Stationary Battery Thermal Management: Analysis of Active Cooling Designs
Abstract
:1. Introduction
2. Literature Review
2.1. Battery Heat Generation and Effects
2.2. Battery Thermal Management (BTM)
2.2.1. Air BTM Systems
2.2.2. Alternative Stationary BTM Systems
- developing several battery rack designs that could be used to increase cooling efficiency,
- investigating performance of each design under several metrics, including resulting battery temperatures,
- developing an experimentally validated computational fluid dynamics model for an active air-based battery cooling system,
- analyzing potential methods for improving air-based cooling system design and derive conclusions and recommendations that could guide future research and potential prototype design.
3. Materials and Methodology
3.1. Model Design
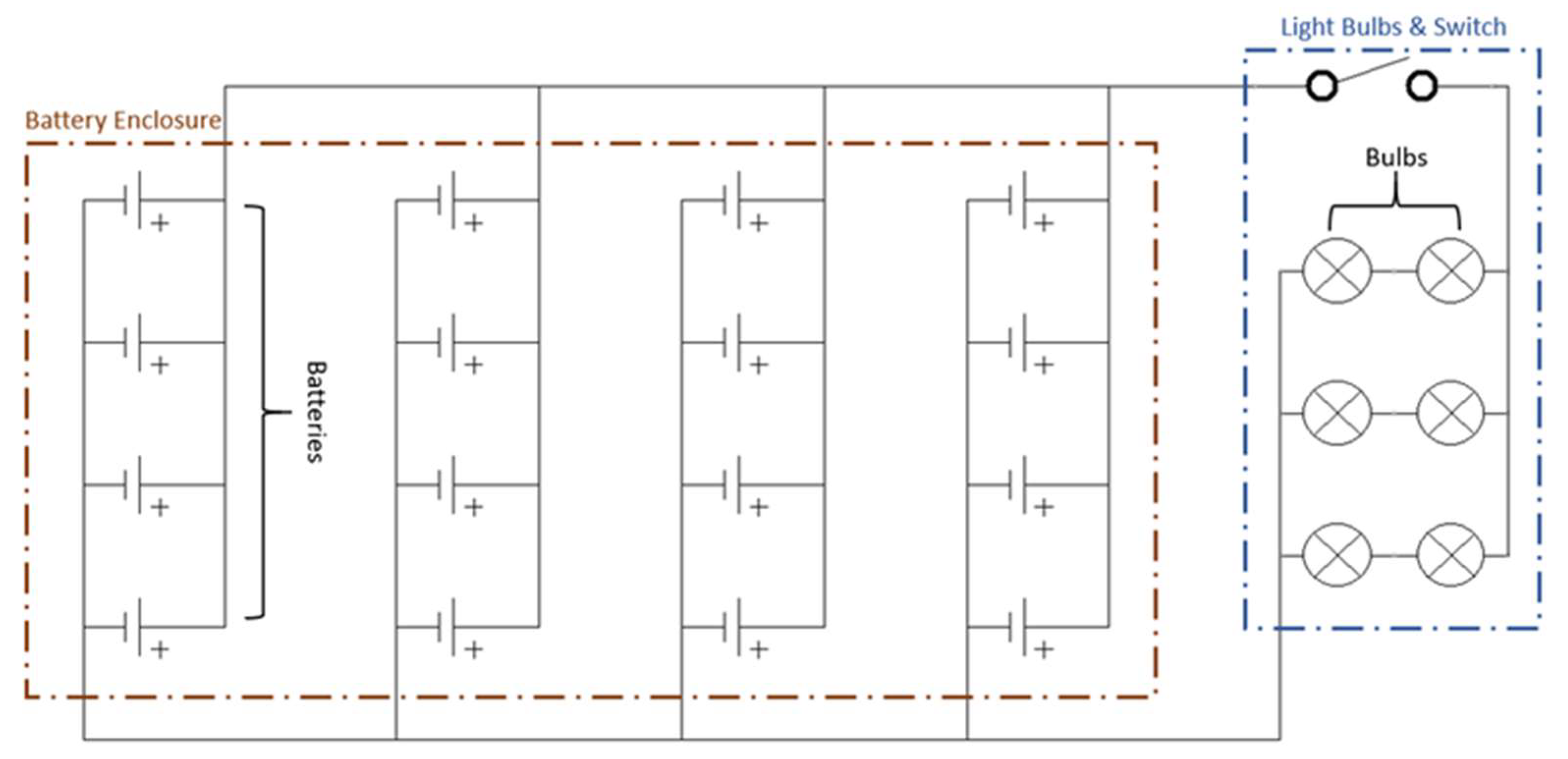
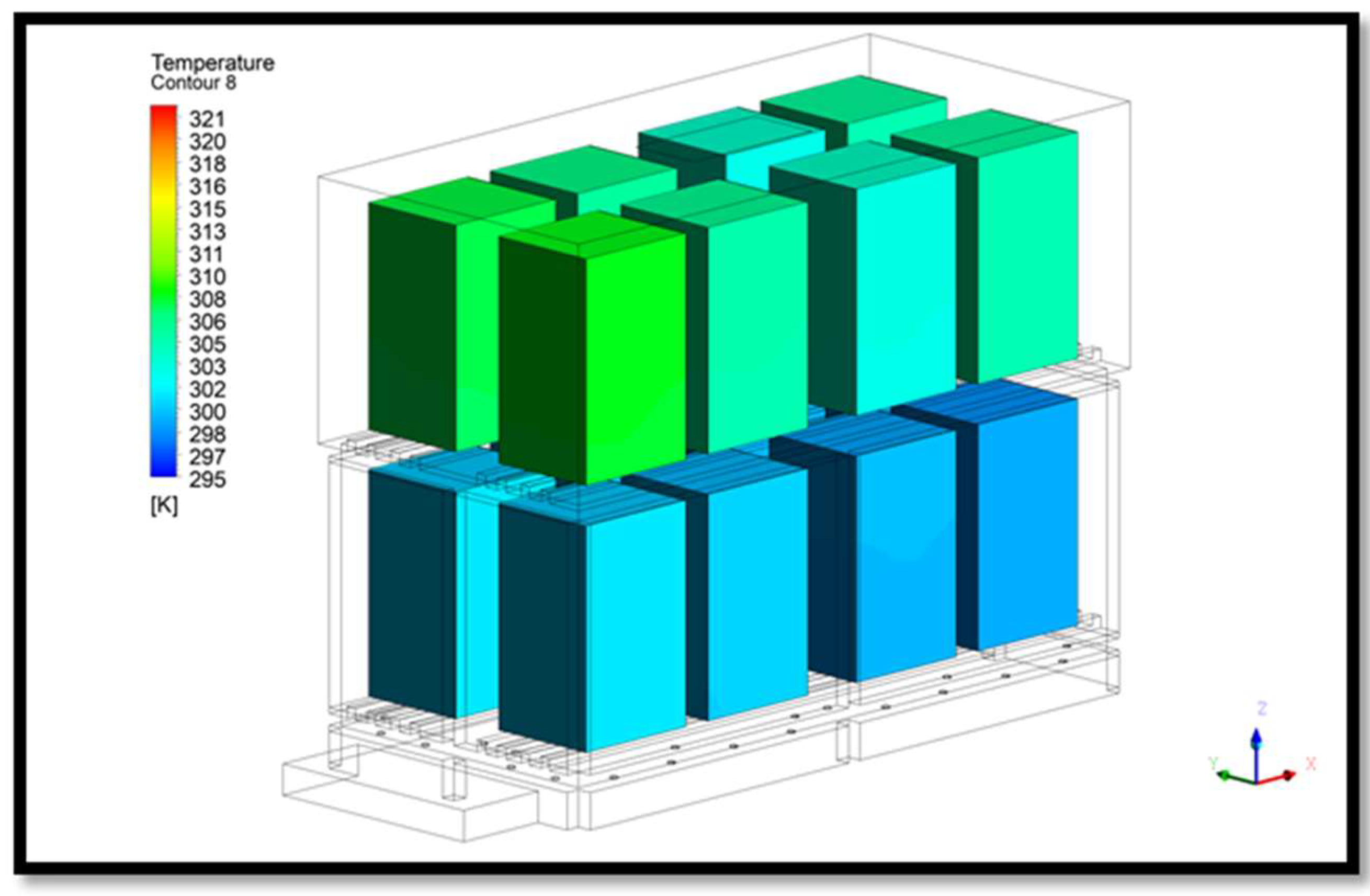
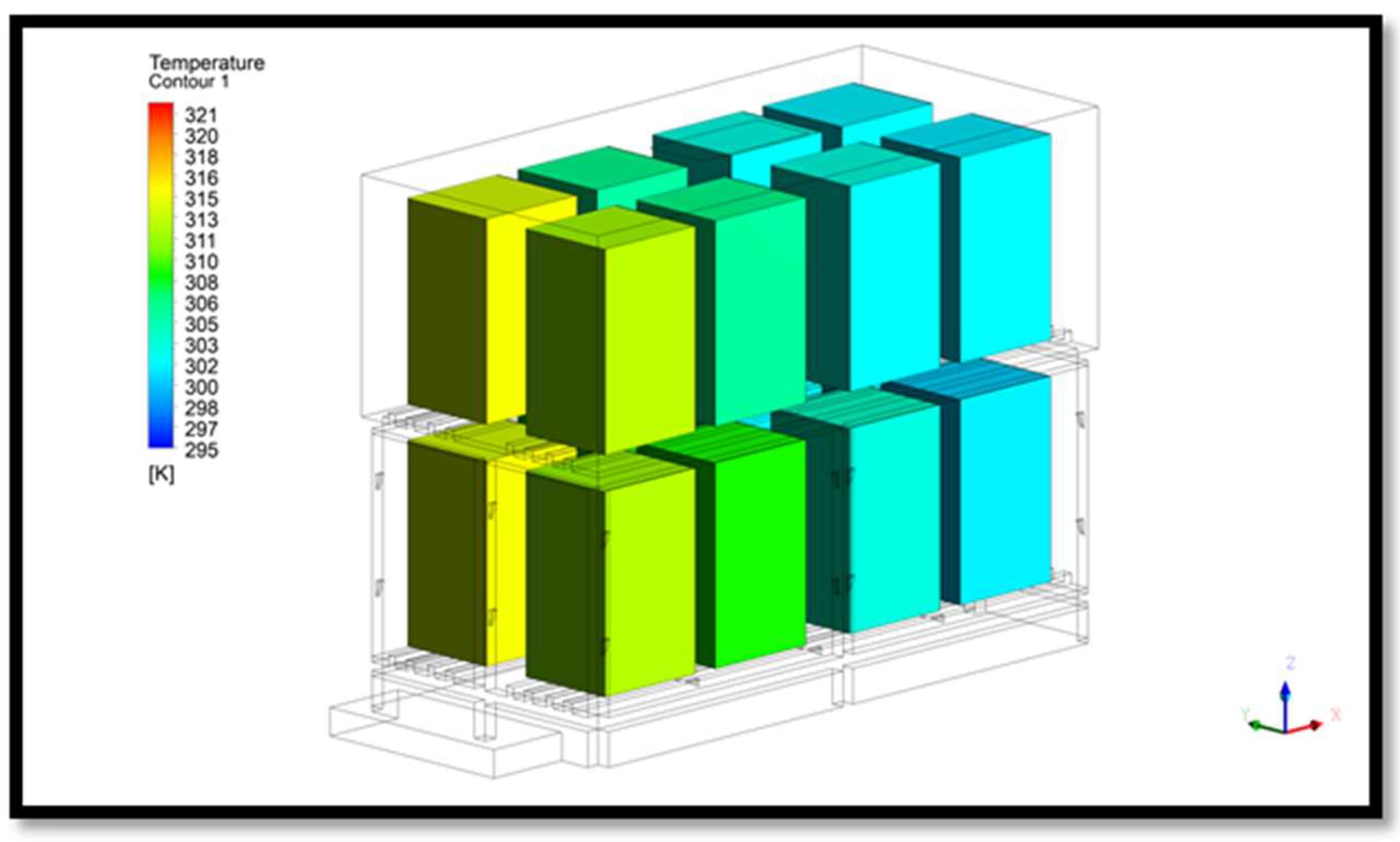
- Default Model: 16 batteries placed on a rack contained within an enclosure with forced air vented underneath. This model is shown in Figure 2.
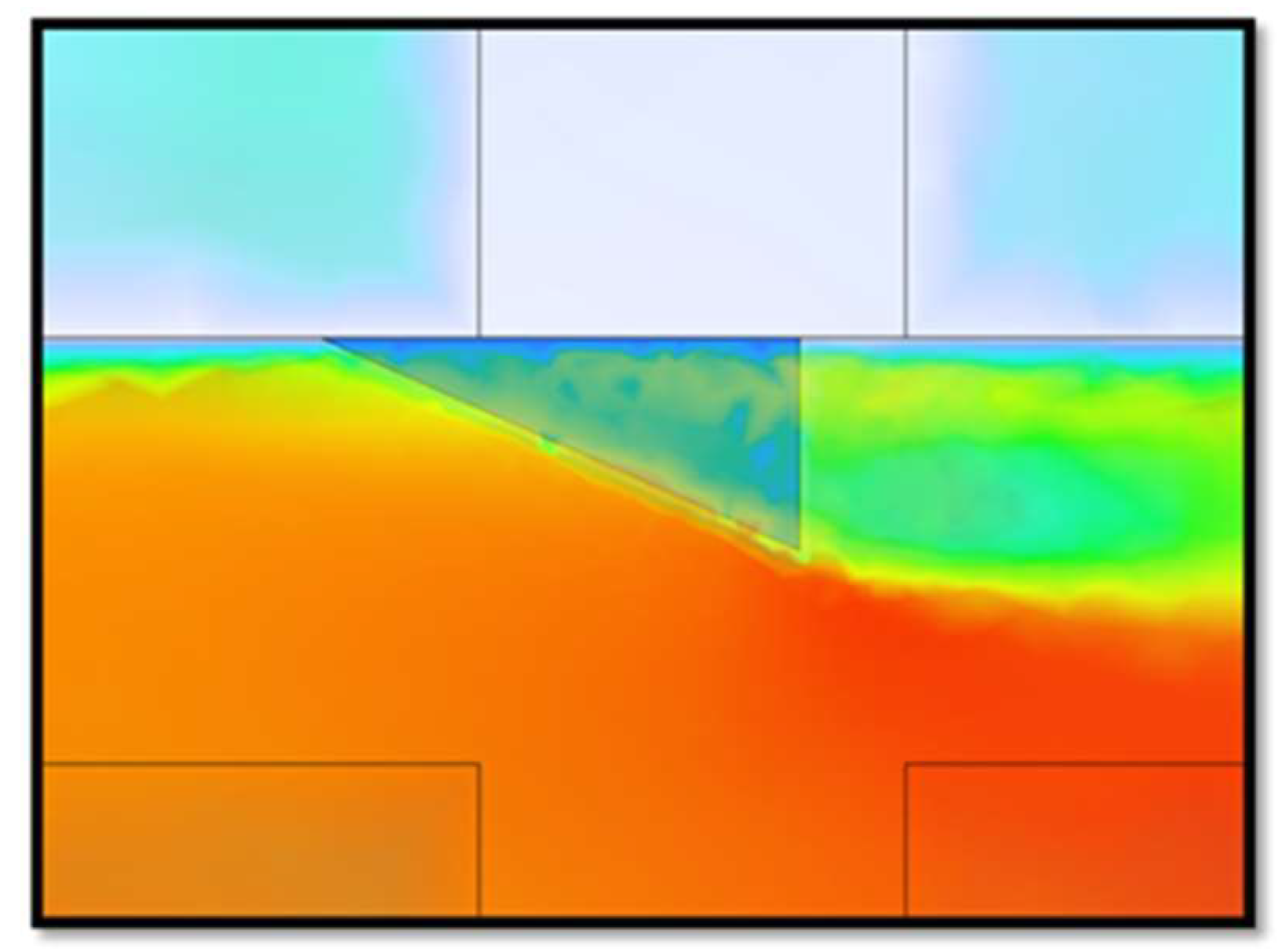
- Vented Model: Same construction as the default model besides the addition of a perforated plate to the bottom of the rack. This can be seen in Figure 3.
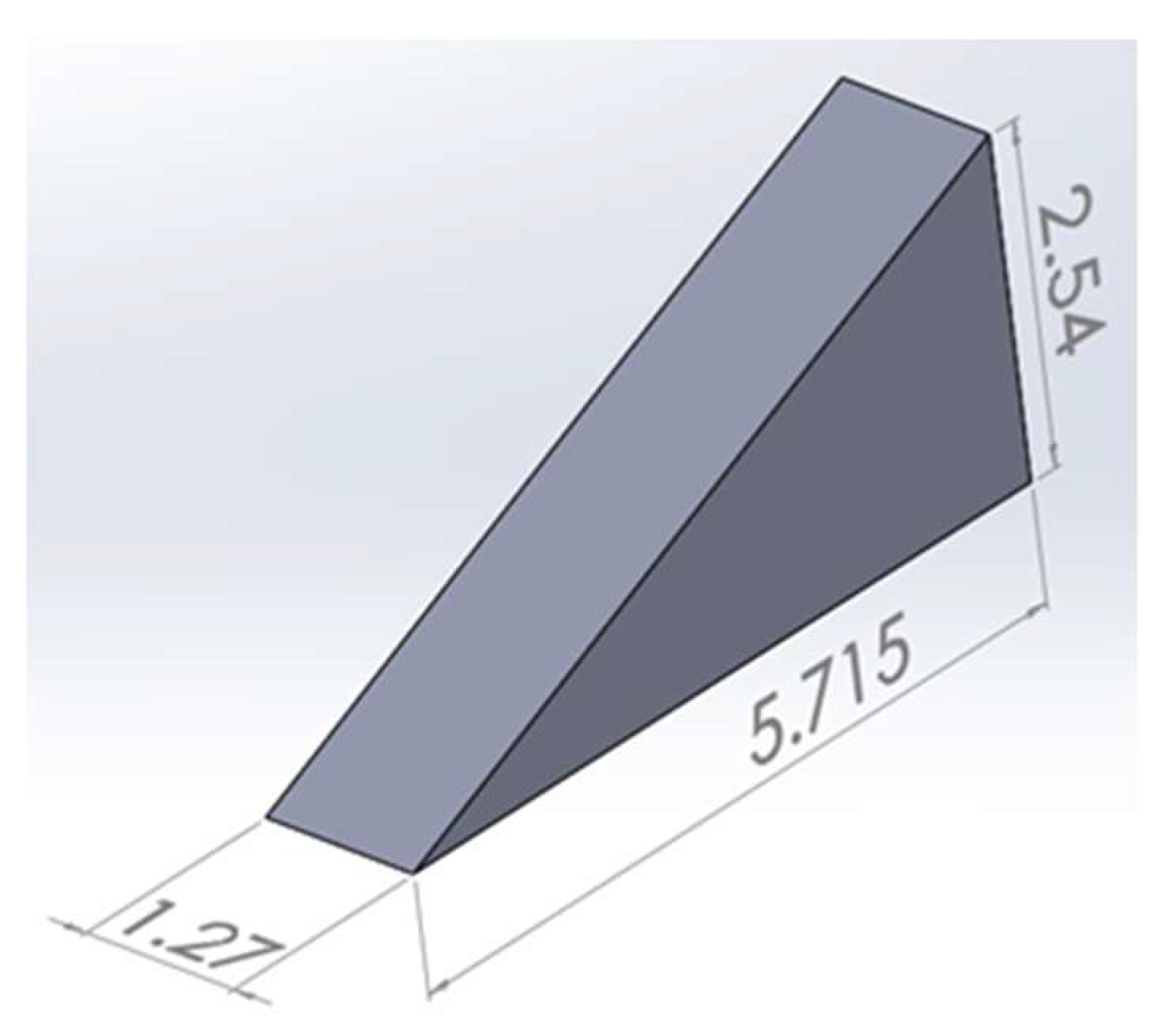
- Vortex Generator Model: Same construction as the default model besides the addition of small vortex generators to the underside and supporting arms of the rack. Attached vortex generators may be observed in Figure 4.
3.2. Experimental Model
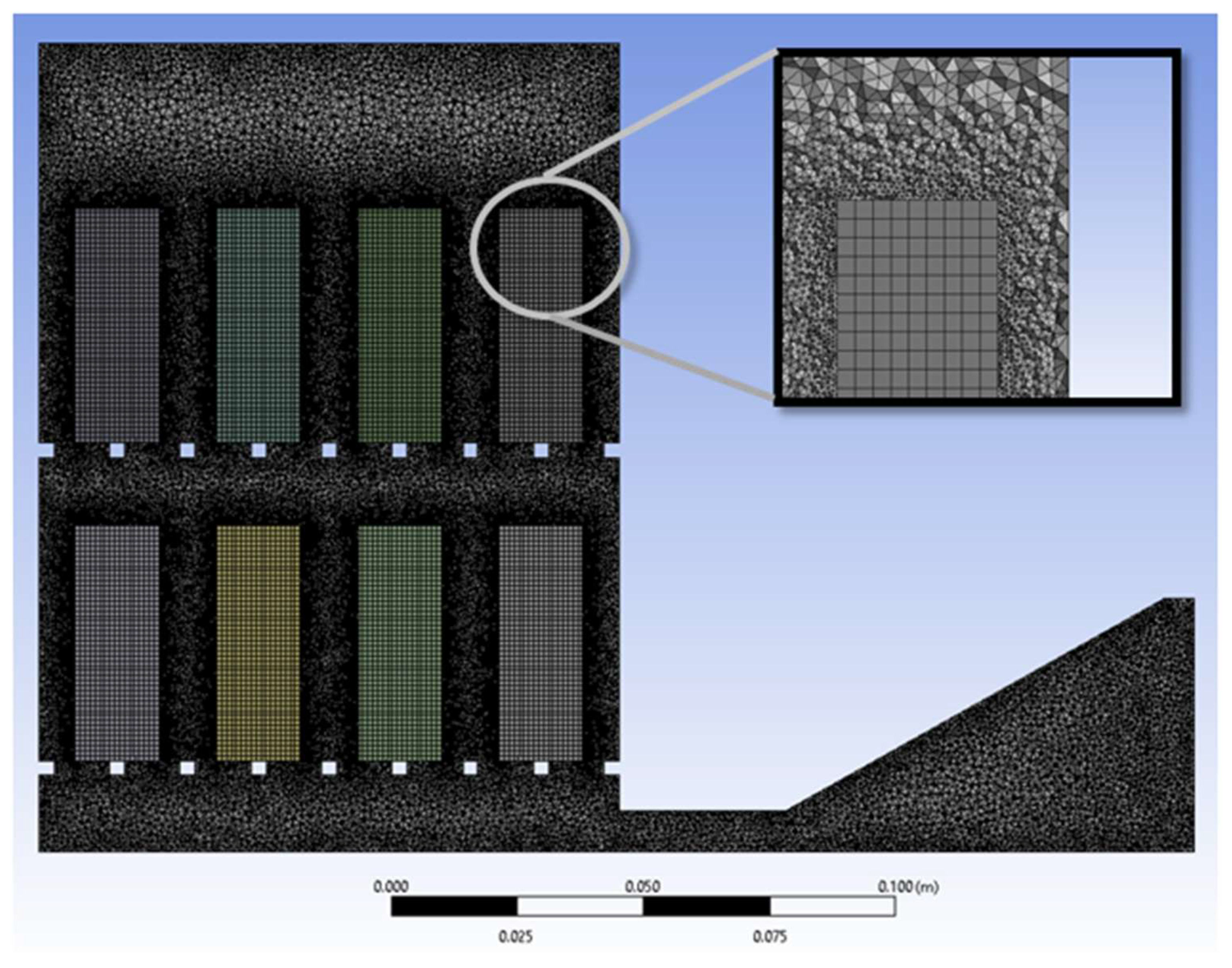
3.3. CFD Simulation
- k—Thermal Conductivity
- t—Time
- u—x-velocity
- V—velocity vector
- v—y-velocity
- w—z-velocity
- μ—Viscosity
- p—Pressure
- Φ—Dissipation Function
- Si—Energy source
- T—Temperature
- ρ—density
3.4. Experimental Model Simulation
3.5. Full-Scale Simulation
- Nu is Nusselt number
- q is heat flux
- T is temperature and
- K is thermal conductivity
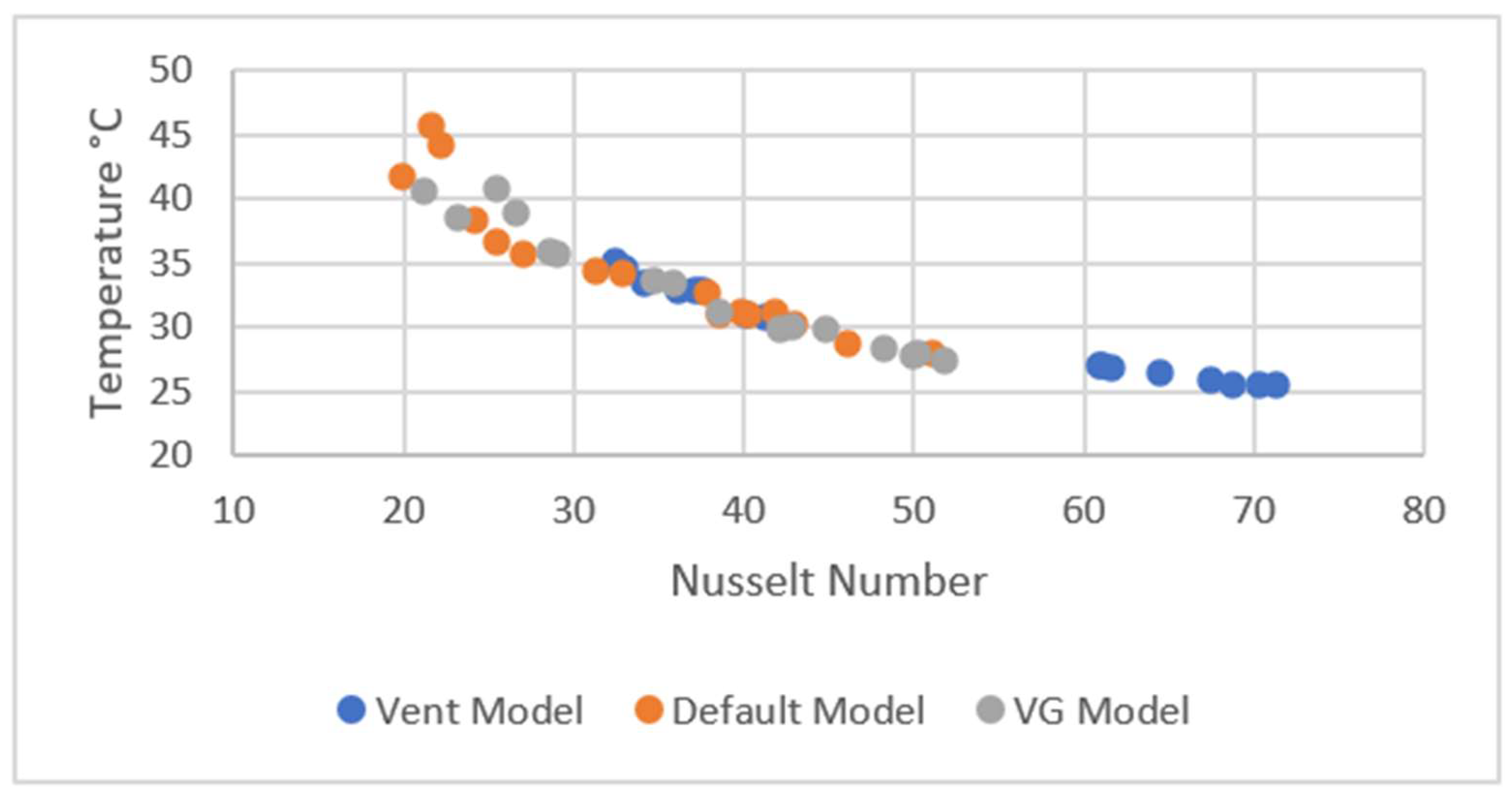
4. Simulation Validation
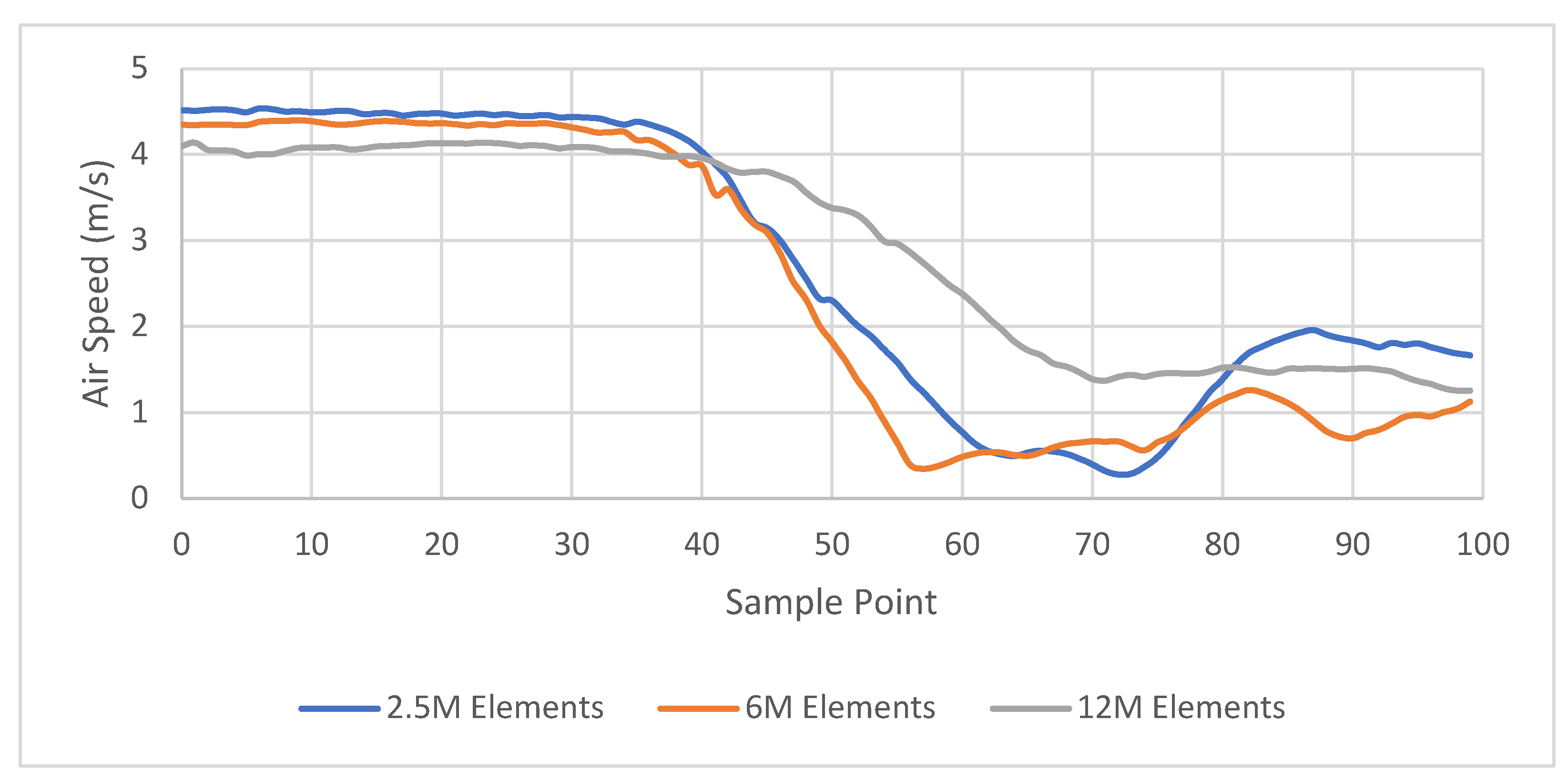
4.1. Simulation Validation
4.2. Full-Scale Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Kreith, F. Principles of Sustainable Energy Systems, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Xia, G.; Cao, L.; Bi, G. A review on battery thermal management in electric vehicle application. J. Power Sources 2017, 367, 90–105. [Google Scholar] [CrossRef]
- Kim, J.; Oh, J.; Lee, H. Review on battery thermal management system for electric vehicles. J. Appl. Therm. Eng. 2019, 149, 192–212. [Google Scholar] [CrossRef]
- Hammond, R.; Everingham, S.; Srinivasan, D. Batteries for Stationary Standby and for Stationary Cycling Applications Part 1: Standby vs. Cycling—Definitions and Concepts. In Proceedings of the IEEE Power Engineering Society General Meeting (IEEE Cat. No.03CH37491), Toronto, ON, Canada, 13–17 July 2003; pp. 141–145. [Google Scholar] [CrossRef]
- Amrouche, S.O.; Rekioua, D.; Rekioua, T.; Bacha, S. Overview of energy storage in renewable energy systems. Int. J. Hydrog. Energy 2016, 41, 20914–20927. [Google Scholar] [CrossRef]
- Divya, K.C.; Østergaard, J. Battery energy storage technology for power systems—An overview. Electr. Power Syst. Res. 2009, 79, 511–520. [Google Scholar] [CrossRef]
- Barton, J.P.; Infield, D.G. Energy Storage and Its Use With Intermittent Renewable Energy. IEEE Trans. Energy Convers. 2004, 19, 441–448. [Google Scholar] [CrossRef]
- Nor, N.M.; Ali, A.; Ibrahim, T.; Romlie, M.F. Battery Storage for the Utility-Scale Distributed Photovoltaic Generations. IEEE Access 2018, 6, 1137–1154. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, J.; Baskaran, S.; Imhoff, C.H.; Holladay, J.D. Enabling renewable energy—And the future grid—With advanced electricity storage. JOM 2010, 62, 14–23. [Google Scholar] [CrossRef]
- Hu, X.; Zou, C.; Zhang, C.; Li, Y. Technological Developments in Batteries: A Survey of Principal Roles, Types, and Management Needs. IEEE Power Energy Mag. 2017, 15, 20–31. [Google Scholar] [CrossRef]
- Lawder, M.T.; Suthar, B.; Northrop, P.W.C.; De, S.; Hoff, C.M.; Leitermann, O.; Crow, M.L.; Santhanagopalan, S.; Subramanian, V.R. Battery Energy Storage System (BESS) and Battery Management System (BMS) for Grid-Scale Applications. Proc. IEEE 2014, 102, 1014–1030. [Google Scholar] [CrossRef]
- McKeon, B.B.; Furukawa, J.; Fenstermacher, S. Advanced Lead–Acid Batteries and the Development of Grid-Scale Energy Storage Systems. Proc. IEEE 2014, 102, 951–963. [Google Scholar] [CrossRef]
- LaCommare, K.; Eto, J. Cost of power interruptions to electricity consumers in the United States (US). Energy 2006, 31, 1845–1855. [Google Scholar] [CrossRef] [Green Version]
- Neacșu, D.O. Telecom Power Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ferraro, M.; Brunaccini, G.; Sergi, F.; Aloisio, D.; Randazzo, N.; Antonucci, V. From Uninterruptible Power Supply to resilient smart micro grid: The case of a battery storage at telecommunication station. J. Energy Storage 2020, 28, 101207. [Google Scholar] [CrossRef]
- Telaretti, E.; Dusonchet, L. Stationary battery technologies in the U.S.: Development Trends and prospects. Renew. Sustain. Energy Rev. 2017, 75, 380–392. [Google Scholar] [CrossRef]
- Corey, G. Batteries for Stationary Standby and for Stationary Cycling Applications Part 6: Alternative Electricity Storage Technologies. In Proceedings of the IEEE Power Engineering Society General Meeting (IEEE Cat. No.03CH37491), Toronto, ON, Canada, 13–17 July 2003; pp. 164–169. [Google Scholar] [CrossRef]
- Schainker, R. Executive Overview: Energy Storage Options for A Sustainable Energy Future. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; pp. 2309–2314. [Google Scholar] [CrossRef]
- Ruetschi, P. Aging mechanisms and service life of lead–acid batteries. J. Power Sources 2004, 127, 33–44. [Google Scholar] [CrossRef]
- Smith, K.; Saxon, A.; Keyser, M.; Lundstrom, B.; Cao, Z.; Roc, A. Life prediction model for grid-connected Li-ion battery energy storage system. In Proceedings of the American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 4062–4068. [Google Scholar] [CrossRef]
- Leng, F.; Tan, C.M.; Pecht, M. Effect of Temperature on the Aging rate of Li Ion Battery Operating above Room Temperature. Sci. Rep. 2015, 5, 12967. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rao, Z.; Wang, S. A review of power battery thermal energy management. Renew. Sustain. Energy Rev. 2011, 15, 4554–4571. [Google Scholar] [CrossRef]
- Liu, L.; Sun, H.; Li, C.; Li, T.; Xin, J.; Zheng, N. Managing Battery Aging for High Energy Availability in Green Datacenters. IEEE Trans. Parallel Distrib. Syst. 2017, 28, 3521–3536. [Google Scholar] [CrossRef]
- Stan, A.-I.; Swierczynski, M.J.; Stroe, D.-I.; Teodorescu, R.; Andreasen, S.J.; Moth, K. A Comparative Study of Lithium Ion to Lead Acid Batteries for Use in UPS Applications. In Proceedings of the IEEE 36th International Telecommunications Energy Conference (IN℡EC), Vancouver, BC, Canada, 28 September–2 October 2014. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Smith, K.; Neubauer, J. Design and Analysis of Large Lithium-Ion Battery Systems; Artech: Norwood, MA, USA, 2014. [Google Scholar]
- Hesse, H.C.; Schimpe, M.; Kucevic, D.; Jossen, A. Lithium-Ion Battery Storage for the Grid—A Review of Stationary Battery Storage System Design Tailored for Applications in Modern Power Grids. Energies 2017, 10, 2107. [Google Scholar] [CrossRef] [Green Version]
- 1187-2013; IEEE Recommended Practice for Installation Design and Installation of Valve-Regulated Lead-Acid Batteries for Stationary Applications; IEEE Std 1187-2013 Revis. IEEE Std 1187-2002. IEEE: New York, NY, USA, 2014. [CrossRef]
- IEEE/ASHRAE. Guide for the Ventilation and Thermal Management of Batteries for Stationary Applications; IEEE Std 1635-2012ASHRAE Guidel. 21-2012; IEEE: New York, NY, USA, 2012; pp. 1–108. [Google Scholar] [CrossRef]
- Jouhara, H.; Khordehgah, N.; Serey, N.; Almahmoud, S.; Lester, S.P.; Machen, D.; Wrobel, L. Applications and thermal management of rechargeable batteries for industrial applications. Energy 2019, 170, 849–861. [Google Scholar] [CrossRef]
- Chiu, K.-C.; Lin, C.-H.; Yeh, S.-F.; Lin, Y.-H.; Huang, C.-S.; Chen, K.-C. Cycle life analysis of series connected lithium-ion batteries with temperature difference. J. Power Sources 2014, 263, 75–84. [Google Scholar] [CrossRef]
- Hart, D.; Sarkissian, A. Deployment of Grid-Scale Batteries in the United States; U.S. Department of Energy: Washington, DC, USA, 2016; p. 31.
- Kosik, B. ASHRAE’s Energy Standard for Data Centers Turns Three. CSE 2019, 56, 24–30. [Google Scholar]
- Zhang, H.; Shao, S.; Xu, H.; Zou, H.; Tian, C. Free cooling of data centers: A review. Renew. Sustain. Energy Rev. 2014, 35, 171–182. [Google Scholar] [CrossRef]
- Daraghmeh, H.M.; Wang, C.-C. A review of current status of free cooling in datacenters. Appl. Therm. Eng. 2017, 114, 1224–1239. [Google Scholar] [CrossRef]
- Mohammadian, S.K.; He, Y.-L.; Zhang, Y. Internal cooling of a lithium-ion battery using electrolyte as coolant through microchannels embedded inside the electrodes. J. Power Sources 2015, 293, 458–466. [Google Scholar] [CrossRef]
- Jaguemont, J.; Van Mierlo, J. A comprehensive review of future thermal management systems for battery-electrified vehicles. J. Energy Storage 2020, 31, 101551. [Google Scholar] [CrossRef]
- Buidin, T.I.C.; Mariasiu, F. Battery thermal management systems: Current status and design approach of cooling technologies. Energies 2021, 14, 4879. [Google Scholar] [CrossRef]
- Spitthoff, L.; Shearing, P.; Burheim, O. Temperature, Ageing and Thermal Management of Lithium-Ion Batteries. Energies 2021, 14, 1248. [Google Scholar] [CrossRef]
- Jeffs, J.; Dinh, T.Q.; Widanage, W.D.; McGordon, A.; Picarelli, A. Optimisation of Direct Battery Thermal Management for EVs Operating in Low-Temperature Climates. Energies 2020, 13, 5980. [Google Scholar] [CrossRef]
- Akinlabi, A.H.; Solyali, D. Configuration, design, and optimization of air-cooled battery thermal management system for electric vehicles: A review. Renew. Sustain. Energy Rev. 2020, 125, 109815. [Google Scholar] [CrossRef]
- Chen, K.; Chen, Y.; She, Y.; Song, M.; Wang, S.; Chen, L. Construction of effective symmetrical air-cooled system for battery thermal management. Appl. Therm. Eng. 2019, 166, 114679. [Google Scholar] [CrossRef]
- Monika, K.; Chakraborty, C.; Roy, S.; Dinda, S.; Singh, S.A.; Datta, S.P. An improved mini-channel based liquid cooling strategy of prismatic LiFePO4 batteries for electric or hybrid vehicles. J. Energy Storage 2021, 35, 102301. [Google Scholar] [CrossRef]
- Dubey, P.; Pulugundla, G.; Srouji, A. Direct Comparison of Immersion and Cold-Plate Based Cooling for Automotive Li-Ion Battery Modules. Energies 2021, 14, 1259. [Google Scholar] [CrossRef]
- Gschwander, S.; Niedermaier, S.; Gamisch, S.; Kick, M.; Klünder, F.; Haussmann, T. Storage Capacity in Dependency of Supercooling and Cycle Stability of Different PCM Emulsions. Appl. Sci. 2021, 11, 3612. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.; Wu, W.; Chen, K.; Hong, S.; Lai, Y. A critical review of battery thermal performance and liquid based battery thermal management. Energy Convers. Manag. 2019, 182, 262–281. [Google Scholar] [CrossRef]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A Critical Review of Thermal Issues in Lithium-Ion Batteries. J. Electrochem. Soc. 2011, 158, R1. [Google Scholar] [CrossRef]
- Khan, M.; Swierczynski, M.; Kær, S. Towards an Ultimate Battery Thermal Management System: A Review. Batteries 2017, 3, 9. [Google Scholar] [CrossRef] [Green Version]
- Yang, N.; Zhang, X.; Shang, B.; Li, G. Unbalanced discharging and aging due to temperature differences among the cells in a lithium-ion battery pack with parallel combination. J. Power Sources 2016, 306, 733–741. [Google Scholar] [CrossRef]
- Brzezińska, D. Ventilation System Influence on Hydrogen Explosion Hazards in Industrial Lead-Acid Battery Rooms. Energies 2018, 11, 2086. [Google Scholar] [CrossRef] [Green Version]
- Al-Zareer, M.; Dincer, I.; Rosen, M.A. A thermal performance management system for lithium-ion battery packs. Appl. Therm. Eng. 2019, 165, 114378. [Google Scholar] [CrossRef]
- Schmidt, R.; Shaukatullah, H. Computer and telecommunications equipment room cooling: A review of literature. IEEE Trans. Components Packag. Technol. 2003, 26, 89–98. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, Z.; Yang, L. A review on airflow distribution and management in data center. Energy Build. 2018, 179, 264–277. [Google Scholar] [CrossRef]
- ASHRAE Technical Committee. Data Center Power Equipment Thermal Guidelines and Best Practices; ASHREA TC99; ASHRAE Technical Committee: Peachtree Corners, GA, USA, 2016; pp. 1–60. [Google Scholar]
- Butler, P.; Dunleavey, J.; Farber-DeAnda, M.; Moseley, P. Performance of valve-regulated lead-acid batteries in real-world stationary applications—Utility installations. J. Power Sources 2001, 96, 94–101. [Google Scholar] [CrossRef]
- Garche, J.; Jossen, A. Battery Management Systems (BMS) for Increasing Battery Life Time. In Proceedings of the ℡ESCON 2000, Third International Telecommunications Energy Special Conference (IEEE Cat. No.00EX424), Dresden, Germany, 7–10 May 2000; pp. 81–88. [Google Scholar]
- Cho, J.; Jeong, S.; Kim, Y. Commercial and research battery technologies for electrical energy storage applications. Prog. Energy Combust. Sci. 2015, 48, 84–101. [Google Scholar] [CrossRef]
- Xie, Q.; Yue, S.; Pedram, M.; Shin, D.; Chang, N.; Qing, X. Adaptive Thermal Management for Portable System Batteries by Forced Convection Cooling. In Proceedings of the Design, Automation Test in Europe Conference Exhibition (DATE), Grenoble, France, 19–22 March 2013; pp. 1225–1228. [Google Scholar] [CrossRef] [Green Version]
- He, F.; Ma, L. Thermal management of batteries employing active temperature control and reciprocating cooling flow. Int. J. Heat Mass Transf. 2015, 83, 164–172. [Google Scholar] [CrossRef]
- Chang, G.; Cui, X.; Li, Y.; Ji, Y. Effects of reciprocating liquid flow battery thermal management system on thermal characteristics and uniformity of large lithium-ion battery pack. Int. J. Energy Res. 2020, 44, 6383–6395. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Tjong, J.; Ahmed, R.; El-Sayed, M.; Habibi, S. Adaptive Temperature Monitoring for Battery Thermal Management. In Proceedings of the IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 16–19 June 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Ali, H.A.A.; Abdeljawad, Z.N. Thermal Management Technologies of Lithium-Ion Batteries Applied for Stationary Energy Storage Systems: Investigation on the Thermal Behavior of Lithium-Ion Batteries. Master’s Thesis, Mälardalens University, Västerås, Sweden, 2020. [Google Scholar]
- Chen, D.; Jiang, J.; Kim, G.-H.; Yang, C.; Pesaran, A. Comparison of different cooling methods for lithium ion battery cells. Appl. Therm. Eng. 2016, 94, 846–854. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Al-Zareer, M.; Dincer, I.; Rosen, M.A. A review of novel thermal management systems for batteries. Int. J. Energy Res. 2018, 42, 3182–3205. [Google Scholar] [CrossRef]
- Wilke, S.; Schweitzer, B.; Khateeb, S.; Al-Hallaj, S. Preventing thermal runaway propagation in lithium ion battery packs using a phase change composite material: An experimental study. J. Power Sources 2017, 340, 51–59. [Google Scholar] [CrossRef]
- Madani, S.S.; Swierczynski, M.J.; Kaer, S.K. A review of Thermal Management and Safety for Lithium Ion Batteries. In Proceedings of the Twelfth International Conference on Ecological Vehicles and Renewable Energies, Monte Carlo, Monaco, 11–13 April 2017; pp. 1–20. [Google Scholar] [CrossRef]
- C&D Technologies. MCT-HP Data Sheet. 2020. Available online: https://cdtechno.com/wp-content/uploads/2020/05/MCT-HP_DataSheet.pdf (accessed on 12 December 2020).
- Bayazit, Y.; Sparrow, E.M.; Joseph, D.D. Perforated plates for fluid management: Plate geometry effects and flow regimes. Int. J. Therm. Sci. 2014, 85, 104–111. [Google Scholar] [CrossRef]
- Ke, Z.; Chen, C.-L.; Li, K.; Wang, S.; Chen, C.-H. Vortex dynamics and heat transfer of longitudinal vortex generators in a rectangular channel. Int. J. Heat Mass Transf. 2018, 132, 871–885. [Google Scholar] [CrossRef]
- Awais, M.; Bhuiyan, A.A. Heat transfer enhancement using different types of vortex generators (VGs): A review on experimental and numerical activities. Therm. Sci. Eng. Prog. 2018, 5, 524–545. [Google Scholar] [CrossRef]
- Saw, B.; Ye, Y.; Tay, A.A.; Chong, W.T.; Kuan, S.H.; Yew, M.C. Computational fluid dynamic and thermal analysis of Lithium-ion battery pack with air cooling. Appl. Energy 2016, 177, 783–792. [Google Scholar] [CrossRef]
- Alonzo-García, A.; del Carmen Gutiérrez-Torres, C.; Jiménez-Bernal, J.A. Computational Fluid Dynamics in Turbulent Flow Applications. Life Sci. 2016. [Google Scholar] [CrossRef]
- Ahn, J.; Sparrow, E.; Gorman, J. Turbulence intensity effects on heat transfer and fluid-flow for a circular cylinder in crossflow. Int. J. Heat Mass Transf. 2017, 113, 613–621. [Google Scholar] [CrossRef]
- Wanko Tchatchouang, C. Effects of Turbulence Modeling in Predicting Flow and Heat Transfer in a Duct with Pin Fins; Purdue University: West Lafayette, IN, USA, 2012. [Google Scholar]
- Freund, S.; Kabelac, S. Investigation of local heat transfer coefficients in plate heat exchangers with temperature oscillation IR thermography and CFD. Int. J. Heat Mass Transf. 2010, 53, 3764–3781. [Google Scholar] [CrossRef]
- Li, W.H.; Ren, J.; Jiang, H.D.; Luan, Y.G.; Ligrani, P. Assessment of six turbulence models for modeling and predicting narrow passage flows, part 2: Pin fin arrays. Numer. Heat Transf. Part A Appl. 2016, 69, 445–463. [Google Scholar] [CrossRef]
- Shabani, B.; Biju, M. Theoretical Modelling Methods for Thermal Management of Batteries. Energies 2015, 8, 10153–10177. [Google Scholar] [CrossRef]
- Shen, M.; Gao, Q. A review on battery management system from the modeling efforts to its multiapplication and integration. Int. J. Energy Res. 2019, 43, 5042–5075. [Google Scholar] [CrossRef]
- Cengel, Y. Heat and Mass Transfer: Fundamentals and Applications; McGraw-Hill Higher Education: New York, NY, USA, 2014. [Google Scholar]
- Choi, K.W.; Yao, N.P. Engineering Analysis of Thermal Phenomena for Lead—Acid Batteries during Recharge Processes; Argonne National Lab. (ANL): Argonne, IL, USA, 1977. [Google Scholar]
- Al Hallaj, S.; Maleki, H.; Hong, J.; Selman, J. Thermal modeling and design considerations of lithium-ion batteries. J. Power Sources 1999, 83, 1–8. [Google Scholar] [CrossRef]
- Moseley, P.; Rand, D.; Garche, J. Lead–Acid Batteries for Future Automobiles; Oxford Elsevier: Oxford, UK, 2017; pp. 601–618. [Google Scholar] [CrossRef]
- Mahamud, R. Advanced Battery Thermal Management for Electrical-Drive Vehicles Using Reciprocating Cooling Flow and Spatial-Resolution, Lumped-Capacitance Thermal Model; University of Nevada: Reno, NV, USA, 2011. [Google Scholar]
- Daud, Z.H.C.; Chrenko, D.; Dos Santos, F.; Aglzim, E.-H.; Keromnes, A.; Le Moyne, L. 3D electro-thermal modelling and experimental validation of lithium polymer-based batteries for automotive applications. Int. J. Energy Res. 2016, 40, 1144–1154. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery thermal models for hybrid vehicle simulations. J. Power Sources 2002, 110, 377–382. [Google Scholar] [CrossRef]
- Peng, X.; Cui, X.; Liao, X.; Garg, A. A Thermal Investigation and Optimization of an Air-Cooled Lithium-Ion Battery Pack. Energies 2020, 13, 2956. [Google Scholar] [CrossRef]
- Shahid, S.; Agelin-Chaab, M. Experimental and numerical studies on air cooling and temperature uniformity in a battery pack. Int. J. Energy Res. 2018, 42, 2246–2262. [Google Scholar] [CrossRef]
- Soltani, M.; Berckmans, G.; Jaguemont, J.; Ronsmans, J.; Kakihara, S.; Hegazy, O.; Van Mierlo, J.; Omar, N. Three dimensional thermal model development and validation for lithium-ion capacitor module including air-cooling system. Appl. Therm. Eng. 2019, 153, 264–274. [Google Scholar] [CrossRef]
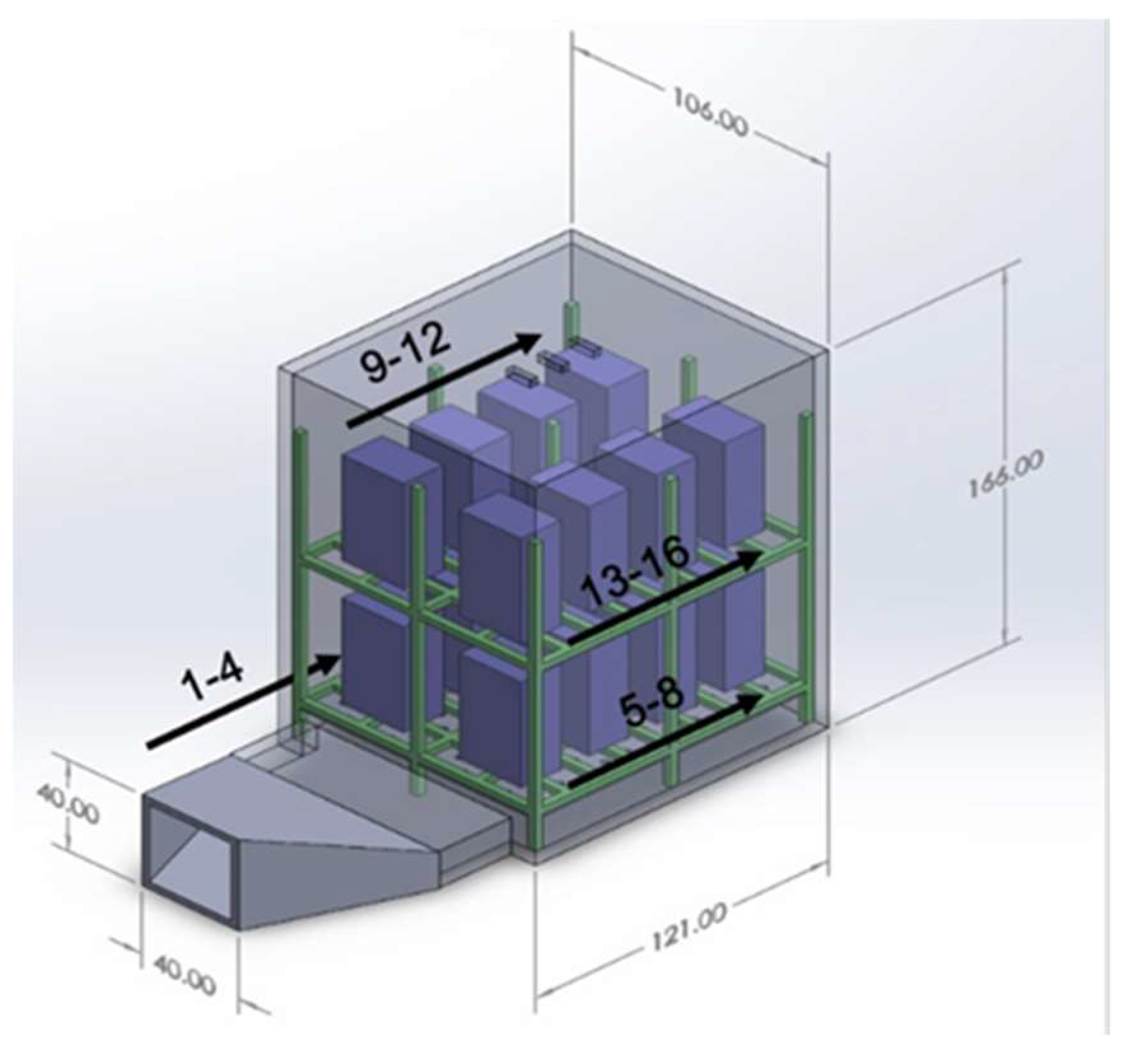
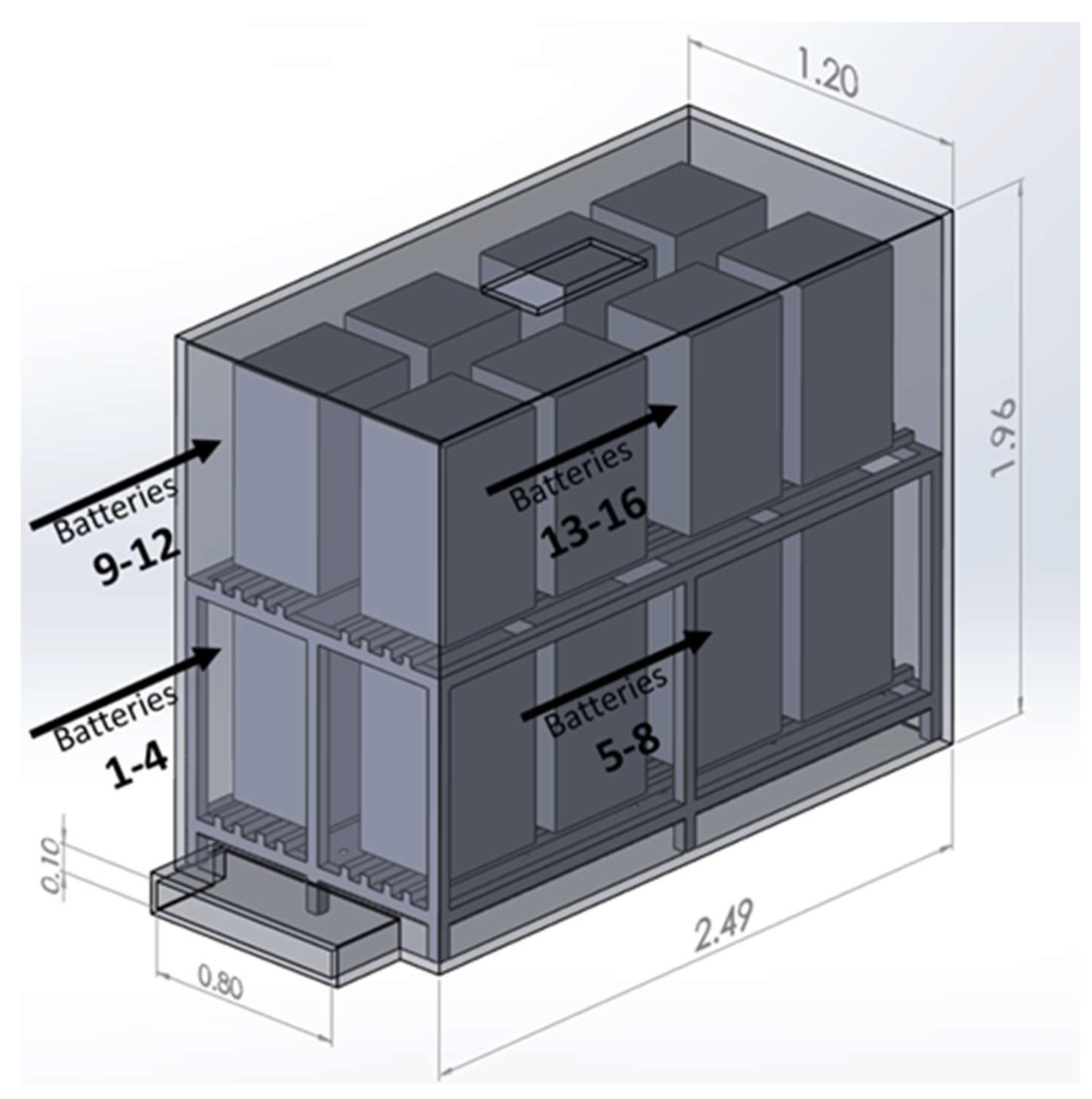
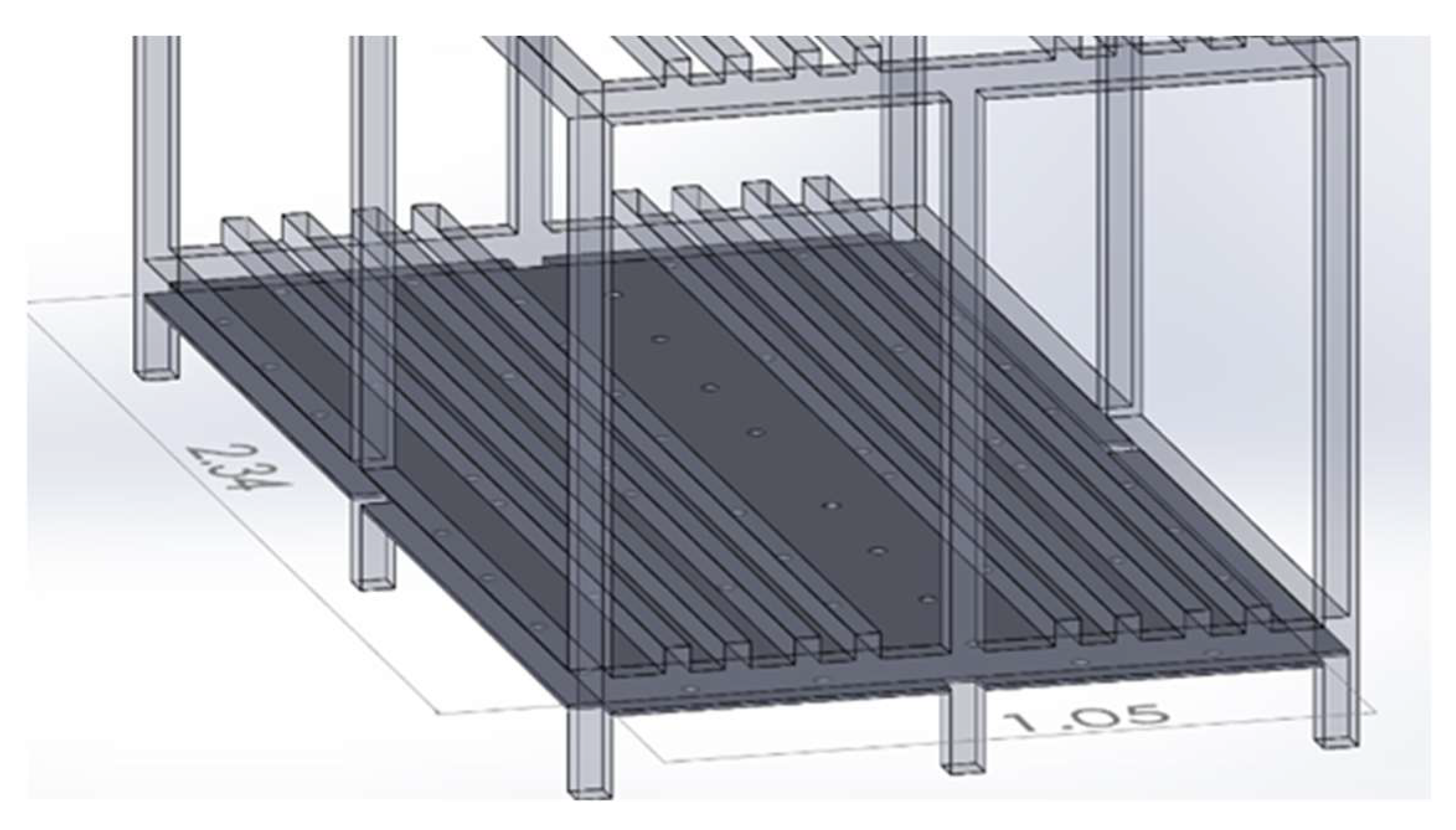
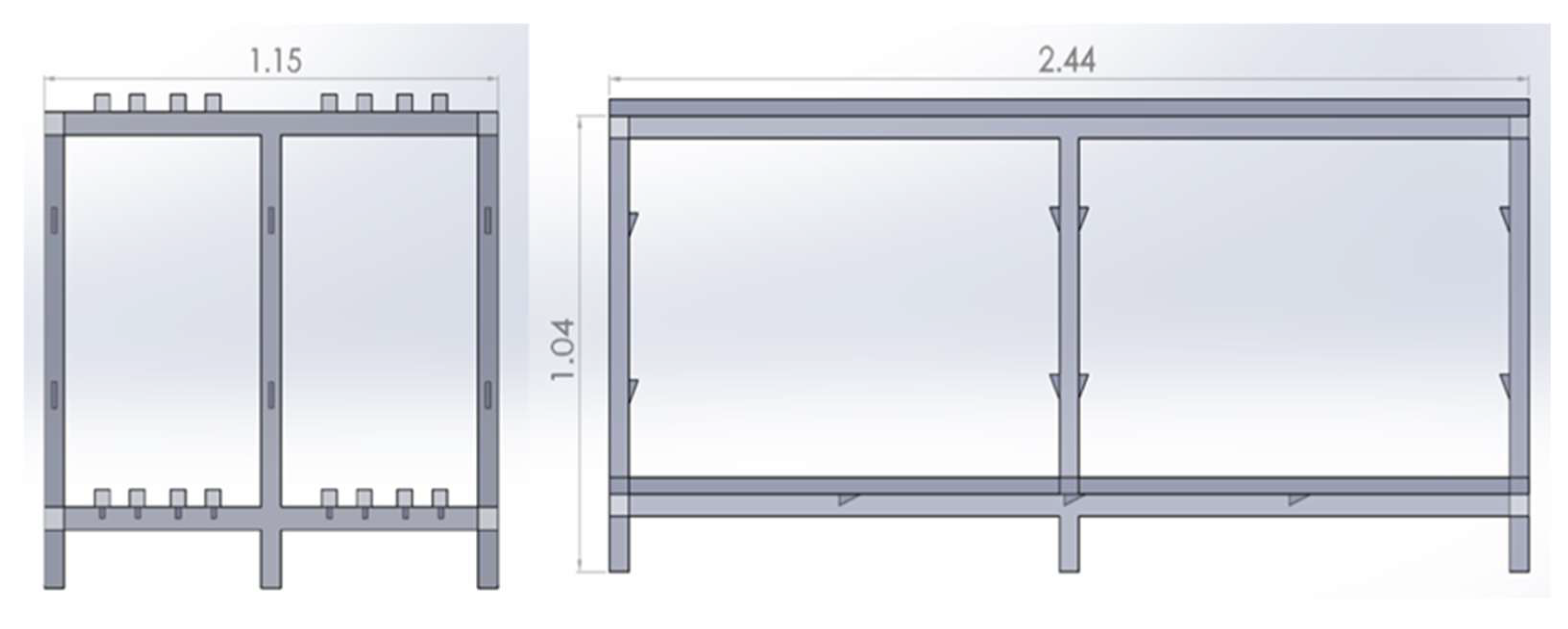








| Manufacturer | Instrument | Quantity Measured |
|---|---|---|
| EXTECH | 40711 Hot Wire Thermo-Anemometer | Airflow Velocity |
| CAMPBELL SCIENTIFIC | Cr1000 × Datalogger | Battery Temperatures |
| CAMPBELL SCIENTIFIC | AM16/32b Channel Multiplexer | Battery Temperatures |
| CAMPBELL SCIENTIFIC | PS100 External Battery | Battery Temperatures |
| KLEIN TOOLS | 600A Clamp Meter CL200 | Battery Voltage |
| BAYIT | DC 5–120 V 100 A Mini Digital Current Ammeter | Circuit Current |
| OMEGA | 5TC-TT-K-30-72 | Battery Temperatures |
| Variable | Value | Unit |
|---|---|---|
| Battery-Specific Heat Capacity | 800 | J/kg-K |
| Battery Conductivity | 250 | W/m-K |
| Inlet Air Temperature | 22 | °C |
| Inlet Air Velocity | 1.7 | m/s |
| Variable | Value | Unit |
|---|---|---|
| Heat Generation per Battery | 75 | Watts |
| Battery-Specific Heat Capacity | 1000 | J/kg-K |
| Battery Conductivity | 250 | W/m-K |
| Inlet Air Temperature | 22 | °C |
| Inlet Air Flowrate | 400 | cfm |
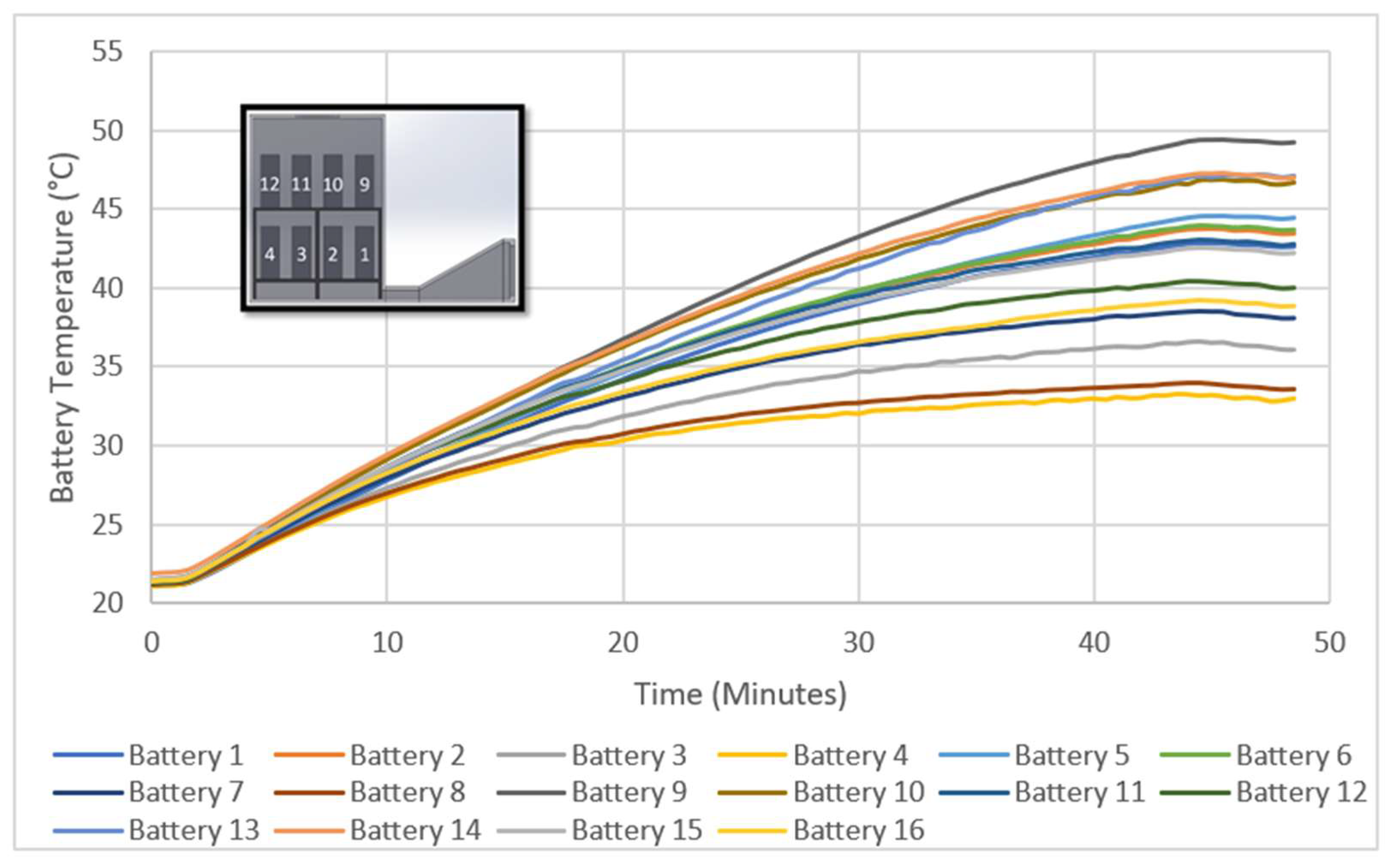
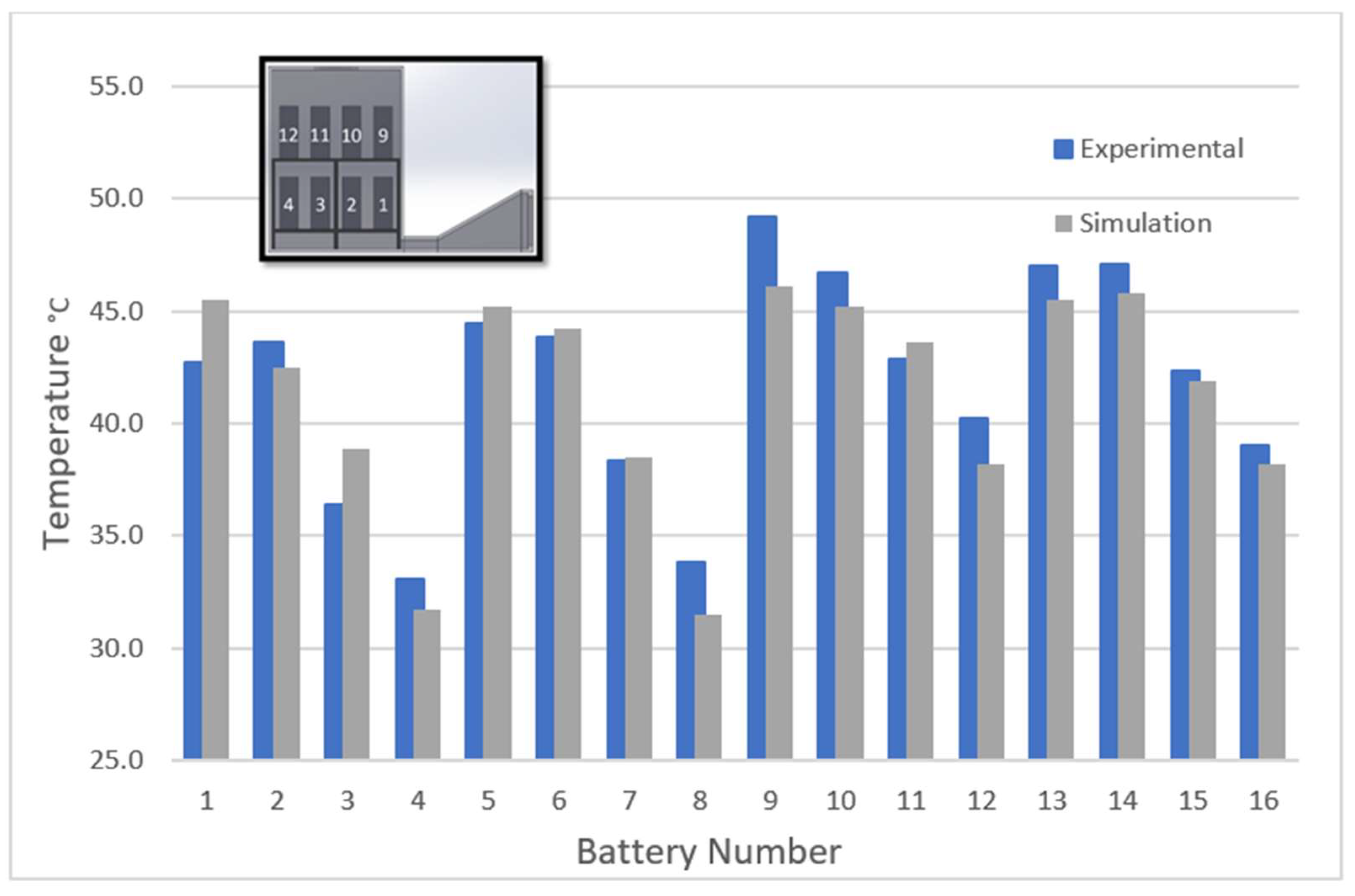
| Battery | Default Experimental Model Steady State Temp °C | Default Simulation Model Temp °C | Absolute Error Temp °C |
|---|---|---|---|
| 1 | 42.7 | 45.5 | 2.8 |
| 2 | 43.6 | 42.5 | 1.1 |
| 3 | 36.4 | 38.9 | 2.5 |
| 4 | 33.1 | 31.7 | 1.4 |
| 5 | 44.4 | 45.2 | 0.8 |
| 6 | 43.8 | 44.2 | 0.4 |
| 7 | 38.3 | 38.5 | 0.2 |
| 8 | 33.8 | 31.5 | 2.3 |
| 9 | 49.2 | 46.1 | 3.1 |
| 10 | 46.7 | 45.2 | 1.5 |
| 11 | 42.9 | 43.6 | 0.7 |
| 12 | 40.2 | 38.2 | 2.0 |
| 13 | 47.0 | 45.5 | 1.5 |
| 14 | 47.1 | 45.8 | 1.3 |
| 15 | 42.3 | 41.9 | 0.4 |
| 16 | 39.1 | 38.2 | 0.9 |
| Average | 41.9 | 41.4 | 1.4 |
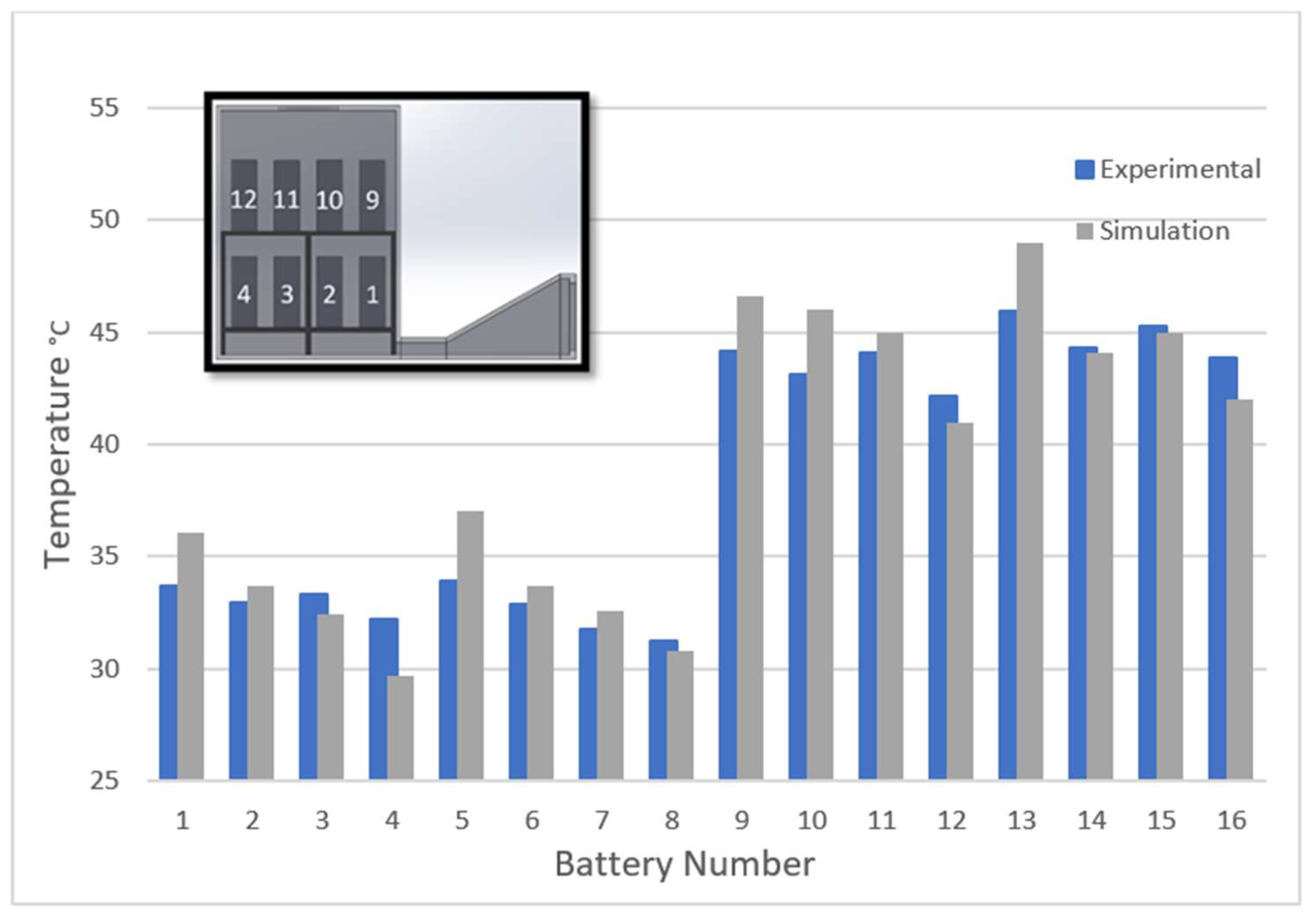
| Battery | Vented Experimental Model Steady State Temp °C | Vented Simulation Model Temp °C | Absolute Error Temp °C |
|---|---|---|---|
| 1 | 33.6 | 36.1 | 2.4 |
| 2 | 32.9 | 33.7 | 0.8 |
| 3 | 33.3 | 32.4 | 0.9 |
| 4 | 32.2 | 29.7 | 2.5 |
| 5 | 33.9 | 37 | 3.05 |
| 6 | 32.9 | 33.7 | 0.8 |
| 7 | 31.8 | 32.6 | 0.8 |
| 8 | 31.2 | 30.8 | 0.4 |
| 9 | 44.2 | 46.6 | 2.4 |
| 10 | 43.1 | 46 | 2.9 |
| 11 | 44.1 | 45 | 0.9 |
| 12 | 42.2 | 41 | 1.2 |
| 13 | 45.9 | 49 | 3.1 |
| 14 | 44.3 | 44.1 | 0.23 |
| 15 | 45.3 | 45 | 1.28 |
| 16 | 43.8 | 42 | 1.8 |
| Average | 38.4 | 39.0 | 1.53 |
| Battery | Default Model Temp (°C) | Vented Model Temp (°C) | Vortex Generator Model Temp (°C) |
|---|---|---|---|
| 1 | 41.5 | 27 | 38.5 |
| 2 | 36.6 | 26.3 | 35.7 |
| 3 | 30.9 | 25.8 | 31.7 |
| 4 | 28.7 | 25.4 | 27.3 |
| 5 | 40.5 | 26.9 | 40.4 |
| 6 | 36 | 26.8 | 35.6 |
| 7 | 30.9 | 25.6 | 29.9 |
| 8 | 28 | 25.4 | 27.6 |
| 9 | 44.6 | 35.1 | 38.7 |
| 10 | 34 | 32.9 | 33.6 |
| 11 | 32.2 | 31 | 30.1 |
| 12 | 31.2 | 32.7 | 28 |
| 13 | 44.4 | 34.7 | 40.7 |
| 14 | 34.1 | 33.5 | 33.3 |
| 15 | 31 | 30.8 | 29.7 |
| 16 | 30 | 32.7 | 28.3 |
| Average: | 34.7 | 29.5 | 33.1 |
| Battery Series | Default Model Temperature Differentials (°C) | Vented Model Temperature Differentials (°C) | Vortex Generator Temperature Differentials (°C) |
|---|---|---|---|
| 1–4 | 12.8 | 1.6 | 11.2 |
| 5–8 | 12.5 | 1.5 | 12.8 |
| 9–12 | 13.4 | 4.1 | 10.7 |
| 13–16 | 14.4 | 3.9 | 12.4 |
| Average: | 13.2 | 2.7 | 11.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hailu, G.; Henke, M.; Petersen, T. Stationary Battery Thermal Management: Analysis of Active Cooling Designs. Batteries 2022, 8, 23. https://doi.org/10.3390/batteries8030023
Hailu G, Henke M, Petersen T. Stationary Battery Thermal Management: Analysis of Active Cooling Designs. Batteries. 2022; 8(3):23. https://doi.org/10.3390/batteries8030023
Chicago/Turabian StyleHailu, Getu, Martin Henke, and Todd Petersen. 2022. "Stationary Battery Thermal Management: Analysis of Active Cooling Designs" Batteries 8, no. 3: 23. https://doi.org/10.3390/batteries8030023
APA StyleHailu, G., Henke, M., & Petersen, T. (2022). Stationary Battery Thermal Management: Analysis of Active Cooling Designs. Batteries, 8(3), 23. https://doi.org/10.3390/batteries8030023






