Real-Time Volume-Rendering Image Denoising Based on Spatiotemporal Weighted Kernel Prediction
Abstract
1. Introduction
- Spatiotemporal VPT Denoising Framework: We propose a flexible framework capable of denoising both single-frame and multi-frame images by effectively combining spatial and temporal information. This approach allows for robust noise reduction across various scenarios.
- Dual-stream Encoder–Decoder Architecture: Our architecture separately processes non-color-related auxiliary features and color-related radiance features. This design leverages low-noise image information more effectively. Additionally, we incorporated gradient loss into the loss function to preserve geometric details and enhance sharpness.
- Multi-head Adaptive Kernel Prediction Module: We introduced a module that predicts adaptive filtering kernels for each pixel. Unlike traditional reprojection algorithms with fixed parameters, our network learns pixel-wise adaptive parameters, enabling better handling of temporal variations and preserving fine details over time.
2. The Related Work
2.1. Learning-Based Direct Prediction Denoiser
2.2. Learning-Based Kernel Prediction Denoiser
2.3. Denoising for DVR
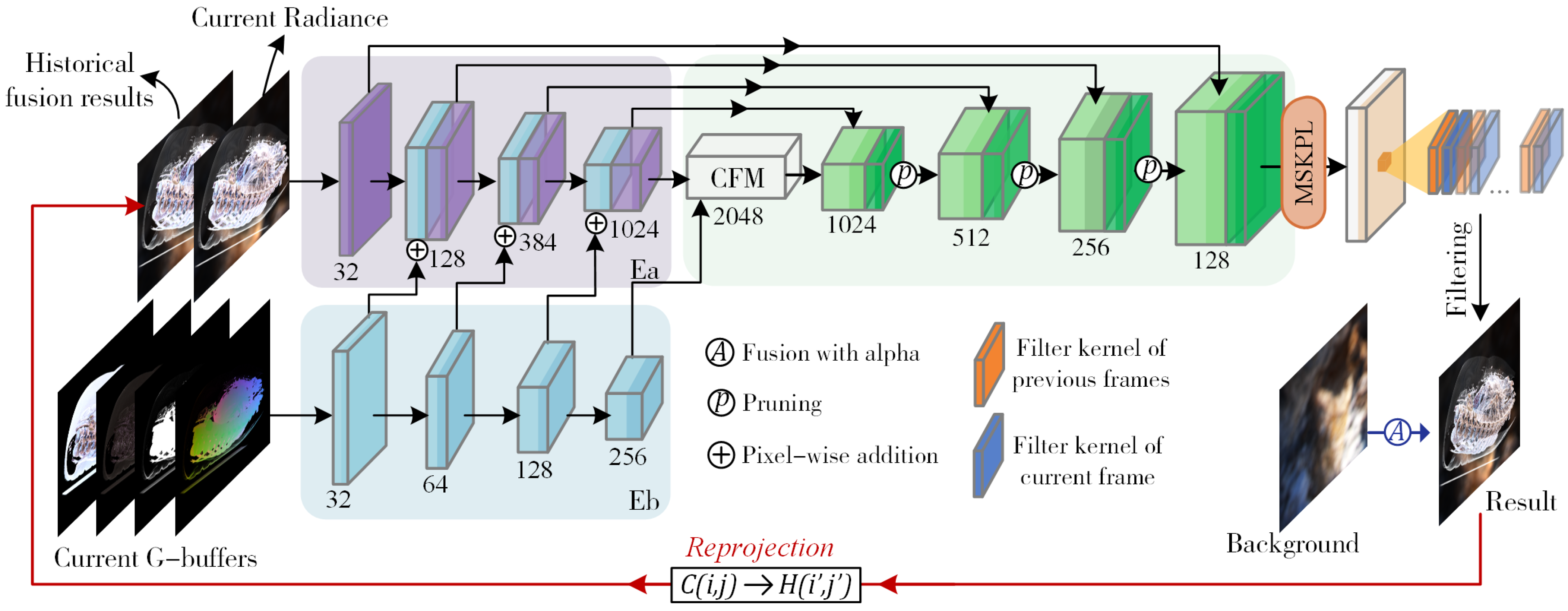
3. Methodology
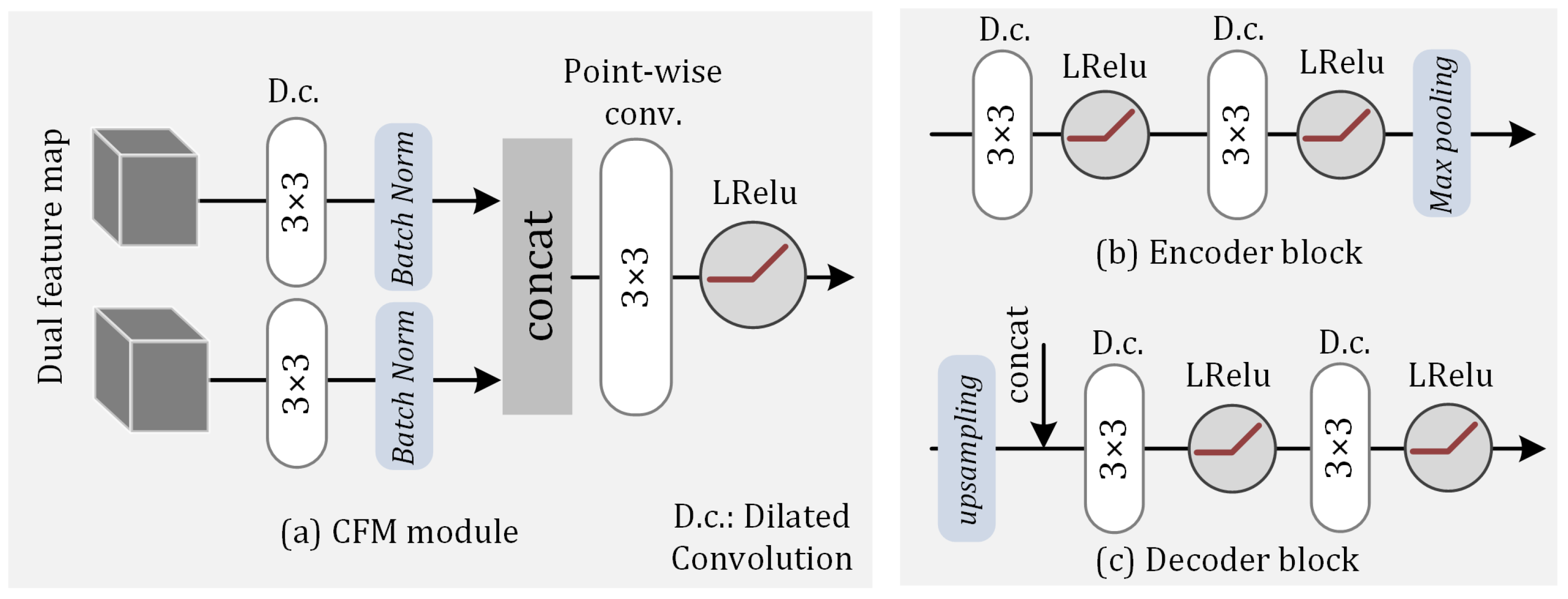
3.1. Dual-Stream Convolutional Encoder–Decoder Network
- 1.
- Parallel encoding: Assuming the input feature map has dimensions (W, H), the output of the i-th layer in is , and the output of the i-th layer in is . The computation process is as follows:
- 2.
- Cascade fusion: The feature maps generated by the dual-stream encoder are fused using our cascade fusion module (CFM). The CFM consists of convolutional layers, batch normalization layers, and pixel-wise convolutional layers to ensure the standardization of the dual-channel feature map distribution and enhance information integration capabilities.
- 3.
- Residual connection and decoding: Assuming the i-th output result of decoder D is , the calculation formula isHere, L represents the number of blocks in both the encoder and decoder. In this study, we set .
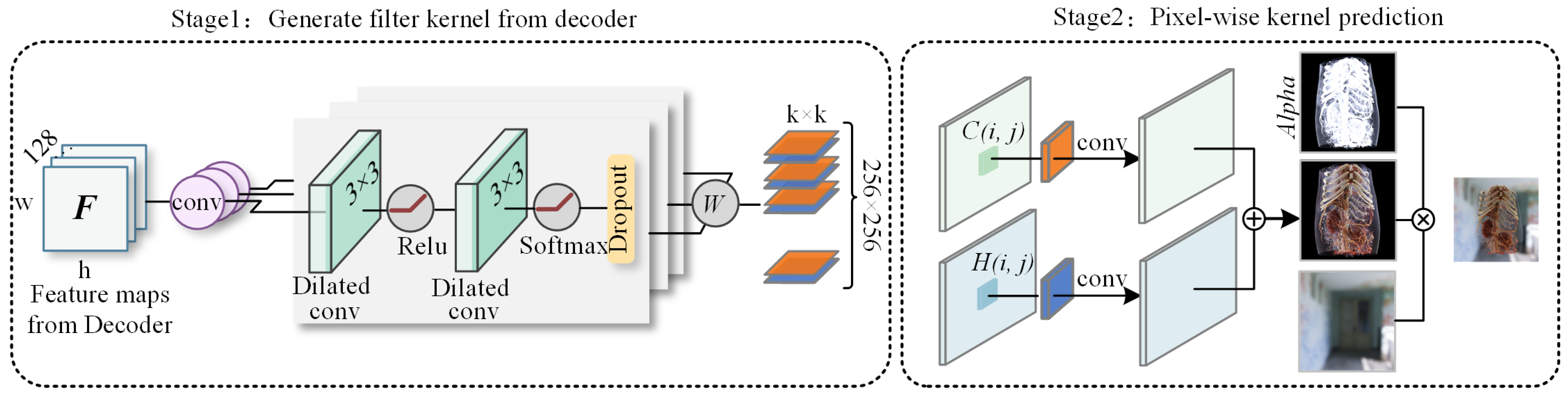
3.2. Multi-Head Space-Time Kernel Prediction Module
3.3. Network Training and Optimization
4. Experimentation and Analysis
4.1. Dataset
4.2. Evaluation Metrics
- 1.
- The PSNR is used to quantify the reconstruction quality of images and videos affected by lossy compression. For an input image I and a reference image R, both with resolution , the PSNR is calculated as follows:where represents the Mean Squared Error between the corresponding pixels of the two images. A higher PSNR indicates a better image quality.
- 2.
- The SSIM represents the image distortion by detecting changes in the structural information. The SSIM is calculated as follows:where and represent the mean values of images I and R, respectively; and denote the standard deviations of the two images; and represents the covariance between the two images. A higher SSIM indicates a greater similarity between I and R.
- 3.
- For temporal sequences, the tPSNR is used to estimate the stability across consecutive frames [29]. It calculates the difference in the PSNR between the current frame and the previous frame to quantify temporal variations:where t represents the time index of the current frame.
4.3. Model Configuration and Experimental Setup
4.3.1. Model Configuration
4.3.2. Experimental Setup
- Scheme 1—comparative experiments: Since the proposed method targets real-time denoising tasks for Monte Carlo rendering images, four state-of-the-art methods were selected for the quality and efficiency evaluations: FDAE [4], WRLS [30], SVGF [10], and WSKP [7]. FDAE is a neural network denoising method based on the U-Net architecture; WRLS reduces noise through linear model fitting; SVGF is a spatiotemporal-filtering-based image denoising algorithm that effectively preserves details; and WSKP is a kernel prediction neural network based on shared parameters. For WSKP, the experiment inputs both noisy radiance and auxiliary features (albedo, gradient, depth). In FDAE, in addition to the albedo and gradient, features from the second scattering event are also included as the input. ONND is trained on a large dataset, and its pre-trained model can be directly used for inference.
- Scheme 2—ablation experiments: In the ablation experiments, four experiments are designed to verify the impact of different model structures on the denoising results: (1) using the network to directly predict radiance values; (2) using only spatial results with a single encoder–decoder structure; (3) using a parallel dual-encoder–decoder structure; and (4) adding historical frame kernel fusion to the parallel encoder–decoder structure. Additionally, the results for images with different noise levels were evaluated to measure the model’s generalization ability.
4.4. Experimental Results and Analysis
4.4.1. Comparative Experiments
4.4.2. Ablation Study
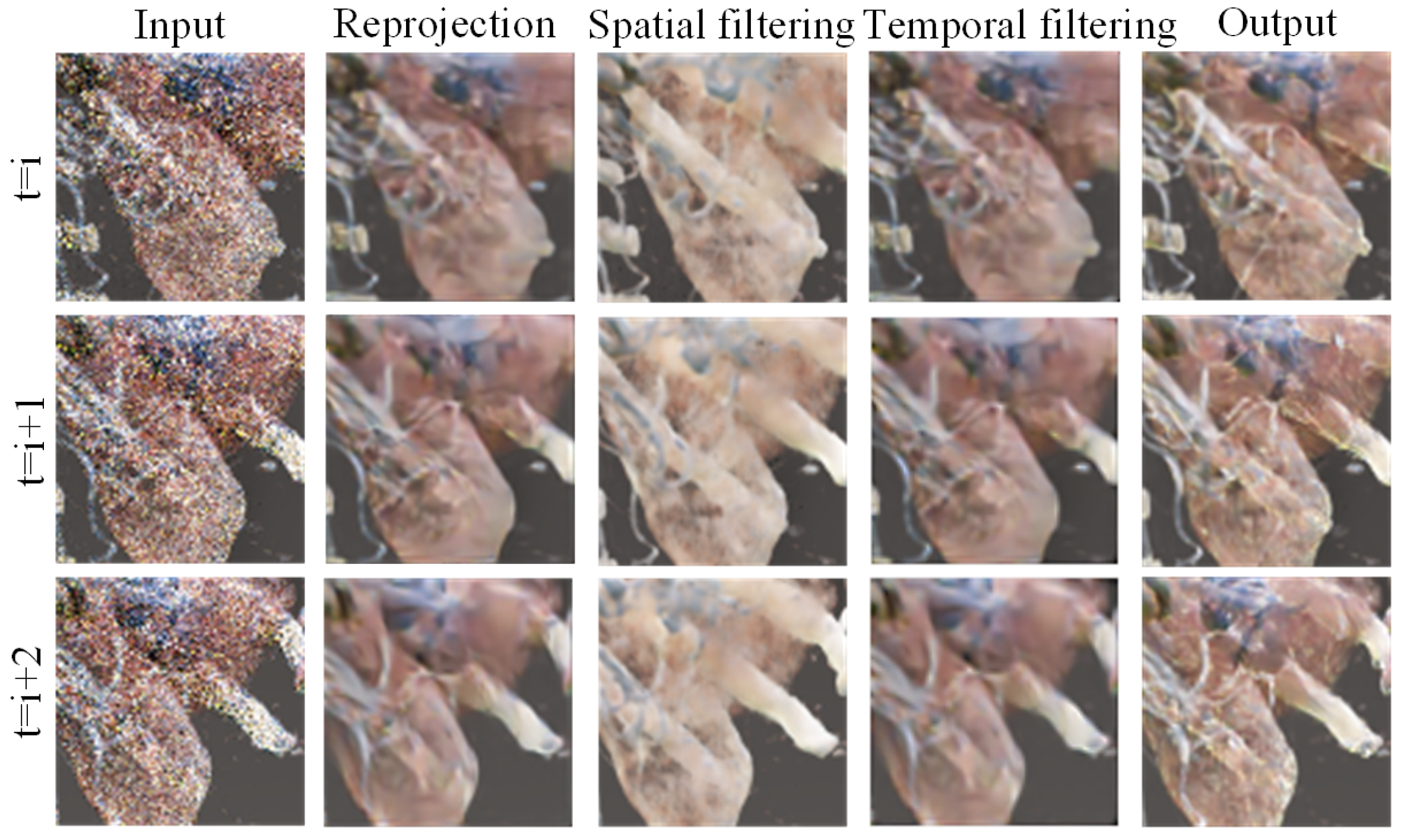
4.4.3. Reliability Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weber, C.; Kaplanyan, A.; Stamminger, M.; Dachsbacher, C. Interactive Direct Volume Rendering with Many-light Methods and Transmittance Caching. In Proceedings of the Vision, Modeling, and Visualization Workshop, Lugano, Switzerland, 11–13 September 2013; pp. 195–202. [Google Scholar]
- Preim, B.; Botha, C.P. Visual Computing for Medicine: Theory, Algorithms, and Applications; Newnes: Oxford, UK, 2013. [Google Scholar]
- Huo, Y.; Yoon, S.e. A survey on deep learning-based Monte Carlo denoising. Comput. Vis. Media 2021, 7, 169–185. [Google Scholar] [CrossRef]
- Hofmann, N.; Martschinke, J.; Engel, K.; Stamminger, M. Neural denoising for path tracing of medical volumetric data. Proc. ACM Comput. Graph. Interact. Tech. 2020, 3, 1–18. [Google Scholar] [CrossRef]
- Chaitanya, C.R.A.; Kaplanyan, A.S.; Schied, C.; Salvi, M.; Lefohn, A.; Nowrouzezahrai, D.; Aila, T. Interactive reconstruction of Monte Carlo image sequences using a recurrent denoising autoencoder. ACM Trans. Graph. (TOG) 2017, 36, 1–12. [Google Scholar] [CrossRef]
- Bako, S.; Vogels, T.; McWilliams, B.; Meyer, M.; Novák, J.; Harvill, A.; Sen, P.; Derose, T.; Rousselle, F. Kernel-predicting convolutional networks for denoising Monte Carlo renderings. ACM Trans. Graph. 2017, 36, 97:1–97:14. [Google Scholar] [CrossRef]
- Fan, H.; Wang, R.; Huo, Y.; Bao, H. Real-time monte carlo denoising with weight sharing kernel prediction network. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2021; Volume 40, pp. 15–27. [Google Scholar]
- Xu, C.; Cheng, H.; Chen, Z.; Wang, J.; Chen, Y.; Zhao, L. Real-time Realistic Volume Rendering of Consistently High Quality with Dynamic Illumination. IEEE Trans. Vis. Comput. Graph. 2024, 1–15. [Google Scholar] [CrossRef]
- Hofmann, N.; Hasselgren, J.; Clarberg, P.; Munkberg, J. Interactive path tracing and reconstruction of sparse volumes. Proc. ACM Comput. Graph. Interact. Tech. 2021, 4, 1–19. [Google Scholar] [CrossRef]
- Schied, C.; Kaplanyan, A.; Wyman, C.; Patney, A.; Chaitanya, C.R.A.; Burgess, J.; Liu, S.; Dachsbacher, C.; Lefohn, A.; Salvi, M. Spatiotemporal variance-guided filtering: Real-time reconstruction for path-traced global illumination. In High Performance Graphics; ACM: New York, NY, USA, 2017; pp. 1–12. [Google Scholar]
- Koskela, M.; Immonen, K.; Mäkitalo, M.; Foi, A.; Viitanen, T.; Jääskeläinen, P.; Kultala, H.; Takala, J. Blockwise multi-order feature regression for real-time path-tracing reconstruction. ACM Trans. Graph. (TOG) 2019, 38, 1–14. [Google Scholar] [CrossRef]
- Xin, H.; Zheng, S.; Xu, K.; Yan, L.Q. Lightweight bilateral convolutional neural networks for interactive single-bounce diffuse indirect illumination. IEEE Trans. Vis. Comput. Graph. 2020, 28, 1824–1834. [Google Scholar] [CrossRef]
- Işık, M.; Mullia, K.; Fisher, M.; Eisenmann, J.; Gharbi, M. Interactive Monte Carlo denoising using affinity of neural features. ACM Trans. Graph. (TOG) 2021, 40, 1–13. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, J.; Wang, R.; Xu, K.; Yang, Y.L.; Li, C.; Tang, R. Adversarial Monte Carlo denoising with conditioned auxiliary feature modulation. ACM Trans. Graph. 2019, 38, 224:1–224:12. [Google Scholar] [CrossRef]
- Igouchkine, O.; Zhang, Y.; Ma, K.L. Multi-material volume rendering with a physically-based surface reflection model. IEEE Trans. Vis. Comput. Graph. 2017, 24, 3147–3159. [Google Scholar] [CrossRef] [PubMed]
- Han, K.B.; Odenthal, O.G.; Kim, W.J.; Yoon, S.E. Pixel-wise Guidance for Utilizing Auxiliary Features in Monte Carlo Denoising. Proc. ACM Comput. Graph. Interact. Tech. 2023, 6, 1–19. [Google Scholar] [CrossRef]
- Vogels, T.; Rousselle, F.; McWilliams, B.; Röthlin, G.; Harvill, A.; Adler, D.; Meyer, M.; Novák, J. Denoising with kernel prediction and asymmetric loss functions. ACM Trans. Graph. (TOG) 2018, 37, 1–15. [Google Scholar] [CrossRef]
- Meng, X.; Zheng, Q.; Varshney, A.; Singh, G.; Zwicker, M. Real-time Monte Carlo Denoising with the Neural Bilateral Grid. In Proceedings of the EGSR (DL), London, UK, 13–24 April 2020; pp. 13–24. [Google Scholar]
- Balint, M.; Wolski, K.; Myszkowski, K.; Seidel, H.P.; Mantiuk, R. Neural Partitioning Pyramids for Denoising Monte Carlo Renderings. In Proceedings of the ACM SIGGRAPH 2023 Conference Proceedings, Sydney, Australia, 12–15 December 2023; pp. 1–11. [Google Scholar]
- Chen, Y.; Lu, Y.; Zhang, X.; Xie, N. Interactive neural cascade denoising for 1-spp Monte Carlo images. Vis. Comput. 2023, 39, 3197–3210. [Google Scholar] [CrossRef]
- Iglesias-Guitian, J.A.; Mane, P.; Moon, B. Real-time denoising of volumetric path tracing for direct volume rendering. IEEE Trans. Vis. Comput. Graph. 2020, 28, 2734–2747. [Google Scholar] [CrossRef] [PubMed]
- Bauer, D.; Wu, Q.; Ma, K.L. Fovolnet: Fast volume rendering using foveated deep neural networks. IEEE Trans. Vis. Comput. Graph. 2022, 29, 515–525. [Google Scholar] [CrossRef]
- Taibo, J.; Iglesias-Guitian, J.A. Immersive 3D Medical Visualization in Virtual Reality using Stereoscopic Volumetric Path Tracing. In Proceedings of the 2024 IEEE Conference Virtual Reality and 3D User Interfaces (VR), Orlando, FL, USA, 16–21 March 2024; pp. 1044–1053. [Google Scholar]
- Schied, C.; Peters, C.; Dachsbacher, C. Gradient estimation for real-time adaptive temporal filtering. Proc. ACM Comput. Graph. Interact. Tech. 2018, 1, 1–16. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Nehab, D.F.; Sander, P.V.; Lawrence, J.; Tatarchuk, N.; Isidoro, J.R. Accelerating real-time shading with reverse reprojection caching. In Proceedings of the GH ’07, San Diego, CA, USA, 4–5 August 2007. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Mueller, J.H.; Neff, T.; Voglreiter, P.; Steinberger, M.; Schmalstieg, D. Temporally adaptive shading reuse for real-time rendering and virtual reality. ACM Trans. Graph. (TOG) 2021, 40, 1–14. [Google Scholar] [CrossRef]
- Thomas, M.M.; Liktor, G.; Peters, C.; Kim, S.; Vaidyanathan, K.; Forbes, A.G. Temporally Stable Real-Time Joint Neural Denoising and Supersampling. Proc. ACM Comput. Graph. Interact. Tech. 2022, 5, 1–22. [Google Scholar] [CrossRef]
- Wang, Z.; Na, Y.; Liu, Z.; Tian, B.; Fu, Q. Weighted Recursive Least Square Filter and Neural Network based Residual Echo Suppression for the AEC-Challenge. arXiv 2021, arXiv:2102.08551. [Google Scholar] [CrossRef]

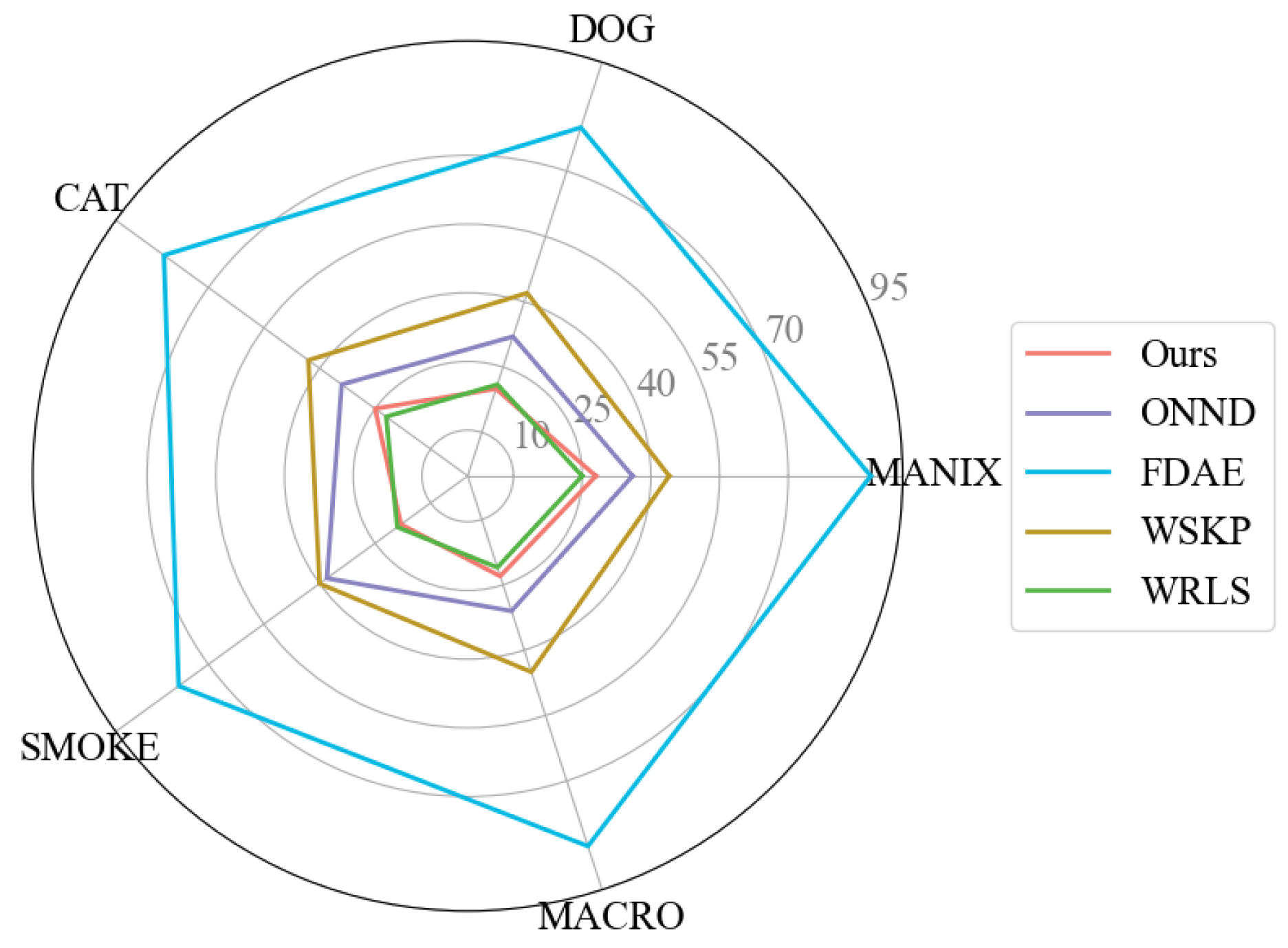

| Methods | Metrics | Manix | Dog | Cat | Artifix | Smoke | Average |
|---|---|---|---|---|---|---|---|
| PSNR | 37.050 | 33.687 | 37.315 | 37.516 | 35.910 | 36.295 | |
| Ours | tPSNR | 40.562 | 37.824 | 41.331 | 39.003 | 38.100 | 39.364 |
| SSIM | 0.931 | 0.933 | 0.941 | 0.963 | 0.969 | 0.947 | |
| PSNR | 24.212 | 23.142 | 25.248 | 24.902 | 26.749 | 24.86 | |
| SVGF | tPSNR | 27.975 | 27.724 | 28.115 | 27.121 | 31.543 | 28.496 |
| SSIM | 0.834 | 0.861 | 0.854 | 0.882 | 0.861 | 0.858 | |
| PSNR | 38.521 | 31.358 | 36.098 | 35.614 | 35.692 | 35.456 | |
| FDAE | tPSNR | 41.163 | 33.534 | 40.664 | 35.765 | 38.122 | 38.650 |
| SSIM | 0.937 | 0.905 | 0.910 | 0.914 | 0.969 | 0.927 | |
| PSNR | 21.741 | 22.255 | 23.241 | 21.962 | 23.751 | 22.59 | |
| WSKP | tPSNR | 25.089 | 25.741 | 27.029 | 25.672 | 24.010 | 25.508 |
| SSIM | 0.827 | 0.793 | 0.813 | 0.867 | 0.873 | 0.834 | |
| PSNR | 28.64 | 31.081 | 32.834 | 30.700 | 31.842 | 31.019 | |
| WRLS | tPSNR | 21.734 | 34.673 | 36.339 | 34.670 | 34.423 | 35.175 |
| SSIM | 0.895 | 0.906 | 0.913 | 0.920 | 0.948 | 0.916 |
| Datasets | Single Encoder | Dual-Stream Encoder | Denoise for One Frame | Space-Time Fusion | ||||
|---|---|---|---|---|---|---|---|---|
| K = 3 | K = 4 | K = 3 | K = 4 | SSIM | PSNR | SSIM | PSNR | |
| Artifix | 0.791 | 0.798 | 0.889 | 0.916 | 0.903 | 32.704 | 0.916 | 34.841 |
| Dog | 0.813 | 0.823 | 0.872 | 0.931 | 0.905 | 32.293 | 0.931 | 34.186 |
| Macro | 0.804 | 0.852 | 0.873 | 0.928 | 0.896 | 31.253 | 0.928 | 33.341 |
| Datasets | Pixel-Wise Weighted | Whole-Image Weighted () | Whole-Image Weighted () | |||
|---|---|---|---|---|---|---|
| SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | |
| Artifix | 0.916 | 34.841 | 0.892 | 30.342 | 0.887 | 30.765 |
| Dog | 0.931 | 34.186 | 0.923 | 32.553 | 0.911 | 32.439 |
| Macro | 0.928 | 33.341 | 0.924 | 31.300 | 0.921 | 31.350 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Xu, C.; Zhao, L. Real-Time Volume-Rendering Image Denoising Based on Spatiotemporal Weighted Kernel Prediction. J. Imaging 2025, 11, 126. https://doi.org/10.3390/jimaging11040126
Xu X, Xu C, Zhao L. Real-Time Volume-Rendering Image Denoising Based on Spatiotemporal Weighted Kernel Prediction. Journal of Imaging. 2025; 11(4):126. https://doi.org/10.3390/jimaging11040126
Chicago/Turabian StyleXu, Xinran, Chunxiao Xu, and Lingxiao Zhao. 2025. "Real-Time Volume-Rendering Image Denoising Based on Spatiotemporal Weighted Kernel Prediction" Journal of Imaging 11, no. 4: 126. https://doi.org/10.3390/jimaging11040126
APA StyleXu, X., Xu, C., & Zhao, L. (2025). Real-Time Volume-Rendering Image Denoising Based on Spatiotemporal Weighted Kernel Prediction. Journal of Imaging, 11(4), 126. https://doi.org/10.3390/jimaging11040126






