A Multimodal Ensemble Driven by Multiobjective Optimisation to Predict Overall Survival in Non-Small-Cell Lung Cancer
Abstract
:1. Introduction
2. Materials
2.1. Imaging
2.2. Clinical Features
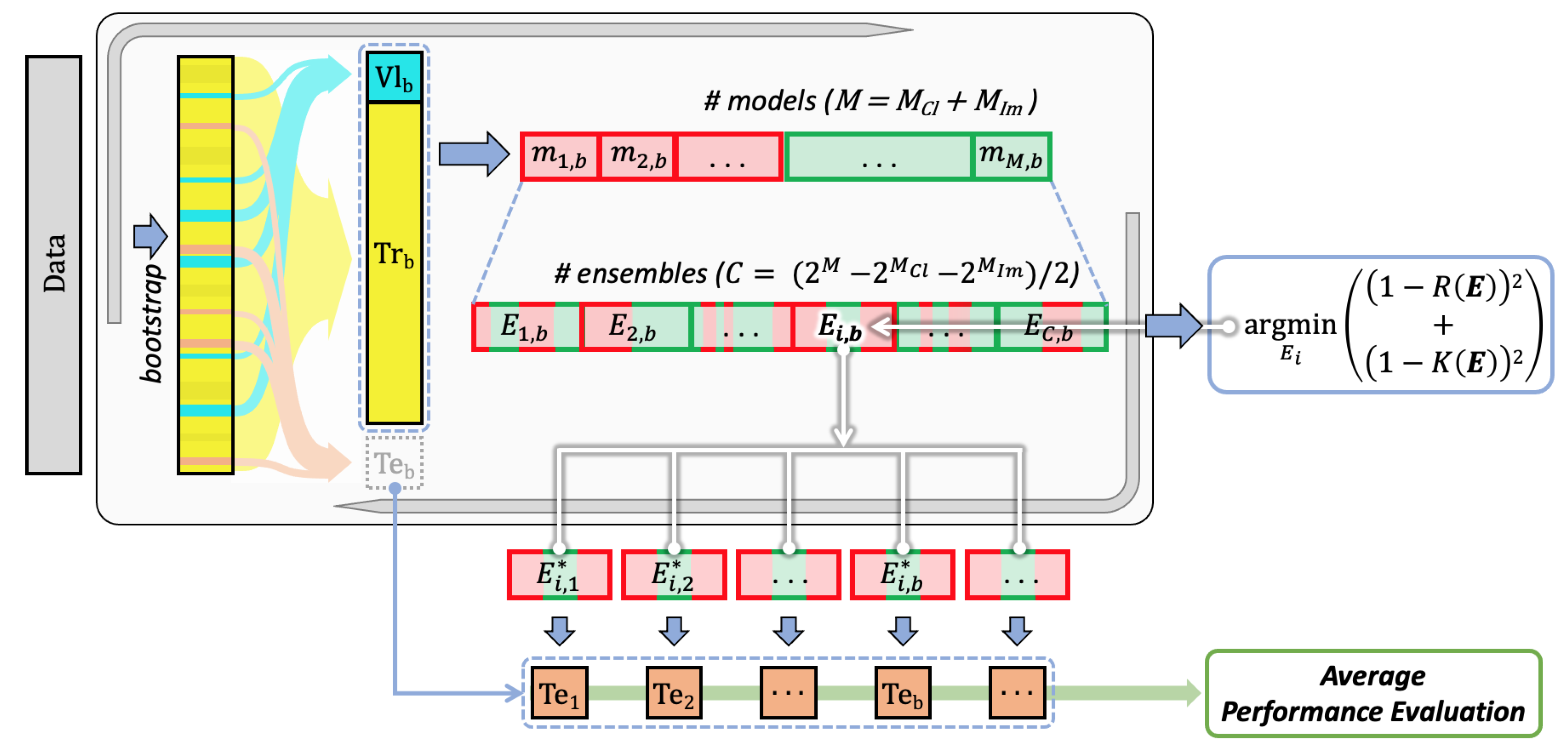
3. Methods
- Training all the available models for every single modality using the training sets defined by the bootstrap validation approach;
- Finding the multimodal set of unimodal models solving a multiobjective optimisation problem working with evaluation and diversity scores, which are computed on the validation sets defined by the same bootstrap approach;
- Computing the performance on the test sets defined by bootstrap, which are then averaged out (block “Average performance evaluation”).
3.1. Training
- AdaBoost as a cascade of classifiers;
- Decision Tree (DT) as tree model;
- Multilayer perceptron (MLP) as neural architecture with one hidden layer with 13 neurons and 1 neuron in the output layer, which use the ReLU and Sigmoid activation functions, respectively;
- Random forest (RF) as an ensemble of trees;
- Support Vector Machine (SVM) as a kernel machine;
- TABNET [35] as a neural architecture;
- XGBoost a variation of the AdaBoost that uses a gradient descent procedure to minimise the loss when adding weak learners.
- AlexNet [37];
- VGG [38]: VGG11, VGG11-BN, VGG13, VGG13-BN, VGG16, VGG16-BN, VGG19, VGG19-BN, where the suffix BN means that batch normalization is used;
- ResNet [39]: ResNet18, ResNet34, ResNet50, ResNet101, ResNet152, ResNeXt50, ResNeXt101, Wide-ResNet50-2, Wide-ResNet101-2;
- DenseNet [40]: DenseNet121, DenseNet169, DenseNet161, DenseNet201;
- GoogLeNet [41];
- ShuffleNet [42]: ShuffleNet-v2-x0-5, ShuffleNet-v2-x1-0, ShuffleNet-v2-x1-5, ShuffleNet-v2-x2-0;
- MobileNetV2 [43];
- MNasNet [44]: MNasNet0-5, MNasNet1-0.
3.2. Optimisation
3.3. Preprocessing
4. Results and Discussion
- : it denotes the average performance for all the possible ensembles;
- : it denotes the performance of the ensemble consisting of the unimodal models with the largest recall, i.e., AdaBoost, ResNet34, and VGG11-BN. In this case, we adopt the subscript post to specify that such three models were a posteriori selected, i.e., they provide the largest performance on the test set, and not on the validation set;
- : it denotes the average performance attained by all the possible ensembles, including the two unimodal classifiers with the largest a posteriori recall, i.e., Adaboost and VGG11-BN, whilst varying the remaining experts included in the ensemble;
- : it denotes the performance of the ensemble obtained relaxing the multimodality constraints, and it is composed of AdaBoost, DT and RF.
5. Conclusions
- Retrieving data at 1-, 2-, and 3-year time points as well as the progression free survival, which would add useful information;
- Provide more complementary information by adding other modalities to improve performance, such as WSI, genome sequencing, etc.;
- Perform different multimodality fusion approaches, such as joint fusion to obtain a end-to-end trainable system able to exploit the inherent correlations between multiple modalities;
- Search for an approach that a priori selects the models to be included in the ensemble, without the need to train them all individually;
- Switch from a classification to a regression task, which will allow predicting the actual survival time, also integrating the “Input doubling method” [52] as a preprocessing tool to augment the training set size.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ML | Machine Learning |
| DL | Deep Learning |
| DT | Decision Tree |
| RF | Random Forest |
| MLP | Multilayer Perceptron |
| CNN | Convolutional Neural Network |
| SVM | Support Vector Machine |
| AUC | Area Under the ROC Curve |
| CT | Computed Tomography |
| MRI | Magnetic Resonance Imaging |
| PET | Positron Emission Tomography |
| WSI | Whole Slide Image |
| TCIA | The Cancer Imaging Archive |
| NSCLC | Non-Small-Cell Lung Cancer |
| OS | Overall Survival |
| CTV | Clinical Target Volume |
References
- Word Health Organisation. LUNG. 2020. Available online: https://gco.iarc.fr/today/data/factsheets/cancers/15-Lung-fact-sheet.pdf (accessed on 18 May 2022).
- Cancer.net. Lung Cancer—Non-Small Cell: Statistics. 2022. Available online: https://www.cancer.net/cancer-types/lung-cancer-non-small-cell/statistics (accessed on 18 May 2022).
- National Cancer Institute. Non-Small Cell Lung Cancer Treatment. 2022. Available online: https://www.cancer.gov/types/lung/hp/non-small-cell-lung-treatment-pdq#_514 (accessed on 18 May 2022).
- Lambin, P.; Rios-Velazquez, E.; Leijenaar, R.; Carvalho, S.; van Stiphout, R.G.; Granton, P.; Zegers, C.M.; Gillies, R.; Boellard, R.; Dekker, A.; et al. Radiomics: Extracting more information from medical images using advanced feature analysis. Eur. J. Cancer 2012, 48, 441–446. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scrivener, M.; de Jong, E.E.C.; van Timmeren, J.E.; Pieters, T.; Ghaye, B.; Geets, X. Radiomics applied to lung cancer: A review. Transl. Cancer Res. 2016, 5, 398–409. [Google Scholar] [CrossRef]
- Ramella, S.; Fiore, M.; Greco, C.; Cordelli, E.; Sicilia, R.; Merone, M.; Molfese, E.; Miele, M.; Cornacchione, P.; Ippolito, E.; et al. A radiomic approach for adaptive radiotherapy in non-small cell lung cancer patients. PLoS ONE 2018, 13, e0207455. [Google Scholar] [CrossRef]
- Sicilia, R.; Cordelli, E.; Ramella, S.; Fiore, M.; Greco, C.; Molfese, E.; Miele, M.; Vinciguerra, E.; Cornacchione, P.; Ippolito, E.; et al. Exploratory radiomics for predicting adaptive radiotherapy in non-small cell lung cancer. In Proceedings of the IEEE 31st International Symposium on Computer-Based Medical Systems (CBMS), Karlstad, Sweden, 18–21 June 2018; pp. 250–255. [Google Scholar] [CrossRef]
- Anzar, I.; Sverchkova, A.; Stratford, R.; Clancy, T. NeoMutate: An ensemble machine learning framework for the prediction of somatic mutations in cancer. BMC Med. Genom. 2019, 12, 63. [Google Scholar] [CrossRef] [Green Version]
- Gupta, R.; Kurc, T.; Sharma, A.; Almeida, J.S.; Saltz, J. The Emergence of Pathomics. Curr. Pathobiol. Rep. 2019, 7, 73–84. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.Z.; Sicilia, R.; Tortora, M.; Cordelli, E.; Nibid, L.; Sabarese, G.; Perrone, G.; Fiore, M.; Ramella, S.; Soda, P. Exploring Deep Pathomics in Lung Cancer. In Proceedings of the 2021 IEEE 34th International Symposium on Computer-Based Medical Systems (CBMS), Aveiro, Portugal, 7–9 June 2021; IEEE: Aveiro, Portugal, 2021; pp. 407–412. [Google Scholar] [CrossRef]
- Aerts, H.J.W.L.; Velazquez, E.R.; Leijenaar, R.T.H.; Parmar, C.; Grossmann, P.; Carvalho, S.; Bussink, J.; Monshouwer, R.; Haibe-Kains, B.; Rietveld, D.; et al. Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach. Nat. Commun. 2014, 5, 4006. [Google Scholar] [CrossRef] [Green Version]
- Huynh, E.; Coroller, T.P.; Narayan, V.; Agrawal, V.; Hou, Y.; Romano, J.; Franco, I.; Mak, R.H.; Aerts, H.J. CT-based radiomic analysis of stereotactic body radiation therapy patients with lung cancer. Radiother. Oncol. 2016, 120, 258–266. [Google Scholar] [CrossRef]
- Fave, X.; Zhang, L.; Yang, J.; Mackin, D.; Balter, P.; Gomez, D.; Followill, D.; Jones, A.K.; Stingo, F.; Liao, Z.; et al. Delta-radiomics features for the prediction of patient outcomes in non–small cell lung cancer. Sci. Rep. 2017, 7, 588. [Google Scholar] [CrossRef]
- Li, H.; Galperin-Aizenberg, M.; Pryma, D.; Simone, C.B.; Fan, Y. Unsupervised machine learning of radiomic features for predicting treatment response and overall survival of early stage non-small cell lung cancer patients treated with stereotactic body radiation therapy. Radiother. Oncol. 2018, 129, 218–226. [Google Scholar] [CrossRef]
- Parmar, C.; Grossmann, P.; Bussink, J.; Lambin, P.; Aerts, H. Machine Learning methods for Quantitative Radiomic Biomarkers. Sci. Rep. 2015, 5, 13087. [Google Scholar] [CrossRef] [Green Version]
- D’Amico, N.C.; Sicilia, R.; Cordelli, E.; Tronchin, L.; Greco, C.; Fiore, M.; Carnevale, A.; Iannello, G.; Ramella, S.; Soda, P. Radiomics-Based Prediction of Overall Survival in Lung Cancer Using Different Volumes-Of-Interest. Appl. Sci. 2020, 10, 6425. [Google Scholar] [CrossRef]
- Heiliger, L.; Sekuboyina, A.; Menze, B.; Egger, J.; Kleesiek, J. Beyond Medical Imaging: A Review of Multimodal Deep Learning in Radiology. techRxiv 2022, 13. [Google Scholar] [CrossRef]
- Stahlschmidt, S.R.; Ulfenborg, B.; Synnergren, J. Multimodal deep learning for biomedical data fusion: A review. Briefings Bioinform. 2022, 23, bbab569. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; He, K.; Guo, Y.; Liu, X.; Yang, Q.; Zhang, C.; Xie, Y.; Mu, S.; Guo, Y.; Fu, Y.; et al. A Novel Multimodal Radiomics Model for Preoperative Prediction of Lymphovascular Invasion in Rectal Cancer. Front. Oncol. 2020, 10, 457. [Google Scholar] [CrossRef] [Green Version]
- Tortora, M.; Cordelli, E.; Sicilia, R.; Nibid, L.; Ippolito, E.; Perrone, G.; Ramella, S.; Soda, P. RadioPathomics: Multimodal Learning in Non-Small Cell Lung Cancer for Adaptive Radiotherapy. arXiv 2022, arXiv:2204.12423. [Google Scholar]
- Cipollari, S.; Guarrasi, V.; Pecoraro, M.; Bicchetti, M.; Messina, E.; Farina, L.; Paci, P.; Catalano, C.; Panebianco, V. Convolutional neural networks for automated classification of prostate multiparametric magnetic resonance imaging based on image quality. J. Magn. Reson. Imaging 2022, 55, 480–490. [Google Scholar] [CrossRef]
- Amini, M.; Nazari, M.; Shiri, I.; Hajianfar, G.; Deevband, M.R.; Abdollahi, H.; Zaidi, H. Multi-Level PET and CT Fusion Radiomics-based Survival Analysis of NSCLC Patients. In Proceedings of the 2020 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), Boston, MA, USA, 31 October–7 November 2020; IEEE: Boston, MA, USA; pp. 1–4. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, J.; Huang, X.; Ling, S.H.; Su, S.W. DeepMMSA: A Novel Multimodal Deep Learning Method for Non-small Cell Lung Cancer Survival Analysis. arXiv 2021, arXiv:2106.06744. [Google Scholar]
- He, Q.; Li, X.; Kim, D.N.; Jia, X.; Gu, X.; Zhen, X.; Zhou, L. Feasibility study of a multi-criteria decision-making based hierarchical model for multi-modality feature and multi-classifier fusion: Applications in medical prognosis prediction. Inf. Fusion 2020, 55, 207–219. [Google Scholar] [CrossRef]
- Vale-Silva, L.A.; Rohr, K. Long-term cancer survival prediction using multimodal deep learning. Sci. Rep. 2021, 11, 13505. [Google Scholar] [CrossRef]
- Bakr, S.; Gevaert, O.; Echegaray, S.; Ayers, K.; Zhou, M.; Shafiq, M.; Zheng, H.; Benson, J.A.; Zhang, W.; Leung, A.; et al. Data for NSCLC Radiogenomics Collection. The Cancer Imaging Archive. 2017. Available online: https://wiki.cancerimagingarchive.net/display/Public/NSCLC+Radiogenomics (accessed on 28 September 2022).
- Aerts, H.J.W.L.; Wee, L.; Rios Velazquez, E.; Leijenaar, R.T.H.; Parmar, C.; Grossmann, P.; Carvalho, S.; Bussink, J.; Monshouwer, R.; Haibe-Kains, B.; et al. Data from NSCLC-Radiomics. The Cancer Imaging Archive. 2019. Available online: https://wiki.cancerimagingarchive.net/display/Public/NSCLC-Radiomics (accessed on 28 September 2022).
- Grossman, R.L.; Heath, A.P.; Ferretti, V.; Varmus, H.E.; Lowy, D.R.; Kibbe, W.A.; Staudt, L.M. Toward a Shared Vision for Cancer Genomic Data. N. Engl. J. Med. 2016, 375, 1109–1112. [Google Scholar] [CrossRef]
- Aggarwal, R.; Sounderajah, V.; Martin, G.; Ting, D.S.; Karthikesalingam, A.; King, D.; Ashrafian, H.; Darzi, A. Diagnostic accuracy of deep learning in medical imaging: A systematic review and meta-analysis. NPJ Digit. Med. 2021, 4, 65. [Google Scholar] [CrossRef] [PubMed]
- Gulum, M.A.; Trombley, C.M.; Kantardzic, M. A review of explainable deep learning cancer detection models in medical imaging. Appl. Sci. 2021, 11, 4573. [Google Scholar] [CrossRef]
- Tortora, M.; Cordelli, E.; Sicilia, R.; Miele, M.; Matteucci, P.; Iannello, G.; Ramella, S.; Soda, P. Deep Reinforcement Learning for Fractionated Radiotherapy in Non-Small Cell Lung Carcinoma. Artif. Intell. Med. 2021, 119, 102137. [Google Scholar] [CrossRef] [PubMed]
- Guarrasi, V.; Soda, P. Multi-objective optimization determines when, which and how to fuse deep networks: An application to predict COVID-19 outcomes. arXiv 2022, arXiv:2204.03772. [Google Scholar]
- Aceña, V.; Martín de Diego, I.; Fernández, R.R.; Moguerza, J.M. Minimally overfitted learners: A general framework for ensemble learning. Knowl.-Based Syst. 2022, 254, 109669. [Google Scholar] [CrossRef]
- Borisov, V.; Leemann, T.; Seßler, K.; Haug, J.; Pawelczyk, M.; Kasneci, G. Deep neural networks and tabular data: A survey. arXiv 2021, arXiv:2110.01889. [Google Scholar]
- Arik, S.O.; Pfister, T. TabNet: Attentive Interpretable Tabular Learning. Proc. AAAI Conf. Artif. Intell. 2019, 35, 6679–6687. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A. One weird trick for parallelizing convolutional neural networks. arXiv 2014, arXiv:1404.5997. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.T.; Sun, J. ShuffleNet V2: Practical guidelines for efficient CNN architecture design. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 116–131. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Tan, M.; Chen, B.; Pang, R.; Vasudevan, V.; Sandler, M.; Howard, A.; Le, Q.V. MnasNet: Platform-aware neural architecture search for mobile. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2820–2828. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Guarrasi, V.; D’Amico, N.C.; Sicilia, R.; Cordelli, E.; Soda, P. Pareto optimization of deep networks for COVID-19 diagnosis from chest X-rays. Pattern Recognit. 2022, 121, 108242. [Google Scholar] [CrossRef] [PubMed]
- Guarrasi, V.; D’Amico, N.C.; Sicilia, R.; Cordelli, E.; Soda, P. A Multi-Expert System to Detect COVID-19 Cases in X-ray Images. In Proceedings of the 2021 IEEE 34th International Symposium on Computer-Based Medical Systems (CBMS), Aveiro, Portugal, 7–9 June 2021; pp. 395–400. [Google Scholar]
- Guarrasi, V.; Soda, P. Optimized Fusion of CNNs to Diagnose Pulmonary Diseases on Chest X-Rays. In Proceedings of the International Conference on Image Analysis and Processing—ICIAP 2022, Lecce, Italy, 23–27 May 2022; Springer: Cham, Switzerland, 2022; pp. 197–209. [Google Scholar] [CrossRef]
- Dietterich, T.G. An experimental comparison of three methods for constructing ensembles of decision trees: Bagging, boosting, and randomization. Mach. Learn. 2000, 40, 139–157. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Brown, G.; Wyatt, J.; Harris, R.; Yao, X. Diversity creation methods: A survey and categorisation. Inf. Fusion 2005, 6, 5–20. [Google Scholar] [CrossRef]
- Izonin, I.; Tkachenko, R.; Shakhovska, N.; Lotoshynska, N. The Additive Input-Doubling Method Based on the SVR with Nonlinear Kernels: Small Data Approach. Symmetry 2021, 13, 612. [Google Scholar] [CrossRef]
| Author | Modalities | Study Population | Number of Patients | Data Representation | Fusion Modality | Learning Model | Performance |
|---|---|---|---|---|---|---|---|
| Amini et al. [22] | CT, PET | NSCLC I-IV stages | 182 | Radiomic features extracted from an image obtained by merging PET and CT scans through a technique based on 3D discrete wavelet transform | Early | Kaplan–Meier method | C-index: 0.708 |
| Wu et al. [23] | CT, clinical data | NSCLC I-III stages | 422 | Concatenation of deep features extracted by a 3D-ResNet34 and an MLP for CT images and clinical data, respectively | Early | MLP | C-index: 0.658 |
| He et al. [24] | CT, clinical data | NSCLC I-III stages | 316 | Clinical data and radiomic features | Late | Modular architecture with SVM, DT, KNN, RF, and XGBoost as base classifiers | AUC: 0.81 |
| Vale-Silva and Rohr [25] | clinical data, gene expression, microRNA expression, DNA methylation, gene copy number variation data, and WSI | 33 different cancer types | 11.081 | Element-wise maxima across the set of representation vectors of single-modality submodels | Joint | Modular architecture, with dedicated input data modality submodels, a data fusion layer, and a final survival prediction MLP submodel | Time-dependent C-index: best 0.822 lung squamous cell carcinoma 0.554 |
| Putting our work in the background | CT, clinical data | NSCLC II-IV stages | 191 | Clinical data and CT slices | Optimisation-driven late | multimodal ensemble of learners trained on different modalities and selected by a multiobjective optimisation algorithm | ACC: 0.75 |
| Feature | Missing Data | Categories | Distribution |
|---|---|---|---|
| Age * | 26 (13.62%) | <71 years | 82 (42.93%) |
| ≥71 years | 83 (43.46%) | ||
| CTV * | 37 (19.37%) | <114.88 | 77 (40.31%) |
| ≥114.88 | 77 (40.31%) | ||
| Sex | 0 (0.00%) | Male | 133 (69.63%) |
| Female | 58 (30.37%) | ||
| Histology | 0 (0.00%) | Adenocarcinoma | 95 (49.74%) |
| Squamous | 59 (30.89%) | ||
| Other | 11 (5.76%) | ||
| Unknown | 26 (13.61%) | ||
| Stage | 0 (0.00%) | II | 4 (2.09%) |
| III | 160 (83.77%) | ||
| IV | 27 (14.14%) | ||
| T stage | 36 (18.85%) | T0 | 1 (0.52%) |
| T1 | 9 (4.71%) | ||
| T2 | 32 (16.75%) | ||
| T3 | 65 (34.03%) | ||
| T4 | 48 (25.13%) | ||
| N stage | 26 (13.61%) | N0 | 15 (7.85%) |
| N1 | 33 (17.28%) | ||
| N2 | 93 (48.69%) | ||
| recurrence N2 | 6 (3.14%) | ||
| N3 | 18 (9.42%) |
| Classifier | Modality | Accuracy | F-Score | Recall |
|---|---|---|---|---|
| AdaBoost | Clinical | 65.00 ± 5.00 | 67.35 ± 6.53 | 74.00 ± 16.73 |
| DT | Clinical | 60.00 ± 3.54 | 59.42 ± 9.15 | 62.00 ± 20.49 |
| MLP | Clinical | 61.00 ± 5.48 | 54.37 ± 23.57 | 60.00 ± 38.08 |
| RF | Clinical | 60.00 ± 6.12 | 60.72 ± 9.74 | 64.00 ± 16.73 |
| SVM | Clinical | 59.00 ± 2.24 | 55.46 ± 10.29 | 54.00 ± 18.17 |
| TABNET | Clinical | 63.00 ± 10.37 | 64.68 ± 11.69 | 70.00 ± 22.36 |
| XGBoost | Clinical | 54.00 ± 8.22 | 49.67 ± 16.74 | 50.00 ± 24.49 |
| AlexNet | Imaging | 50.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 |
| DenseNet121 | Imaging | 62.00 ± 19.24 | 59.97 ± 27.79 | 66.00 ± 35.07 |
| DenseNet161 | Imaging | 69.00 ± 6.52 | 68.28 ± 8.88 | 70.00 ± 20.00 |
| DenseNet169 | Imaging | 71.00 ± 17.82 | 72.28 ± 17.44 | 76.00 ± 20.74 |
| DenseNet201 | Imaging | 63.00 ± 16.05 | 65.95 ± 16.37 | 74.00 ± 23.02 |
| GoogLeNet | Imaging | 60.00 ± 6.12 | 50.04 ± 19.69 | 48.00 ± 31.14 |
| MNasNet0-5 | Imaging | 51.00 ± 13.42 | 45.65 ± 19.37 | 44.00 ± 23.02 |
| MNasNet1-0 | Imaging | 62.00 ± 7.58 | 65.11 ± 9.94 | 74.00 ± 20.74 |
| MobileNetV2 | Imaging | 67.00 ± 17.18 | 68.61 ± 17.17 | 74.00 ± 23.02 |
| ResNet101 | Imaging | 51.00 ± 5.48 | 49.97 ± 20.44 | 60.00 ± 38.08 |
| ResNet152 | Imaging | 71.00 ± 7.42 | 63.65 ± 19.16 | 60.00 ± 30.82 |
| ResNet18 | Imaging | 64.00 ± 18.84 | 58.74 ± 29.30 | 60.00 ± 33.91 |
| ResNet34 | Imaging | 70.00 ± 11.73 | 71.71 ± 10.51 | 78.00 ± 22.80 |
| ResNet50 | Imaging | 69.00 ± 11.40 | 69.45 ± 17.58 | 78.00 ± 27.75 |
| ResNeXt101 | Imaging | 69.00 ± 7.42 | 68.95 ± 8.46 | 70.00 ± 15.81 |
| ResNeXt50 | Imaging | 63.00 ± 10.37 | 64.35 ± 19.82 | 78.00 ± 33.47 |
| ShuffleNet-v2-x0-5 | Imaging | 74.00 ± 10.25 | 74.66 ± 11.07 | 78.00 ± 16.43 |
| ShuffleNet-v2-x1-0 | Imaging | 67.00 ± 17.18 | 67.14 ± 20.74 | 72.00 ± 26.83 |
| ShuffleNet-v2-x1-5 | Imaging | 74.00 ± 13.87 | 72.3 ± 19.53 | 74.00 ± 27.02 |
| ShuffleNet-v2-x2-0 | Imaging | 73.00 ± 9.08 | 71.23 ± 11.99 | 70.00 ± 20.00 |
| VGG11 | Imaging | 50.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 |
| VGG11-BN | Imaging | 74.00 ± 16.36 | 75.03 ± 16.37 | 78.00 ± 19.24 |
| VGG13 | Imaging | 50.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 |
| VGG13-BN | Imaging | 64.00 ± 8.22 | 61.58 ± 25.24 | 72.00 ± 35.64 |
| VGG16 | Imaging | 50.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 |
| VGG16-BN | Imaging | 71.00 ± 13.42 | 72.19 ± 10.95 | 74.00 ± 13.42 |
| VGG19 | Imaging | 50.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 |
| VGG19-BN | Imaging | 59.00 ± 15.17 | 51.68 ± 32.01 | 58.00 ± 38.99 |
| Wide-ResNet101-2 | Imaging | 68.00 ± 10.95 | 69.84 ± 9.55 | 76.00 ± 20.74 |
| Wide-ResNet50-2 | Imaging | 64.00 ± 13.87 | 66.02 ± 12.41 | 70.00 ± 18.71 |
| E | Multimodal | 75.00 ± 16.20 | 77.70 ± 13.83 | 84.00 ± 15.17 |
| Multimodal | 60.00 ± 6.12 | 58.15 ± 9.40 | 58.00 ± 17.89 | |
| Multimodal | 61.00 ± 5.48 | 62.02 ± 9.58 | 66.00 ± 16.73 | |
| Multimodal | 66.58 ± 11.30 | 61.44 ± 15.13 | 62.35 ± 22.00 | |
| Multimodal | 72.00 ± 12.04 | 75.41 ± 10.68 | 83.00 ± 15.17 | |
| Multimodal | 70.94 ± 10.90 | 71.79 ± 10.21 | 74.91 ± 13.86 | |
| Multimodal | 61.00 ± 2.24 | 61.09 ± 8.11 | 64.00 ± 18.17 | |
| DeepMMSA [23] | Multimodal | 59.00 ± 6.52 | 58.07 ± 12.32 | 52.00 ± 32.71 |
| MCF [24] | Multimodal | 62.00 ± 2.74 | 61.04 ± 10.53 | 64.00 ± 23.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caruso, C.M.; Guarrasi, V.; Cordelli, E.; Sicilia, R.; Gentile, S.; Messina, L.; Fiore, M.; Piccolo, C.; Beomonte Zobel, B.; Iannello, G.; et al. A Multimodal Ensemble Driven by Multiobjective Optimisation to Predict Overall Survival in Non-Small-Cell Lung Cancer. J. Imaging 2022, 8, 298. https://doi.org/10.3390/jimaging8110298
Caruso CM, Guarrasi V, Cordelli E, Sicilia R, Gentile S, Messina L, Fiore M, Piccolo C, Beomonte Zobel B, Iannello G, et al. A Multimodal Ensemble Driven by Multiobjective Optimisation to Predict Overall Survival in Non-Small-Cell Lung Cancer. Journal of Imaging. 2022; 8(11):298. https://doi.org/10.3390/jimaging8110298
Chicago/Turabian StyleCaruso, Camillo Maria, Valerio Guarrasi, Ermanno Cordelli, Rosa Sicilia, Silvia Gentile, Laura Messina, Michele Fiore, Claudia Piccolo, Bruno Beomonte Zobel, Giulio Iannello, and et al. 2022. "A Multimodal Ensemble Driven by Multiobjective Optimisation to Predict Overall Survival in Non-Small-Cell Lung Cancer" Journal of Imaging 8, no. 11: 298. https://doi.org/10.3390/jimaging8110298
APA StyleCaruso, C. M., Guarrasi, V., Cordelli, E., Sicilia, R., Gentile, S., Messina, L., Fiore, M., Piccolo, C., Beomonte Zobel, B., Iannello, G., Ramella, S., & Soda, P. (2022). A Multimodal Ensemble Driven by Multiobjective Optimisation to Predict Overall Survival in Non-Small-Cell Lung Cancer. Journal of Imaging, 8(11), 298. https://doi.org/10.3390/jimaging8110298










