Ambiguity in Solving Imaging Inverse Problems with Deep-Learning-Based Operators
Abstract
:1. Introduction
1.1. Model-Based Mathematical Formulation
1.2. Deep-Learning-Based Formulation
1.3. Contributions of the Article
1.4. Structure of the Article
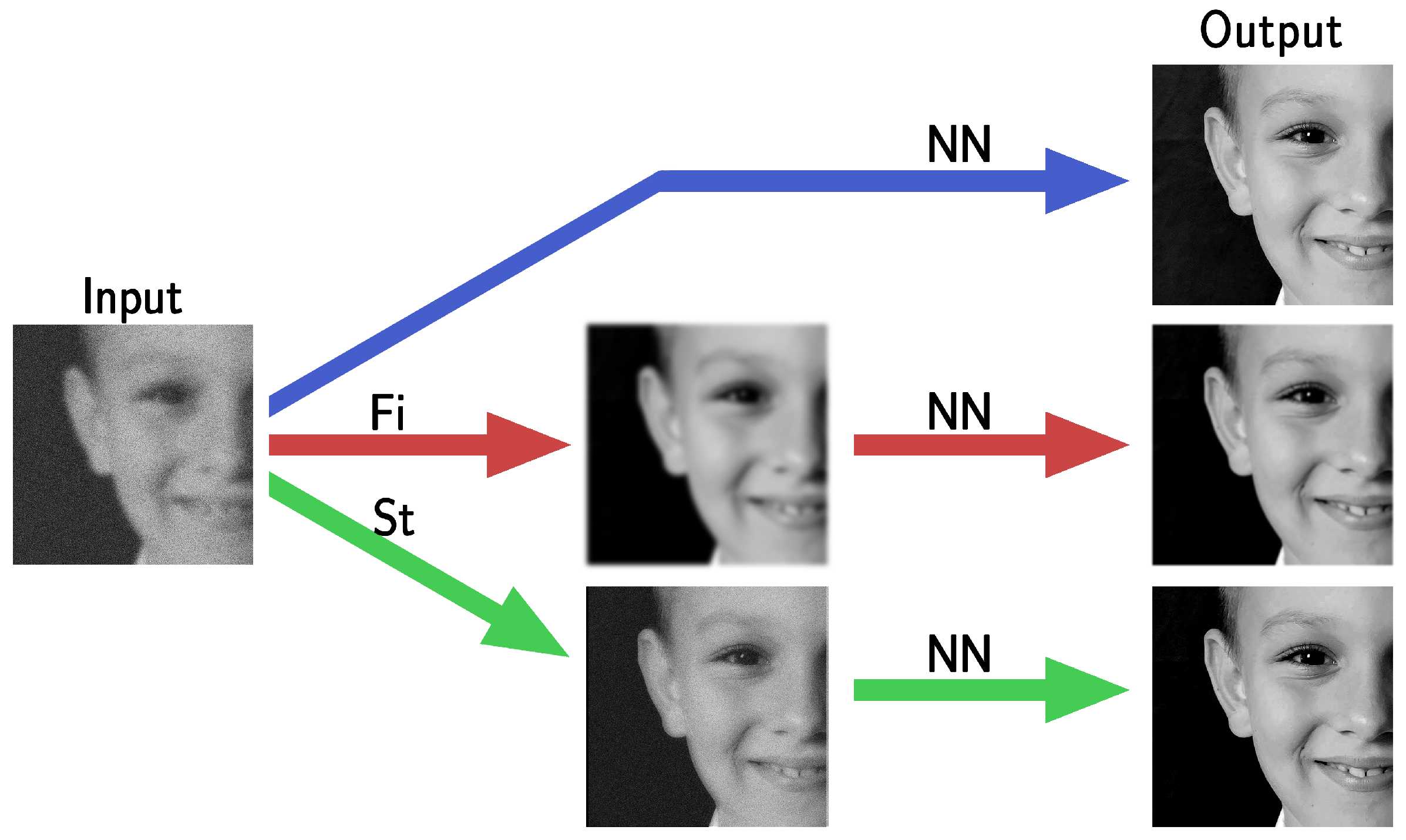
2. Solving Imaging Inverse Problems with Deep-Learning-Based Operators
3. Experimental Setting
3.1. Network Architectures
3.2. Data Set
3.3. Neural Networks Training and Testing
3.4. Robustness of the End-to-End NN Approach
4. Improving Noise-Robustness in Deep-Learning-Based Reconstructors
4.1. Stabilized Neural Network (StNN) Based on the Imaging Model
4.2. Filtered Neural Network (FiNN)
5. Results
5.1. Results of Experiment A
5.2. Results of Experiment B
5.3. Analysis with Noise Varying on the Test Set
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hansen, P.C.; Nagy, J.G.; O’leary, D.P. Deblurring Images: Matrices, Spectra, and Filtering; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Whyte, O.; Sivic, J.; Zisserman, A.; Ponce, J. Non-uniform deblurring for shaken images. Int. J. Comput. Vis. 2012, 98, 168–186. [Google Scholar] [CrossRef] [Green Version]
- Raskar, R.; Agrawal, A.; Tumblin, J. Coded exposure photography: Motion deblurring using fluttered shutter. In ACM Siggraph 2006 Papers; ACM: New York, NY, USA, 2006; pp. 795–804. [Google Scholar]
- Bertero, M.; Boccacci, P.; De Mol, C. Introduction to Inverse Problems in Imaging; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Zhang, K.; Ren, W.; Luo, W.; Lai, W.S.; Stenger, B.; Yang, M.H.; Li, H. Deep image deblurring: A survey. Int. J. Comput. Vis. 2022, 130, 2103–2130. [Google Scholar] [CrossRef]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Springer Science & Business Media: New York, NY, USA, 1996. [Google Scholar]
- Scherzer, O.; Grasmair, M.; Grossauer, H.; Haltmeier, M.; Lenzen, F. Variational Methods in Imaging; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Venkatakrishnan, S.V.; Bouman, C.A.; Wohlberg, B. Plug-and-play priors for model based reconstruction. In Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013; pp. 945–948. [Google Scholar]
- Kamilov, U.S.; Mansour, H.; Wohlberg, B. A plug-and-play priors approach for solving nonlinear imaging inverse problems. IEEE Signal Process. Lett. 2017, 24, 1872–1876. [Google Scholar] [CrossRef]
- Cascarano, P.; Piccolomini, E.L.; Morotti, E.; Sebastiani, A. Plug-and-Play gradient-based denoisers applied to CT image enhancement. Appl. Math. Comput. 2022, 422, 126967. [Google Scholar] [CrossRef]
- Hansen, P.C. Discrete Inverse Problems: Insight and Algorithms; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Lazzaro, D.; Piccolomini, E.L.; Zama, F. A nonconvex penalization algorithm with automatic choice of the regularization parameter in sparse imaging. Inverse Probl. 2019, 35, 084002. [Google Scholar] [CrossRef]
- Hradiš, M.; Kotera, J.; Zemcık, P.; Šroubek, F. Convolutional neural networks for direct text deblurring. In Proceedings of the BMVC, Swansea, UK, 7–10 September 2015; Volume 10. [Google Scholar]
- Koh, J.; Lee, J.; Yoon, S. Single-image deblurring with neural networks: A comparative survey. Comput. Vis. Image Underst. 2021, 203, 103134. [Google Scholar] [CrossRef]
- Sun, J.; Cao, W.; Xu, Z.; Ponce, J. Learning a convolutional neural network for non-uniform motion blur removal. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 769–777. [Google Scholar]
- Zhang, K.; Luo, W.; Zhong, Y.; Ma, L.; Stenger, B.; Liu, W.; Li, H. Deblurring by realistic blurring. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2737–2746. [Google Scholar]
- Gottschling, N.M.; Antun, V.; Hansen, A.C.; Adcock, B. The Troublesome Kernel—On Hallucinations, No Free Lunches and the Accuracy-Stability Trade-Off in Inverse Problems. arXiv 2020, arXiv:2001.01258. [Google Scholar]
- Amjad, J.; Sokolić, J.; Rodrigues, M.R. On deep learning for inverse problems. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Roma, Italy, 3–7 September 2018; pp. 1895–1899. [Google Scholar]
- Bastounis, A.; Hansen, A.C.; Vlačić, V. The mathematics of adversarial attacks in AI–Why deep learning is unstable despite the existence of stable neural networks. arXiv 2021, arXiv:2109.06098. [Google Scholar]
- Evangelista, D.; Nagy, J.; Morotti, E.; Piccolomini, E.L. To be or not to be stable, that is the question: Understanding neural networks for inverse problems. arXiv 2022, arXiv:2211.13692. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Chen, L.; Chu, X.; Zhang, X.; Sun, J. Simple baselines for image restoration. In Proceedings of the Computer Vision—ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Proceedings, Part VII. Springer: Berlin/Heidelberg, Germany, 2022; pp. 17–33. [Google Scholar]
- Morotti, E.; Evangelista, D.; Loli Piccolomini, E. A green prospective for learned post-processing in sparse-view tomographic reconstruction. J. Imaging 2021, 7, 139. [Google Scholar] [CrossRef] [PubMed]
- Nah, S.; Kim, T.H.; Lee, K.M. Deep Multi-Scale Convolutional Neural Network for Dynamic Scene Deblurring. In Proceedings of the CVPR, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Bishop, C.M. Training with noise is equivalent to Tikhonov regularization. Neural Comput. 1995, 7, 108–116. [Google Scholar] [CrossRef]
- Gonzalez, R.C. Digital Image Processing; Pearson Education India: Delhi, India, 2009. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 29 October–1 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]








| UNet | 0.118 | 0.085 | 0.087 | 36.572 | 2.519 | 0.878 |
| 3L-SSNet | 0.082 | 0.055 | 0.072 | 2.563 | 0.148 | 0.243 |
| NAFNet | 0.104 | 0.080 | 0.078 | 15.624 | 1.053 | 0.434 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Evangelista, D.; Morotti, E.; Piccolomini, E.L.; Nagy, J. Ambiguity in Solving Imaging Inverse Problems with Deep-Learning-Based Operators. J. Imaging 2023, 9, 133. https://doi.org/10.3390/jimaging9070133
Evangelista D, Morotti E, Piccolomini EL, Nagy J. Ambiguity in Solving Imaging Inverse Problems with Deep-Learning-Based Operators. Journal of Imaging. 2023; 9(7):133. https://doi.org/10.3390/jimaging9070133
Chicago/Turabian StyleEvangelista, Davide, Elena Morotti, Elena Loli Piccolomini, and James Nagy. 2023. "Ambiguity in Solving Imaging Inverse Problems with Deep-Learning-Based Operators" Journal of Imaging 9, no. 7: 133. https://doi.org/10.3390/jimaging9070133
APA StyleEvangelista, D., Morotti, E., Piccolomini, E. L., & Nagy, J. (2023). Ambiguity in Solving Imaging Inverse Problems with Deep-Learning-Based Operators. Journal of Imaging, 9(7), 133. https://doi.org/10.3390/jimaging9070133








