Doing for Circular Time What Shoemaker Did for Time without Change: How One Could Have Evidence That Time Is Circular Rather than Linear and Infinitely Repeating
Abstract
:1. Introduction
2. An Analogy
Shoemaker’s argument, while open to objections, is plausible and can be amplified to make it considerably more plausible. Rather than consider his case in any detail, I will strengthen his conclusion by offering the same style of argument based on a different fantasy world. Basically, both Shoemaker’s argument and mine are designed to show that talk of time without change has sense through providing a description of conditions under which we would be warranted in asserting the existence of temporal vacua.
3. The Issue
“[Line Hypothesis] and [Circle Hypothesis] are clearly incompatible theories. However, any observation that supports [Line Hypothesis] supports [Circle Hypothesis] equally and vice versa… Consider two possible worlds, A and B. We stipulate that in A time is linear and change precisely cyclical so that [Line Hypothesis] is true of this world. We stipulate that in B time is closed so that [Circle Hypothesis] is true of B. In addition we decree that the entire set of states constituting B is qualitatively identical to the sequence of states in any one [epoch] of A. Imagine that you are to be placed in one of these worlds without being told which world it is. The question then is—just what possible observation could you make to ascertain whether you are in A or in B? My suggestion has been that there is nothing you could do. While these are apparently very different kinds of worlds the question as to which world it is that you are in is empirically undecidable.”
“But is there any reason to believe that time is closed? Perhaps not. But neither, it seems, is there any reason to believe that time is linear. For all we know, both alternatives seem equally possible. Both are equally compatible with all possible empirical evidence. Furthermore, it seems unlikely that simplicity could break the tie… We may conclude, then, that closed time is a realistic possibility, which in turn appears to imply a plausible version of eternal recurrence.”
4. The Challenge
- Consult historical records and find that (O1) there was an earlier time qualitatively exactly like the present time? No, this is exactly what you would expect to find even were Line Hypothesis true. O1 supports Line Hypothesis to the same degree that it supports Circle Hypothesis.
- Consult historical records and find that (O2) numerically the same time, hosting numerically the same people participating in numerically the same events, occurred in the past? No. Though O2 would support Circle Hypothesis over Line Hypothesis, O2 is not observable4. There is no observable difference between O2 and O2*, which results from replacing each occurrence of ‘numerically the same’ with ‘qualitatively the same but numerically distinct’.
- Live long enough to see an event, e.g., a particular basketball game, that you remember seeing earlier in your life and observe that (O3) game1 is earlier than game2, and game1 = game2? No. O3 would support Circle Hypothesis over Line Hypothesis, but O3 is not observable. There is no observable difference between O3 and O3*, which stands to O3 as O2* stands to O2.
- Live a life that has no beginning or end, no birth or death, but rather a life whose topology and metric matches time itself, and come to believe, on the basis of introspection and memory, that (O4) you had this particular token experience some years ago? No. O4 would favor Circle Hypothesis, but neither introspection nor memory could justify the belief that the experience that you had some years ago was this token experience, as opposed to a numerically distinct qualitative duplicate.
- Leave a trail of breadcrumbs and eventually observe that (O5) you have returned to the time and approximate place of your earlier dropping of a breadcrumb? No. See #3 above.
5. Other Routes to Knowledge
5.1. Evidence That Is Not Ordinary Empirical Evidence
PII: Necessarily, if x and y have exactly the same purely qualitative properties, then x = y.
5.2. Weir’s Indeterministic Case
“An empirical consideration has recently been suggested by Susan Weir. We should first need some evidence to narrow the correct choice of descriptions down to these two, the circular and repetitive descriptions. We should need evidence, that is, that everything had happened in exactly the same way before. Perhaps inhabitants of circular time could remember things as having happened in exactly the same way before and even remember remembering. But we must be careful that this first piece of evidence is not of a totally deterministic character, suggesting that everything happens inevitably. For the second piece of evidence we want is something that suggests that a few things at least are not required to happen as they do. Taking those two pieces of evidence together, we could reason that it was not likely that world history would repeat itself exactly again and again, unless it was actually required to do so. Since the evidence of indeterminism would show that it was not required to do so, we should have reason to side against the hypothesis of repetition and to prefer the hypothesis of a single circle of time.”
6. The Main Argument
- (i)
- Either Line Hypothesis is true or Circle Hypothesis is true11.
- (ii)
- All F particles have a duration of exactly 12,000 years12.
- (iii)
- o is an F particle.
- (iv)
- o never begins to exist, never ceases to exist, and exists at all times; it has a career that is topologically and metrically like time as a whole. If Line Hypothesis is true, then o has an infinite duration, not a duration of exactly 12,000 years. If Circle Hypothesis is true, then o has a duration of exactly 12,000 years, not an infinite duration14.
7. Objections and Replies
- (i)
- Either Line Hypothesis is true or Circle Hypothesis is true.
- (ii)
- An F particle begins to exist in a region r at a time t if and only if two G particles collide there and then.
- (iii)
- An F particle ceases to exist in a region r at a time t if and only if two G particles are emitted there and then.
- (iv)
- For each F particle x, the duration-in-years of x is equal to 12,000 + n, where n is x’s ‘mileage’, the total spatial distance it has traveled through absolute space, in thousands of astronomical units (kau) (1 kau = 1000 au.).
- (v)
- No F particles move faster than 0.9 kau per year.
- (vi)
- o is an F particle.
- (vii)
- o is always absolutely at rest.
- (viii)
- o never begins to exist, never ceases to exist, and exists at all times; it has a career that is topologically and metrically like time as a whole. If Line Hypothesis is true, then o has an infinite duration, not a duration of exactly 12,000 years. If Circle Hypothesis is true, then o has a duration of exactly 12,000 years, not an infinite duration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1. | We model this speech on a passage from Newton-Smith [2] that we quote below. |
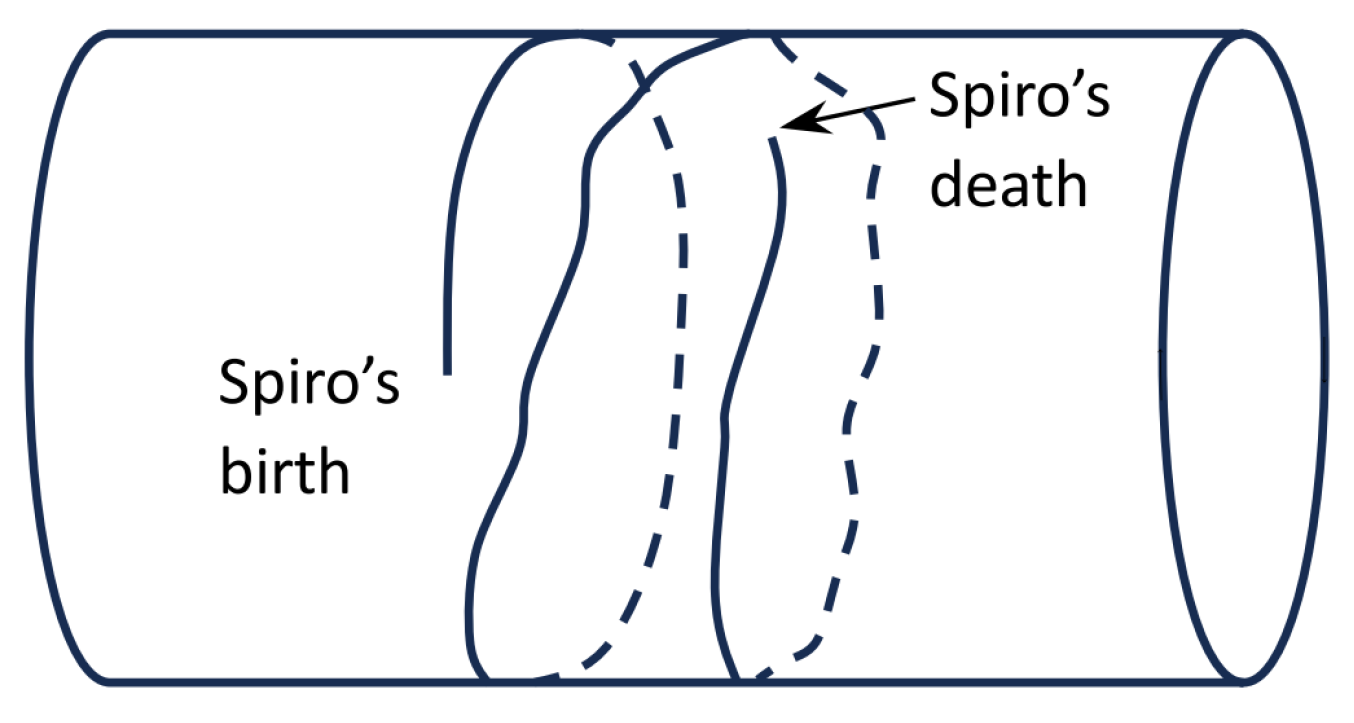
| 2. | By a cylinder of time, we mean a cylindrical spacetime in which the temporal dimension is finite and closed, forming a loop. Figure 2 represents such a spacetime. To interpret Figure 2, start with a circle, where the circle represents circular time and where each point on the circle represents an instant. Now, replace each point on that circle with a line, where each line represents all of three-dimensional space at a particular instant. The result is (or is analogous to) a cylinder. Thanks to an anonymous reviewer for prompting us to clarify this expression. |
| 3. | Lewis [8,9] distinguishes between external time (time itself) and the personal time of a particular person (or other object), which is, roughly, what would be measured by the person’s wristwatch. In a relativistic version of this case, Spiro’s worldline would have a proper time length of 70 years, whereas there would be inertial closed timelike curves whose proper time length is only 30 years. A timelike curve is a spacetime path that could be the worldline of an object with mass, always traveling at less than light speed. A closed timelike curve forms a loop. On the distinction between relativistic proper time and Lewisian personal time, in connection with relativistic spacetimes whose temporal dimension forms a loop, see Gilmore [10] and Eagle [11]. |
| 4. | Similar points have been made in connection with Nietzsche’s theory of eternal recurrence. See especially Jenkins [13] (p. 209–213). |
| 5. | What about the other way around? To acquire evidence that favors Line Hypothesis over Circle Hypothesis, could you observe that (O6) your birth occurred, and before that an exactly similar birth occurred, and before that an exactly similar birth occurred, and so on? No. O6 may be observable, but it supports Circle Hypothesis to the same degree that it supports Line Hypothesis. Could you observe that (O7) your birth occurred, and before that an exactly similar but numerically distinct birth occurred, and . . . ? No. O7 is not observable. Perhaps one could have other kinds of ordinary empirical evidence that would favor Line Hypothesis over Circle Hypothesis. On this question we take no stand. |
| 6. | Typically, one’s evidence for the disjunction of Circle Hypothesis (C) and Line Hypothesis (L) will be empirical. Strictly speaking, our focus is on arguments for the conditional claim: (C ∨ L)→C. When an argument for this conditional claim relies on an empirical premise, we classify the argument as empirical, and when it only relies on a priori premises, we classify it as a priori. Mutatis mutandis for arguments for (C ∨ L)→L. |
| 7. | Grünbaum [14] (p. 202) writes that ‘there is a rather simple way of seeing how manlike beings might discover that the cosmic time of their universe is closed, despite the seriality of the local segment of cosmic time accessible to their experience’. He then suggests that they might acquire empirical evidence for the disjunction of Circle Hypothesis and Line Hypothesis and then invoke PII to rule out Line Hypothesis. We classify this as an a priori argument for Circle Hypothesis on the grounds that Grünbaum’s argument for (C ∨ L)→C is a priori. See note 6. |
| 8. | |
| 9. | One might suggest that the notion of ordinary empirical evidence can be characterized simply as non-testimonial empirical evidence. We have doubts about this suggestion. First, ordinary empirical evidence often involves testimony. Second, and conversely, we might be able to describe cases in which we have non-testimonial evidence that is relevantly oracle-like and therefore not ordinary empirical evidence. We could discover a natural phenomenon that, perhaps as a matter of weird, brute fact, in effect, functions as an oracle. Suppose we discover that there is a tree with the following feature: if one writes a question on a piece of paper, crumples it up, and stuffs it into a hole in its trunk, the tree delivers an answer one year later, which can be read off a core sample of its tree rings when those rings are decoded according to a simple rule. We could then acquire evidence of the tree’s reliability in a straightforward way. Such a tree might yield evidence that Circle Hypothesis is true, and this might count as non-testimonial evidence. But such evidence would still be relevantly similar to evidence from an oracle in that it would not be ordinary empirical evidence. |
| 10. | Sorabji [5] (p. 180) states that Malcolm Murchison suggested a similar idea in conversation with Sorabji. |
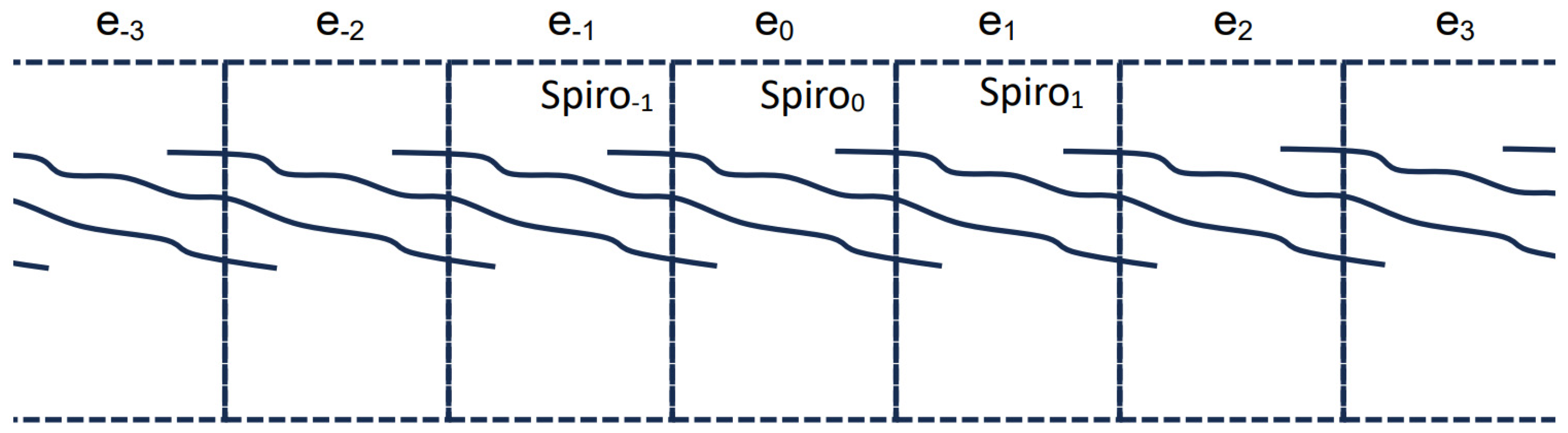
| 11. | Newton-Smith seems willing to grant that this is possible, somehow. The details can be filled in in various ways. Perhaps, on your hard-drive, you have snapshots, of various resolutions and quality, of the whole internet taken at 1 s intervals. You have 12,000,000 years worth of such snapshots, divided into 1000 volumes, arranged from the most pristine to the most corrupted. Each volume covers a 12,000-year epoch of the internet. All evidence indicates that the epoch, call it e0, running from the present time back to 12,000 years ago, is a perfect duplicate of the immediately preceding 12,000-year epoch, call it e-1, and that e-1 is a perfect duplicate of the 12,000-year epoch, call it e-2, immediately preceding it, and so on back to e−999, though at that point, the files are highly corrupted and unreliable. Likewise, as time passes, the pattern continues to play out as one would expect: the snapshots of the internet taken tomorrow match those taken 12,000 years earlier, 24,000 years earlier, 36,000 years earlier, and so on for 1000 iterations. Your computer and hard-drive might be objects that have persisted through an interval that is at least 12,000,000 years long and contains 1000 duplicate epochs, or they might be objects that have ‘wound around’ the 12,000-year-long circle of time at least 1000 times, having, at each moment, 1000 different token representations of the same 12,000-year epoch. |
| 12. | That an epoch, or circular time itself, has a duration of 12,000 years does not guarantee that a particle will not last longer than 12,000 years; see the discussion in Section 3. |
| 13. | For neatness, let us suppose that each F particle, or its corresponding worldline, is topologically open at its beginning and topologically closed at its end, if it has a beginning and end. |
| 14. | If Circle Hypothesis is true, o never begins to exist and never ceases to exist because its career is a loop, i.e., because it is an ‘object loop’, not because it winds around circular time (in the way discussed in Section 3) infinitely into o’s personal past and infinitely into o’s personal future. Regarding object loops, see Sorabji [5] (pp. 165–188), [10] (pp. 320–322), Hanley [19], Gilmore [15,20], Eagle [16,21], and Lewis [9] (pp. 35–37). |
| 15. | This dialectic precisely mirrors an aspect of Shoemaker [6] (p. 368). |
| 16. | An anonymous reviewer raised a related concern, framed as an inductive argument to support the hypothesis that there are two different kinds of F particles, finite and infinite: “Now, in the 12,000 year history of the universe, surely the scientific understanding developed. First, mass was discovered, later charge, then spin,… As such, the scientists of this world would have thought that all particles of the same mass were of the same sort until they discovered charge, then they could distinguish different classes. Then they later discovered spin, and so what were thought to be the members of a single category were again divided. So, now we have F particles with a finite life and F particles with an infinite life. Just another similar step in the progress of science. Wouldn’t we thus have empirical evidence that disallows the inference to circular time?”. We reply first by conceding that there are worlds, similar to our F particle world, in which some observers have inductive evidence for believing that there are both finite and infinite F particles. However, we can add further detail to our case to guarantee that no one in that case has such evidence. We can stipulate that the evidence indicates that all particles with the same mass also have the same charge, the same spin, etc., so that there are no inductive reasons to expect F particles to subdivide into two natural subspecies, finite and infinite. Given all of this, the evidence does not directly support the hypothesis that some F particles are infinite in duration. Rather, it directly supports the hypothesis that some F particles exist at all times, never begin or cease to exist, and have a topology and duration that matches the topology and duration of time as whole. It does not follow from this that some F particles are infinite in duration. We thank the reviewer for pressing us to address this point. |
References
- Quine, W.V. Comments on Newton-Smith. Analysis 1979, 39, 66–67. [Google Scholar] [CrossRef]
- Newton-Smith, W.H. The Structure of Time; Routledge & Kegan Paul: London, UK, 1980. [Google Scholar]
- Bergström, L. Death and Eternal Recurrence. In The Oxford Handbook of the Philosophy of Death; Bradley, B., Feldman, F., Johansson, J., Eds.; Oxford University Press: Oxford, UK, 2013; pp. 167–185. [Google Scholar]
- Weir, S. An Enquiry into the Possibility and Implications of a Closed Temporal Topology. Ph.D. Thesis, University of Bristol, Bristol, UK, 1986. [Google Scholar]
- Sorabji, R. Matter, Space, and Motion: Theories in Antiquity and Their Sequel; Cornell University Press: Ithaca, NY, USA, 1988. [Google Scholar]
- Shoemaker, S. Time without Change. J. Philos. 1969, 66, 363–381. [Google Scholar] [CrossRef]
- Lewis, D. On the Plurality of Worlds; Blackwell: Oxford, UK, 1986. [Google Scholar]
- Lewis, D. The Paradoxes of Time Travel. Am. Philos. Q. 1976, 13, 145–152. [Google Scholar]
- Lewis, D. The Paradoxes of Time Travel: The Gavin David Young Lectures at the University of Adelaide. In Philosophical Manuscripts; Janssen-Lauret, F., MacBride, F., Eds.; Oxford University Press: Oxford, UK, 2023; pp. 1–56. [Google Scholar]
- Gilmore, C. Coinciding Objects and Duration Properties: Reply to Eagle. In Oxford Studies in Metaphysics; Zimmerman, D.W., Ed.; Oxford University Press: Oxford, UK, 2010; Volume 5, pp. 95–111. [Google Scholar]
- Eagle, A. Duration in Relativistic Spacetime. In Oxford Studies in Metaphysics; Zimmerman, D.W., Ed.; Oxford University Press: Oxford, UK, 2010; Volume 5, pp. 113–117. [Google Scholar]
- Sorabji, R. Self: Ancient and Modern Insights about Individuality, Life, and Death; University of Chicago Press: Chicago, IL, USA, 2006. [Google Scholar]
- Jenkins, S.D. Time and Personal Identity in Nietzsche’s Theory of Eternal Recurrence. Philos. Compass 2012, 7, 208–217. [Google Scholar] [CrossRef]
- Plantinga, A. Is Belief in God Properly Basic? Noûs 1981, 15, 41–51. [Google Scholar] [CrossRef]
- Mellor, D.H. Real Time; Cambridge University Press: Cambridge, UK, 1981. [Google Scholar]
- Weir, S. Closed Time and Causal Loops: A Defence against Mellor. Analysis 1988, 48, 203–209. [Google Scholar] [CrossRef]
- Grünbaum, A. Philosophical Problems of Space and Time; Alfred A. Knopf: New York, NY, USA, 1963. [Google Scholar]
- Loeb, P. The Death of Nietzsche’s Zarathustra; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Hanley, R. No end in sight: Causal loops in philosophy, physics and fiction. Synthese 2004, 141, 123–152. [Google Scholar] [CrossRef]
- Gilmore, C. Time Travel, Coinciding Objects, and Persistence. In Oxford Studies in Metaphysics; Zimmerman, D.W., Ed.; Oxford University Press: Oxford, UK, 2007; Volume 3, pp. 177–198. [Google Scholar]
- Eagle, A. Location and Perdurance. In Oxford Studies in Metaphysics; Zimmerman, D.W., Ed.; Oxford University Press: Oxford, UK, 2010; Volume 5, pp. 53–94. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gilmore, C.; Kierland, B. Doing for Circular Time What Shoemaker Did for Time without Change: How One Could Have Evidence That Time Is Circular Rather than Linear and Infinitely Repeating. Philosophies 2024, 9, 92. https://doi.org/10.3390/philosophies9040092
Gilmore C, Kierland B. Doing for Circular Time What Shoemaker Did for Time without Change: How One Could Have Evidence That Time Is Circular Rather than Linear and Infinitely Repeating. Philosophies. 2024; 9(4):92. https://doi.org/10.3390/philosophies9040092
Chicago/Turabian StyleGilmore, Cody, and Brian Kierland. 2024. "Doing for Circular Time What Shoemaker Did for Time without Change: How One Could Have Evidence That Time Is Circular Rather than Linear and Infinitely Repeating" Philosophies 9, no. 4: 92. https://doi.org/10.3390/philosophies9040092
APA StyleGilmore, C., & Kierland, B. (2024). Doing for Circular Time What Shoemaker Did for Time without Change: How One Could Have Evidence That Time Is Circular Rather than Linear and Infinitely Repeating. Philosophies, 9(4), 92. https://doi.org/10.3390/philosophies9040092




