Thermoluminescence as a Research Tool to Investigate Luminescence Mechanisms
Abstract
:1. Introduction
2. Theoretical Background
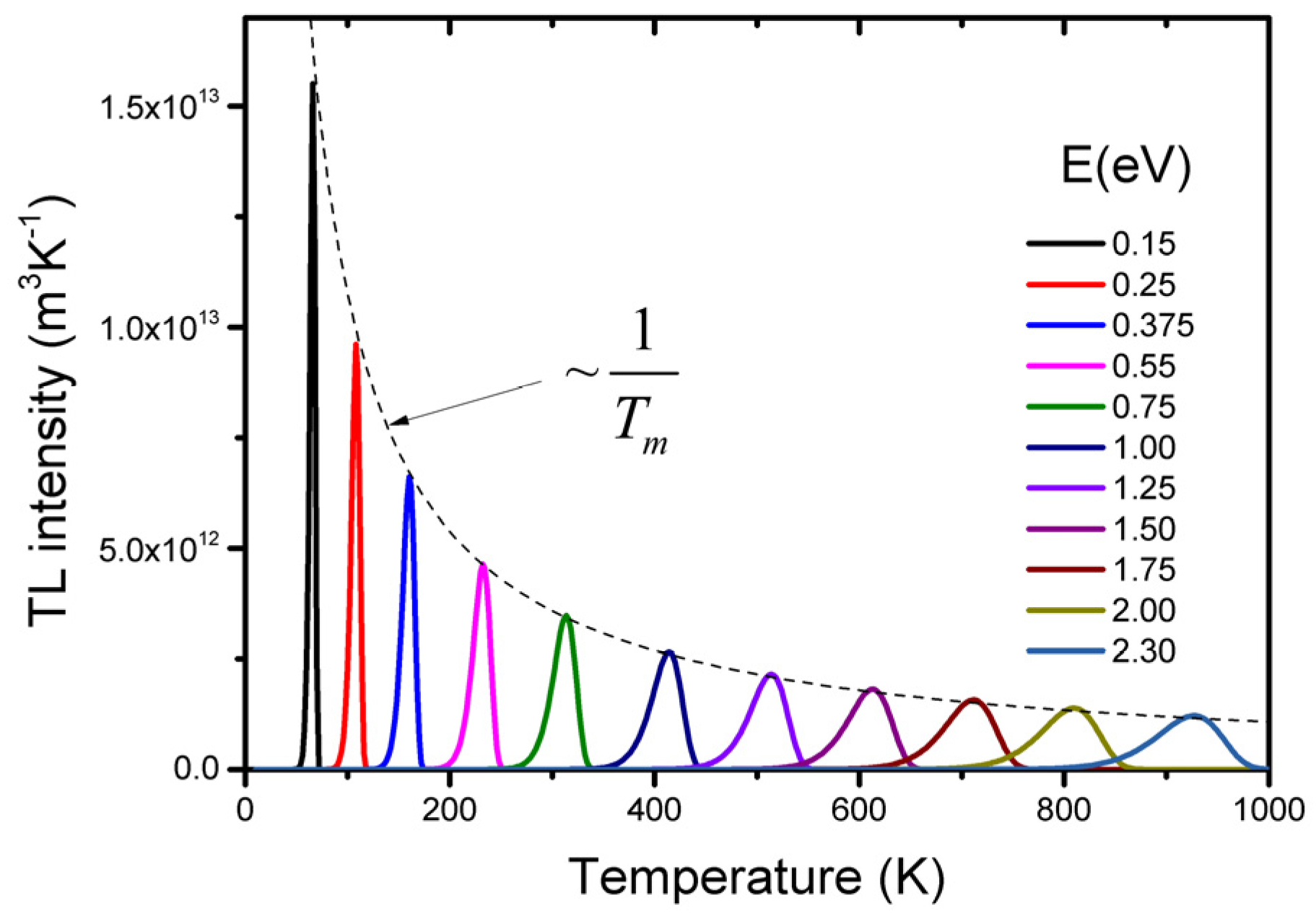
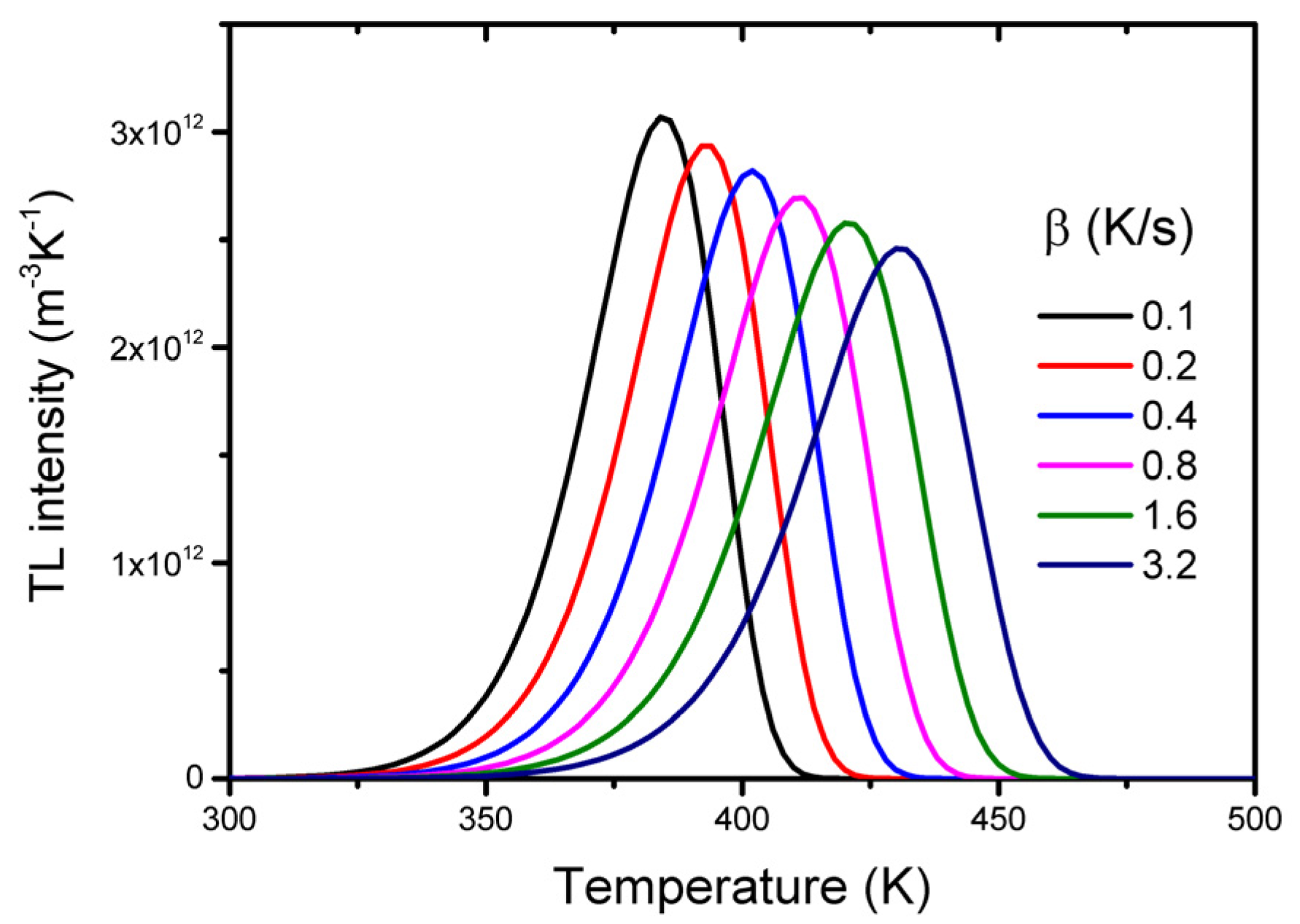
2.1. Simple Model and Characteristics of TSL
2.2. Deviations from the Simple Model
2.3. Methods for Extracting Trap Parameters
3. Instrumentation
4. Thermoluminescence as a Research Tool
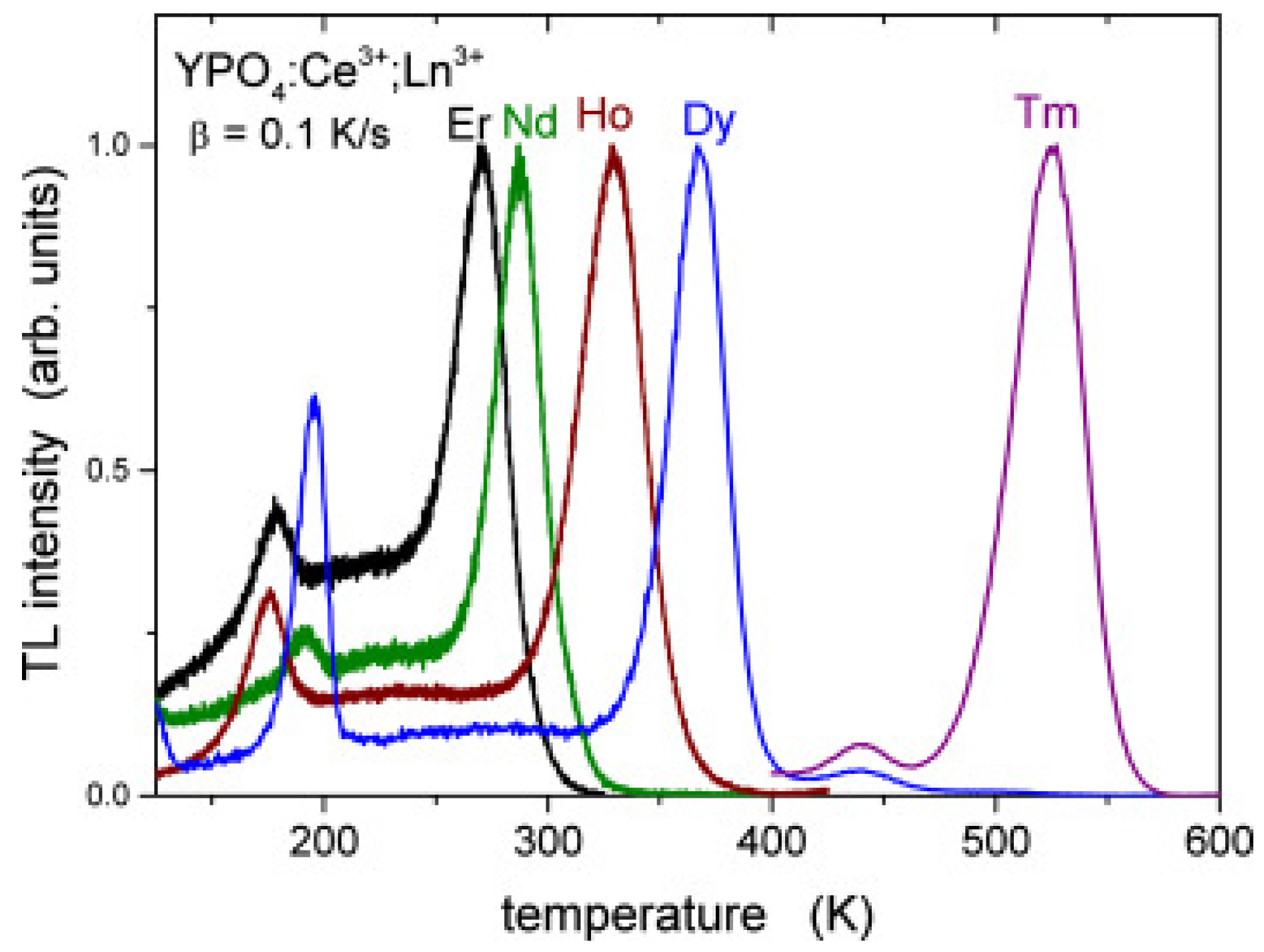
4.1. Energy Level Positions
4.2. Persistent Luminescence
4.3. Band Gap Engineering
4.4. Tunnelling
4.5. Thermal Quenching
4.6. Photosynthesis
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Daniels, F.; Boyd, C.; Saunders, D. Thermoluminescence as a Research Tool. Science 1953, 117, 343–349. [Google Scholar] [CrossRef] [PubMed]
- Martini, M.; Meinardi, F. Thermally stimulated luminescence: New perspectives in the study of defects in solids. La Riv. del Nuovo Cim. 1997, 20, 1–71. [Google Scholar] [CrossRef]
- Murthy, K.V.R. Thermoluminescence and its Applications: A Review. Defect Diffus. Forum 2013, 347, 35–73. [Google Scholar] [CrossRef]
- Mihóková, E.; Nikl, M. Luminescent materials: Probing the excited state of emission centers by spectroscopic methods. Meas. Sci. Technol. 2015, 26, 12001. [Google Scholar] [CrossRef]
- Bos, A.J.J. Theory of thermoluminescence. Radiat. Meas. 2006, 41, 45–56. [Google Scholar] [CrossRef]
- McKeever, S.W.S. Thermoluminescence of Solids; Cambridge University Press: Cambridge, UK, 1988; ISBN 0521368111. [Google Scholar]
- Chen, R.; McKeever, S.W.S. Theory of Thermoluminescence and Related Phenomena; World Scientific: Singapore, 1997; ISBN 0810222955. [Google Scholar]
- Chen, R.; Pagonis, V. Thermally and Optically Stimulated Luminescence—A Simulation Approach; John Wiley: Chichester, UK, 2011; ISBN 978-0-470-74927-2. [Google Scholar]
- Sunta, C.M. Unraveling Thermoluminescence; Springer Series in Materials Science; Springer: New Delhi, India, 2015; Volume 202, ISBN 978-81-322-1939-2. [Google Scholar]
- Randall, J.T.; Wilkins, M.H.F. The Phosphorescence of Various Solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 1945, 184, 347–364. [Google Scholar] [CrossRef]
- Randall, J.T.; Wilkins, M.H.F. Phosphorescence and Electron Traps. II. The Interpretation of Long-Period Phosphorescence. Proc. R. Soc. A Math. Phys. Eng. Sci. 1945, 184, 390–407. [Google Scholar] [CrossRef]
- Randall, J.; Wilkins, M. Phosphorescence and Electron Traps I. The Study of Trap Distributions. Proc. R. Soc. A Math. Phys. Eng. Sci. 1945, 184, 366–389. [Google Scholar] [CrossRef]
- Hoogenboom, J.E.; De Vries, W.; Dielhof, J.B.; Bos, A.J.J. Computerized analysis of glow curves from thermally activated processes. J. Appl. Phys. 1988, 64, 3193–3200. [Google Scholar] [CrossRef]
- Urbach, F. Zur Lumineszenz der Alkalihalogenide. Sitzungsberichte Akad. der Wiss. Wien 1930, 139, 363–372. [Google Scholar] [CrossRef]
- Murthy, K.V.R.; Virk, H.S. Luminescence Phenomena: An Introduction. Defect Diffus. Forum 2014, 347, 1–34. [Google Scholar] [CrossRef]
- Pagonis, V.; Kitis, G. Prevalence of first-order kinetics in thermoluminescence materials: An explanation based on multiple competition processes. Phys. Status Solidi Basic Res. 2012, 249, 1590–1601. [Google Scholar] [CrossRef]
- Pagonis, V.; Morthekai, P.; Kitis, G. Kinetic analysis of thermoluminescence glow curves in feldspar: Evidence for a continuous distribution of energies. Geochronometria 2014, 41, 168–177. [Google Scholar] [CrossRef]
- Gómez-Ros, J.M.; Correcher, V.; García-Guinea, J.; Delgado, A. Evolution of the trapped charge distribution due to trap emptying processes in a natural aluminosilicate. Radiat. Prot. Dosim. 2006, 119, 93–97. [Google Scholar] [CrossRef] [PubMed]
- Correcher, V.; Gomez-Ros, J.M.; Garcia-Guinea, J.; Lis, M.; Sanchez-Muñoz, L. Calculation of the activation energy in a continuous trap distribution system of a charoite silicate using initial rise and TL glow curve fitting methods. Radiat. Meas. 2008, 43, 269–272. [Google Scholar] [CrossRef]
- Srivastava, J.K.; Supe, S.J. Trap distribution analysis for thermoluminescence of CaSO4:Dy. J. Phys. D Appl. Phys. 1983, 16, 1813–1818. [Google Scholar] [CrossRef]
- Srivastava, J.K.; Supe, S.J. The thermoluminescence characterisation of Li2B4O7 doped with Cu. J. Phys. D Appl. Phys. 1989, 22, 1537–1543. [Google Scholar] [CrossRef]
- Whitley, V.H.; Larsen, N.A.; McKeever, S.W.S. Determination of ionisation energies and attempt-to-escape factors using thermally stimulated conductivity. Radiat. Prot. Dosim. 2002, 100, 147–152. [Google Scholar] [CrossRef]
- Botterman, J.; Smet, P.F. Persistent phosphor SrAl2O4:Eu,Dy in outdoor conditions: Saved by the trap distribution. Opt. Express 2015, 23, A868–A881. [Google Scholar] [CrossRef] [PubMed]
- Aitasalo, T.; Hölsä, J.; Jungner, H.; Krupa, J.-C.; Lastusaari, M.; Legendziewicz, J.; Niittykoski, J. Effect of temperature on the luminescence processes of SrAl2O4:Eu2+. Radiat. Meas. 2004, 38, 727–730. [Google Scholar] [CrossRef]
- Van Den Eeckhout, K.; Bos, A.J.J.; Poelman, D.; Smet, P.F. Revealing trap depth distributions in persistent phosphors. Phys. Rev. B-Condens. Matter Mater. Phys. 2013, 87, 1–11. [Google Scholar] [CrossRef]
- Pan, Z.; Lu, Y.-Y.; Liu, F. Sunlight-activated long-persistent luminescence in the near-infrared from Cr3+-doped zinc gallogermanates. Nat. Mater. 2011, 11, 58–63. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, Y.; Ueda, J.; Tanabe, S.; Dorenbos, P. Band-gap variation and a self-redox effect induced by compositional deviation in ZnxGa2O3+x:Cr3+ persistent phosphors. J. Mater. Chem. C 2014, 2, 5502. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Wang, Y.; Chen, W.; Zeng, W.; Han, S.; Li, G.; Li, Y. Controlling and revealing the trap distributions of Ca6BaP4 O17:Eu2+,R3+ (R = Dy, Tb, Ce, Gd, Nd) by codoping different trivalent lanthanides. J. Mater. Chem. C 2015, 3, 11212–11218. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Liu, Y.; Dong, H.; Lei, B.; Zheng, M.; Xiao, Y.; Peng, M.; Wang, J. Insights into luminescence quenching and detecting trap distribution in Ba2Si5N8:Eu2+ phosphor with comprehensive considerations of temperature-dependent luminescence behaviors. J. Mater. Chem. C 2015, 3, 9572–9579. [Google Scholar] [CrossRef]
- Brylew, K.; Drozdowski, W.; Wojtowicz, A.J.; Kamada, K.; Yoshikawa, A. Studies of low temperature thermoluminescence of GAGG:Ce and LuAG:Pr scintillator crystals using the Tmax-Tstop method. J. Lumin. 2014, 154, 452–457. [Google Scholar] [CrossRef]
- Lecointre, A.; Bessière, A.; Bos, A.J.J.; Dorenbos, P.; Viana, B.; Jacquart, S. Designing a red persistent luminescence phosphor: The example of YPO4:Pr3+,Ln3+ (Ln = Nd, Er, Ho, Dy). J. Phys. Chem. C 2011, 115, 4217–4227. [Google Scholar] [CrossRef]
- Luo, H.; Bos, A.J.J.; Dorenbos, P. Charge Carrier Trapping Processes in RE2O2S (RE = La, Gd, Y and Lu). J. Phys. Chem. C 2017. [Google Scholar] [CrossRef] [PubMed]
- Hoogenstraaten, W. Electron traps in ZnS phosphors. Philips Res. Rep. 1958, 13, 515–693. [Google Scholar]
- Kitis, G.; Tuyn, J.W.N. A simple method to correct for the temperature lag in TL glow-curve measurements. J. Phys. D. Appl. Phys. 1998, 31, 2065–2073. [Google Scholar] [CrossRef]
- Piters, T.M.; Bos, A.J.J. Effects of non-ideal heat transfer on the glow curve in thermoluminescence experiments. J. Phys. D Appl. Phys. 1999, 27, 1747–1756. [Google Scholar] [CrossRef]
- Garlick, G.F.J.; Gibson, A.F. The Electron Trap Mechanism of Luminescence in Sulphide and Silicate Phosphors. Proc. Phys. Soc. 1948, 60, 574–590. [Google Scholar] [CrossRef]
- Pagonis, V.; Kitis, G.; Furetta, C. Numerical and Practical Exercises in Thermoluminescence; Springer: New York, NY, USA, 2006; ISBN 0-387-26063-3. [Google Scholar]
- Chen, R.; Haber, G.A. Calculation of glow curves’ activation energies by numerical initial rise method. Chem. Phys. Lett. 1968, 2, 483–485. [Google Scholar] [CrossRef]
- Horowitz, Y.S.; Yossin, D. Computerized Glow curve deconvolution: Application to thermoluminescence dosimetry. Radiat. Prot. Dosim. 1995, 60, 1–114. [Google Scholar]
- Van Dijk, J.W.E. Thermoluminescence glow curve deconvolution and its statistical analysis using the flexibility of spreadsheet programs. Radiat. Prot. Dosim. 2006, 119, 332–338. [Google Scholar] [CrossRef] [PubMed]
- Stadtmann, H.; Wilding, G. Glow curve deconvolution for the routine readout of LiF:Mg,Ti thermoluminescent detectors. Radiat. Meas. 2017. [Google Scholar] [CrossRef]
- Chen, R.; Pagonis, V.; Lawless, J.L. Evaluated thermoluminescence trapping parameters-What do they really mean? Radiat. Meas. 2016, 91, 21–27. [Google Scholar] [CrossRef]
- Chen, R.; Pagonis, V. The role of simulations in the study of thermoluminescence (TL). Radiat. Meas. 2014, 71, 8–14. [Google Scholar] [CrossRef]
- Rappaport, F.; Lavergne, J. Thermoluminescence: Theory. Photosynth. Res. 2009, 101, 205–216. [Google Scholar] [CrossRef] [PubMed]
- Repetto, G.; Zurita, J.L.; Roncel, M.; Ortega, J.M. Thermoluminescence as a complementary technique for the toxicological evaluation of chemicals in photosynthetic organisms. Aquat. Toxicol. 2015, 158, 88–97. [Google Scholar] [CrossRef] [PubMed]
- Ducruet, J.M.; Vass, I. Thermoluminescence: Experimental. Photosynth. Res. 2009, 101, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Townsend, P.D.; Kirsh, Y. Spectral measurement during thermoluminescence—An essential requirement. Contemp. Phys. 1989, 30, 337–354. [Google Scholar] [CrossRef]
- Piters, T.M.; Meulemans, W.H.; Bos, A.J.J. An automated research facility for measuring thermoluminescence emission spectra using an optical multichannel analyzer. Rev. Sci. Instrum. 1993, 64, 109. [Google Scholar] [CrossRef]
- Rhodes, M.W.; Wanwilairat, S.; Vilaithong, T.; Hoffmann, W. Low cost high resolution thermoluminescence spectrometer. Rev. Sci. Instrum. 2000, 71, 2053. [Google Scholar] [CrossRef]
- Bos, A.J.J.; Winkelman, A.J.M.; Le Masson, N.J.M.; Sidorenko, A.V.; Van Eijk, C.W. A TL/OSL Emission Spectrometer Extension of the. Radiat. Meas. 2002, 101, 111–114. [Google Scholar]
- Yoshizumi, M.T.; Caldas, L.V.E. TL emission spectra measurements using a spectrometer coupled to the Risoe TL/OSL reader. Radiat. Phys. Chem. 2014, 104, 292–296. [Google Scholar] [CrossRef]
- Bos, A.J.J.; Dorenbos, P.; Bessière, A.; Viana, B. Lanthanide energy levels in YPO4. Radiat. Meas. 2008, 43, 222–226. [Google Scholar] [CrossRef]
- Bos, A.J.J.; Van Duijvenvoorde, R.M.; Van Der Kolk, E.; Drozdowski, W.; Dorenbos, P. Thermoluminescence excitation spectroscopy: A versatile technique to study persistent luminescence phosphors. J. Lumin. 2011, 131, 1465–1471. [Google Scholar] [CrossRef]
- Thomsen, K.J.; Bøtter-Jensen, L.; Jain, M.; Denby, P.M.; Murray, A.S. Recent instrumental developments for trapped electron dosimetry. Radiat. Meas. 2008, 43, 414–421. [Google Scholar] [CrossRef]
- Lapp, T.; Jain, M.; Thomsen, K.J.; Murray, A.S.; Buylaert, J.P. New luminescence measurement facilities in retrospective dosimetry. Radiat. Meas. 2012, 47, 803–808. [Google Scholar] [CrossRef]
- Lapp, T.; Kook, M.; Murray, A.S.; Thomsen, K.J.; Buylaert, J.P.; Jain, M. A new luminescence detection and stimulation head for the Risø TL/OSL reader. Radiat. Meas. 2014, 81, 178–184. [Google Scholar] [CrossRef] [Green Version]
- Richter, D.; Richter, A.; Dornich, K. Lexsyg—A new system for luminescence research. Geochronometria 2013, 40, 220–228. [Google Scholar] [CrossRef]
- Richter, D.; Richter, A.; Dornich, K. Lexsyg smart—A luminescence detection system for dosimetry, material research and dating application. Geochronometria 2015, 42, 202–209. [Google Scholar] [CrossRef]
- Richter, D.; Mittelstraß, D.; Kreutzer, S.; Pintaske, R.; Dornich, K.; Fuchs, M. A new fully integrated X-ray irradiator system for dosimetric research. Appl. Radiat. Isot. 2016, 112, 122–130. [Google Scholar] [CrossRef] [PubMed]
- Dorenbos, P. Systematic behaviour in trivalent lanthanide charge transfer energies. J. Phys. Condens. Matter 2003, 15, 8417–8434. [Google Scholar] [CrossRef]
- Dorenbos, P. A Review on How Lanthanide Impurity Levels Change with Chemistry and Structure of Inorganic Compounds. ECS J. Solid State Sci. Technol. 2013, 2, R3001–R3011. [Google Scholar] [CrossRef]
- Dorenbos, P. The electronic structure of lanthanide doped compounds with 3d, 4d, 5d, or 6d conduction band states. J. Lumin. 2014, 151, 224–228. [Google Scholar] [CrossRef]
- Dorenbos, P. Charge transfer bands in optical materials and related defect level location. Opt. Mater. (Amst) 2017, 69, 8–22. [Google Scholar] [CrossRef]
- Dorenbos, P. Valence stability of lanthanide ions in inorganic compounds. Chem. Mater. 2005, 17, 6452–6456. [Google Scholar] [CrossRef]
- Bos, A.J.J.; Dorenbos, P.; Bessire, A.; Lecointre, A.; Bedu, M.; Bettinelli, M.; Piccinelli, F. Study of TL glow curves of YPO4 double doped with lanthanide ions. Radiat. Meas. 2011, 46, 1410–1416. [Google Scholar] [CrossRef]
- You, F.; Bos, A.J.J.; Shi, Q.; Huang, S.; Dorenbos, P. Thermoluminescence investigation of donor (Ce3+, Pr3+, Tb3+) acceptor (Eu+, Yb3+) pairs in Y3Al5O12. Phys. Rev. B-Condens. Matter Mater. Phys. 2012, 85, 1–7. [Google Scholar] [CrossRef]
- Krumpel, A.H.; Bos, A.J.J.; Bessière, A.; Van Der Kolk, E.; Dorenbos, P. Controlled electron and hole trapping in YPO4: Ce3+, Ln3+ and LuPO4: Ce3+, Ln3+ (Ln = Sm, Dy, Ho, Er, Tm). Phys. Rev. B-Condens. Matter Mater. Phys. 2009, 80, 1–10. [Google Scholar] [CrossRef]
- Luo, H.; Bos, A.J.J.; Dobrowolska, A. Low-temperature VUV photoluminescence and thermoluminescence of UV excited afterglow phosphor Sr3AlxSi1−xO5:Ce3+, Ln3+ (Ln = Er, Nd, Sm, Dy and Tm). Phys. Chem. Chem. Phys. 2015, 17, 15419–15427. [Google Scholar] [CrossRef] [PubMed]
- Yukihara, E.G.; Milliken, E.D.; Oliveira, L.C.; Orante-Barrón, V.R.; Jacobsohn, L.G.; Blair, M.W. Systematic development of new thermoluminescence and optically stimulated luminescence materials. J. Lumin. 2013, 133, 203–210. [Google Scholar] [CrossRef]
- Oliveira, L.C.; Yukihara, E.G.; Baffa, O. MgO:Li,Ce,Sm as a high-sensitivity material for Optically Stimulated Luminescence dosimetry. Sci. Rep. 2016, 6, 24348. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Bos, A.J.J.; Dorenbos, P. Controlled Electron-Hole Trapping and Detrapping Process in GdAlO3 by Valence Band Engineering. J. Phys. Chem. C 2016, 120, 5916–5925. [Google Scholar] [CrossRef]
- You, F.; Bos, A.J.J.; Shi, Q.; Huang, S.; Dorenbos, P. Electron transfer process between Ce3+ donor and Yb3+ acceptor levels in the bandgap of Y3Al5O12 (YAG). J. Phys. Condens. Matter 2011, 23, 215502. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, D.S.; Gayen, S.K.; Pogatshnik, G.J.; Ghen, R.D.; Miniscalco, W.J. Optical-absorption and photoionization measurements from the excited states of Ce3+:Y3Al5O12. Phys. Rev. B 1989, 39, 8807–8815. [Google Scholar] [CrossRef]
- Babin, V.; Hanus, M.; Krasnikov, A.; Kučera, M.; Nikl, M.; Zazubovich, S. Determination of the position of the 5d excited levels of Ce3+ ions with respect to the conduction band in the epitaxial films of the multicomponent (Lu,Gd)3(Ga,Al)5O12:Ce garnets. Opt. Mater. (Amst) 2016, 62, 465–474. [Google Scholar] [CrossRef]
- Wu, Y.; Nikl, M.; Jary, V.; Ren, G. Thermally induced ionization of 5d1 state of Ce3+ ion in Gd3Ga3Al2O12 host. Chem. Phys. Lett. 2013, 574, 56–60. [Google Scholar] [CrossRef]
- Matsuzawa, T.; Aoki, Y.; Takeuchi, N.; Murayama, Y. A New Long Phosphorescent Phosphor with High Brightness, SrAl2O4:Eu2+,Dy3+. J. Electrochem. Soc. 1996, 143, 2670. [Google Scholar] [CrossRef]
- Ueda, J.; Hashimoto, A.; Takemura, S.; Ogasawara, K.; Dorenbos, P.; Tanabe, S. Vacuum referred binding energy of 3 d transition metal ions for persistent and photostimulated luminescence phosphors of cerium-doped garnets. J. Lumin. 2017, 192, 371–375. [Google Scholar] [CrossRef]
- Aitasalo, T.; Ho, J.; Lastusaari, M.; Niittykoski, J. Thermoluminescence Study of Persistent Luminescence Materials: Eu2+- and R3+-Doped Calcium Aluminates, CaAl2O4:Eu2+,R3+. J. Phys. Chem. B 2006, 110, 4589–4598. [Google Scholar] [CrossRef] [PubMed]
- Asami, K.; Ueda, J.; Tanabe, S. Trap depth and color variation of Ce3+-Cr3+ co-doped Gd3(Al,Ga)5O12 garnet persistent phosphors. Opt. Mater. (Amst) 2016, 62, 171–175. [Google Scholar] [CrossRef]
- Bessière, A.; Lecointre, A.; Priolkar, K.R.; Gourier, D. Role of crystal defects in red long-lasting phosphorescence of CaMgSi2O6:Mn diopsides. J. Mater. Chem. 2012, 22, 19039. [Google Scholar] [CrossRef]
- Brito, H.F.; Hölsä, J.; Jungner, H.; Laamanen, T.; Lastusaari, M.; Malkamäki, M.; Rodrigues, L.C.V. Persistent luminescence fading in Sr2MgSi2O7:Eu2+,R3+ materials: A thermoluminescence study. Opt. Mater. Express 2012, 2, 287. [Google Scholar] [CrossRef]
- Denis, G.; Deniard, P.; Rocquefelte, X.; Benabdesselam, M.; Jobic, S. The thermally connected traps model applied to the thermoluminescence of Eu2+ doped Ba13−xAl22−2xSi10+2xO66 materials (x∼0.6). Opt. Mater. (Amst) 2010, 32, 941–945. [Google Scholar] [CrossRef]
- Dobrowolska, A.; Karsu, E.C.; Bos, A.J.J.; Dorenbos, P. Spectroscopy, thermoluminescence and afterglow studies of CaLa4(SiO4)3O:Ln (Ln = Ce, Nd, Eu, Tb, Dy). J. Lumin. 2015, 160, 321–327. [Google Scholar] [CrossRef]
- Feng, P.; Zhang, J.; Wu, C.; Liu, X.; Wang, Y. Self-activated afterglow luminescence of un-doped Ca2ZrSi4O12 material and explorations of new afterglow phosphors in a rare earth element-doped Ca2ZrSi4O12 system. Mater. Chem. Phys. 2013, 141, 495–501. [Google Scholar] [CrossRef]
- Ju, G.; Hu, Y.; Chen, L.; Wang, X. Investigation of the persistent luminescence of LiBaPO4:Eu2+. J. Mater. Res. 2014, 29, 519–526. [Google Scholar] [CrossRef]
- Katayama, Y.; Kobayashi, H.; Ueda, J.; Viana, B.; Tanabe, S. Persistent luminescence properties of Cr3+-Sm3+ activated LaAlO3 perovskite. Opt. Mater. Express 2016, 6, 1500. [Google Scholar] [CrossRef]
- Li, Y.; Gecevicius, M.; Qiu, J. Long persistent phosphors—From fundamentals to applications. Chem. Soc. Rev. 2016, 45, 2090–2136. [Google Scholar] [CrossRef] [PubMed]
- Liepina, V.; Millers, D.; Smits, K. Tunneling luminescence in long lasting afterglow of SrAl2O4:Eu,Dy. J. Lumin. 2017, 185, 151–154. [Google Scholar] [CrossRef]
- Rosticher, C.; Chaneac, C.; Bos, A.J.J.; Viana, B. Study on the persistent luminescence of diopside nanotracers CaMgSi2O6: Eu2+, Mn2+, Pr3+. Proc. SPIE 2016, 9749, 97490–97491. [Google Scholar] [CrossRef]
- Singh, T.B.; Mashangva, M.; Gartia, R.K. Trap spectroscopy and thermoluminescence of persistent luminescent materials. Indian J. Pure Appl. Phys. 2013, 51, 223–229. [Google Scholar]
- Tang, W.; Wang, M.; Meng, X.; Lin, W. Luminescence properties of tunable white-light long-lasting phosphor YPO4: Eu3+, Tb3+, Sr2+, Zr4+. Opt. Mater. (Amst) 2016, 54, 120–125. [Google Scholar] [CrossRef]
- Van den Eeckhout, K.; Poelman, D.; Smet, P. Persistent Luminescence in Non-Eu2+-Doped Compounds: A Review. Materials (Basel) 2013, 6, 2789–2818. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van den Eeckhout, K.; Smet, P.F.; Poelman, D. Persistent Luminescence in Eu2+-Doped Compounds: A Review. Materials (Basel) 2010, 3, 2536–2566. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Ma, X.; Qin, Q.; Shi, L.; Sun, J.; Zhou, M.; Liu, B.; Wang, Y. The synthesis and afterglow luminescence properties of a novel red afterglow phosphor: SnO2:Sm3+,Zr4+. Mater. Chem. Phys. 2012, 136, 320–324. [Google Scholar] [CrossRef]
- Zúñiga-Rivera, N.J.; Salas-Castillo, P.; Chernov, V.; Díaz-Torres, L.A.; Meléndrez, R.; García-Gutierrez, R.; Carrillo-Torres, R.C.; Barboza-Flores, M. Thermally and optically stimulated luminescence in long persistent orthorhombic strontium aluminates doped with Eu, Dy and Eu, Nd. Opt. Mater. (Amst) 2017, 67, 91–97. [Google Scholar] [CrossRef]
- Zuo, Y.; Chen, X.; Liu, X. Long lasting phosphorescence properties and multi-peak fitting on thermoluminescence of red LaAlO3:Eu3+ phosphor. Chem. Res. Chin. Univ. 2015, 31, 427–429. [Google Scholar] [CrossRef]
- Fasoli, M.; Vedda, A.; Nikl, M.; Jiang, C.; Uberuaga, B.P.; Andersson, D.A.; McClellan, K.J.; Stanek, C.R. Band-gap engineering for removing shallow traps in rare-earth Lu3Al5O12 garnet scintillators using Ga3+ doping. Phys. Rev. B-Condens. Matter Mater. Phys. 2011, 84, 1–4. [Google Scholar] [CrossRef]
- Nikl, M.; Mihokova, E.; Pejchal, J.; Vedda, A.; Zorenko, Y.; Nejezchleb, K. The antisite LuAl defect-related trap in Lu3Al5O12:Ce single crystal. Phys. Status Solidi 2005, 242, R119–R121. [Google Scholar] [CrossRef]
- Ueda, J.; Dorenbos, P.; Bos, A.J.J.; Kuroishi, K.; Tanabe, S. Control of electron transfer between Ce3+ and Cr3+ in the Y3Al5−xGaxO12 host via conduction band engineering. J. Mater. Chem. C 2015, 12, 19–21. [Google Scholar] [CrossRef]
- Katayama, Y.; Hashimoto, A.; Xu, J.; Ueda, J.; Tanabe, S. Thermoluminescence investigation on Y3Al5−xGaxO12:Ce3+-Bi3+ green persistent phosphors. J. Lumin. 2017, 183, 355–359. [Google Scholar] [CrossRef]
- Luo, J.; Wu, Y.; Zhang, G.; Zhang, H.; Ren, G. Composition–property relationships in (Gd3−xLux)(GayAl5−y)O12:Ce (x = 0, 1, 2, 3 and y = 0, 1, 2, 3, 4) multicomponent garnet scintillators. Opt. Mater. (Amst) 2013, 36, 476–481. [Google Scholar] [CrossRef]
- Visocekas, R.; Ceva, T.; Marti, C.; Lefaucheux, F.; Robert, M.C. Tunneling processes in afterglow of calcite. Phys. Status Solidi 1976, 35, 315–327. [Google Scholar] [CrossRef]
- Visocekas, R.; Barthou, C.; Blanc, P. Thermal quenching of far-red Fe3+ thermoluminescence of volcanic K-feldspars. Radiat. Meas. 2014, 61, 52–73. [Google Scholar] [CrossRef]
- Avouris, P.; Morgan, T.N. A tunneling model for the decay of luminescence in inorganic phosphors: The case of Zn2SiO4:Mn. J. Chem. Phys. 1981, 74, 4347–4355. [Google Scholar] [CrossRef]
- Delbecq, C.J.; Toyozaka, Y.; Yuster, P.H. Tunneling recombination of trapped electrons and holes in KCl: AgCl and KCl: TlCl. Phys. Rev. B 1974, 9, 4497–4505. [Google Scholar] [CrossRef]
- Dobrowolska, A.; Bos, A.J.J.; Dorenbos, P. Electron tunnelling phenomena in YPO4: Ce,Ln (Ln = Er, Ho, Nd, Dy). J. Phys. D Appl. Phys. 2014, 47, 335301. [Google Scholar] [CrossRef]
- Kitaura, M.; Sato, A.; Kamada, K.; Ohnishi, A.; Sasaki, M. Phosphorescence of Ce-doped Gd3Al2Ga3O12 crystals studied using luminescence spectroscopy. J. Appl. Phys. 2014, 115, 83517. [Google Scholar] [CrossRef]
- Vedda, A.; Nikl, M.; Fasoli, M.; Mihokova, E.; Pejchal, J.; Dusek, M.; Ren, G.; Stanek, C.R.; McClellan, K.J.; Byler, D.D. Thermally stimulated tunneling in rare-earth-doped oxyorthosilicates. Phys. Rev. B-Condens. Matter Mater. Phys. 2008, 78, 1–8. [Google Scholar] [CrossRef]
- Poolton, N.R.J.; Kars, R.H.; Wallinga, J.; Bos, A.J.J. Direct evidence for the participation of band-tails and excited-state tunnelling in the luminescence of irradiated feldspars. J. Phys. Condens. Matter 2009, 21, 485505. [Google Scholar] [CrossRef] [PubMed]
- Şahiner, E.; Kitis, G.; Pagonis, V.; Meriç, N.; Polymeris, G.S. Tunnelling recombination in conventional, post-infrared and post-infrared multi-elevated temperature IRSL signals in microcline K-feldspar. J. Lumin. 2017, 188, 514–523. [Google Scholar] [CrossRef]
- Jain, M.; Guralnik, B.; Andersen, M.T. Stimulated luminescence emission from localized recombination in randomly distributed defects. J. Phys. Condens. Matter 2012, 24, 385402. [Google Scholar] [CrossRef] [PubMed]
- Pagonis, V.; Chen, R.; Kulp, C.; Kitis, G. An overview of recent developments in luminescence models with a focus on localized transitions. Radiat. Meas. 2017. [Google Scholar] [CrossRef]
- Akselrod, M.S.; Agersnap Larsen, N.; Whitley, V.; McKeever, S.W.S. Thermal quenching of F-center luminescence in Al2O3:C. J. Appl. Phys. 1998, 84, 3364–3373. [Google Scholar] [CrossRef]
- Mandowski, A.; Bos, A.J.J.; Mandowska, E.; Orzechowski, J. Monte-Carlo method for determining the quenching function from variable heating rate measurements. Radiat. Meas. 2010, 45, 284–287. [Google Scholar] [CrossRef]
- Bos, A.J.J.; Poolton, N.R.J.; Wallinga, J.; Bessire, A.; Dorenbos, P. Energy levels in YPO4:Ce3+,Sm3+ studied by thermally and optically stimulated luminescence. Radiat. Meas. 2010, 45, 343–346. [Google Scholar] [CrossRef]
- Mandowski, A.; Bos, A.J.J. Explanation of anomalous heating rate dependence of thermoluminescence in YPO4:Ce3+,Sm3+ based on the semi-localized transition (SLT) model. Radiat. Meas. 2011, 46, 1376–1379. [Google Scholar] [CrossRef]
- Ueda, J.; Dorenbos, P.; Bos, A.J.J.; Meijerink, A.; Tanabe, S. Insight into the Thermal Quenching Mechanism for Y3Al5O12:Ce3+ through Thermoluminescence Excitation Spectroscopy. J. Phys. Chem. C 2015, 119, 25003–25008. [Google Scholar] [CrossRef]
- Arnold, B.Y.W.; Sherwood, H.K. Are Chloroplasts Semiconductors? Proc. Natl. Acad. Sci. USA 1957, 43, 105–114. [Google Scholar] [CrossRef]
- Vass, I. The history of photosynthetic thermoluminescence. Photosynth. Res. 2003, 76, 303–318. [Google Scholar] [CrossRef] [PubMed]
- Ducruet, J.-M. Chlorophyll thermoluminescence of leaf discs: simple instruments and progress in signal interpretation open the way to new ecophysiological indicators. J. Exp. Bot. 2003, 54, 2419–2430. [Google Scholar] [CrossRef] [PubMed]
- Havaux, M. Spontaneous and thermoinduced photon emission: New methods to detect and quantify oxidative stress in plants. Trends Plant Sci. 2003, 8, 409–413. [Google Scholar] [CrossRef]











© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bos, A.J.J. Thermoluminescence as a Research Tool to Investigate Luminescence Mechanisms. Materials 2017, 10, 1357. https://doi.org/10.3390/ma10121357
Bos AJJ. Thermoluminescence as a Research Tool to Investigate Luminescence Mechanisms. Materials. 2017; 10(12):1357. https://doi.org/10.3390/ma10121357
Chicago/Turabian StyleBos, Adrie J. J. 2017. "Thermoluminescence as a Research Tool to Investigate Luminescence Mechanisms" Materials 10, no. 12: 1357. https://doi.org/10.3390/ma10121357
APA StyleBos, A. J. J. (2017). Thermoluminescence as a Research Tool to Investigate Luminescence Mechanisms. Materials, 10(12), 1357. https://doi.org/10.3390/ma10121357




