A Study on the Impact of Environmental Factors on Chub Mackerel Scomber japonicus Fishing Grounds Based on a Linear Mixed Model
Abstract
1. Introduction
2. Materials and Methods
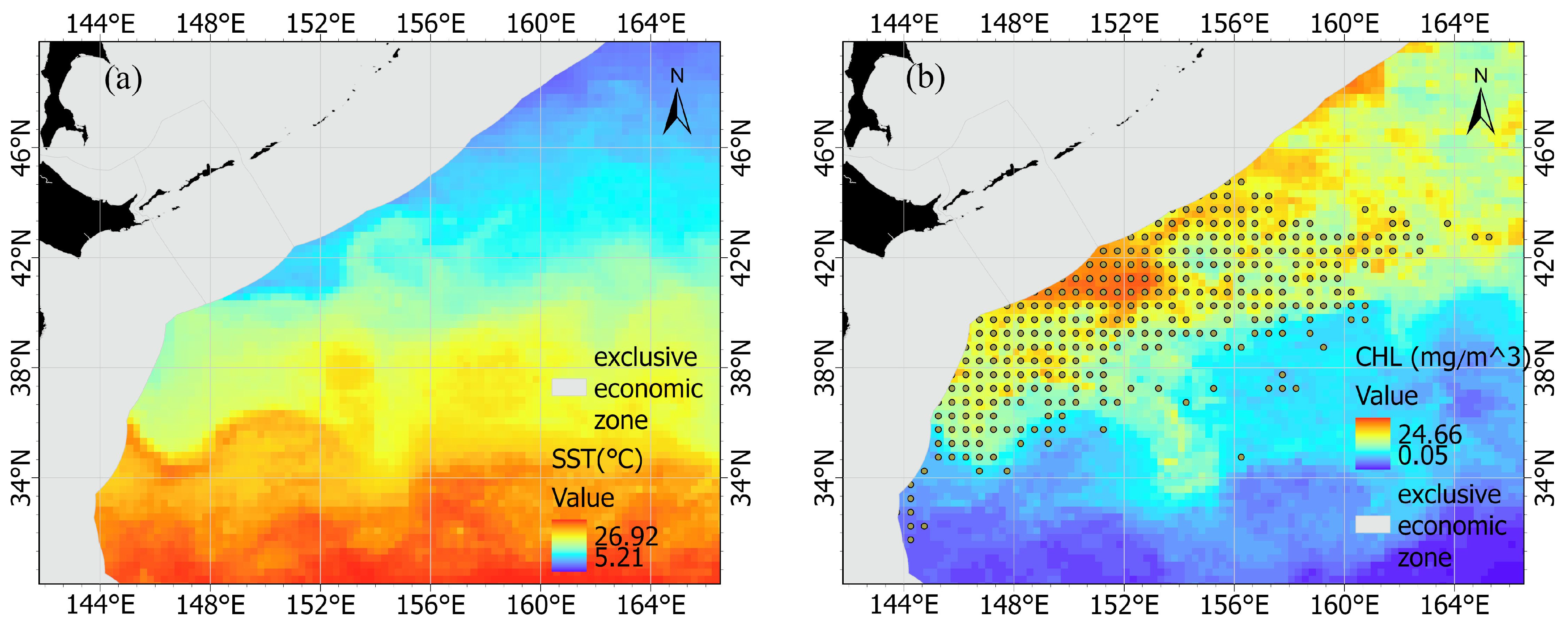
2.1. Environmental and Fishery Data
2.2. Normalization and Multicollinearity Detection of Variables
2.3. Linear Mixed Model
2.4. Selection of the Optimal Model
3. Results
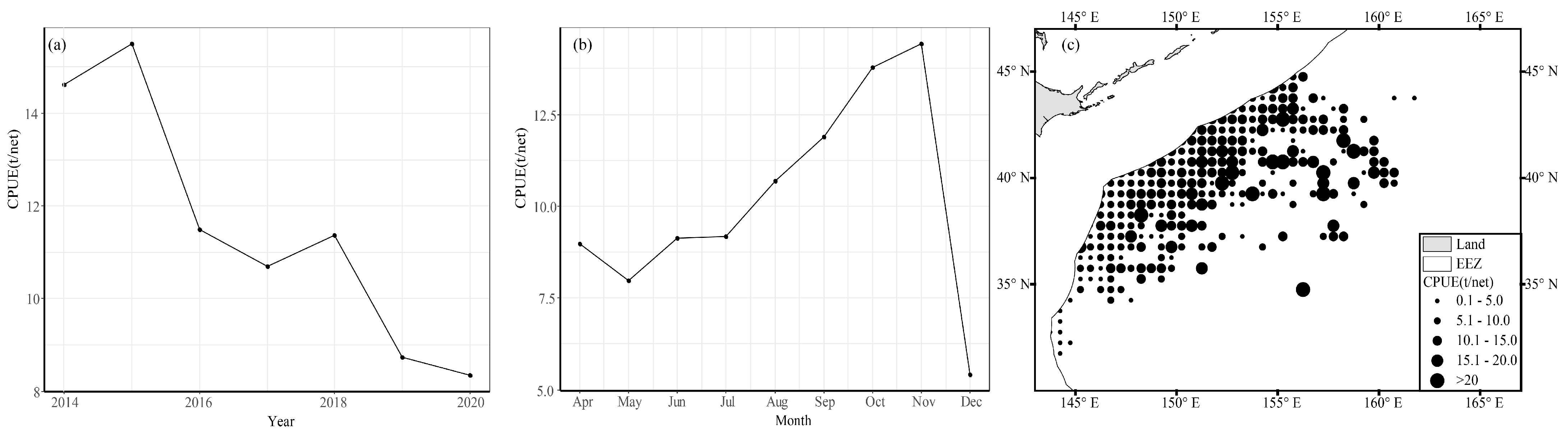
3.1. Seasonal Variation and Spatial Distribution of CPUE
3.2. Optimal Linear Mixed Model
3.3. Mixed Effects of SST and logCHL on CPUE
3.3.1. Fixed Effect Parameters
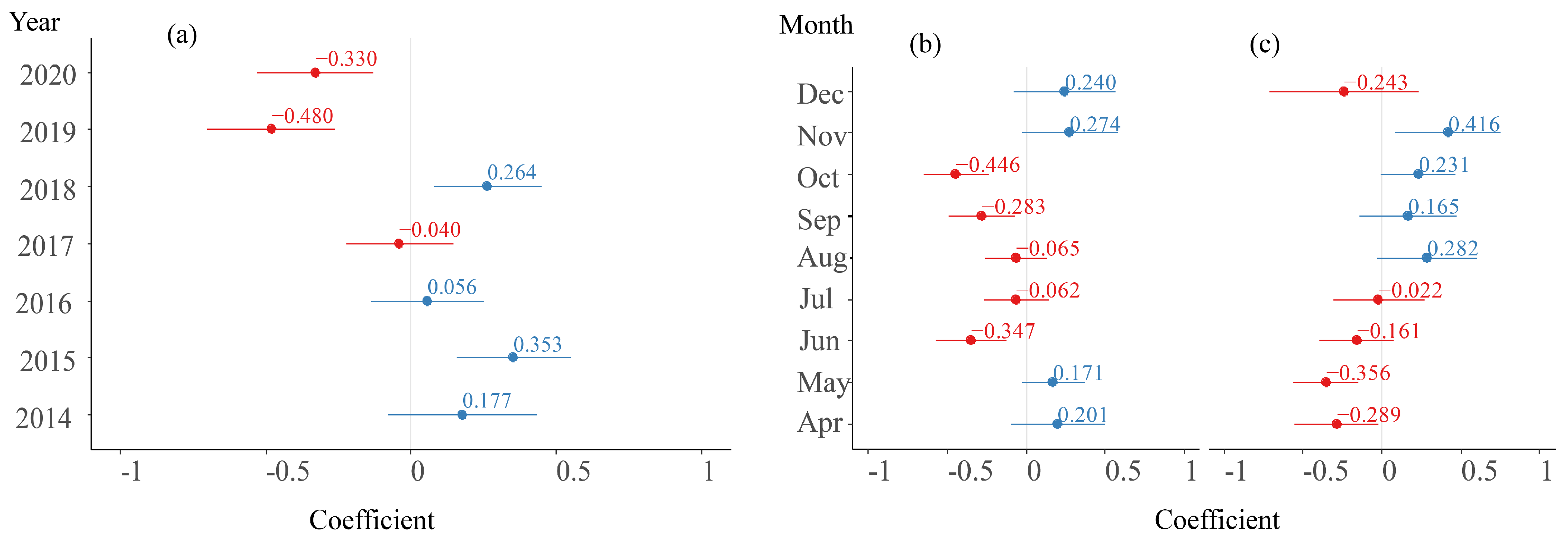
3.3.2. Random Effect Parameters
3.4. Residual Test
4. Discussion
4.1. Influence of SST on Chub Mackerel
4.2. The Effect of Chlorophyll-a Concentration on Chub Mackerel
4.3. Implications of Intercepts in Random Effects of Year and Zone
4.4. Scalability of Linear Mixed-Effects Regression
4.5. Limitations
5. Conclusions
- (1)
- SST is a fixed effect and there exists a negative correlation between SST and CPUE;
- (2)
- The effect of chlorophyll concentration (logCHL) on the CPUE does not have a fixed effect, but the coefficient of the covariate (logCHL) for the Month group shows significance, and it will have different effects on CPUE with seasonal changes. Chlorophyll concentration is positively correlated with CPUE during wintering and spawning periods and is negatively correlated with CPUE during feeding periods;
- (3)
- The inherent differences in CPUE in time and space can be captured through random intercepts, thereby enhancing the accuracy and generalization ability of the model. This flexibility enables the model to more comprehensively describe the structure and variability in the CPUE, helping us better reveal the complex relationships and patterns behind the changes in chub mackerel CPUE.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, C.; Ito, S.; Kamimura, Y.; Xiu, P. Evaluating the Influence of Environmental Factors on the Early Life History Growth of Chub Mackerel (Scomber japonicus) Using a Growth and Migration Model. Prog. Oceanogr. 2022, 206, 102821. [Google Scholar] [CrossRef]
- Shiraishi, T.; Okamoto, K.; Yoneda, M.; Sakai, T.; Ohshimo, S.; Onoe, S.; Yamaguchi, A.; Matsuyama, M. Age Validation, Growth and Annual Reproductive Cycle of Chub Mackerel Scomber japonicus off the Waters of Northern Kyushu and in the East China Sea. Fish. Sci. 2008, 74, 947–954. [Google Scholar] [CrossRef]
- Torrejón-Magallanes, J.; Ángeles-González, L.E.; Csirke, J.; Bouchon, M.; Morales-Bojórquez, E.; Arreguín-Sánchez, F. Modeling the Pacific Chub Mackerel (Scomber japonicus) Ecological Niche and Future Scenarios in the Northern Peruvian Current System. Prog. Oceanogr. 2021, 197, 102672. [Google Scholar] [CrossRef]
- Wang, L.; Ma, S.; Liu, Y.; Li, J.; Liu, S.; Lin, L.; Tian, Y. Fluctuations in the Abundance of Chub Mackerel in Relation to Climatic/Oceanic Regime Shifts in the Northwest Pacific Ocean since the 1970s. J. Mar. Syst. 2021, 218, 103541. [Google Scholar] [CrossRef]
- Wang, Z.; Ito, S.; Yabe, I.; Guo, C. Development of a Bioenergetics and Population Dynamics Coupled Model: A Case Study of Chub Mackerel. Front. Mar. Sci. 2023, 10, 1142899. [Google Scholar] [CrossRef]
- Yukami, R.; Nishijima, S.; Kamimura, Y.; Furuichi, S. Stock Assessment and Evaluation for Chub Mackerel (Fiscal Year 2022). In Marine Fisheries Stock Assessment and Evaluation for Japanese Waters; Japan Fisheries Agency and Japan Fisheries Research and Education Agency: Tokyo, Japan, 2022; pp. 39–42. [Google Scholar]
- Taga, M.; Kamimura, Y.; Yamashita, Y. Effects of Water Temperature and Prey Density on Recent Growth of Chub Mackerel Scomber japonicus Larvae and Juveniles along the Pacific Coast of Boso–Kashimanada. Fish. Sci. 2019, 85, 931–942. [Google Scholar] [CrossRef]
- Cui, K.; Chen, X. Study of the relationships between SST and mackerel abundances in the Yellow and East China Seas. South China Fish. Sci. 2007, 3, 20–25. [Google Scholar]
- Guan, W.; Chen, X.; Gao, F.; Li, G. Environmental Effects on Fishing Efficiency of Scomber japonicus for Chinese Large Lighting Purse Seine Fishery in the Yellow and East China Seas. J. Fish. Sci. China 2009, 16, 949–958. [Google Scholar]
- Han, H.; Yang, C.; Jiang, B.; Shang, C.; Sun, Y.; Zhao, X.; Xiang, D.; Zhang, H.; Shi, Y. Construction of Chub Mackerel (Scomber japonicus) Fishing Ground Prediction Model in the Northwestern Pacific Ocean Based on Deep Learning and Marine Environmental Variables. Mar. Pollut. Bull. 2023, 193, 115158. [Google Scholar] [CrossRef]
- Dai, S.; Tang, F.; Fan, W.; Zhang, H.; Cui, X. Distribution of Resource and Environment Characteristics of Fishing Ground of Scomber Japonicas in the North Pacific High Seas. Mar. Fish. 2017, 39, 372–382. [Google Scholar]
- Miao, Z. Relation between Pneumatophorus and Carangidae Fishing Grounds in the Summer-Autumn and Ocean Hydrologic Environment in the Northern Part of the East China Sea. J. Zhejiang Coll. Fish. 1993, 12, 32–39. [Google Scholar]
- Sassa, C.; Tsukamoto, Y. Distribution and Growth of Scomber japonicus and S. Australasicus Larvae in the Southern East China Sea in Response to Oceanographic Conditions. Mar. Ecol. Prog. Ser. 2010, 419, 185–199. [Google Scholar] [CrossRef]
- Wang, L.; Ma, S.; Liu, Y.; Li, J.; Sun, D.; Tian, Y. Climate-Induced Variation in a Temperature Suitability Index of Chub Mackerel in the Spawning Season and Its Effect on the Abundance. Front. Mar. Sci. 2022, 9, 996626. [Google Scholar] [CrossRef]
- Owiredu, S.A.; Onyango, S.O.; Song, E.-A.; Kim, K.-I.; Kim, B.-Y.; Lee, K.-H. Enhancing Chub Mackerel Catch Per Unit Effort (CPUE) Standardization through High-Resolution Analysis of Korean Large Purse Seine Catch and Effort Using AIS Data. Sustainability 2024, 16, 1307. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, X.; Yang, S.; Dai, Y.; Cui, X.; Wu, Y.; Zhang, S.; Fan, W.; Han, H.; Zhang, H.; et al. Construction of CPUE Standardization Model and Its Simulation Testing for Chub Mackerel (Scomber japonicus) in the Northwest Pacific Ocean. Ecol. Indic. 2023, 155, 111022. [Google Scholar] [CrossRef]
- Li, Y.; Pan, L.; Yan, L.; Chen, X. Individual-based model study on the fishing ground of chub mackerel in the East China Sea. Acta Oceanol. Sin. 2014, 36, 67–74. [Google Scholar] [CrossRef]
- Chen, L.F.; Zhu, G.P. Analysis of Influence on Spatial Distribution of Fishing Ground for Antarctic Krill Fishery in the Northern South Shetland Islands Based on GWR Model. Ying Yong Sheng Tai Xue Bao 2018, 29, 938–944. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, M.; Nishijima, S.; Yukami, R.; Watanabe, C.; Kamimura, Y.; Furuichi, S.; Ichinokawa, M.; Okamura, H. Spatiotemporal Dynamics of the Pacific Chub Mackerel Revealed by Standardized Abundance Indices. Fish. Res. 2019, 219, 105315. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, H.; Ma, Q.; Yang, C.; Zhao, G. Standardized CPUE of Chub Mackerel (Scomber japonicas) Caught by the China’s Lighting Purse Seine Fishery up to 2019; NPFC-2021-TWG CMSA04-WP17; East China Sea Fisheries Research Institute, Chinese Academy of Fishery Sciences: Shanghai, China, 2021. [Google Scholar]
- Chen, X.; Li, G.; Feng, B.; Tian, S. Habitat Suitability Index of Chub Mackerel (Scomber japonicus) from July to September in the East China Sea. J. Oceanogr. 2009, 65, 93–102. [Google Scholar] [CrossRef]
- Lee, D.; Son, S.; Kim, W.; Park, J.M.; Joo, H.; Lee, S.H. Spatio-Temporal Variability of the Habitat Suitability Index for Chub Mackerel (Scomber japonicus) in the East/Japan Sea and the South Sea of South Korea. Remote Sens. 2018, 10, 938. [Google Scholar] [CrossRef]
- Xiao, G. Construction and Comparison of Fishing Ground Forecast Model of Chub Mackerel (Scomber japonicus) in Pacific Northwest (Master). Master’s Thesis, Shanghai Ocean University, Shanghai, China, 2022. [Google Scholar]
- Gilbert, C.S.; Gentleman, W.C.; Johnson, C.L.; DiBacco, C.; Pringle, J.M.; Chen, C. Modeling Dispersal of Sea Scallop (Placopecten Magellanicus) Larvae on Georges Bank: The Influence of Depth-Distribution, Planktonic Duration and Spawning Seasonality. Prog. Oceanogr. 2010, 87, 37–48. [Google Scholar] [CrossRef]
- Brochier, T.; Colas, F.; Lett, C.; Echevin, V.; Cubillos, L.A.; Tam, J.; Chlaida, M.; Mullon, C.; Freon, P. Small Pelagic Fish Reproductive Strategies in Upwelling Systems: A Natal Homing Evolutionary Model to Study Environmental Constraints. Prog. Oceanogr. 2009, 83, 261–269. [Google Scholar] [CrossRef]
- Li, J.; Cui, X.; Tang, F.; Fan, W.; Han, Z.; Wu, Z. Spatiotemporal Analysis of Marine Environmental Influence on the Distribution of Chub Mackerel in the Northwest Pacific Ocean Based on Geographical and Temporal Weighted Regression. J. Sea Res. 2024, 200, 102514. [Google Scholar] [CrossRef]
- Hyun, S.-Y.; Cadrin, S.X.; Roman, S. Fixed and Mixed Effect Models for Fishery Data on Depth Distribution of Georges Bank Yellowtail Flounder. Fish. Res. 2014, 157, 180–186. [Google Scholar] [CrossRef]
- Kanamori, Y.; Takasuka, A.; Nishijima, S.; Okamura, H. Climate Change Shifts the Spawning Ground Northward and Extends the Spawning Period of Chub Mackerel in the Western North Pacific. Mar. Ecol. Prog. Ser. 2019, 624, 155–166. [Google Scholar] [CrossRef]
- Wootton, R.J. Ecology of Teleost Fishes; Springer: Dordrecht, The Netherlands, 1989; ISBN 978-94-010-6859-8. [Google Scholar]
- Yasuda, T.; Kawabe, R.; Takahashi, T.; Murata, H.; Kurita, Y.; Nakatsuka, N.; Arai, N. Habitat Shifts in Relation to the Reproduction of Japanese Flounder Paralichthys Olivaceus Revealed by a Depth-Temperature Data Logger. J. Exp. Mar. Biol. Ecol. 2010, 385, 50–58. [Google Scholar] [CrossRef]
- Akinwande, M.O.; Dikko, H.G.; Samson, A. Variance Inflation Factor: As a Condition for the Inclusion of Suppressor Variable(s) in Regression Analysis. Open J. Stat. 2015, 5, 754–767. [Google Scholar] [CrossRef]
- Pinheiro, J.C.; Bates, D.M. (Eds.) Linear Mixed-Effects Models: Basic Concepts and Examples. In Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2000; pp. 3–56. ISBN 978-0-387-22747-4. [Google Scholar]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Linear Mixed Models. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Montesinos López, O.A., Montesinos López, A., Crossa, J., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 141–170. ISBN 978-3-030-89010-0. [Google Scholar]
- Chen, Z.; Zhu, S.; Niu, Q.; Zuo, T. Knowledge Discovery and Recommendation with Linear Mixed Model. IEEE Access 2020, 8, 38304–38317. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using Lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Akoglu, H. User’s Guide to Correlation Coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef]
- Bates, M.D.; Castellano, K.E.; Rabe-Hesketh, S.; Skrondal, A. Handling Correlations Between Covariates and Random Slopes in Multilevel Models. J. Educ. Behav. Stat. 2014, 39, 524–549. [Google Scholar] [CrossRef]
- Chung, Y.; Gelman, A.; Rabe-Hesketh, S.; Liu, J.; Dorie, V. Weakly Informative Prior for Point Estimation of Covariance Matrices in Hierarchical Models. J. Educ. Behav. Stat. 2015, 40, 136–157. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Zhang, R.; Tian, Y.; Zhang, J.; Lin, L. Relationship between the Resource Distribution of Scomber japonicus and Seawater Temperature Vertical Structure of Northwestern Pacific Ocean. Period. Ocean. Univ. China 2019, 49, 29–38. [Google Scholar] [CrossRef]
- Kamimura, Y.; Takahashi, M.; Yamashita, N.; Watanabe, C.; Kawabata, A. Larval and Juvenile Growth of Chub Mackerel Scomber japonicus in Relation to Recruitment in the Western North Pacific. Fish. Sci. 2015, 81, 505–513. [Google Scholar] [CrossRef]
- Cui, G.; Zhu, W.; Dai, Q. Temporal and Spatial Distribution of the Mackerel Fishing Ground in the Northwest Pacific and Its Relationship with Sea Surface Temperature and Chlorophyll Concentration. Ocean. Dev. Manag. 2021, 38, 95–99. [Google Scholar]
- Li, X.; Pang, Z.; Zhu, J.; Ying, Y.; Sun, S. Spatial-Temporal Patterns in Fishing Ground of Scomber japonicus in Center Eastern Central Atlantic Ocean. Fish. Sci. 2018, 37, 31–37. [Google Scholar] [CrossRef]
- Suda, M.; Watanabe, C.; Akamine, T. Two-Species Population Dynamics Model for Japanese Sardine Sardinops Melanostictus and Chub Mackerel Scomber japonicus off the Pacific Coast of Japan. Fish. Res. 2008, 94, 18–25. [Google Scholar] [CrossRef]
- Yatsu, A.; Watanabe, T.; Ishida, M.; Sugisaki, H.; Jacobson, L.D. Environmental Effects on Recruitment and Productivity of Japanese Sardine Sardinops Melanostictus and Chub Mackerel Scomber japonicus with Recommendations for Management. Fish. Oceanogr. 2005, 14, 263–278. [Google Scholar] [CrossRef]
- Cheung, W.W.L.; Watson, R.; Pauly, D. Signature of Ocean Warming in Global Fisheries Catch. Nature 2013, 497, 365–368. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Xu, Z.; Zhou, J. Effect of Global Warming on the Distribution of Lucifer Intermedius and L. hanseni (Decapoda) in the Changjiang Estuary. Prog. Nat. Sci. 2009, 19, 1389–1395. [Google Scholar] [CrossRef]
- Zhao, G.; Wu, Z.; CUI, X.; FAN, W.; Shi, Y.; Xiao, G.; Tang, F. Spatial Temporal Patterns of Chub Mackerel Fishing Ground in the Northwest Pacific Based on Spatial Autocorrelation Model. Haiyang Xuebao 2022, 44, 22–35. [Google Scholar] [CrossRef]
- Caramantin-Soriano, H.; Vega-Pérez, L.A.; Ñiquen, M. The Influence of the 1992–1993 El Niño on the Reproductive Biology of Scomber japonicus Peruanus (Jordán & Hubb, 1925). Braz. J. Oceanogr. 2009, 57, 263–272. [Google Scholar] [CrossRef]
- Yu, W.; Wen, J.; Chen, X.; Li, G.; Li, Y.; Zhang, Z. Effects of Climate Variability on Habitat Range and Distribution of Chub Mackerel in the East China Sea. J. Ocean. Univ. China 2021, 20, 1483–1494. [Google Scholar] [CrossRef]
- Lin, P.; Ma, J.; Chai, F.; Xiu, P.; Liu, H. Decadal Variability of Nutrients and Biomass in the Southern Region of Kuroshio Extension. Prog. Oceanogr. 2020, 188, 102441. [Google Scholar] [CrossRef]
- Ozawa, T.; Kawai, K.; Uotani, I. Stomach Content Analysis of Chub Mackerel Scomber japonicus Larvae by Quantification I Method. Nippon Suisan Gakkaishi 1991, 57, 1241–1245. [Google Scholar] [CrossRef]
- Smith, R.C.; Dustan, P.; Au, D.; Baker, K.S.; Dunlap, E.A. Distribution of Cetaceans and Sea-Surface Chlorophyll Concentrations in the California Current. Mar. Biol. 1986, 91, 385–402. [Google Scholar] [CrossRef]
- Watanabe, C.; Yatsu, A. Long-Term Changes in Maturity at Age of Chub Mackerel (Scomber japonicus) in Relation to Population Declines in the Waters off Northeastern Japan. Fish. Res. 2006, 78, 323–332. [Google Scholar] [CrossRef]
- Watanabe, C.; Nishida, H. Development of Assessment Techniques for Pelagic Fish Stochs: Applications of Daily Egg Production Method and Pelagic Trawl in the Northestern Pacific Ocean. Fish. Sci. 2002, 68, 97–100. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Watanabe, T. Morphology and Ecology of Early Stages of Life in Japanese Common Mackerel, Scomber japonicus Houttuyn, with Special Reference to Fluctuation of Population. Bull. Tokai Reg. Fish. Res. Lab. 1970, 62, 1–283. [Google Scholar]
- Shen, H.; Hong, M. Marine Environment and Distribution of Major Pelagic Fishes in the Northwest Pacific Ocean. Morden Fish. Inf. 1986, 2, 4–8. [Google Scholar]
- Fan, W.; Cui, X.; Yumei, W.U. The Study on Fishing Ground of Neon Flying Squid, Ommastrephes Bartrami, and Ocean Environment Based on Remote Sensing Data in the Northwest Pacific Ocean. Chin. J. Oceanol. Limnol. 2009, 27, 408–414. [Google Scholar] [CrossRef]
- Wang, Y.; Bi, R.; Zhang, J.; Gao, J.; Takeda, S.; Kondo, Y.; Chen, F.; Jin, G.; Sachs, J.P.; Zhao, M. Phytoplankton Distributions in the Kuroshio-Oyashio Region of the Northwest Pacific Ocean: Implications for Marine Ecology and Carbon Cycle. Front. Mar. Sci. 2022, 9, 865142. [Google Scholar] [CrossRef]
- Guo, A.; Zhang, Y.; Yu, W.; Chen, X.J.; Qian, W. Influence of El Niño and La Niña with Different Intensity on Habitat Variation of Chub Mackerel Scomber Japonicas in the Coastal Waters of China. Haiyang Xuebao 2018, 40, 58–67. [Google Scholar]
- Kuroda, H.; Suyama, S.; Miyamoto, H.; Setou, T.; Nakanowatari, T. Interdecadal Variability of the Western Subarctic Gyre in the North Pacific Ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 2021, 169, 103461. [Google Scholar] [CrossRef]
- Qiu, B. Kuroshio and Oyashio Currents. In Encyclopedia of Ocean Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 384–394. ISBN 978-0-12-813082-7. [Google Scholar]
- Abbas-Aghababazadeh, F.; Lu, P.; Fridley, B.L. Nonlinear Mixed-Effects Models for Modeling in Vitro Drug Response Data to Determine Problematic Cancer Cell Lines. Sci. Rep. 2019, 9, 14421. [Google Scholar] [CrossRef]
- Aiadi, O.; Kherfi, M.L. A New Method for Automatic Date Fruit Classification. Int. J. Comput. Vis. Robot. 2017, 7, 692. [Google Scholar] [CrossRef]
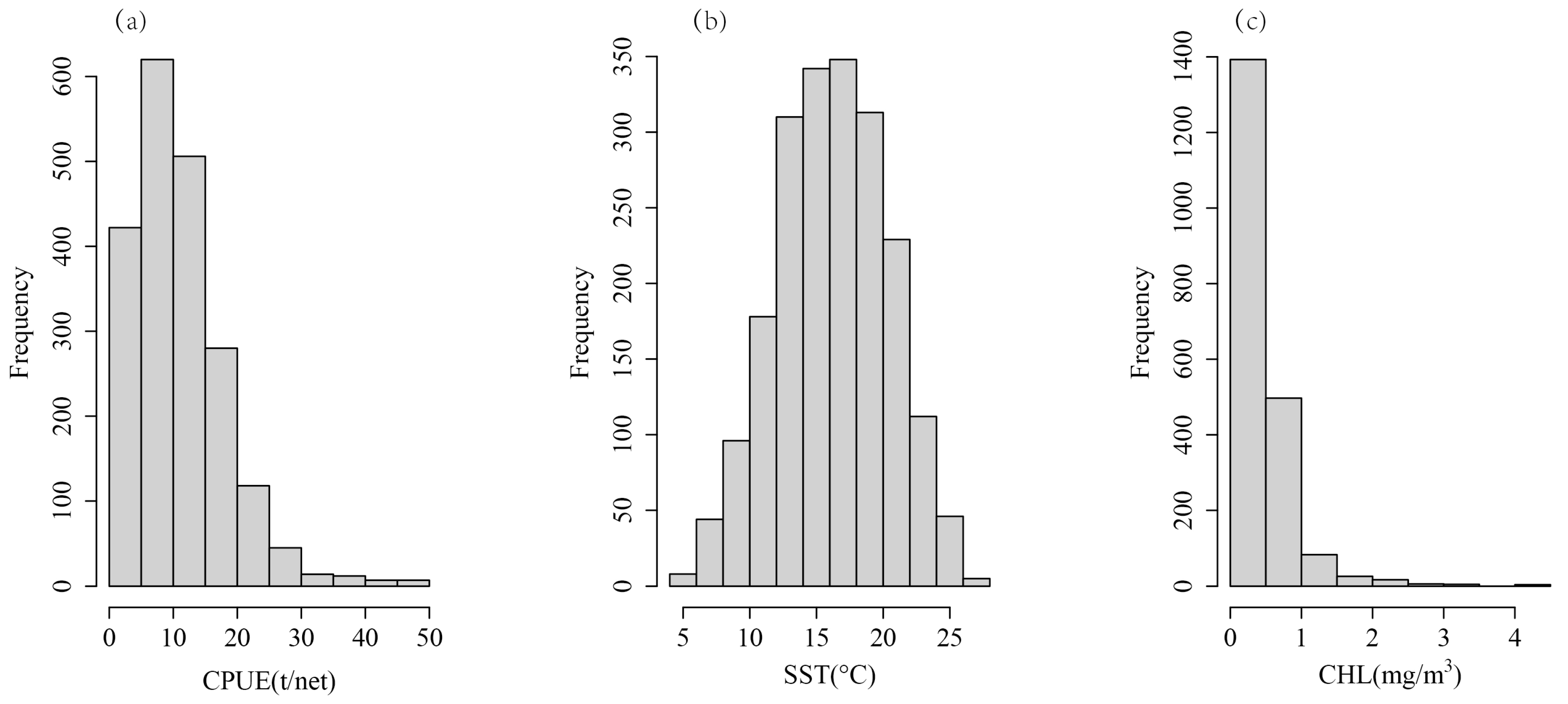
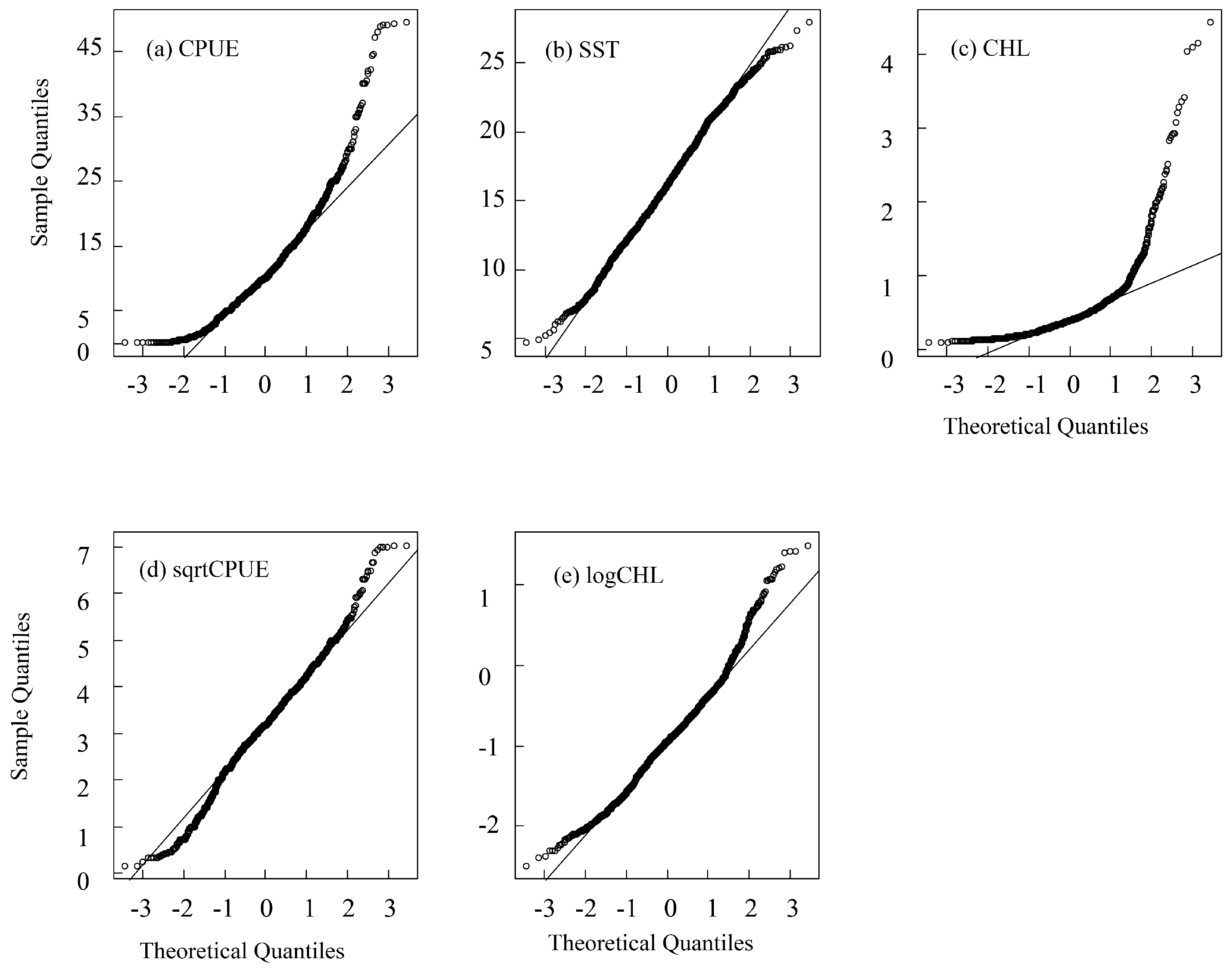


| Variable | Original Distribution | Distribution after Transformation | ||||
|---|---|---|---|---|---|---|
| Square Root | Natural logarithm | |||||
| Skewness | Kurtosis | Skewness | Kurtosis | Skewness | Kurtosis | |
| CPUE | 1.318 | 6.337 | −0.002 | 3.459 | −1.957 | 9.027 |
| SST | −0.021 | 2.610 | −0.373 | 2.952 | −0.789 | 3.842 |
| CHL | 4.077 | 27.165 | 1.958 | 9.613 | 0.511 | 3.763 |
| Scenario | Model Structure | AIC | BIC | logLik | Deviance |
|---|---|---|---|---|---|
| 0 | 1 + sst + logCHL | 6.265 | 6.287 | −3.128 | 2.589 |
| 1 | 1 + (1|Year) + (1|Month) + (1|Zone) | 6.077 | 6.105 | −3.034 | 6.067 |
| 2 | 1 + (1|Year) + (1 + logCHL|Month) + (1|Zone) | 6.055 | 6.094 | −3.020 | 6.041 |
| 3 | 1 + (1 + logCHL|Year) + (1 + logCHL|Month) + (1|Zone) | 6.056 | 6.106 | −3.019 | 6.038 |
| 4 | 1 + sst + (1|Year) + (1|Month) + (1|Zone) | 6.058 | 6.091 | −3.023 | 6.045 |
| 5 | 1 + sst + (1|Year) + (1 + logCHL|Month) + (1|Zone) | 6.035 | 6.080 | −3.010 | 6.019 |
| 6 | 1 + sst + logCHL + (1|Year) + (1|Month) + (1|Zone) | 6.054 | 6.093 | −3.020 | 6.040 |
| Variable | Estimate | Std. Error | Degree of Freedom | T | p |
|---|---|---|---|---|---|
| (Intercept) | 3.794 | 0.211 | 27.275 | 17.974 | 0.000 *** |
| SST | −0.050 | 0.010 | 366.871 | −4.933 | 0.000 *** |
| Groups | Coefficient | Variance | Std. Dev. | Correlation |
|---|---|---|---|---|
| Zone | (Intercept) | 0.031 | 0.175 | / |
| Month | (Intercept) | 0.094 | 0.307 | −0.070 |
| logCHL | 0.084 | 0.289 | ||
| Year | (Intercept) | 0.093 | 0.304 | / |
| Residual | 1.075 | 1.037 | / | |
| Deleted Single Term | The Number of Parameters | Log-LPT | AIC | LRT | Degree of Freedom | p |
|---|---|---|---|---|---|---|
| None | 8 | −3009.6 | 6035.1 | |||
| (1|year) | 7 | −3055.4 | 6124.9 | 91.772 | 1 | 0.000 *** |
| logCHL in (1 + logCHL|m) | 6 | −3022.8 | 6057.6 | 26.424 | 2 | 0.000 *** |
| (1|zone) | 7 | −3012.3 | 6038.6 | 5.483 | 1 | 0.019 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Tang, F.; Wu, Y.; Zhang, S.; Zhou, W.; Cui, X. A Study on the Impact of Environmental Factors on Chub Mackerel Scomber japonicus Fishing Grounds Based on a Linear Mixed Model. Fishes 2024, 9, 323. https://doi.org/10.3390/fishes9080323
Li J, Tang F, Wu Y, Zhang S, Zhou W, Cui X. A Study on the Impact of Environmental Factors on Chub Mackerel Scomber japonicus Fishing Grounds Based on a Linear Mixed Model. Fishes. 2024; 9(8):323. https://doi.org/10.3390/fishes9080323
Chicago/Turabian StyleLi, Jiasheng, Fenghua Tang, Yumei Wu, Shengmao Zhang, Weifeng Zhou, and Xuesen Cui. 2024. "A Study on the Impact of Environmental Factors on Chub Mackerel Scomber japonicus Fishing Grounds Based on a Linear Mixed Model" Fishes 9, no. 8: 323. https://doi.org/10.3390/fishes9080323
APA StyleLi, J., Tang, F., Wu, Y., Zhang, S., Zhou, W., & Cui, X. (2024). A Study on the Impact of Environmental Factors on Chub Mackerel Scomber japonicus Fishing Grounds Based on a Linear Mixed Model. Fishes, 9(8), 323. https://doi.org/10.3390/fishes9080323








