Energy Structure of Yb³⁺-Yb³⁺ Paired Center in LiNbO₃ Crystal

Abstract

Within the framework of Dexter’s theory, we calculate the energies of the Stark levels of Yb³⁺-Yb³⁺ paired centers in lithium niobate doped with Yb³⁺ ions (LiNbO₃:Yb³⁺) crystal, considering the interaction of optical electrons of ytterbium ions forming the paired center. The calculated Stark level energies are shown to correspond well with the observed cooperative luminescence wavelengths.

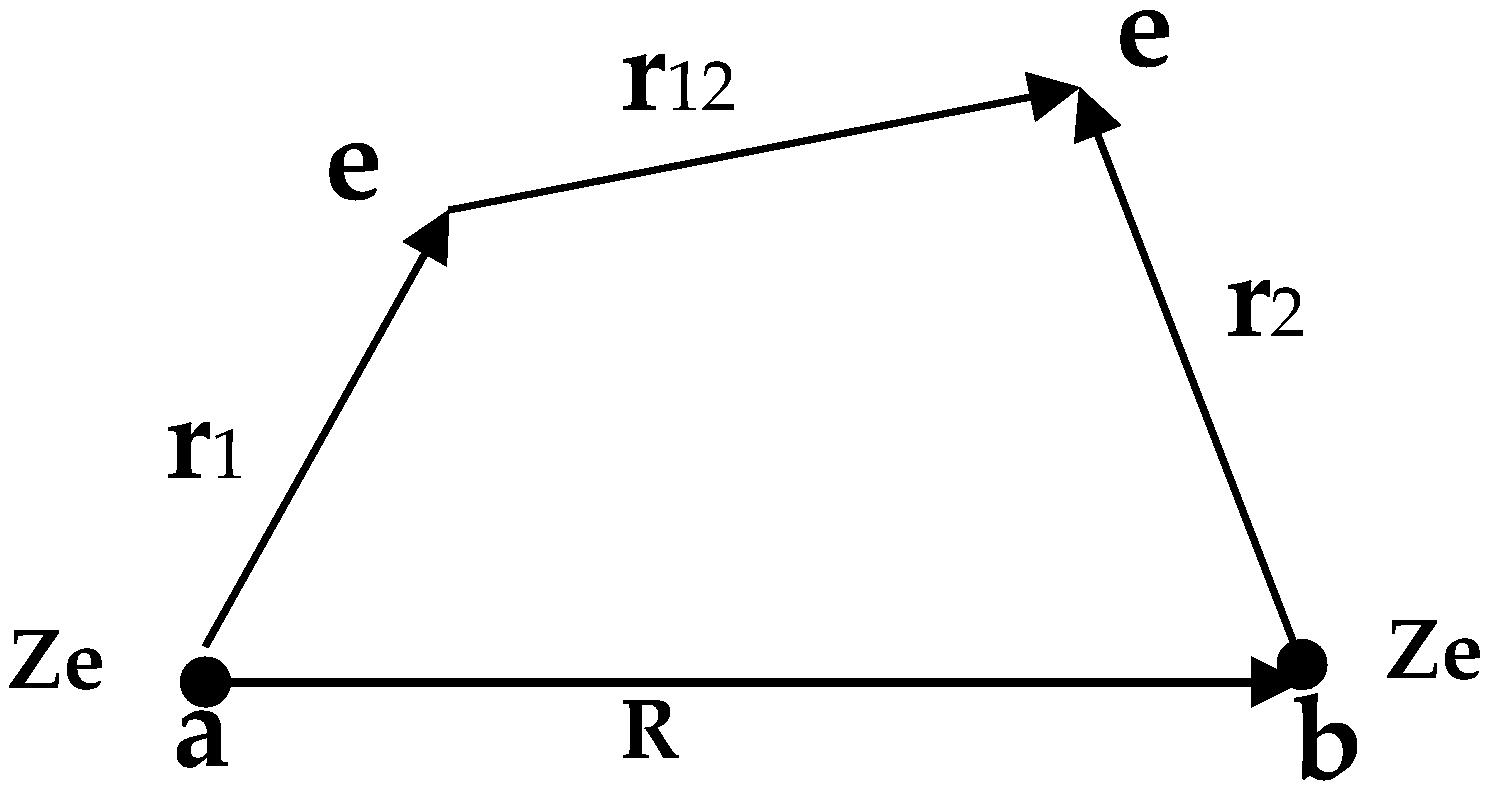
1. Introduction

The lattice structure of the LiNbO₃ (LN) crystal, belonging to the space group R3c (C_3v), consists of chains of trigonally distorted octahedrons aligned along the crystallographic optical axis. The rhombohedral unit cell contains four formula units, with lattice constants at room temperature of a = 5.1483 Å and c = 13.8631 Å [1]. In the LN crystal lattice, trivalent rare-earth (RE³⁺) impurity ions can predominantly occupy the positions of Li⁺ ions or replace Nb⁵⁺ ions at Li⁺ sites (anti-sites), ensuring charge compensation [2,3]. The location and local symmetry of RE³⁺ impurity ions in the LN lattice have been extensively studied using electron paramagnetic resonance (EPR) spectroscopy (see, for example, [4,5,6,7]). Specifically, studies [6] have demonstrated that RE³⁺ ions occupy octahedral sites with either C₃ or C₁ local symmetry. Furthermore, the research in [7] confirmed the presence of Yb³⁺-Yb³⁺ paired centers in the LN crystal matrix, with an interionic distance of 3.1 Å.

Thus, in the LN crystal lattice, in addition to single impurity centers, paired centers (dimers) can form due to the close proximity of RE³⁺ ions. These paired centers influence both the spectroscopic properties (such as cooperative luminescence) and the kinetic characteristics of the LN crystal [8]. Experimental and theoretical studies on cooperative luminescence (CL) in Yb-doped crystals have been conducted in [9,10,11,12,13,14,15]. Notably, [9] investigated cooperative luminescence in LN:x%Yb³⁺ (x = 0.7%, 1.2%, and 4%) crystals at 12 K under 920 nm excitation. Analysis of the experimental data revealed that approximately 10.4% of Yb³⁺ ions in the LN matrix form paired Yb³⁺-Yb³⁺ centers, where one Yb³⁺ ion resides at a Li⁺ site and the other at a Nb⁵⁺ site. Cooperative luminescence (CL) was observed in Li₆Y(BO₃)₃:x%Yb³⁺ (x = 1, 5, 20) crystals within the 526–476 nm wavelength range at temperatures of 6–300 K, under both continuous and pulsed excitation at 972.3 nm [10]. In [11], the effects of cooperative luminescence and absorption in Yb-doped fibers (YFs) were extensively studied under continuous excitation at 980 nm. It was shown that Yb³⁺ ion pairs significantly influence both the nonlinear transmittance of YF at λ_ex = 980 nm and the relaxation dynamics of the excited Yb³⁺ state. In [12], blue emission was observed in Yb³⁺-activated Y₄Al₂O₉ crystals (10 at.%) under infrared site-selective laser excitation. A detailed analysis of the absorption and emission spectra, along with measurements of emission intensity dependence on excitation power and relaxation time, confirmed that CL is responsible for the observed emission. Similarly, in [13], UV emission was detected in Yb³⁺:CaF₂ upon near-IR excitation. The UV emission intensity exhibited a cubic dependence on pump power, while the luminescence lifetime was approximately one-third that of isolated Yb³⁺ ions. The observed spectral features matched the self-convoluted spectra of three individual Yb³⁺ ions, confirming that the UV emission originates from the cooperative luminescence of three Yb³⁺ ions. CL also plays a role in sensitization within the Yb/Tb system, where energy transfer occurs from the excited states of Yb³⁺ ion pairs to Tb³⁺ ions [14].

In this study, we employ Dexter’s theory to calculate the Stark level energies of Yb³⁺-Yb³⁺ paired centers in LN, explicitly accounting for the interaction of optical electrons between the ytterbium ions forming the paired center.

2. Materials and Methods

Within the framework of Dexter’s theory [15], we assume that the interaction between impurity ions in an RE³⁺-RE³⁺ paired center is significantly weaker than the interaction between the crystal field (CF) and an individual RE³⁺ ion. Consequently, the Hamiltonian for the RE³⁺-RE³⁺ paired center can be expressed as follows:

$$\widehat{H}={\widehat{H}}_a+{\widehat{H}}_b+{\widehat{V}}_{ab}$$

(1)

where ${\widehat{H}}_a={\widehat{H}}_{ao}+{\widehat{V}}_{CF}$ and ${\widehat{H}}_b={\widehat{H}}_{bo}+{\widehat{V}}_{CF}$ are the Hamiltonians for single Yb³⁺ ions, numbered with indices “a” and “b”, ${\widehat{H}}_{ao}$ (${\widehat{H}}_{bo}$) is the Hamiltonian of the interaction of an optical electron with its own nuclear core, ${\widehat{V}}_{CF}$ is the CF Hamiltonian. Thus,

$${\widehat{H}}_a\left|\lambda ,{\overrightarrow{r}}_1⟩\right.=\left({\widehat{H}}_{ao}+{\widehat{V}}_{CF}\right)\left|\lambda ,{\overrightarrow{r}}_1⟩\right.=E_{a\lambda }\left|\lambda ,{\overrightarrow{r}}_1⟩\right.$$

(2a)

$${\widehat{H}}_b\left|\mu ,{\overrightarrow{r}}_2⟩\right.=\left({\widehat{H}}_{bo}+{\widehat{V}}_{CF}\right)\left|\mu ,{\overrightarrow{r}}_2⟩\right.=E_{b\mu }\left|\mu ,{\overrightarrow{r}}_2⟩\right.$$

(2b)

where $E_{a\lambda }$ and $E_{b\mu }$ (${\psi }_{a\lambda }\left({\stackrel{\rightharpoonup }{r}}_1\right)=\left|\lambda ,{\overrightarrow{r}}_1〉\right.$ and ${\mathsf{\Psi }}_{b\mu }\left(\stackrel{\rightharpoonup }{r}\right)=\left|\begin{array}{c}\mu \\ \stackrel{\rightharpoonup }{r}\end{array}\right.〉$ are the energies (wave functions) of the $\lambda \mathrm{t}\mathrm{h}$ and μth Stark states of “a” and “b” ytterbium ions, respectively. Representing the electron wave functions of a paired center as a product of one-electron wave functions of ions “a” and “b”, ${\psi }_{ab}\left(\lambda ,{\overrightarrow{r}}_1;\mu ,{\overrightarrow{r}}_2\right)={\psi }_a\left(\lambda ,{\overrightarrow{r}}_1\right){\psi }_b\left(\mu ,{\overrightarrow{r}}_2\right)$, for the eigenvalues of Hamiltonian (1), we obtain

$$E\left(a\lambda ,b\mu \right)=E_{a\lambda }+E_{b\mu }+⟨{\psi }_a\left(\lambda ,{\overrightarrow{r}}_1\right)|{\widehat{V}}_{ab}|{\psi }_b\left(\mu ,{\overrightarrow{r}}_2\right)⟩$$

(3)

where ${\overrightarrow{r}}_1$ and ${\overrightarrow{r}}_2$ are the radius vectors of the optical electrons of ions “a” and “b” (Figure 1).

We will consider the Coulomb interaction of the optical electrons of “a” and “b” ions with each other. Then,

$${\widehat{V}}_{ab}={\displaystyle \frac{e^2}{\left|{\overrightarrow{r}}_{12}\right|}}={\displaystyle \frac{e^2}{\left|\overrightarrow{R}+{\overrightarrow{r}}_2-{\overrightarrow{r}}_1\right|}}$$

(4)

where $\overrightarrow{R}$ is the distance between the nuclei of ions “a” and “b”.

Expanding the right-hand side of (4) in a series in the powers of ${\overrightarrow{r}}_1$ and ${\overrightarrow{r}}_2$ $\left(\left|{\overrightarrow{r}}_1\right|, \left|{\overrightarrow{r}}_2\right|\ll \left|\overrightarrow{R}\right|\right)$ and moving to spherical coordinates $\left(r_1,{\theta }_1,{\phi }_1\right)$ and $\left(r_2,{\theta }_2,{\phi }_2\right)$, we obtain

$${\widehat{V}}_{ab}={\sum }_{l_1{l}_2}{\sum }_m{\displaystyle \frac{4\pi e^2}{R^{l_1+l_2+1}}}{F}_{l_1{l}_2}{C}_{l_{1}m l_2-m }^{l0}{D}_{l_{1}m}\left({\omega }_1\right)D_{l_2-m}\left({\omega }_2\right)$$

(5)

where the following notations are introduced,

$$F_{l_1{l}_2}={\left(-1\right)}^{l_2}\sqrt{{\displaystyle \frac{\left(2l_1+2l_2\right)!}{\left(2l_1+1\right)!\left(2l_2+1\right)!}}}$$

(6)

$$D_{l_{1}m}\left({\omega }_1\right)=r_1^{l_1}{Y}_{l_{1}m}\left({\omega }_1\right); D_{l_2-m}\left({\omega }_2\right)=r_2^{l_2}{Y}_{l_2-m}\left({\omega }_2\right)$$

(7)

where ${\omega }_1\equiv \left({\theta }_1,{\phi }_1\right)$, ${\omega }_2\equiv \left({\theta }_2,{\phi }_2\right)$, $Y_{kq}\left(\theta ,\phi \right)$ is the spherical function, and $C_{l_1{m}_1 l_2{m}_{2 } }^{lm}$ is the Clebsch–Gordan coefficient. Using (5) and (7), we represent the third term of Formula (3) in the form

$$\begin{gathered} ⟨{\psi }_a\left(\lambda ,{\overrightarrow{r}}_1\right){\psi }_b\left(\mu ,{\overrightarrow{r}}_2\right)|{\widehat{V}}_{ab}|{\psi }_a\left(\lambda ,{\overrightarrow{r}}_1\right){\psi }_b\left(\mu ,{\overrightarrow{r}}_2\right)⟩= \\ {\sum }_{l_1{l}_2}{\sum }_m{\displaystyle \frac{4\pi e^2}{R^{l_1+l_2+1}}}{F}_{l_1{l}_2}{C}_{\begin{array}{cc}{l}_{1}m& l_2-m\end{array}}^{l_1+l_{2 }0}⟨{\psi }_a\left(\lambda ,{\overrightarrow{r}}_1\right)|r_1^{l_1}{Y}_{l_{1}m}\left({\omega }_1\right)|{\psi }_a\left(\lambda ,{\overrightarrow{r}}_1\right)⟩⟨{\psi }_b\left(\mu ,{\overrightarrow{r}}_2\right)|r_2^{l_2}{Y}_{l_2-m}\left({\omega }_2\right)|{\psi }_b\left(\mu ,{\overrightarrow{r}}_2\right)⟩ \end{gathered}$$

(8)

In this case, due to the selection rules, the non-zero contributions are given by the terms $l_1, l_2=0, 2, 4, 6$. At the same time, the term $l_1=l_2=0$ can be discarded, since taking it into account leads to a uniform shift in energy levels.

3. Results

Within the weak crystal-field (CF) approximation, the wave functions of the Stark levels for a single RE³⁺ center, expressed in the LSJM representation, take the form

$$|\psi \left(\nu ,\overrightarrow{r}\right)⟩=R_{RE}\left(r\right){\sum }_{JM}{d}_{LSJM}^{\left(\nu \right)}|LSJM⟩$$

(9)

where $R_{RE}\left(r\right)$ are the Hartree–Fock radial wave functions of the RE³⁺ ion, the explicit form of which for RE³⁺ ions is given in [16], $d_{LSJM}^{\left(\nu \right)}$ are the numerical coefficients, L, S, and J are the orbital, spin, and total angular momenta, and M is the projection of the total angular momentum. Thus, calculating the matrix elements in Equation (8) reduced to calculation matrix elements that are diagonal in S, L, and J,$⟨LSJM|\sum _i{r}_i^l{Y}_{lm}\left(i\right)|LSJM\prime ⟩$, where summation is performed over the equivalent optical electrons of the RE³⁺ ion. By applying the Wigner–Eckart theorem [17] and transitioning to unit tensor operators $U_l$, we obtain the following:

$$⟨LSJM|{\sum }_i{r}_i^l{Y}_{lm}\left(i\right)|LSJM\prime ⟩={\left(-1\right)}^{l+f}\overline{r^l}\sqrt{{\displaystyle \frac{7\left(2l+1\right)}{4\pi \left(2J+1\right)}}}{C}_{\begin{array}{cc}30& l0\end{array}}^{30}{C}_{\begin{array}{cc}JM& lm\end{array}}^{J{M}^{\prime }}⟨LSJ|\left|U_l\right||LSJ⟩$$

(10)

The given matrix element $〈LSJ‖U_l‖LSJ〉$ is calculated using the Racah scheme [17,18].

$$\begin{gathered} ⟨LSJ|\left|U_l\right||LSJ⟩={\left(-1\right)}^{S+J+L}N\left(2J+1\right)(2L+ \\ 1)\left\{\begin{array}{ccc}J& l& J\\ L& S& L\end{array}\right\}{\sum }_{L_1{S}_1}{\left(-1\right)}^{L_1}\left\{\begin{array}{ccc}L& 3& L_1\\ 3& L& l\end{array}\right\}{\left[G_{L_1{S}_1}^{LS}\right]}^2 \end{gathered}$$

(11)

In (10) and (11), the following notations are introduced: N is the number of equivalent electrons (holes) of an unfilled electron shell, $\left\{\begin{array}{ccc}.& .& .\\ .& .& .\end{array}\right\}$ represents the 6j symbols, $G_{L_1{S}_1}^{LS}$ is the fractional parentage coefficient of Racah, the numerical values of which for pⁿ, dⁿ, and fⁿ electron shells are tabulated in [19], and $\overline{r^l}={\displaystyle \underset{0}{\overset{\infty }{\int }}{\left[R_{4f}\left(r\right)\right]}^2\hspace{0.17em}{r}^{l+2}\hspace{0.17em}dr}$ is the average value of the radius vector of the optical electron of the impurity ion.

For Yb³⁺ ions, the reduced matrix elements, calculated using Formula (11), are equal to $⟨{\displaystyle \frac{7}{2}}\Vert U_2\Vert {\displaystyle \frac{7}{2}}⟩={\displaystyle \frac{5\sqrt{2}}{7}}$, $⟨{\displaystyle \frac{7}{2}}\Vert U_4\Vert {\displaystyle \frac{7}{2}}⟩={\displaystyle \frac{6}{7}}$, $⟨{\displaystyle \frac{7}{2}}\Vert U_6\Vert {\displaystyle \frac{7}{2}}⟩=\sqrt{{\displaystyle \frac{2}{7}}}$, $⟨{\displaystyle \frac{5}{2}}\Vert U_2\Vert {\displaystyle \frac{5}{2}}⟩={\displaystyle \frac{6}{7}}$, $⟨{\displaystyle \frac{5}{2}}\Vert U_4\Vert {\displaystyle \frac{5}{2}}⟩={\displaystyle \frac{\sqrt{22}}{7}}$, $⟨{\displaystyle \frac{5}{2}}\Vert U_6\Vert {\displaystyle \frac{5}{2}}⟩=0$. The average values of the radius vector of the optical electron of the Yb³⁺ ion are given in [16]: $\overline{r^2}=0.613 a.e.$, $\overline{r^4}=0.96 a.e.$, $\overline{r^6}=3.104 a.e$.

4. Discussion

As is well known, the ground electronic configuration (4f¹³) of the Yb³⁺ ion comprises an eight-fold degenerate ground-state manifold, ²F_7/2, and a six-fold degenerate excited-state manifold, ²F_5/2. The crystal field (CF) splits these manifolds into four and three Kramers doublets, respectively. The spectroscopic properties of LN:Yb crystals with varying impurity ion concentrations were thoroughly investigated in [2,20,21,22]. Specifically, in [20], the wave functions of the Stark states of the Yb³⁺ ion were constructed within the LSJM representation using the weak CP approximation (12), as detailed below.

$$\begin{array}{l}{E}_{a1}=E_{b1}=0;\mathrm{c}{\mathrm{m}}^{-1}\dots \dots \left|{\nu }_{\hspace{0.17em}1}\right.〉=\pm 0.509416\hspace{0.17em}\hspace{0.17em}\left|{\displaystyle \frac{7}{2}}\hspace{0.17em}\pm {\displaystyle \frac{1}{2}}\right.〉-0.616433\hspace{0.17em}\left|{\displaystyle \frac{7}{2}}\hspace{0.17em}\mp {\displaystyle \frac{5}{2}}\right.〉-0.600421\hspace{0.17em}\left|{\displaystyle \frac{7}{2}}\hspace{0.17em}\pm {\displaystyle \frac{7}{2}}\right.〉\hspace{0.17em},\\ E_{a2}=E_{b2}=303\dots \dots \left|{\nu }_{\hspace{0.17em}2}\right.〉=\pm 0.804567\hspace{0.17em}\hspace{0.17em}\left|{\displaystyle \frac{7}{2}}\hspace{0.17em}\pm {\displaystyle \frac{1}{2}}\right.〉+0.093697\hspace{0.17em}\left|{\displaystyle \frac{7}{2}}\hspace{0.17em}\mp {\displaystyle \frac{5}{2}}\right.〉+0.586424\hspace{0.17em}\hspace{0.17em}\left|{\displaystyle \frac{7}{2}}\hspace{0.17em}\pm {\displaystyle \frac{7}{2}}\right.〉\hspace{0.17em},\\ E_{a3}=E_{b3}=495\dots \dots \left|{\nu }_3\right.〉=\pm 0.305234\hspace{0.17em}\hspace{0.17em}\left|{\displaystyle \frac{7}{2}}\hspace{0.17em}\pm {\displaystyle \frac{1}{2}}\right.〉+0.781812\hspace{0.17em}\left|{\displaystyle \frac{7}{2}}\hspace{0.17em}\mp {\displaystyle \frac{5}{2}}\right.〉-0.543692\hspace{0.17em}\left|{\displaystyle \frac{7}{2}}\hspace{0.17em}\pm {\displaystyle \frac{7}{2}}\right.〉\hspace{0.17em},\\ E_{a4}=E_{b4}=769\dots \dots \left|{\nu }_{\hspace{0.17em}4}\right.〉=\left|{\displaystyle \frac{7}{2}}\hspace{0.17em}\pm {\displaystyle \frac{3}{2}}\right.〉\hspace{0.17em},\\ E_{a5}=E_{b5}=\mathrm{10,204}\dots \dots \left|{\nu }_{\hspace{0.17em}5}\right.〉=-0.442843\hspace{0.17em}\hspace{0.17em}\left|{\displaystyle \frac{5}{2}}\hspace{0.17em}\pm {\displaystyle \frac{1}{2}}\right.〉\pm 0.896599\hspace{0.17em}\left|{\displaystyle \frac{5}{2}}\hspace{0.17em}\mp {\displaystyle \frac{5}{2}}\right.〉\hspace{0.17em},\\ E_{a6}=E_{b6}=\mathrm{10,471}\dots \dots \left|{\nu }_{\hspace{0.17em}6}\right.〉=0.896599\hspace{0.17em}\hspace{0.17em}\left|{\displaystyle \frac{5}{2}}\hspace{0.17em}\pm {\displaystyle \frac{1}{2}}\right.〉\pm 0.442843\hspace{0.17em}\left|{\displaystyle \frac{5}{2}}\hspace{0.17em}\mp {\displaystyle \frac{5}{2}}\right.〉\hspace{0.17em},\\ E_{a7}=E_{b7}=\mathrm{10,893}\dots \dots \left|{\nu }_{\hspace{0.17em}7}\right.〉=\pm \hspace{0.17em}\left|{\displaystyle \frac{5}{2}}\hspace{0.17em}\pm {\displaystyle \frac{3}{2}}\right.〉\hspace{0.17em},\end{array}$$

(12)

As a result of the interaction (4), the Kramers states ${\nu }_i$ and ${\nu }_j$ of individual Yb³⁺ ions forming a paired center become mixed, giving rise to seven four-fold and twenty-one eight-fold degenerate states $\left({\nu }_i, {\nu }_j\right)$, The energies of these states are determined by the expression (3). The values of the energy levels of the paired center Yb³⁺-Yb³⁺ calculated using the above formulas are shown in

Table 1. Energy levels $\left({\nu }_i, {\nu }_j\right)$ of the paired center Yb³⁺-Yb³⁺ in LN.

N	a Levels of Yb-Yb	b $⟨\mathit{a}\mathit{\lambda };\mathit{b}\mathit{\mu }⟩$ in cm−1	c $\mathit{E}\left(\mathit{a}\mathit{\lambda };\mathit{b}\mathit{\mu }\right)$ cm−1	d Levels of Yb-Yb	d $\mathit{E}\left(\mathit{a}\mathit{\lambda };\mathit{b}\mathit{\mu }\right)$ cm−1
1	(1,1)	11.0	11.0	(1,1)	11	0
2	(1,2) and (2,1)	32.2	335.2	(1,2) and (2,1)	335.2	324.2
3	(1,3) and (3,1)	−35.4	459.6	(1,3) and (3,1)	459.6	448.6
4	(1,4) and (4,1)	13.3	782.3	(2,2)	660.8	649.8
5	(1,5) and (5,1)	183.3	10,387.3	(1,4) and (4,1)	782.3	771.3
6	(1,6) and (6,1)	7.9	10,478.9	(2,3) and (3,2)	812.4	801.4
7	(1,7) and (7,1)	175.4	11,068.4	(3,3)	908.2	897.2
8	(2,2)	54.8	660.8	(2,4) and (4,2)	1108.5	1097.5
9	(2,3) and (3,2)	14.4	812.4	(3,4) and (4,3)	1230.4	1219.4
10	(2,4) and (4,2)	36.5	1108.5	(4,4)	1556.9	1545.9
11	(2,5) and (5,2)	203.9	10,710.9	(1,5) and (5,1)	10,387.3	10,376.3
12	(2,6) and (6,2)	31.2	10,805.2	(1,6) and (6,1)	10,478.9	10,467.9
13	(2,7) and (7,2)	−153.2	11,042.8	(2,5) and (5,2)	10,710.9	10,699.9
14	(3,3)	−81.8	908.2	(2,6) and (6,2)	10,805.2	10,794.2
15	(3,4) and (4,3)	−33.6	1230.4	(3,5) and (5,3)	10,836	10,825.0
16	(3,5) and (5,3)	137.0	10,836.0	(3,6) and (6,3)	10,927	10,916.0
17	(3,6) and (6,3)	−39.0	10,927.0	(2,7) and (7,2)	11,042.8	11,031.8
18	(3,7) and (7,3)	−122.1	11,265.9	(1,7) and (7,1)-	11,068.4	11,057.4
19	(4,4)	18.9	1556.9	(4,5) and (5,4)	11,157.1	11,146.1
20	(4,5) and (5,4)	184.1	11,157.1	(4,6) and (6,4)	11,253.8	11,242.8
21	(4,6) and (6,4)	13.8	11,253.8	(3,7) and (7,3)	11,265.9	11,254.9
22	(4,7) and (7,4)	−171.5	11,490.5	(4,7) and (7,4)	11,490.5	11,479.5
23	(5,5)	356.5	20,764.5	(5,5)	20,764.5	20,753.5
24	(5,6) and (6,5)	178.6	20,853.6	(5,6) and (6,5)	20,853.6	20,842.6
25	(5,7) and (7,5)	3.8	21,100.8	(6,6)	20,950.3	20,939.3
26	(6,6)	8.3	20,950.3	(5,7) and (7,5)	21,100.8	21,089.8
27	(6,7) and (7,6)	−176.9	21,187.1	(6,7) and (7,6)	21,187.1	21,176.1
28	(7,7)	−360.0	21,426.0	(7,7)	21,426	21,415.0

^a Stark levels of Yb³⁺-Yb³⁺ pair. ^b Matrix elements of the ${\widehat{V}}_{ab}$. ^c Energy of the $\left(a\lambda ;b\mu \right)$ level. ^d Stark levels ordered by energy scale.

. As shown in Table 1, the energy levels of the Yb³⁺-Yb³⁺ center are clustered into three distinct regions (last column of Table 1), 0–1545.9 cm⁻¹, 10,376.3–11,479.5 cm⁻¹, and 20,753.5–21,415 cm⁻¹, separated by approximately 9000 cm⁻¹. The energy separation between levels within each group ranges from approximately 100 to 300 cm⁻¹. Consequently, the levels (1,5) and (5,5) are metastable, allowing for possible luminescence under appropriate excitation conditions. To facilitate comparison with experimentally observed cooperative luminescence wavelengths [9],

Table 2. Calculated and measured values of the wavelengths of CL at 12 K.

Transition	${\mathit{\lambda }}_{\mathit{c}\mathit{a}\mathit{l}}$, nm	${\mathit{\lambda }}_{\mathit{e}\mathit{x}\mathit{p}}$, nm [11]
$\left(\mathrm{5,5}\right)\to \left(\mathrm{1,2}\right)$	489.5	490.0
$\left(\mathrm{5,5}\right)\to \left(\mathrm{2,2}\right)$	497.4	497.3
$\left(\mathrm{5,5}\right)\to \left(\mathrm{3,3}\right)$	503.6	505.0
$\left(\mathrm{5,5}\right)\to \left(\mathrm{2,4}\right)$	508.8	510.0
$\left(\mathrm{5,5}\right)\to \left(\mathrm{2,4}\right)$	512.0	513.1
$\left(\mathrm{5,5}\right)\to \left(\mathrm{4,4}\right)$	520.6	522.0

presents the transition wavelengths from the metastable level (5,5), calculated based on the data in Table 1. It is evident that the calculated values closely match the measured wavelengths, with an accuracy comparable to the spectral line widths $\left(∆\lambda ~1÷1.5 \mathrm{n}\mathrm{m}\right)$.

It should be noted that to reconstruct the cooperative luminescence spectrum, $F\left(\lambda \right)$, of the Yb³⁺-Yb³⁺ dimer, the self-convolution of the spectrum,$f\left(\lambda \right)$, of an individual Yb³⁺ ion is used:

$$F\left(\lambda \right)={\int }_{-\infty }^{\infty }f\left({\lambda }^{\prime }\right)f\left(\lambda -{\lambda }^{\prime }\right)d{\lambda }^{\prime }$$

(13)

It is evident that when using the luminescence spectrum of Yb³⁺ in the infrared region (900–1200 nm), the cooperative luminescence spectrum, calculated using Equation (13), falls within the visible wavelength range (450–600 nm), as observed in [10,11,12,13,14].

For LN:Yb at low temperatures, this corresponds to transitions from level (5,5) to levels (i, j), where i, j = 1, 2, 3, and 4 (Table 2). However, the absorption and emission spectra of the Yb³⁺ ion theoretically include lines in the Long-Wave Infrared (LWIR) region, originating from transitions between Stark levels within the same multiplet. However, due to strong phonon suppression, these lines are so weak that they remain experimentally unobservable and are therefore neglected when analyzing the spectra of individual Yb³⁺ centers. However, incorporating these transitions into $f\left(\lambda \right)$ in the calculation using Equation (13) results in the appearance of an additional set of lines in the infrared region (10,376.3–11,479.5 cm⁻¹, Table 1). Notably, the numerous additional lines observed in the infrared absorption and luminescence spectra of Yb³⁺-containing materials (e.g., [2,13,23]) may also originate from transitions between the energy levels of Yb³⁺-Yb³⁺ paired centers.

It is worth noting that at sufficiently high concentrations of paired centers, the absorption spectrum contains lines in the wavelength range of 460–480 nm [11]. However, to our knowledge, no experimental studies have been conducted to measure the absorption of LN: Yb³⁺ crystals in this spectral region.

5. Conclusions

Considering the interaction of optical electrons within the impurity ion paired center significantly alters the energy-level structure, distinguishing three groups of levels in the regions 0–1545.9 cm⁻¹, 10,376.3–11,479.5 cm⁻¹, and 20,753.5–21,415 cm⁻¹, separated by approximately 9000 cm⁻¹. Within each group, the energy spacing between levels ranges from approximately 100 to 300 cm⁻¹. As shown in Table 1, the energy spectrum of the Yb³⁺-Yb³⁺ paired center includes two metastable levels, (5,1) and (5,5), which are separated from the nearest lower level by energy gaps of 8830.4 cm⁻¹ and 9274 cm⁻¹, respectively. The presence of the metastable level (5,1) enables the excitation of the (5,5) level when pumped at a wavelength of 955 nm through two mechanisms: reabsorption from the (1,5) level

$$\left(\mathrm{1,1}\right)\stackrel{955 \mathrm{n}\mathrm{m}}{\to }\left(\mathrm{1,6}\right)⇝\left(\mathrm{1,5}\right)\stackrel{955\mathrm{nm}}{\to }\left(\mathrm{6,5}\right)⇝\left(\mathrm{5,5}\right)$$

(14)

and cross-relaxation transition according to the scheme

$$\left(\mathrm{1,5}\right)⟶\left(\mathrm{1,1}\right):\left(\mathrm{1,5}\right)⟶\left(\mathrm{5,5}\right)$$

(15)

The calculated and observed wavelengths of cooperative luminescence at low temperatures [11] show a satisfactory agreement, with an accuracy of ∆λ~1 ÷ 1.5 nm (Table 2).

Notably, the cooperative luminescence spectrum of the Yb³⁺-Yb³⁺ paired center is determined by the self-convolution of the luminescence spectrum of a single Yb³⁺ ion (Equation (13)). In this approach, the spectra of single centers in the infrared (IR) region are used, which is a reasonable assumption. Consequently, only lines in the visible region are observed, corresponding to transitions from the (5, k) (k = 5, 6, and 7) levels to the levels (j, i) (i, j = 1, 2, 3, and 4) levels. However, considering that the absorption and emission spectra of the Yb³⁺ ion theoretically also contain lines in the Long-Wave Infrared (LWIR) region due to Stark intra-manifold transitions, self-convolution should also yield lines in the IR region. These lines are caused by transitions from the (5, k) (k = 5, 6, and 7) levels to the (j, i) (j = 1, 2, 3, 4 and i = 5, 6, 7) levels or from the (j, i) (j = 1, 2, 3, 4 and i = 5, 6, 7) levels to the (j, i) (i, j = 1, 2, 3, and 4) levels (Table 1).

Additionally, we note that the weakly intense lines observed in the low-temperature emission and absorption spectra of a single Yb³⁺ center (see, for example, [15,22,23]) may originate from transitions between the (1,5) level and lower Stark levels, as well as from transitions of the type (1,1) → $\left(\lambda ,\mu \right)$, at $\lambda =1, 2, 3, 4; \mu =5, 6, 7$.