Second-Neighbor Hopping Effects in the Two-Dimensional Attractive Hubbard Model
Abstract
:1. Introduction
2. Model and Methodology
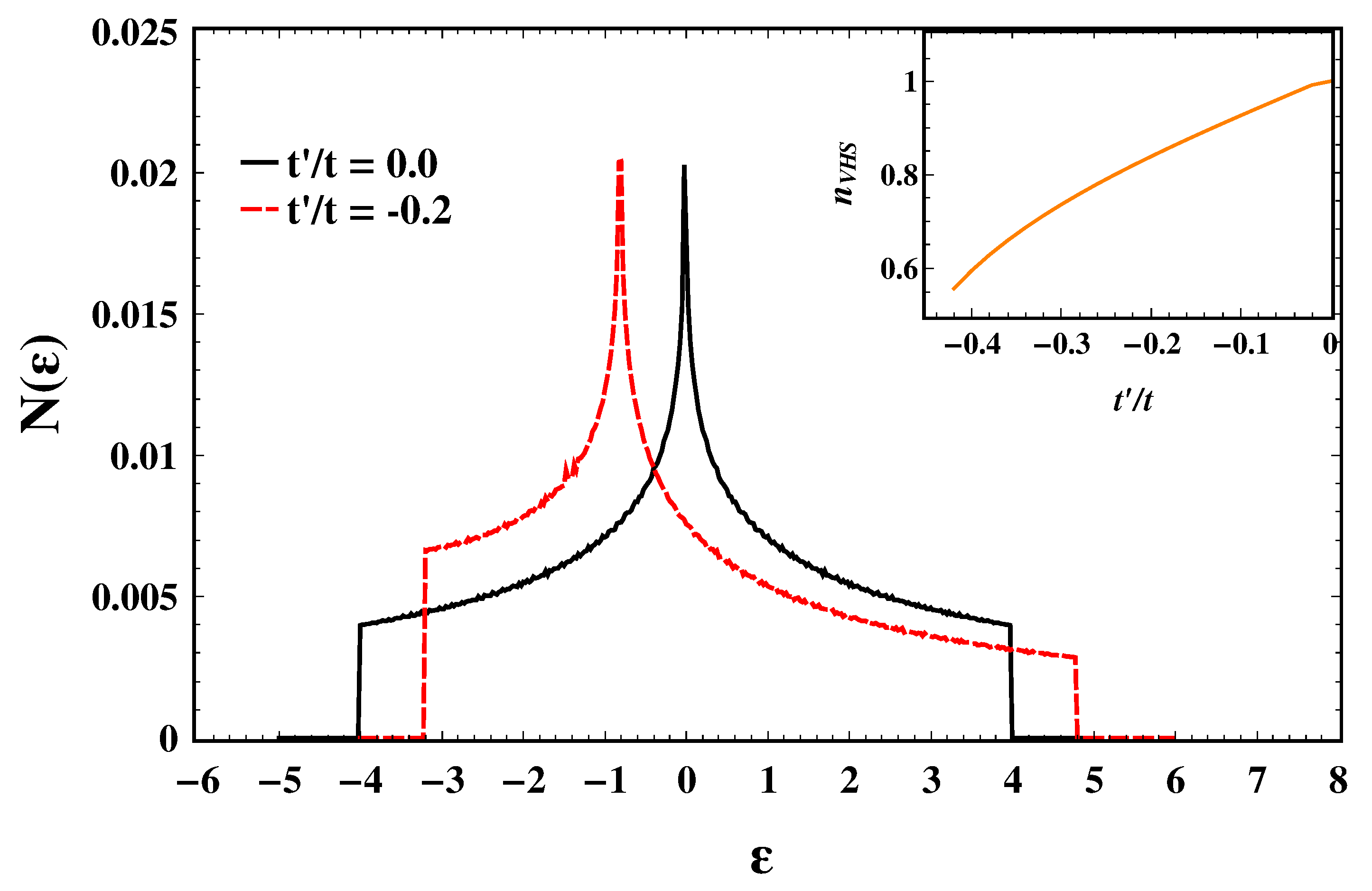
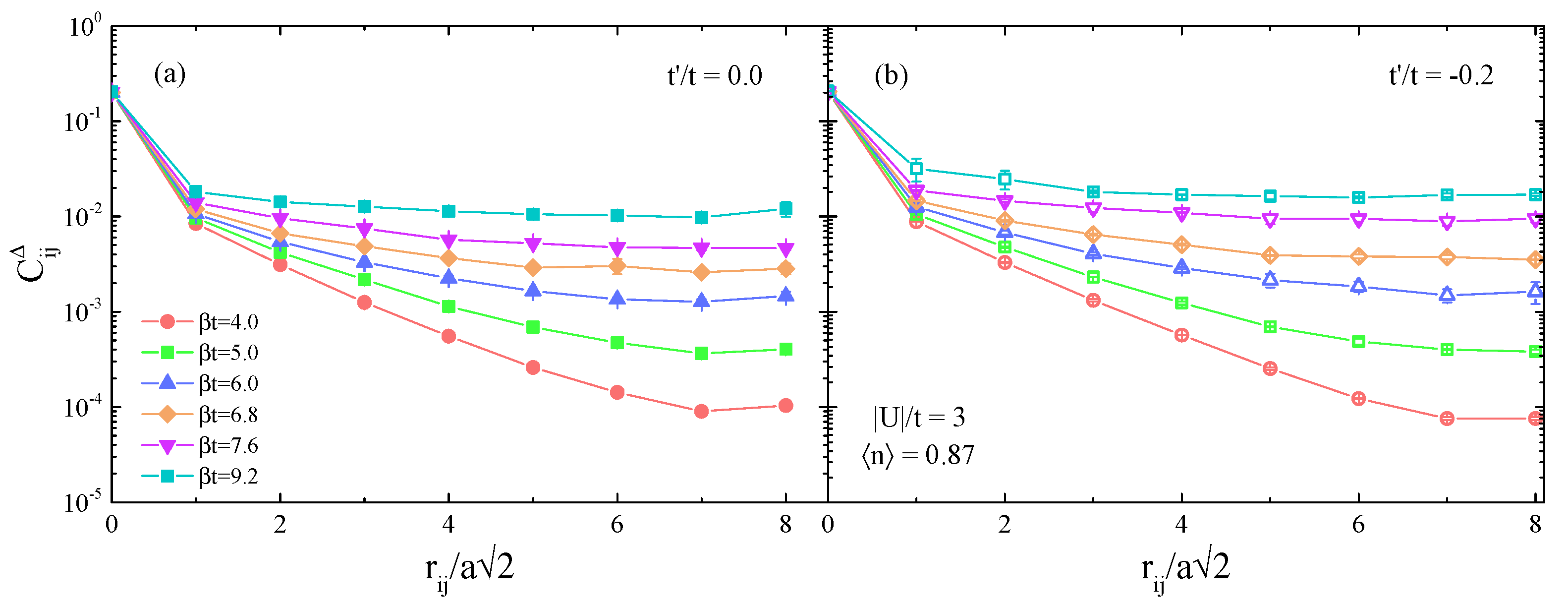
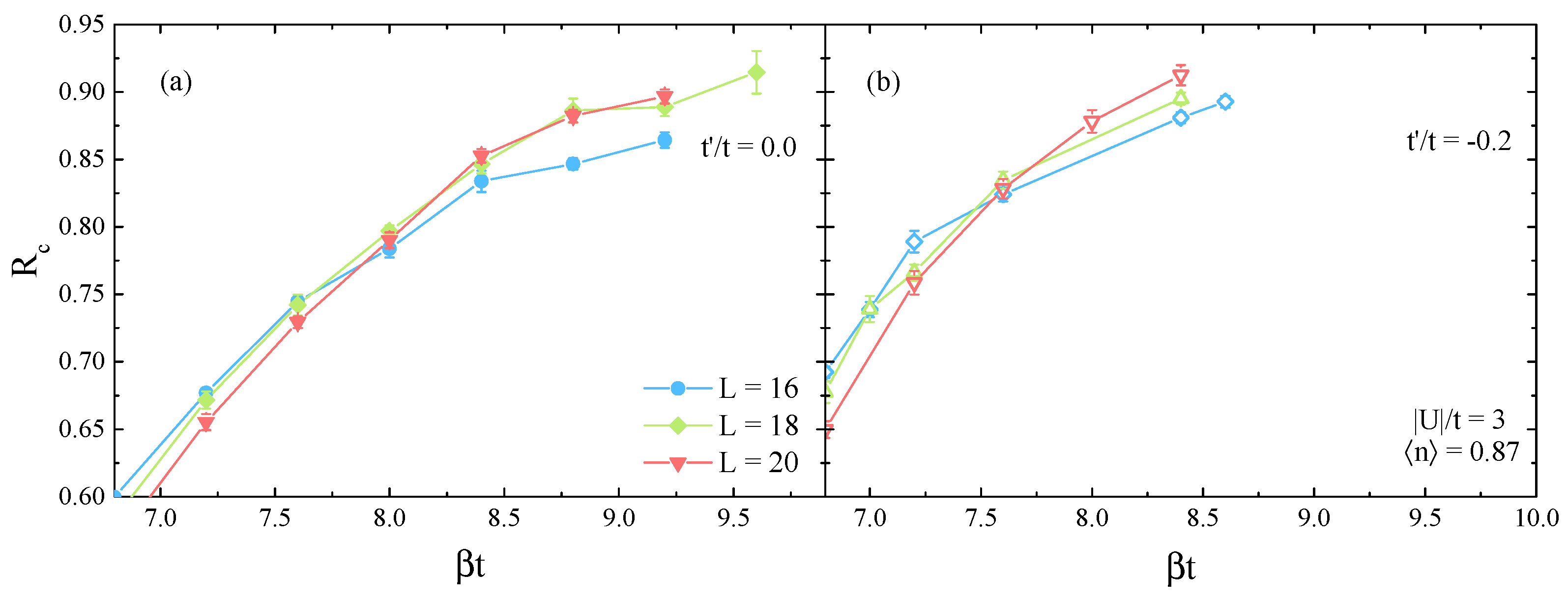
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHM | Attractive Hubbard model |
| CDW | Charge-density wave |
| DOS | density of states |
| NN | nearest neighbor |
| NNN | next-nearest neighbor |
| QMC | Quantum Monte Carlo |
| DQMC | Determinant Quantum Monte Carlo |
References
- Micnas, R.; Ranninger, J.; Robaszkiewicz, S. Superconductivity in narrow-band systems with local nonretarded attractive interactions. Rev. Mod. Phys. 1990, 62, 113–171. [Google Scholar] [CrossRef]
- Anderson, P.W. Model for the Electronic Structure of Amorphous Semiconductors. Phys. Rev. Lett. 1975, 34, 953–955. [Google Scholar] [CrossRef]
- Hirsch, J.E. Two-dimensional Hubbard model: Numerical simulation study. Phys. Rev. B 1985, 31, 4403–4419. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.C.; Ogata, M.; Rice, T.M. Attractive interaction and superconductivity for K3C60. Phys. Rev. Lett. 1991, 67, 3452–3455. [Google Scholar] [CrossRef]
- Wilson, J.A. Developments in the negative-U modelling of the cuprate HTSC systems. J. Phys. Condens. Matter 2001, 13, R945–R977. [Google Scholar] [CrossRef]
- Fontenele, R.A.; Costa, N.C.; dos Santos, R.R.; Paiva, T. Two-dimensional attractive Hubbard model and the BCS-BEC crossover. Phys. Rev. B 2022, 105, 184502. [Google Scholar] [CrossRef]
- Chin, C.; Grimm, R.; Julienne, P.; Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010, 82, 1225–1286. [Google Scholar] [CrossRef]
- Jaksch, D.; Zoller, P. The cold atom Hubbard toolbox. Ann. Phys. 2005, 315, 52. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885. [Google Scholar] [CrossRef]
- Esslinger, T. Fermi-Hubbard Physics with Atoms in an Optical Lattice. Annu. Rev. Condens. Matter Phys. 2010, 1, 129–152. [Google Scholar] [CrossRef]
- McKay, D.C.; DeMarco, B. Cooling in strongly correlated optical lattices: Prospects and challenges. Rep. Prog. Phys. 2011, 74, 054401. [Google Scholar] [CrossRef]
- Mitra, D.; Brown, P.T.; Guardado-Sanchez, E.; Kondov, S.S.; Devakul, T.; Huse, D.A.; Schauss, P.; Bakr, W.S. Quantum gas microscopy of an attractive Fermi?Hubbard system. Nat. Phys. 2018, 14, 173–177. [Google Scholar] [CrossRef]
- Hirsch, J.E.; Scalapino, D.J. Enhanced Superconductivity in Quasi Two-Dimensional Systems. Phys. Rev. Lett. 1986, 56, 2732–2735. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, R.R. Second-neighbor hopping in the attractive Hubbard model. Phys. Rev. B 1992, 46, 5496–5498. [Google Scholar] [CrossRef]
- Yang, J.; Liu, L.; Mongkolkiattichai, J.; Schauss, P. Site-Resolved Imaging of Ultracold Fermions in a Triangular-Lattice Quantum Gas Microscope. PRX Quantum 2021, 2, 020344. [Google Scholar] [CrossRef]
- Lin, H.Q.; Hirsch, J.E. Two-dimensional Hubbard model with nearest- and next-nearest-neighbor hopping. Phys. Rev. B 1987, 35, 3359–3368. [Google Scholar] [CrossRef]
- Blankenbecler, R.; Scalapino, D.J.; Sugar, R.L. Monte Carlo calculations of coupled boson-fermion systems. I. Phys. Rev. D 1981, 24, 2278–2286. [Google Scholar] [CrossRef]
- Hirsch, J.E. Discrete Hubbard-Stratonovich transformation for fermion lattice models. Phys. Rev. B 1983, 28, 4059. [Google Scholar] [CrossRef]
- White, S.R.; Scalapino, D.J.; Sugar, R.L.; Loh, E.Y.; Gubernatis, J.E.; Scalettar, R.T. Numerical study of the two-dimensional Hubbard model. Phys. Rev. B 1989, 40, 506–516. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, R.R. Introduction to quantum Monte Carlo simulations for fermionic systems. Braz. J. Phys. 2003, 33, 36–54. [Google Scholar] [CrossRef]
- Kaul, R.K. Spin Nematics, Valence-Bond Solids, and Spin Liquids in SO(N) Quantum Spin Models on the Triangular Lattice. Phys. Rev. Lett. 2015, 115, 157202. [Google Scholar] [CrossRef]
- Sato, T.; Assaad, F.F.; Grover, T. Quantum Monte Carlo Simulation of Frustrated Kondo Lattice Models. Phys. Rev. Lett. 2018, 120, 107201. [Google Scholar] [CrossRef] [PubMed]
- Darmawan, A.S.; Nomura, Y.; Yamaji, Y.; Imada, M. Stripe and superconducting order competing in the Hubbard model on a square lattice studied by a combined variational Monte Carlo and tensor network method. Phys. Rev. B 2018, 98, 205132. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133–1136. [Google Scholar] [CrossRef]
- Daul, S.; Noack, R.M. Ferromagnetic transition and phase diagram of the one-dimensional Hubbard model with next-nearest-neighbor hopping. Phys. Rev. B 1998, 58, 2635–2650. [Google Scholar] [CrossRef]
- Huse, D.A. Ground-state staggered magnetization of two-dimensional quantum Heisenberg antiferromagnets. Phys. Rev. B 1988, 37, 2380–2382. [Google Scholar] [CrossRef] [PubMed]
- Hurt, D.; Odabashian, E.; Pickett, W.E.; Scalettar, R.T.; Mondaini, F.; Paiva, T.; dos Santos, R.R. Destruction of superconductivity by impurities in the attractive Hubbard model. Phys. Rev. B 2005, 72, 144513. [Google Scholar] [CrossRef]
- Mondaini, F.; Paiva, T.; dos Santos, R.R.; Scalettar, R.T. Disordered two-dimensional superconductors: Roles of temperature and interaction strength. Phys. Rev. B 2008, 78, 174519. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fontenele, R.A.; Vasconcelos, N.; Costa, N.C.; Paiva, T.; dos Santos, R.R. Second-Neighbor Hopping Effects in the Two-Dimensional Attractive Hubbard Model. Condens. Matter 2023, 8, 11. https://doi.org/10.3390/condmat8010011
Fontenele RA, Vasconcelos N, Costa NC, Paiva T, dos Santos RR. Second-Neighbor Hopping Effects in the Two-Dimensional Attractive Hubbard Model. Condensed Matter. 2023; 8(1):11. https://doi.org/10.3390/condmat8010011
Chicago/Turabian StyleFontenele, Rodrigo Alves, Nathan Vasconcelos, Natanael Carvalho Costa, Thereza Paiva, and Raimundo Rocha dos Santos. 2023. "Second-Neighbor Hopping Effects in the Two-Dimensional Attractive Hubbard Model" Condensed Matter 8, no. 1: 11. https://doi.org/10.3390/condmat8010011
APA StyleFontenele, R. A., Vasconcelos, N., Costa, N. C., Paiva, T., & dos Santos, R. R. (2023). Second-Neighbor Hopping Effects in the Two-Dimensional Attractive Hubbard Model. Condensed Matter, 8(1), 11. https://doi.org/10.3390/condmat8010011







