Spin Transport in Magnetically Ordered Systems: Ferromagnets, Antiferromagnets and Frustrated Systems

Abstract

In this review, we outline the important results on the resistivity encountered by an electron in magnetically ordered materials. The mechanism of the collision between the electron and the lattice spins is shown. Experiments on the spin resistivity in various magnetic materials as well as the theoretical background are recalled. We focus on our works of 15 years of principally using Monte Carlo simulations. In these works, we have studied the spin resistivity in various kinds of magnetic systems ranging from ferromagnets and antiferromagnets to frustrated spin systems. It is found that the spin resistivity shows a broad peak at the transition temperature in systems with a second-order phase transition, while it undergoes a discontinuous jump at the transition temperature of a first-order transition. New results on the hexagonal-close-packed (HCP) antiferromagnet are also shown in extended detail for the Ising case in both the frustrated and non-frustrated parameter regions.

1. Introduction

The resistivity encountered by the displacement of an electron driven by an applied electric field in a material is due to its collisions with the material constituents, such as atoms. In general these collisions are caused not by direct contacts but by various potentials and magnetic and electric fields from different sources. As a matter of fact, the motion of the electron is slowed down except in the superconducting regime. One can mention many simple examples such as the motion of an electron in a magnet or in a lattice with vibrating atoms (phonons) under an applied electric field.

The investigation of the resistivity is one of the most important tasks in condensed matter physics. Apart from the desire to understand the mechanisms lying behind the resistivity, numerous applications using the transport properties of electrons in electronic devices have motivated an increasing number of studies—experimentally, theoretically and numerically. The study of the resistivity started after the discovery of the electron more than a century ago by the simple free-electron Drude theory, which takes into account the relaxation time $\tau$ between two successive collisions due to atoms. The following relation has been established:

$$\sigma = \frac{n{e}^2\tau }{m}$$

(1)

where $\sigma$ is the conductivity, e the electron charge, $\tau$ the electron relaxation time, m the electron mass and n the number of electrons crossing a unit’s surface per unit of time.

Over the years, there has been a large number of more realistic theories of resistivity that take into account different interactions. Nevertheless, this relation is still valid if the electron mass m is replaced by its effective mass $m^{*}$, which includes effects of the interactions of the electron with its environment. The relaxation time $\tau$ should also be modified; it is no more a constant, but it depends on the collision mechanism. In a crystal, it is known that the effective mass of the electron can be “heavier” or “lighter” than its mass at rest $m_0$ because it contains the effects of various interactions. This strongly modifies the mobility of the electron in crystals. As for $\tau$, it has a strong effect on the temperature dependence of the resistivity. It has been established that $\tau$ depends on a power of the electron energy. This power depends on the collision process, such as collisions with charged impurities, neutral impurities, magnetic impurities, phonons, magnons, etc. Thus, in a crystal, the total resistivity ${\rho }_t(T)$ is a sum of the contributions coming from various collision processes. At low temperature (T), it is given by

$${\rho }_t(T) = {\rho }_0 + A_1{T}^2 + A_2{T}^5 + A_{3}ln\frac{\mu }{T}$$

(2)

where $A_1$, $A_2$ and $A_3$ are constants. The first term is T-independent, the second term, proportional to $T^2$, stems from the scattering of the conducting electron at low T by lattice spin-waves. Note that the resistivity caused by a Fermi liquid is also proportional to $T^2$ with another coefficient. The $T^5$ term that is observed in metals comes from the diffusion of conduction electrons by atomic vibrations. However, the resistivity in metals show a linear T dependence at high T. The last term expresses the contribution from the quantum Kondo effect, namely the scattering of conduction electrons by magnetic impurities at extremely low T.

In this review, we focus our attention on the resistivity $\rho$ due to the spin of the conduction electron in magnetically ordered materials. For short, let us call it the “spin resistivity” hereafter. This spin resistivity has been widely studied both experimentally and theoretically for more than five decades. The rapid development of the field is due mainly to many applications in spintronics.

We are interested in magnetic materials that show a phase transition from a magnetically ordered phase, such as ferromagnets and antiferromagnets, to the paramagnetic state. Let us mention in the following some experiments that have been performed in magnetic materials, including metals, semiconductors and superconductors. These experiments carried out on various materials show different shapes of the spin resistivity around the phase-transition temperature: SrRuO${}_3$ thin films [1], Ru-doped La${}_{0.4}$Ca${}_{0.6}$MnO${}_3$ [2], antiferromagnetic $ϵ$-(Mn${}_{1 - x}$Fe${}_x$)${}_{3.25}$Ge [3], semiconducting Pr${}_{0.7}$Ca${}_{0.3}$MnO${}_3$ thin films [4], superconducting BaFe${}_2$As${}_2$ single crystals [5], LaFeAsO [6] and La${}_{1 - x}$Sr${}_x$MnO${}_3$ [7]. We see in these works that, depending on the nature of the compound, $\rho$ can have a pronounced peak [8], a change of its slope or a curvature change at the transition temperature $T_C$. Note that in the last case, one has a maximum of the differential resistivity $d\rho /dT$ [9,10].

Theoretically, the $T^2$ magnetic contribution in Equation (2) has been obtained by Kasuya [11] by taking into account the scattering of the electron spin by the spin waves at low T. However, at higher T, specifically in the region of the phase transition of the magnetic lattice, there have been no such clear mechanisms explaining different experimental behaviors of the spin resistivity. The researchers de Gennes and Friedel [12] have conjectured that the spin resistivity has its origin in the spin–spin correlation, so it should behave as the magnetic susceptibility. As a consequence, it should diverge at $T_C$. However, Fisher and Langer [13] and Kataoka [14] have made the observation that the range of spin–spin correlation should not be infinite at $T_C$ due to collisions. This changes the shape of $\rho$ with respect to the magnetic susceptibility near the phase transition. Let us mention that the resistivity due to magnetic impurities has been calculated by Zarand et al. [15] as a function of the Anderson’s localization length. This parameter expresses, in fact, a kind of correlation sphere induced around each impurity. Their result shows that the resistivity peak depends on this parameter, and is thus in agreement with the spin–spin correlation idea.

Note that the spin resistivity depends on the spin orientation of the environment: the electron encounters less resistance in a ferromagnet with spins parallel to its spin than in a ferromagnet with spins antiparallel to its spin. Imagine a film composed of three ferromagnetic layers where the middle one is a soft ferromagnet. In the layer-coupling configuration $\uparrow - \uparrow - \uparrow$, the movement of an up spin perpendicular to the film encounters a resistance $R_{\uparrow }$. One now applies an external magnetic field in the negative direction, small enough to reverse the spins in the (middle) soft layer: one has the three-layer configuration $\uparrow - \downarrow - \uparrow$. The up spin is found to encounter much difficulty crossing the three layers: the resistance is $R_{\downarrow }$, which is much larger than $R_{\uparrow }$. This is the phenomenon of Giant-Magneto-Resistance (GMR) discovered in Refs. [16,17,18] that has many applications in spintronics.

The absence of Monte Carlo (MC) simulations in the literature on spin resistivity has motivated our works since 2007: we have studied the spin current in a number of systems including ferromagnets [19,20,21] and antiferromagnets [22,23,24,25] by MC simulations. The behavior of $\rho$ as a function of T has been shown to be in general agreement with the experiments and theories mentioned above. In addition to ferromagnets and antiferromagnets, we have also studied the spin resistivity in frustrated spin systems [26,27]. These systems, discovered in the early 1980s, have been intensively studied. Many unusual properties have been found. The reader is referred to reference [28] for reviews on various frustrated spin systems. In this paper, we summarize the most important aspects and results of works on the spin resistivity in ferromagnets, antiferromagnets and in some frustrated magnets.

In Section 2, we present our generic model and the MC method that we employ to study the spin resistivity. Section 3 is devoted to the presentation of our main MC results since 2007. Comparisons between some experiments are made in this section. In Section 4, we show new results in the case of a hexagonal-close-packed (HCP) crystal, where we tune a frustration parameter, allowing study of both the non-frustrated case and the frustrated case in the phase space. Concluding remarks are given in Section 5.

2. Model and Method

2.1. Model

We have investigated the spin resistivity in magnetically ordered materials by using a newly-devised efficient MC simulation method [23,24]. The success of the method was demonstrated when we studied the semiconducting MnTe, where the agreement with the experiment is excellent [25]. This case is reviewed below. In ferromagnets, we found that the spin resistivity has a high peak at the lattice order–disorder transition temperature $T_C$. As said earlier, this anomaly comes from the spin–spin correlation [12,13,14] but remains finite at $T_C$. In antiferromagnets, one observes only a broad maximum [29]. In addition to ferromagnets and antiferromagnets, we have investigated the spin resistivity in the following two frustrated systems: the face-centered cubic (FCC) lattice with Ising spins [26] and the $J_1 - J_2$ simple cubic (SC) lattice [27]. We found that the first-order phase transition in these frustrated systems causes a discontinuity of the spin resistivity at $T_C$.

Let us recall here the model and method that were used in our early works, shown in Refs. [23,26]: simulations were carried out to calculate the current of itinerant spins moving in the system under the action of an electric field $\overrightarrow{ϵ}$ applied in the x direction. The itinerant spin ${\sigma }_i$ carried by a conduction electron interacting with its surrounding lattice spins inside a sphere of radius $D_1$ centered at its position at time t on its trajectory across the crystal. The Hamiltonian is supposed to be

$${\mathcal{H}}_l = -\sum _j{I}_{ij}{\overrightarrow{\sigma }}_i·{\overrightarrow{S}}_j$$

(3)

where the sum is carried over all lattice spins in the sphere centered at the itinerant Ising spin ${\overrightarrow{\sigma }}_i$. $I_{ij}$ denotes the distance-dependent interaction between ${\overrightarrow{\sigma }}_i$ and ${\overrightarrow{S}}_j$. To be general, we also consider the following interaction between an electron spin with neighboring conduction spins within a sphere of radius $D_2$:

$${\mathcal{H}}_i = -\sum _j{K}_{ij}{\overrightarrow{\sigma }}_i·{\overrightarrow{\sigma }}_j$$

(4)

For simplicity, we suppose the distance-dependent interactions are

$$\begin{array}{ccc}\hfill I_{ij}& = & I_{0}exp(-B{r}_{ij})\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill K_{ij}& = & K_{0}exp(-C{r}_{ij})\hfill \end{array}$$

(6)

where $I_0$, B, $K_0$ and C are constants to be chosen so that the energy of a conduction electron spin is much smaller than that of a lattice spin. This choice is made from a physical consideration: in choosing so, we avoid the influence of itinerant spins on the ordering of the lattice spins. Note that this choice is justified in the almost-free electron model, where $I_0 \simeq K_0 \simeq 0$, and in semiconductors, where they are larger but still weak with respect to the exchange integrals of the lattice spins $J_1$ and $J_2$. A discussion in detail on the choice of these parameters is given, for example, in reference [23].

Let us assume in the following a concentration of one itinerant electron per two lattice cells. This concentration is thus of the order of electron concentration in normal metals, which is ${10}^{23}$/cm${}^3$. With this concentration, it is obvious that the averaged distance between two conduction electrons is much larger than the cutoff distance $D_2$, which is of the order of the lattice constant. However, due to the attractive nature of the electron–electron interaction, Equation (5), it is necessary to introduce a chemical potential term to insure that itinerant spins are uniformly dispersed in the crystal and that they do not form clusters. This chemical potential is written as

$${\mathcal{H}}_p = D[n(\overrightarrow{r}) - n_0]$$

(7)

where D is a positive constant, $n(\overrightarrow{r})$ denotes the concentration of conduction spins in the sphere of cutoff radius $D_2$ centered at the position $\overrightarrow{r}$ of the conduction spin under consideration, and $n_0$ is the averaged electron concentration.

$I_0$ is defined in Equation (5) and represents the magnitude of the interaction between a conduction electron and a localized lattice spin (Equation (3)). $K_0$ is the magnitude of the interaction between two conduction electrons (see Equations (4) and (6)). D is the magnitude of the chemical potential (Equation (7)). When we simulate a real material, if we have experimental data on the resistivity and the exchange interactions, such as in the case of MnTe presented in Section 3.3, we can estimate the values of these coefficients.

2.2. Simulation Method

Let us study a film of size $N_x \times N_y \times N_z$, where $N_z$ is the film thickness, which is much smaller than the sizes $N_x$ and $N_y$ in the x and y directions, respectively. Usually, we use $N_z = 4 - 8$ and $N_x = N_y = 20 - 60$. Itinerant spins move under the action of an electric field acting on the electron charge, applied in the direction x. The electric field energy is

$${\mathcal{H}}_E = -e\overrightarrow{ϵ}·\overrightarrow{\ell }$$

(8)

where e is the electron charge, $\overrightarrow{ϵ}$ the applied electrical field and $\overrightarrow{\ell }$ the displacement vector of the electron.

The interaction between the lattice spins is given by the Hamiltonian

$${\mathcal{H}}_L = -J\sum _{i,j}\overrightarrow{S_i}·\overrightarrow{S_j}$$

(9)

where J is the exchange interaction between nearest neighbors (NN) ${\overrightarrow{S}}_i$ and ${\overrightarrow{S}}_j$. For ferromagnets, $J > 0$; and for antiferromagnets, $J < 0$.

We use the standard Monte Carlo (MC) method to thermalize the lattice alone at T. Next, we introduce the electrons into the lattice. We suppose that each electron spin interacts with the surrounding lattice spins inside a sphere centered at its position and of radius $D_1$. The electron spin also interacts with other electron spins within a sphere of radius $D_2$. Electrons move under the applied electric field.

In order to obtain the spin current, we have to thermalize the state of the spins of conduction electrons in the lattice. This is done by the following steps:

(i)

We take a conduction spin and calculate its actual energy $E_{old}$ using the different interactions mentioned above.

(ii)

We make a trial move $\overrightarrow{\ell }$ for the electron in a random direction between 0 and a, where a is the lattice constant. If the move $\overrightarrow{\ell }$ takes the itinerant electron outside the sample, then we put it inside on the other sample end by virtue of the periodic boundary condition.

(iii)

We then calculate the new energy $E_{new}$. If $E_{new} < E_{old}$, then the trial position is accepted. Otherwise, it is accepted with the probability $exp[-(E_{new} - E_{old})/(k_{B}T)]$.

(iv)

We take another conduction electron and repeat the three steps above. We continue with other electrons until all electrons are considered: this accomplishes one MC step/spin. A large number of MC steps/spins are necessary to arrive at a steady current state. We next average physical quantities of interest at the temperature T under consideration.

(v)

We take another T and repeat the above four steps. We should cover the temperature region of interest.

This paper is a review of our publications over the past 15 years. In each publication, we used various sample sizes to detect finite size effects. We increased the sample size until the results did not depend anymore on the size. The results are considered as valid thermodynamically. The finite size effect and the finite size scaling are what the simulators do before reaching conclusions. This problem is particularly important when one wants to study the criticality or the order of a phase transition. In the review, we do not repeat these details, which depend on the studied system. Rather, we emphasize the results. The reader interested in the details of the simulation methods is referred to each original publication.

We calculate the spin resistivity $\rho$ as:

$$\begin{array}{ccc}\hfill \rho & = & \frac{1}{N_s}\hfill \end{array}$$

(10)

where $N_s$ is the number of mobile electrons passing through a unit surface perpendicular to the direction of the applied electric field x per MC time unit. An application with a real material using real units is presented in Section 3.3.

For a good thermal average, we have to perform very long MC runs, and we proceed as follows: for each configuration of the lattice spins, we average the spin resistivity over $N_1$ MC steps; then, we again thermalize the lattice with $N_2$ MC steps to get rid of the correlation between lattice spin configurations before again averaging the resistivity for $N_1$ MC steps. We repeat this $N_1 + N_2$ cycle for a large number of times $N_3$. The total MC steps of resistivity averaging is about $4 \times {10}^5$ steps per spin in our runs. We found by comparison that this “multi-step” averaging method strongly suppresses statistical fluctuations seen in our earlier work [20].

It is obvious that larger $N_1$ and $N_2$ values yield better statistics. We know that, depending on T, the relaxation time ${\tau }_L$ of the lattice spins varies. We have to compare ${\tau }_L$ with the relaxation time ${\tau }_I$ of conduction electron spins in order to choose a right value of $N_1$ in order to calculate the average of the resistivity with one lattice spin configuration at T. We know the two limiting cases. The first case is when ${\tau }_L \simeq {\tau }_I$. In this case, we have to take $N_1 = 1$; namely, the lattice spin configuration should change with each move of itinerant spins. The second case is when ${\tau }_L \gg {\tau }_I$. In this case, itinerant spins can be scattered many times along the trajectory across the same lattice configuration and for many times across the lattice.

In order to choose a right value of $N_1$, we consider the following temperature dependence of ${\tau }_L$ in non-frustrated spin systems. The relaxation time is expressed in this case as [30,31,32]

$${\tau }_L = \frac{A}{|1 - T/T_C{|}^{z\nu }}$$

(11)

where A is a constant, $\nu$ the correlation critical exponent, and z the dynamic exponent, which depends on the spin model and space dimension. For a 3D Ising model, $\nu = 0.638$ and $z = 2.02$. From this expression, we see that as T tends to $T_C$, ${\tau }_L$ diverges. In the critical region around $T_C$, the system thus encounters the so-called “critical slowing down”: the spin relaxation is extremely long due to the divergence of the spin–spin correlation. When we take into account the temperature dependence of ${\tau }_L$, the shape of the resistivity is strongly modified near $T_C$, where ${\tau }_L$ is very long, in contrast to the paramagnetic phase, where the relaxation time is very short due to rapid thermal fluctuations. We should emphasize that at low T, $\rho$ does not depend on ${\tau }_L$, since in that temperature range, where the ordering of the lattice spins is almost perfect, the spin landscape from one microscopic state to another does not change significantly; so the motion of the itinerant electron spin does not significantly vary (see reference [24]).

Finally, we note that we have also used the Boltzmann’s equation combined with MC data to study the spin resistivity [21]. However, the shape of the resistivity peak at the transition temperature does not agree well with experiments, unlike that obtained from direct MC simulations, as shown below. This proves the efficiency of MC simulations for the calculation of the spin resistivity in magnetically ordered materials. The present review therefore aims to promote this method.

3. Review

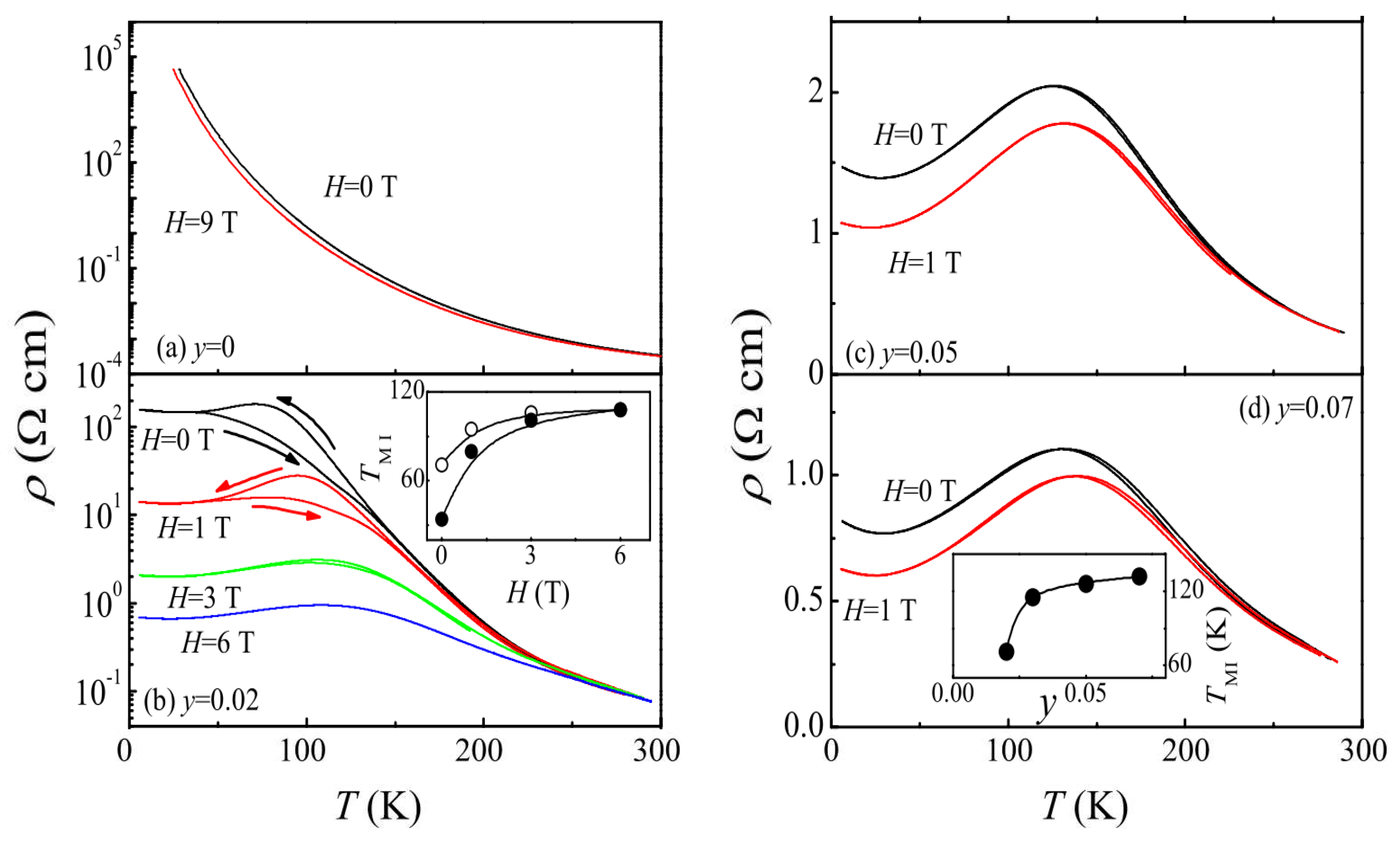
3.1. Spin Resistivity in Ferromagnets and Antiferromagnets

The experiments mentioned above, amongst numerous other data, show that the spin resistivity in ferromagnets has a sharp peak at the transition temperature $T_C$ of the lattice. We know by the theory of phase transitions and critical phenomena that in the region around $T_C$, the so-called “critical slowing-down” phenomenon happens, resulting in extremely large ${\tau }_L$. The peak in $\rho$ is due to this phenomenon via Equation (11), where ${\tau }_L$ diverges at $T_C$. Our MC simulations using the method described above in the case of a ferromagnet where the lattice spins are of the Ising type show a sharp peak at $T_C$ (see Figure 1) in agreement with experimental data. We note that the spin resistivity for ferromagnets (as well as for antiferromagnets) increases with decreasing T at low T. This can be explained by several causes: the freezing or crystallization of conduction electrons takes place at low T so that just a small number of conduction spins with decreasing T are mobile, or it may be the classical counter-effect of the quantum Kondo electron-impurity scattering if one considers the few excited lattice spins at low T are independent impurities; see the last term of Equation (2). Note that the shape of $\rho$ depends on the lattice type, interaction strengths encountered by the conduction electrons, electron concentration, relaxation time, spin model, applied magnetic-field amplitude, etc. In [23], we have shown that a decrease in the interaction between conduction spins, $K_0$, reduces the increase of $\rho$ as $T \to 0$, an applied magnetic field reduces the height of the resistivity peak, and larger electron density reduces $\rho$. Finally, we emphasize that $\rho$ depends on the material intrinsically via the critical exponents $\nu$ and z; see Equation (11).

If we wish to compare simulated spin resistivity to experimental measurements performed on a given material, we have to use in the simulation the available experimental physical parameters of that material. An example of quantitative comparison for semiconductor MnTe is shown in Section 3.3.

Note that the magnetic field applied on the system reduces the peak height, as shown in our work [23] and in agreement with the experiments in [2].

Unlike ferromagnets, antiferromagnets have not been studied much. Haas [29] has shown that—in contrast to ferromagnets, where the resistivity $\rho$ has a sharp peak at the order–disorder transition of the lattice spins—in antiferromagnets, there is no such a peak. Using MC simulations, we found that the peak does exist in an antiferromagnet, but it is less sharp compared to that of a ferromagnet, as seen in Figure 1. We think that the alternate change of sign of the spin–spin correlation with distance may have something to do with the absence of a sharp peak. We have tested this idea on the effect of the cut-off distance $D_1$ [26]: in an antiferromagnet, when we increase $D_1$, we include successive up-spin shells and down-spin shells in the sphere of radius $D_1$. Consequently, the difference between the numbers of up and down spins in the sphere oscillates with varying $D_1$, giving rise to the oscillatory behavior of $\rho$ observed at small $D_1$, unlike in ferromagnets.

At this stage, we note that the presence of an itinerant spin will break the invariance between a ferromagnet and its antiferromagnet counterpart in the local Mattis transformation ($J_{ij} \to -J_{ij},{\overrightarrow{S}}_j \to -{\overrightarrow{S}}_j$).

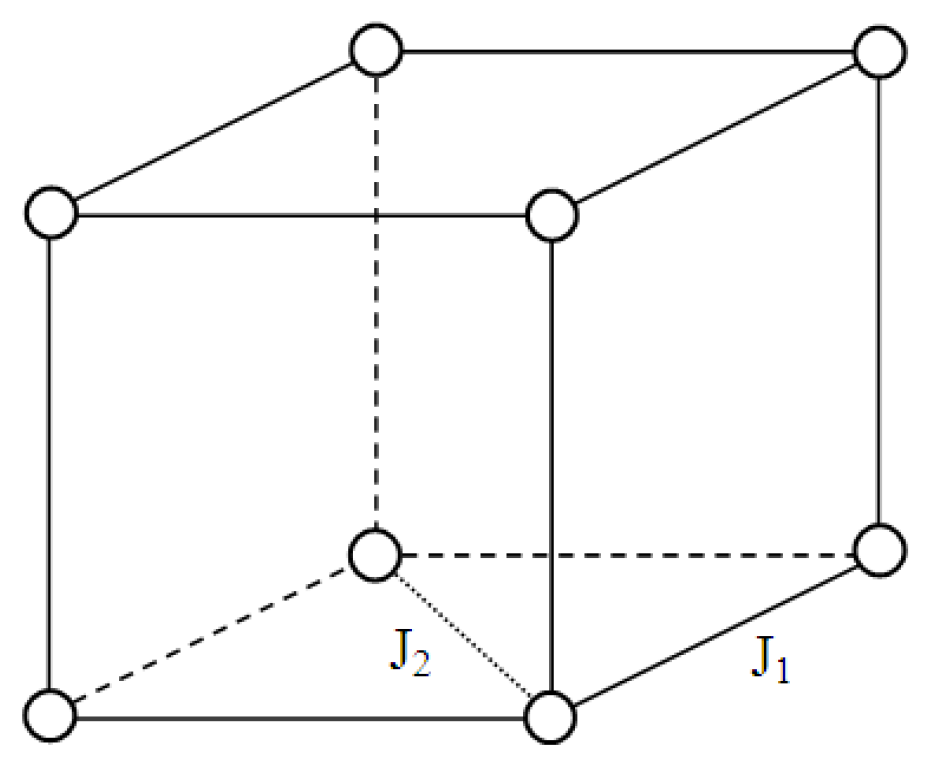
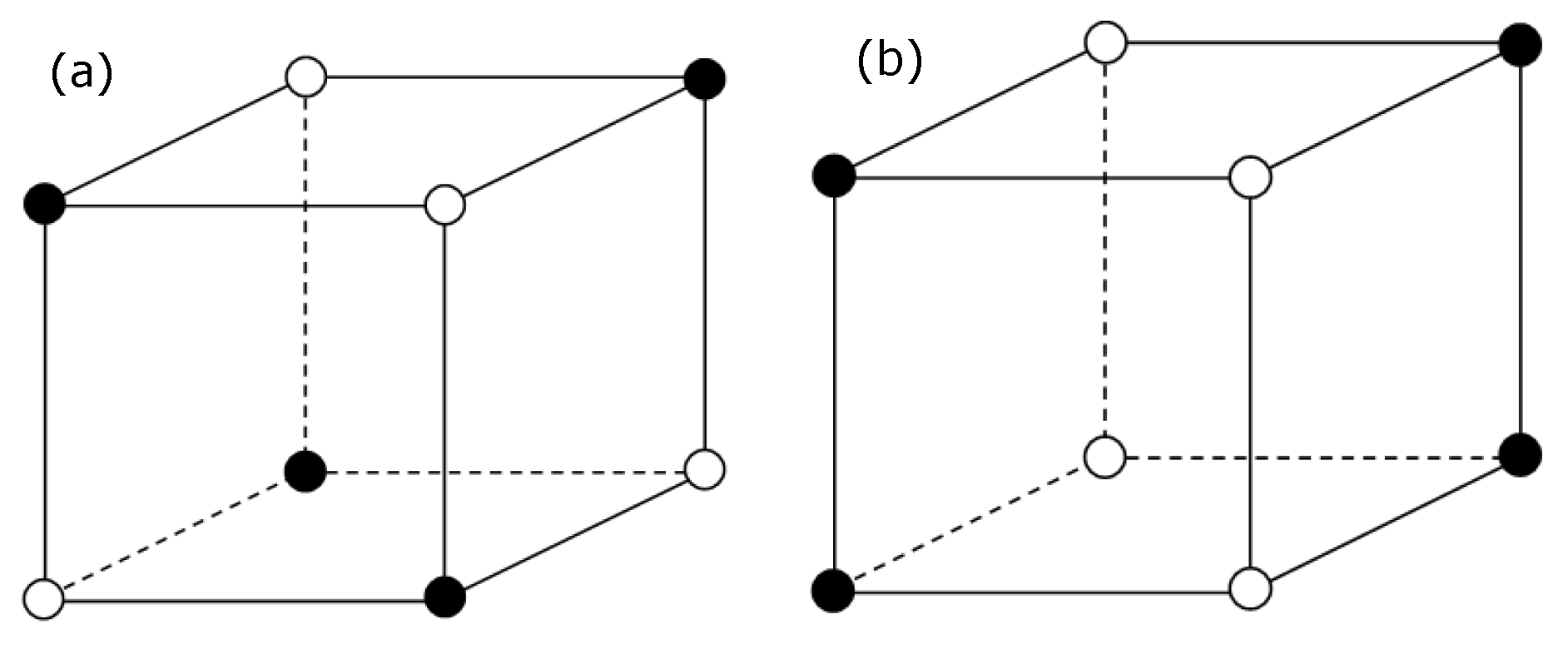
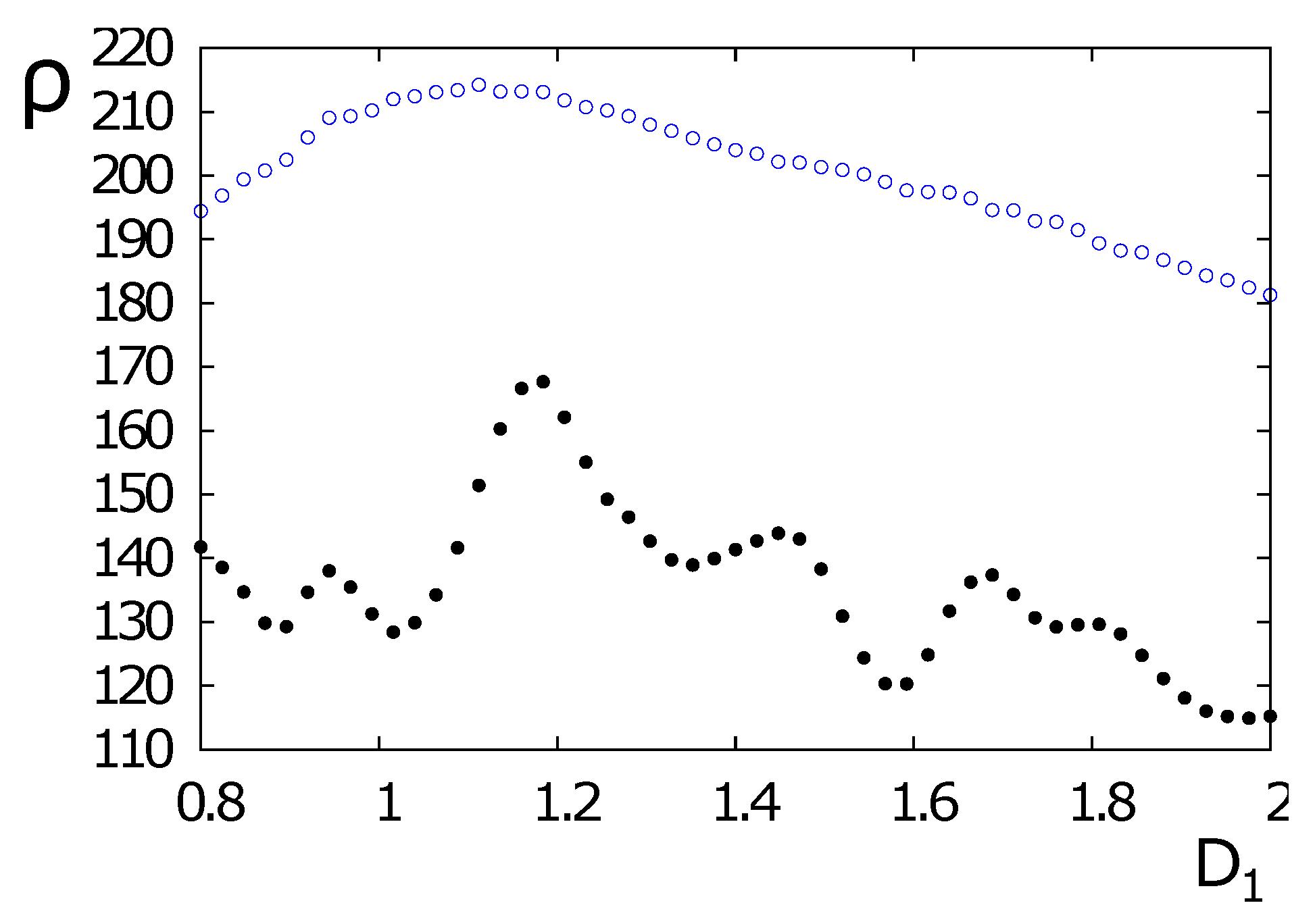
3.2. Frustrated $J_1–J_2$ Model on a Simple Cubic Lattice

Let us consider the simple cubic lattice with NN and NNN interactions, as shown in Figure 2. The Hamiltonian is written as

$$\mathcal{H} = -J_1\sum _{(i,j)}{\overrightarrow{S}}_i·{\overrightarrow{S}}_j - J_2\sum _{(i,m)}{\overrightarrow{S}}_i·{\overrightarrow{S}}_m$$

(12)

where the first sum ${\sum }_{(i,j)}$ is made over the NN Ising spin pairs ${\overrightarrow{S}}_i$ and ${\overrightarrow{S}}_j$ with interaction $J_1$, and the second sum ${\sum }_{(i,m)}$ is performed over the NNN pairs with interaction $J_2$.

We focus our attention on the region of parameters that gives rise to a frustration. For that purpose, we assume that $J_1$ is an antiferromagnetic interaction, namely, $J_1 = -J < 0$ ($J > 0$), and $J_2$ is also antiferromagnetic. We put $J_2 = -\eta J$, where $\eta$ is a positive parameter. The ground state (GS) of this system can be obtained by minimizing the energy or by comparing the energies of different spin configurations. We can also numerically minimize the energy by using the steepest descent method [33]. We obtain the GS antiferromagnetic configuration shown Figure 3a for $|J_2| < 0.25|J_1|$ and the GS spin configuration shown in Figure 3b for $|J_2| > 0.25|J_1|$. This latter configuration is three-fold degenerate because we can choose the parallel NN spins either on the x, y or z axis. In addition, with the permutation of black and white spins, we have the total degeneracy equal to six.

We note in passing that in the case of the Heisenberg model in the frustrated region ($|J_2| > 0.25|J_1|$), the phase transition has been shown to be of the first order [34]. The system is very unstable due to its large degeneracy. In the case of the Ising spin on the SC lattice treated here, we found that the first-order character of the phase transition is even stronger [27].

We use $J_1 = -J = -1$ (AF interaction) for the coupling between NN lattice spins in the simulations. The energy is thus measured in the unit of J, and the temperature is in the unit of $J/k_B$. All distances ($D_1$ and $D_2$) are in the unit of the lattice constant a.

Simulations have been carried out by using the temperature-dependent relaxation time of the lattice spins given by Equation (11), where we have taken $A = 1$ and ${\tau }_L = 1$ at $T = 2T_C$, far from $T_C$. Such a choice leads to ${\tau }_L = 1$ at that temperature, for which fast thermal fluctuations in the paramagnetic phase far above $T_C$ are expected.

Since we suppose that the interaction between conduction electron spins is attractive, a chemical potential is required to avoid the collapse of the system, namely, to avoid all conduction spins forming a cluster (cf. Equation (7)). The chemical potential in thermodynamics makes the particle uniformly distributed in the space. Its strength is expressed by D, which has to be chosen in accordance with $K_0$. Figure 4 displays the phase diagram in the space $(K_0,D)$, which shows the collapse region. This allows us to avoid this region and choose an appropriate value of D for a given $K_0$.

To see the effect of the nature of the phase transition on the spin resistivity, in the following, we focus on two typical cases: $\eta = 0.2$ and $\eta = 0.26$, which belong, respectively, to the regions of second- and first-order transition.

A. 

For $\eta = 0.2$:

The spin resistivity at temperatures below $T_N$ oscillates with varying $D_1$. By analyzing the ratio of the number of up spins to the number of down spins in the sphere of radius $D_1$, we found that it oscillates with varying $D_1$: the maxima (minima) of $\rho$ correspond to the case of largest (smallest) numbers of parallel (antiparallel) spins in the sphere [26,27]. At very high temperatures, where the lattice spins are disordered, the number of up spins and down spins in the sphere of radius $D_1$ should be equal. There is, however, a very small oscillation if the temperature is close to $T_N$ and if $D_1$ is small.

Figure 5 displays the resistivity versus T for $D_1 = 1.2$. The spin resistivity shows a rounded maximum at the transition temperature. This is in agreement with the curve experimentally observed in La${}_{0.4}$Ca${}_{0.6}$MnO${}_3$ by Lu et al. [2] (see Figure 6, right panel).

For $D_1 = 0.8$ or $D_1 = 1$, the resistivity is smaller below the transition temperature, as seen in Figure 7. This shows the importance of the effect of the interaction range on the spin resistivity in materials.

B. 

For $\eta = 0.26$:

At this value of $\eta$, the transition of the lattice spins is of first order. The dependence of the resistivity on $D_1$ is very similar to that of the second-phase transition, namely, the resistivity at a given T oscillates as $D_1$ varies. The physical meaning of the oscillation has been given above. More details can be found in Refs. [26,27]. We found that the resistivity $\rho$ in the frustrated regime can go downward or upward at the transition temperature depending on $D_1$ [27], unlike in non-frustrated ferromagnets and antiferromagnets as shown earlier. This is displayed in Figure 8 for two values of $D_1$, where one observes the discontinuity of $\rho$ at the transition temperature. The discontinuity of $\rho$ has also been found in other frustrated antiferromagnets, such as the FCC antiferromagnet [26].

From the results shown above for the $J_1 - J_2$ model, we come to the conclusion that the behavior of the spin resistivity is a consequence of the nature of the lattice transition. If the lattice transition is of second order, then the resistivity of itinerant spins has a rounded peak, while if the lattice transition is of first order, the resistivity is discontinuous at the transition temperature.

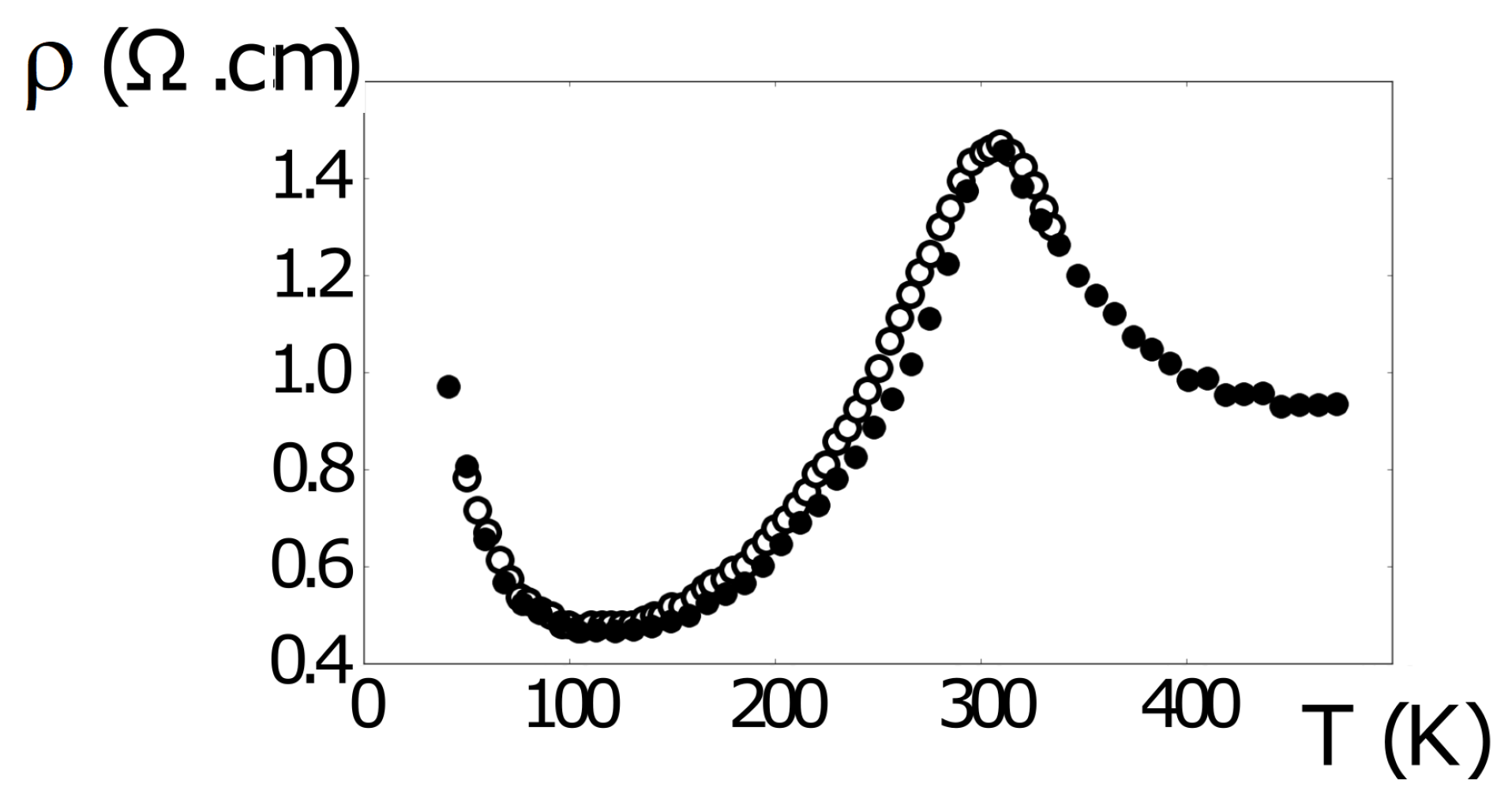
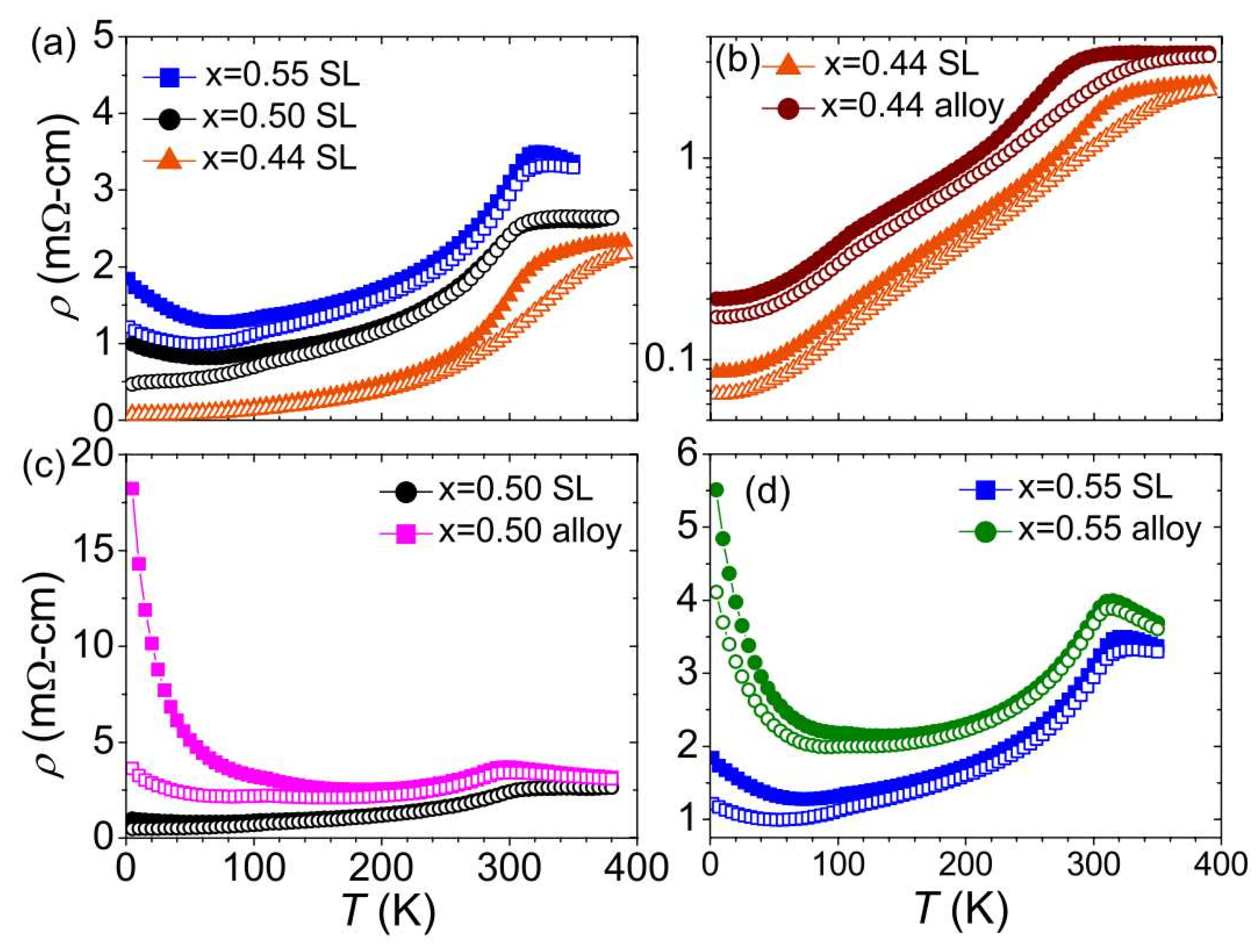
3.3. The Case of MnTe

The pure semiconductor MnTe has two kinds of structures: the zinc-blend structure or the hexagonal NiAs one (shown in Figure 9) [35]. We focus on the second structure, where the Néel temperature is $T_N = 310$ K [36] and where many other experimental data are available. MnTe is a semiconductor with a large gap (1.27 eV) and a carrier concentration $n = 4.3 \times {10}^{17}$cm${}^{-3}$ at room temperature [37,38]. Without doping, MnTe is non degenerate. The crystal is formed by ferromagnetic $xy$ hexagonal planes antiferromagnetically stacked in the c direction. The NN distance in the c direction is $c/2 \simeq 3.36$ Å, and the in-plane NN distance is $a = 4.158$ Å. From neutron scattering experiments, it was found that the main exchange interactions between Mn spins in MnTe are the interaction between NN along the c axis with the value $J_1/k_B = -21.5 \pm 0.3$ K, the ferromagnetic exchange $J_2/k_B \approx 0.67 \pm 0.05$ K between in-plane neighboring Mn (they are next NN by distance), and the third NN antiferromagnetic interaction $J_3/k_B \simeq -2.87 \pm 0.04$ K (see Figure 9). The spins lie in the $xy$ plane perpendicular to the c direction with a small in-plane easy-axis anisotropy $D_a$ [36]. Let us emphasize that the values of the exchange integrals given above were deduced from experimental data by fitting with a free spin-wave theory [36]. Other fittings with mean-field theories give slightly different values: $J_1/k_B = -16.7$ K, $J_2/k_B = 2.55$ K and $J_3/k_B = -0.28$ K [37]. Note that the Mn spin is experimentally known to be of the Heisenberg model with magnitude $S = 5/2$ [36].

We write the following Hamiltonian for the lattice spins:

$$\begin{array}{ccc}\hfill \mathcal{H}& = & -J_1\sum _{(i,j)}{\overrightarrow{S}}_i·{\overrightarrow{S}}_j - J_2\sum _{(i,m)}{\overrightarrow{S}}_i·{\overrightarrow{S}}_m - J_3\sum _{(i,k)}{\overrightarrow{S}}_i·{\overrightarrow{S}}_k\hfill \\ & & -D_a\sum _i{(S_i^x)}^2\hfill \end{array}$$

(13)

where the first sum is performed over the NN spin pairs, the second sum over the NNN pairs and the third one over the third NN pairs. $D_a > 0$ is an anisotropy constant that favors the in-plane x easy-axis spin configuration.

The behavior of $\rho$ in MnTe as a function of T has been experimentally shown in several works [39,40,41,42,43]. Using MC simulations, we have studied the spin resistivity in MnTe with the above Hamiltonian [25]. Let us summarize this work here.

For MC simulations, we suppose the following Hamiltonian of the itinerant spins:

$${\mathcal{H}}_i = -\sum _{n}I(\overrightarrow{r} - {\overrightarrow{R}}_n)\overrightarrow{\sigma }·{\overrightarrow{S}}_n$$

(14)

where the sum is performed by counting all the lattice spins ${\overrightarrow{S}}_n$ inside the sphere of radius $D_1 = a$ centered at $\overrightarrow{r}$. $I(\overrightarrow{r} - {\overrightarrow{R}}_n) > 0$ is the ferromagnetic distance-dependent interaction between the itinerant electron spin $\overrightarrow{\sigma }$ at $\overrightarrow{r}$ and the Mn spin ${\overrightarrow{S}}_n$ at ${\overrightarrow{R}}_n$.

The electron spin is supposed to be of the Ising type. We neglect, therefore, the quantum effects that may be important at very low T, but our attention is focused on the region of T high enough so that quantum effects may be neglected. We assume the following form of $I(\overrightarrow{r} - {\overrightarrow{R}}_n)$:

$$I(\overrightarrow{r} - {\overrightarrow{R}}_n) = I_{0}exp[-\alpha (\overrightarrow{r} - {\overrightarrow{R}}_n)]$$

(15)

where the constants $I_0$ and $\alpha$ are chosen in such a way that the interaction ${\mathcal{H}}_i$ yields an energy much smaller than the lattice energy given by $\mathcal{H}$ (see the guide for the choice of different constants given below for Equation (5) and in reference [23]). It is noted that the cut-off distance $D_1$ is rather short so that only the first few neighbors are inside the sphere; the results shown below do not, therefore, depend significantly on the choice of the value of $\alpha$ in the exponential. Finally, note that the concentration of conduction electrons in MnTe is $n = 4.3 \times {10}^{17}$ cm${}^{ - 3}$, which is five orders lower than the concentration of its surrounding lattice spins, which is ≃${10}^{22}$ cm${}^{ - 3}$. This observation justifies that the interaction between conduction electrons for MnTe can be neglected. We have assumed this in the simulations shown in the following.

As mentioned above, the exchange interactions deduced from experimental data have slightly different values; they depend on the theoretical Hamiltonian and the approximations used to deduce it (often the mean-field approximation is used; see a detailed example in [44]). Note that in semiconductors, the carrier concentration varies with T, but since this concentration is very low, we do not take into account its variation. Consequently, the number of conduction electron spins used in the simulation is important only for the statistical average. The current obtained is proportional to the number of itinerant spins, but there are no extra effects within our assumptions mentioned above.

We have calculated $\rho$ of MnTe using the exchange integrals slightly modified with respect to the ones given above in order to obtain the best fit. The obtained resistivity $\rho$ is shown in Figure 10. Let us note that we have taken $J_3$ slightly larger in magnitude than the value deduced from experiments by mean-field approximation. Our value of $J_3$ was chosen in order to obtain $T_N = 310$ K, which is in excellent agreement with experiments. However, the most striking feature is that the simulated $\rho$ shows a sharp maximum at $T_N$ and coincides with the experimental data over the whole temperature range. Note that we have used $A = 1$ and the well-known Heisenberg critical exponents $\nu = 0.707$, $z = 1.97$ [31] for the lattice spins. It is remarkable that with the same set of parameters, we obtain excellent agreement with experiments in the temperature regions below $T < 140$ K and above $T_N$. We note that we tried earlier to use the Boltzmann’s equation [22], but the obtained result was not as good as the MC result presented above.

From the simulated $\rho$, we can calculate the relaxation time of conduction spins; we obtain ${\tau }_I \simeq 0.1$ ps. The mean free path can be also estimated; it is equal to $\overline{l} \simeq 20$ Åat the critical temperature.

4. Phase Transition and Spin Resistivity in the Ising HCP Lattice

4.1. Hamiltonian and Ground State

The lattice we consider is the HCP structure illustrated in Figure 11. The $xy$ planes are triangular (hexagonal), and the stacking direction is z. We suppose the following Hamiltonian:

$$\mathcal{H} = -\sum _{(i,j)}{J}_{i,j}{\overrightarrow{S}}_i·{\overrightarrow{S}}_j$$

(16)

where $J_{ij}$ is the AF interaction between nearest-neighbors (NN) ${\overrightarrow{S}}_i$ and ${\overrightarrow{S}}_j$. We denote $J_{ij} = J_1$ if the NN are on the $xy$ triangular plane and $J_{ij} = J_2$ if the NN are on two adjacent planes (see Figure 11). The GS can be determined by minimization of the local energy of each spin and doing this for all spins, then repeating many times until the total energy converges to a minimum. Normally, with a system without bond disordering, this method needs just a small number of iterations. The GS can be checked by looking at the final snapshot: it should be periodic. This procedure of local energy minimization is called in the literature “the steepest-descent method”. The implementation of this method is very simple [33]: (i) We first create an initial random configuration. (ii) We then calculate the local field acting at a spin by its neighbors using (16). (iii) We align the spin under consideration along the calculated local field; in doing so, its energy is minimum. (iv) We take another spin and repeat the three preceding steps until all spins are considered: this step completes one sweep. (v) We start another sweep and realize a large number of sweeps until the total energy is minimum.

One can also analytically minimize the interaction energy as shown below to find the GS. Let us assume that both interactions $J_1$ and $J_2$ are antiferromagnetic. For simplicity, we fix $J_2 = -1$ and vary $J_1$.

The case of isotropic interaction, namely $J_1 = J_2$, has been studied in [45]. We summarize the results here: for the HCP structure, each spin is common for eight tetrahedra (four in the upper half-space and four in the lower half-space along the z axis) and an NN bond is shared by two tetrahedra. The GS spin configuration of the system is formed by stacking neighboring tetrahedra. In the GS, one has two pairs of antiparallel spins on each tetrahedron. Their axes form an arbitrary angle $\alpha$. The GS degeneracy is therefore infinite (see Figure 2a of [45]). Note that the periodic boundary conditions reduce a number of the GS configurations, but the degeneracy is still infinite. One particular family of configurations of interest for both XY and Heisenberg cases is when $\alpha = 0$. The GS is then collinear with two spins up and the other two down. The stacking sequence is simple because there are three equivalent configurations due to the fact that there are three ways to choose the parallel spin pair in the original tetrahedron.

The case where $J_1 \ne J_2$ has been studied in [46] for the Ising and XY cases. Let us recall some results concerning the Ising case that allow us to understand the new results on the spin resistivity presented below.

We use the steepest-descent method described above with varying $J_1$ ($J_2 = -1$)—we find two kinds of GS spin configuration: the first consists of $xy$ ferromagnetic planes stacked antiferromagnetically along the z direction, while the second one is the stacking of $xy$ AF planes such that each tetrahedron has two up and two down spins. The transition between the two configurations is determined as follows: one simply writes down the respective energies of a tetrahedron and compares them:

$$\begin{array}{ccc}\hfill E_1& = & 3(-J_1 + J_2)\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill E_2& = & J_1 + J_2\hfill \end{array}$$

(18)

One sees that $E_1 < E_2$ when $J_1 > 0.5J_2$, i.e., $|J_1| < 0.5|J_2|$. Thus the first configuration is more stable when $|J_1| < 0.5|J_2|$.

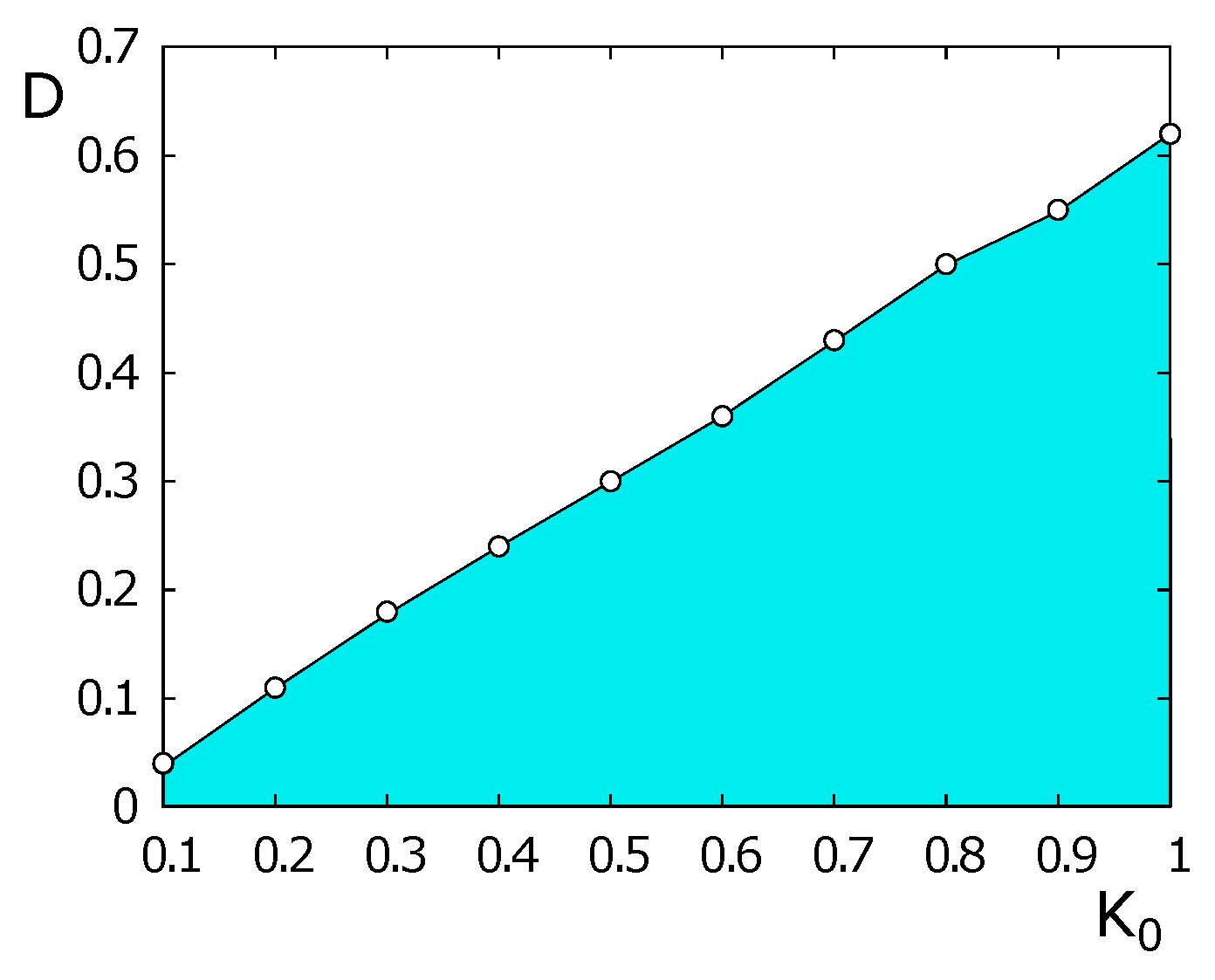
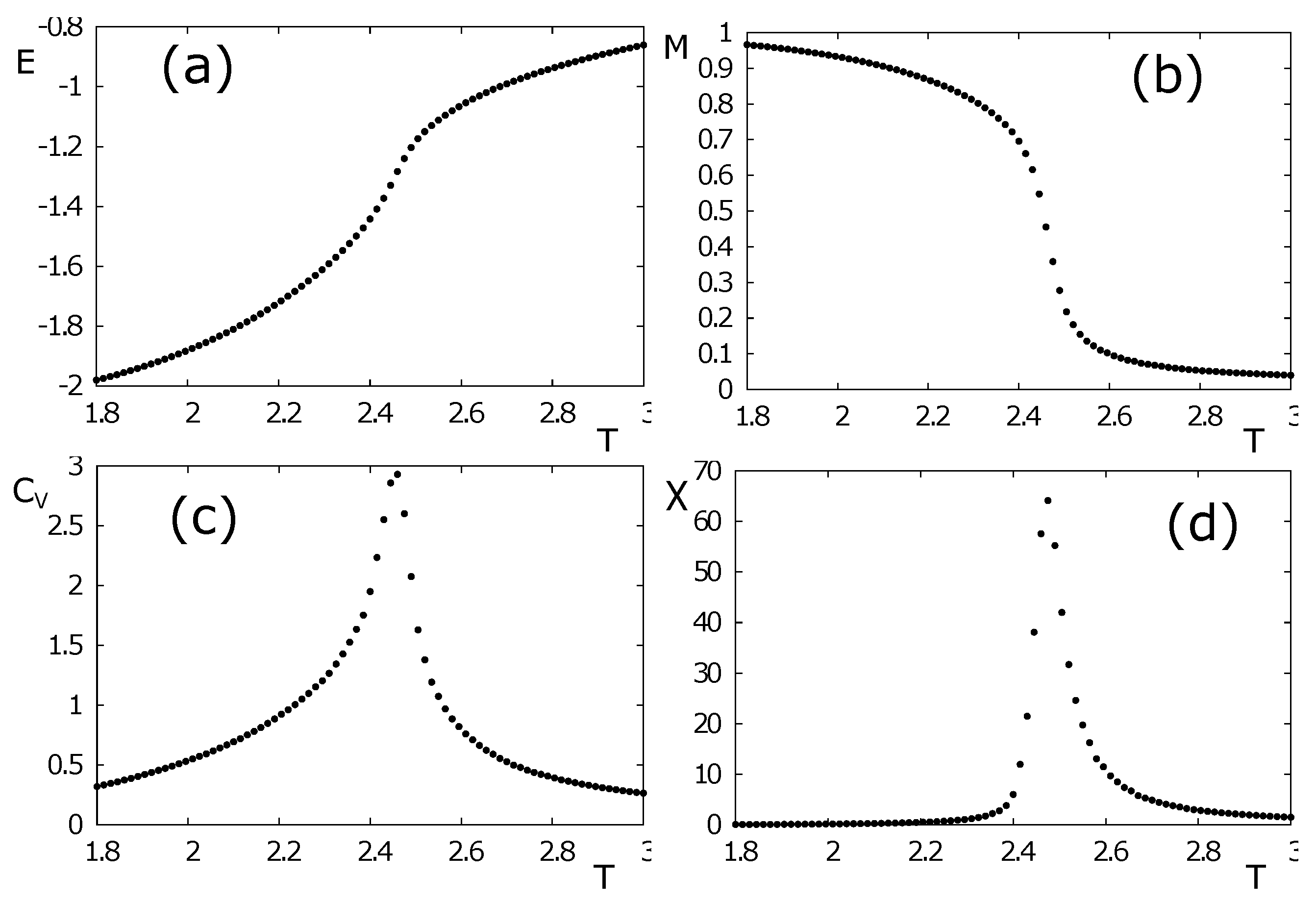
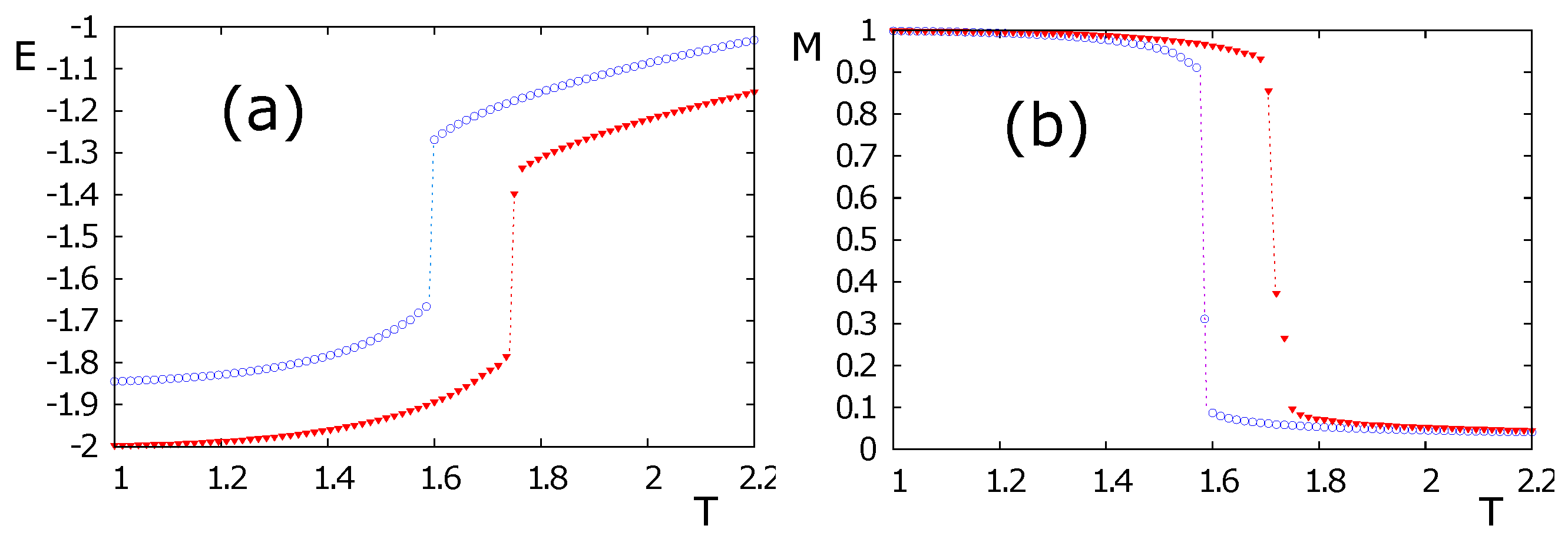
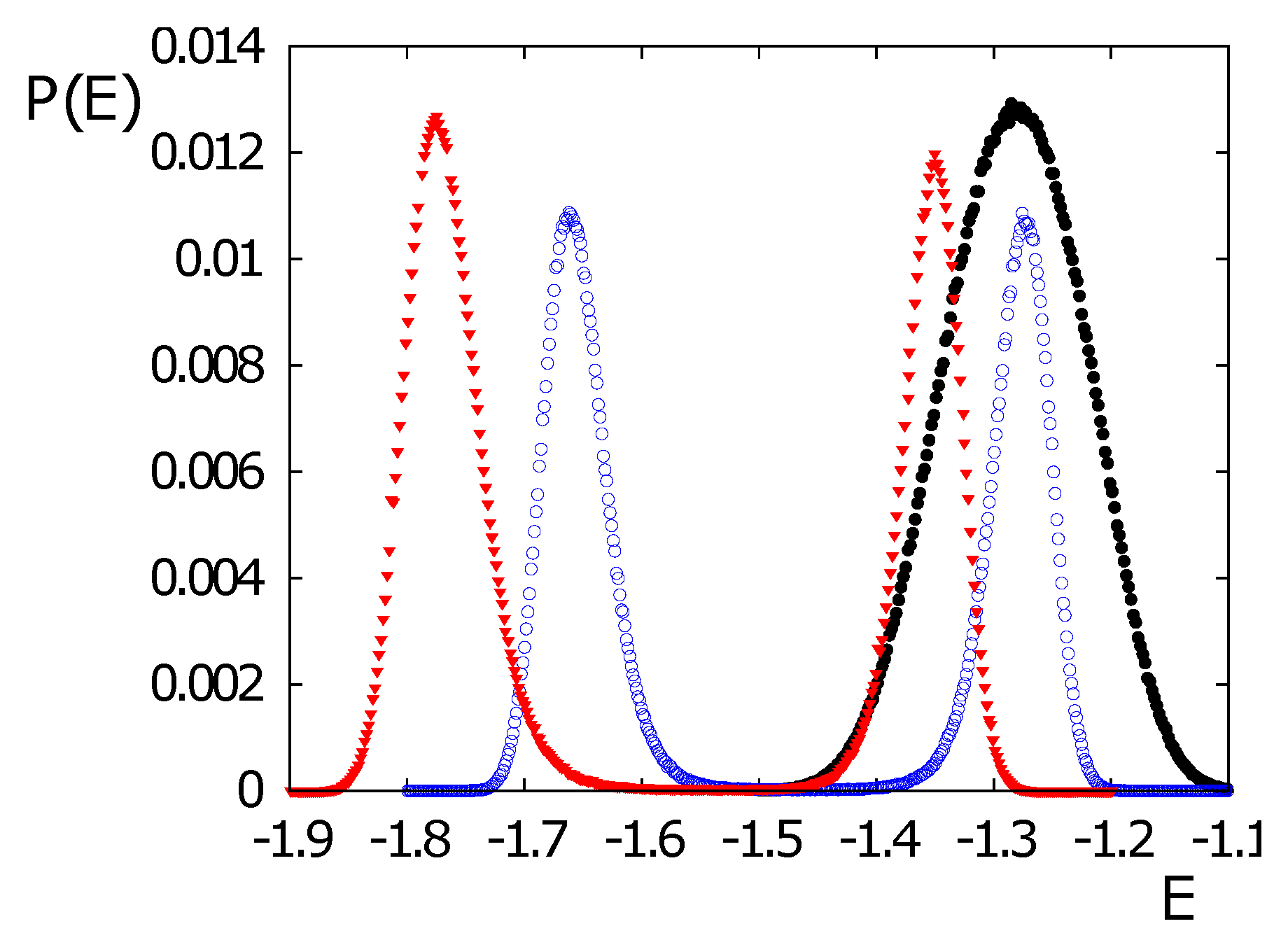
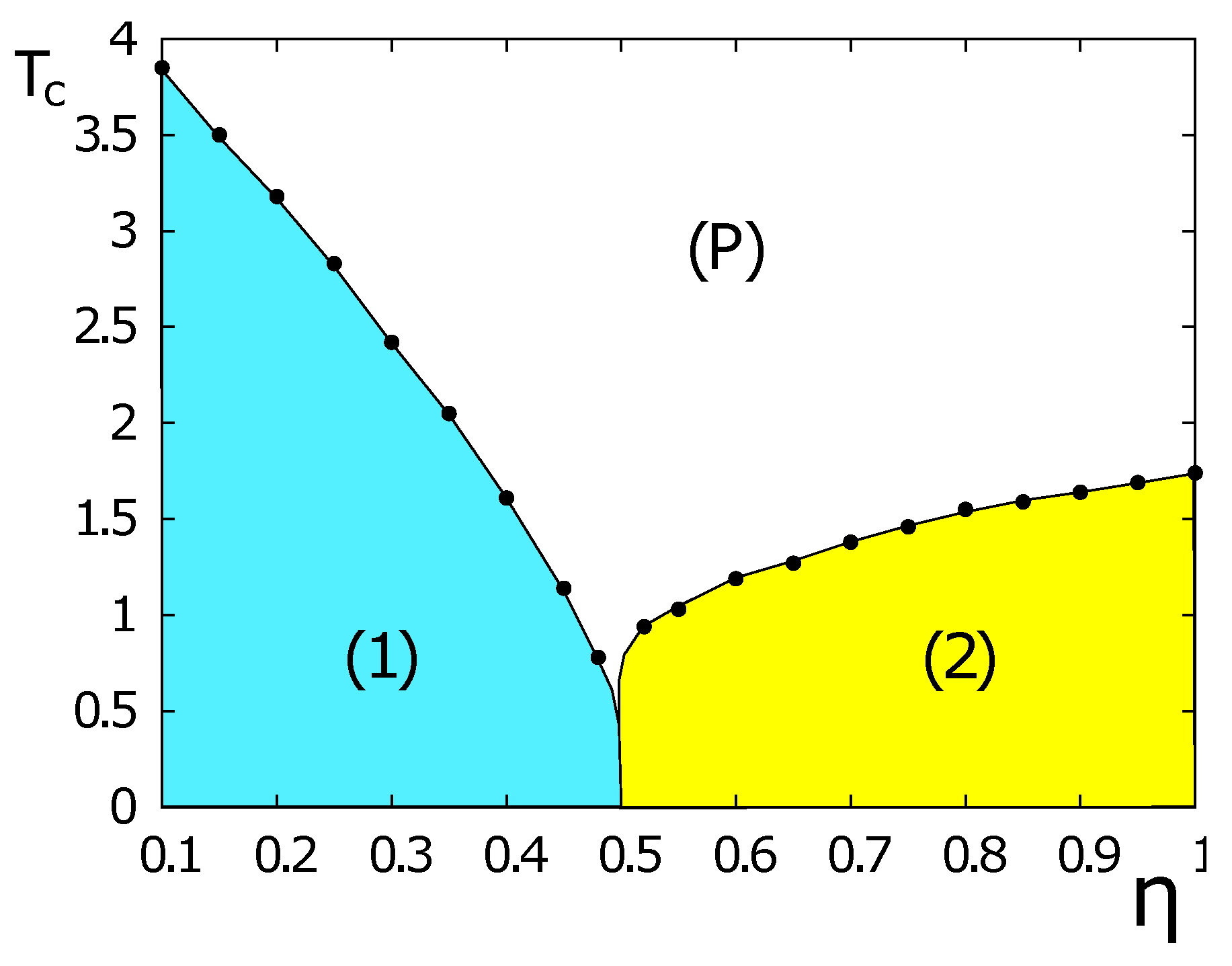
4.2. Phase Transition in the Case of Ising Spins on the HCP Lattice

In the following, we present the results of simulations using the Hamiltonian Equation (16). We use the sample size $N_x \times N_y \times N_z$ with $N_x = N_y = 18$ and $N_z = 8$, namely, 16 atomic planes along the z axis and the periodic boundary conditions in all directions. We use the first ${10}^6$ MC steps per spin to reach equilibrium, and we average physical quantities with the next ${10}^6$ MC steps per spin. The energy is expressed in the unit of $|J_2| = 1$.

Let us define $\eta = J_1/J_2$. We have seen that the GS changes at ${\eta }_c = 0.5$, so we show below the properties of the system on both sides of this value. Figure 12 displays the averaged energy per spin, the order parameter (staggered magnetization), the specific heat and the susceptibility for $\eta = 0.3$. As seen, the transition is of second order since there is no discontinuity of the energy and the order parameter at the transition temperature.

For $\eta = J_1/J_2 > 0.5$, Figure 13 for $\eta = 0.85$ and 1 shows that the discontinuity of E and M at the transition is very large, which is a signature of a strong first-order transition in both cases.

In order to confirm the order of the phase transition, we measure the energy histogram taken during the averaged MC time. Figure 14 shows the energy histogram taken at the transition temperature for $\eta = 0.3$ (black), $0.85$ (blue) and 1 (red). We observe here that the first case is a Gaussian distribution indicating a second-order transition, in contrast to the last two cases that show double-peak histograms confirming a first-order transition.

Figure 15 displays the phase diagram in the space $(T_C,\eta )$, where zone (1) and zone (2) denote the ordering of the first and second kinds, respectively; (P) indicates the paramagnetic phase. Note that the transition line between (1) and (P) is a second-order line, while that between (2) and (P) is a first-order line.

Note that in the $XY$ case, the change of the GS takes place at ${\eta }_c = 1/3$. We have studied this case in detail in [46].

Finally, let us emphasize that all 3D frustrated systems we know so far undergo a first-order transition [28], including the much-studied antiferromagnetic stacked triangular lattice [47,48,49,50,51], the FCC antiferromagnets [52], the simple cubic fully frustrated lattices [53,54,55,56], helimagnets [57] and the antiferromagnetic HCP lattice studied here (see more details in [45,46]).

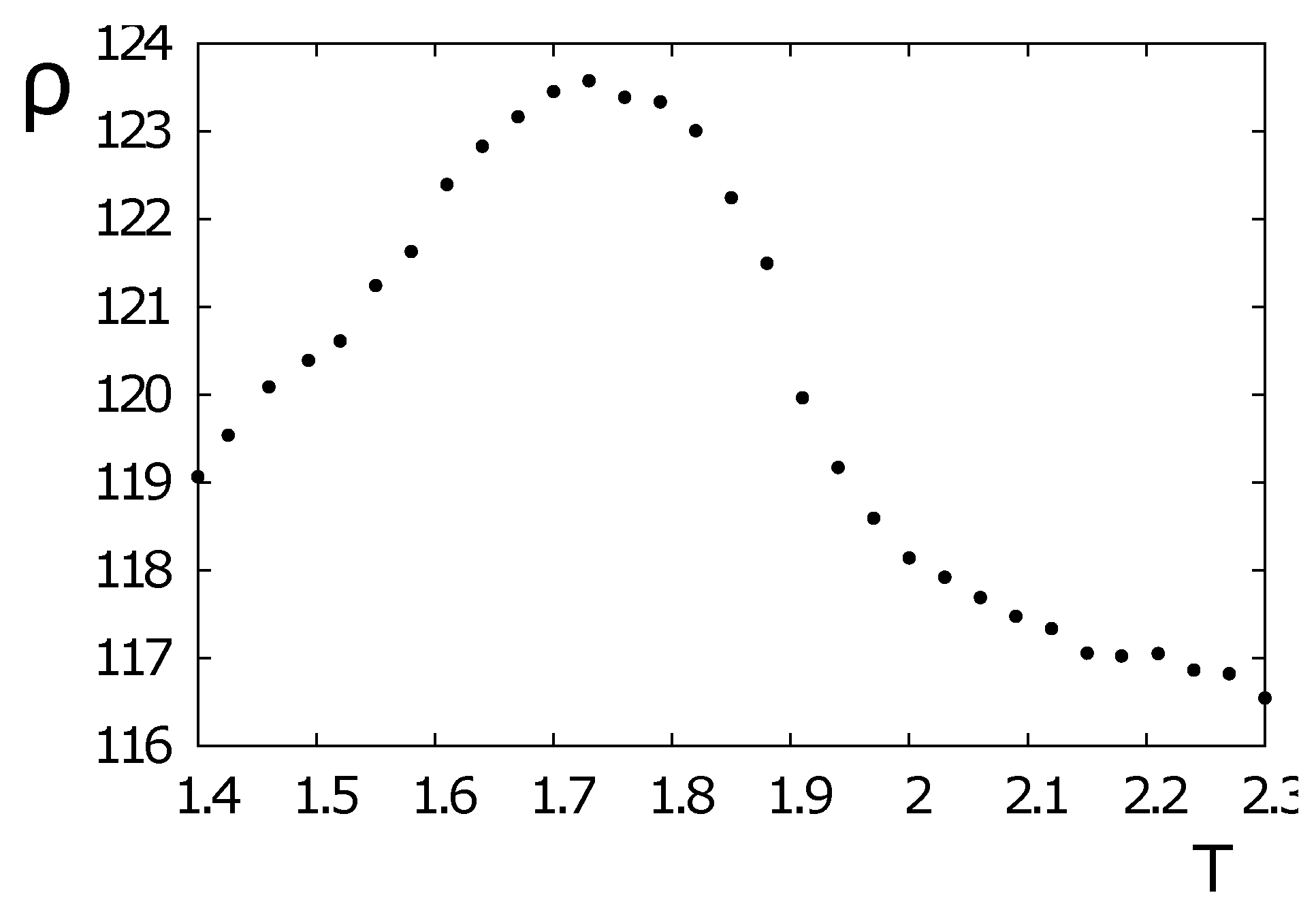
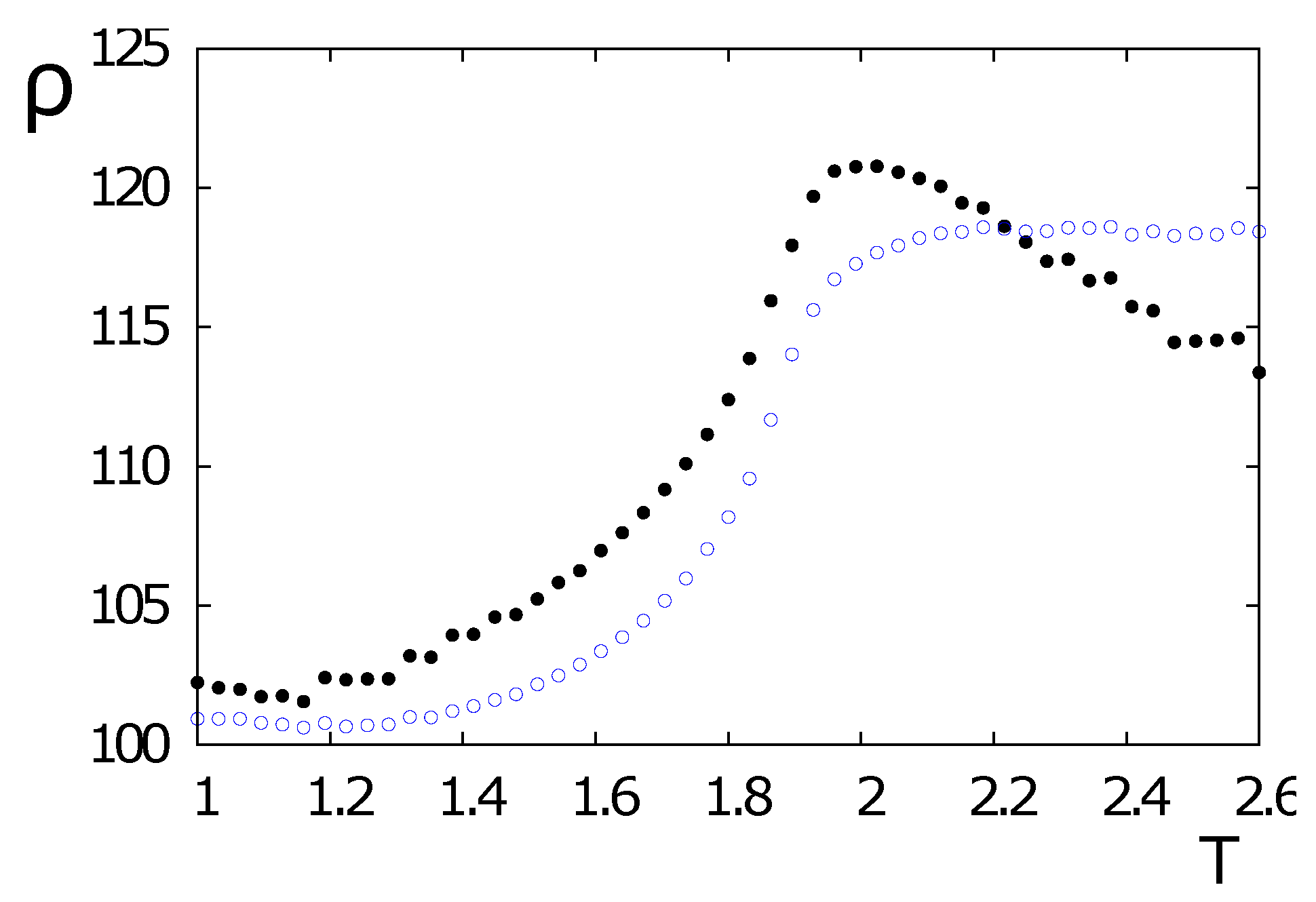
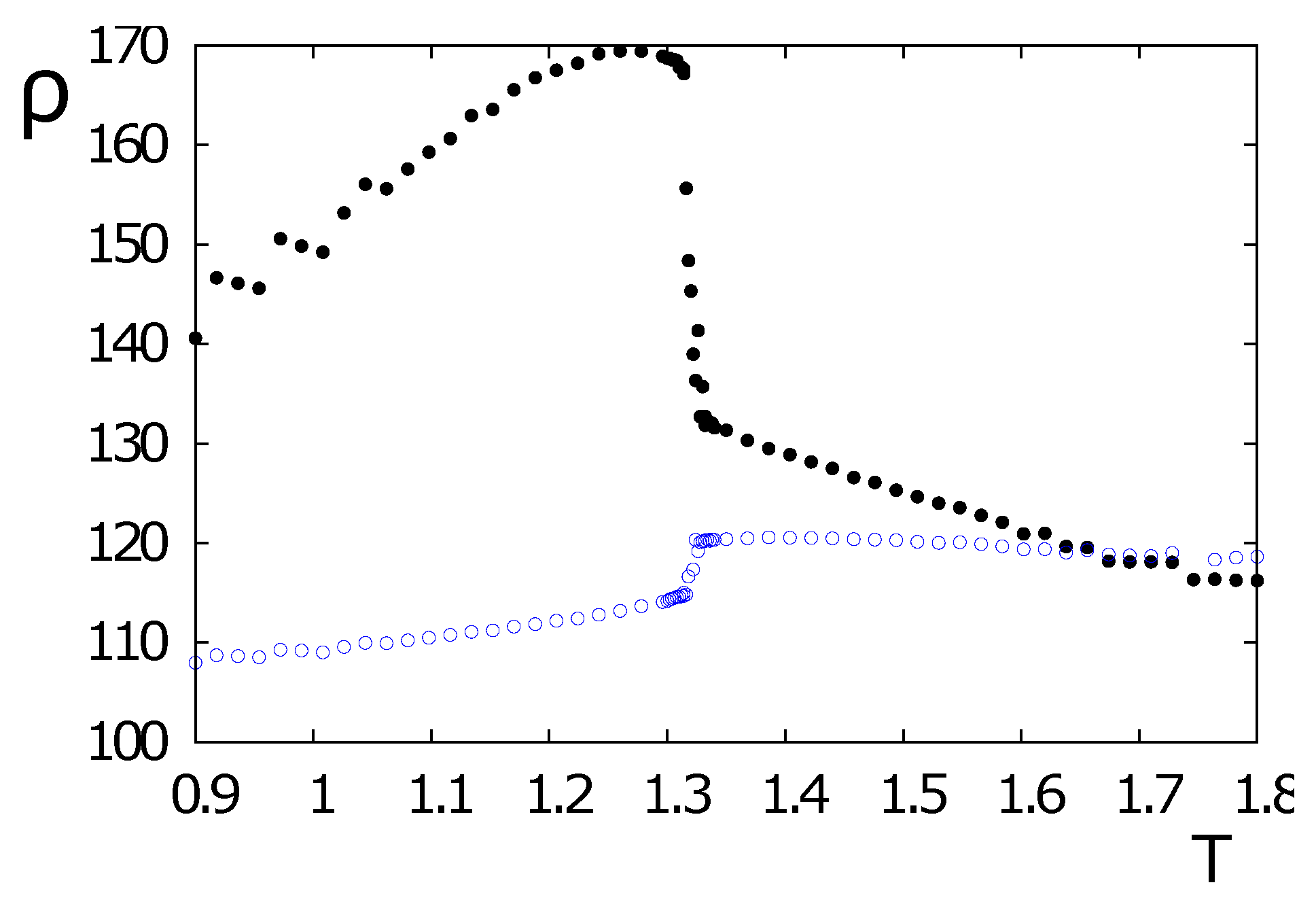
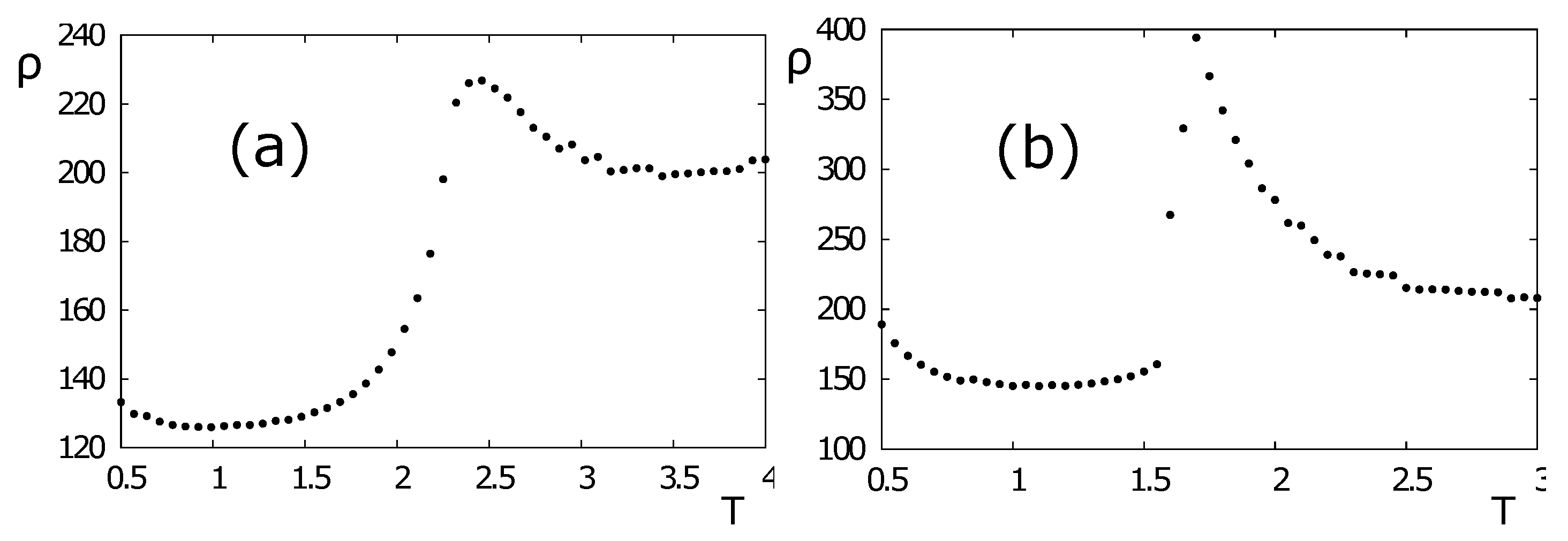
4.3. Spin Resistivity in the HCP Lattice with Ising Spins

The results in this subsection are new; they have not been published so far. Using the method described in Section 2, we carry out MC simulations to study the spin resistivity in the Ising case. We show in Figure 16 the resistivity at two temperatures, below and above the transition temperature, as a function of $D_1$ for the GS belonging to Phase (1). We show in Figure 17 the case of a GS belonging to Phase (2) (see Figure 15). Similar to the case of the $J_1 - J_2$ model on the simple cubic lattice considered in [26,27], we find here an oscillation of $\rho$ at low temperature. Note that $\rho$ is always smaller at low temperature than at high temperature, whatever the value of $D_1$ is. The physical origin of the oscillation has been discussed above.

(i)

At very low temperatures, the resistivity increases with decreasing temperature. This behavior can be understood by the freezing of the itinerant spins due to low T: the energy of itinerant spins is low; they occupy the low-energy positions in the periodic lattice; it is difficult to move them out by the insufficient thermal energy. They are somewhat frozen in almost periodic positions; namely, a pseudo crystallization occurs. Note that the increase of resistivity with decreasing T at very low T has been observed in many experiments on various materials and is not limited to ferromagnets [3,5,7,40]. This increase of $\rho$ with decreasing T in the quantum case has been explained by J. Kondo using a third-order perturbation theory [58]: the scattering of s-electrons by d-electrons of localized magnetic impurities gives rise to a resistivity minimum at a finite T. We have also found here this minimum of $\rho$ at low T with the classical spin model. The similarity with the quantum Kondo effect can be explained by the fact that an excited localized lattice down-spin (in a very small number at low T) can be viewed as an impurity that captures nearby conduction up-spins.

(ii)

Outside this low-T region, when T increases, the thermal energy progressively unfreezes the itinerant spins. As a consequence, $\rho$ decreases and passes through a minimum (see discussion above). However, at higher T, the scattering with the lattice spins is stronger; $\rho$ increases up to the transition temperature.

(iii)

At the transition temperature, $\rho$ shows a peak. The physical mechanism leading to the peak can be explained: in a previous work [21], it was found from our simulations that the peak is due to scattering of the itinerant spins by antiparallel-spin clusters that are numerous in the transition region. When one gets close to the transition point, the number of clusters of down spins are the most numerous, giving rise to the peak in $\rho$. Note that the “defects” clusters (i.e., clusters of antiparallel spins) have an energy barrier to resist the passage of itinerant spins. This is also the origin of the extremely long relaxation time in the critical region.

(iv)

Well above the transition temperature, in the paramagnetic phase, as temperature increases, clusters of down and up spins are increasingly broken into independent disordered spins, namely, spins with zero energy; itinerant spins move easily on their trajectory, decreasing $\rho$ with the increasing T.

The spin resistivity $\rho$ for $\eta = 0.3$ and 1 is shown in Figure 18 as a function of T; here, the distances $D_1$ and $D_2$ are in units of the distance between the NN lattice spins, and $I_0$, $K_0$ and D, which have energy dimensions, are in units of $|J_2| = 1$. As in the frustrated $J_1 - J_2$ model shown above, one finds here that $\rho$ has a broad peak in the second-order region, in contrast to the first-order region, where it undergoes a discontinuous jump at the phase transition. Some remarks are in order.

Note that we have also varied the radius $D_1$ to see its effect on $\rho$ at the transition in the present frustrated HCP model. We found the same effect seen in other antiferromagnets we studied previously [26,27]: at a given temperature, an oscillation of $\rho$ with varying $D_1$ oscillates slightly with distance. The origin of this oscillation has been analyzed above in the $J_1 - J_2$ model.

Finally, let us look at some experimental data obtained for ferromagnets and antiferromagnets. Figure 19 shows experiments by Du et al. performed on $\epsilon$-(Mn${}_{1 - x}$Fe${}_x{)}_{3.25}$Ge antiferromagnets [3], experiments by McGuire et al. performed on antiferromagnetic superconductors LaFeAsO [6] and by Chandra et al. on thin Cd${}_{1 - x}$Mn${}_x$Te films [39]. Experiments by Santos et al. on antiferromagnetic La${}_{1 - x}$Sr${}_x$MnO${}_3$ [7] are shown in Figure 20. We see here that our results on the shape of the spin resistivity are in agreement with these experiments. With the lack of physical data on these experimental materials, we cannot make a quantitative comparison as we did in the MnTe case presented above.

5. Conclusions

In this paper, we have reviewed some important works published on the spin resistivity in magnetically ordered systems. We have focused on our works published over the past 15 years using mainly Monte Carlo simulations. These works were motivated by the absence of Monte Carlo works, even at the present time, except ours, in spite of the fact that this method of simulation has proven to be very efficient when comparing its results with experimental data. In the case of MnTe, for which there are sufficient experimental data, we have made a quantitative comparison between experimental and simulated spin resistivities. The agreement between experiments and simulations is excellent. This review therefore aims at promoting this method to study more realistic cases.

As demonstrations, we have used this method to study the spin resistivity in generic ferromagnets and antiferromagnets. The cases of frustrated systems have also been presented: the $J_1 - J_2$ model and the antiferromagnetic HCP lattice.

Let us summarize the results on the two frustrated systems.

The $J_1 - J_2$ model is a simple cubic lattice with Ising spins interacting with each other via NN and NNN antiferromagnetic interactions, $J_1$ and $J_2$, respectively. The GS of this model is determined by the ratio $\eta = J_2/J_1$. We have shown that the GS changes at the critical value ${\eta }_c = 0.25$. For the non-frustrated region in the phase space, namely $\eta < 0.25$, the GS is simply composed periodically of two interpenetrated tetrahedra formed by the NNN sites. In the frustrated region, namely $\eta > 0.25$, the GS can be described as composed of one line of spin up and one line of spin down alternately in one crystal direction. The degeneracy is three because there is the freedom to choose one direction among three. The total degeneracy is six if we count the states of reverse spins. The transition in the frustrated region is theoretically of first order since the present six-fold GS is equivalent to the q-state Potts model with $q = 6$. We know that in three dimensions, the transition of the Potts model is of first order from $q = 3$. We found this directly from the simulation. In the non-frustrated region, namely $\eta < 0.25$, the transition is found to be of second order. We performed MC simulations to obtain $\rho$ of the conduction spins. We found that $\rho$ displays a broad maximum at the second-order phase transition while it undergoes a discontinuous change at the first-order transition.

The Ising model on the antiferromagnbetic HCP lattice has been also studied in this review. We assumed an in-plane interaction $J_1$ and an inter-plane interaction $J_2$, both antiferromagnetic. We found that the GS changes at the critical value ${\eta }_c = 0.5$, below (above) which the spins in the $xy$ planes are ferromagnetic (antiferromagnetic). The nature of the transition changes in these two regions: it is of second order below ${\eta }_c$ and of first order above ${\eta }_c$. The spin resistivity has been simulated in both regions of $\eta$. In the second-order region, it shows a broad maximum, while in the first-order region, the resistivity $\rho$ makes a discontinuous jump at the transition. This feature is what we also found in other frustrated spin systems.

These findings reviewed in this paper show a close relationship between the nature of the phase transition and the shape of the spin resistivity in real materials. We hope that this review convinces the magnetic community of the use of MC simulations for transport phenomena.