Approximate Closed-Form Solution of the Differential Equation Describing Droplet Flight during Sprinkler Irrigation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Closed-Form Solution and Mathematical Modeling
- Flow of water completely disintegrates into droplets of various diameters in the outlet section of the sprinkler nozzle;
- All droplets have the same initial velocity, which is equal to the average velocity of the water flow in the exit section of the nozzle;
- Each droplet of water is considered alone along the trajectory, i.e., without collisions with the other droplets;
- Water droplets are considered rigid spheres upon exiting the nozzle and remain spherical during flight;
- Water droplets are not subject to evaporation, so their diameters remain unchanged throughout their trajectory;
- No wind.
2.1.1. Ascending Portion of the Trajectory
2.1.2. Descending Portion of the Trajectory
2.2. Numerical Solution
3. Results and Discussion
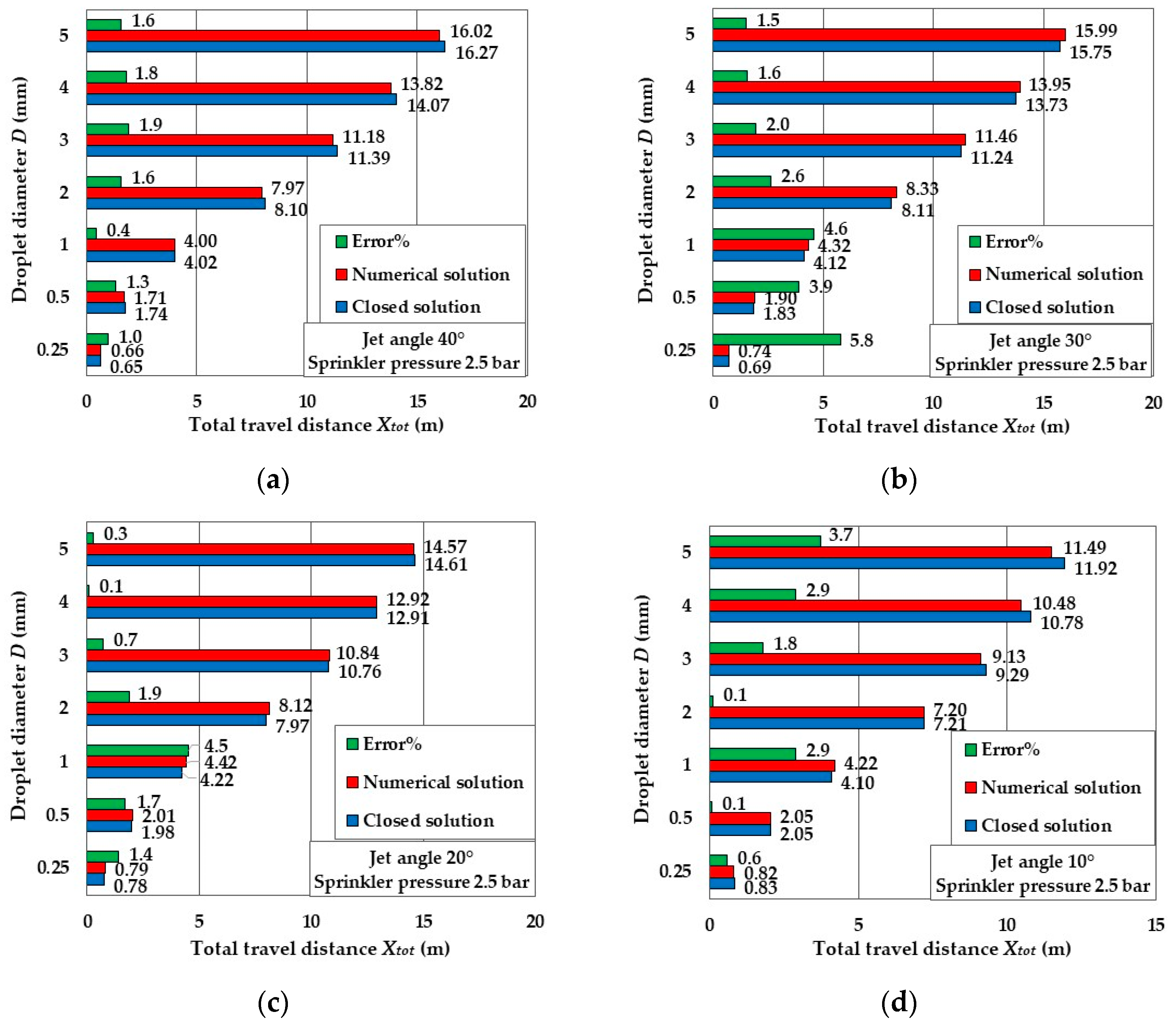
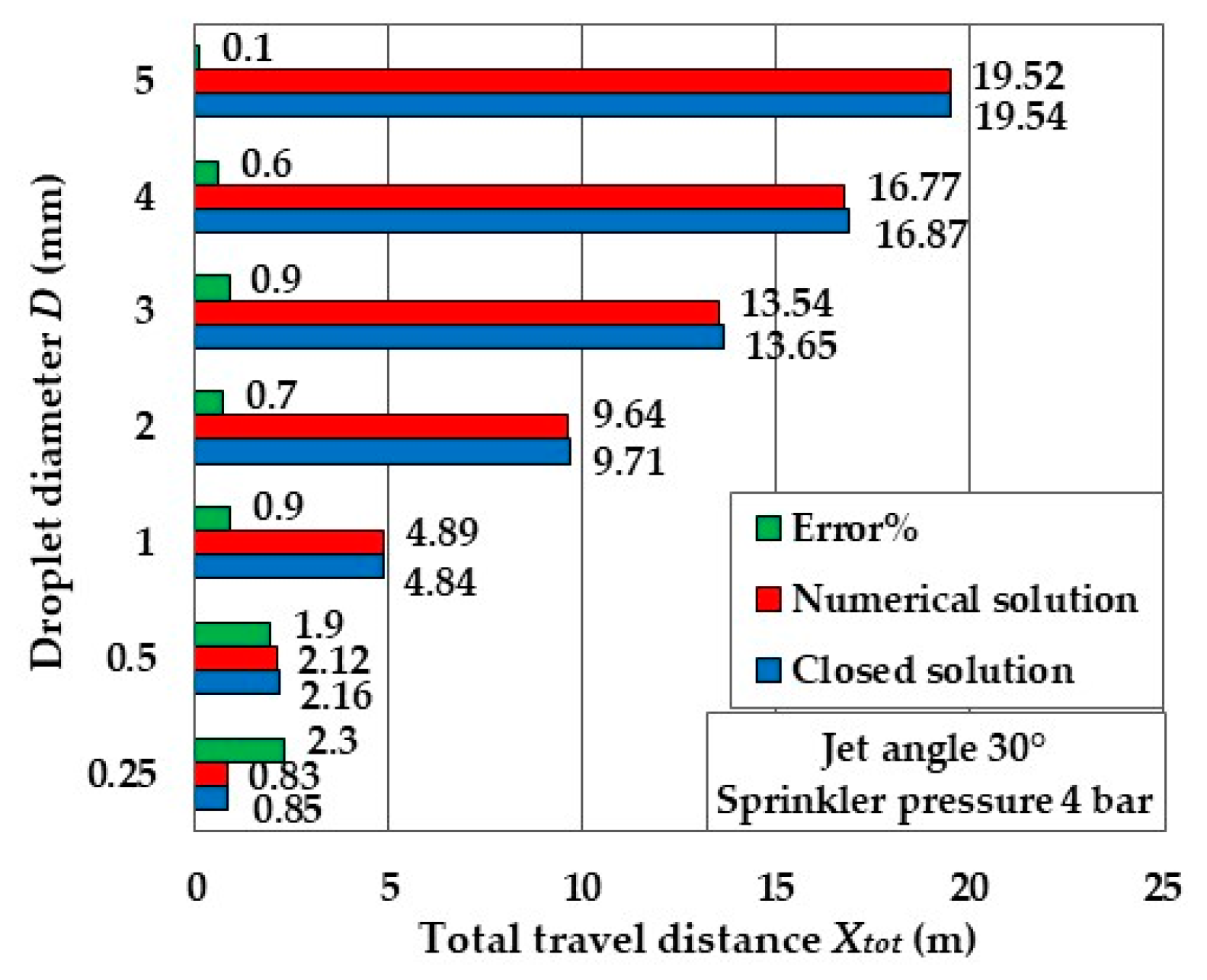
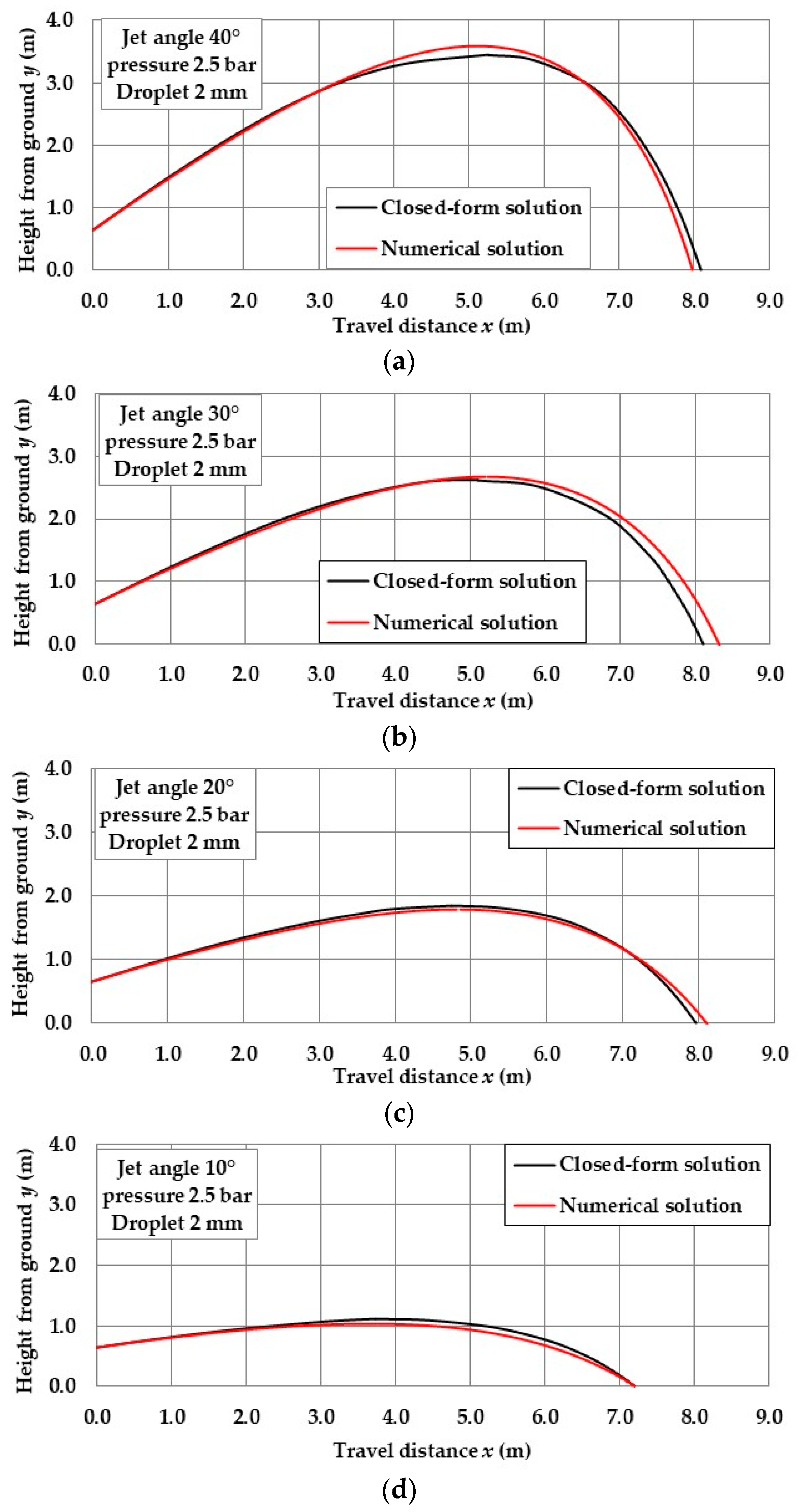
3.1. Comparison between Approximate Closed-Form Solution and Exact Numerical Solution
3.2. Comparison between Approximate Closed-Form Solution and Experimental Data
3.3. Modification of the Drag Coefficient Formula to Consider the Deformation of the Droplets
3.4. Synoptic Table of the Definitive Analytical Modeling Based on Approximated Closed-Form Solution with the Drag Coefficient according to Park’s Values with Equations (59) and (60)
3.5. Results of the Application of Definitive Analytical Modeling
3.6. Analytical Modeling and Droplet Evaporation
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Regression Equations for Linearization Coefficients
References
- Hui, X.; Zhao, H.; Zhang, H.; Wang, W.; Wang, J.; Yan, H. Specific power or droplet shear stress: Which is the primary cause of soil erosion under low-pressure sprinklers? Agric. Water Manag. 2023, 286, 108376. [Google Scholar] [CrossRef]
- Chen, R.; Li, H.; Wang, J.; Song, Z. Critical factors influencing soil runoff and erosion in sprinkler irrigation: Water application rate and droplet kinetic energy. Agric. Water Manag. 2023, 283, 108299. [Google Scholar] [CrossRef]
- Hui, X.; Zheng, Y.; Muhammad, R.S.; Tan, H.; Yan, H. Non-negligible factors in low-pressure sprinkler irrigation: Droplet impact angle and shear stress. J. Arid Land 2022, 14, 1293–1316. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhu, D.; Ge, M. The spatial variation mechanism of size, velocity, and the landing angle of throughfall droplets under maize canopy. Water 2021, 13, 2083. [Google Scholar] [CrossRef]
- Chen, R.; Li, H.; Wang, J.; Guo, X. Analysis of droplet characteristics and kinetic energy distribution for fixed spray plate sprinkler at low working pressure. Trans. ASABE 2021, 64, 447–460. [Google Scholar] [CrossRef]
- Ge, M.; Wu, P.; Zhu, D.; Zhang, L. Analysis of kinetic energy distribution of big gun sprinkler applied to continuous moving hose-drawn traveler. Agric. Water Manag. 2018, 201, 118–132. [Google Scholar] [CrossRef]
- Félix-Félix, J.R.; Salinas-Tapia, H.; Bautista-Capetillo, C.; Garcia-Aragon, J.; Burguete, J.; Playan, E. A modified particle tracking velocimetry technique to characterize sprinkler irrigation drops. Irrig. Sci. 2017, 35, 515–531. [Google Scholar] [CrossRef]
- Hua, L.; Li, H.; Bortolini, L.; Jiang, Y. A model for predicting effects of rotation variation on water distribution of rotary sprinkler. Irrig. Sci. 2023, in press. [CrossRef]
- Zerihun, D.; Sanchez, C.A.; Warrick, A.W. Sprinkler irrigation droplet dynamics. I: Review and theoretical development. J. Irrig. Drain. Eng. 2016, 142, 04016007. [Google Scholar] [CrossRef]
- Zerihun, D.; Sanchez, C.A.; Warrick, A.W. Sprinkler irrigation droplet dynamics. II: Numerical solution and model evaluation. J. Irrig. Drain. Eng. 2016, 142, 04016008. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Y.; Zhu, D.; Wu, P.; Zheng, C.; Zhang, X.; Khudayberdi, N.; Liu, C. Simulating droplet distribution characteristics for sprinkler irrigation with a modified ballistic model. Comput. Electron. Agric. 2023, 215, 108437. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Y.; Zhu, D.; Zhang, X.; Gao, F.; Zheng, C. Modelling the spray range of rotating nozzles based on modified ballistic trajectory equation parameters. Irrig. Drain. 2023, 72, 343–357. [Google Scholar] [CrossRef]
- Seginer, I. Tangential velocity in sprinkler drops. Trans. ASAE 1965, 8, 90–93. [Google Scholar] [CrossRef]
- Fukui, Y.; Nakanish, K.; Okamura, S. Computer evaluation of sprinkler irrigation uniformity. Irrig. Sci. 1980, 2, 23–32. [Google Scholar] [CrossRef]
- von Bernuth, R.D.; Gilley, J.R. Sprinkler droplet size distribution estimation from single leg test data. Trans. ASAE 1984, 27, 1435–1441. [Google Scholar] [CrossRef]
- Vories, E.D.; Von Bernuth, R.D.; Mickelson, R.H. Simulating sprinkler performance in wind. J. Irrig. Drain. Eng. 1987, 113, 119–130. [Google Scholar] [CrossRef]
- Seginer, I.; Nir, D.; von Bernuth, R.D. Simulation of wind distorted sprinkler patterns. J. Irrig. Drain. Eng. 1991, 117, 285–306. [Google Scholar] [CrossRef]
- Carrion, P.; Tarjuelo, J.M.; Montero, J. SIRIAS: A simulation model for sprinkler irrigation. I: Description. Irrig. Sci. 2001, 20, 73–84. [Google Scholar] [CrossRef]
- Playan, E.; Burguete, J.; Zapata, N.; Salvador, R.; Bautista-Capetillo, C.; Cavero, J.; Martinez-Cob, A.; Faci, J.; Dechimi, F. Mathematical Problems and Solutions in Sprinkler Irrigation; Monografıas de la Real Academia de Ciencias 31: Zaragoza, Spain, 2009; pp. 153–174. [Google Scholar]
- Lorenzini, G. Simplified modelling of sprinkler droplet dynamics. Biosyst. Eng. 2004, 87, 1–11. [Google Scholar] [CrossRef]
- Yan, H.J.; Bai, G.; He, J.Q.; Li, Y.J. Model of droplet dynamics and evaporation for sprinkler irrigation. Biosyst. Eng. 2010, 106, 440–447. [Google Scholar] [CrossRef]
- Ben Charfi, I.; Corbari, C.; Skokovic, D.; Sobrino, J.; Mancini, M. Modeling of water distribution under center pivot irrigation technique. J. Irrig. Drain. Eng. 2021, 147, 04021024. [Google Scholar] [CrossRef]
- Friso, D. A new mathematical model for food thermal process prediction. Modell. Simul. Eng. 2013, 2013, 569473. [Google Scholar] [CrossRef]
- Bird, R.B.; Steward, W.E.; Lightfoot, E.N. Transport Phenomena; Wiley & Sons: New York, NY, USA, 1960; pp. 185–187. [Google Scholar]
- Friso, D. Mathematical modelling of particle terminal velocity for improved design of clarifiers, thickeners and flotation devices for wastewater treatment. Clean Technol. 2023, 5, 921–933. [Google Scholar] [CrossRef]
- Lapple, C.E.; Shepherd, C.B. Calculation of particle trajectories. Ind. Eng. Chem. 1940, 32, 605–617. [Google Scholar] [CrossRef]
- Thompson, A.L.; Gilley, J.R.; Norman, J.M. A sprinkler water droplet evaporation and plant canopy model: I Model development. Trans. ASAE 1993, 36, 735–741. [Google Scholar] [CrossRef]
- Thompson, A.L.; Gilley, J.R.; Norman, J.M. A sprinkler water droplet evaporation and plant canopy model: II. Model application. Trans. ASAE 1993, 36, 743–750. [Google Scholar] [CrossRef]
- Kincaid, D.C. Spray drop kinetic energy from irrigation sprinklers. Trans. ASAE 1996, 39, 847–853. [Google Scholar] [CrossRef]
- Park, S.W.; Mitchell, J.K.; Bubenzer, G.D. Splash erosion modeling: Physical analysis. Trans. ASAE 1982, 25, 357–361. [Google Scholar] [CrossRef]
- Park, S.W.; Mitchell, J.K.; Bubenzer, G.D. Rainfall characteristics and their relation to splash erosion. Trans. ASAE 1983, 26, 795–804. [Google Scholar] [CrossRef]
- Laws, J.O. Measurements of the fall velocity of waterdrops and raindrops. Trans. Am. Geophys. Union 1941, 22, 709–721. [Google Scholar] [CrossRef]
- Gunn, R.; Kinzer, G.D. The terminal velocity of fall for water droplets in stagnant air. J. Meteorol. 1949, 6, 243–248. [Google Scholar] [CrossRef]
- Kincaid, D.C.; and Longley, T.S. A water droplet evaporation and temperature model. Trans. ASAE 1989, 32, 457–462. [Google Scholar] [CrossRef]
- Friso, D. Conveyor-belt dryers with tangential flow for food drying: Mathematical modelling and design guidelines for final moisture content higher than the critical value. Inventions 2020, 5, 22. [Google Scholar] [CrossRef]


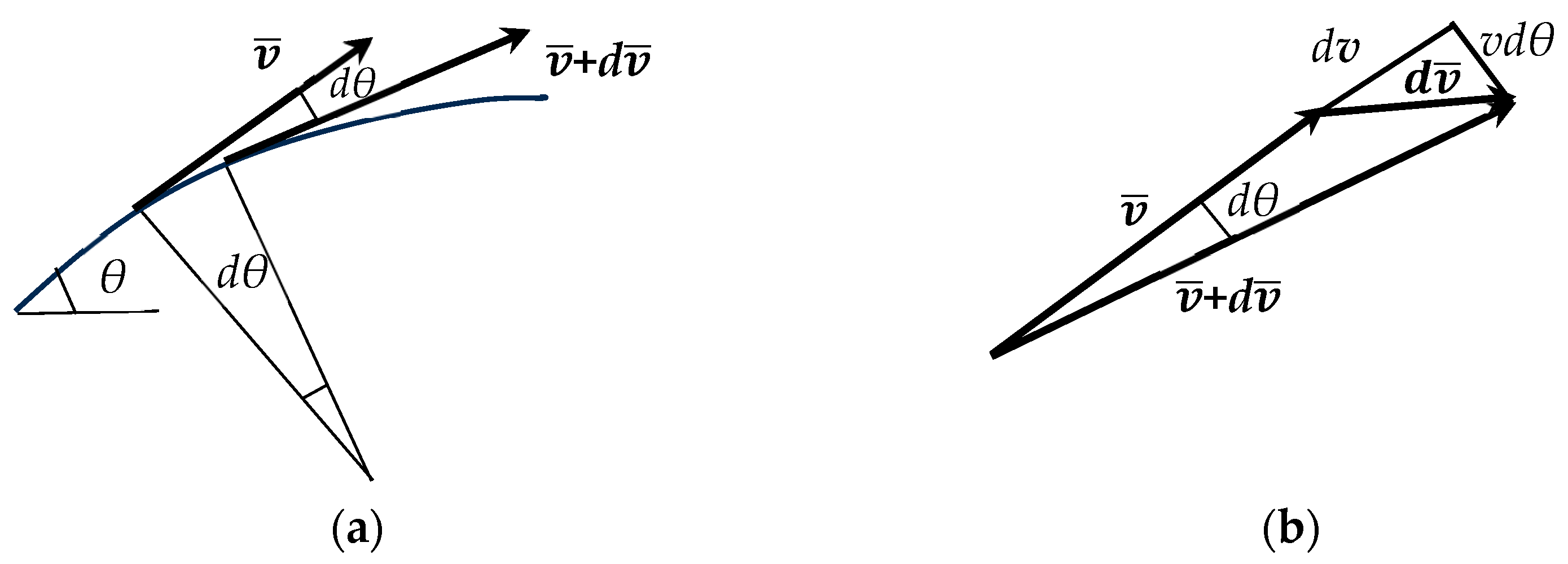
| Droplet Diameter D (mm) | Travel Distance xtot (m) Tompson et al. [27,28] | Travel Distance xtot (m) This Study | Relative Error (%) |
|---|---|---|---|
| 0.3 | 1.30 | 1.27 | −2.6 |
| 0.9 | 5.22 | 5.20 | −0.3 |
| 1.8 | 10.00 | 10.92 | +9.2 |
| 3.0 | 13.48 | 17.27 | +28.2 |
| 5.1 | 17.83 | 25.76 | +44.5 |
| Droplet Diameter D (mm) | Flight Time ttot (s) Tompson et al. [27,28] | Flight Time ttot (s) This Study | Relative Error (%) |
|---|---|---|---|
| 0.3 | 2.63 | 1.03 | −60.9 |
| 0.9 | 1.54 | 1.66 | +7.7 |
| 1.8 | 1.63 | 1.97 | +20.8 |
| 3.0 | 1.75 | 2.17 | +24.1 |
| 5.1 | 1.84 | 2.38 | +29.4 |
| Droplet Diameter D (mm) | Re0 Tompson et al. [27,28] | Drag Coefficient cd Equation (4) Based on SDC | Drag Coefficient cd Equation (58) Park et al. [30,31] |
|---|---|---|---|
| 0.3 | 554 | 0.572 | - |
| 0.9 | 1661 | 0.442 | 0.443 |
| 1.8 | 3323 | 0.400 | 0.464 |
| 3.0 | 5538 | 0.383 | 0.499 |
| 5.1 | 9414 | 0.376 | 0.570 |
| Droplet Diameter D (mm) | Travel Distance xtot (m) Tompson et al. [27,28] | Travel Distance xtot (m) This Study with Equation (60) | Relative Error (%) |
|---|---|---|---|
| 0.3 | 1.30 | 1.27 | −2.6 |
| 0.9 | 5.22 | 5.10 | −2.4 |
| 1.8 | 10.00 | 9.60 | −4.0 |
| 3.0 | 13.48 | 13.61 | +1.0 |
| 5.1 | 17.83 | 18.23 | +2.3 |
| Droplet Diameter D (mm) | Total Flight Time ttot (s) Tompson et al. [27,28] | Total Flight Time ttot (s) This Study with Equation (60) | Relative Error (%) |
|---|---|---|---|
| 0.3 | 2.63 | 1.03 | −60.9 |
| 0.9 | 1.54 | 1.63 | +5.8 |
| 1.8 | 1.63 | 1.85 | +13.3 |
| 3.0 | 1.75 | 1.94 | +11.0 |
| 5.1 | 1.84 | 2.01 | +9.0 |
| Symbol | Unity of Measurement | Description |
|---|---|---|
| a | m s−2 | acceleration |
| Ar | - | Archimedes number |
| C | - | integration constant |
| cd | - | drag coefficient |
| D | m | droplet diameter |
| g | m s−2 | gravity acceleration |
| h | m | nozzle height from the ground |
| m | kg | mass |
| n | axis normal to the trajectory | |
| p | bar | nozzle pressure |
| Re | - | Reynolds number |
| s | m | axis tangential to the trajectory and/or length of the trajectory |
| t | s | time |
| v | m s−1 | droplet velocity |
| u, w, z | - | auxiliary variables |
| x | m | travel distance |
| y | m | height of trajectory |
| Greek symbol | Unity of measurement | Description |
| α | - | linearization coefficient |
| β | - | Exponent in the drag coefficient formula for ascending trajectory |
| γ | - | linearization coefficient |
| δ | - | Exponent in the drag coefficient formula for descending trajectory |
| ε | - | linearization coefficient |
| η | - | “ |
| θ | ° | trajectory angle |
| λ | - | linearization coefficient |
| μ | Pa s | viscosity |
| ρ | kg m3 | density |
| σ | - | linearization coefficient |
| φ | - | “ |
| ψ | - | “ |
| Subscript | Description | |
| a | ascending portion of trajectory | |
| air | air | |
| ave | average | |
| d | descending portion of trajectory | |
| D | droplet | |
| end | end of trajectory | |
| top | top of trajectory | |
| ua | integration constant of auxiliary variable u of ascending trajectory | |
| ud | integration constant of auxiliary variable u of descending trajectory | |
| w | water | |
| 0 | start of trajectory |
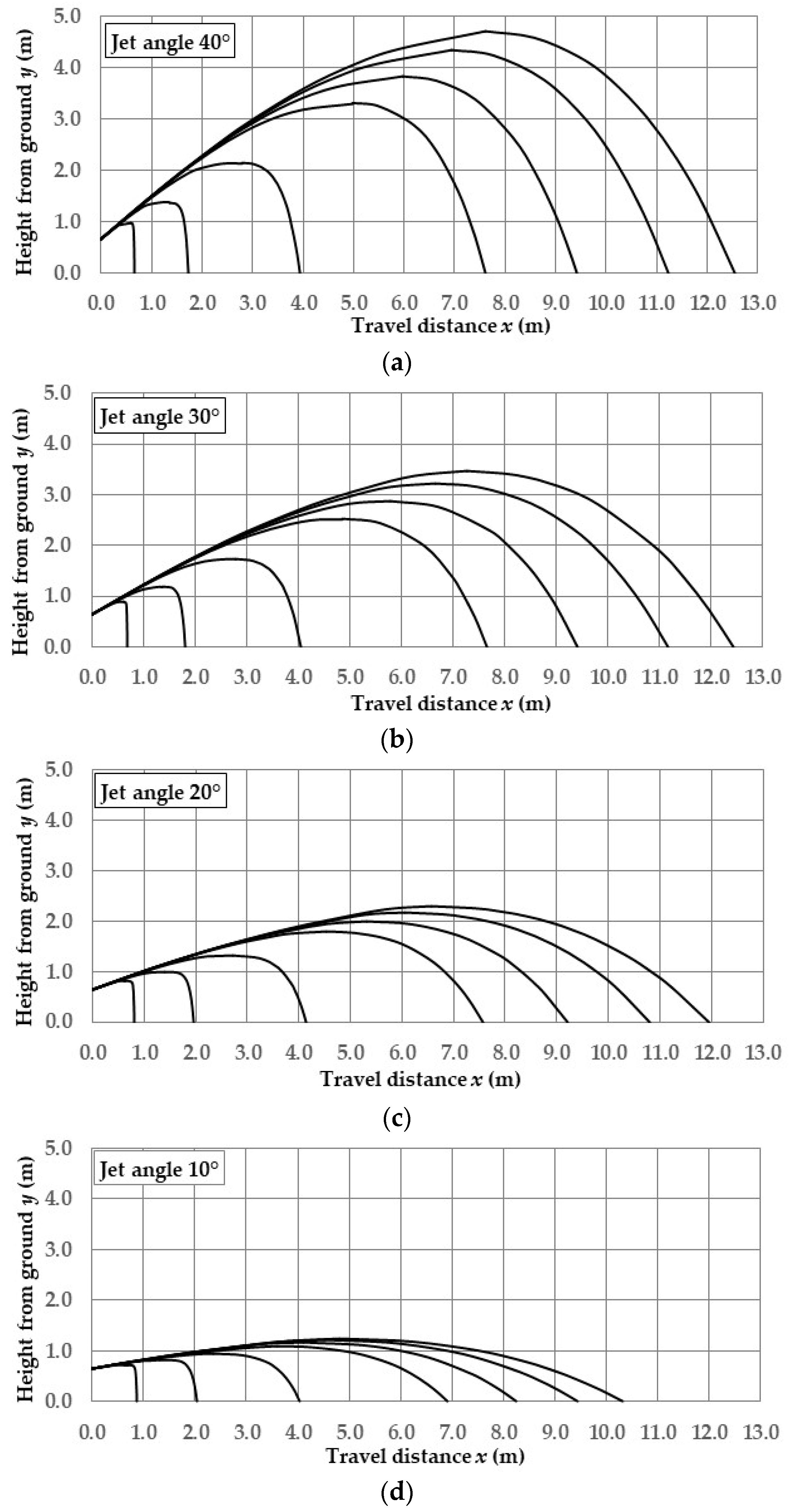
| Jet Angle θ0 (°) | Droplet Diameter D (mm) | Travel Distance xtot (m) | Top Height from Ground ytop + h (m) | Landing Angl e θend (°) | Terminal Velocity vend (m/s) |
|---|---|---|---|---|---|
| 0.25 | 0.65 | 0.96 | 89.5 | 1.9 | |
| 0.5 | 1.73 | 1.37 | 87.2 | 3.2 | |
| 1 | 3.94 | 2.14 | 82.0 | 4.7 | |
| 40° | 2 | 7.62 | 3.30 | 75.0 | 6.4 |
| 3 | 9.43 | 3.83 | 71.7 | 7.2 | |
| 4 | 11.24 | 4.34 | 69.0 | 7.9 | |
| 5 | 12.55 | 4.69 | 67.0 | 8.4 | |
| 0.25 | 0.69 | 0.88 | 89.4 | 1.8 | |
| 0.5 | 1.82 | 1.18 | 86.5 | 3.0 | |
| 1 | 4.05 | 1.72 | 79.5 | 4.3 | |
| 30° | 2 | 7.65 | 2.52 | 69.9 | 5.8 |
| 3 | 9.43 | 2.88 | 65.4 | 6.5 | |
| 4 | 11.17 | 3.22 | 61.7 | 7.2 | |
| 5 | 12.44 | 3.46 | 59.2 | 7.7 | |
| 0.25 | 0.81 | 0.80 | 89.2 | 1.7 | |
| 0.5 | 1.97 | 1.00 | 85.3 | 2.8 | |
| 1 | 4.15 | 1.33 | 75.3 | 3.9 | |
| 20° | 2 | 7.57 | 1.79 | 61.1 | 5.3 |
| 3 | 9.22 | 1.99 | 54.9 | 6.1 | |
| 4 | 10.80 | 2.17 | 50.1 | 6.8 | |
| 5 | 11.96 | 2.30 | 47.0 | 7.4 | |
| 0.25 | 0.87 | 0.73 | 88.7 | 1.6 | |
| 0.5 | 2.04 | 0.81 | 83.0 | 2.4 | |
| 1 | 4.04 | 0.94 | 66.9 | 3.3 | |
| 10° | 2 | 6.91 | 1.10 | 45.4 | 5.1 |
| 3 | 8.25 | 1.16 | 37.6 | 6.2 | |
| 4 | 9.45 | 1.21 | 32.3 | 7.3 | |
| 5 | 10.32 | 1.25 | 29.2 | 8.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friso, D. Approximate Closed-Form Solution of the Differential Equation Describing Droplet Flight during Sprinkler Irrigation. Inventions 2024, 9, 73. https://doi.org/10.3390/inventions9040073
Friso D. Approximate Closed-Form Solution of the Differential Equation Describing Droplet Flight during Sprinkler Irrigation. Inventions. 2024; 9(4):73. https://doi.org/10.3390/inventions9040073
Chicago/Turabian StyleFriso, Dario. 2024. "Approximate Closed-Form Solution of the Differential Equation Describing Droplet Flight during Sprinkler Irrigation" Inventions 9, no. 4: 73. https://doi.org/10.3390/inventions9040073
APA StyleFriso, D. (2024). Approximate Closed-Form Solution of the Differential Equation Describing Droplet Flight during Sprinkler Irrigation. Inventions, 9(4), 73. https://doi.org/10.3390/inventions9040073






