Mathematical Modeling of Oxygen Transfer Using a Bubble Generator at a High Reynolds Number: A Partial Differential Equation Approach for Air-to-Water Transfer
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Fine Bubble Generator with the Plate with Orifices in Rotational Motion
- -
- A high Reynolds number indicates turbulent flow, which enhances mixing and mass transfer rates.
- -
- The bubbles have a constant size, neglecting variations due to changes in hydrostatic pressure or coalescence/breakup dynamics.
- -
- The bubbles are uniformly distributed within the fluid.
- -
- Homogeneity in fluid properties (density, viscosity, diffusivity).
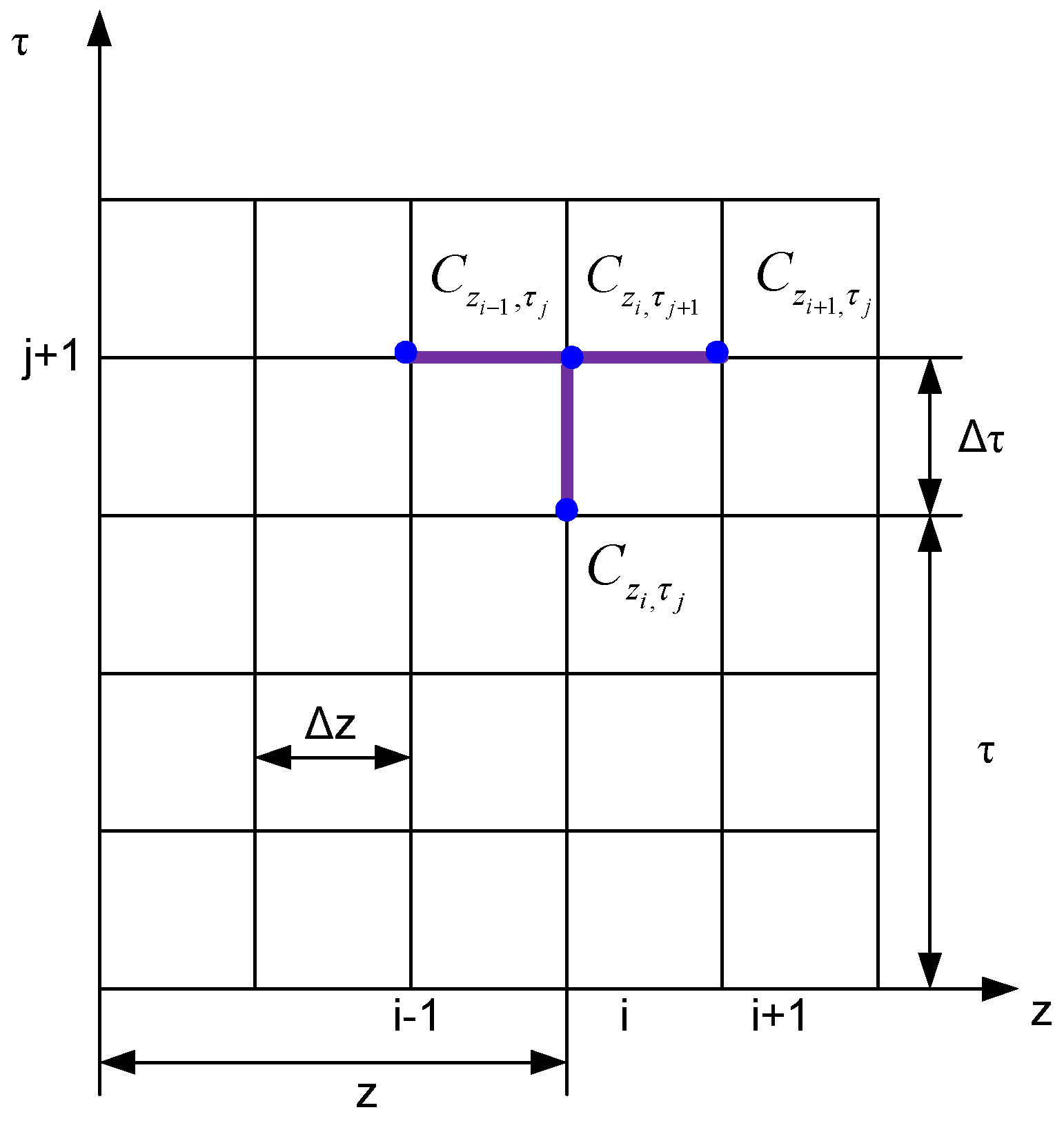
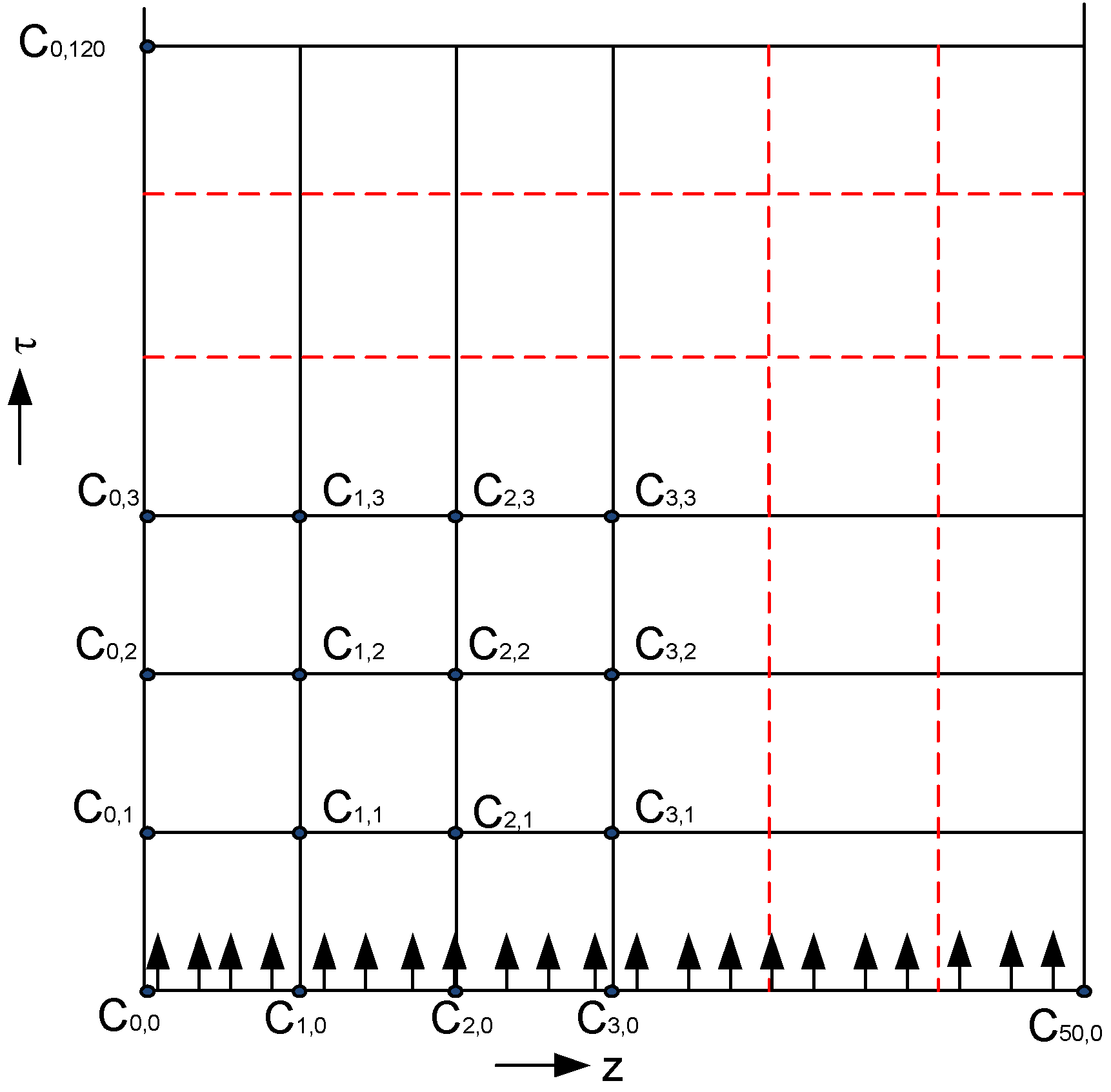
2.2. Solving the Differential Equation of Diffusion with the Term “Source”
- -
- According to the order of the partial derivatives, they are classified into first-order, second-order, and n-order equations;
- -
- According to the character of linearity, they are divided into linear, quasi-linear, and nonlinear equations;
- -
- According to the type of influence of the integration domain on the solution at a point, they are divided into elliptic, parabolic, and hyperbolic equations;
- -
- According to the general form of a linear differential equation with partial derivatives with two variables [29]
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cashel, F.S.; Knightes, C.D.; Lupo, C.; Iott, T.; Streich, K.; Conville, C.J.; Bridges, T.W.; Dombroski, I. Using monitoring and mechanistic modeling to improve understanding of eutrophication in a shallow New England estuary. J. Environ. Manag. 2024, 355, 120478. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Wang, Y.; Yang, H.; Lan, S.; Chen, C.; Dai, B.; Wang, C.; Li, X.; Xie, Y. Using intermittent moving aeration to repair hypereutrophic pond: Nutrient removal efficiency and microbial diversity analysis. Environ. Sci. Pollut. Res. 2023, 30, 46697–46710. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Jin, H.; Chen, J.; Wang, D.; Yang, Z.; Wang, B.; Zhuang, Y.; Wang, R. Nitrogen removal through sediment denitrification in the Yangtze Estuary and its adjacent East China Sea: A nitrate limited process during summertime. Sci. Total Environ. 2021, 795, 148616. [Google Scholar] [CrossRef] [PubMed]
- Saleh, A.; Ibrahim, F.N.; Sharaf, M.A.M. Mathematical model for expanding suitable areas for fish survival in a polluted river by using the solution of the two coupled pollution and aeration equations. Model. Earth Syst. Environ. 2024, 10, 1803–1813. [Google Scholar] [CrossRef]
- Hessen, D.O.; Andersen, T.; Armstrong McKay, D.; Kosten, S.; Meerhoff, M.; Pickard, A.; Spears, B.M. Lake ecosystem tipping points and climate feedbacks. Earth Syst. Dynam. 2024, 15, 653–669. [Google Scholar] [CrossRef]
- Fengbo, L.; Zhiping, S.S.; Hangying, Q.; Xiyue, Z.; Chunchun, X.; Dianxin, W.; Fuping, F.; Jinfei, F.; Ning, Z. Effects of Rice-Fish Co-culture on Oxygen Consumption in Intensive Aquaculture Pond. Rice Sci. 2019, 26, 50–59. [Google Scholar]
- Maßmig, M.; Cisternas-Novoa, C.; Engel, A. Uncovering the role of oxygen on organic carbon cycling: Insights from a continuous culture study with a facultative anaerobic bacterioplankton species (Shewanella baltica). Front. Mar. Sci. 2024, 11, 1328392. [Google Scholar] [CrossRef]
- Welker, T.L.; Overturf, K.; Abernathy, J. Effect of aeration and oxygenation on growth and survival of rainbow trout in a commercial serial-pass, flow-through raceway system. Aquac. Rep. 2019, 14, 100194. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Tran-Nguyen, P.L.; Chau Vo, T.T.B. Advances in aeration and wastewater treatment in shrimp farming: Emerging trends, current challenges, and future perspectives. AQUA-Water Infrastruct. Ecosyst. Soc. 2024, 73, 902–916. [Google Scholar] [CrossRef]
- Tong, C.; He, K.; Hu, H. Design and Application of New Aeration Device Based on Recirculating Aquaculture System. Appl. Sci. 2024, 14, 3401. [Google Scholar] [CrossRef]
- Benigno, P.; Legamia, P.D., Jr.; Adriano, B.; Singian, D. Evaluating the Efficiency of a Modified Solar Powered Pond Aerator System. Int. J. Eng. Technol. 2018, 7, 613–616. [Google Scholar]
- Nguyen, N.T.; Matsuhashi, R.; Bich Chau Vo, T.T. A design on sustainable hybrid energy systems by multi-objective optimization for aquaculture industry. Renew. Energy 2021, 163, 1878–1894. [Google Scholar] [CrossRef]
- Imani, M.; Fakour, H.; Lo, S.-L.; Yuan, M.-H.; Chen, C.-K.; Mobasser, S.; Muangthai, I. Aquavoltaics Feasibility Assessment: Synergies of Solar PV Power Generation and Aquaculture Production. Water 2023, 15, 987. [Google Scholar] [CrossRef]
- Tănase, B.; Constantin, M.; Zamfir, M.; Băran, N.; Păun, R.; Roza, A. Energy optimization of water oxygenation processes. UPB Sci. Bull. Ser. D 2018, 80, 103–114. [Google Scholar]
- Vlăsceanu, M.; Dan Robescu, D.; Căluşaru, M. Theoretical and experimental research concerning the modification of dissolved oxygen concentration in aeration tanks equipped with surface aerators. UPB Sci. Bull. Ser. D 2015, 77, 177–184. [Google Scholar]
- Căluşaru, I.M.; Băran, N.; Costache, A. The determination of dissolved oxygen concentration in stationary water. Appl. Mech. Mater. Trans. Tech. Publ. 2013, 436, 233. [Google Scholar] [CrossRef]
- Căluşaru, I.M.; Băran, N.; Costache, A. Determination of dissolved oxygen concentration in stationary water. J. Chem. 2012, 63, 1312–1315. [Google Scholar] [CrossRef]
- Căluşaru, I.M.; Băran, N.; Pătulea, A. The influence of the constructive solution of fine bubble generators on the concentration of dissolved oxygen in water. Adv. Mater. Res. 2012, 538–541, 2304. [Google Scholar] [CrossRef]
- Pătulea, A.; Căluşaru, I.M.; Băran, N. Research regarding the measurements of the dissolved concentration in water. Adv. Mater. Res. 2012, 550–553, 3388. [Google Scholar] [CrossRef]
- Căluşaru, I.M.; Costache, A.; Băran, N.; Ionescu, G.L.; Donţu, O. A new solution to increase the performance of the water oxygenation process. J. Chem. 2013, 64, 1143–1145. [Google Scholar]
- Băran, N.; Constantin, M.; Tănase, B.; Moraru, E.; Ioana Moga, C.I. Influence of Fine Bubble Generator Architecture on Time Variation of Dissolved Oxygen Concentration in Water. J. Chem. 2019, 70, 2132–2135. [Google Scholar] [CrossRef]
- Căluşaru, I.M.; Băran, N.; Ionescu, G.L.; Donţu, O. Influence of fine bubble generators nozzles diameter on the dissolved O2 concentration. Environ. Eng. Man. J. 2018, 17, 1029–1033. [Google Scholar]
- Martakidis, K.; Gavril, D. Extending the study of mass transport across the gas-liquid interface by reversed-flow gas chromatography. J. Chromatogr. A 2019, 1605, 460370. [Google Scholar] [CrossRef]
- Lewis, W.K.; Whitman, W.G. Principles of Gas Absorption. Ind. Eng. Chem. 1994, 16, 1215–1220. [Google Scholar] [CrossRef]
- Heyland, A.; Roszell, J.; Chau, J.; Chai, K.; Eaton, A.; Nolan, K.; Madden, K.; Ahmed, W.H. Mass transfer and flow characterization of novel algae-based nutrient removal system. Biotechnol. Biofuels 2021, 14, 104. [Google Scholar] [CrossRef]
- Pătulea, A.S. Influenţa Parametrilor Funcţionali şi a Arhitecturii Generatoarelor de Bule Fine Asupra Eficienţei Instalaţiilor de Aerare. Ph.D. Thesis, University Politechnica of Bucharest, București, Romania, 2012. [Google Scholar]
- Gupta, R.K. Numerical Methods, Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Lee, B. Least angle regression, relaxed lasso, and elastic net for algebraic multigrid of systems of elliptic partial differential equations. In Numerical Linear Algebra with Applications; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2024. [Google Scholar]
- Arendt, W.; Urban, K. Partial Differential Equations. In An Introduction to Analytical and Numerical Methods; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Chapiro, G.; Mazorche, S.R.; Norman, J.H.; Roche, J.R. Solution of the Non-Liniar Parabolic Problems Using Complementary Algorithm (FDA-NCP); Mecánica Computacional: Buenos Aires, Argentina, 2010; Volume 29, pp. 2141–2153. [Google Scholar]
- Avramescu, A.-M. Etude prospective sur l’exploitation des materiaux naturels compares aux materiaux synthetiques. U.P.B. Sci. Bull. Ser. B 2023, 85, 235–247. [Google Scholar]
- Ciobanu, R.; Rizescu, C.I.; Rizescu, D.; Gramescu, B. Surface Durability of 3D-Printed Polymer Gears. Appl. Sci. 2024, 14, 2531. [Google Scholar] [CrossRef]
- Mateescu, G.M. Hidro-Gazo-Dinamica Generatoarelor de Bule Fine. Ph.D. Thesis, University Politechnica of Bucharest, Bucharest, Romania, 2011. [Google Scholar]
- Donisan, E.; Constantin, M.; Băran, N.; Toader, A. A new system for measuring the liquids flow rates. UPB Sci. Bull. Ser. D 2017, 79, 259–266. [Google Scholar]
- Băran, N.; Căluşaru, I.M.; Mateescu, G. Influence of the architecture of fine bubble generators on the variation of the concentration of oxygen dissolved in water. UPB Sci. Bull. Ser. D 2013, 75, 225–236. [Google Scholar] [CrossRef]
- Băran, N.; Constantin, I.M.; Tănase, E.B.; Mlisan, R. Research regarding water oxygenation with fine air bubbles. UPB Sci. Bull. Ser. D 2016, 78, 167–178. [Google Scholar]


| Characteristic | Notation | Value |
|---|---|---|
| Initial dissolved oxygen concentration | C0 | 3.12 mg/dm3 |
| Dissolved oxygen concentration at saturation | Cs | 8.3 mg/dm3 |
| Water temperature | t | 24 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Constantin, M.; Dobre, C.; Oprea, M. Mathematical Modeling of Oxygen Transfer Using a Bubble Generator at a High Reynolds Number: A Partial Differential Equation Approach for Air-to-Water Transfer. Inventions 2024, 9, 76. https://doi.org/10.3390/inventions9040076
Constantin M, Dobre C, Oprea M. Mathematical Modeling of Oxygen Transfer Using a Bubble Generator at a High Reynolds Number: A Partial Differential Equation Approach for Air-to-Water Transfer. Inventions. 2024; 9(4):76. https://doi.org/10.3390/inventions9040076
Chicago/Turabian StyleConstantin, Mihaela, Cătălina Dobre, and Mugurel Oprea. 2024. "Mathematical Modeling of Oxygen Transfer Using a Bubble Generator at a High Reynolds Number: A Partial Differential Equation Approach for Air-to-Water Transfer" Inventions 9, no. 4: 76. https://doi.org/10.3390/inventions9040076
APA StyleConstantin, M., Dobre, C., & Oprea, M. (2024). Mathematical Modeling of Oxygen Transfer Using a Bubble Generator at a High Reynolds Number: A Partial Differential Equation Approach for Air-to-Water Transfer. Inventions, 9(4), 76. https://doi.org/10.3390/inventions9040076






