Abstract
Orthotropic steel deck (OSD) bridges are lightweight constructions which are convenient, especially for the achievement of long spans. Conversely, due to the stress concentration in correspondence to the numerous and unavoidable welded construction details, this bridge typology is prone to fatigue cracking under the effect of cyclic loading with high-stress amplitudes. Existing OSD bridges are particularly vulnerable to fatigue damage accumulation because of the dated standards adopted at the time of their design and the fact that heavy lorries have increased in travel frequency and weight. In the present paper, a case study of a northern Italian existing highway viaduct, built in the 1990s, is presented and analyzed. The fatigue damage accumulation was carried out according to the fatigue load models for road bridges reported in Eurocode EN 1991-2 and the assessment criteria indicated in EN 1993-1-9. The stress amplitude, in correspondence to the critical details of the bridge, is assessed by means of detailed finite-element calculations carried out with the software MIDAS GEN®. The amplitude and frequency of the travelling weights are assessed based on real traffic monitoring from the highway. Moreover, an automatic “rain-flow” algorithm is implemented, which is able to detect each nominal stress variation above the fatigue limit. In general, the bridge is not fully compliant with today’s standards when considering the entire duration of the prescribed life of the design. Countermeasures, like lane number reductions and lane reshaping, are critically analyzed since their effectiveness is questionable as far as the reduction in heavy traffic is concerned. Other interventions, like the replacement of the pavement in order to improve the stress redistribution upon the connection details below the wheel footprint, and continuous bridge inspections or monitoring, look more promising.
1. Introduction
Light orthotropic slab decks have brought significant benefits as far as the design of bridges with long spans is concerned. The traffic loads acting on an OSD system are redistributed in two orthogonal directions, which are characterized by different stiffness properties. In addition, deflection-induced secondary stresses [1] take place, and the actual stress state is difficult to assess. As shown in the literature [2], it is possible to break down the system into several independent subsystems that can be separately analyzed [3] and then combined with the superposition principle of the effects to obtain the total linear elastic response, especially when manual calculations are involved.
At the same time, they require a significant number of elements welded or bolted together. In correspondence to these connections, the presence of welding residual stresses [4,5,6] and stress concentrations are superimposed on the oscillating stresses due to the travelling loads, especially caused by heavy lorry traffic. During the last few decades, fatigue cracks were often observed in correspondence to the welded and bolted joints of in-service OSD bridges since they act as crack initiation sites. Hence, the orthotropic steel deck bridges are prone to fatigue cracks, which can substantially affect the service and ultimate state of such structures [7].
As stated in [8], the most common fatigue-prone details in the OSD bridges are the rib-to-deck welded connections, the rib-to-floor beam welded joint, the floor beam cutout details, and the butt weldings in the longitudinal ribs.
During the bridge inspections, it was noticed that most of the fatigue cracks initiate at the root or toe of the rib-to-deck welded joints and subsequently propagate within the steel deck [9]. Kainuma et al. [10] performed cyclic tests on 19 full-scale orthotropic steel deck specimens by using a servo-hydraulic testing machine in order to study the behavior of fatigue cracks at the weld root of the rib-to-deck joints. A total of six different kinds of OSD specimens were fabricated with different plate thicknesses and weld penetration rates. In particular, the effects of the plate thickness and the weld penetration rate were investigated by measuring the crack length and crack depth during the fatigue test. Subsequently, a finite element analysis was performed to check the stress distribution close to the weld root, which confirmed the test results. Bohai et al. [11] performed FEM analyses to study the root-deck-fatigue performance of the Taizhou Bridge in China. An equivalent stress range of multi-axles was adopted by using the Palmgren–Miner rule. Furthermore, the pavement-deck interaction was analyzed in terms of stress ranges that occurred close to the weld root and fatigue lifetime. Three different configurations between the deck plate and pavement were considered in the analyses, i.e., without interaction, dispersal model, and with interaction. It was found that a decrement of 70% in the stress range can be achieved by considering explicitly the pavement flexural rigidity with respect to the without interaction case. As a consequence, by considering the pavement-deck interaction, it was demonstrated that the predicted life of the root-deck fatigue cracks increased by more than 20 times with respect to those obtained without interaction. A similar study was conducted by Wang et al. [12], who investigated the effect of load dispersal through asphalt surfacing on the fatigue behavior of rib-to-deck welds. Different deck plate thicknesses and temperatures were considered in the analyses, demonstrating the overall positive benefits of loading dispersal on the fatigue performance of rib-to-deck welded joints. Zhang et al. [9] proposed an innovative rib-to-deck joint in OSD bridges with both-sided fillet welded joints to enhance their fatigue lifetime. The fatigue analysis was performed by adopting the effective notch stress approach. Finite element simulations demonstrated that the use of this innovative welded joint reduced the effective notch stresses compared to those obtained with conventional single partial penetration weldings. Wang et al. [13] performed fatigue tests on rib-to-deck welded joint specimens. All the specimens failed due to fatigue cracks initiated at the weld root of the rib-to-deck welded joints due to the lack of penetration and high-tensile residual stresses. Furthermore, strain gauges were applied to the specimens to monitor the continuous degradation of the OSDs during the tests. A stiffness redistribution was found during the crack propagation between the damaged material and the section not yet cracked. In addition, significant differences in terms of fatigue performance were found between root-deck and toe-deck crack failure modes, independently of using the nominal and hot-spot stresses. Thus, it was concluded that the assessment of fatigue performance of root-deck failures by adopting S-N design curves obtained for the toe-deck crack mode can be unsafe since it can lead to an overestimation of the actual fatigue lifetime of OSD bridges.
Another critical point in OSDs is represented by the fatigue cracks at the rib-to-floor beam welded joints, which can accelerate the damage to this kind of bridge. To this aim, Huang et al. [14] performed fatigue tests on nine rib-to-crossbeam welded specimens in order to investigate their fatigue cracking features and their fatigue resistance. It was found that fatigue cracks had initiated from the weld toe of the rib-to-floor beam and subsequently propagated at the rib wall in the longitudinal direction. Furthermore, the nominal fatigue resistance of the tests was compared with S-N curves from different standards. Subsequently, the hot-spot stress and effective notch stress methods were adopted to assess the fatigue resistance of rib-to-floor beam joints. In this way, it was possible to obtain the corresponding S-N curves, which were subsequently compared with the fatigue data available in the literature. A more recent study on the fatigue behavior of rib-to-floor beam welded joints was performed by Cheng et al. [15]. More specifically, they investigated the positive effect of ultra-high-performance concrete-reinforced slabs to extend the fatigue lifetime of OSDs. To this aim, three full-scale rib-to-floor beam welded joints were subjected to fatigue loadings to investigate their fatigue failure modes, crack initiation modes, crack propagation paths, vertical rigidity degradation, and fatigue life. It was found that the application of the UHPC-reinforced slabs on the OSD led to an important increment in the fatigue lifetime compared to those of unreinforced specimens, as well as a sensible reduction in vertical displacement and flexural rigidity being obtained.
The fatigue failure could also occur at the cutout detail. In fact, during a visual inspection of the Pingsheng Bridge located in China, several cracks were found on the web of the floor beam near the cutout detail [16]. More in detail, it was observed that the fatigue cracks initiated at the cutout detail and propagated on the floor beam web. Therefore, several countermeasures were adopted. In particular, 13 uniaxial strain gauges were applied on the floor beam web around the cutout. In this way, it was possible to conduct long-time field measurements under actual traffic loading to monitor the stress distribution around the cutout detail. After that, the stress range spectrum was obtained, so that the equivalent constant-amplitude stress range was assessed according to AASHTO LRFD. Therefore, the fatigue lifetime of this existing bridge for the cutout detail was estimated under the current traffic demand, which was much lower than the design life of the bridge prescribed by the standards. After that, multilevel FEM models were performed by adopting the fatigue track of AASHTO LRFD. It was found that the fatigue lifetime of the cutout detail is close to the experimentally observed one, differing only by adopting the fatigue category B of AASHTO LRFD. Finally, the influence of web thickness on fatigue life was studied. From these analyses, it emerged that infinite fatigue life could be expected only if a diaphragm thickness of 14 mm is adopted. At the same time, Zhu et al. [17] studied the fatigue performance of two new types of cutout geometries based on field monitoring and FEM analysis. The experimental and numerical results demonstrated that the new cutout geometry led to an increment in the stress range in the floor beam web, resulting in a decrement in the fatigue life. Conversely, a reduction in the out-of-plane stress of the floor beam web was found.
Another location in OSD bridges that is prone to fatigue cracks is the rib butt-welded and bolted joints. To this aim, Chen et al. [18] performed experimental fatigue tests under a constant cyclic loading amplitude to investigate the fatigue behavior of U-rib connections. The fatigue cracks occurred in the connection regions. After that, the equivalent amplitude stress range was assessed for the four different welded and bolted joints so that it was possible to plot an S-N diagram. From a comparison with S-N curves, given by AASHTO and Eurocode, it emerged that the fatigue-resistance of full penetration butt weldings is much higher than those recommended in the standards. Eventually, FEM analysis was performed to quantify the stress range reduction in the butt-welded joints due to an increment in the rib thickness and a decrement in the weld size. Analogously, stress amplitude reduction can be obtained for the bolted joints by adopting thicker and wider splice plates. The fatigue response of a U-rib can also be improved by introducing inner bulkheads and stiffeners. To this aim, Zhu et al. [19] performed fatigue tests on full-scale OSD specimens stiffened with the application of inner bulkheads. The strain gauge measurements showed an important decrement close to the stress amplitude in the rib-floor beam connection due to the application of the inner bulkheads. This experimental evidence was confirmed by FEM analyses, through which the hot-spot stresses were assessed. Similar studies were carried out by Li and Zhu [20], who investigated the effect of full internal bulkheads on the fatigue performance of OSDs by means of strain gauge monitoring.
The fatigue life assessment of the OSD details is mostly based on the application of the American Association of State Highway and Transportation Officials-LRFD Bridge Design Specifications, Eurocode 3, and International Institute of Welding Recommendations. The use of both nominal and hot-spot normal stresses are allowed for the fatigue checking of the details.
As far back as two decades ago, Dong [21] proposed a new mesh-size, insensitive, traction, structural-stress method. In this context, based on equilibrium conditions, Dong derived an analytical expression for simple structural stress distribution in the form of a membrane and bending components, which is equivalent to the local trough-thickness stress distribution close to the welded joint and is mesh-size independent. A few years later, the same author [22,23] introduced the concept of equivalent structural stress range parameters with the aim of collapsing fatigue data collected from different joint geometries, thicknesses, and loading modes onto a unique “master” S-N curve. More recently, Yang et al. [24] performed tests on six full-scale OSD specimens to study the fatigue cracks initiated from the toe of the rib-to-deck welded connections with the application of the equivalent traction structural stress-range parameter. The existing fatigue experimental results and those obtained by Yang et al. were used to derive a master S-N curve for weld toe-U rib failures. Furthermore, the same authors [25] studied the effect of the length scale, residual stress, angular misalignment, and stress ratio on the fatigue behavior of single- and double-sided U-rib weldings with the application of the equivalent traction structural stress range parameter. In addition, an enhancement of the traction structural stress was proposed by Yang et al. [26] to analyze OSDs under multiaxial states, whereas Pei et al. [27,28] introduced the concept of the equivalent structural strain-range parameter to model the fatigue performance of welded structures from the LCF to HCF regime. Another method to predict the fatigue strength of welded joints is based on the notch-stress method approach. Sonsino [29] and subsequently Karakas et al. [30] investigated the influence of fictitious notch radii on the fatigue resistance of wrought magnesium alloy AZ31 by means of Neuber’s stress averaging method so that local stress-based S-N curves could be derived. At the same time, an alternative local stress approach, based on the critical distance concept, was used to assess the fatigue resistance of magnesium-welded joints [31]. From this study, it was found that the critical distance was constant with the notch radius, as well as a lower scatter of the existing fatigue experimental data. Therefore, it was concluded that the critical distance method was more effective to predict the fatigue strength of welded joints compared to Neuber’s stress averaging approach. Luo et al. [32] proposed the application of an averaged strain energy density method for the fatigue assessment of rib-to-deck welded joints in OSDs. After that, fatigue tests on full-scale OSD specimens were carried out, and the corresponding averaged SED-N curve was obtained.
An alternative way to assess the fatigue lifetime of OSD bridges is based on the application of linear elastic fracture mechanics. To this aim, Wu et al. [33] investigated the fatigue crack of rib-to-deck welded joints initiating from the weld toe. More in detail, the effect of different initial crack depths and crack shapes, as well as different welding profiles, was investigated via LEFM. The same method, based on LEFM, was exploited by Maljaars et al. [34], who studied the fatigue behavior of fatigue cracks initiated from the weld root. From the application of this model, an S-N curve was provided, which was compared with existing experimental results. A good agreement between the predicted S-N curve and the experimental results was found. Wang et al. [35] applied Paris’ law to predict the propagation of toe-deck fatigue crack in rib-to-deck weldings. Furthermore, the effects of welding residual stresses, the initial crack aspect ratio, the loading amplitude, and the deck thickness on fatigue crack propagation were also investigated. Xiao et al. [36] explored the effect of incomplete weld penetration on butt-welded joints in terms of fatigue life by using the LEFM. More in detail, different depths of incomplete penetration were adopted in the simulation, and the corresponding S-N curve was assessed. It was found that incomplete penetration of 3–4 mm could lead to a very short fatigue life for the U-rib welded joint, and as a consequence, single side groove-butt weldings should be avoided.
Finally, it is worth noting that the phenomenon of fatigue can be dramatically worsened in the case of poor maintenance of the bridge [37,38]. In fact, corrosion not only provides a decrease in the resisting cross-section of the structural element, but the crack nucleation and the subsequent propagation can be substantially affected. As a result, the fatigue limit can diminish or even vanish, and, in general, the fatigue life reduces due to the increased crack propagation rate. Recently, some of the authors of the present paper have shown that the phenomenon can be particularly subtle when small amplitudes are combined with a very high number of cycles (the so-called very-high cycle fatigue (VHCF)) and corrosion, even for other viaduct typologies [39,40].
2. The Orthotropic Bridge Deck Structural System
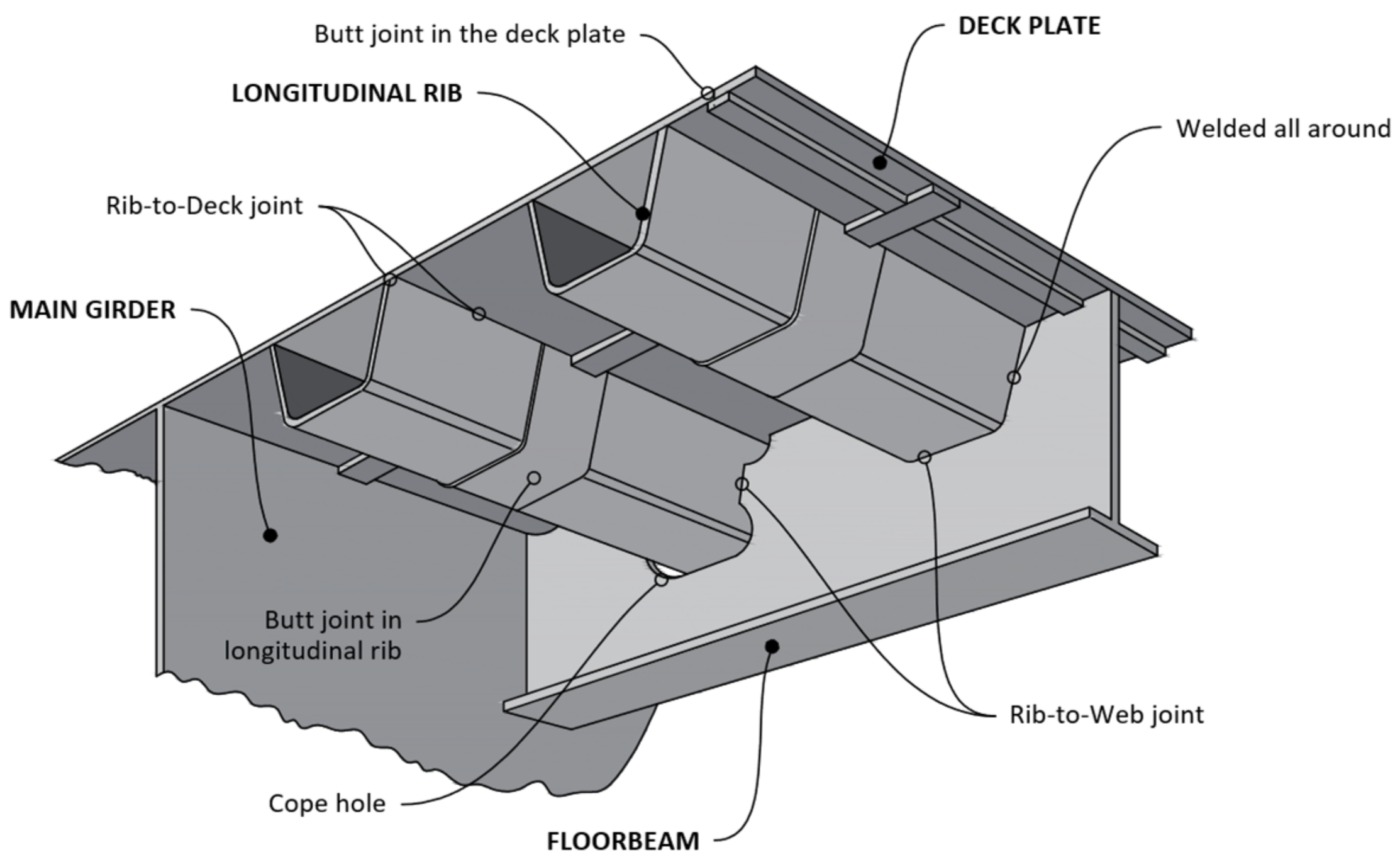
The orthotropic bridge deck slabs consist of a thin plate stiffened by longitudinal “ribs” and supported by transverse “floor beams” that provide different stiffnesses in the two orthogonal directions (Figure 1).
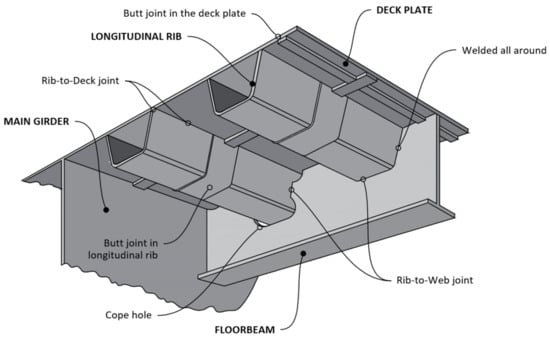
Figure 1.
Components of an orthotropic slab deck (re-adapted from [3]).
This construction system originated in America in 1930 from the AISC (American Institute of Steel Construction), which proposed a new approach aimed at the design of bridges [41], with particular attention paid to their weight to ease the design and the construction of bridges made completely from steel [42].
According to the description available in the literature [3], since the longitudinal ribs and transverse beams are orthogonal “ORTHOgonal” and since, in both directions, their elastic properties are different or anisotropic “anisoTROPIC”, the whole system became known as orthogonal-anisotropic or, briefly, orthotropic. The word “orthotropic” is attributed to German engineers, and the patent was registered in 1948 [2].
Orthotropic steel plate (OSD) decks were used extensively after the Second World War in large-span bridges due to many advantages, such as low weight, high strength, fewer connections, durability, quick construction, and life cycle economy [43].
2.1. Fatigue Phenomenon in the Orthotropic Plates
The phenomenon of fatigue on steel bridges began to be studied in the 1960s when many structures in America and Europe showed structural collapses with fatigue fractures.
According to ASTM standards [44], “Fatigue is a permanent, progressive and localized process of structural change in a material subject to conditions of stress and deformation that vary over time and can lead to the formation of cracks and/or fracture after a sufficient number of cycles”.
The life of a structural element subjected to fatigue is divided into three phases:
- Nucleation: the period of life for the detail from the undamaged state up to the formation of a superficial defect starting from the initial microscopic damage;
- Stable propagation: increase in the size of the damage inside the material in a direction orthogonal to the applied stress field;
- Collapse and final failure: following the propagation of the crack, the resistant section is no longer able to withstand the applied load.
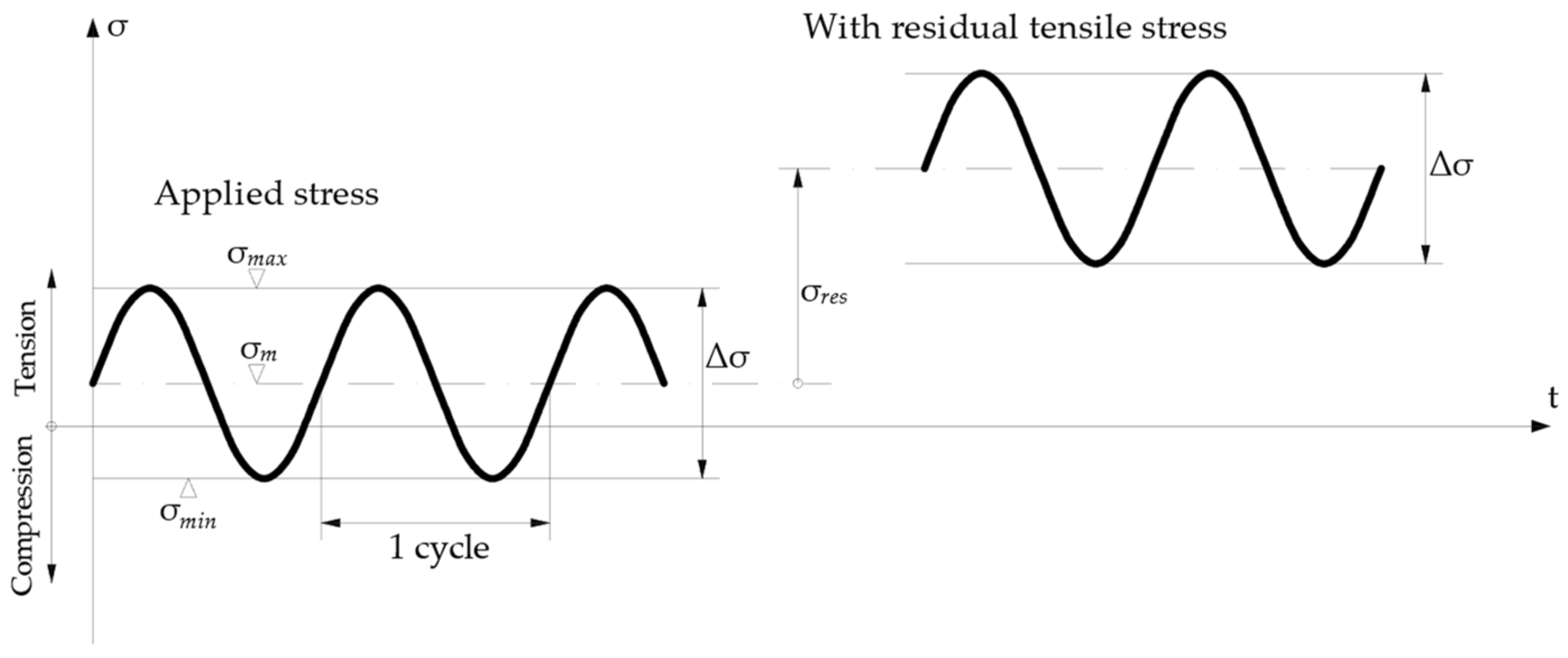
The mean stress has a significant influence on fatigue behavior since tensile mean stress tends to decrease fatigue life, whereas compression mean stress increases the fatigue resistance of the structural elements [45]. In addition, as far as the mean stress is concerned, the additional presence of residual stress must carefully be accounted for (Figure 2).
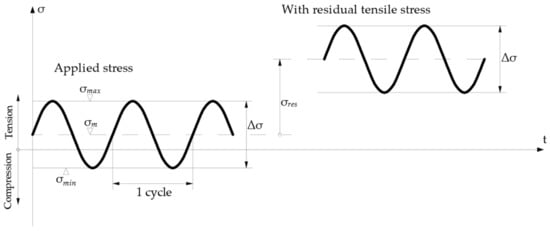
Figure 2.
Parameters of cyclic action and influence of residual stresses.
Based on experience, damage due to fatigue in orthotropic plate bridges can be potentially caused by:
- Defects in the welds;
- Local vibration of the ribs and plates;
- Adoption of construction details that are not very suitable for fatigue resistance;
- Exposure to the corrosive environment;
- Development of surface defects;
- Onset of secondary stresses not foreseen in the project.
Traffic loads induce cyclic stresses in a large number of critical points of the orthotropic plate [46], causing failure potentially at:
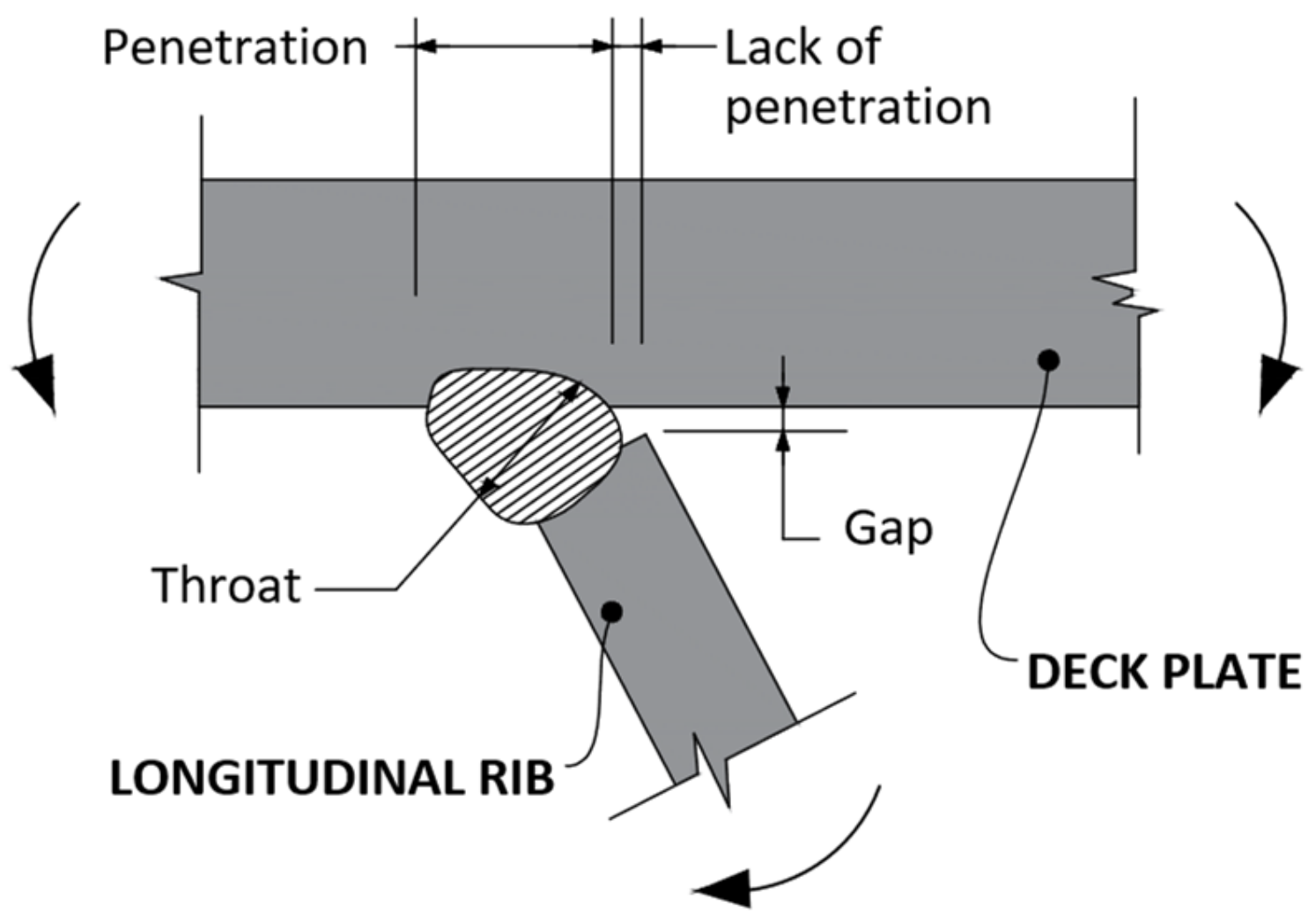
- Rib weld-deck: this connection is particularly stressed during out-of-plane bending (Figure 3);
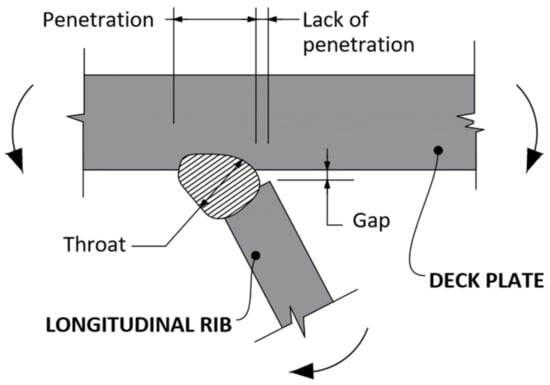 Figure 3. Rib-deck connection [46].
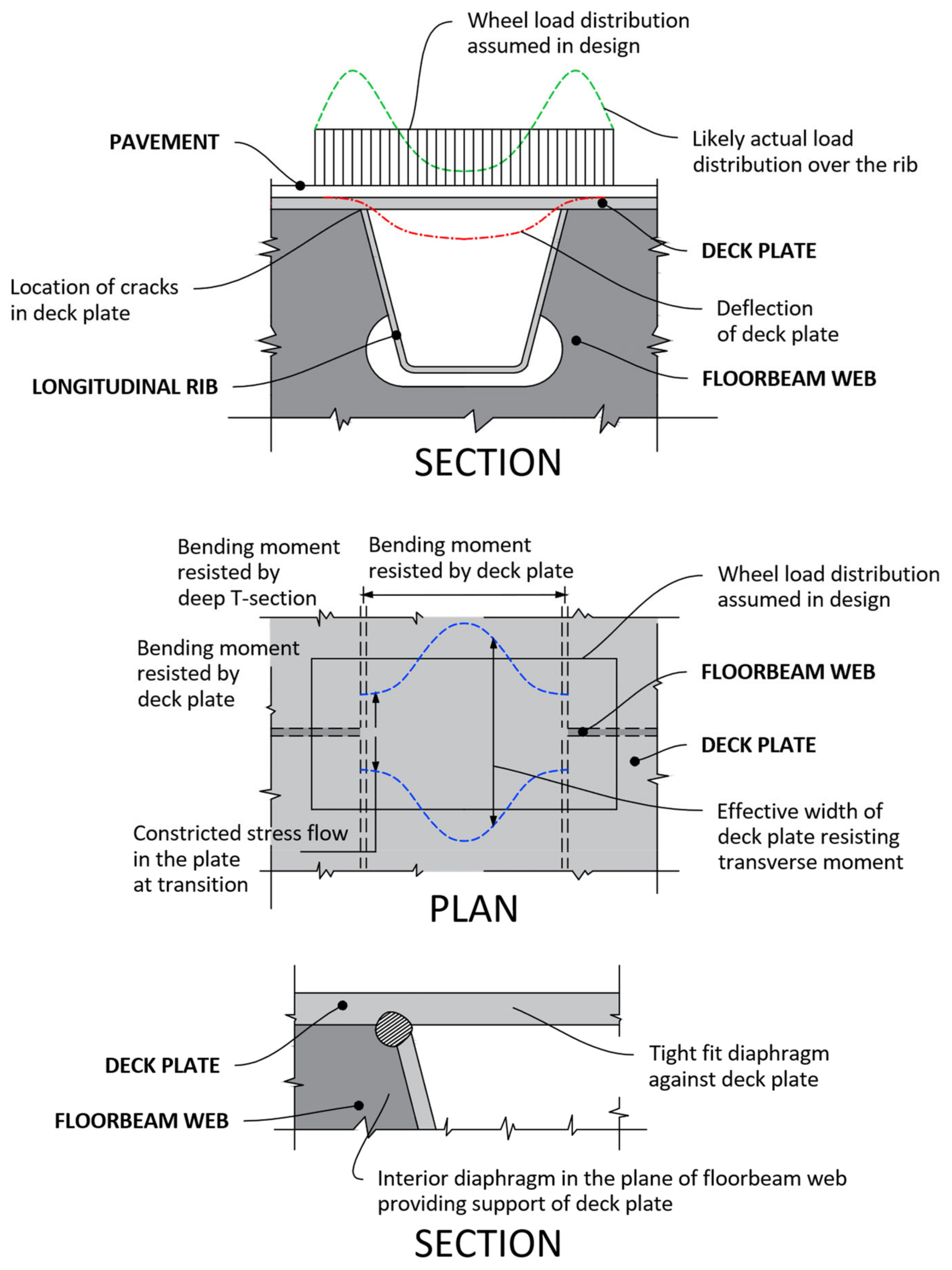
Figure 3. Rib-deck connection [46]. - Rib weld-transversal beams: stress concentration is mainly caused by vehicular transit;
- Web-beam welds: where normal, tangential, and bending stresses are observed in the two different planes (Figure 4).
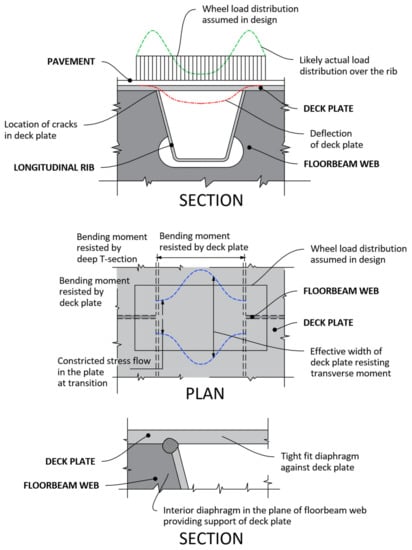 Figure 4. Rib connection-cross beam [46].
Figure 4. Rib connection-cross beam [46].
2.2. Models for the Fatigue Assessment
2.2.1. Wöhler’s Curve
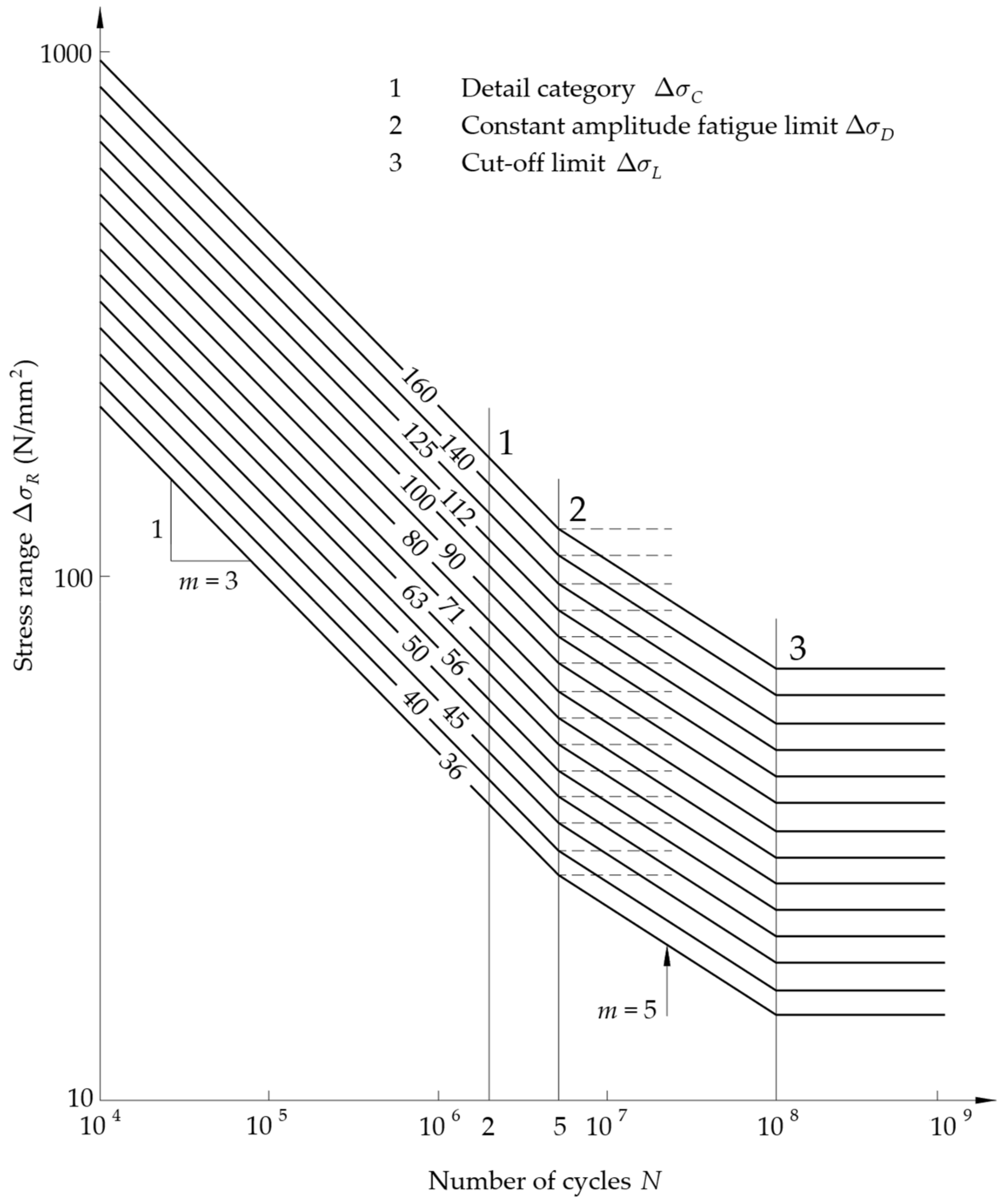
Wöhler’s curves are obtained through uniaxial cyclic load tests [47,48,49,50,51,52] at a constant amplitude up to failure on the virgin specimens. These curves are plotted on a bi-logarithmic scale and relate the nominal stress range, (normal or tangential components), with the number of cycles that lead to failure, N (Figure 5). In general, due to the nature of travelling loads, the stress range is not constant. Therefore, a stress range spectrum must be considered, and a criterion to assess the overall fatigue damage accumulation is necessary.
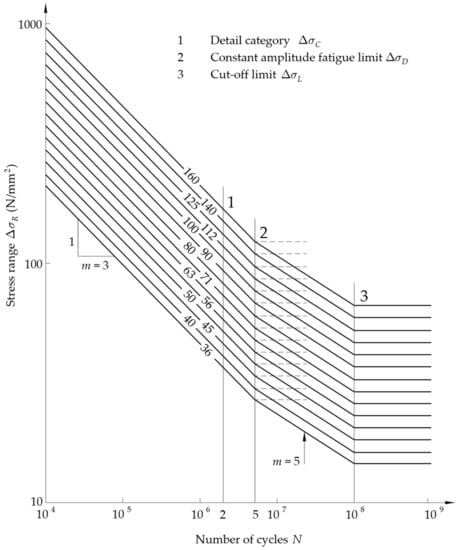
Figure 5.
Fatigue resistance Wöhler’s curves based on the nominal stress range [53].
2.2.2. Palmgreen–Miner Linear Damage Accumulation Criterion
It is assumed that each stress range is responsible for the accumulation of a fraction of damage, which is proportional to the elapsed fatigue life at each stress range. Therefore, the overall damage, , will be the sum of each induced by the application of load cycles, with a constant stress range, , as follows:
where:
- : number of cycles with a constant stress range obtained by the load spectrum;
- : fatigue life for constant stress range , obtained from the S-N curve provided in the standards [53,54].
Note that if 0 < < 1, then the detail is damaged, while if ≥ 1, fatigue failure occurs. Moreover, it is obvious that if for a certain stress amplitude, the fatigue failure is immediately achieved, whereas the fatigue collapse can be reached even if none of the single stress ranges alone has accumulated .
2.3. Normative Approach
Traffic on bridges produces a stress amplitude spectrum that can cause fatigue damage. The fatigue spectrum depends on the geometry and weight of the vehicles, the number of axles, the distance between a vehicle and the following one, and the composition of traffic and its dynamic effects. The European standards (EN 1991-2 e EN 1991-9) explicitly define five fatigue load models to be adopted for the fatigue assessment of road bridges.
In section §4.6 of the UNI EN 1991-2, the following fatigue models are defined:
- Fatigue load model 1 (FLM1), prescribes infinite fatigue lifetime, stress range is assumed based on static calculation without any calculation of load cycles, very conservative;
- Fatigue load model 2 (FLM2), prescribes infinite fatigue lifetime, stress range is assumed from an ideal frequent configuration without any calculation of load cycles, conservative;
- Fatigue load model 3 (FLM3), prescribes the assessment of damage accumulation with an equivalent stress range and traffic volume;
- Fatigue load model 4 (FLM4), prescribes the assessment of damage accumulation based on a set of heavy lorries with assigned relative traffic frequency;
- Fatigue load model 5 (FLM5), prescribes the assessment of damage accumulation based on the experimental assessment of the fatigue spectrum.
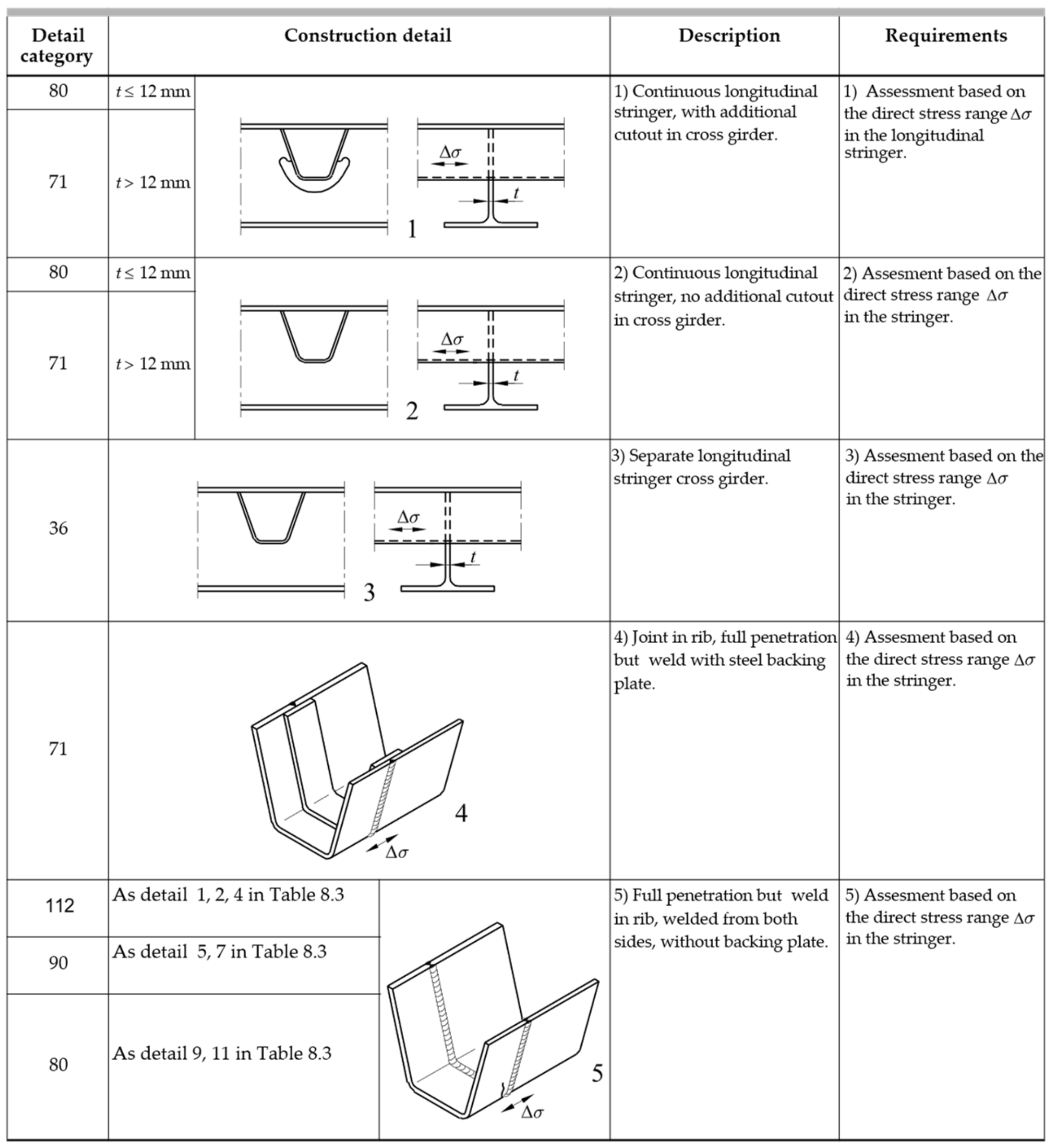
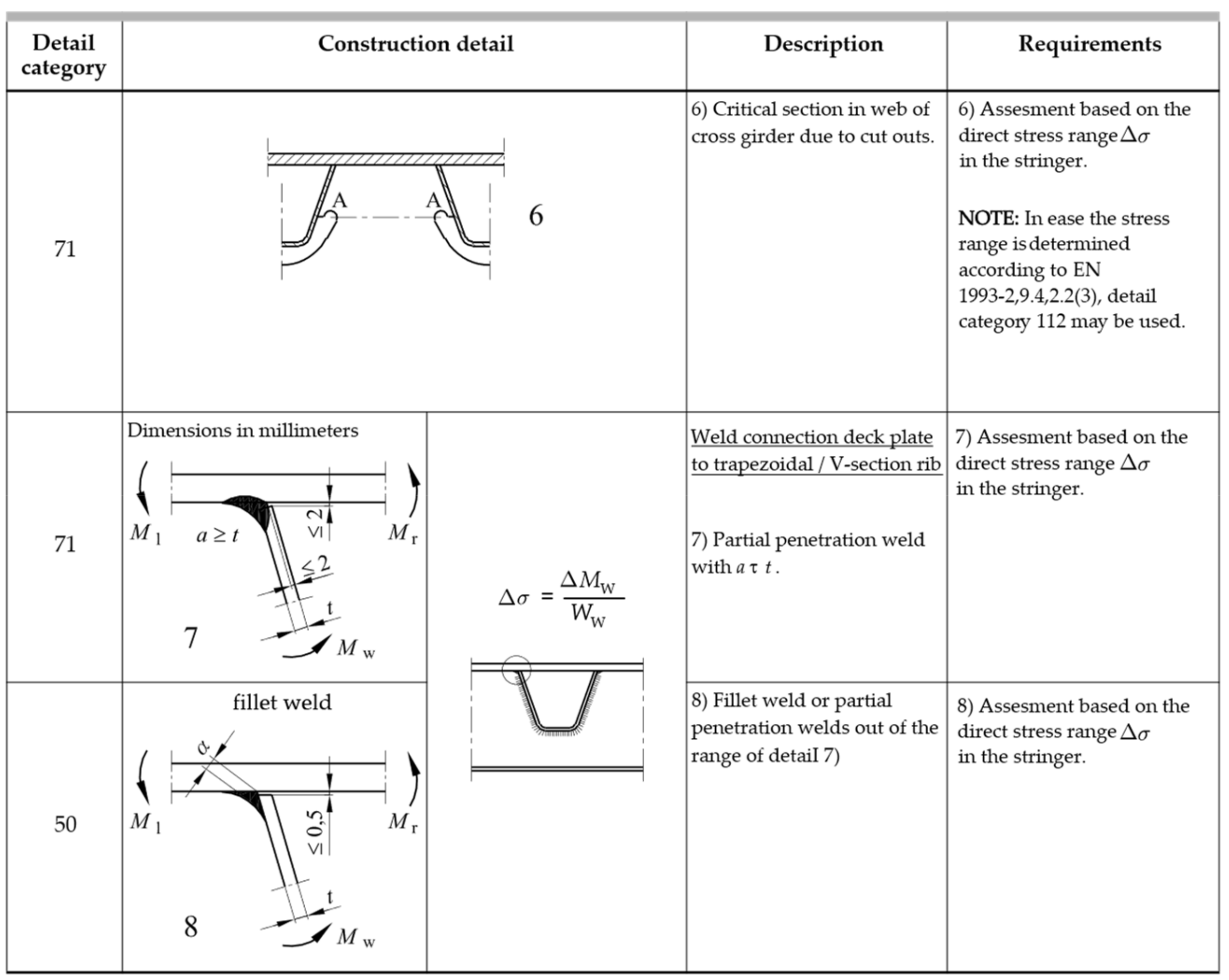
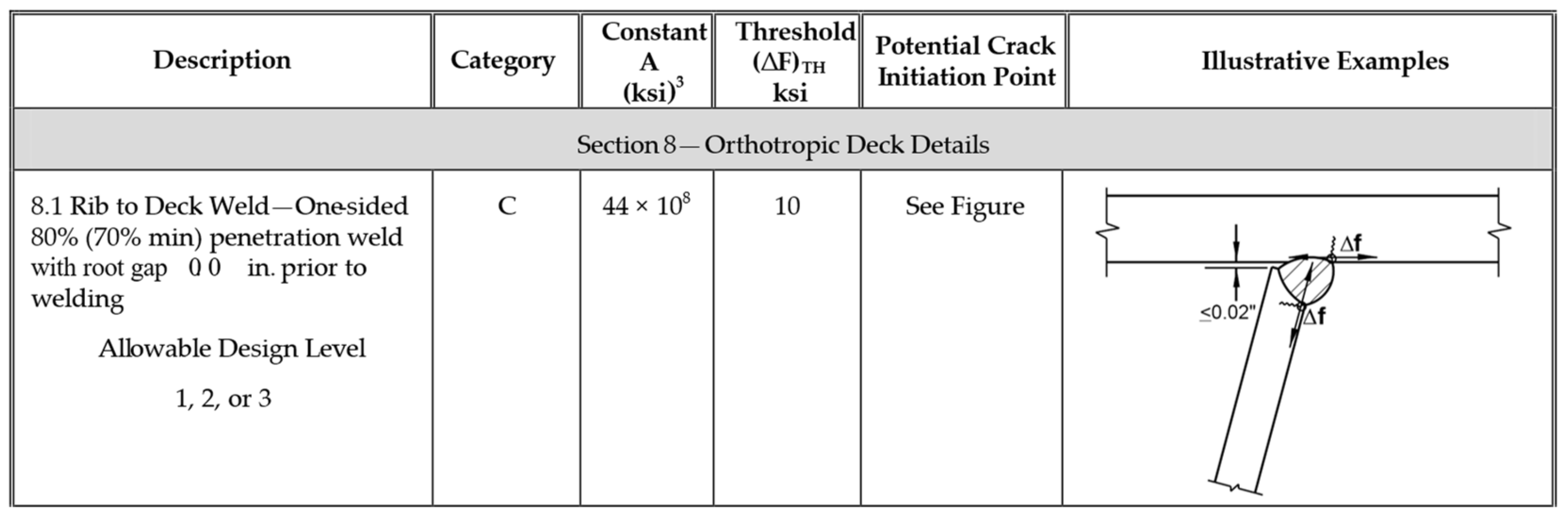
Welded joints can be categorized according to their connected elements. EN1993-1-9 associates a category and a characteristic resistance to each type of joint, as shown in Figure 6, Figure 7 and Figure 8 and Table 1:

Figure 6.
Nomenclature details—Eurocodice EN1993-1-9.
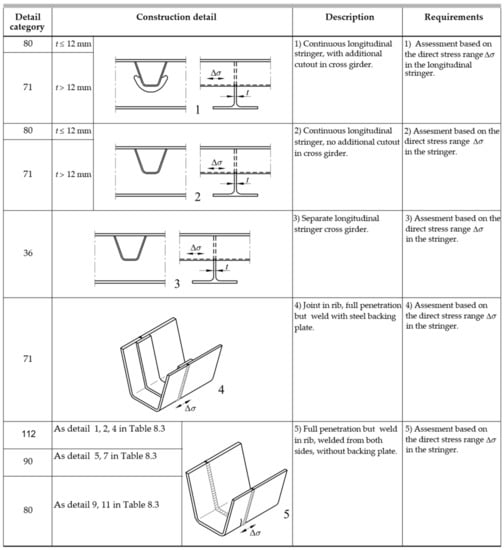
Figure 7.
Table 8.8 UNI EN 1993-1-9—Construction details of closed rib in orthotropic plates (1/2) [53].
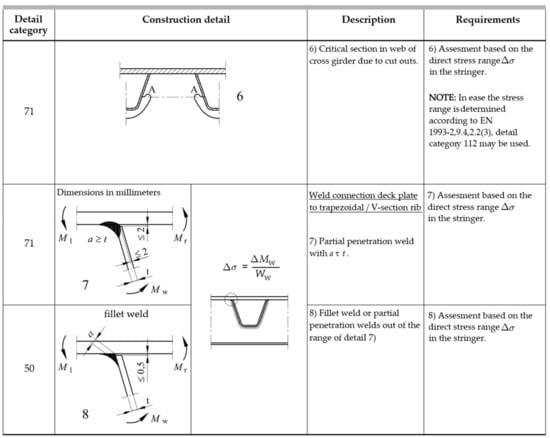
Figure 8.
Table 8.8 UNI EN 1993-1-9—Construction details of closed rib in orthotropic plates (2/2) [53].

Table 1.
Detailed categories according to the Eurocode EN1993-1-9.
To verify the fatigue life in practice, a load spectrum is assigned, which provides the number of repetitions of each level of the design actions in a reference time interval, depending on the intended use of the structure and the intensity of use.
For the fatigue checks, the design stress range, , is identified by multiplying the stress range spectrum, , by the partial safety factor for fatigue checks, (Table 2).

Table 2.
Partial safety factor for fatigue checks.
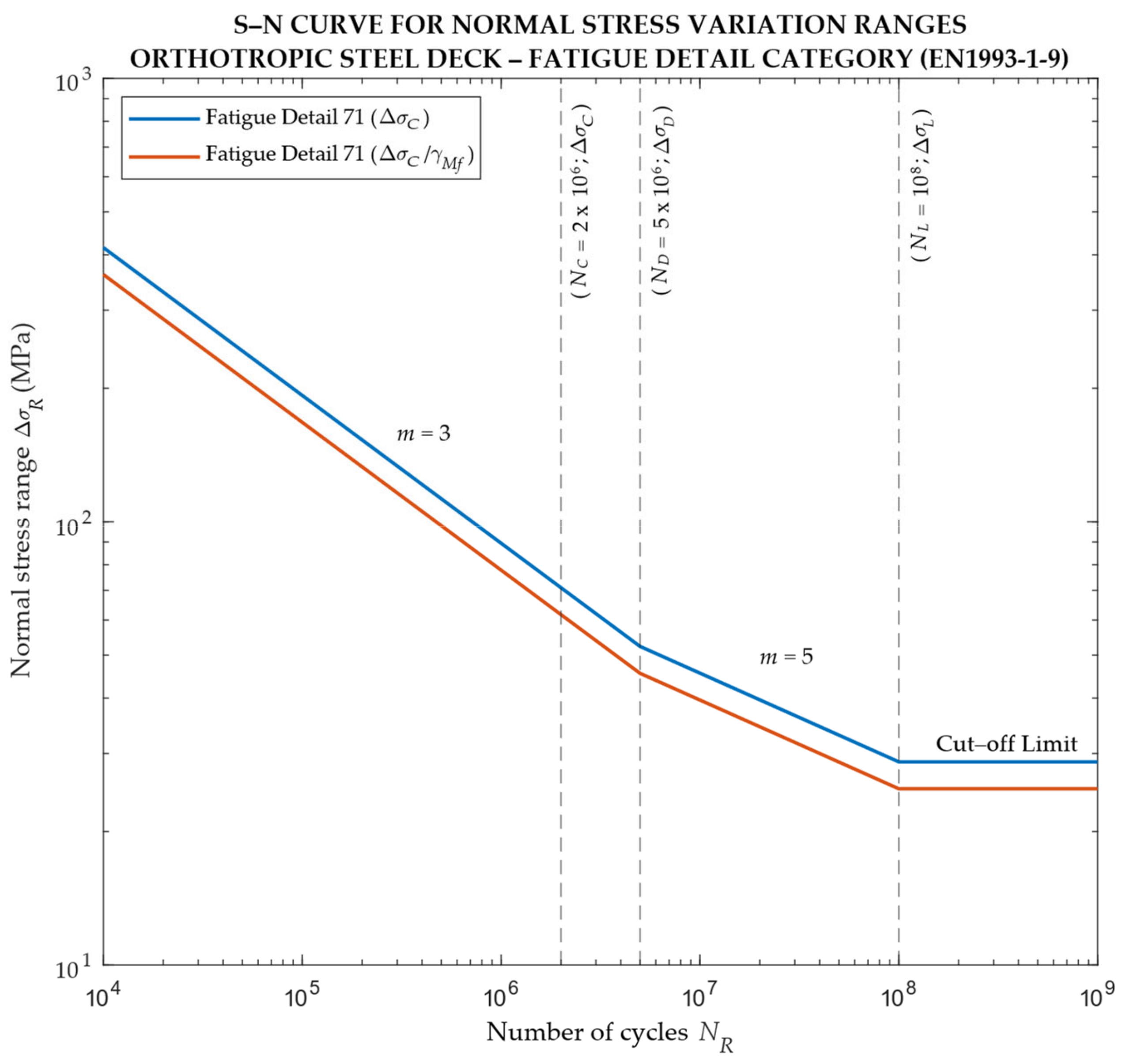
2.3.1. Normative S-N Curve
According to the geometry of the element and the type of welding, the UNI EN 1993-1-9 [53] provides (at §7.1) the Wöhler’s curves, indicating the stress range (normal or tangential) vs. the fatigue lifetime on a bi-logarithmic scale. All curves composing the set are parallel, and each curve is characterized by convention, detail category, and (value of the fatigue strength at 2 million cycles, expressed in N/mm2). It is also characterized by the constant amplitude fatigue limit (CAFL), , at 5 million cycles, which represents about 74% of . The slope coefficient, , is equal to 3 for lives shorter than 5 million cycles. For constant stress amplitude equal to or below the CAFL, the fatigue life is infinite. The CAFL is fixed at 5 million cycles for all detail categories. This is not exactly the case in real fatigue behavior but has advantages for damage sum computations. Under variable amplitude loadings, the CAFL does not exist but still has an influence. Thus, a change in the slope coefficient is made, with the value = 5 being used between 5 million and 100 million cycles. This last value corresponds to the cut-off limit, , which corresponds to about 40% of . By definition, all cycles with stress ranges equal to or below can be neglected when the fatigue damage sum is computed [45].
The equation for the S-N curve for nominal normal stresses is defined piecewise:
where:
2.3.2. Unlimited Fatigue Life Approach
This verification, adopted for FLM1 and FLM2, is conservative and can be used for all types of details subject to fatigue actions. EN 1993-1-9 does not explicitly provide a specified relationship [45], but this arises as a logical consequence of the acceptance of a fatigue limit at 5106 cycles (total number of cycles from the stress histogram).
For structural steels, the fatigue tests at stress intervals of variable amplitudes show that the fatigue life of the structural details is unlimited and, therefore, not sensitive to the phenomenon of fatigue if the maximum design value of the stress amplitudes remains below the calculated value of the design fatigue limit /.
where:
- max (): design value of the maximum stress range spectrum and induced in detail from FLM2, with ;
- : fatigue strength taken as the constant amplitude fatigue limit of the considered construction details;
- : partial factor for stress range;
- : partial factor for fatigue strength.
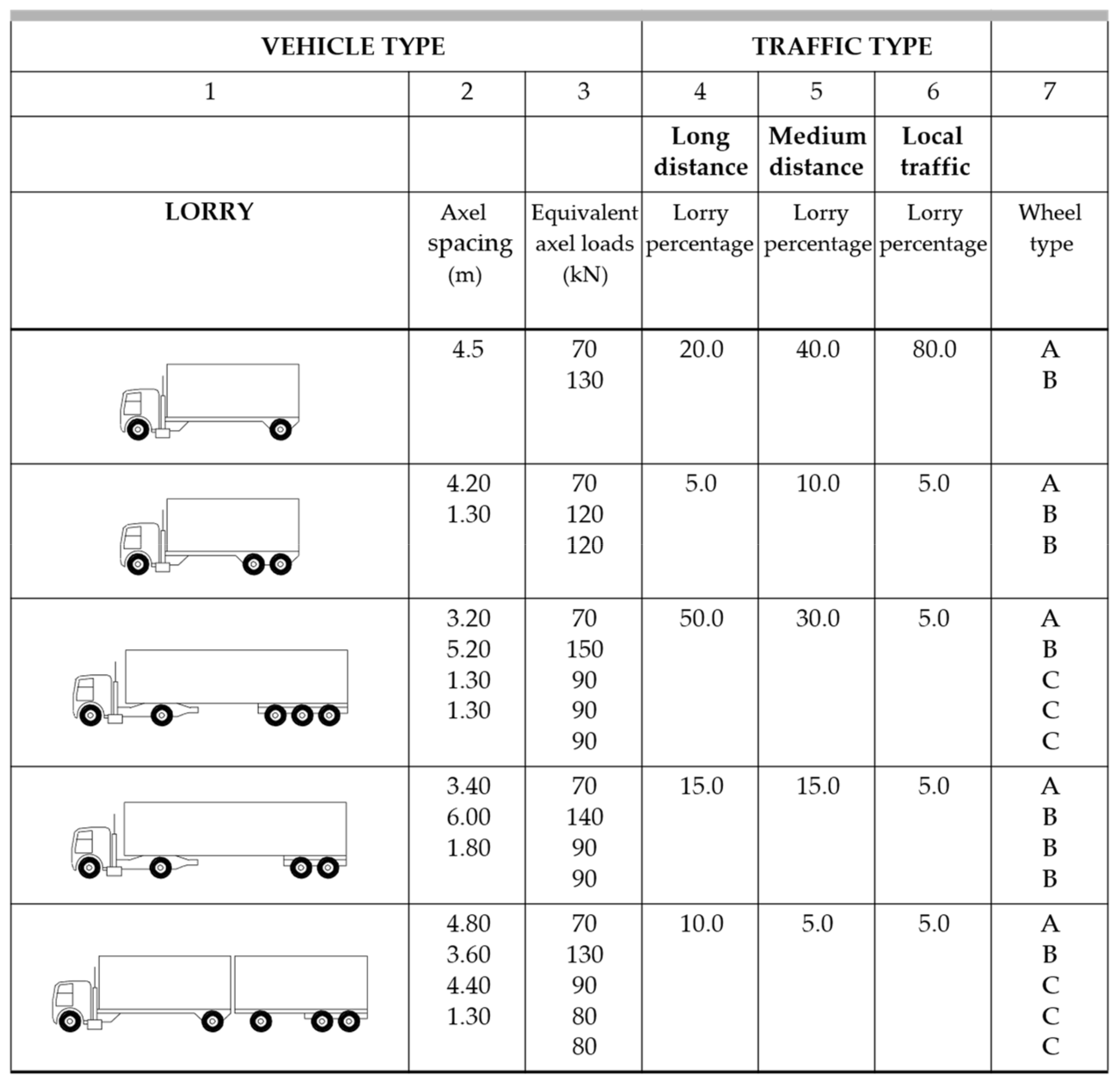
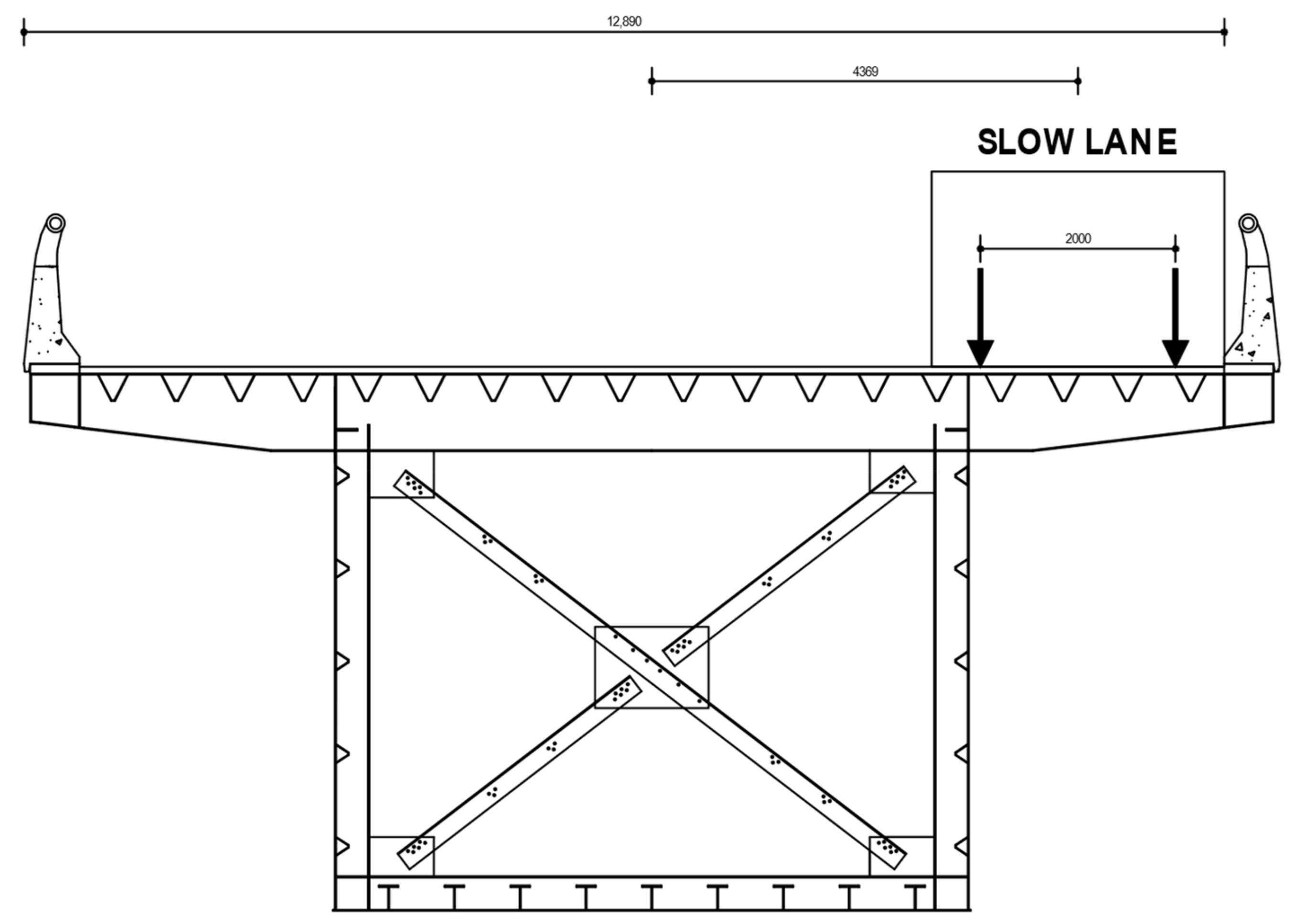
This fatigue load model consists of a set of five idealized lorries defined by axle arrangement and frequent loads for Qki axles [55] located in the slow lane (Figure 9).
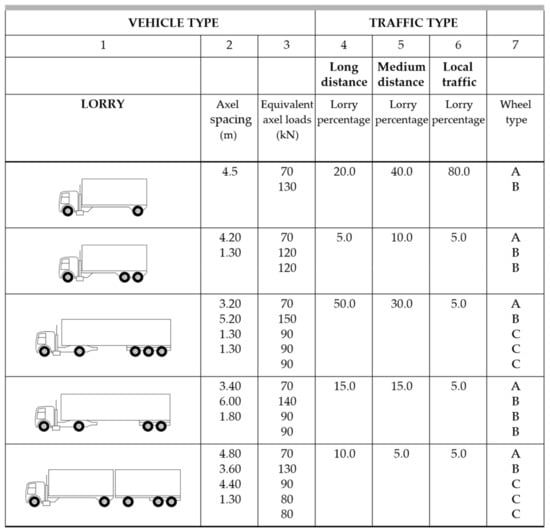
Figure 9.
Table 4.7 UNI EN 1991-2—Set of equivalent lorries of FLM4 [55].
The shape that produces the maximum stress range, or , on the details is accounted for by the assessment. Usually, a preliminary check is always performed according to the unlimited fatigue life approach, thanks to the simplicity of the method. If the check is failed, the designer must rely on more demanding calculations based on the assessment of fatigue damage accumulation.
2.3.3. Fatigue Damage Accumulation Approach
If the service loads are known, the assessment can be alternatively performed on the basis of damage accumulation [56,57], as indicated in EN 1993-1-9 according to FLM3, FLM4, and FLM5.
The fatigue load spectrum can be evaluated with two cyclic counting methods: the rain-flow method or the reservoir method. These two methods can determine:
- the stress variation intervals and their number of cycles;
- the mean stress, where it is necessary to consider the influence of the mean stress.
It is necessary to check that the damage induced by the stress range spectrum of the FLM4, evaluated by the Palmgren–Miner law, is less than the limit damage, :
where:
- : number of cycles with a constant stress range induced by the load spectrum during the lifetime prescribed for the analysis;
- : resistance (in cycles) obtained for a constant stress range , considering the partial factors, and , derived from the design S-N curve for the considered detail;
- = 1: limit damage value.
In the case of the presence of both normal and tangential stresses, the assessment of fatigue strength shall consider their combined effects using appropriate damage combination criteria.
The S-N curves that are available in the consolidated literature refer to the nominal stresses. For the construction details of which the fatigue resistance curve is not known, the stress range may refer to geometric or peak stresses, which apply to the main stresses in the base metal near the potential crack according to the specific modalities and limitations of the method in the field of fracture mechanics.
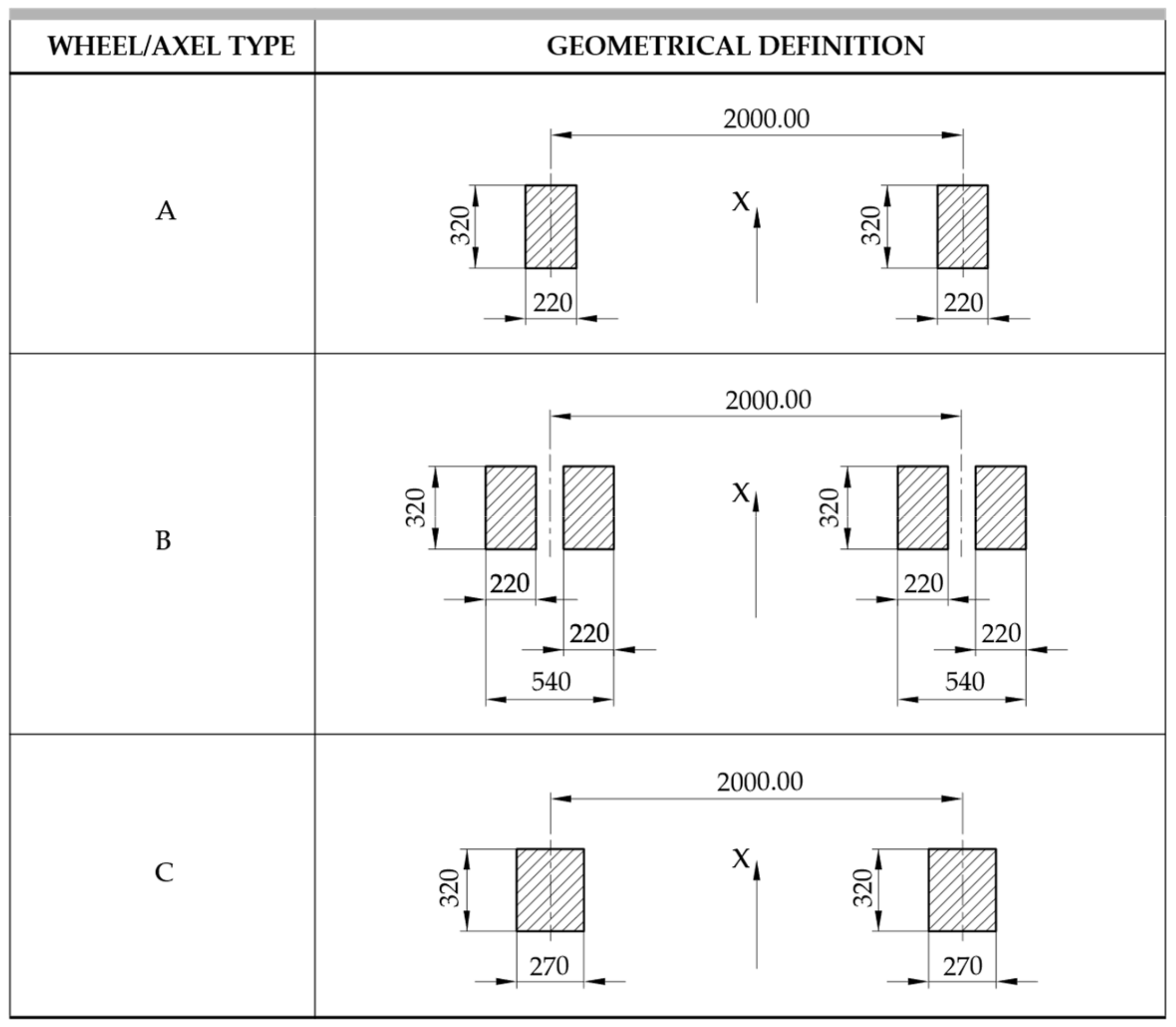
The lorries of the FLM4 have three types of axes (Figure 10) because they differ in wheel spacing and wheel size (A-B-C).
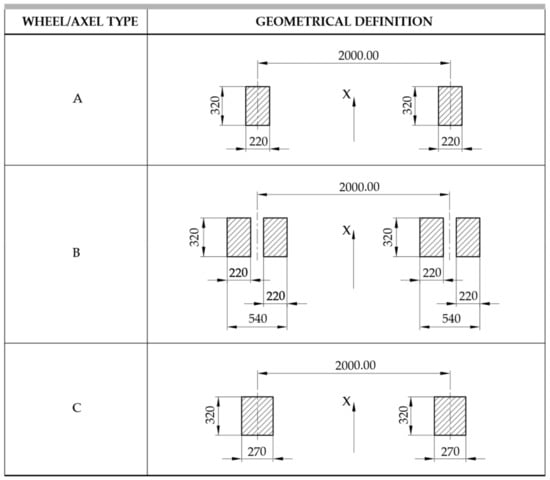
Figure 10.
Table 4.8 UNI EN 1991-2—Dimensions of axles and footprints for equivalent vehicles [55].
3. Case Study: Fatigue Life Assessment of an Existing OSD Viaduct
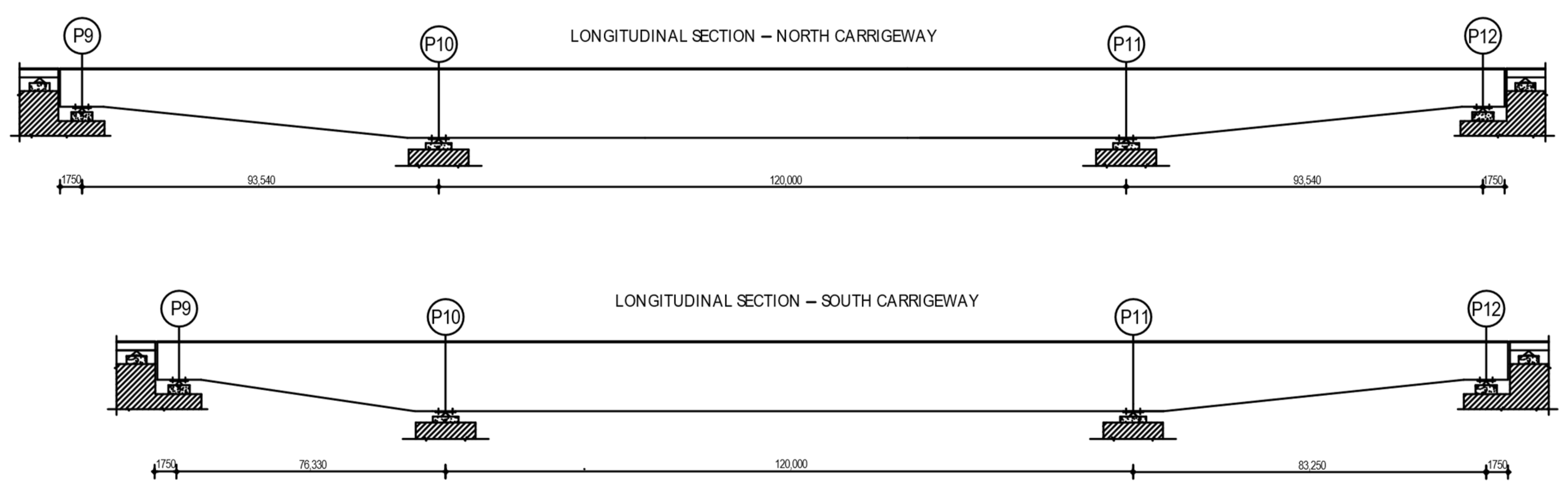
The case study of a northern Italian existing highway viaduct designed at the end of the 1980s is here considered in order to provide a fatigue life assessment according to today’s standards, briefly described in the previous section. The steel viaduct is composed of two independent carriageways, both with three spans supported by four 35.00 m high reinforced concrete piers (Figure 11). The orthotropic steel deck (OSD) of each carriage is a box girder (Figure 12 and Figure 13) with variable depths ranging between 3 m in correspondence to the two transversal joints and 5.00 m along the central span.

Figure 11.
Longitudinal view of the two carriageways of the case study.
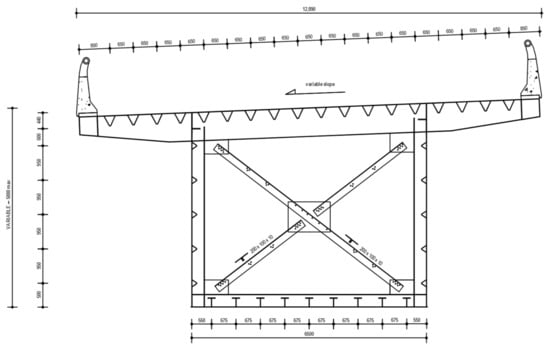
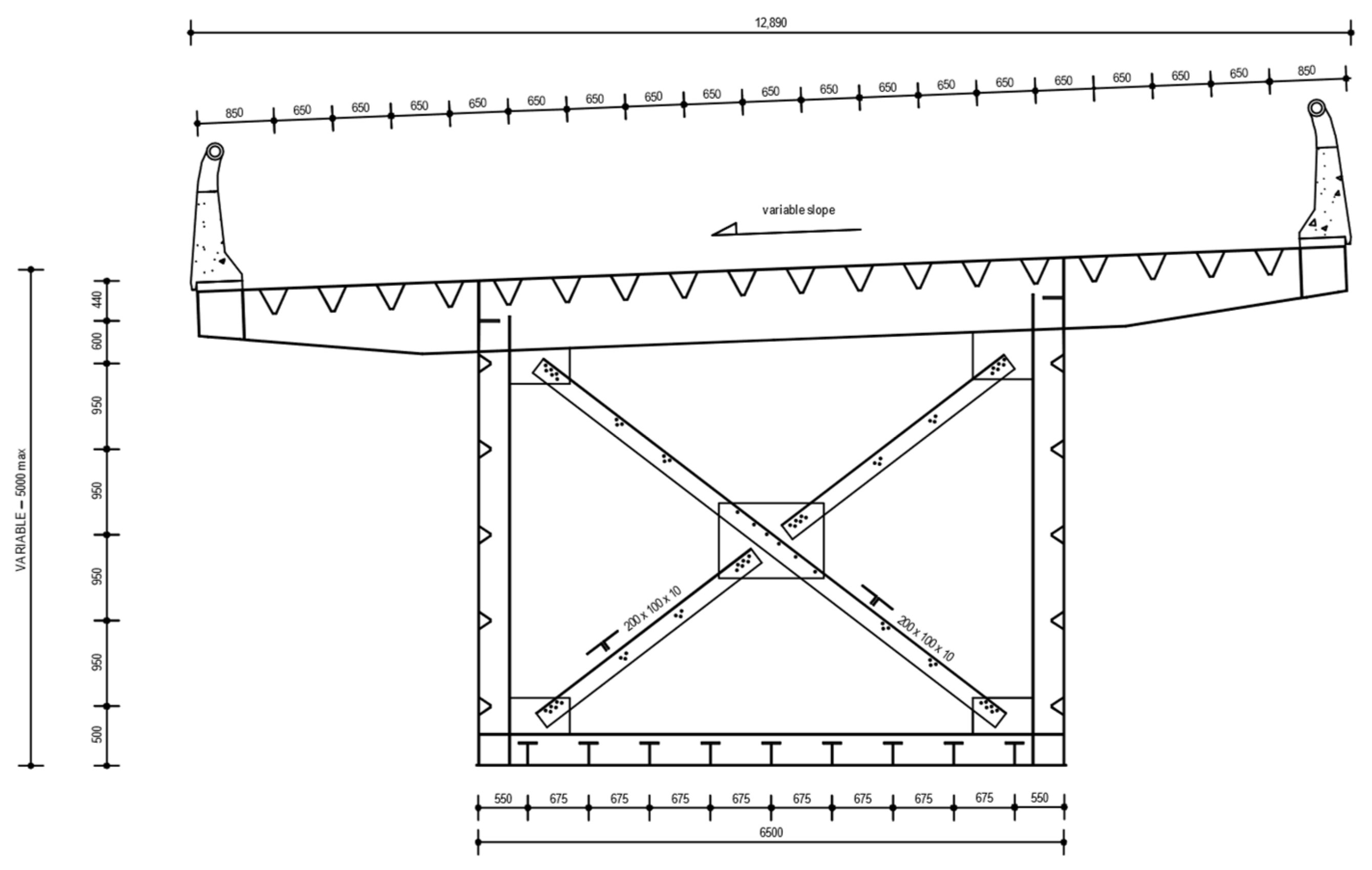
Figure 12.
Transversal section of the case study.

Figure 13.
View of the right cantilever of the deck of the case study.
3.1. Numerical Model
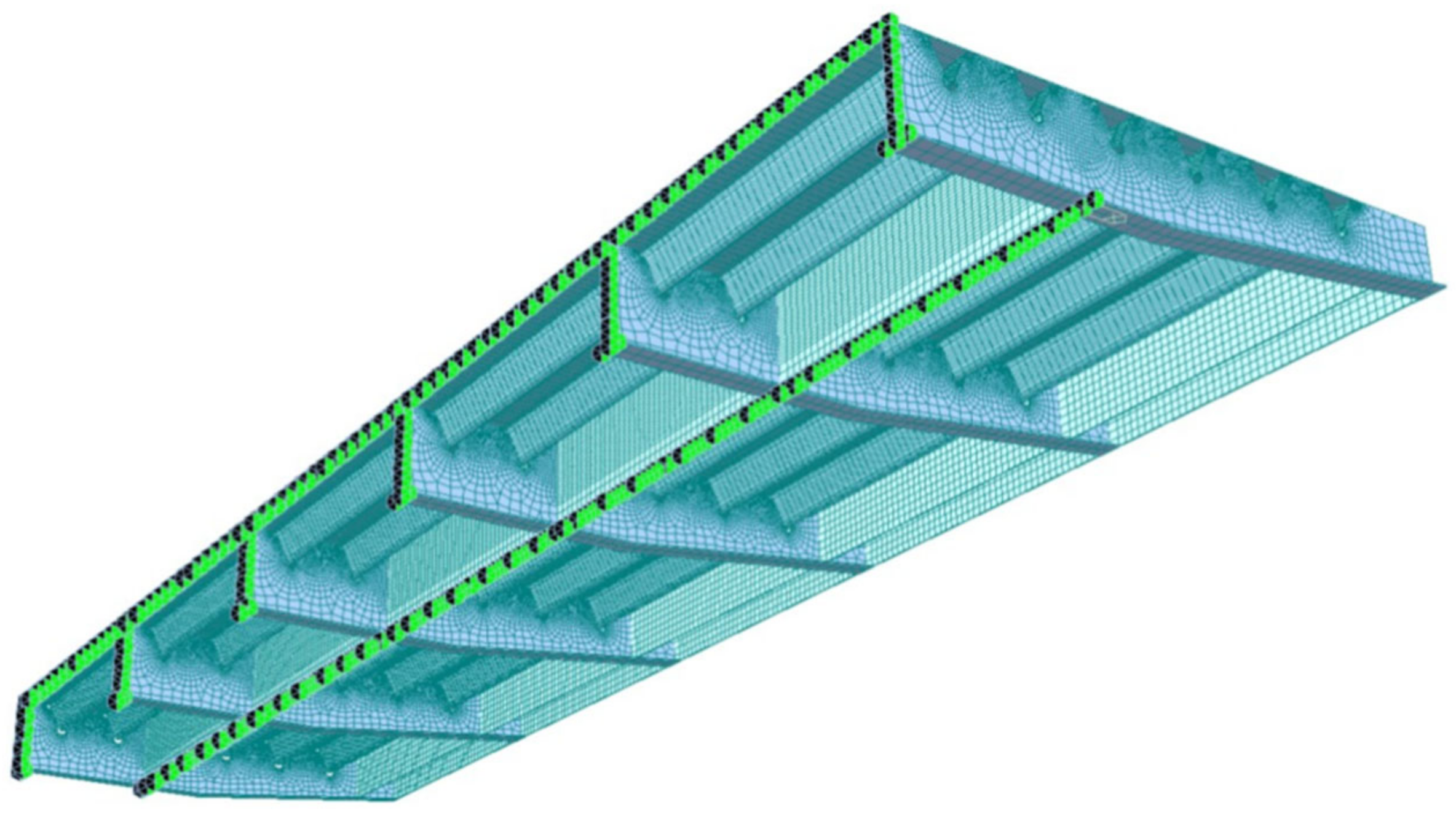
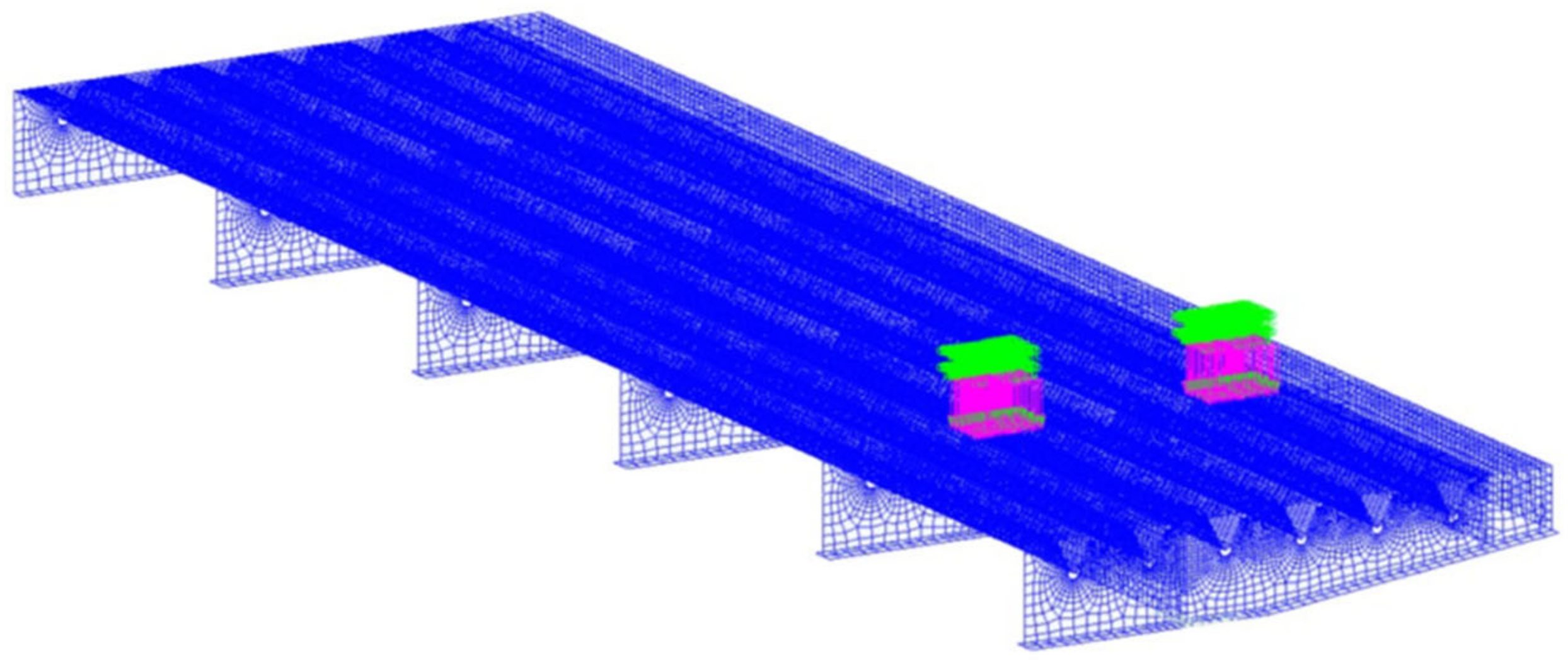
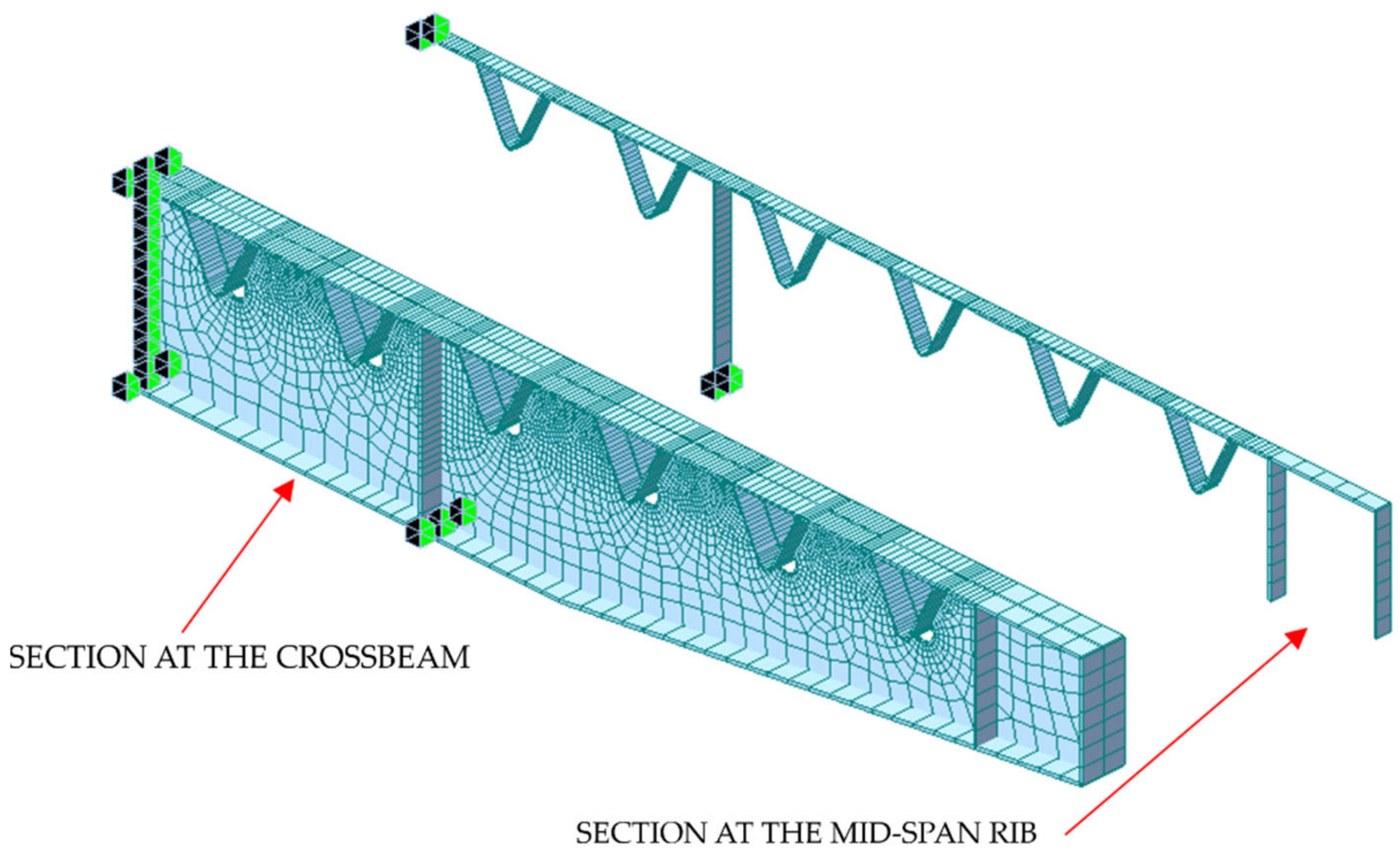
In order to calculate the stress state in the connection details of the orthotropic steel deck for subsequent fatigue life assessments, a finite element model of a deck portion, having a size of 4.54 m in the transverse direction, 15.0 m in the longitudinal direction, and 0.79 m in height, was utilized (Figure 14).
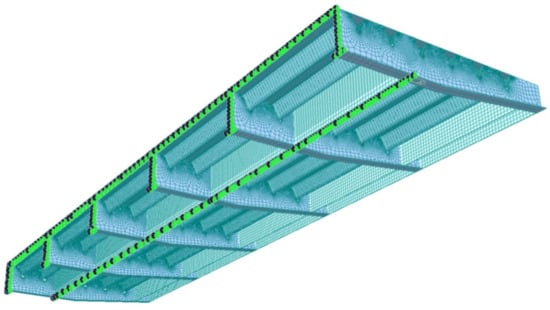
Figure 14.
Representation of the shell structural model for nominal stress assessment in the connection details carried out with the MIDAS GEN® software (version GEN2021 v3.2, MIDAS Information Technology Co.Ltd., Milan, Italy).
The preliminary checks according to FLM2 failed; therefore, the FLM4 was chosen based on the available information about the traffic loads.
The commercial finite element software MIDAS GEN® [58] was used. The program allows for automatic mesh refinement, thanks to an “Edge Size Control” subroutine aimed at optimizing the mesh by making it finer close to the notches and the stress concentration regions.
The thicknesses assigned in the FEM were: 10 mm for the top plate of the platform, 7 mm for the “v” rib, 10 mm for the web of the transverse beams, and 12 mm for the thickness of the box.
The geometry of the model was built with the module MIDAS GEN®. The following four steps were carried out:
- Longitudinal extrusion of the upper plate of the deck with a mesh of 10 cm;
- Simulation of structural continuity through the assignment of “supports”: displacements in the three global directions were constrained in correspondence to the core of the transverse rib, the upper plate, and the core of the body;
- Rib copying with a step of 3 m for five times;
- Assignment of static “pressure moving load loads” (Figure 15).
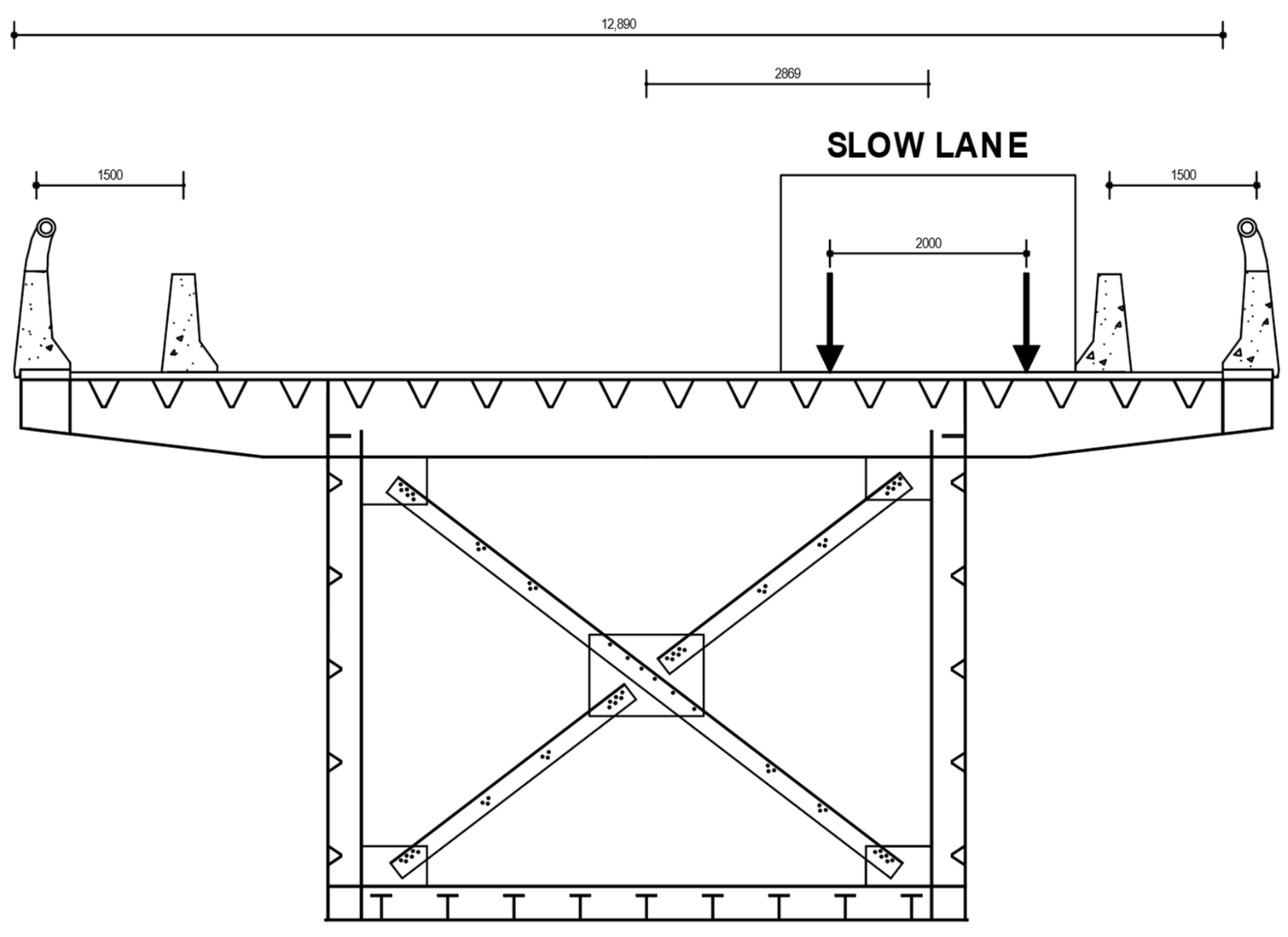
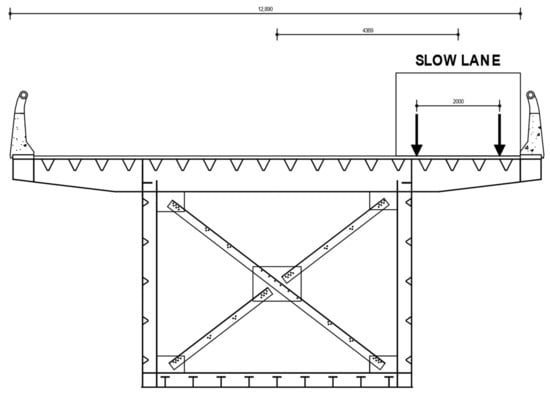 Figure 15. Slow lane—Cross section of the case study.
Figure 15. Slow lane—Cross section of the case study.
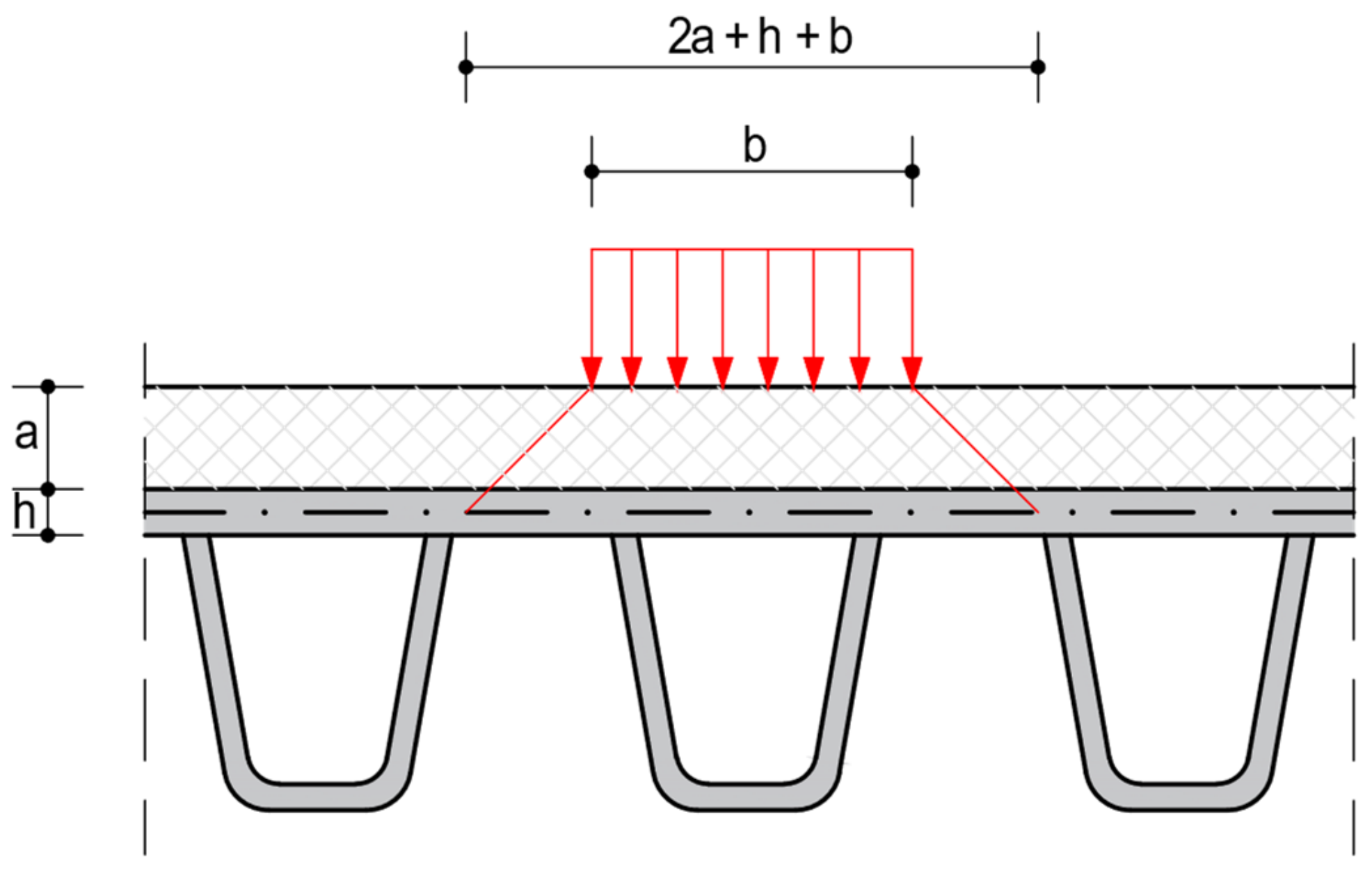
In the structural analysis, the pavement layer (Figure 16) was not explicitly modelled, but the effect of stress diffusion was accounted for by considering 45 degree-diffusions of the loads through the pavement and the consequent enlargement of the conventional footprint of the trucks on the orthotropic plate [55].
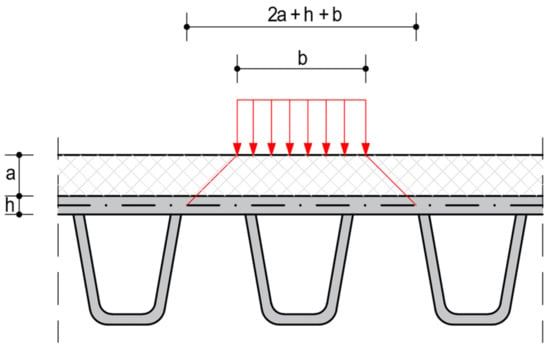
Figure 16.
Diffusion of the concentrated loads in orthotropic slab decks.
Finally, the effect of the transit of each of the five lorries from the FLM4 (a minimum of 3 and a maximum of 6 axles) was implemented in MIDAS GEN® in order to obtain the stress spectrum in correspondence to the details to be checked. In general, the decomposition of the structural finite element model in different substructures, with increasing levels of details, allows for a notable reduction in the computational effort.
3.2. Fatigue Analysis
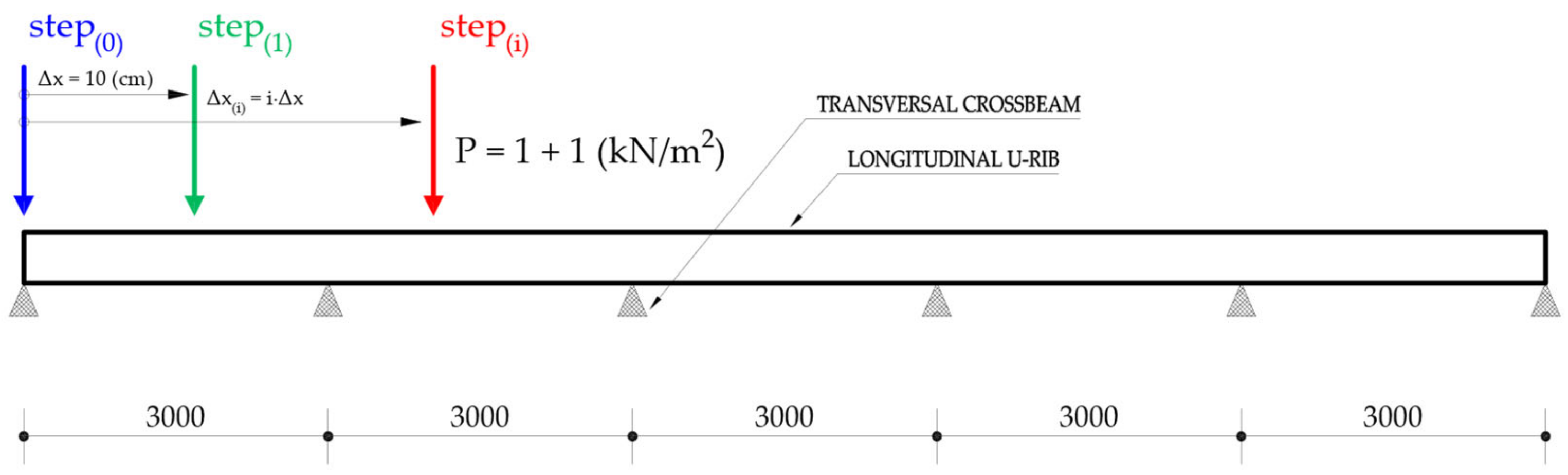
A linear elastic pseudo-static dynamic analysis was performed, thus allowing us to exploit the superposition principle. Three moving unit loads, A-B-C, were considered, with fixed relative distances and given diffusion footprints. The transit of the load mask over the bridge was discretized in 50 steps [58] (Figure 17 and Figure 18), which corresponds to about 30 cm, with the entire length of the model equal to 15 m.
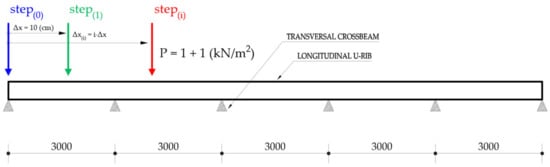
Figure 17.
Loading steps—Footprint with unitary pressures.
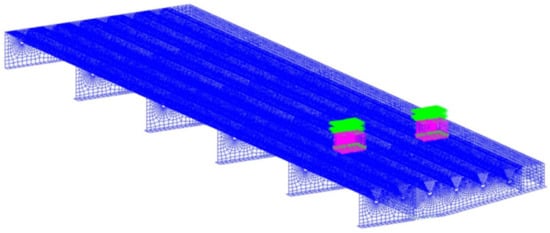
Figure 18.
Position of the diffused footprints type B from the FLM4—step n°10 (rib’s mid-span)—load acting on the slow lane.
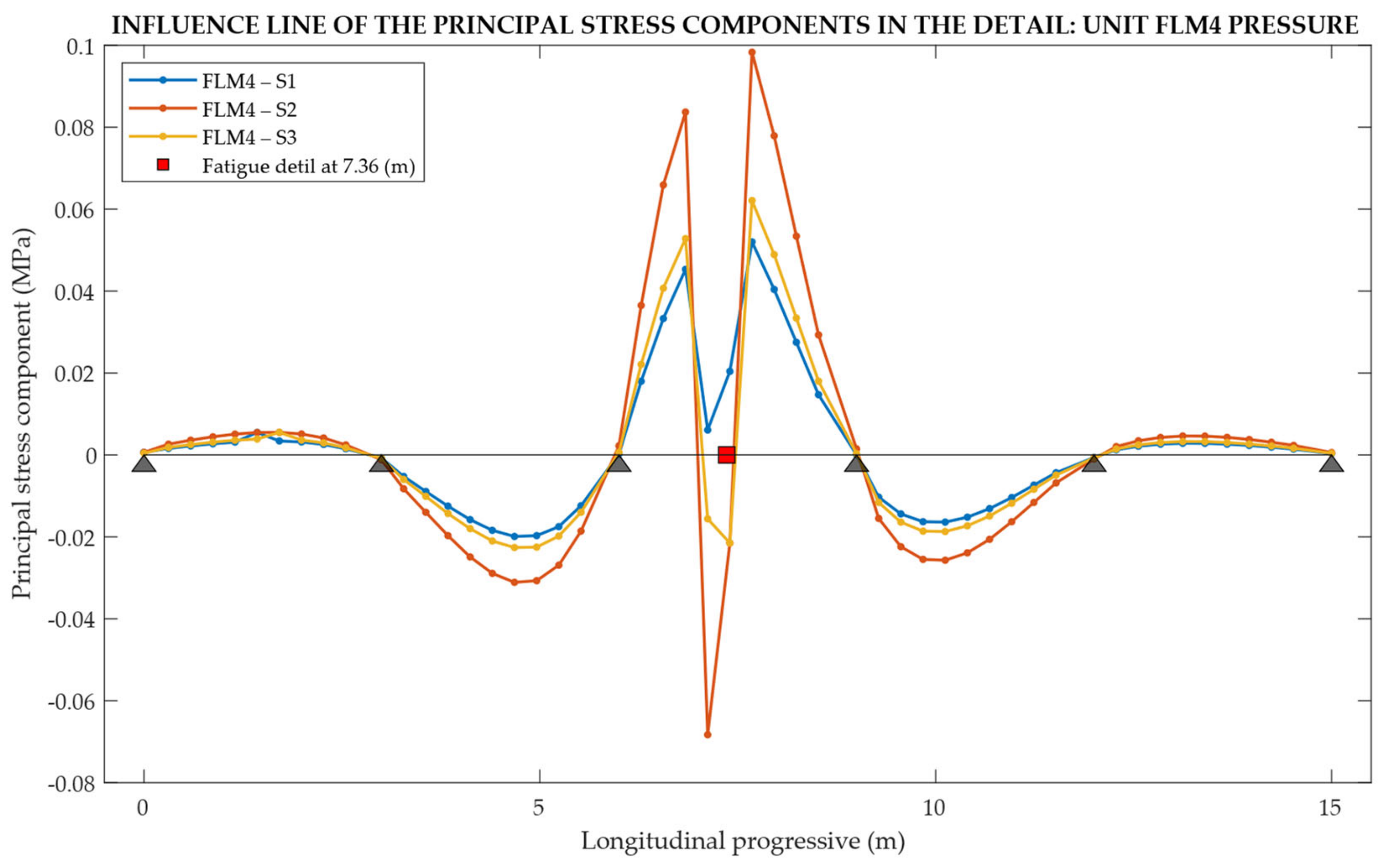
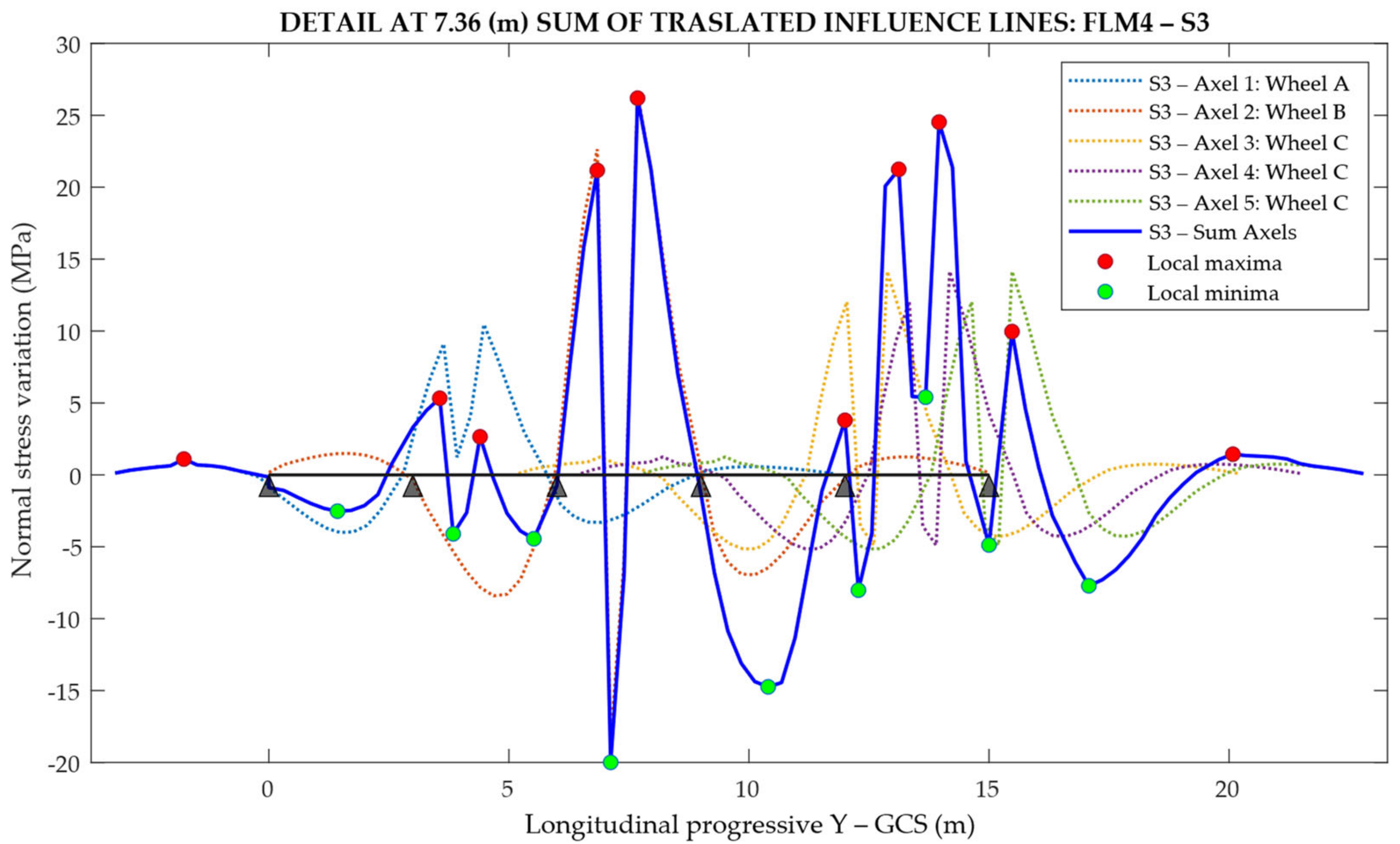
In this way, by performing several linear elastic analyses, it was possible to obtain the influence line of the three principal stress components for the connection details for assessment (Figure 19).
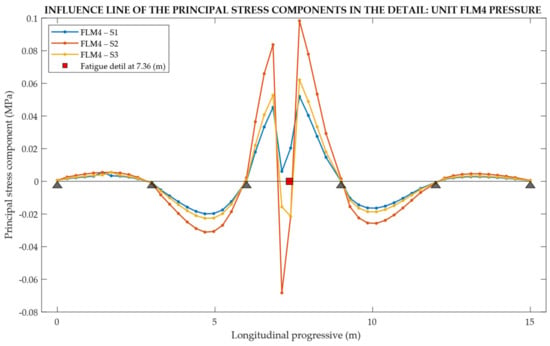
Figure 19.
Principal stress components influence line for a fatigue detail at 7.36 m, exported from MIDAS GEN®.
3.2.1. Number of Fatigue Cycles
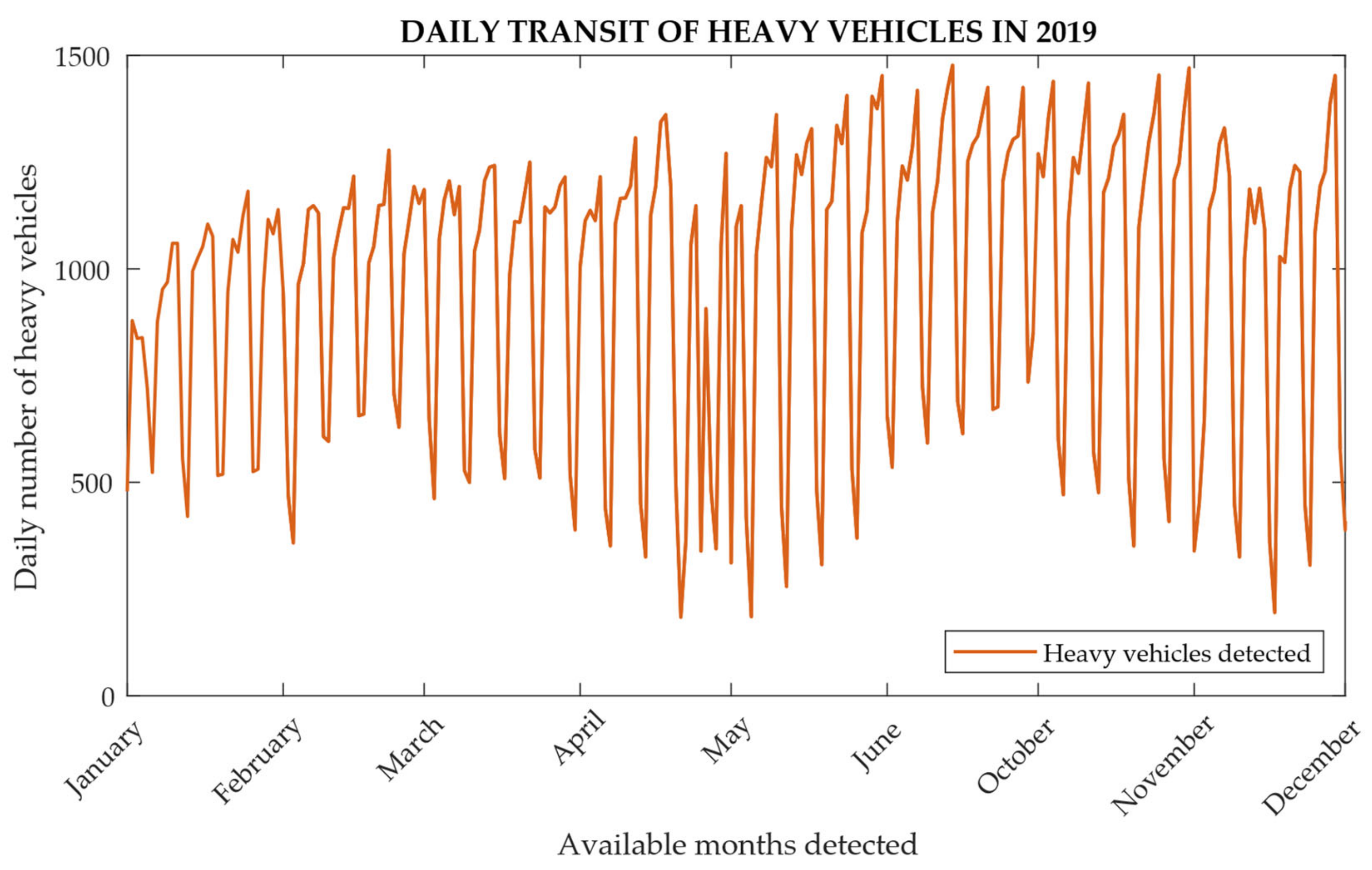
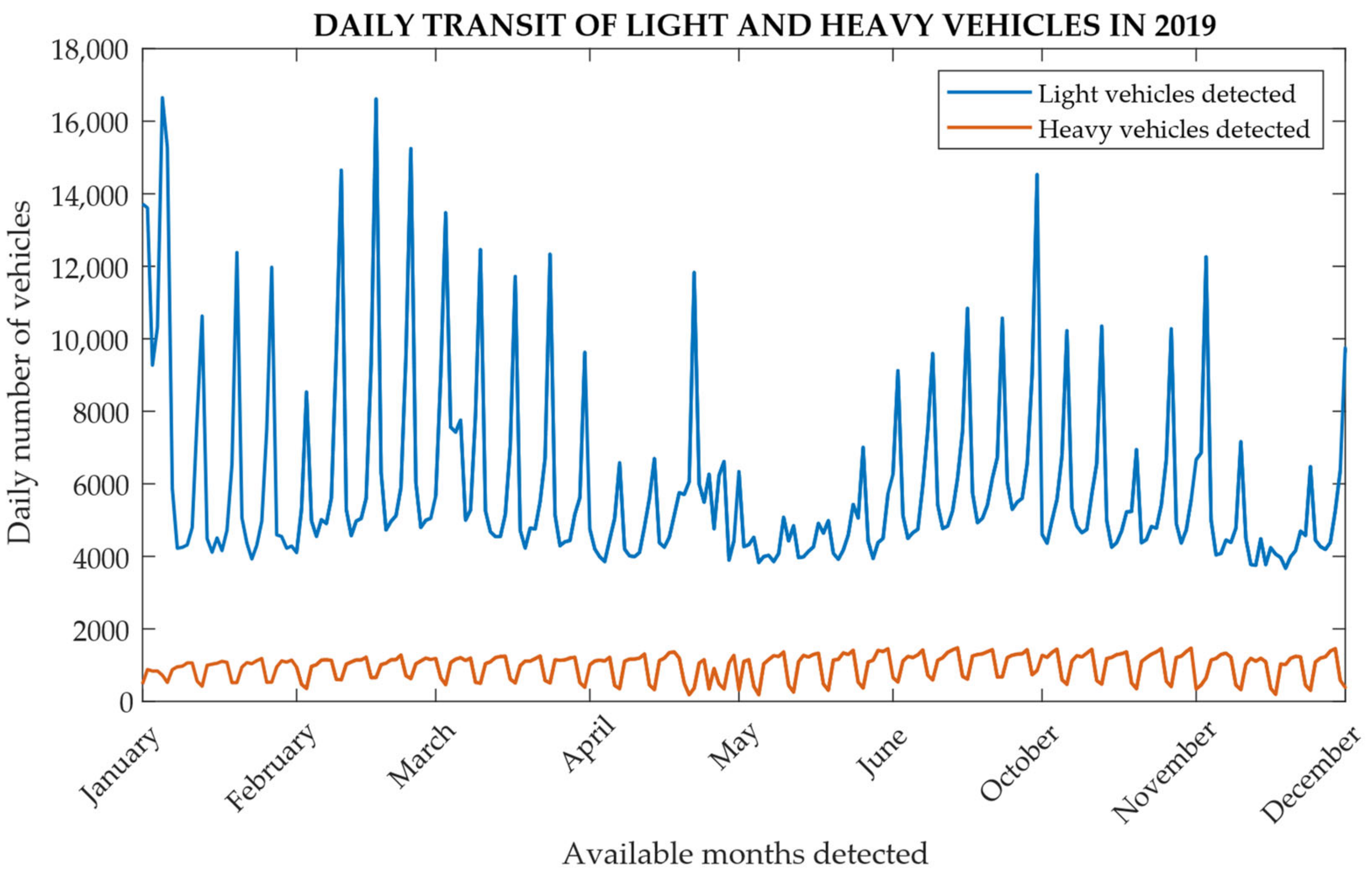
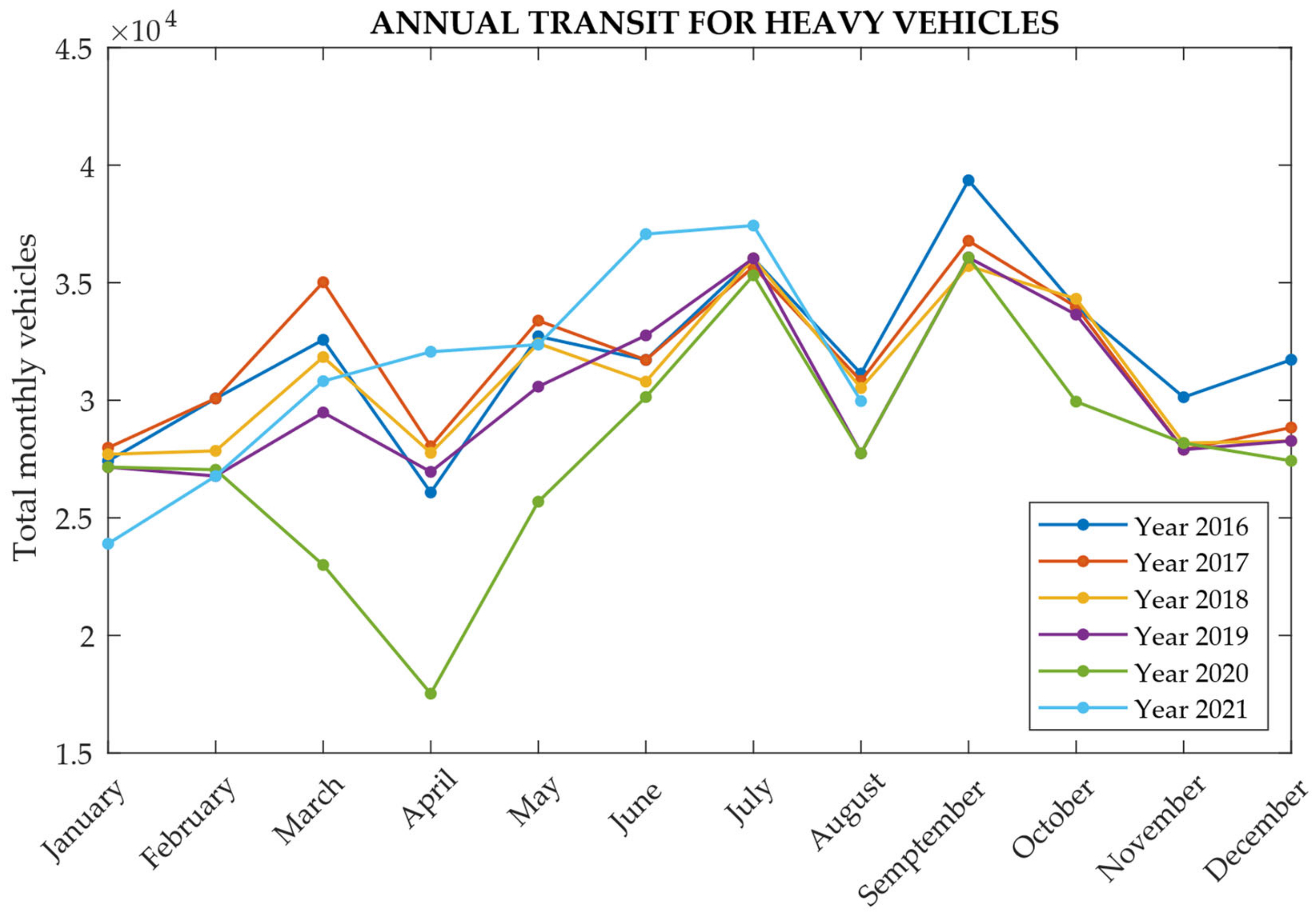
The daily artificial data representative of traffic available for the months of June–October 2019 for the continuous monitoring campaign of the support excursion [59,60,61] were used (Figure 20, Figure 21 and Figure 22). The choice of the traffic volume for the fatigue calculation with FLM4, with reference to Table 4.7 UNI EN 1993-2 (Figure 10), was considered for the fatigue assessment and was deduced by also analyzing the potential flow of the vehicles which affected the relevant motorway section in previous and subsequent years [60].
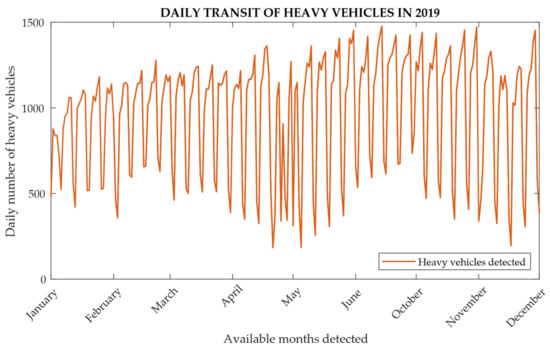
Figure 20.
Data of the daily transit of heavy vehicles between October and June recorded in 2019 in the highway section of the case study viaduct.
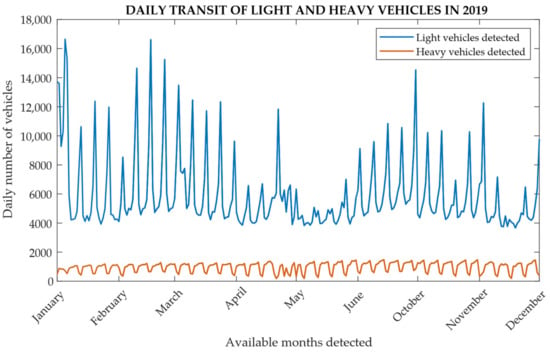
Figure 21.
Data of the daily transit of light and heavy vehicles between October and June recorded in 2019 in the highway section of the case study viaduct.
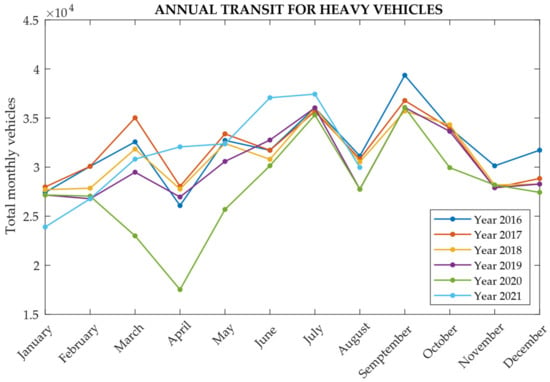
Figure 22.
Data on the monthly transit of heavy vehicles between 2016 and 2021, obtained starting from 2019 in the highway section of the case study viaduct.
These values were obtained through the “Measured Mobility Index” [61]. These indices are calculated as arithmetic averages of the values available for the counting sections of the aggregate for the two macro classes of vehicles: light vehicles with a capacity of less than 3.5 t and heavy vehicles, which instead have a capacity greater than 3.5 t.
3.2.2. Post-Processing
Thanks to the linear elastic analysis, it was possible to obtain the spectrum of the induced stresses for each detail due to the transit of each of the single axis with unitary pressure loads or the three lines of influence for the principal stress components.
Exploiting linear elasticity, the line of influence corresponding to the transit of each of the five shapes of the trucks (Table 3) could easily be obtained by scaling the stresses already obtained for the moving-unit pressure and to translate the line of influence of the single axis previously obtained as a function of the distance between the axles of the vehicles of the FLM4.

Table 3.
Composition of annual heavy vehicle traffic according to the five truck templates of FLM4 [60].
Through an automated peak-to-peak recognition process implemented in Matlab®, the maximum and minimum peaks of the influence lines were recognized, and the load cycles were counted using the “Rain-flow Method”. The Matlab® subroutine returns “Load histograms” in which, for each shape of the FLM4, the stress variation is sorted in descending order.
3.2.3. Fatigue Assessment
For the fatigue life assessment of the rib, the safety factor is assumed to be γMf = 1.15 [53]; thus, with this assumption, the structural element is sensitive to failure due to fatigue but with moderate consequences since load redistribution among parallel ribs is allowed. The reduction in the stress range ( = ) due to the mean stress was accounted for. According to EN 1993-1-9, the detail has a reference value of the fatigue strength = 71 MPa.
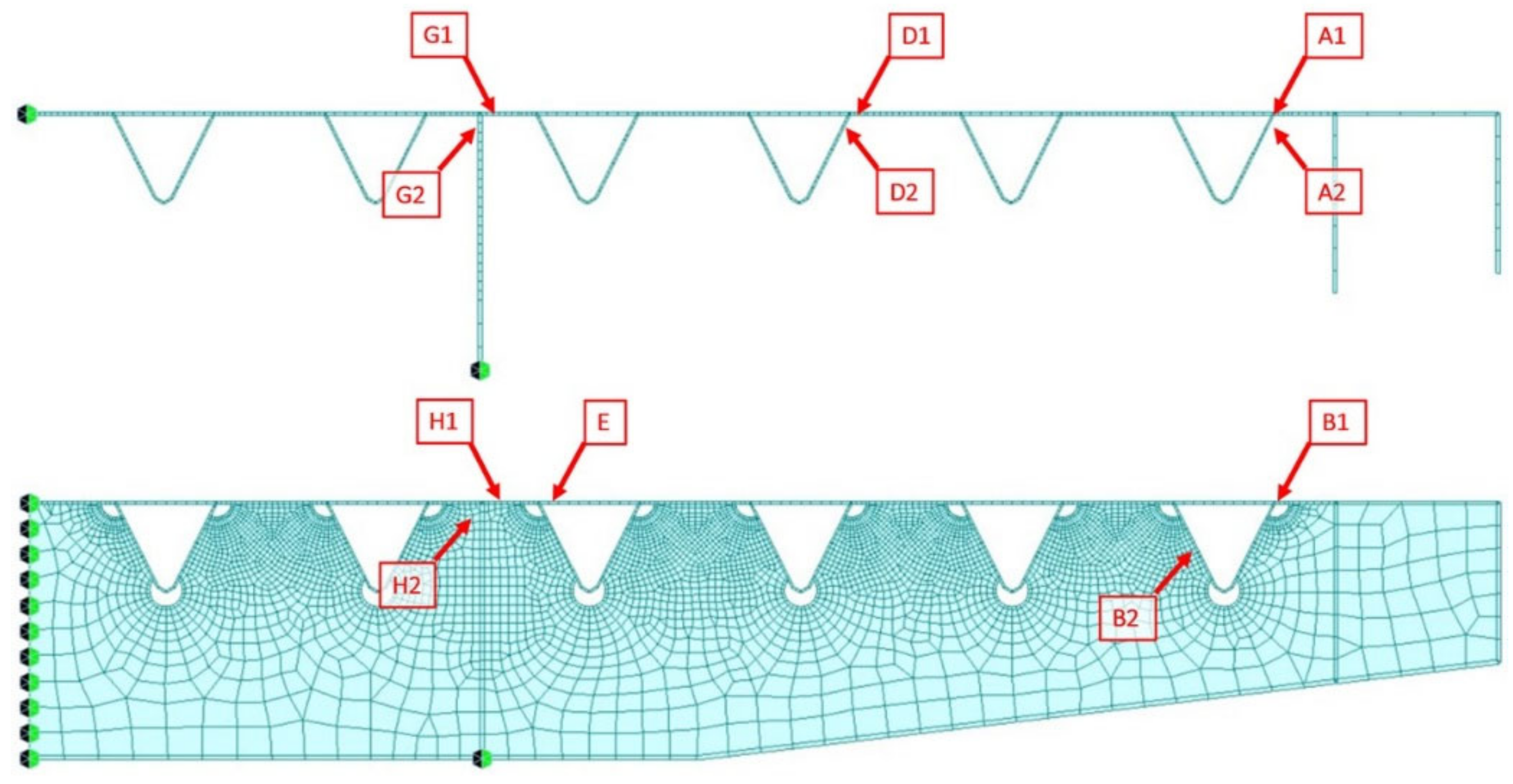
The checks were carried out in the section at about 7.36 m (mid-span of the rib span) and at 6.00 m (section at the second rib) (Figure 23) from the origin of the reference system of the structural model. In fact, the two details considered for the checks correspond to the limit case for the maximum and minimum stiffness of the transverse structural element, respectively.
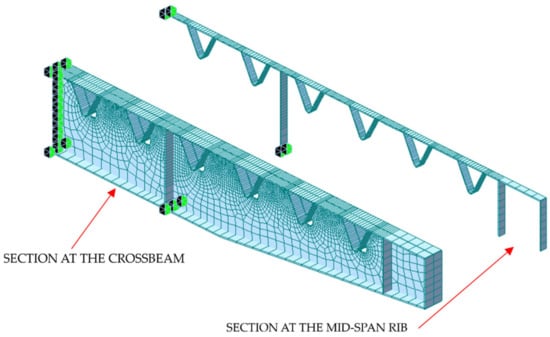
Figure 23.
Locations of the performed fatigue damage check sections in the FEM model.
3.3. Results and Discussion
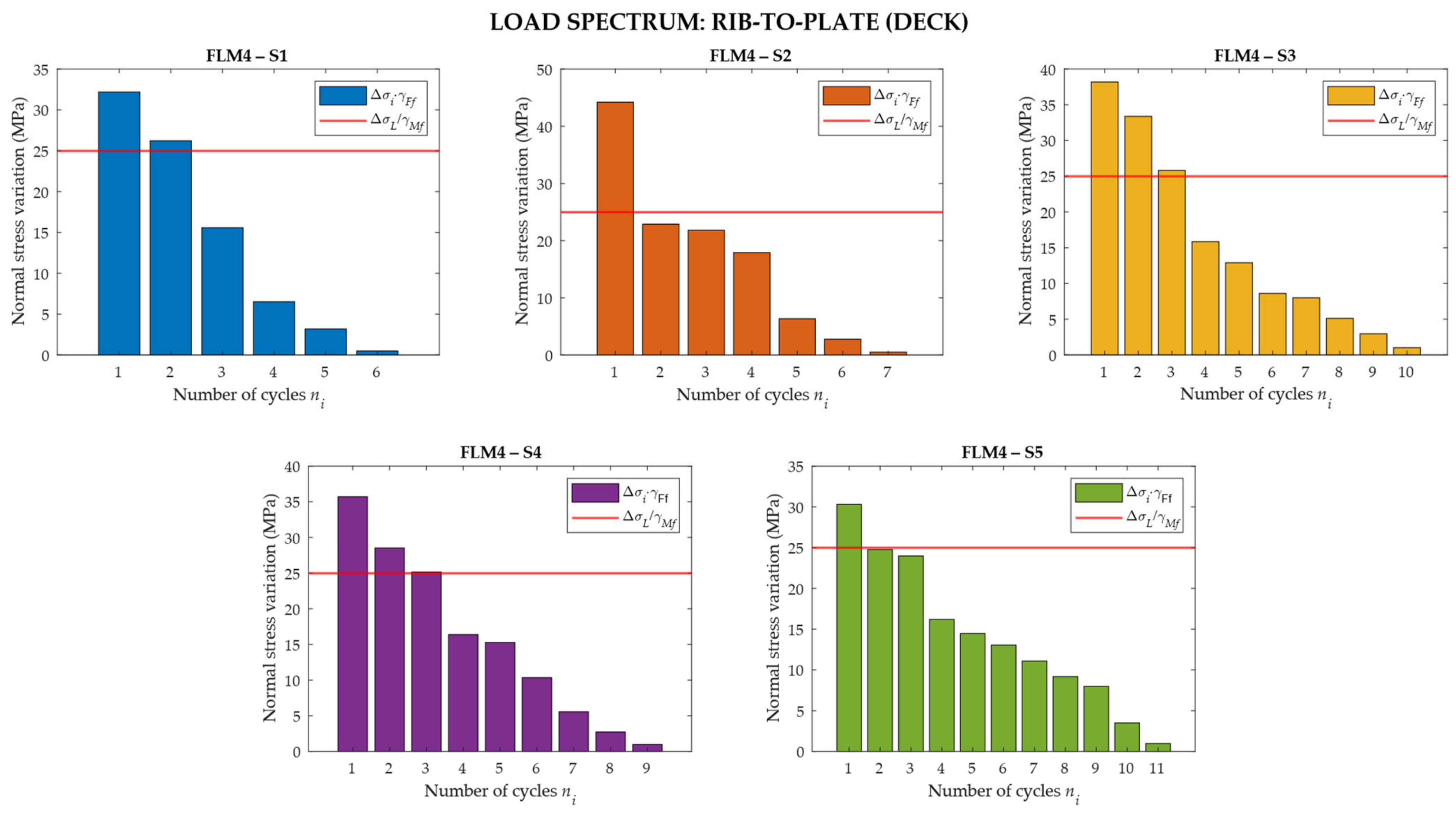
The number of details to be checked with respect to fatigue resistance is very high, but the procedure is quite recursive. Therefore, for the sake of brevity, only one detail will be fully described, while the other ones will be only summarized (see Table 4 and the following ones).

Table 4.
Distinction of detail assessment: Rib-to-Plate—FLM4 S1.
Some Dutch authors [62] have observed that the rib-to-plate detail is where (based on practical experience) fatigue cracks take place more often. The rib-to-plate detail (Figure 24) corresponds to the intersection of the cross-beam and longitudinal Rib in the deck plate. The crack usually nucleates at the root of the longitudinal corner weld or between the core of the channel and the deck plate at the intersection of the cross-piece and the longitudinal closed trapezoidal stiffeners. Then, the crack first propagates through the deck plate thickness and afterwards longitudinally beside the stiffener.
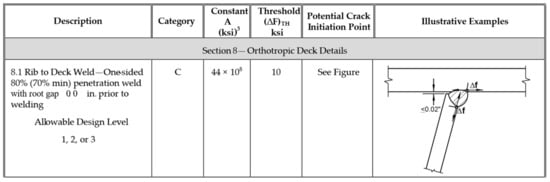
Figure 24.
Table 6.6.1.2.3-1 LRFD AASHTO—Detail categories for load-induced fatigue [63].
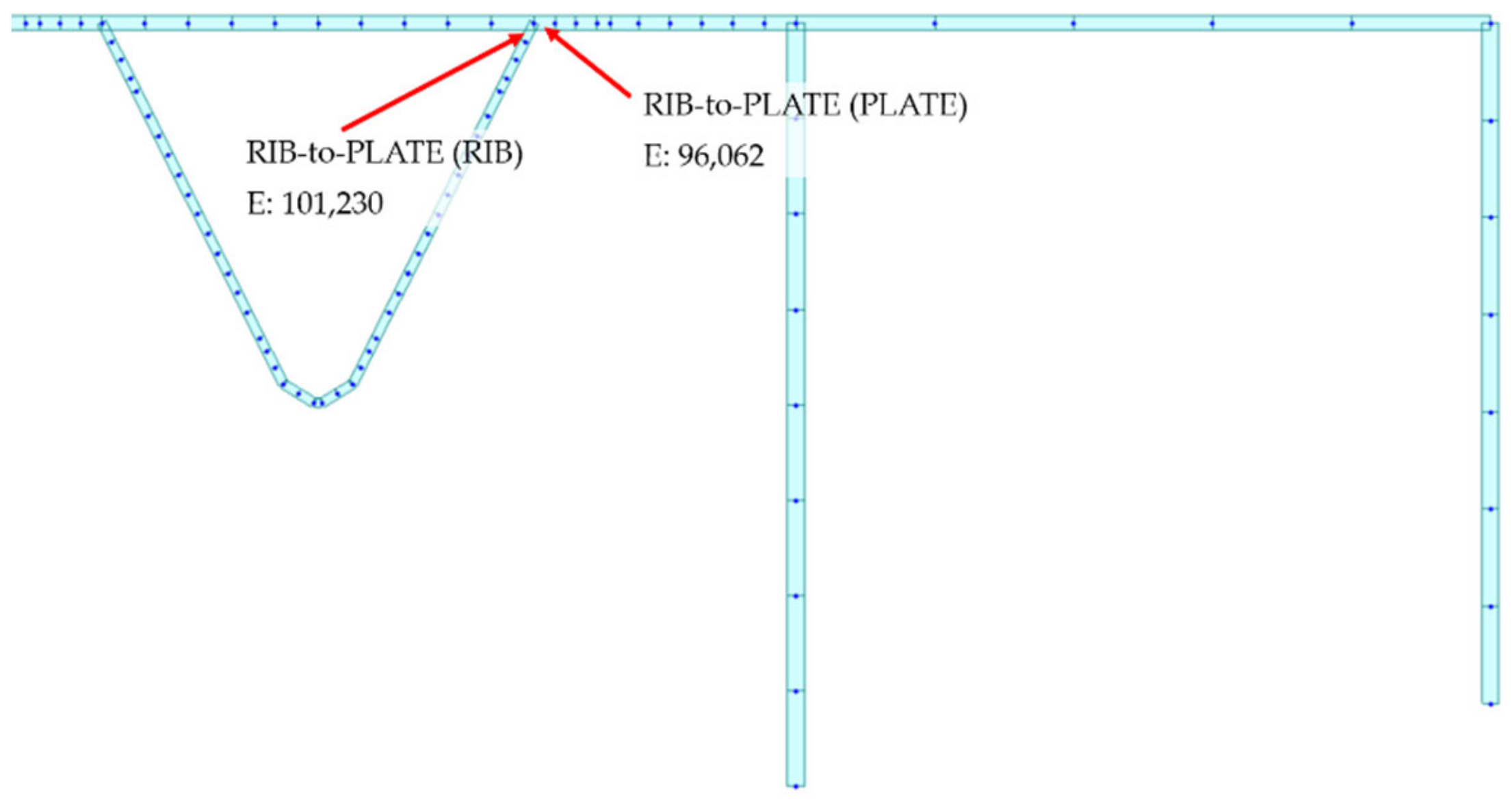
3.3.1. Rib-to-Deck (Plate) Detail
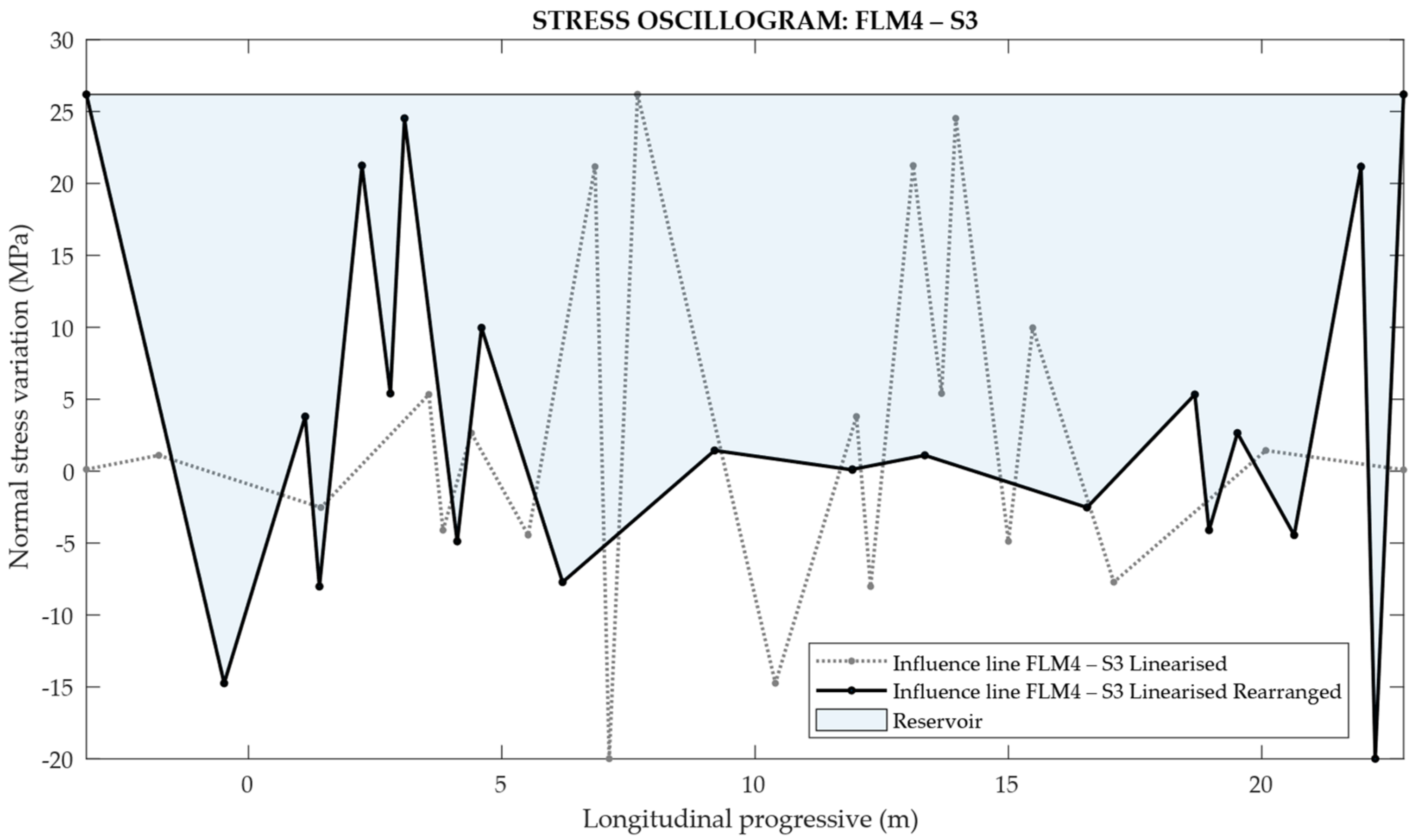
In order to calculate the mean stress state and the stress range in correspondence to the fatigue detail, the plate element n° 96,062 of the deck FEM model (Figure 25) was considered. Then, for each lorry typology, the stress is assessed by superimposing the results obtained from the line of influence of unit pressure wheel footprints: A, B, C, previously multiplied by the corresponding load factor (which depends on the lorry type). In addition, the stress due to longitudinal bending of the box girder, depending on dead weights and on the moving lorry position being extracted from the whole viaduct FEM model, is also added in correspondence to the points where the fatigue check is carried out. This procedure provides the stress spectrum (Figure 26). Finally, the reservoir method diagrams can also be obtained for manual or automatic cycle counts (Figure 27).
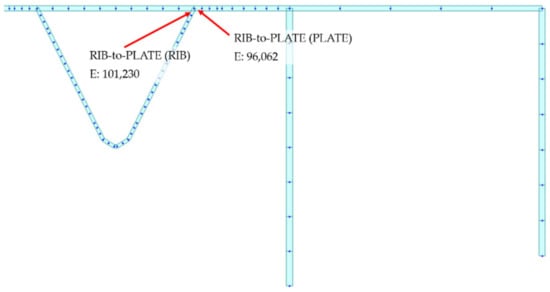
Figure 25.
Rib-to-Plate detail location in the finite element model.
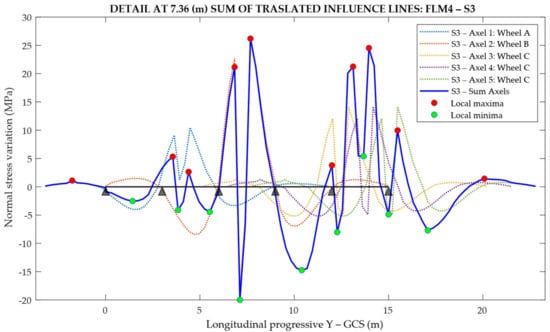
Figure 26.
Stress spectrum for the transit of the lorry silhouette 3 from the FLM4.
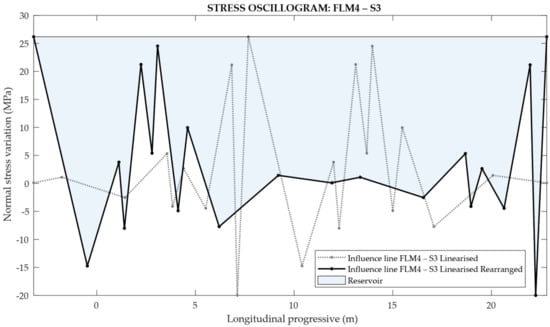
Figure 27.
Reservoir method for the transit of the lorry silhouette 3 for the FLM4.
A Matlab® subroutine has been implemented to automatize the application of the two-parameter rain-flow method. Note that the local maxima and minima of the stress spectrum can be interpreted as the load history due to each lorry transit. Therefore, the sequence of load reversal can be automatically detected, and the fatigue stress spectrum obtained for each lorry typology (Figure 28).
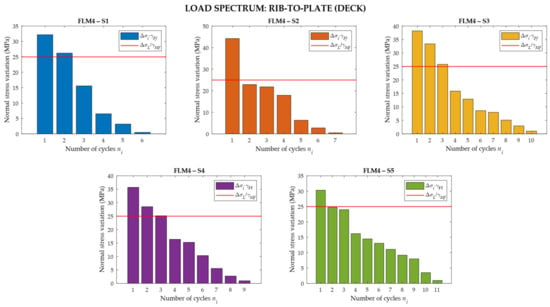
Figure 28.
Tension load history for the transit of the five lorries from the FLM4.
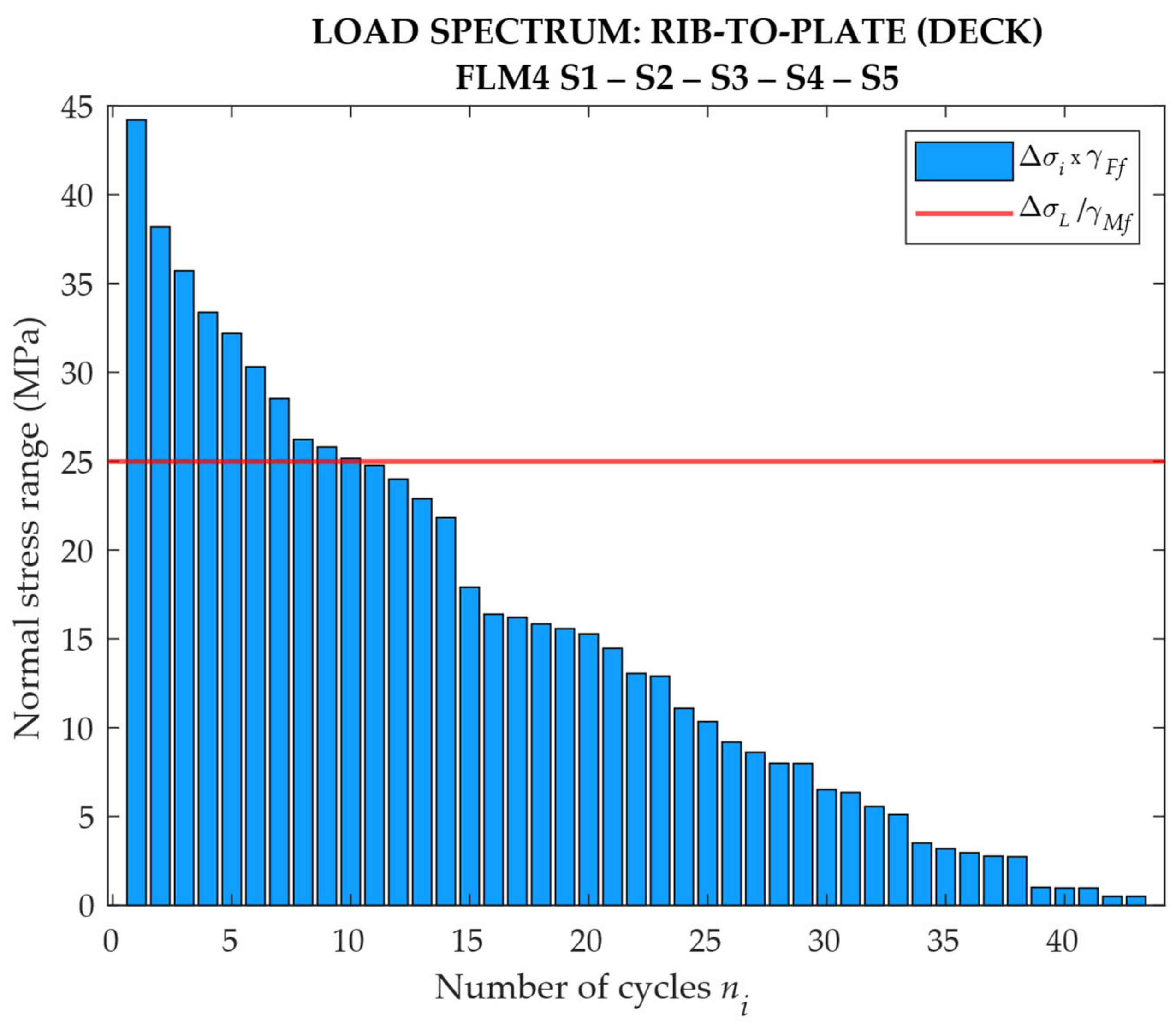
The total number of lorries that travelled above the viaduct was deduced using information (about monitoring) with the system PANAMA (“Platform for the monitoring and analysis of traffic” of the Italian government-owned company for road ANAS), which was carried out during 2019. In addition, to calculate the amount of traffic due to each singular heavy lorry typology, reference is made to Table 4.7 of the UNI EN 1991-2 (average distance, as the highway on which the case study is located has a length of less than 100 km) which provides the frequency percentages of the annual volume. For each shape, the actual number of annual cycles that produce fatigue damage is calculated in detail by filtering the Matlab output, i.e., considering only the variations in stresses above the fatigue limit (see Figure 29 and Figure 30).
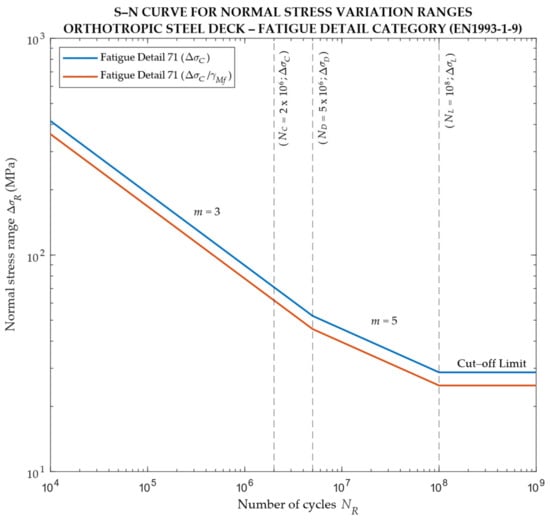
Figure 29.
Design S-N curve for detail 71 from UNI EN 1993-1-9 [53].
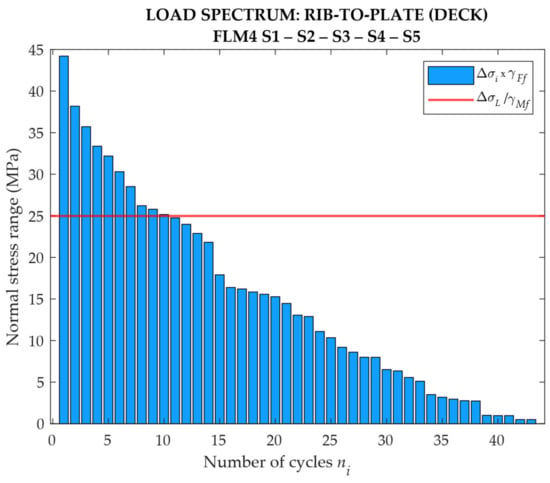
Figure 30.
Load spectrum for the FLM4 in detail considered.
The annual damage accumulation for the transit of the five lorries silhouette for the FLM4 is summarized in Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9.

Table 5.
Distinction of detail assessment: Rib-to-Plate—FLM4 S2.

Table 6.
Distinction of detail assessment: Rib-to-Plate—FLM4 S3.

Table 7.
Distinction of detail assessment: Rib-to-Plate—FLM4 S4.

Table 8.
Distinction of detail assessment: Rib-to-Plate—FLM4 S5.

Table 9.
Distinction of detail assessment: Rib-to-Plate.
Table 4, Table 5, Table 6, Table 7 and Table 8 can be integrated over the nominal design life duration to assess whether the detail fatigue resistance is compliant with the present standard.
The detail Rib-to-Plate does not suffer from fatigue during the nominal design life of 50 years.
3.3.2. Verification Summary
In order to provide an assessment of the fatigue lifetime of the existing viaduct with respect to the present standards, the whole set of details vulnerable to fatigue must be considered. In addition, the calculation must account for a change in the loading configuration due to a limitation of the lane which took place (since 2019) after the positioning of two additional New Jersey barriers, which is shown in Figure 31.
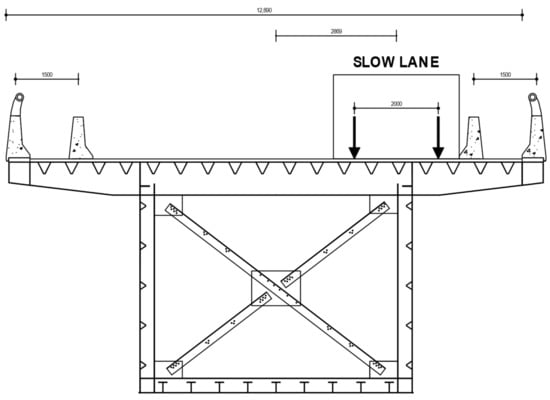
Figure 31.
Slow lane position from around 2019, following the positioning of additional New Jersey barriers.
The set of details for which the checks are carried out is shown in Figure 32.
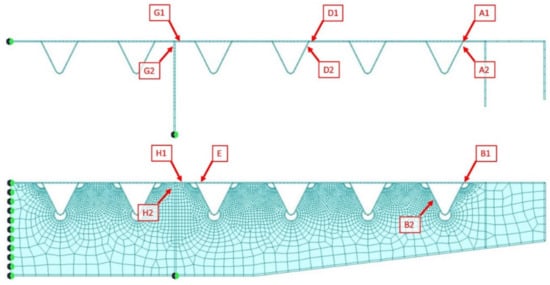
Figure 32.
Details subjected to assessment from the section 7.36 m from the first rib (mid-span of the rib) and 6.00 m from the first rib (cross-beam).
The following tables summarize the partial damage accumulation, providing the number of years after which the total damage becomes equal to one. The details over the slow lane are divided into two groups, located respectively on the left or the right side of the additional barrier. This subdivision is meaningful since the details on the left will continue to accumulate fatigue damage after the placement of the additional New Jersey barriers, whereas the details on the right will be unloaded. The groups are as follows:
- Group 1 (R): A1, A2, B1, and B2: critical details in the original condition. After the lane number reduction and placement of the additional New Jersey barrier, these details are unloaded;
- Group 2 (L): D1, D2, G1, G2, H1, and H2: those details are less critical in the original condition, though some of them will accumulate damage after the lane reduction due also to the overlapping of the load silhouette (Figure 32).
Table 10 and Table 11 reassume the fatigue damage assessment carried out in the original configuration. The number of cycles and the accumulated fatigue damage per year are reported for each FLM4 heavy lorry category. In the last two columns, the fatigue life of the detail and the expected year for unit fatigue damage accumulation are reported. The calculations reveal that the detail rib-to-plate A2 is the most critical since the European standards provide a fatigue life equal to 21 years.

Table 10.
Results of damage checks in the original configuration—Group 1 (R).

Table 11.
Results of damage checks in the original configuration–Group 2 (L).
In Table 12, the yearly damage accumulation is assessed in correspondence to reduced lanes and the placement of additional barriers. Only details belonging to Group 2 (L) are reported since details of Group 1 (R) are unloaded and do not accumulate any further fatigue damage.

Table 12.
Yearly fatigue damage accumulation—Group 2(L), with the additional New Jersey barriers and lane reduction since 2019.
Finally, Table 13 shows the fatigue assessment for the actual load history. The calculation is carried out in two steps; firstly, the original configuration, valid between 1994 and 2019, and secondly, the reduced line and additional barriers configuration, valid from 2019 onward. The calculated yearly fatigue damage is integrated over the corresponding duration, and the level of traffic is assumed to be approximately constant since 1994.

Table 13.
Results of damage checks—Group 2(Left)—Accumulation of damage due to the actual full load history.
In the last columns, the total fatigue damage and the expected year for unit damage accumulation are reported. The analyzed detail results are compliant with the preset European Standard as far as fatigue resistance is concerned.
4. Conclusions
The phenomenon of fatigue in orthotropic steel deck bridges has been briefly summarized, together with the normative approach of the UNI EN 1993 European standard.
An existing orthotropic steel deck viaduct, located on a northern Italy highway and designed at the end of the 1980s, is adopted as a case study to assess its compliance with today’s standards. The calculation exploited finite element simulations carried out on the structure and on more detailed substructures. The information on the number of load cycles was derived with the support of experimental monitoring with the system: PANAMA (“Platform for the monitoring and analysis of traffic” of the Italian government-owned company for road ANAS).
The results show that the viaduct in the original configuration was not fully compliant with the standards as far as fatigue resistance is concerned. In fact, the ultimate limit state with respect to fatigue damage accumulation was first reached in detail A2 in 2015.
It is expected that similar viaducts of the same age are probably in analogous conditions. Particular care should be devoted to bridges that could be in the worst maintenance condition due to the decrease in fatigue resistance induced by corrosion.
On the other hand, the lane number reduction, and the placement of additional New Jersey barriers in 2019, provided unloading conditions for the most critical details and interrupted further fatigue damage accumulation. Consequently, the damage checks were verified, and the structure is now compliant with fatigue resistance requirements.
Nevertheless, in general, the reduction in the total number of lanes does not provide an automatic reduction in heavy lorry traffic, which mainly takes place in the slow lane. Moreover, details, such as B2, are still suffering from fatigue damage accumulation due to the overlapping of wheel footprints in both the original and the reduced lane conditions, thus deserving special attention. Therefore, further interventions, like the replacement of the pavement in order to improve the stress redistribution upon the connection details below the wheel footprint, and continuous bridge inspections or monitoring, are suggested.
Author Contributions
Conceptualization, M.M., R.A., D.M., S.I., F.M. and A.C.; methodology, M.M., D.M., S.I., F.M. and A.C.; software, M.M.; validation, M.M., D.M., S.I., F.M. and A.C.; formal analysis, M.M., R.A., D.M., S.I., F.M. and A.C.; investigation, M.M., D.M., S.I., F.M. and A.C.; data curation, M.M., D.M., S.I., F.M. and A.C.; writing—original draft preparation, M.M., R.A., S.I. and F.M.; writing—review and editing, M.M., D.M., S.I., F.M. and A.C.; supervision, R.A., D.M., S.I., F.M. and A.C.; funding acquisition, D.M., S.I. and A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- AISC. Design Manual for Orthotropic Steel Plate Deck Bridges; American Institute of Steel Construction: New York, NY, USA, 1963; ISBN 978-1-56424-004-0. [Google Scholar]
- Connor, R.J.; Federal Highway Administration; Fisher, J.; Gatti, W.; Gopalartnam, V.; Kozy, B. Manual for Design, Construction and Maintenance of Orthotropic Steel Deck Bridges; Federal Highway Administration, U.S. Department of Transportation: Washington, DC, USA, 2012. [Google Scholar]
- Troitsky, M.S. Orthotropic Bridges—Theory and Design, 2nd ed.; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1987; pp. 57–63. [Google Scholar]
- Russo, F.; Mertz, D.R.; Frank, K.H.; Wilson, K.E. Design and Evaluation of Steel Bridges for Fatigue and Fracture—Reference Manual; National Highway Institute (US): Vienna, VA, USA, 2016; ISBN 979-8611492352. [Google Scholar]
- Tecchio, G.; Lorenzoni, F.; Caldon, M.; Donà, M.; Da Porto, F.; Modena, C. Monitoring of orthotropic steel decks for experimental evaluation of residual fatigue life. J. Civ. Struct. Health Monit. 2017, 3, 517–539. [Google Scholar] [CrossRef]
- Yan, F.; Chen, W.; Lin, Z. Prediction of fatigue life of welded details in cable-stayed orthotropic steel deck bridges. Eng. Struct. 2016, 127, 344–368. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Y.; Bao, Y.; Jia, D.; Bu, Y.; Li, Q. Fatigue Performance of Orthotropic Steel-Concrete Composite Deck with Large-Size Longitudinal U-Shaped Ribs. Eng. Struct. 2017, 150, 864–874. [Google Scholar] [CrossRef]
- Zou, S.; Cao, R.; Deng, L.; Wang, W. Effect of stress reversals on fatigue life evaluation of OSD considering the transverse distribution of vehicle loads. Eng. Struct. 2022, 265, 114400. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J.; Yuan, D.; Bu, Y. Fatigue performance of rib-to-deck joint in orthotropic steel bridge deck with new type of both-side fillet welded joints. In Proceedings of the IABSE Symposium Nantes 2018: Tomorrow’s Megastructures, Nantes, France, 19–21 September 2018; pp. S7-19–S7-26. [Google Scholar]
- Kainuma, S.; Yang, M.; Jeong, Y.S.; Inokuchi, S.; Kawabata, A.; Uchida, D. Experimental investigation for structural parameter effects on fatigue behavior of rib-to-deck welded joints in orthotropic steel decks. Eng. Fail. Anal. 2017, 79, 520–537. [Google Scholar] [CrossRef]
- Ji, B.; Liu, R.; Chen, C.; Maeno, H.; Chen, X. Evaluation on root-deck fatigue of orthotropic steel bridge deck. J. Constr. Steel Res. 2013, 90, 174–183. [Google Scholar] [CrossRef]
- Wang, Q.; Ji, B.; Xia, J.; Fu, Z. Fatigue assessment of rib-deck welds in orthotropic steel decks integrating the effect of load dispersal through asphalt surfacing. Structures 2020, 28, 1701–1712. [Google Scholar] [CrossRef]
- Wang, D.; Xiang, C.; Ma, Y.; Chen, A.; Wang, B. Experimental study on the root-deck fatigue crack on orthotropic steel decks. Mater. Des. 2021, 203, 109601. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Q.; Bao, Y.; Bu, Y. Fatigue assessment of longitudinal rib-to-crossbeam welded joints in orthotropic steel bridge decks. J. Constr. Steel Res. 2019, 159, 53–66. [Google Scholar] [CrossRef]
- Cheng, B.; Abdelbaset, H.; Li, H.T.; Tian, L.; Zhao, J. Fatigue behavior of rib-to-floorbeam welded connection in UHPC reinforced OSDs subjected to longitudinal flexural. Eng. Fail. Anal. 2022, 137, 106383. [Google Scholar] [CrossRef]
- Zhu, Z.; Xiang, Z.; Li, J.; Carpinteri, A. Fatigue damage investigation on diaphragm cutout detail on orthotropic bridge deck based on field measurements and FEM. Thin-Walled Struct. 2020, 157, 107106. [Google Scholar] [CrossRef]
- Zhu, Z.; Xiang, Z.; Li, J.; Huang, Y.; Ruan, S. Fatigue behavior of orthotropic bridge decks with two types of cutout geometry based on field monitoring and FEM analysis. Eng. Struct. 2020, 209, 109926. [Google Scholar] [CrossRef]
- Chen, S.; Huang, Y.; Zhou, C.; Gu, P. Experimental and numerical study on fatigue performance of U-rib connections. J. Constr. Steel Res. 2019, 163, 105796. [Google Scholar] [CrossRef]
- Zhu, A.; Li, M.; Zhu, H.; Xiao, H.; Ge, H. Fatigue behaviour of orthotropic steel bridge decks with inner bulkheads. J. Constr. Steel Res. 2018, 146, 63–75. [Google Scholar] [CrossRef]
- Li, J.; Zhu, Z. Effects of full internal bulkheads on fatigue behaviors of orthotropic steel decks. J. Constr. Steel Res. 2022, 196, 107400. [Google Scholar] [CrossRef]
- Dong, P. A structural stress definition and numerical implementation for fatigue analysis of welded joints. Int. J. Fatigue 2001, 23, 865–876. [Google Scholar] [CrossRef]
- Dong, P. A robust structural stress method for fatigue analysis of offshore/marine structures. Trans. ASME 2005, 127, 68–74. [Google Scholar] [CrossRef]
- Dong, P.; Prager, M.; Osage, D. The design master S-N curve in ASME Div 2 rewrite and its validations. Weld. World 2007, 51, 53–63. [Google Scholar] [CrossRef]
- Yang, H.; Wang, P.; Qian, H.; Dong, P. Analysis of fatigue test conditions for reproducing weld toe cracking into U-rib wall in orthotropic bridge decks. Int. J. Fatigue 2022, 162, 106976. [Google Scholar] [CrossRef]
- Yang, H.; Wang, P.; Qian, H.; Niu, S.; Dong, P. An experimental investigation into fatigue behaviors of single- and double-sided U rib welds in orthotropic bridge decks. Int. J. Fatigue 2022, 159, 106827. [Google Scholar] [CrossRef]
- Yang, H.; Wang, P.; Qian, H. Fatigue behaviors of typical of orthotropic steel bridges in multiaxial stress states using traction structural stress. Int. J. Fatigue 2020, 141, 105862. [Google Scholar] [CrossRef]
- Pei, X.; Dong, P.; Xing, S. A structural strain parameter for a unified treatment of fatigue behaviors of welded components. Int. J. Fatigue 2019, 124, 444–460. [Google Scholar] [CrossRef]
- Pei, X.; Dong, P.; Kim, M.H. A simplified structural strain method for low-cycle fatigue evaluation of girth-welded pipe connections. Int. J. Fatigue 2020, 139, 105732. [Google Scholar] [CrossRef]
- Sonsino, C.M. Consideration of allowable equivalent stresses for fatigue design of welded joints according to the notch stress concept with the reference radii rref = 1.00 and 0.05 mm. Weld. World 2009, 53, 64–75. [Google Scholar] [CrossRef]
- Karakas, Ö.; Baumgartner, J.; Susmel, L. On the use of fictitious notch radius equal to 0.3 mm to design against fatigue welded joints made of wrought magnesium alloy AZ31. Int. J. Fatigue 2020, 139, 105747. [Google Scholar] [CrossRef]
- Karakas, Ö.; Zhang, G.; Sonsino, C.M. Critical distance approach for the fatigue strength assessment of magnesium welded joints in contrast to Neuber’s effective stress method. Int. J. Fatigue 2018, 112, 21–35. [Google Scholar] [CrossRef]
- Luo, P.; Zhang, Q.; Bao, Y.; Zhou, A. Fatigue evaluation of rib-to-deck welded joint using averaged strain energy density method. Eng. Struct. 2018, 177, 682–694. [Google Scholar] [CrossRef]
- Wu, W.; Kolstein, H.; Veljkovic, M. Fatigue resistance of rib-to-deck welded joint in OSDs, analysed by fracture mechanics. J. Constr. Steel Res. 2019, 162, 105700. [Google Scholar] [CrossRef]
- Maljaars, J.; Bonet, E.; Pijpers, R.J.M. Fatigue resistance of the deck plate in steel orthotropic deck strcutures. Eng. Fract. Mech. 2018, 201, 214–228. [Google Scholar] [CrossRef]
- Wang, Q.; Ji, B.; Li, C.; Fu, Z. Fatigue evaluation of rib-to-deck welds: Crack-propagation-life predictive model and parametric analysis. J. Constr. Steel Res. 2020, 173, 106248. [Google Scholar] [CrossRef]
- Xiao, Z.G.; Yamada, K.; Inoue, J.; Yamaguchi, K. Fatigue cracks in longitudinal ribs of steel orthotropic deck. Int. J. Fatigue 2006, 28, 409–416. [Google Scholar] [CrossRef]
- Invernizzi, S.; Montagnoli, F.; Carpinteri, A. Fatigue Assessment of the Collapsed XXth Century Cable-Stayed Polcevera Bridge in Genoa. Procedia Struct. Integr. 2019, 18, 237–244. [Google Scholar] [CrossRef]
- Invernizzi, S.; Montagnoli, F.; Carpinteri, A. The collapse of the Morandi’s bridge: Remarks about fatigue and corrosion. In Proceedings of the IABSE Symposium Wroclaw 2020: Synergy of Culture and Civil Engineering—History and Challenges, Wroclaw, Poland, 7–9 October 2020; pp. 1040–1047. [Google Scholar]
- Invernizzi, S.; Montagnoli, F.; Carpinteri, A. Corrosion Fatigue Investigation on the Possible Collapse Reasons of Polcevera Bridge in Genoa. Lect. Notes Mech. Eng. 2020, 151–159. [Google Scholar] [CrossRef]
- Invernizzi, S.; Montagnoli, F.; Carpinteri, A. Very high cycle corrosion fatigue study of the collapsed Polcevera Bridge, Italy. J. Bridge Eng. 2022, 27, 04021102. [Google Scholar] [CrossRef]
- Chen, W.-F.; Duan, L. Bridge Engineering Handbook: Construction and Maintenance: Chapter 14, Orthotropic Deck Bridges; Mangus, A.R., Sun, S., Eds.; CRC Press: Boca Raton, FL, USA, 2014; ISBN 978-1-4398-5233-0. [Google Scholar]
- Masera, D.; Mairone, M.; Asso, R. Il Fenomeno della Fatica nei Ponti in Acciaio a Piastra Ortotropa. Strade Autostrade 2021, 149, 57–63. [Google Scholar]
- Qian, Z.H.; Abruzzese, D. Fatigue failure of welded connections at orthotropic bridges. Frat. E Integrità Strutt. 2009, 3, 105–112. [Google Scholar] [CrossRef]
- ASTM. American National Standard ANSI/ASTM E206-72; ASTM: West Conshohocken, PA, USA, 1979. [Google Scholar]
- Nussbaumer, A.; Borges, L.; Davaine, L. Fatigue Design of Steel and Composite Structures: Eurocode 3: Design of Steel Structures, Part 1–9 Fatigue; Eurocode 4: Design of Composite Steel and Concrete Structures; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 978-3-433-60120-4. [Google Scholar]
- Wolchuk, R. Steel Orthotropic Decks: Developments in the 1990s. Transp. Res. Rec. 1999, 1688, 30–37. [Google Scholar] [CrossRef]
- Carpinteri, A.; Montagnoli, F.; Invernizzi, S. Scaling and fractality in fatigue resistance: Specimen-size effects on Wöhler’s curve and fatigue limit. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1869–1879. [Google Scholar] [CrossRef]
- Carpinteri, A.; Montagnoli, F. Scaling and fractality in subcritical fatigue crack growth: Crack-size effects on Paris’ law and fatigue threshold. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 788–801. [Google Scholar] [CrossRef]
- Carpinteri, A.; Montagnoli, F. Scaling and fractality in fatigue crack growth: Implications to Paris’ law and Wöhler’s curve. Procedia Struct. Integr. 2019, 14, 957–963. [Google Scholar] [CrossRef]
- Montagnoli, F.; Invernizzi, S.; Carpinteri, A. Fractality and size effect in fatigue damage accumulation: Comparison between Paris and Wöhler’s curve. Lect. Notes Mech. Eng. 2020, 188–196. [Google Scholar] [CrossRef]
- Invernizzi, S.; Montagnoli, F.; Carpinteri, A. Experimental evidence of specimen-size effects on EN-AW6082 aluminum alloy in VHCF regime. Appl. Sci. 2021, 11, 4272. [Google Scholar] [CrossRef]
- Invernizzi, S.; Paolino, D.; Montagnoli, F.; Tridello, A.; Carpinteri, A. Comparison between fractal and statistical approaches to model size effects in VHCF. Metals 2022, 12, 1499. [Google Scholar] [CrossRef]
- European Committee for Standardization. EN 1993-1-9 Eurocode 3: Design of Steel Structures Part 1–9 Fatigue; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- European Committee for Standardization. EN 1993-2 Eurocode 3: Design of Steel Structures: Steel Bridges. Brussels, European Committee for Standardization Part 2: Steel Bridges; European Committee for Standardization: Brussels, Belgium, 2007. [Google Scholar]
- European Committee for Standardization. EN 1991-2 Eurocode 1: Actions on Structures Part 2: Traffic Loads on Bridges; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Miner, M.A. Cumulative Damage in Fatigue. J. Appl. Mech. 1945, 12, 149–164. [Google Scholar] [CrossRef]
- Palmgren, A. “Die Lebensdauer von Kugellagern” (The Service Life of Ball Bearings). Z. Des Ver. Dtsch. 1924, 68, 339–341. [Google Scholar]
- Masera, D.; Mairone, M. Modellazione e Analisi di un Viadotto Esistente con Impalcato a Cassone in Acciaio a Piastra Ortotropa. Available online: https://www.harpaceas.it/case-studies/modellazione-e-analisi-di-un-viadotto-esistente-con-impalcato-a-cassone-in-acciaio-a-piastra-ortotropa (accessed on 2 July 2022).
- Asso, R.; Cucuzza, R.; Rosso, M.M.; Masera, D.; Marano, G.C. Bridges Monitoring: An Application of AI with Gaussian Processes. In Proceedings of the 4th International Conference on Evolutionary and Deterministic Methods for Design, Optimization and Control; Institute of Structural Analysis and Antiseismic Research National Technical University of Athens, Athens, Greece, 28–30 June 2021. [Google Scholar]
- Mairone, M. Study of an Existing Viaduct with Box-Girder Orthotropic Steel Deck. Master’s Thesis, Politecnico di Torino, Turin, Italy, 2021. [Google Scholar]
- Traffic Observatory Archive. Available online: https://www.stradeanas.it/it/le-strade/osservatorio-del-traffico/archivio-osservatorio-del-traffico (accessed on 1 September 2021).
- De Jong, F.B.P.; Bijlaard, F.S.K. Renovation Techniques for Fatigue Cracked Orthotropic Steel Bridge Decks; Technische Universiteit Delft: Delft, The Netherlands, 2007; ISBN 978-90-90-21412-2. [Google Scholar]
- AASHTO. LRFD Bridge Design Specifications; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).