Spatial and Temporal Analysis of Drought Forecasting on Rivers of South India
Abstract
:1. Introduction
2. Methodology
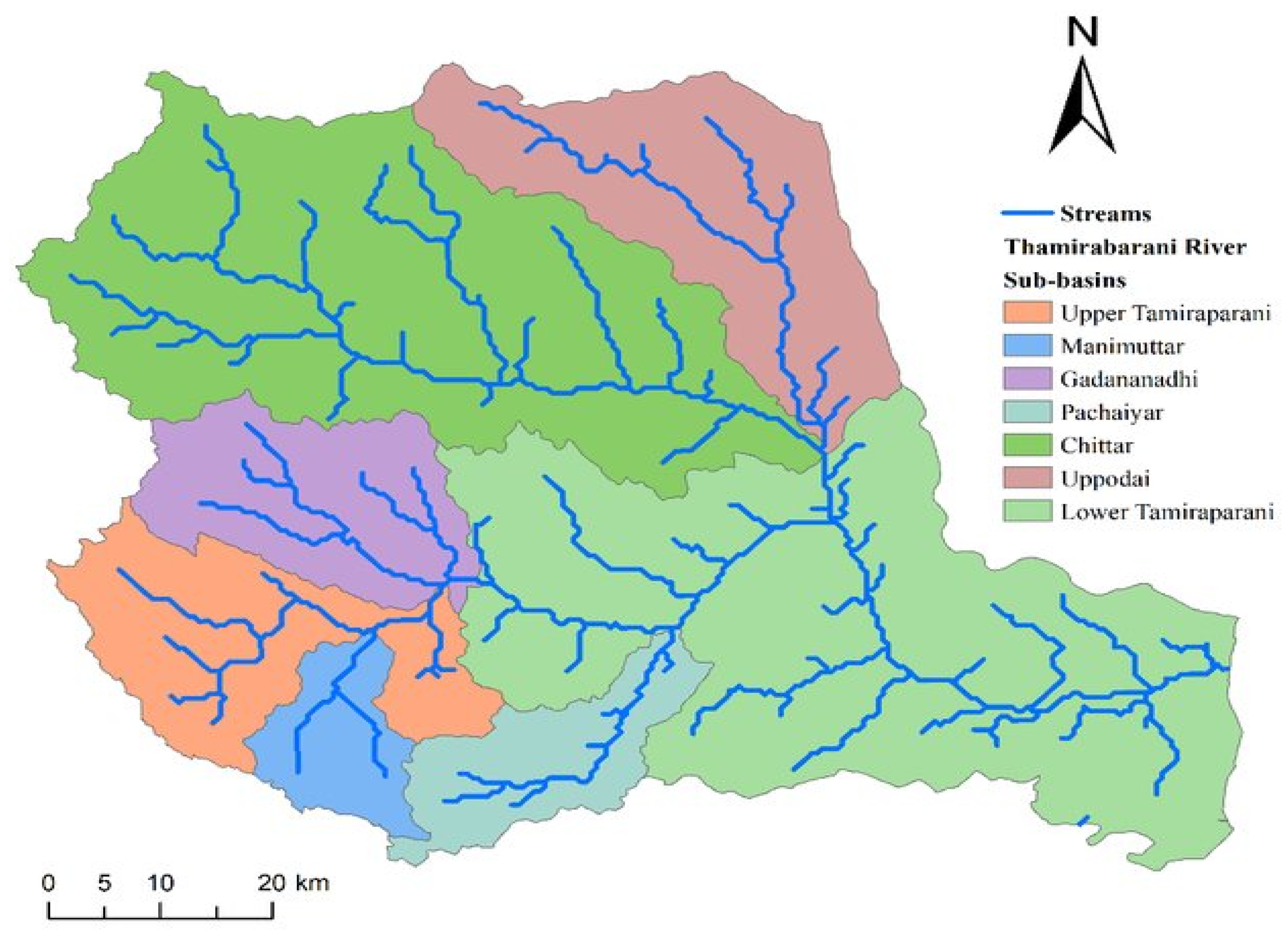
2.1. Study Area
2.2. Data Collected
2.2.1. Meteorological Data
2.2.2. Hydraulic and Hydrological Data
2.2.3. Agricultural Data
3. Fuzzy Rule-Based Drought Forecasting
Estimation of the Standardized Precipitation Index
4. Results and Discussion
4.1. Meteorological Drought Risk Index
4.2. Drought Forecasting Using Fuzzy Logic
4.2.1. Analysis of SPI for Drought Forecasting
4.2.2. Drought Forecasting
4.2.3. Performance of Fuzzy-Based Drought Forecasting
4.2.4. Defuzzification of the Forecasted Ranks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nagarajan, R. Drought Assessment; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Haied, N.; Foufou, A.; Chaab, S.; Azlaoui, M.; Khadri, S.; Benzahia, K.; Benzahia, I. Drought assessment and monitoring using meteorological indices in a semi-arid region. Energy Procedia 2017, 119, 518–529. [Google Scholar] [CrossRef]
- Dutta, D.; Kundu, A.; Patel, N.R.; Saha, S.K.; Siddiqui, A.R. Assessment of agricultural drought in Rajasthan (India) using remote sensing derived Vegetation Condition Index (VCI) and Standardized Precipitation Index (SPI). Egypt. J. Remote Sens. Space Sci. 2015, 18, 53–63. [Google Scholar] [CrossRef]
- Bhunia, P.; Das, P.; Maiti, R. Meteorological drought study through SPI in three drought prone districts of West Bengal, India. Earth Syst. Environ. 2020, 4, 43–55. [Google Scholar] [CrossRef]
- Ekundayo, O.Y.; Abiodun, B.J.; Kalumba, A.M. Global quantitative and qualitative assessment of drought research from 1861 to 2019. Int. J. Disaster Risk Reduct. 2022, 70, 102770. [Google Scholar] [CrossRef]
- Lakshmi, S.V.; Ramalakshmi, M.; Rakshith, R.K.; Christobel, M.J.; Kumar, P.P.; Priyadharshini, B.; Kumar, P.R. An integration of geospatial technology and standard precipitation index (SPI) for drought vulnerability assessment for a part of Namakkal district, South India. Mater. Today Proc. 2020, 33, 1206–1211. [Google Scholar] [CrossRef]
- Pai, D.S.; Sridhar, L.; Guhathakurta, P.; Hatwar, H.R. District-wide drought climatology of the southwest monsoon season over India based on standardized precipitation index (SPI). Nat. Hazards 2011, 59, 1797–1813. [Google Scholar] [CrossRef]
- Dhangar, N.; Vyas, S.; Guhathakurta, P.; Mukim, S.; Tidke, N.; Balasubramanian, R.; Chattopadhyay, N. Drought monitoring over India using multi-scalar standardized precipitation evapotranspiration index. Mausam 2019, 70, 833–840. [Google Scholar] [CrossRef]
- Halide, H.; Ridd, P. Modelling coral bleaching events using a fuzzy logic technique. In Fuzzy Logic; Physica: Heidelberg, Germany, 2002; pp. 352–362. [Google Scholar]
- Wong, K.W.; Wong, P.M.; Gedeon, T.D.; Fung, C.C. Rainfall prediction model using soft computing technique. Soft Comput. 2003, 7, 434–438. [Google Scholar] [CrossRef]
- Karamouz, M.; Kerachian, R.; Zahraie, B. Monthly water resources and irrigation planning: Case study of conjunctive use of surface and groundwater resources. J. Irrig. Drain. Eng. 2004, 130, 391–402. [Google Scholar] [CrossRef]
- Annas, S.; Kanai, T.; Koyama, S. Neuro-fuzzy approaches for modeling the wet season tropical rainfall. Agric. Inf. Res. 2006, 15, 331–341. [Google Scholar] [CrossRef]
- Subramanian, C.; Manry, M.T.; Naccarino, J. Reservoir inflow forecasting using neural networks. In Proceedings of the American Power Conference, Chicago, IL, USA, 6–8 April 1999; Volume 61, pp. 220–225. Available online: https://www.researchgate.net/profile/Michael-Manry/publication/2311940_Reservoir_Inflow_Forecasting_Using_Neural_Networks/links/0912f50bfb6f172b7b000000/Reservoir-Inflow-Forecasting-Using-Neural-Networks.pdf (accessed on 22 March 2023).
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; Volume 30.
- St George, S.; Meko, D.M.; Cook, E.R. The seasonality of precipitation signals embedded within the North American Drought Atlas. Holocene 2010, 20, 983–988. [Google Scholar] [CrossRef]
- Shewale, M.P.; Kumar, S. Climatological features of drought incidences in India. In Meteorological Monograph (Climatology 21/2005); National Climate Centre, Indian Meteorological Department: Delhi, India, 2005. [Google Scholar]
- Ravikumar, G. Multi Criteria Analysis for Drought Assessment Using Remote Sensing and GIS. 2017, Anna University, India. Available online: https://shodhganga.inflibnet.ac.in/handle/10603/10086 (accessed on 23 March 2023).
- Ray, K.S.; Shewale, M.P. Probability of occurrence of drought in various sub-divisions of India. Mausam 2001, 52, 541–546. [Google Scholar] [CrossRef]
- Herbst, P.H.; Bredenkamp, D.; Barker, H.M.G. A technique for the evaluation of drought from rainfall data. J. Hydrol. 1966, 4, 264–272. [Google Scholar] [CrossRef]
- Chow, V.T. Handbook of Applied Hydrology; McGraw Hill: New York, NY, USA, 1959. [Google Scholar]
- Mohan, S.; Rangacharya, N.C.V. A modified method for drought identification. Hydrol. Sci. J. 1991, 36, 11–21. [Google Scholar] [CrossRef]
- Yevjevich, V.M. Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts. Doctoral Dissertation, Colorado State University, Fort Collins, CO, USA, 1967. [Google Scholar]
- Beersma, J.J.; Buishand, T.A. Drought in The Netherlands—Regional frequency analysis versus time series simulation. J. Hydrol. 2007, 347, 332–346. [Google Scholar] [CrossRef]
- Pongracz, R.; Bogardi, I.; Duckstein, L. Application of fuzzy rule-based modeling technique to regional drought. J. Hydrol. 1999, 224, 100–114. [Google Scholar] [CrossRef]
- Ross, T.J. Fuzzy Logic with Engineering Applications; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Paulo, A.A.; Ferreira, E.; Coelho, C.; Pereira, L.S. Drought class transition analysis through Markov and Loglinear models, an approach to early warning. Agric. Water Manag. 2005, 77, 59–81. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Rouault, M.; Richard, Y. Intensity and spatial extension of drought in South Africa at different time scales. Water SA 2003, 29, 489–500. [Google Scholar] [CrossRef]
- Wu, H.; Hayes, M.J.; Wilhite, D.A.; Svoboda, M.D. The effect of the length of record on the standardized precipitation index calculation. Int. J. Climatol. J. R. Meteorol. Soc. 2005, 25, 505–520. [Google Scholar] [CrossRef]







| S. No. | SPI Values | Drought Category |
|---|---|---|
| 1 | 2 and above | Extremely wet |
| 2 | 1.5–1.99 | Very wet |
| 3 | 1.0–1.49 | Moderately wet |
| 4 | −0.99–0.99 | Normal |
| 5 | −1.0 to −1.49 | Moderately dry |
| 6 | −1.5 to −1.99 | Severe dry |
| 7 | −2.0 or less | Extreme dry |
| Sr. No | Name of Station | Year Wise Drought Severity | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1971 | 1972 | 1973 | 1974 | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 | 1983 | 1984 | 1985 | ||
| 1 | Sivagiri | M1 | M0 | M0 | M2 | M3 | M1 | M0 | M1 | M0 | M0 | M3 | M3 | M2 | M0 | M0 |
| 2 | Gadana dam | M3 | M0 | M0 | M3 | M2 | M2 | M0 | M1 | M0 | M2 | M1 | M1 | M1 | M0 | M0 |
| 3 | Kannadian anicut | M0 | M1 | M0 | M2 | M2 | M1 | M0 | M0 | M0 | M1 | M1 | M1 | M2 | M0 | M1 |
| 4 | Papanasam | M3 | M3 | M3 | M3 | M3 | M3 | M3 | M3 | M3 | M1 | M1 | M1 | M1 | M0 | M1 |
| 5 | Dam Camp | M3 | M3 | M3 | M3 | M3 | M3 | M3 | M3 | M3 | M0 | M0 | M1 | M0 | M0 | M0 |
| 6 | Ambasamudram | M1 | M2 | M0 | M2 | M3 | M2 | M0 | M0 | M0 | M2 | M1 | M3 | M2 | M0 | M0 |
| 7 | Manimuttar | M0 | M0 | M0 | M2 | M2 | M1 | M0 | M1 | M0 | M1 | M1 | M2 | M2 | M0 | M2 |
| 8 | Cheranmadevi | M3 | M3 | M1 | M3 | M3 | M2 | M0 | M2 | M0 | M2 | M2 | M2 | M2 | M0 | M0 |
| 9 | Nanguneri | M0 | M0 | M0 | M2 | M2 | M1 | M0 | M0 | M0 | M1 | M2 | M1 | M2 | M0 | M2 |
| 10 | Radhapuram | M0 | M2 | M0 | M3 | M2 | M1 | M0 | M0 | M0 | M0 | M2 | M3 | M2 | M1 | M2 |
| 11 | Nilaparai | M0 | M1 | M1 | M2 | M0 | M0 | M0 | M1 | M0 | M0 | M0 | ||||
| 12 | Thirunelveli | M0 | M0 | M0 | M0 | M3 | M1 | M1 | M2 | M0 | M3 | M2 | M1 | M2 | M0 | M0 |
| 13 | Palayankottai | M0 | M0 | M0 | M3 | M3 | M0 | M0 | M1 | M0 | M0 | M1 | M1 | M2 | M0 | M0 |
| 14 | Senkottai | M2 | M2 | M0 | M0 | M0 | M2 | M0 | M1 | M0 | M2 | M1 | M2 | M2 | M0 | M1 |
| 15 | Tenkasi | M0 | M0 | M0 | M1 | M1 | M2 | M0 | M0 | M0 | M1 | M2 | M0 | M1 | M0 | M1 |
| 16 | Karuppanadhi anicut | M0 | M0 | M0 | M0 | M2 | M0 | M2 | M1 | M1 | ||||||
| 17 | Ayikudi | M1 | M0 | M0 | M2 | M1 | M1 | M0 | M0 | M0 | M1 | M2 | M0 | M0 | M0 | M0 |
| 18 | Kadauanallur | M0 | M0 | M0 | M3 | M3 | M2 | M0 | M0 | M0 | M0 | M2 | M0 | M2 | M2 | M1 |
| 19 | Sankarankovil | M0 | M0 | M0 | M2 | M3 | M0 | M0 | M2 | M0 | M0 | M1 | M0 | M1 | M1 | M2 |
| 20 | Kovilpatti | M0 | M0 | M0 | M3 | M1 | M1 | M0 | M1 | M0 | M2 | M2 | M1 | M0 | M0 | M1 |
| 21 | Kayattar | M1 | M2 | M0 | M1 | M1 | M3 | M2 | M1 | M1 | M3 | M1 | M3 | M3 | M3 | M2 |
| 22 | Otappidaram | M0 | M0 | M0 | M3 | M2 | M1 | M0 | M2 | M0 | M1 | M1 | M2 | M0 | M0 | M1 |
| 23 | Thoothukudi | M0 | M0 | M0 | M3 | M3 | M0 | M0 | M0 | M0 | M1 | M2 | M0 | M1 | M0 | M0 |
| 24 | Srivaikuntam | M0 | M0 | M1 | M3 | M2 | M0 | M0 | M0 | M0 | M0 | M0 | M1 | M2 | M0 | M0 |
| 25 | Santtankulam | M0 | M0 | M0 | M3 | M3 | M1 | M0 | M0 | M0 | M1 | M2 | M1 | M2 | M0 | M0 |
| 26 | Tiruchendur | M0 | M0 | M0 | M2 | M2 | M1 | M0 | M0 | M1 | M1 | M1 | M0 | M3 | M0 | M0 |
| S. No. | Range | Drought Severity |
|---|---|---|
| 1 | 1.0–1.41 | Very mild |
| 2 | 1.41–1.82 | Mild |
| 3 | 1.82–2.23 | Moderate |
| 4 | 2.23–2.64 | Severe |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaikh, A.; Sharma, K.V.; Kumar, V.; Singh, K. Spatial and Temporal Analysis of Drought Forecasting on Rivers of South India. Urban Sci. 2023, 7, 88. https://doi.org/10.3390/urbansci7030088
Shaikh A, Sharma KV, Kumar V, Singh K. Spatial and Temporal Analysis of Drought Forecasting on Rivers of South India. Urban Science. 2023; 7(3):88. https://doi.org/10.3390/urbansci7030088
Chicago/Turabian StyleShaikh, Ayub, Kul Vaibhav Sharma, Vijendra Kumar, and Karan Singh. 2023. "Spatial and Temporal Analysis of Drought Forecasting on Rivers of South India" Urban Science 7, no. 3: 88. https://doi.org/10.3390/urbansci7030088
APA StyleShaikh, A., Sharma, K. V., Kumar, V., & Singh, K. (2023). Spatial and Temporal Analysis of Drought Forecasting on Rivers of South India. Urban Science, 7(3), 88. https://doi.org/10.3390/urbansci7030088







