A Numerical Study of Nonlinear Fractional Order Partial Integro-Differential Equation with a Weakly Singular Kernel
Abstract
:1. Introduction
2. Preliminaries
Temporal Approximation
- and as
- for
3. Derivation of the Procedure
4. Stability and Convergence Analysis
5. Numerical Implementation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atangana, A.; Secer, A. A Note on Fractional Order Derivatives and Table of Fractional Derivatives of Some Special Functions. Abstr. Appl. Anal. 2013, 2013, 279681. [Google Scholar] [CrossRef] [Green Version]
- Noeiaghdam, S.; Dreglea, A.; Iįk, H.; Suleman, M. A Comparative Study between Discrete Stochastic Arithmetic and Floating-Point Arithmetic to Validate the Results of Fractional Order Model of Malaria Infection. Mathematics 2021, 9, 1435. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Micula, S.; Nieto, J. A Novel Technique to Control the Accuracy of a Nonlinear Fractional Order Model of COVID-19: Application of the CESTAC Method and the CADNA Library. Mathematics 2021, 9, 1321. [Google Scholar] [CrossRef]
- Ali, Z.; Nia, S.N.; Rabiei, F.; Shah, K.; Tan, M.K. A Semianalytical Approach to the Solution of Time-Fractional Navier-Stokes Equation. Adv. Math. Phys. 2021, 2021, 13. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Zaslavsky, G.M. Hamiltonian Chaos and Fractional Dynamics; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Gurtin, M.E.; Pipkin, A.C. A general theory of heat conduction with finite wave speeds. Arch. Ration. Mech. Anal. 1968, 31, 113–126. [Google Scholar] [CrossRef]
- Pao, C.V.; Payne, L.; Amann, H. Bifurcation analysis of a nonlinear diffusion system in reactor dynamics. Appl. Anal. 2007, 9, 107–119. [Google Scholar] [CrossRef]
- Zadeh, K.S. An integro-partial differential equation for modeling biofluids flow in fractured biomaterials. J. Theor. Biol. 2011, 273, 72–79. [Google Scholar] [CrossRef]
- Hepperger, P. Hedging electricity swaptions using partial integro-differential equations. Stoch. Process. Their Appl. 2012, 122, 600–622. [Google Scholar] [CrossRef] [Green Version]
- Larsson, S.; Racheva, M.; Saedpanah, F. Discontinuous Galerkin method for an integro-differential equation modeling dynamic fractional order viscoelasticity. Comput. Methods Appl. Mech. Eng. 2015, 283, 196–209. [Google Scholar] [CrossRef] [Green Version]
- Mirzaee, F.; Alipour, S. A hybrid approach of nonlinear partial mixed integro-differential equations of fractional order. Iran. J. Sci. Technol. Trans. Sci. 2020, 44, 725–737. [Google Scholar] [CrossRef]
- Ng, F.S. Statistical mechanics of normal grain growth in one dimension: A partial integro-differential equation model. Acta Mater. 2016, 120, 453–462. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Xu, D.; Qiu, W. A finite difference scheme for the nonlinear time-fractional partial integro-differential equation. Math. Methods Appl. Sci. 2020, 43, 1–21. [Google Scholar] [CrossRef]
- Hu, L.; Ren, Y.; Sakthivel, R. Existence and uniqueness of mild solutions for semilinear integro-differential equations of fractional order with nonlocal conditions. Semigroup Forum 2009, 79, 507–514. [Google Scholar] [CrossRef]
- Li, F.; Liang, J.; Xu, H.K. Existence of mild solutions for fractional integro-differential equations of Sobolev type with nonlocal conditions. J. Math. Anal. Appl. 2012, 391, 510–525. [Google Scholar] [CrossRef] [Green Version]
- Karthikeyan, K.; Trujillo, J.J. Existence and uniqueness results for fractional integrodifferential equations with boundary value conditions. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4037–4043. [Google Scholar] [CrossRef]
- Chuong, N.M.; Ke, T.D.; Quan, N.N. Stability for a class of fractional partial integro-differential equations. J. Integral Equ. Appl. 2014, 26, 145–170. [Google Scholar] [CrossRef]
- Jaradat, H.; Awawdeh, F.; Rawashdeh, E.A. Analytic solution of fractional integro-differential equations. Ann. Univ. Craiova 2011, 38, 1–10. [Google Scholar]
- Hussain, A.K.; Rusli, N.; Fadhel, F.S.; Yahya, Z.R. Solution of one-dimensional fractional order partial integro-differential equations using variational iteration method. Aip Conf. Proc. 2016, 1775, 030096. [Google Scholar]
- Mittal, R.C.; Nigam, R. Solution of fractional integro-differential equations by Adomian decomposition method. Int. J. Appl. Math. Mech. 2008, 4, 87–94. [Google Scholar]
- Rawashdeh, E. Numerical solution of fractional integro-differential equations by collocation method. Appl. Math. Comput. 2006, 176, 1–6. [Google Scholar] [CrossRef]
- Eslahchi, M.R.; Dehghan, M.; Parvizi, M. Application of the collocation method for solving nonlinear fractional integro-differential equations. J. Comput. Appl. Math. 2014, 257, 105–128. [Google Scholar] [CrossRef]
- Zhao, J.; Xiao, J.; Ford, N.J. Collocation methods for fractional integro-differential equations with weakly singular kernels. Numer. Algor. 2014, 65, 723–743. [Google Scholar] [CrossRef]
- Arshed, S. B-Spline solution of fractional integro partial differential equation with a weakly singular kernel. Numer. Methods Partial. Differ. Equ. 2017, 33, 1565–1581. [Google Scholar] [CrossRef]
- Unhale, S.I.; Kendre, S.D. Numerical solution of nonlinear fractional integro-differential equation by Collocation method. Malaya J. Mat. 2018, 6, 73–79. [Google Scholar] [CrossRef] [Green Version]
- Avazzadeh, Z.; Heydari, M.H.; Cattani, C. Legendre wavelets for fractional partial integro-differential viscoelastic equations with weakly singular kernels. Eur. Phys. J. Plus 2019, 134, 368. [Google Scholar] [CrossRef]
- Dehestani, H.; Ordokhani, Y.; Razzaghi, M. Numerical solution of variable-order time fractional weakly singular partial integro-differential equations with error estimation. Math. Model. Anal. 2020, 25, 680–701. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Akram, T.; Abbas, M.; Ismail, A.I.; Ali, N.M. A fully implicit finite difference scheme based on extended cubic B-splines for time fractional advection-diffusion equation. Adv. Differ. Equ. 2018, 2018, 109. [Google Scholar] [CrossRef] [Green Version]
- Akram, T.; Abbas, M.; Ismail, A.I. An extended cubic B-spline collocation scheme for time fractional sub-diffusion equation. Aip Conf. Proc. 2019, 2184, 060017. [Google Scholar]
- Akram, T.; Abbas, M.; Ismail, A.I. Numerical solution of fractional cable equation via extended cubic B-spline. Aip Conf. Proc. 2019, 2138, 030004. [Google Scholar]
- Yaseen, M.; Abbas, M. An efficient computational technique based on cubic trigonometric B-splines for time fractional Burger’s equation. Int. J. Comput Math. 2019, 97, 725–738. [Google Scholar] [CrossRef] [Green Version]
- Jafari, H.; Khalique, M.; Ramezani, M.; Tajadodi, H. Numerical solution of fractional differential equations by using fractional B-spline. Cent. Eur. J. Phys. 2013, 11, 1372–1378. [Google Scholar] [CrossRef] [Green Version]
- Akram, T.; Abbas, M.; Ali, A.; Iqbal, A.; Baleanu, D. A Numerical Approach of a Time Fractional Reaction- Diffusion Model with a Non-Singular Kernel. Symmetry 2020, 12, 1653. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Ismail, A.I.; Ali, N.M.; Baleanu, D. Extended cubic B-splines in the numerical solution of time fractional telegraph equation. Adv. Differ. Equ. 2019, 2019, 365. [Google Scholar] [CrossRef] [Green Version]
- Akram, T.; Abbas, M.; Iqbal, A.; Baleanu, D.; Asad, J. Novel Numerical Approach Based on Modified Extended Cubic B-Spline Functions for Solving Non-Linear Time-Fractional Telegraph Equation. Symmetry 2020, 12, 1154. [Google Scholar] [CrossRef]
- Han, L.X.; Liu, S.J. An extension of the cubic uniform B-spline curves. J. Comput Aided Des. Comput. Graph. 2003, 15, 576–578. [Google Scholar]
- Akram, T.; Abbas, M.; Riaz, M.B.; Ismail, A.I.; Ali, N.M. An efficient numerical technique for solving time fractional Burgers equation. Alex. Eng. J. 2020, 59, 2201–2220. [Google Scholar] [CrossRef]
- Rubin, S.G.; Graves, R.A. A Cubic Spline Approximation for Problems in Fluid Mechanics; NASA Technical Report; U.S. National Aeronautics and Space Administration: Washington, DC, USA, 1975; Available online: https://books.google.com.my/books?id=tzbGKg7dV-IC (accessed on 2 August 2021).
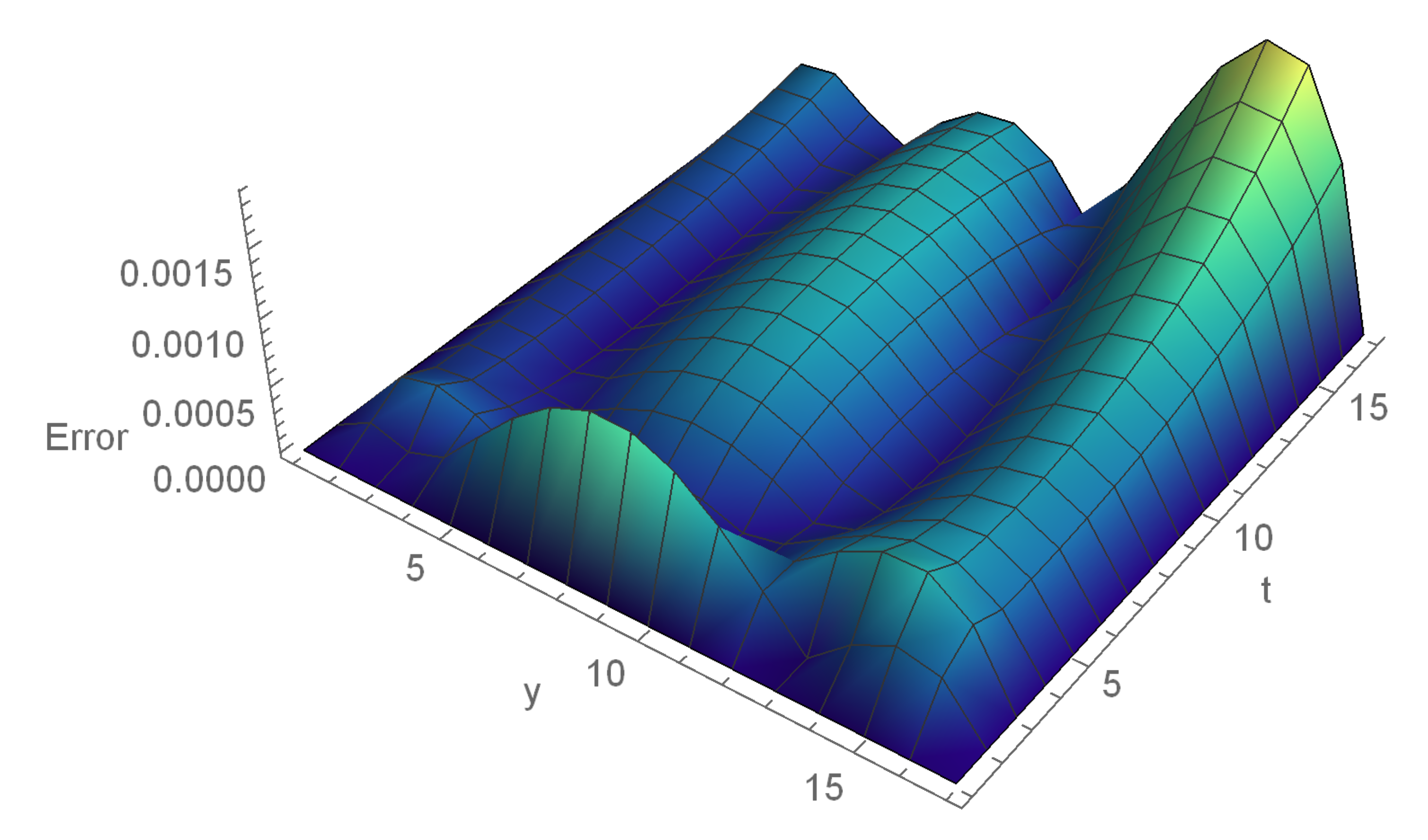
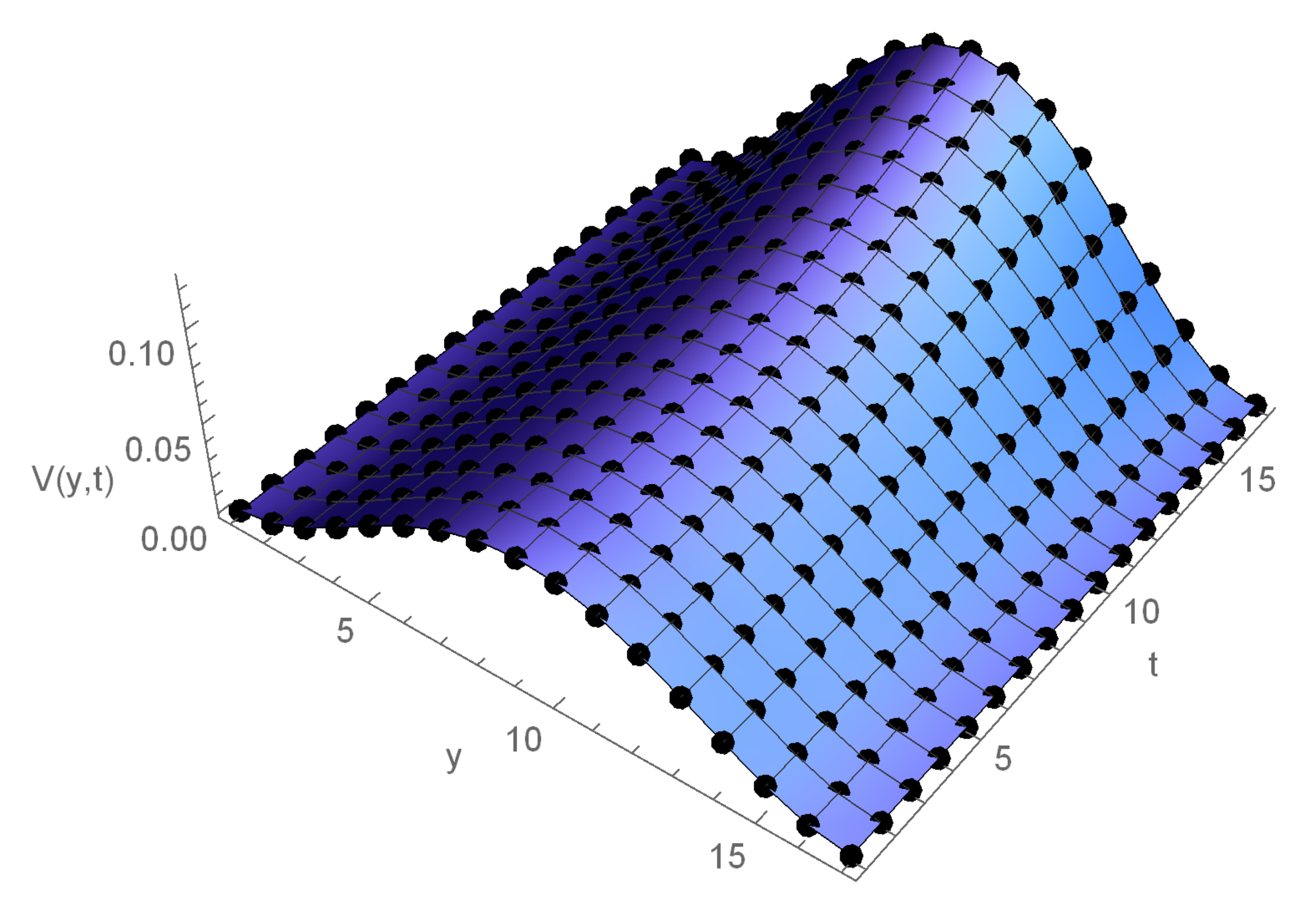


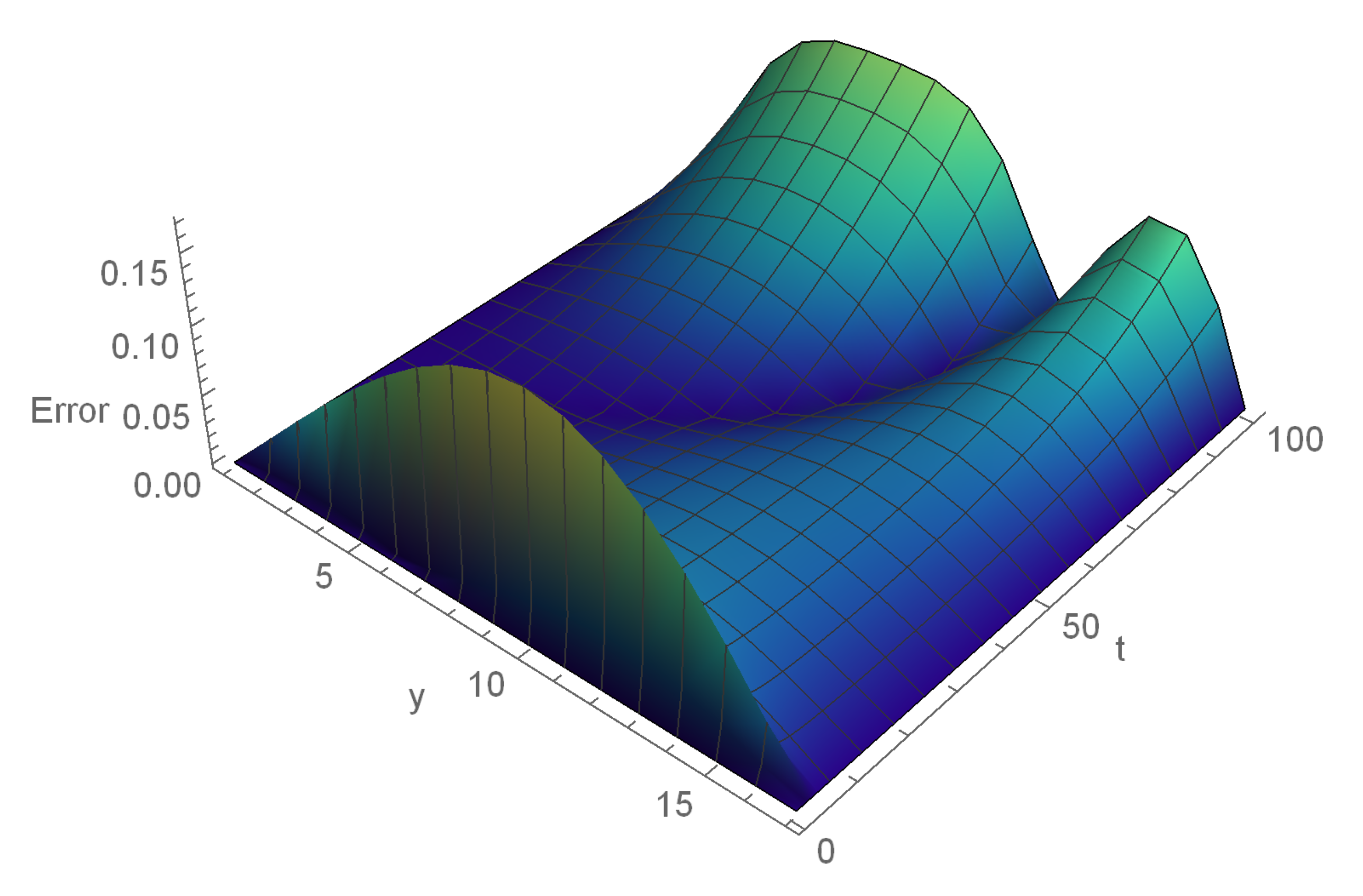
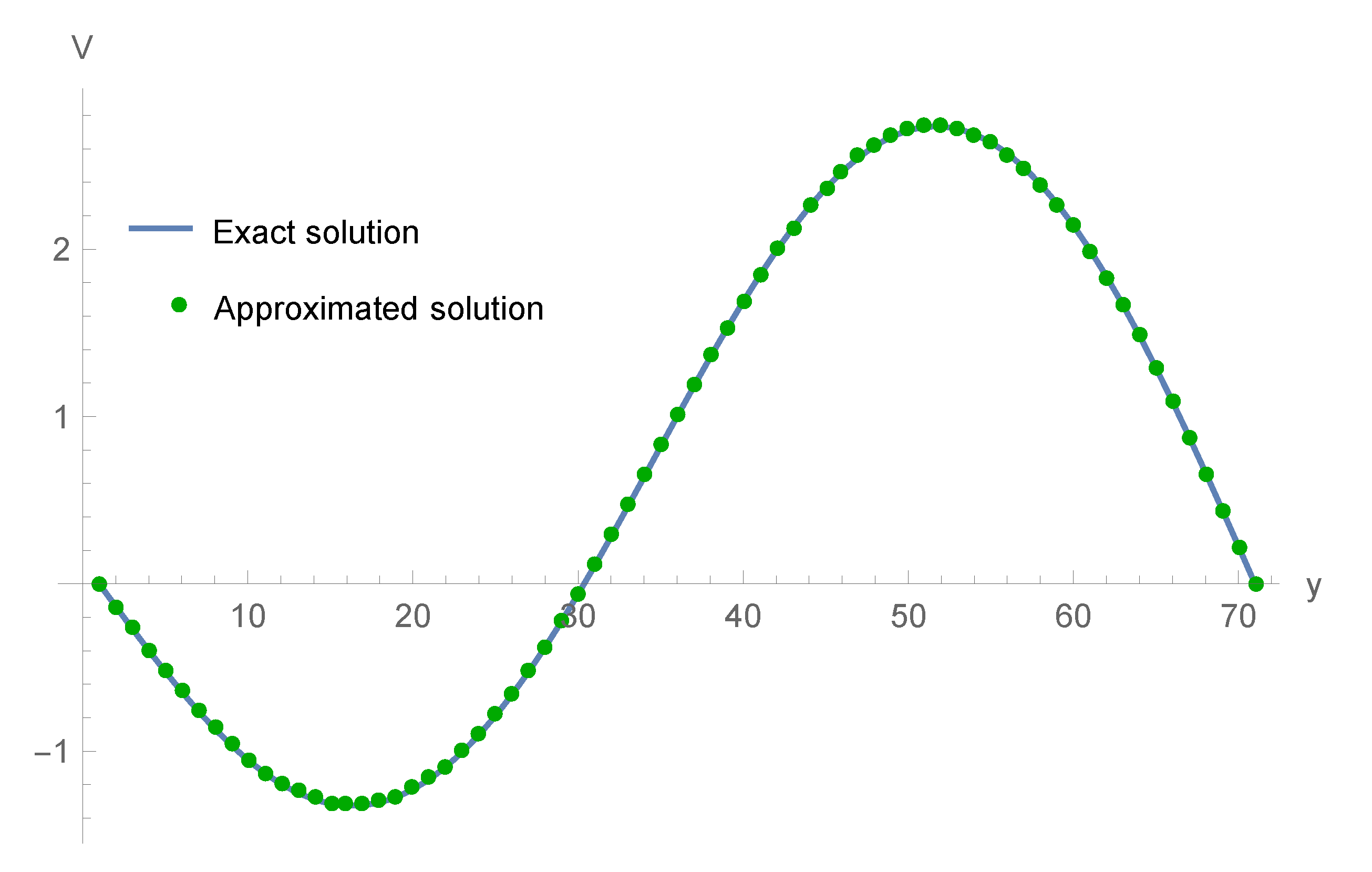
| ECBS | |||||
|---|---|---|---|---|---|
| [16] | Order | ||||
| 0.25 | 1/4 | 0.000338928 | 0.000102331 | 0.005061940 | … |
| 0.25 | 1/8 | 0.000095387 | 0.000031934 | 0.001507530 | 1.74750 |
| 0.25 | 1/16 | 0.000026007 | 0.000008542 | 0.000445685 | 1.75809 |
| 0.25 | 1/32 | 0.000006788 | 0.000001882 | 0.000133631 | 1.73777 |
| 0.5 | 1/4 | 0.000336809 | 0.000102183 | 0.00505510 | … |
| 0.5 | 1/8 | 0.000050628 | 0.000031976 | 0.00151014 | 1.74750 |
| 0.5 | 1/16 | 0.000025630 | 0.000008178 | 0.00045565 | 1.72618 |
| 0.5 | 1/32 | 0.000006784 | 0.000001955 | 0.00013491 | 1.75595 |
| h | ECBS | ||||
|---|---|---|---|---|---|
| [16] | Order | ||||
| 0.5 | 1/4 | 0.0223389 | 0.01822370 | 0.0549348 | … |
| 0.5 | 1/8 | 0.0055991 | 0.00345180 | 0.0136426 | 2.00960 |
| 0.5 | 1/16 | 0.0014002 | 0.00078340 | 0.0033125 | 2.04213 |
| 0.5 | 1/32 | 0.0003501 | 0.00002505 | 0.00080164 | 2.04690 |
| y | ||||
|---|---|---|---|---|
| 0.1 | 0.0002278 | 0.0002393 | 0.0002611 | 0.0000426 |
| 0.2 | 0.0018783 | 0.0019005 | 0.0019430 | 0.0011812 |
| 0.3 | 0.0035717 | 0.0036034 | 0.0036639 | 0.0023206 |
| 0.4 | 0.0042866 | 0.0043257 | 0.0043997 | 0.0026410 |
| 0.5 | 0.0034757 | 0.0035196 | 0.0036008 | 0.0017125 |
| 0.6 | 0.0011975 | 0.0012421 | 0.0013230 | 0.0003752 |
| 0.7 | 0.0017931 | 0.0017525 | 0.0016805 | 0.0029206 |
| 0.8 | 0.0040788 | 0.0040474 | 0.0039930 | 0.0046428 |
| 0.9 | 0.0038964 | 0.0038792 | 0.0038497 | 0.0039922 |
| [16] | Order | |||
|---|---|---|---|---|
| 0.5 | 1/4 | 0.0177409 | 0.0130166 | … |
| 0.5 | 1/8 | 0.0051229 | 0.0050567 | 1.489999 |
| 0.5 | 1/16 | 0.0014272 | 0.0011256 | 1.495493 |
| 0.5 | 1/32 | 0.0003866 | 0.0003048 | 1.497291 |
| h | [16] | Order | ||
|---|---|---|---|---|
| 0.5 | 1/4 | 0.3295713 | 0.2219332 | … |
| 0.5 | 1/8 | 0.0750875 | 0.0456438 | 1.489999 |
| 0.5 | 1/16 | 0.0183464 | 0.0058752 | 1.495493 |
| 0.5 | 1/32 | 0.0045605 | 0.0006886 | 1.497291 |
| y | ||||
|---|---|---|---|---|
| 0.1 | 0.0237447 | 0.0216525 | 0.0224432 | 0.0224217 |
| 0.2 | 0.0364358 | 0.0332549 | 0.0344475 | 0.0344188 |
| 0.3 | 0.0390615 | 0.0364304 | 0.0373676 | 0.0373676 |
| 0.4 | 0.0391821 | 0.0387213 | 0.0388031 | 0.0388078 |
| 0.5 | 0.0363214 | 0.0389181 | 0.0377829 | 0.0378141 |
| 0.6 | 0.0214206 | 0.0267798 | 0.0245592 | 0.0246163 |
| 0.7 | 0.0062788 | 0.0004300 | 0.0256691 | 0.0022242 |
| 0.8 | 0.0292914 | 0.0232263 | 0.0039930 | 0.0255941 |
| 0.9 | 0.0270044 | 0.0234284 | 0.0248600 | 0.0248123 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akram, T.; Ali, Z.; Rabiei, F.; Shah, K.; Kumam, P. A Numerical Study of Nonlinear Fractional Order Partial Integro-Differential Equation with a Weakly Singular Kernel. Fractal Fract. 2021, 5, 85. https://doi.org/10.3390/fractalfract5030085
Akram T, Ali Z, Rabiei F, Shah K, Kumam P. A Numerical Study of Nonlinear Fractional Order Partial Integro-Differential Equation with a Weakly Singular Kernel. Fractal and Fractional. 2021; 5(3):85. https://doi.org/10.3390/fractalfract5030085
Chicago/Turabian StyleAkram, Tayyaba, Zeeshan Ali, Faranak Rabiei, Kamal Shah, and Poom Kumam. 2021. "A Numerical Study of Nonlinear Fractional Order Partial Integro-Differential Equation with a Weakly Singular Kernel" Fractal and Fractional 5, no. 3: 85. https://doi.org/10.3390/fractalfract5030085
APA StyleAkram, T., Ali, Z., Rabiei, F., Shah, K., & Kumam, P. (2021). A Numerical Study of Nonlinear Fractional Order Partial Integro-Differential Equation with a Weakly Singular Kernel. Fractal and Fractional, 5(3), 85. https://doi.org/10.3390/fractalfract5030085








