Parametric Family of Root-Finding Iterative Methods: Fractals of the Basins of Attraction
Abstract
1. Introduction
2. Convergence Analysis
3. Stability Analysis
- Attractive if .
- Parabolic or Neutral if .
- Repulsive if .
- Superattractive if .
- (a)
- If , then .
- (b)
- Except for some specific values of the simplifying the operator, is an strange fixed point of rational operator .
- (c)
- The stability function of two conjugate fixed points coincide,
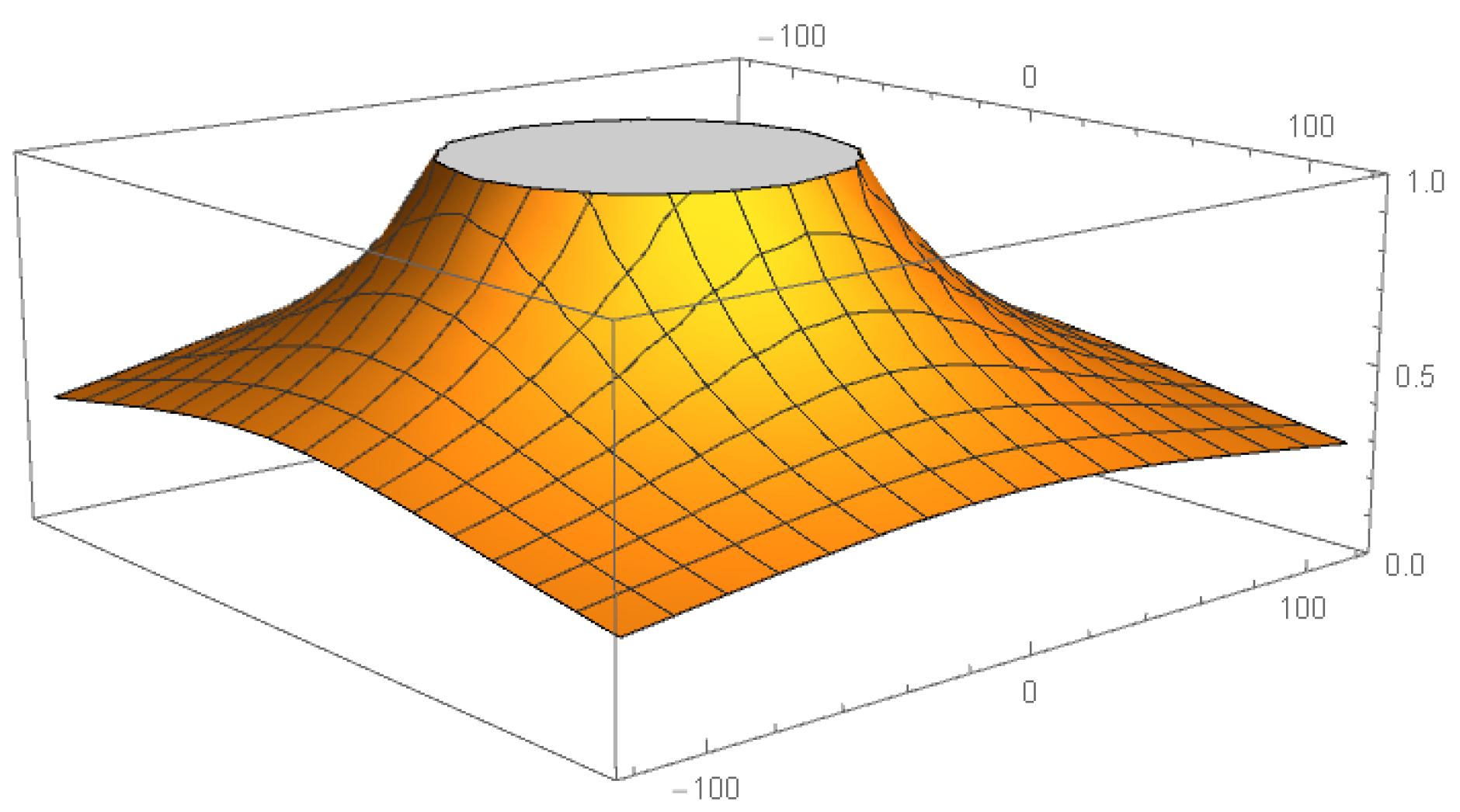
3.1. Performance of the Strange Fixed Points
- andare conjugate and repulsive, with independence of the value of parameter α.
- andare attractors for values of α in small regions of the complex plane, inside the complex areaand. Moreover, both are superattracting for.
- andare conjugate and attractors for values of α inside the complex area. Moreover, both are superattracting for.
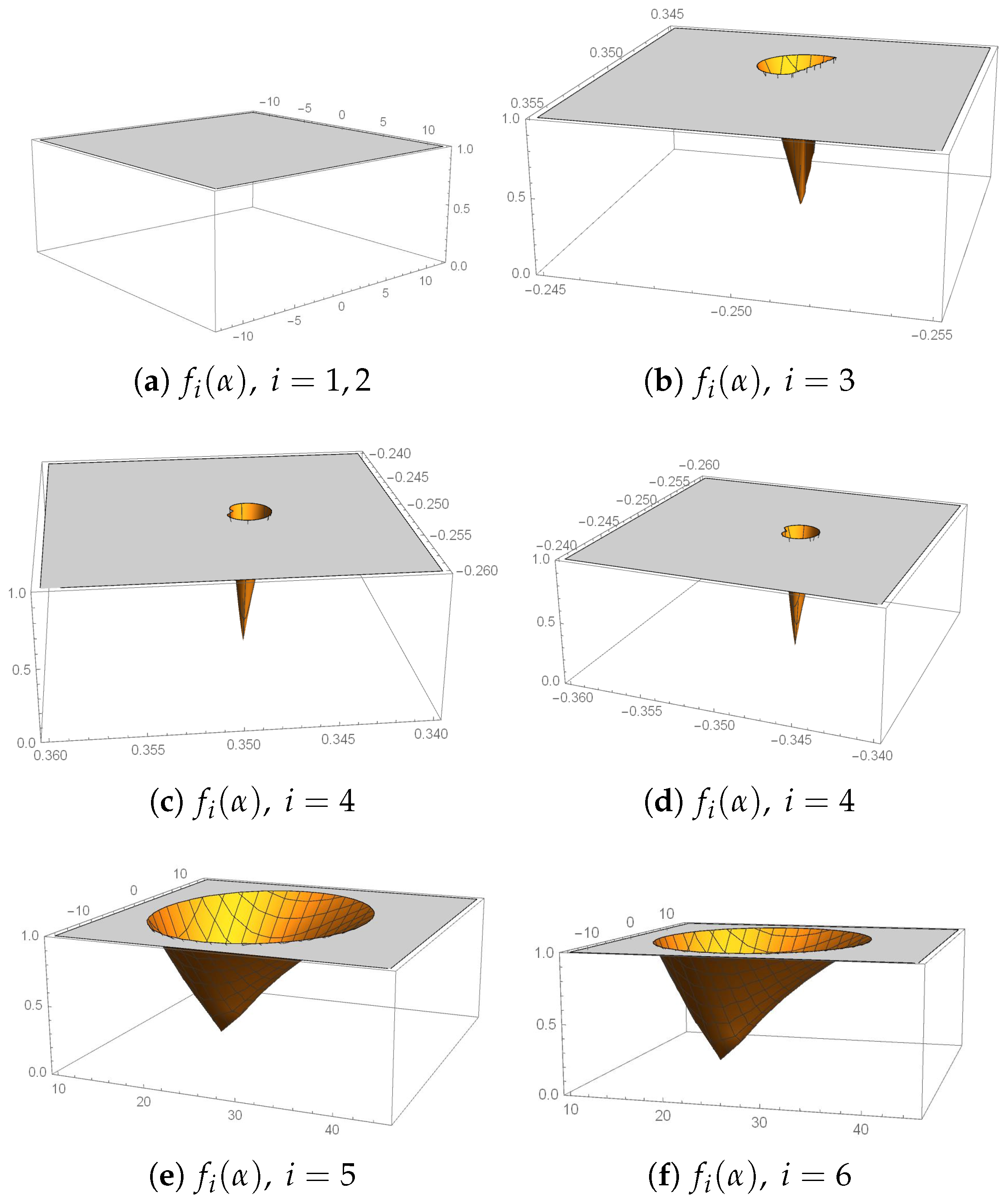
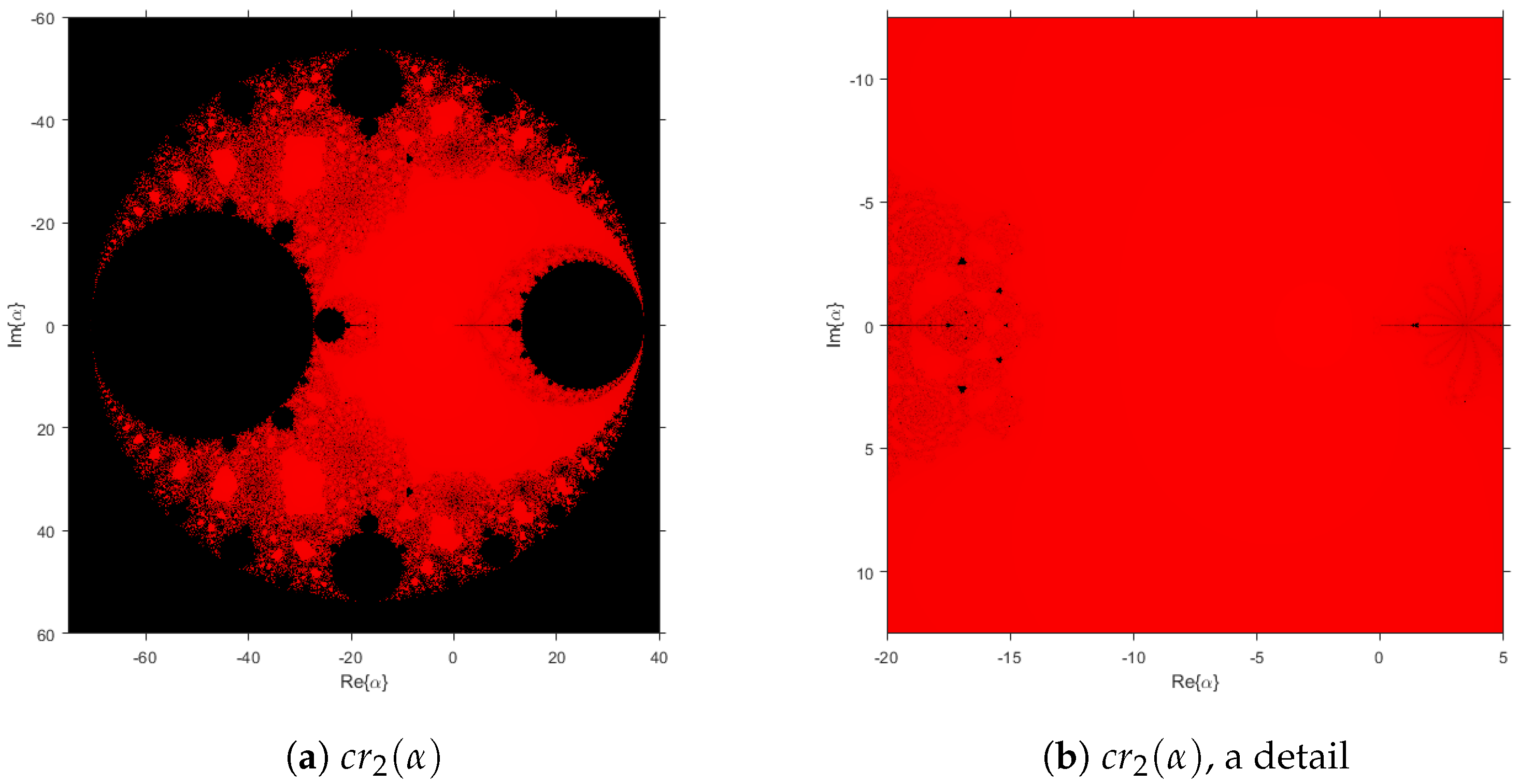
3.2. Critical Points and Parameter Planes
- One, ifor. In these cases, the reduced rational operator is:whose only free critical point is, that is a pre-image of.
- Three, ifand, as in this case, they are defined as:
- (a)
- If , then , and it is a pre-image of the fixed point : . As is repulsive for , . Thus, has only two invariant Fatou components, and .
- (b)
- If , then , and . As is not a fixed point when , then and its orbit will remain at Julia set until the rounding error makes it fall into the basin of attraction of or .
- (c)
- For the rest of the values of , we gave three critical points.
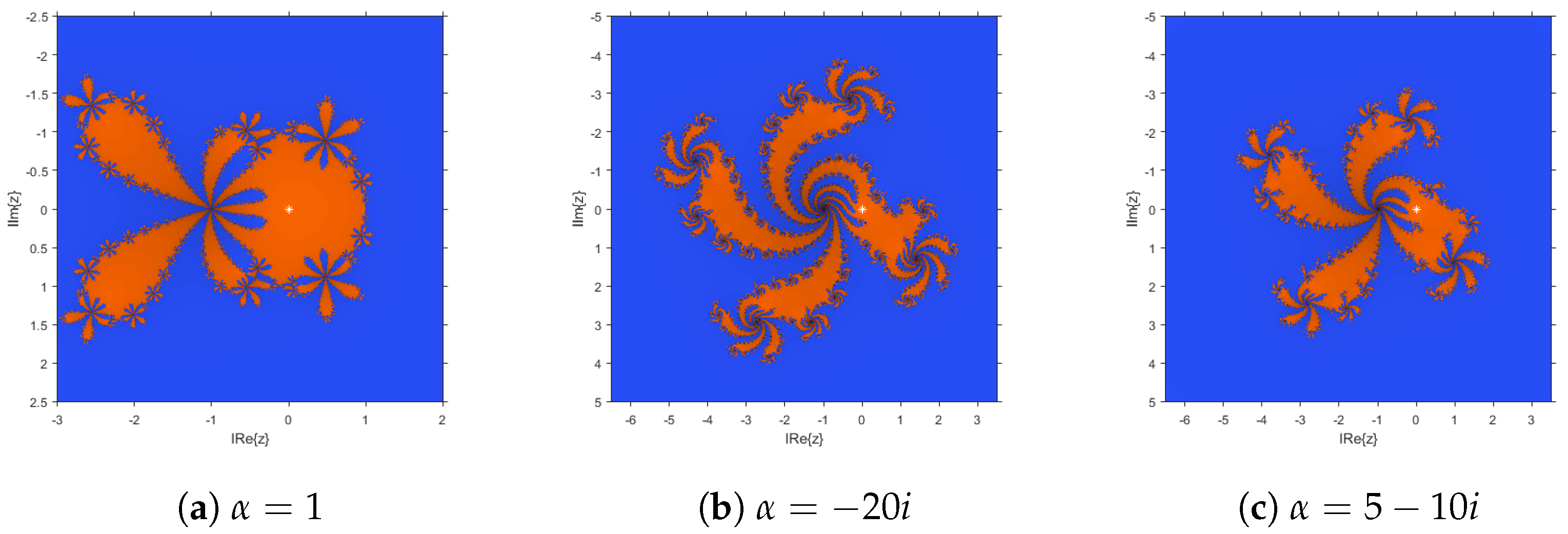
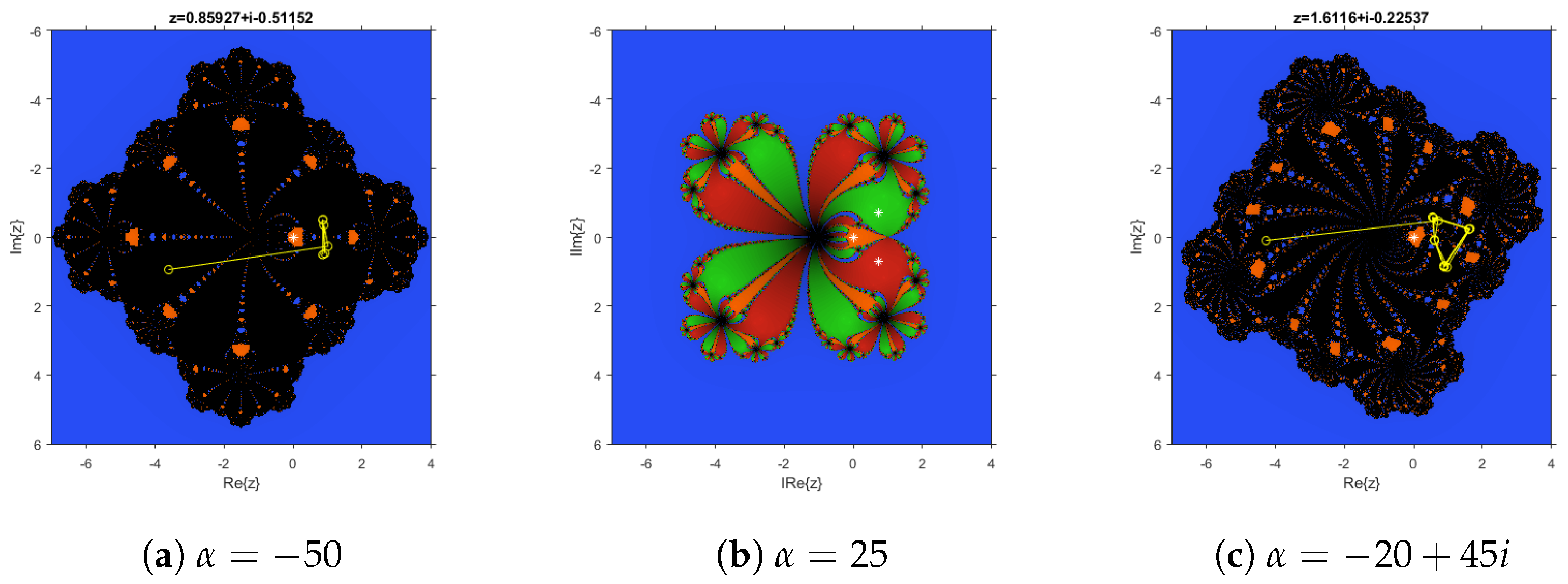
3.3. Dynamical Planes
4. Numerical Results
- , with two real roots at and .
- , with real roots at , and , among others.
- Colebrook-White function [27] , with a real root at , among others.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bruns, D.D.; Bailey, J.E. Nonlinear feedback control for operating a nonisothermal CSTR near an unstable steady state. Chem. Eng. Sci. 1977, 32, 257–264. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Gutiérrez, J.M.; Hernández, M.A.; Salanova, M.A. Chebyshev-like methods and quadratic equations. Rev. Anal. Num. Th. Approx. 1999, 28, 23–35. [Google Scholar]
- Constantinides, A.; Mostoufi, N. Numerical Methods for Chemical Engineers with MATLAB Applications; Prentice-Hall: Boston, MA, USA, 1999. [Google Scholar]
- White, F.M. Fluid Mechanics; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multi-pointiteration. J. Assoc. Comput. Math. 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Li, W.; Pang, Y. Application of Adomian decomposition method to nonlinear systems. Adv. Differ. Equ. 2020, 67. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; Chelsea Publishing Company: New York, NY, USA, 1982. [Google Scholar]
- Chun, C.; Neta, B.; Kozdon, J.; Scott, M. Choosing weight functions in iterative methods for simple roots. Appl. Math. Comput. 2014, 227, 788–800. [Google Scholar] [CrossRef]
- Artidiello, S.; Chicharro, F.; Cordero, A.; Torregrosa, J.R. Local convergence and dynamical analysis of a new family of optimal fourth-order iterative methods. Int. J. Comput. Math. 2013, 90, 2049–2060. [Google Scholar] [CrossRef]
- Lotfi, T.; Sharifi, S.; Salimi, M.; Siegmund, S. A new class of three-point method with optimal convergence order eight and its dynamics. Numer. Algor. 2015, 68, 261–288. [Google Scholar] [CrossRef]
- Budzko, D.; Cordero, A.; Torregrosa, J.R. A new family of iterative methods widening areas of convergence. Appl. Math. Comput. 2015, 252, 405–417. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S.; Plaza, S. Review of some iterative root-finding methods from a dynamical point of view. Sci. Ser. A Math. Sci. 2004, 10, 3–35. [Google Scholar]
- Cordero, A.; García-Maimó, J.; Torregrosa, J.R.; Vassileva, M.P.; Vindel, P. Chaos in King’s iterative family. Appl. Math. Lett. 2013, 26, 842–848. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R.; Vindel, P. Dynamics of a family of Chebyshev-Halley type methods. Appl. Math. Comput. 2013, 219, 8568–8583. [Google Scholar] [CrossRef]
- Chicharro, F.I.; Cordero, C.; Garrrido, N.; Torregrosa, J.R. Wide stability in a new family of optimal fourth-order iterative methods. Comp. Math. Methods 2019, 2019, e1023. [Google Scholar] [CrossRef]
- Sharma, D.; Argyros, I.K.; Parhi, S.K.; Sunanda, S.K. Local Convergence and Dynamical Analysis of a Third and Fourth Order Class of Equation Solvers. Fractal Fract. 2021, 5, 27. [Google Scholar] [CrossRef]
- Capdevila, R.R.; Cordero, A.; Torregrosa, J.R. Isonormal surfaces: A new tool for the multi-dimensional dynamical analysis of iterative methods for solving nonlinear systems. Math. Meth. Appl. Sci. 2021, 1–16. [Google Scholar] [CrossRef]
- Kou, J.; Li, Y. A family of new Newton-like methods. Appl. Math. Comput. 2007, 192, 162–167. [Google Scholar] [CrossRef]
- Petković, M.S.; Neta, B.; Petković, L.D.; Džunić, J. Multipoint methods for solving nonlinear equations: A survey. Appl. Math. Comput. 2014, 226, 635–660. [Google Scholar] [CrossRef]
- Jarratt, P. Some fourth order multipoint iterative methods for solving equations. Math. Comput. 1966, 20, 434–437. [Google Scholar] [CrossRef]
- Hueso, J.L.; Martínez, E.; Teruel, C. Convergence, efficiency and dynamics of new fourth and sixth order families of iterative methods for nonlinear systems. Comput. Appl. Math. 2015, 275, 412–420. [Google Scholar] [CrossRef]
- Khattri, S.K.; Abbasbandy, S. Optimal fourth order family of iterative methods. Mat. Vesn. 2011, 63, 67–72. [Google Scholar]
- Blanchard, P. The dynamics of Newton’s Method. Proc. Symp. Appl. Math. 1994, 49, 139–154. [Google Scholar]
- Chicharro, F.I.; Cordero, A.; Torregrosa, J.R. Drawing Dynamical and Parameters Planes of Iterative Families and Methods. Sci. World 2013, 2013, 780153. [Google Scholar] [CrossRef] [PubMed]
- Beardon, A.F. Iteration of Rational Functions: Complex Analytic Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000; Volume 132. [Google Scholar]
- Cordero, A.; Torregrosa, J.R. Variants of Newton’s Method using fifth-order quadrature formulas. Appl. Math. Comput. 2007, 190, 686–698. [Google Scholar] [CrossRef]
- Menon, E.S. Fluid Flow in Pipes. In Transmission Pipeline Calculations and Simulations Manual; Gulf Professional Publishing: Amsterdam, The Netherlands, 2015; Chapter 5; pp. 149–234. [Google Scholar] [CrossRef]
- Wang, X.; Kou, J.; Li, Y. Modified Jarratt method with sixth-order convergence. Appl. Math. Lett. 2009, 22, 1798–1802. [Google Scholar] [CrossRef]
- Chun, C. Some improvements of Jarratt’s method with sixth-order convergence. Appl. Math. Comput. 2007, 190, 1432–1437. [Google Scholar] [CrossRef]
| Solution | Iterations | ACOC | Time (s) | |||
|---|---|---|---|---|---|---|
| −50 | 7.0883 | 8.4884 | −1.4044 | 8 | 4.0 | 0.3223 ± 0.2001 |
| −40 | 0 | 1.4357 | −1.4044 | 29 | 4.0 | 0.9086 ± 0.5325 |
| −20 + 45i | d | d | d | d | d | d |
| −16 − 45i | 2.4842 | 5.1013 | 1.4044 | 10 | 4.0 | 0.3597 ± 0.1498 |
| 1 | 0 | 1.8974 | 1.4044 | 6 | 4.0 | 0.2188 0.2253 ± 0.0838 |
| −20i | 7.0302 | 8.8753 | 1.4044 | 7 | 4.0 | 0.2487 ± 0.0415 |
| 5 − 10i | 0.0 | 1.4936 | 1.4044 | 7 | 4.0 | 0.2481 0.2419 ± 0.0176 |
| −4.5 + 10i | 3.5457 | 1.0501 | 1.4044 | 6 | 4.0 | 0.2223 ± 0.0224 |
| 1.4479 | 8.6274 | 1.4044 | 10 | 2.0 | 0.2033 ± 0.0248 | |
| 0.0 | 9.6997 | 1.4044 | 6 | 4.0 | 0.1970 ± 0.0200 | |
| 0.0 | 4.9393 | 1.4044 | 5 | 6.0 | 0.2264 ± 0.0419 | |
| 0.0 | 1.5533 | 1.4044 | 5 | 6.0 | 0.2334 ± 0.0619 | |
| 0.0 | 9.821 | 1.4044 | 5 | 6.0 | 0.2158 ± 0.0185 |
| Solution | Iterations | ACOC | Time (s) | |||
|---|---|---|---|---|---|---|
| −50 | 0 | 1.5957 | 1.4044 | 7 | 4.0 | 0.2347 ± 0.0293 |
| −40 | 0 | 3.5896 | 1.4044 | 7 | 4.0 | 0.2420 ± 0.0614 |
| −20 + 45i | 1.1188 | 1.475 | 1.4044 | 8 | 4.0 | 0.2589 ± 0.0262 |
| −16 − 45i | 2.9743 | 8.4532 | 1.4044 | 8 | 4.0 | 0.2603 ± 0.0305 |
| 1 | 0 | 7.1697 | 1.4044 | 7 | 4.0 | 0.2263 ± 0.0155 |
| −20i | 1.1363 | 6.6845 | 1.4044 | 7 | 4.0 | 0.2347 ± 0.0266 |
| 5 − 10i | 3.0563 | 2.6576 | 1.4044 | 7 | 4.0 | 0.2314 ± 0.0152 |
| −4.5 + 10i | 0 | 3.7277 | 1.4044 | 7 | 4.0 | 0.2302 ± 0.0129 |
| 1.6796 | 2.9384 | 1.4044 | 11 | 2.0 | 0.2013 ± 0.0128 | |
| 0.0 | 1.7167 | 1.4044 | 7 | 4.0 | 0.1970 ± 0.0200 | |
| 0.0 | 7.3559 | 1.4044 | 5 | 6.0 | 0.2177 ± 0.0203 | |
| 0.0 | 2.2786 | 1.4044 | 5 | 6.0 | 0.2100 ± 0.0144 | |
| 0.0 | 9.2909 | 1.4044 | 5 | 6.0 | 0.2083 ± 0.0436 |
| Solution | Iterations | ACOC | Time (s) | |||
|---|---|---|---|---|---|---|
| −50 | 1.0082 | 4.6325 | −14.137 | 8 | 4.0 | 0.2728 ± 0.0657 |
| −40 | d | d | d | d | d | d |
| −20 + 45i | 2.9787 | 2.2945 | −17.278 | 12 | 4.0 | 0.3858 ± 0.0756 |
| −16 − 45i | d | d | d | d | d | d |
| 1 | 0 | 5.7578 | 0.517 | 6 | 4.0 | 0.2247 ± 0.0474 |
| −20i | 1.9236 | 6.3944 | 0.517 | 7 | 4.0 | 0.2566 ± 0.0551 |
| 5 − 10i | 0.0 | 6.7181 | 0.517 | 7 | 4.0 | 0.2797 ± 0.0715 |
| −4.5 + 10i | 3.0281 | 1.7704 | 0.517 | 7 | 4.0 | 0.3034 ± 0.0963 |
| 1.4521 | 7.5503 | 0.517 | 10 | 2.0 | 0.2075 ± 0.0499 | |
| 0.0 | 3.9685 | 0.517 | 6 | 4.0 | 0.2198 ± 0.0529 | |
| 0.0 | 4.9393 | 1.4044 | 5 | 6.0 | 0.1923 ± 0.0152 | |
| 0.0 | 1.5533 | 1.4044 | 5 | 6.0 | 0.1922 ± 0.0168 | |
| 0.0 | 9.821 | 1.4044 | 5 | 6.0 | 0.2158 ± 0.0185 |
| Solution | Iterations | ACOC | Time (s) | |||
|---|---|---|---|---|---|---|
| −50 | 1.4177 | 5.6457 | −1.8639 | 6 | 4.0 | 0.1848 ± 0.0133 |
| −40 | 1.4177 | 5.1924 | −1.8639 | 7 | 4.0 | 0.2048 ± 0.0155 |
| −20 + 45i | d | d | d | d | d | d |
| −16 − 45i | d | d | d | d | d | d |
| 1 | 0 | 1.6078 | 0.5177 | 8 | 4.0 | 0.2273 ± 0.0189 |
| −20i | 1.0214 | 1.0043 | −1.8639 | 9 | 4.0 | 0.2553 ± 0.0230 |
| 5 − 10i | 0.0 | 4.4053 | 0.5177 | 22 | 4.0 | 0.5289 ± 0.0233 |
| −4.5 + 10i | 1.4234 | 2.2838 | −29.8451 | 9 | 4.0 | 0.2653 ± 0.0487 |
| 2.4269 | 3.0867 | 0.5177 | 12 | 2.0 | 0.1956 ± 0.0260 | |
| 0.0 | 1.0119 | 0.5177 | 7 | 4.0 | 0.1909 ± 0.0243 | |
| 0.0 | 4.8037 | 0.5177 | 6 | 6.0 | 0.2230 ± 0.0273 | |
| 0.0 | 1.5709 | 0.5177 | 6 | 6.0 | 0.2208 ± 0.0261 | |
| 0.0 | 9.7594 | 0.5177 | 5 | 6.0 | 0.2106 ± 0.0218 |
| Solution | Iterations | ACOC | Time (s) | |||
|---|---|---|---|---|---|---|
| −50 | 2.2683 | 5.9163 | 0.01885050 | 6 | 4.0 | 0.4098 ± 0.1367 |
| −40 | 1.1341 | 3.1316 | 0.01885050 | 6 | 4.0 | 0.3978 ± 0.0532 |
| −20 + 45i | 2.4166 | 0.0 | 0.01885050 | 6 | 4.0 | 0.4517 ± 0.1145 |
| −16 − 45i | 1.5247 | 1.4073 | 0.01885050 | 6 | 4.0 | 0.4555 ± 0.0999 |
| 1 | 1.1341 | 2.2713 | 0.01885050 | 5 | 4.0 | 0.3361 ± 0.0419 |
| −20i | 4.0218 | 9.0943 | 0.01885050 | 5 | 4.0 | 0.3386 ± 0.0255 |
| 5 − 10i | 1.5202 | 8.1035 | 0.01885050 | 5 | 4.0 | 0.3744 ± 0.0241 |
| −4.5 + 10i | 3.2812 | 5.7307 | 0.01885050 | 5 | 4.0 | 0.3706 ± 0.0178 |
| 2.9268 | 5.9571 | 0.01885050 | 9 | 2.0 | 0.3630 ± 0.0332 | |
| 1.1341 | 2.0266 | 0.01885050 | 5 | 4.0 | 0.3319 ± 0.0655 | |
| 1.1341 | 2.0266 | 0.01885050 | 5 | 4.0 | 0.3447 ± 0.0301 | |
| 1.1341 | 2.0266 | 0.01885050 | 5 | 4.0 | 0.3494 ± 0.0252 | |
| 1.1341 | 2.0266 | 0.01885050 | 5 | 4.0 | 0.3400 ± 0.0208 |
| Solution | Iterations | ACOC | Time (s) | |||
|---|---|---|---|---|---|---|
| −50 | d | d | d | d | d | d |
| −40 | d | d | d | d | d | d |
| −20 + 45i | d | d | d | d | d | d |
| −16 − 45i | d | d | d | d | d | d |
| 1 | 2.3085 | 4.1347 | 0.01885050 | 6 | 4.0 | 0.3880 ± 0.0206 |
| −20i | 2.2683 | 1.9203 | 0.01885050 | 9 | 4.0 | 0.6564 ± 0.0519 |
| 5 − 10i | 1.2533 | 2.48 | 0.01885050 | 7 | 4.0 | 0.5059 ± 0.0328 |
| −4.5 + 10i | 2.2683 | 2.5742 | 0.01885050 | 7 | 4.0 | 0.5020 ± 0.0177 |
| 2.0584 | 4.9958 | 0.01885050 | 10 | 2.0 | 0.3942 ± 0.0227 | |
| 1.1341 | 1.1036 | 0.01885050 | 5 | 4.0 | 0.3200 ± 0.0233 | |
| 0 | 1.8787 | 0.01885050 | 5 | 6.0 | 0.4191 ± 0.0255 | |
| 0 | 1.8799 | 0.01885050 | 5 | 6.0 | 0.4194 ± 0.0354 | |
| 0 | 1.8793 | 0.01885050 | 5 | 6.0 | 0.4064 ± 0.0168 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Padilla, J.J.; Chicharro, F.I.; Cordero, A.; Torregrosa, J.R. Parametric Family of Root-Finding Iterative Methods: Fractals of the Basins of Attraction. Fractal Fract. 2022, 6, 572. https://doi.org/10.3390/fractalfract6100572
Padilla JJ, Chicharro FI, Cordero A, Torregrosa JR. Parametric Family of Root-Finding Iterative Methods: Fractals of the Basins of Attraction. Fractal and Fractional. 2022; 6(10):572. https://doi.org/10.3390/fractalfract6100572
Chicago/Turabian StylePadilla, José J., Francisco I. Chicharro, Alicia Cordero, and Juan R. Torregrosa. 2022. "Parametric Family of Root-Finding Iterative Methods: Fractals of the Basins of Attraction" Fractal and Fractional 6, no. 10: 572. https://doi.org/10.3390/fractalfract6100572
APA StylePadilla, J. J., Chicharro, F. I., Cordero, A., & Torregrosa, J. R. (2022). Parametric Family of Root-Finding Iterative Methods: Fractals of the Basins of Attraction. Fractal and Fractional, 6(10), 572. https://doi.org/10.3390/fractalfract6100572











