A Variable-Order Fractional Constitutive Model to Characterize the Rate-Dependent Mechanical Behavior of Soft Materials
Abstract
:1. Introduction
2. Preliminary Knowledge of Fractional Calculus
3. Numerical Discretization Method Based on the GL Derivative
4. The Proposed Variable-Order Fractional Constitutive Model
4.1. Model Development
4.2. Validity of the Proposed Model under Tensile Tests
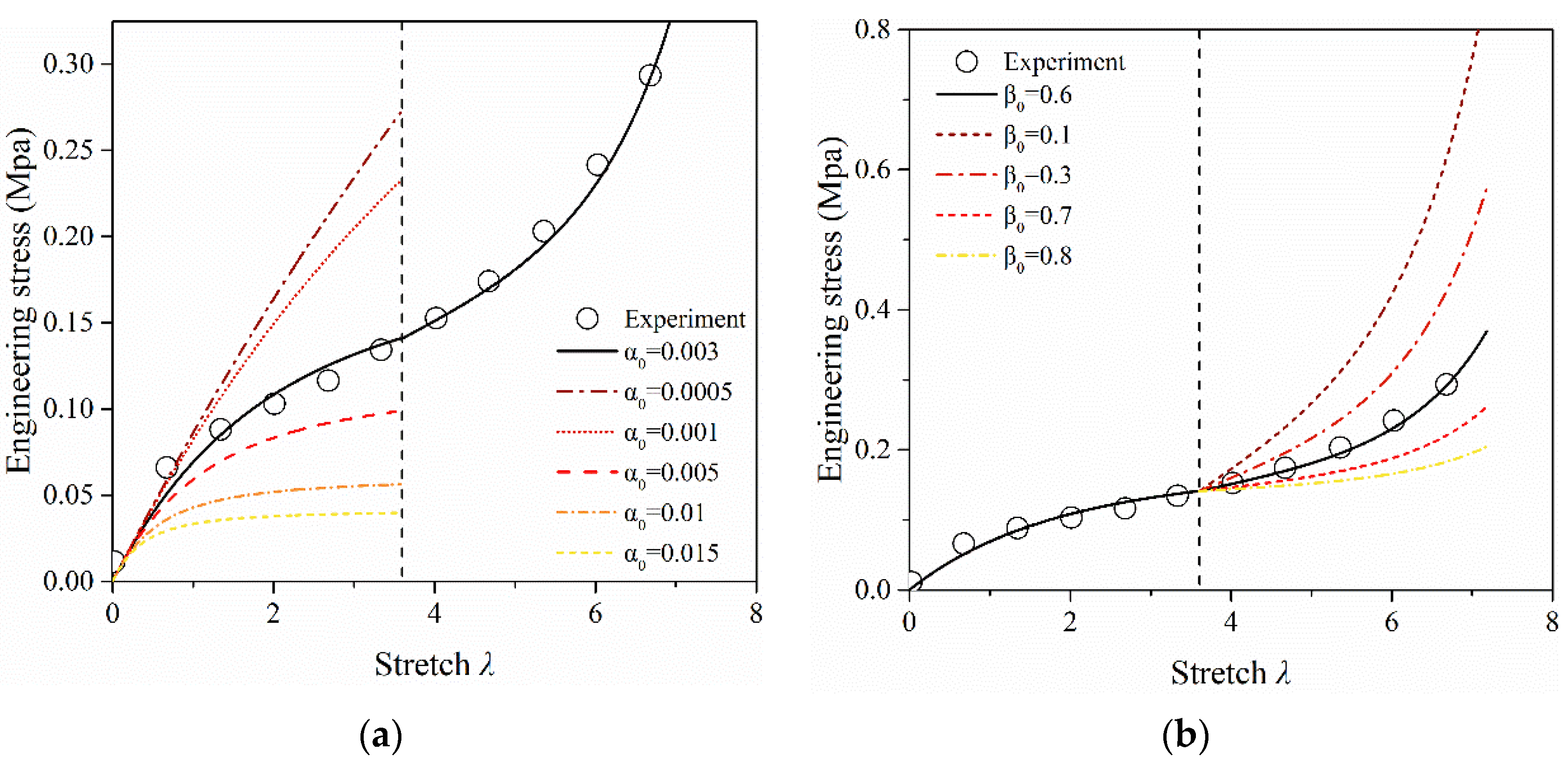
4.2.1. Results for Nitrile Rubber
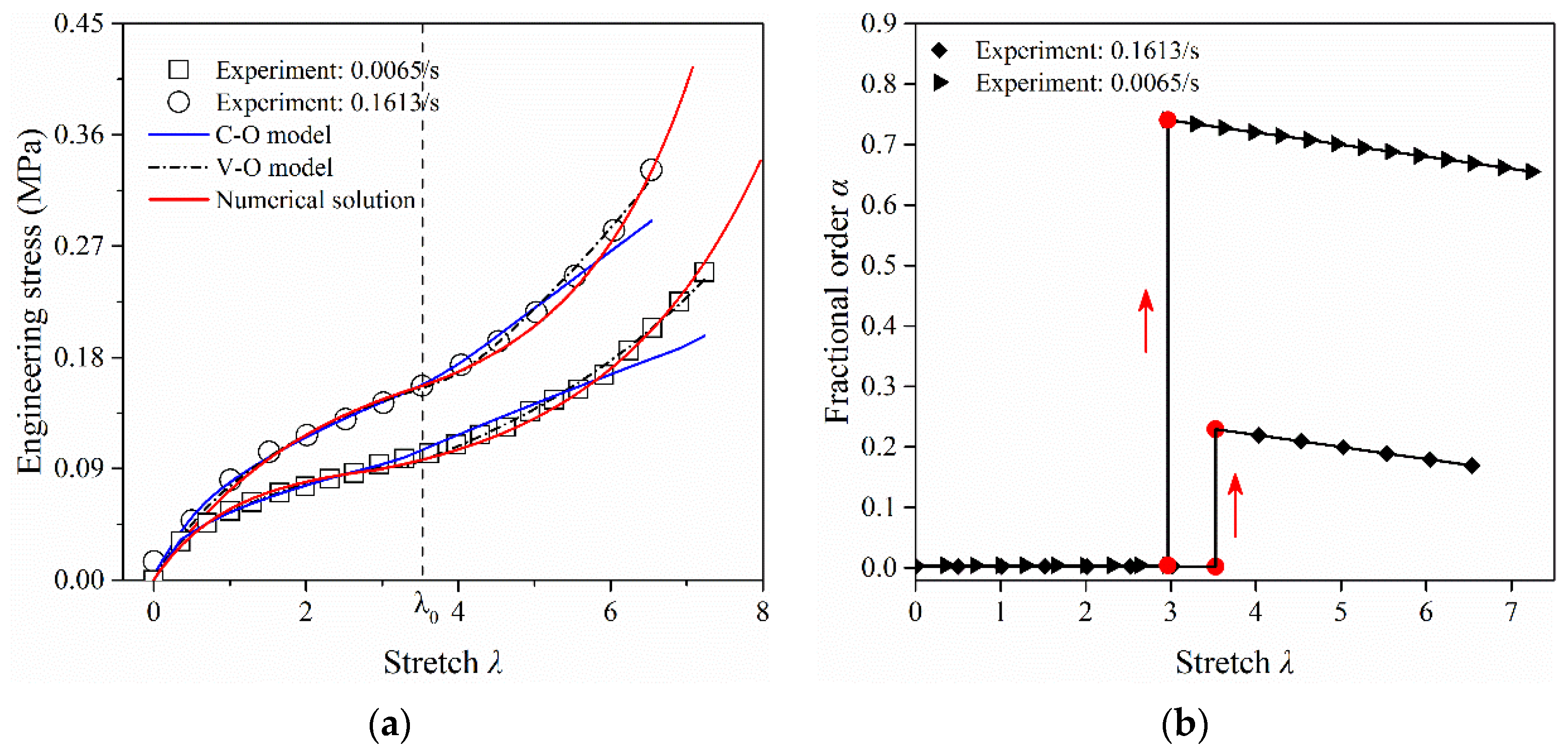
4.2.2. Results for Soft Elastomer
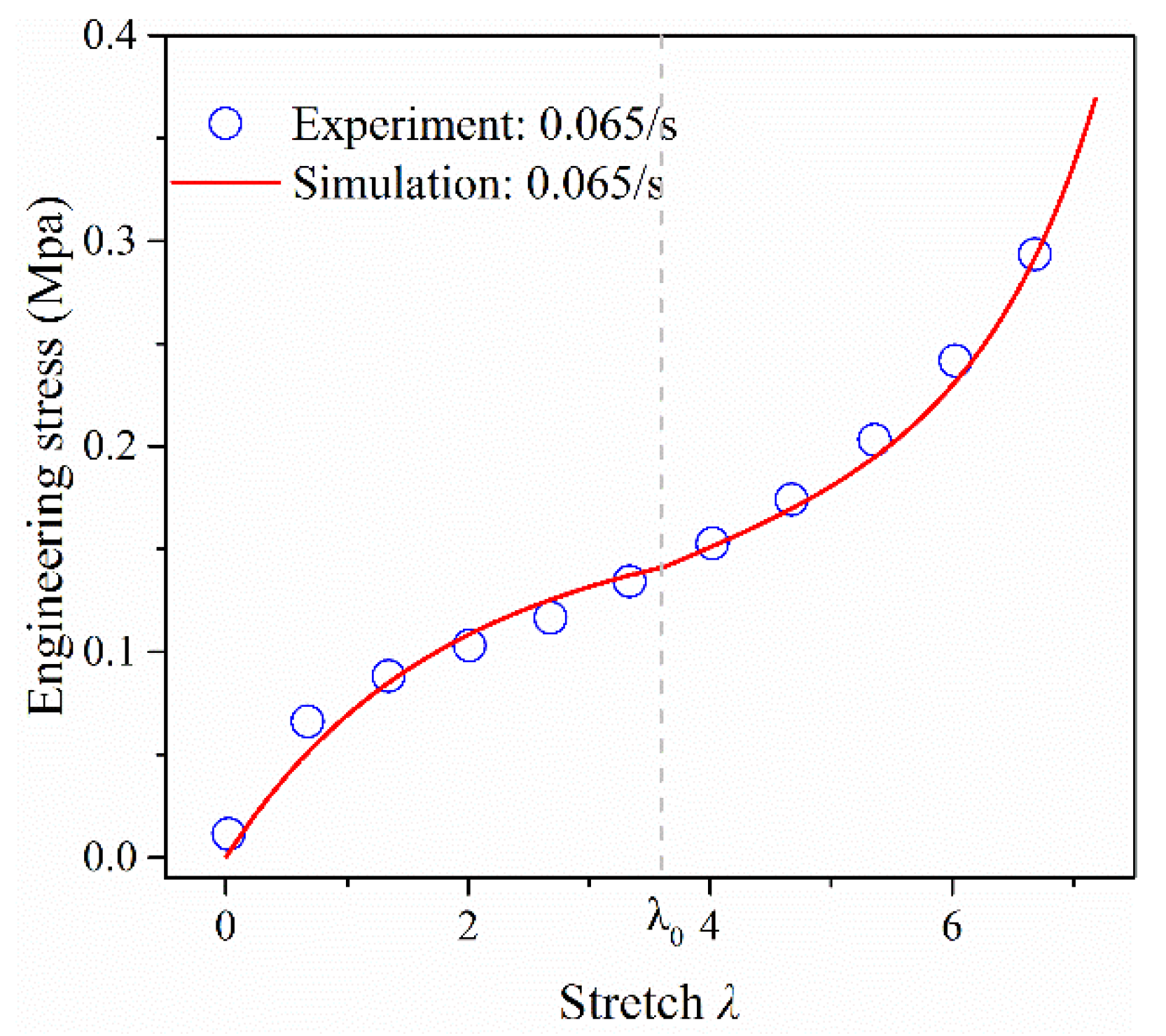
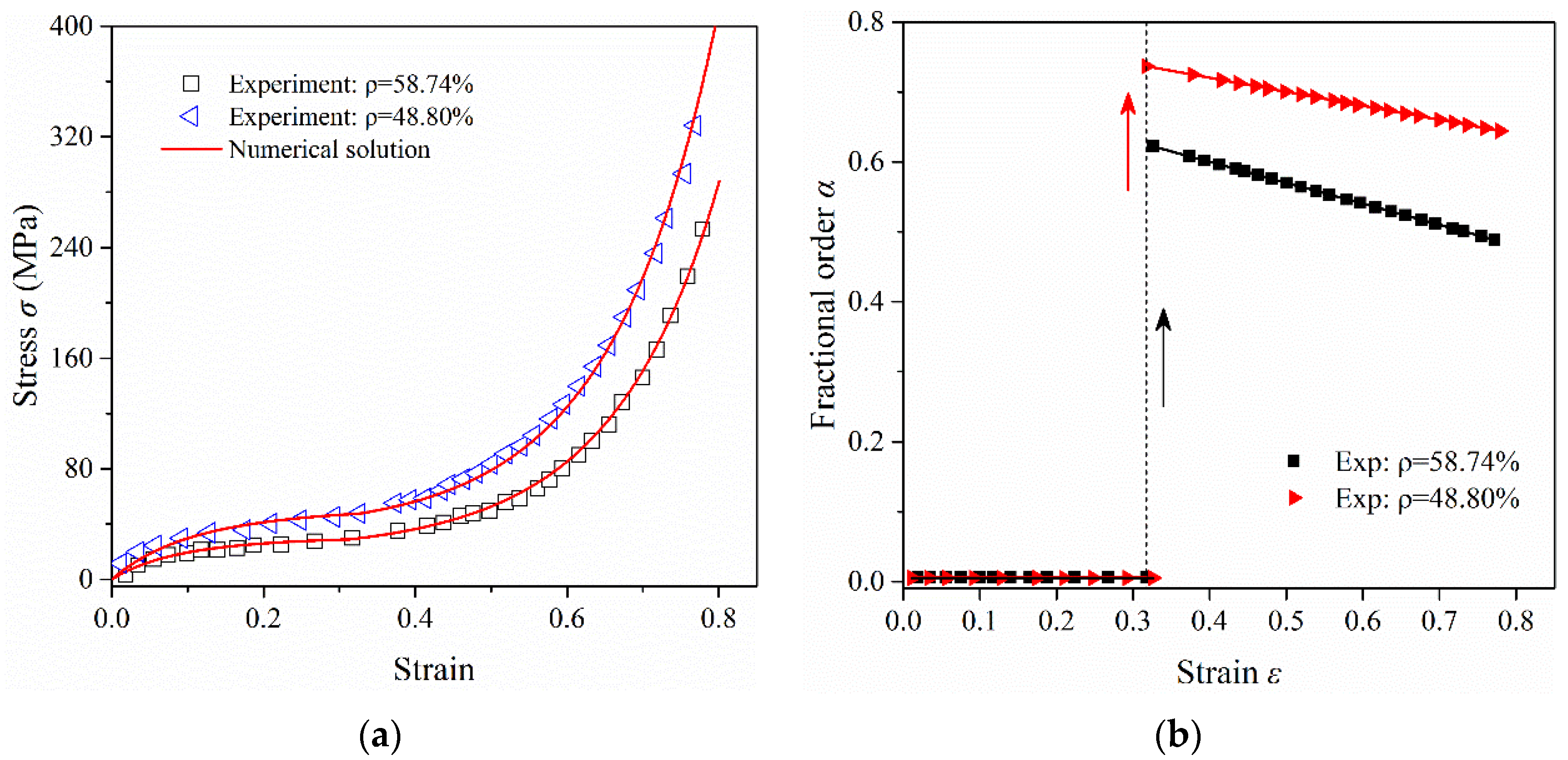
4.3. Validity of the Proposed Model under Compression
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
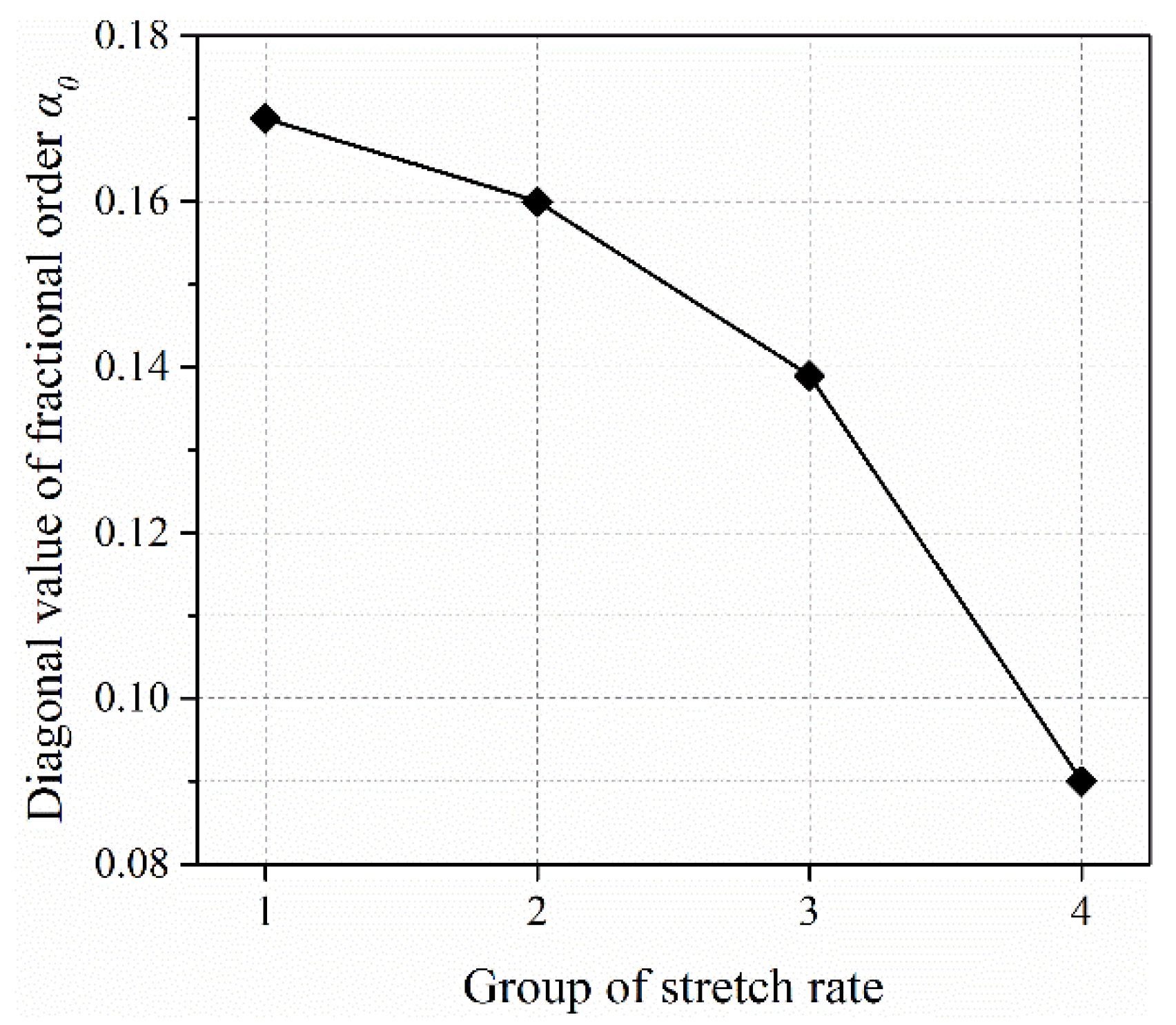
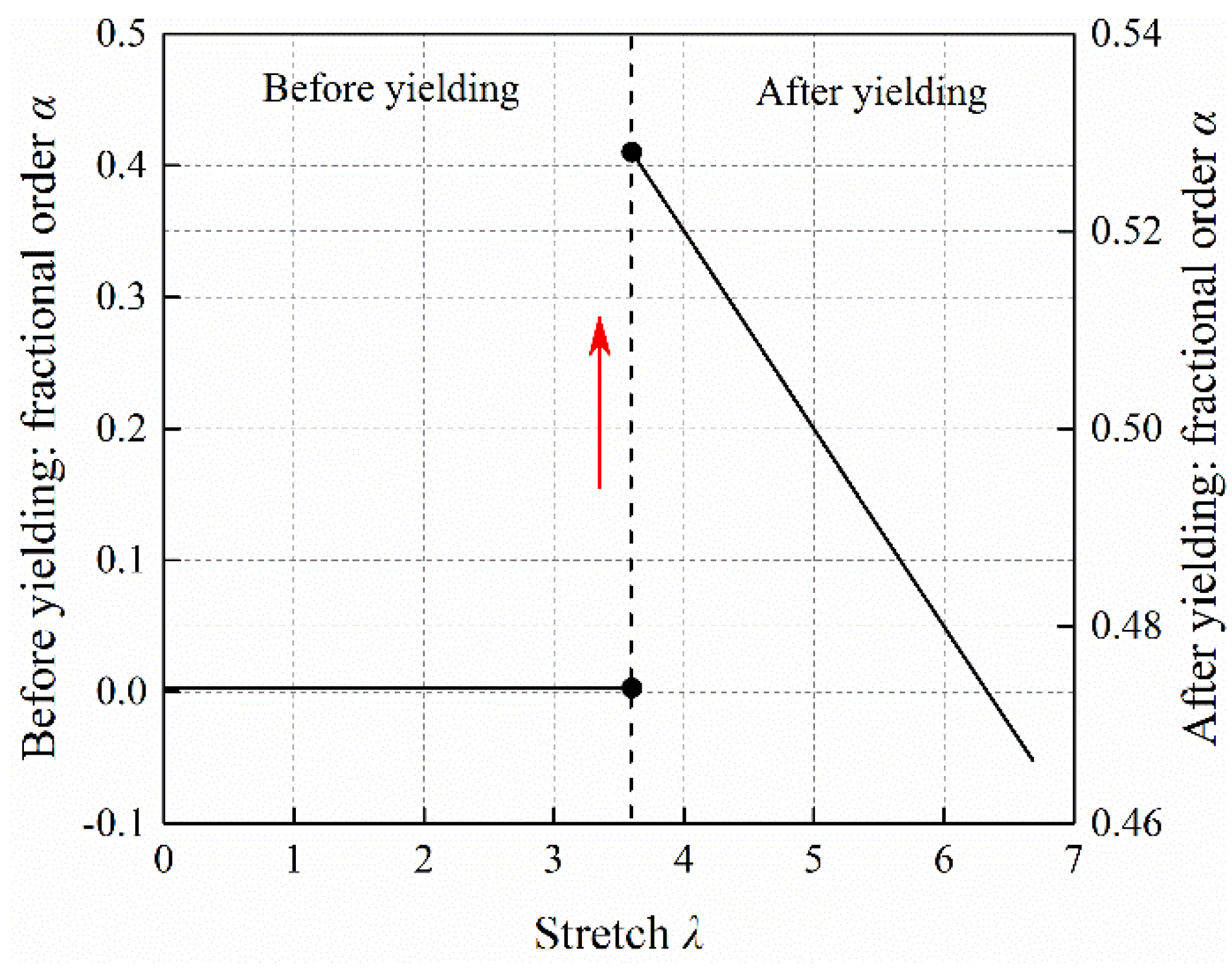
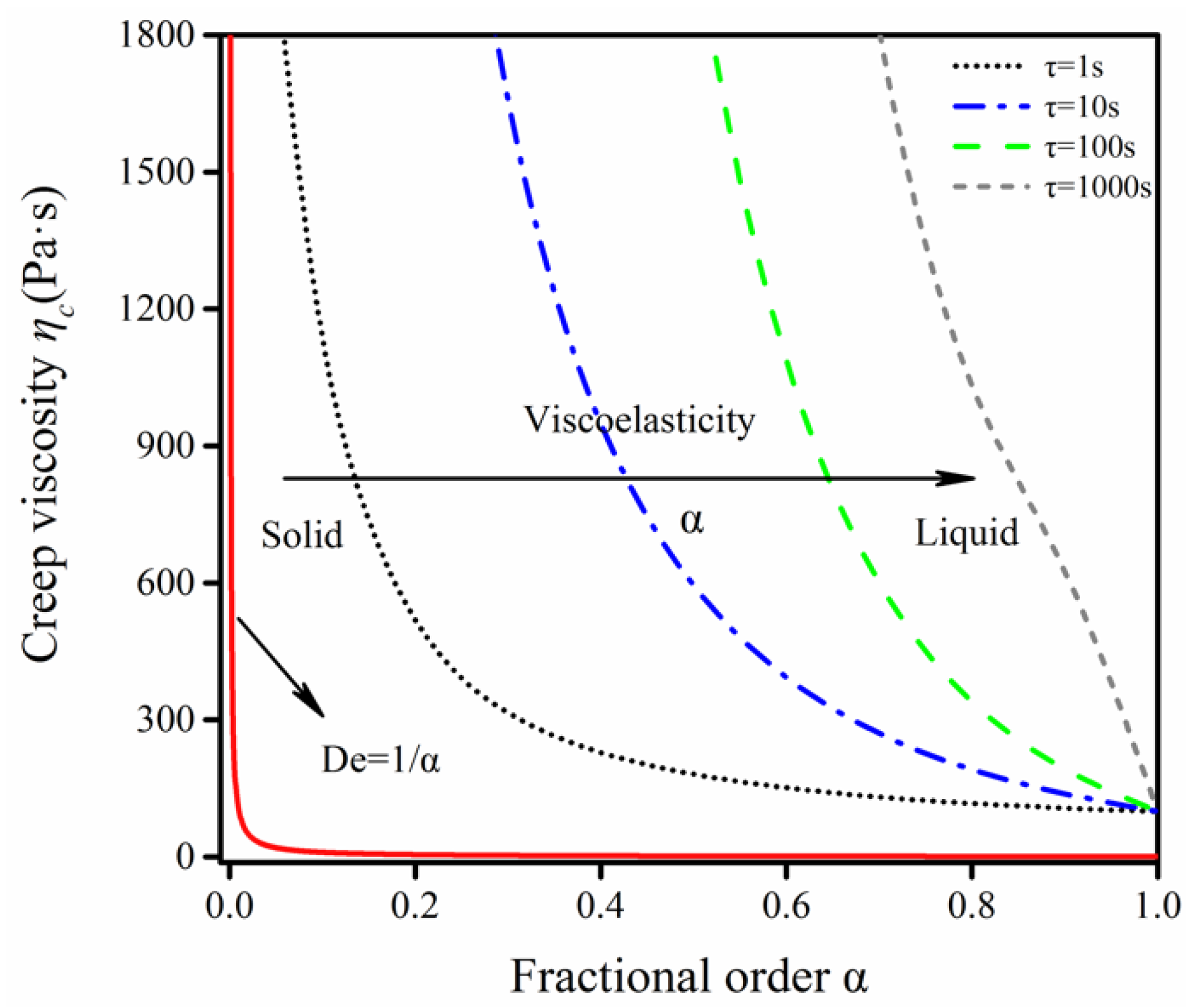
Appendix A. Physical Interpretation of Fractional Order
References
- Lin, S.; Liu, X.; Liu, J.; Yuk, H.; Loh, H.-C.; Parada, G.A.; Settens, C.; Song, J.; Masic, A.; McKinley, G.H.; et al. Anti-fatigue-fracture hydrogels. Sci. Adv. 2018, 5, eaau8528. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, C.; Suo, Z. Hydrogel ionotronics. Nat. Rev. Mater. 2018, 3, 125–142. [Google Scholar] [CrossRef]
- Lendlein, A. Fabrication of reprogrammable shape-memory polymer actuators for robotics. Sci. Robot. 2018, 3, eaat9090. [Google Scholar] [CrossRef] [PubMed]
- Xiang, G.; Yin, D.; Meng, R.; Lu, S. Creep model for natural fiber polymer composites (NFPCs) based on variable order fractional derivatives: Simulation and parameter study. J. Appl. Polym. Sci. 2019, 137, 48796. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Shah, N.A.; Wakif, A.; Mahanthesh, B.; Sivaraj, R.; Koriko, O.K. Ratio of Momentum Diffusivity to Thermal Diffusivity: Introduction, Meta-Analysis, and Scrutinization, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Hepburn, C. Polyurethane Elastomers; Springer: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Qi, H.J.; Boyce, M.C. Stress-strain behavior of thermoplastic polyurethanes. Mech. Mater. 2005, 37, 817–839. [Google Scholar] [CrossRef]
- Qi, H.J.; Boyce, M.C. Constitutive model for stretch-induced softening of the stress-stretch behavior of elastomeric materials. J. Mech. Phys. Solids 2004, 52, 2187–2205. [Google Scholar] [CrossRef]
- Chen, L.L.; Lian, H.; Natarajan, S.; Zhao, W.; Chen, X.Y.; Bordas, S.P.A. Multi-frequency acoustic topology optimization of sound-absorption materials with isogeometric boundary element methods accelerated by frequency-decoupling and model order reduction techniques. Comput. Methods Appl. Mech. Eng. 2022, 395, 114997. [Google Scholar] [CrossRef]
- Chen, L.; Cheng, R.; Li, S.; Lian, H.; Zheng, C.; Bordas, S.P.A. A sample-efficient deep learning method for multivariate uncertainty qualification of acoustic–vibration interaction problems. Comput. Methods Appl. Mech. Eng. 2022, 393, 114784. [Google Scholar] [CrossRef]
- Qu, S.; Li, K.; Li, T.; Jiang, H.; Wang, M.; Li, Z. Rate dependent stress-stretch relation of dielectric elastomers subjected to pure shear like loading and electric field. Acta Mech. Solida Sin. 2012, 25, 542–549. [Google Scholar] [CrossRef]
- Wissler, M.; Mazza, E. Mechanical behavior of an acrylic elastomer used in dielectric elastomer actuators. Sens. Actuators A Phys. 2007, 134, 494–504. [Google Scholar] [CrossRef]
- Foo, C.C.; Cai, S.; Koh, S.; Bauer, S.G.; Suo, Z. Model of dissipative dielectric elastomers. J. Appl. Phys. 2012, 111, 34102. [Google Scholar] [CrossRef]
- Zhao, X.; Koh, S.; Suo, Z. Nonequilibrium thermodynamics of dielectric elastomers. Int. J. Appl. Mech. 2011, 3, 203–217. [Google Scholar] [CrossRef]
- Xiang, G.; Yin, D.; Cao, C.; Gao, Y. Fractional description of creep behavior for fiber reinforced concrete: Simulation and parameter study. Constr. Build. Mater. 2022, 318, 126101. [Google Scholar] [CrossRef]
- Meng, R.; Yin, D.; Drapaca, C.S. Variable-order fractional description of compression deformation of amorphous glassy polymers. Comput. Mech. 2019, 64, 163–171. [Google Scholar] [CrossRef]
- Gao, Y.; Zhao, B.; Yin, D. A general fractional model of creep response for polymer materials: Simulation and model comparison. J. Appl. Polym. Sci. 2022, 139, 51577. [Google Scholar] [CrossRef]
- Su, X.; Chen, W.; Xu, W.; Liang, Y. Non-local structural derivative Maxwell model for characterizing ultra-slow rheology in concrete. Constr. Build. Mater. 2018, 190, 342–348. [Google Scholar] [CrossRef]
- Fernandes, V.A.; De Focatiis, D.S.A. The role of deformation history on stress relaxation and stress memory of filled rubber. Polym. Test. 2014, 40, 124–132. [Google Scholar] [CrossRef] [Green Version]
- Spathis, G.; Kontou, E. Creep failure time prediction of polymers and polymer composites. Compos. Sci. Technol. 2012, 72, 959–964. [Google Scholar] [CrossRef]
- Ding, H.; Xin, Z.; Yang, Y.; Luo, Y.; Xia, K.; Wang, B.; Sun, Y.; Wang, J.; Zhang, Y.; Wu, H.; et al. Ultrasensitive, Low–Voltage Operational, and Asymmetric Ionic Sensing Hydrogel for Multipurpose Applications. Adv. Funct. Mater. 2020, 30, 1909616. [Google Scholar] [CrossRef]
- Gong, J.P. Materials both tough and soft. Science 2014, 344, 161–162. [Google Scholar] [CrossRef]
- Highley, C.B.; Rodell, C.B.; Burdick, J.A. Direct 3D Printing of Shear-Thinning Hydrogels into Self-Healing Hydrogels. Adv. Mater. 2015, 27, 5075–5079. [Google Scholar] [CrossRef]
- Hong, S.; Sycks, D.; Chan, H.F.; Lin, S.; Lopez, G.P.; Guilak, F.; Leong, K.W.; Zhao, X. 3D Printing of Highly Stretchable and Tough Hydrogels into Complex, Cellularized Structures. Adv. Mater. 2015, 27, 4035–4040. [Google Scholar] [CrossRef] [Green Version]
- Mao, G.; Huang, X.; Liu, J.; Li, T.; Qu, S.; Yang, W. Dielectric elastomer peristaltic pump module with finite deformation. Smart Mater. Struct. 2015, 24, 075026. [Google Scholar] [CrossRef]
- Yang, W.; Chen, X.; Jiang, Z.; Zhang, X.; Zheng, L. Effect of slip boundary condition on flow and heat transfer of a double fractional Maxwell fluid. Chin. J. Phys. 2020, 68, 214–223. [Google Scholar] [CrossRef]
- Sun, H.; Chen, W.; Chen, Y. Variable-order fractional differential operators in anomalous diffusion modeling. Phys. A Stat. Mech. Its Appl. 2009, 388, 4586–4592. [Google Scholar] [CrossRef]
- Umarov, S.; Steinberg, S. Variable order differential equations and diffusion with changing modes. Z. fur Anal. Und Ihre Anwend. 2009, 28, 431–450. [Google Scholar] [CrossRef]
- Yin, D.; Wang, Y.; Li, Y.; Cheng, C. Variable-order fractional mean square displacement function with evolution of diffusibility. Phys. A Stat. Mech. Its Appl. 2013, 392, 4571–4575. [Google Scholar] [CrossRef]
- Sheng, H.; Sun, H.; Chen, Y.; Qiu, T. Synthesis of multifractional Gaussian noises based on variable-order fractional operators. Signal Process. 2011, 91, 1645–1650. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Tarasova, V.V. Macroeconomic models with long dynamic memory: Fractional calculus approach. Appl. Math. Comput. 2018, 338, 466–486. [Google Scholar] [CrossRef]
- Mehta, P.P.; Pang, G.; Song, F.; Karniadakis, G.E. Discovering a universal variable-order fractional model for turbulent Couette flow using a physics-informed neural network. Fract. Calc. Appl. Anal. 2019, 22, 1675–1688. [Google Scholar] [CrossRef]
- Coimbra, C.F.M. Mechanics with variable-order differential operators. Ann. Phys. 2003, 12, 692–703. [Google Scholar] [CrossRef]
- Ingman, D.; Suzdalnitsky, J. Application of differential operator with servo-order function in model of viscoelastic deformation process. J. Eng. Mech. 2005, 131, 763–767. [Google Scholar] [CrossRef]
- Ramirez, L.E.S.; Coimbra, C.F.M. A variable order constitutive relation for viscoelasticity. Ann. Phys. 2007, 16, 543–552. [Google Scholar] [CrossRef]
- Garrappa, R.; Giusti, A.; Mainardi, F. Variable-order fractional calculus: A change of perspective. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105904. [Google Scholar] [CrossRef]
- Di Paola, M.; Alotta, G.; Burlon, A.; Failla, G. A novel approach to nonlinear variable-order fractional viscoelasticity. Philos. Trans. A Math. Phys. Eng. Sci. 2020, 378, 20190296. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, F.; Yu, Q.; Li, T. Review of fractional epidemic models. Appl. Math. Model. 2021, 97, 281–307. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Defferential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; High Education Press: Beijing, China, 2011. [Google Scholar]
- Colinas-Armijo, N.; Di Paola, M. Step-by-step integration for fractional operators. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 292–305. [Google Scholar] [CrossRef]
- Di Paola, M.; Granata, M.F. Fractional model of concrete hereditary viscoelastic behaviour. Arch. Appl. Mech. 2016, 87, 335–348. [Google Scholar] [CrossRef]
- Podlubny, I. Matrix approach to discrete fractional calculus. Fract. Calc. Appl. Anal. 2000, 3, 359–386. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Yin, D. A full-stage creep model for rocks based on the variable-order fractional calculus. Appl. Math. Model. 2021, 95, 435–446. [Google Scholar] [CrossRef]
- Gao, Y.; Yin, D.; Zhao, B. Fractional description for the rate-dependent viscoelastic response of tough hydrogels. Polym. Adv. Technol. 2022, 33, 2708–2719. [Google Scholar] [CrossRef]
- Gao, Y.; Yin, D.; Zhao, B. A bridge between the fractional viscoelasticity and time-varying viscosity model: Physical interpretation and constitutive modeling. Mech. Time-Depend. Mater. 2022; in production. [Google Scholar] [CrossRef]
- Burlon, A.; Alotta, G.; Di Paola, M.; Failla, G. An original perspective on variable-order fractional operators for viscoelastic materials. Meccanica 2021, 56, 769–784. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Dabiri, A.; Machado, J.A.T. Application of variable-order fractional calculus in solid mechanics. In Applications in Engineering, Life and Social Sciences, Part A; Bvaleanu, D., Lopes, A.M., Eds.; De Gruyter: Berlin, Germamy, 2019; Volume 7, pp. 207–224. [Google Scholar]
- Manish, V.; Arockiarajan, A.; Tamadapu, G. Influence of water content on the mechanical behavior of gelatin based hydrogels: Synthesis, characterization, and modeling. Int. J. Solids Struct. 2021, 233, 111219. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhong, D.; Wang, P.; Yin, T.; Zhou, H.; Yu, H.; Baliga, C.; Qu, S.; Yang, W. A physically based visco-hyperelastic constitutive model for soft materials. J. Mech. Phys. Solids 2019, 128, 208–218. [Google Scholar] [CrossRef]
- Wu, F.; Gao, R.; Liu, J.; Li, C. New fractional variable-order creep model with short memory. Appl. Math. Comput. 2020, 380, 125278. [Google Scholar] [CrossRef]
- Cai, W.E.I.; Wang, P. A Nonlinear Strain-Dependent Variable-Order Fractional Model with Applications To Aluminum Foams. Fractals 2021, 30, 2250021. [Google Scholar] [CrossRef]
- Wang, Z.G.; Cai, P.; Ying, J.Z.; Li, S.Q.; Hu, J.Z. Mechanical properties and energy absorption capability of closed-cell Al foam. Mater. Rev. 2012, 26, 152–155. [Google Scholar]
- Yang, X.J. New rheological problems involving general fractional derivatives with nonsingular power-law kernels. Proc. Rom. Acad.—Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2018, 19, 45–52. [Google Scholar]
- Su, X.; Xu, W.; Chen, W.; Yang, H. Fractional creep and relaxation models of viscoelastic materials via a non-Newtonian time-varying viscosity: Physical interpretation. Mech. Mater. 2020, 140, 103222. [Google Scholar] [CrossRef]
- Metzler, R.; Nonnenmacher, T.F. Fractional relaxation processes and fractional rheological models for the description of a class of viscoelastic materials. Int. J. Plast. 2003, 19, 941–959. [Google Scholar] [CrossRef]
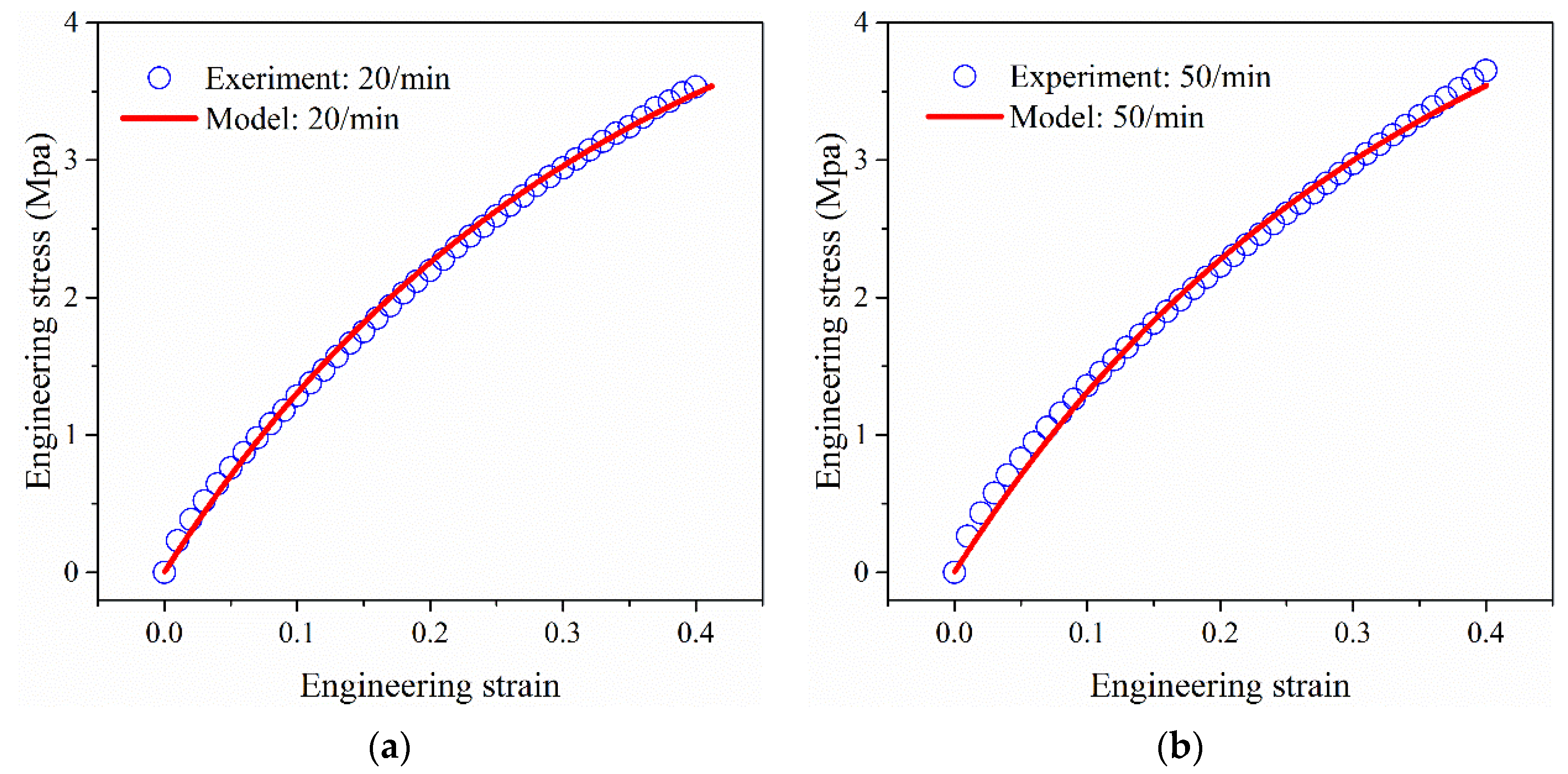
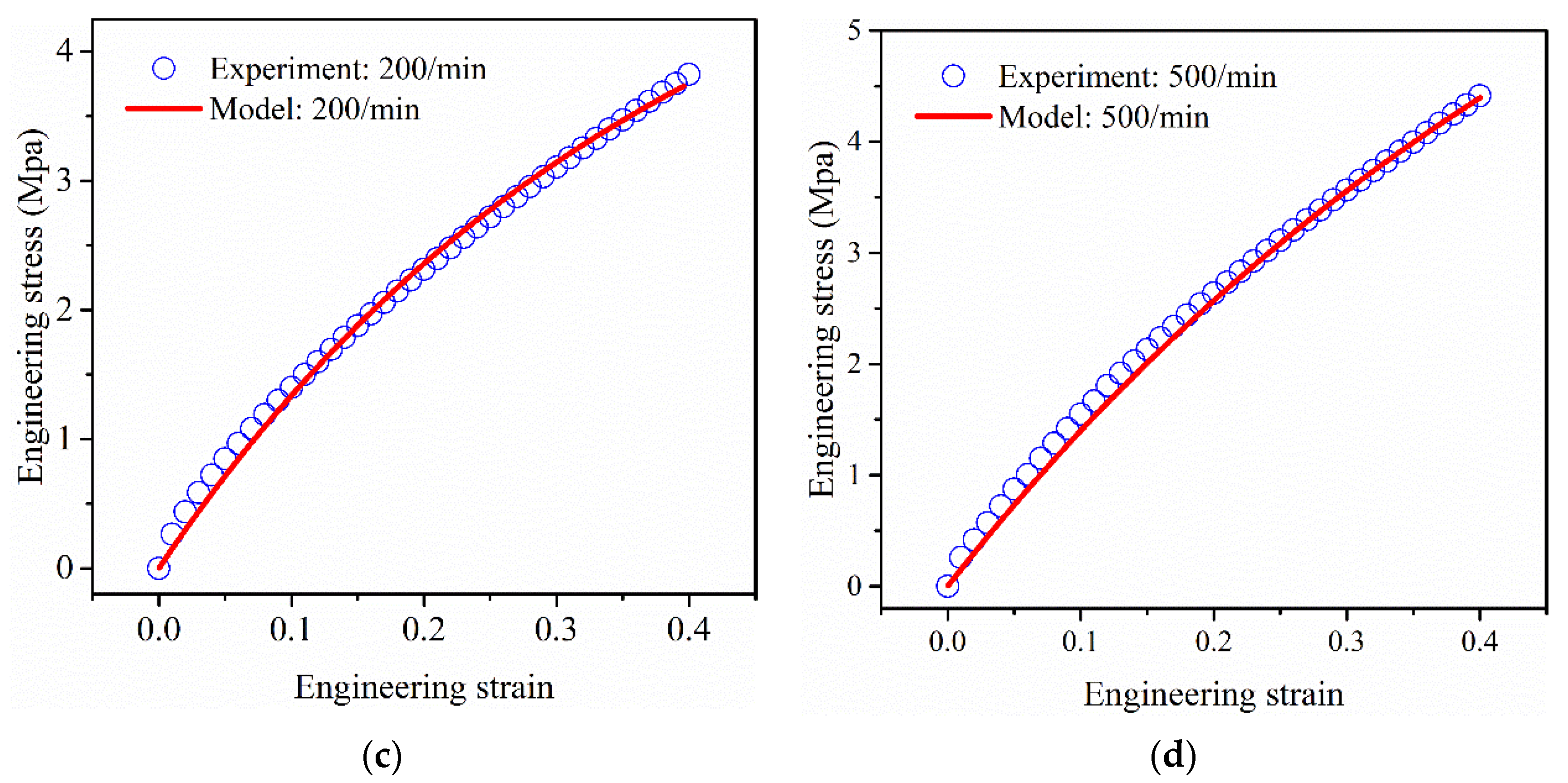
| 20/min | 50/min | 200/min | 500/min | ||
|---|---|---|---|---|---|
| SSE | |||||
| 15.16 | 10.98 | 1.81 × 10−5 | 3.29 × 10−5 | 6.72 × 10−5 | 2.48 × 10−4 |
| SSE | ||||
|---|---|---|---|---|
| 90.26 | 142 | 36.03 | 0.142 | 6.232 × 10−4 |
| Model Parameters | Stretch Rate | SSE | |||
|---|---|---|---|---|---|
| Before yielding | 0.0065/s | 0.9621 | 0.6044 | 0.5105 | 9.6 × 10−6 |
| 0.1613/s | 1.107 | 0.9647 | 0.462 | 1.7 × 10−4 | |
| After yielding | 0.0065/s | 0.6412 | 0.7345 | 0.2 | 4.9 × 10−3 |
| 0.1613/s | 0.8307 | 0.6957 | 0.1 | 2.5 × 10−3 |
| Model Parameters | Stretch Rate | SSE | ||||
|---|---|---|---|---|---|---|
| Before yielding | 0.0065/s | 0.2997 | 4.819 | 0.07 | 0.5126 | 3.6 × 10−3 |
| 0.1613/s | 1.302 | 0.5482 | 0.0336 | 0.295 | 2.1 × 10−4 | |
| After yielding | 0.0065/s | 0.5976 | 1.355 | −0.1016 | 0.8475 | 7.2 × 10−3 |
| 0.1613/s | 0.455 | 485.1 | 0.0131 | 0.0191 | 5.7 × 10−4 |
| Porosity (%) | SSE | ||||
|---|---|---|---|---|---|
| Case 1: 48.80 | 460 | 8 | 460 | 0.00056 | 3.25 × 10−5 |
| Case 2: 58.74 | 325 | 12.9 | 325 | 0.00071 | 2.23 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Yin, D.; Zhao, B. A Variable-Order Fractional Constitutive Model to Characterize the Rate-Dependent Mechanical Behavior of Soft Materials. Fractal Fract. 2022, 6, 590. https://doi.org/10.3390/fractalfract6100590
Gao Y, Yin D, Zhao B. A Variable-Order Fractional Constitutive Model to Characterize the Rate-Dependent Mechanical Behavior of Soft Materials. Fractal and Fractional. 2022; 6(10):590. https://doi.org/10.3390/fractalfract6100590
Chicago/Turabian StyleGao, Yunfei, Deshun Yin, and Bin Zhao. 2022. "A Variable-Order Fractional Constitutive Model to Characterize the Rate-Dependent Mechanical Behavior of Soft Materials" Fractal and Fractional 6, no. 10: 590. https://doi.org/10.3390/fractalfract6100590
APA StyleGao, Y., Yin, D., & Zhao, B. (2022). A Variable-Order Fractional Constitutive Model to Characterize the Rate-Dependent Mechanical Behavior of Soft Materials. Fractal and Fractional, 6(10), 590. https://doi.org/10.3390/fractalfract6100590







