Numerical Simulations of the Oscillating Second-Grade Fluid through a Rectangular Cross Duct with Fractional Constitution Relationship
Abstract
:1. Introduction
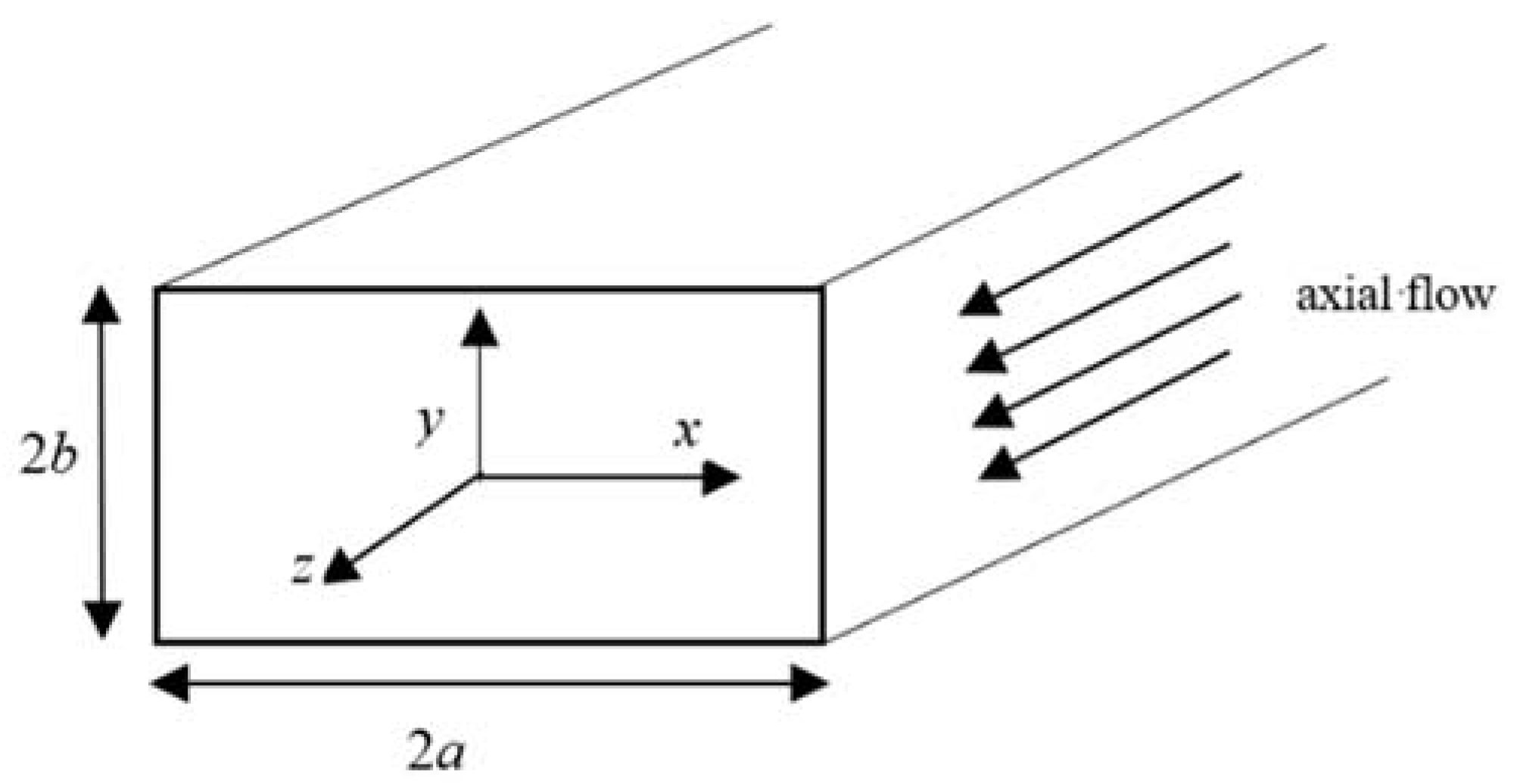
2. The Derivation of the Mathematical Model
3. Analytical Solution
4. Numerical Discretization Method
Numerical Scheme
5. Feasibility Analysis
5.1. Solvability
5.2. Stability
5.3. Convergence
6. Acceleration of the Fractional Derivative
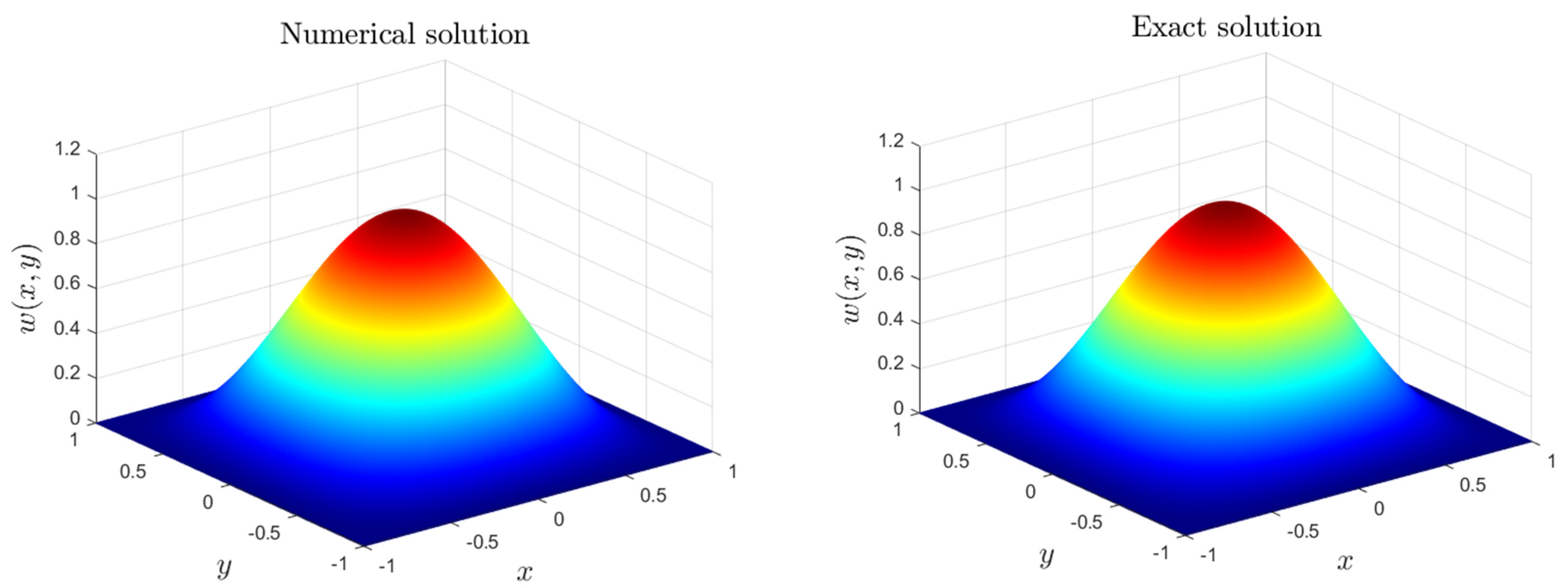
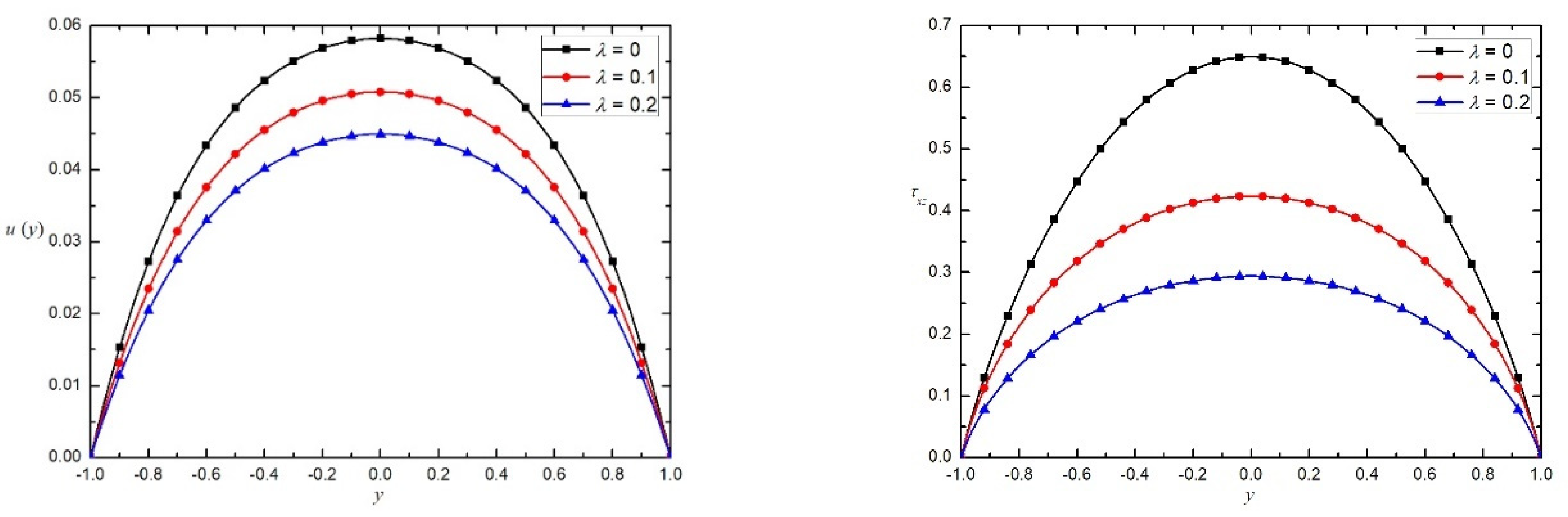
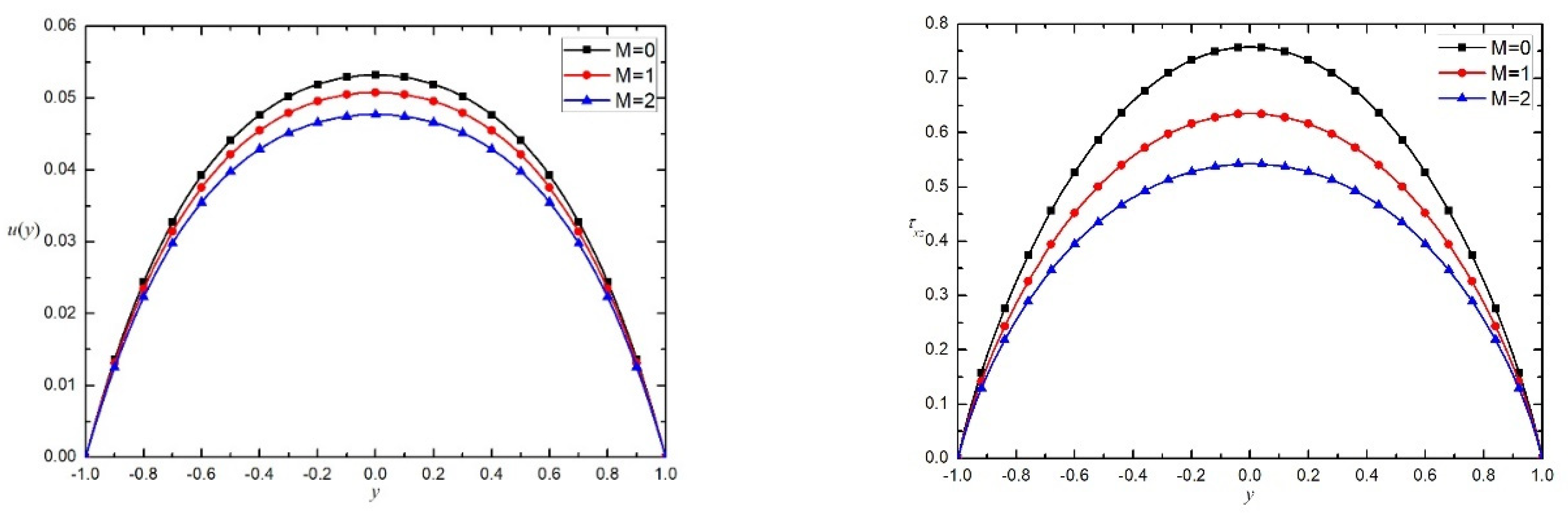
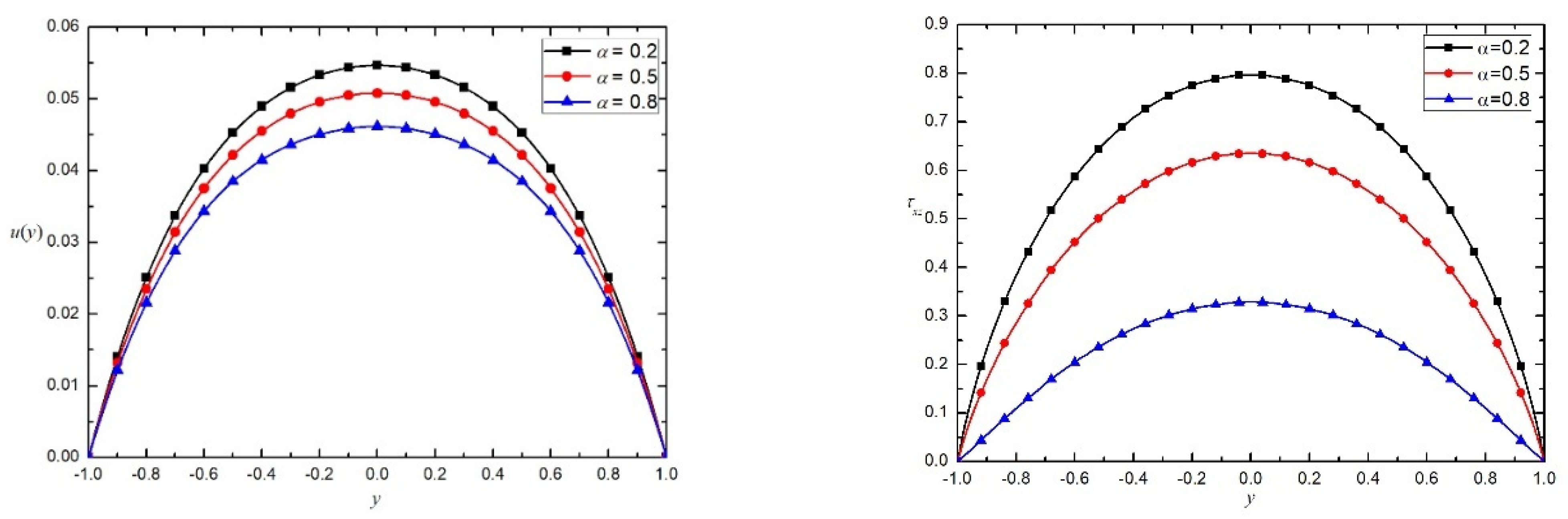
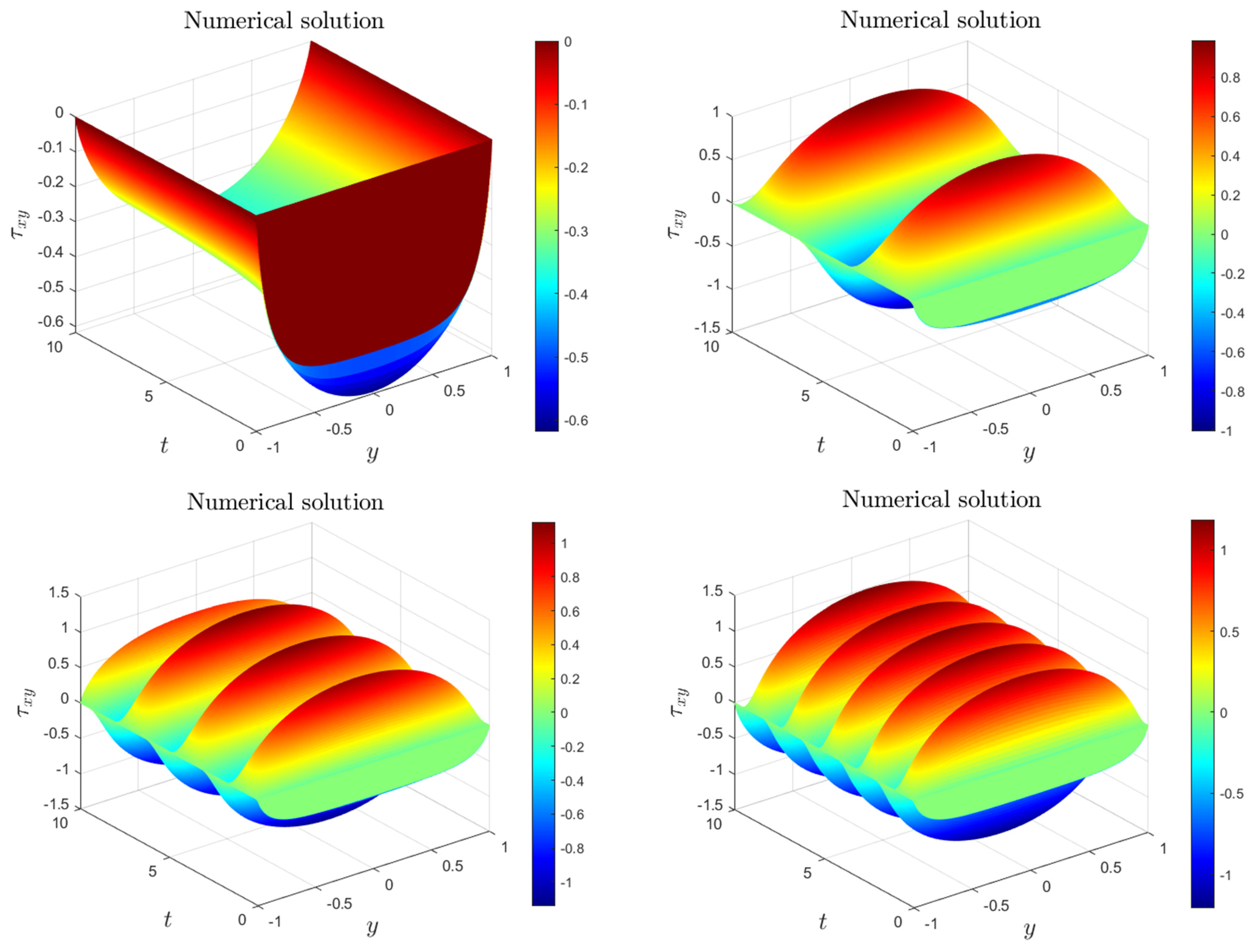
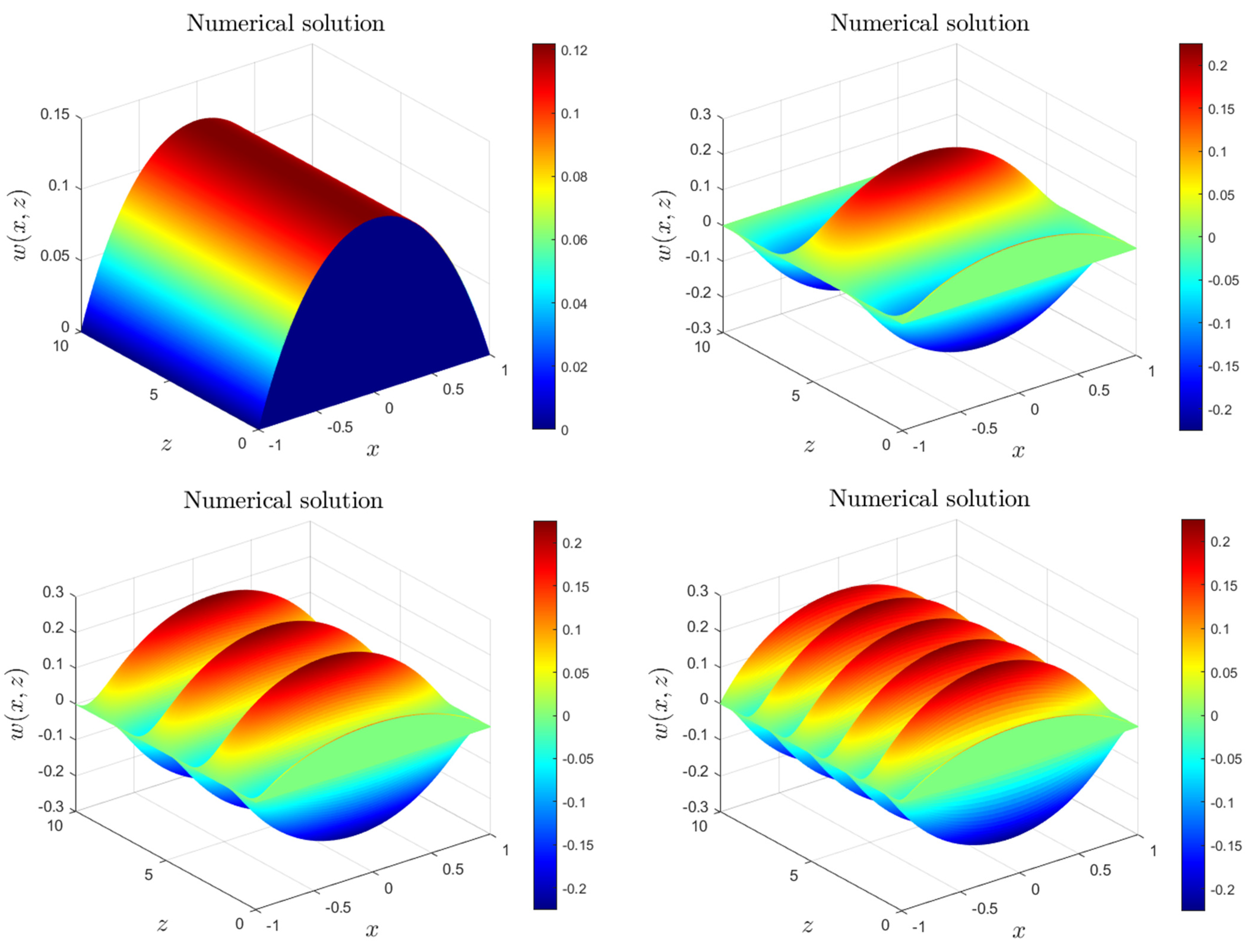
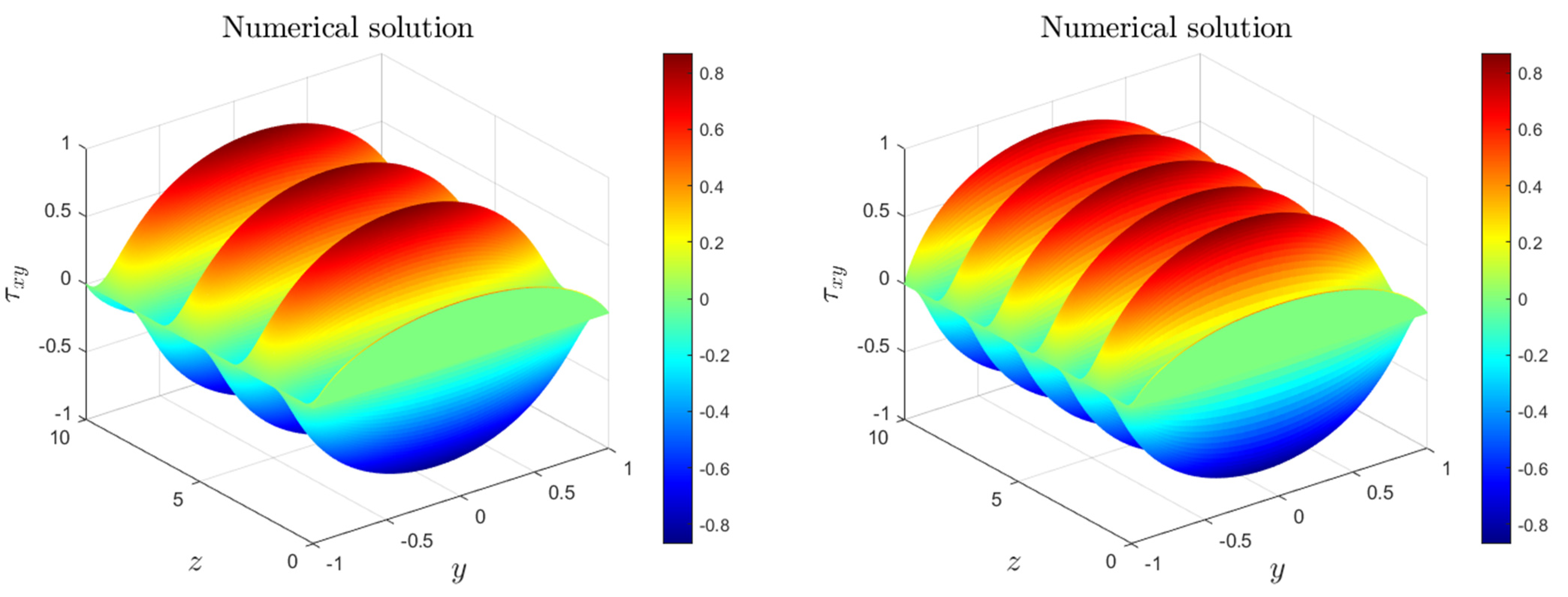
7. Results and Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Barna, I.F.; Bognár, G.; Hriczó, K. Self-similar analytic solution of the two dimensional Navier-Stokes equation with a non-Newtonian type of viscosity. Math. Model. Anal. 2016, 21, 83–94. [Google Scholar] [CrossRef] [Green Version]
- Markovitz, H.; Coleman, B.D. Incompressible second-order fluids. Adv. Appl. Mech. 1964, 8, 69–101. [Google Scholar]
- Coleman, B.D.; Noll, W. An approximation theorem for functionals, with applications in continuum mechanics. Arch. Ration. Mech. Anal. 1960, 6, 355–370. [Google Scholar] [CrossRef]
- Kaloni, P.N. Some remarks on “useful theorems for the second order fluid”. J. Non-Newton. Fluid Mech. 1989, 31, 115–120. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.S.; Mandal, A.C. Transient growth in a flat plate boundary layer under a stream with uniform shear. Phys. Fluids 2022, 33, 114101. [Google Scholar] [CrossRef]
- Bognár, G. Similarity solution of boundary layer flows for non-Newtonian fluids. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 1555–1566. [Google Scholar] [CrossRef]
- Chaves-Guerrero, A.; Peña-Cruz, V.A.; Rinaldi, C.; Fuentes-Díaz, D. Spin-up flow in non-small magnetic fields: Numerical evaluation of the predictions of the common magnetization relaxation equations. Phys. Fluids 2017, 29, 073102. [Google Scholar] [CrossRef]
- Galionis, I.; Hall, P. Stability of the flow in a slowly diverging rectangular duct. J. Fluid Mech. 2006, 555, 43–58. [Google Scholar] [CrossRef]
- Escudier, M.P.; Nickson, A.K.; Poole, R.J. Influence of outlet geometry on strongly swirling turbulent flow through a circular tube. Phys. Fluids 2006, 18, 125103. [Google Scholar] [CrossRef]
- Gao, S.; Hartnett, J.P. Heat transfer behavior of Reiner-Rivlin fluids in rectangular ducts. Int. J. Heat Mass Transf. 1996, 39, 1317–1324. [Google Scholar] [CrossRef]
- Erdoǧan, M.E.; İmrak, C.E. Effects of the side walls on the unsteady flow of a second-grade fluid in a duct of uniform cross-section. Int. J. Non-Linear Mech. 2004, 39, 1379–1384. [Google Scholar] [CrossRef]
- Alamri, S.Z.; Khan, A.A.; Azeez, M.; Ellahi, R. Effects of mass transfer on MHD second-grade fluid towards stretching cylinder: A novel perspective of Cattaneo-Christov heat flux model. Phys. Lett. A 2018, 383, 276–281. [Google Scholar] [CrossRef]
- Bernard, J.M. Problem of second-grade fluids in convex polyhedrons. SIAM J. Math. Anal. 2012, 44, 2018–2038. [Google Scholar] [CrossRef] [Green Version]
- Erdoǧan, M.E.; İmrak, C.E. On unsteady unidirectional flows of a second-grade fluid. Int. J. Non-Linear Mech. 2005, 40, 1238–1251. [Google Scholar] [CrossRef]
- Wang, X.; Qiao, Y.; Qi, H.; Xu, H. Numerical study of pulsatile non-Newtonian blood flow and heat transfer in small vessels under a magnetic field. Int. Commun. Heat Mass Transf. 2022, 133, 105930. [Google Scholar] [CrossRef]
- Feng, L.; Liu, F.; Turner, I.; Zheng, L. Novel numerical analysis of multi-term time fractional viscoelastic non-Newtonian fluid models for simulating unsteady MHD Couette flow of a generalized Oldroyd-B fluid. Fract. Calc. Appl. Anal. 2018, 21, 1073–1103. [Google Scholar] [CrossRef] [Green Version]
- Brunner, H.; Ling, L.; Yamamoto, M. Numerical simulations of 2D fractional subdiffusion problems. J. Comput. Phys. 2010, 229, 6613–6622. [Google Scholar] [CrossRef]
- Feng, C.; Li, B.; Si, X.; Wang, W.; Zhu, J. The electro-osmotic flow and heat transfer of generalized Maxwell fluids with distributed-order time-fractional characteristics in microtubules under an alternating field. Phys. Fluids 2021, 33, 113105. [Google Scholar] [CrossRef]
- Feng, L.; Liu, F.; Turner, I.; Zhuang, P. Numerical methods and analysis for simulating the flow of a generalized Oldroyd-B fluid between two infinite parallel rigid plates. Int. J. Heat Mass Transf. 2017, 115, 1309–1320. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.; Anjum, A.; Fetecau, C.; Qi, H. Exact solutions for some oscillating motions of a fractional Burgers’ fluid. Math. Comput. Model. 2010, 51, 682–692. [Google Scholar] [CrossRef]
- Tan, W.; Xu, M. The impulsive motion of flat plate in a generalized second-grade fluid. Mech. Res. Commun. 2002, 29, 3–9. [Google Scholar] [CrossRef]
- Bazhlekova, E.; Jin, B.; Lazarov, R.; Zhou, Z. An analysis of the Rayleigh-Stokes problem for a generalized second-grade fluid. Numer. Math. 2015, 131, 1–31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khan, M.; Wang, S. Flow of a generalized second-grade fluid between two side walls perpendicular to a plate with a fractional derivative model. Nonlinear Anal. Real World Appl. 2009, 10, 203–208. [Google Scholar] [CrossRef]
- Li, J.; Si, X.; Li, B.; Cao, L.; Zhang, P. The effects of depletion layer for electro-osmotic flow of fractional second-grade viscoelastic fluid in a micro-rectangle channel. Appl. Math. Comput. 2020, 385, 125409. [Google Scholar] [CrossRef]
- Sun, X.; Wang, S.; Zhao, M. Oscillatory flow of Maxwell fluid in a tube of isosceles right triangular cross section. Phys. Fluids 2019, 31, 123101. [Google Scholar]
- Xu, H.; Wang, S.; Zhao, M. Oscillatory flow of second-grade fluid in a straight rectangular duct. J. Non-Newton. Fluid Mech. 2020, 279, 104245. [Google Scholar] [CrossRef]
- Fetecau, C.; Hayat, T.; Fetecau, C. Starting solutions for oscillating motions of Oldroyd-B fluids in cylindrical domains. J. Non-Newton. Fluid Mech. 2008, 153, 191–201. [Google Scholar] [CrossRef]
- Fetecau, C.; Hayat, T.; Khan, M.; Fetecau, C. A note on longitudinal oscillations of a generalized Burgers fluid in cylindrical domains. J. Non-Newton. Fluid Mech. 2010, 165, 350–361. [Google Scholar] [CrossRef]
- Manzini, G. An efficient and conservative hybrid method for solving multi-dimensional conservation laws. Numer. Methods Partial. Diff. Eqs. 2009, 25, 1029–1066. [Google Scholar] [CrossRef]
- Harris, P.A.; Garra, R. Nonlinear time-fractional dispersive equations. Commun. Appl. Ind. Math. 2014, 6, e487. [Google Scholar]
- Barna, I.F.; Mátyás, L. Advanced Analytic Self-Similar Solutions of Regular and Irregular Diffusion Equations. Mathematics 2022, 10, 3281. [Google Scholar] [CrossRef]
- Khan, M.; Fetecau, C.; Hayat, T. MHD transient flows in a channel of rectangular cross-section with porous medium. Phys. Lett. A 2007, 369, 44–54. [Google Scholar] [CrossRef]
- Nadeem, S.; Asghar, S.; Hayat, T.; Hussain, M. The rayleigh stokes problem for rectangular pipe in maxwell and second-grade fluid. Meccanica 2008, 43, 495–504. [Google Scholar] [CrossRef]
- Christov, I.C. Stokes first problem for some non-Newtonian fluids: Results and mistakes. Mech. Res. Commun. 2010, 37, 717–723. [Google Scholar] [CrossRef] [Green Version]
- Christov, I.C. On a difficulty in the formulation of initial and boundary conditions for eigenfunction expansion solutions for the start-up of fluid flow. Mech. Res. Commun. 2013, 51, 86–92. [Google Scholar] [CrossRef] [Green Version]
- Majak, J.; Shvartsman, B.; Pohlak, M.; Karjust, K.; Eerme, M.; Tungel, E. Solution of fractional order differential equation by the Haar Wavelet method. Numerical convergence analysis for most commonly used approach. AIP Conf. Proc. 2016, 1738, 480110. [Google Scholar]
- Sun, Z.; Wu, X. A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 2006, 56, 193–209. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, J.; Zhang, Q.; Zhang, Z. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Commun. Comput. Phys. 2015, 21, 650–678. [Google Scholar] [CrossRef] [Green Version]
- Yan, Y.; Sun, Z.; Zhang, J. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations: A second-order scheme. Commun. Comput. Phys. 2017, 22, 1028–1048. [Google Scholar] [CrossRef]
- Gao, G.; Yang, Q. Fast evaluation of linear combinations of caputo fractional derivatives and its applications to multi-Term time-fractional sub-diffusion equations. Numer. Math. Theory Methods Appl. 2020, 13, 433–451. [Google Scholar]
- Lyu, P.; Liang, Y.; Wang, Z. A fast linearized finite difference method for the nonlinear multi-term time-fractional wave equation. Appl. Numer. Math. 2020, 151, 448–471. [Google Scholar] [CrossRef] [Green Version]
- Ran, M.; Lei, X. A fast difference scheme for the variable coefficient time-fractional diffusion wave equations. Appl. Numer. Math. 2021, 167, 31–44. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Dunn, J.E.; Fosdick, R.L. Thermodynamics, stability, and boundedness of fluids of complexity 2 and fluids of second-grade. Arch. Ration. Mech. Anal. 1974, 56, 191–252. [Google Scholar] [CrossRef]
- Dunn, J.E.; Rajagopal, K.R. Fluids of differential type: Critical review and thermodynamic analysis. Int. J. Eng. Sci. 1995, 33, 689–729. [Google Scholar] [CrossRef] [Green Version]
- Shen, S.; Liu, F.; Anh, V.V. The analytical solution and numerical solutions for a two-dimensional multi-term time fractional diffusion and diffusion-wave equation. J. Comput. Appl. Math. 2019, 345, 515–534. [Google Scholar] [CrossRef]
- Neudecker, H. A note on kronecker products and matrix equation systems. SIAM J. Appl. Math. 1969, 17, 603–606. [Google Scholar] [CrossRef]
- Berardi, M.; Difonzo, F.V. A quadrature-based scheme for numerical solutions to Kirchhoff transformed Richards’ equation. J. Comput. Dyn. 2022, 9, 69–84. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Topics in Matrix Analysis; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Fu, H.; Liu, H.; Wang, H. A finite volume method for two-dimensional Riemann-Liouville space-fractional diffusion equation and its efficient implementation. J. Comput. Phys. 2019, 388, 316–334. [Google Scholar] [CrossRef]
- Sun, H.; Sun, Z. A fast temporal second-order compact ADI difference scheme for the 2D multi-term fractional wave equation. Numer. Algorithms 2021, 86, 761–797. [Google Scholar] [CrossRef]


| Normal L1 Method | Fast Algorithm | |||||
|---|---|---|---|---|---|---|
| Error | Order | Time (s) | Error | Order | TIME (s) | |
| 6.58 | ||||||
| 2.00 | 317.32 | 2.00 | 8.78 | |||
| 2.00 | 2737.48 | 2.00 | 14.61 | |||
| 2.00 | 16,424.92 | 2.00 | 43.06 | |||
| 1.99 | 59,840.35 | 1.99 | 185.47 | |||
| Normal Scheme | Fast Scheme | |||||
|---|---|---|---|---|---|---|
| Error | Order | Time (s) | Error | Order | Time (s) | |
| 2749.74 | 6.83 | |||||
| 1.02 | 2851.14 | 1.02 | 14.90 | |||
| 1.02 | 3057.22 | 1.02 | 33.67 | |||
| 1.02 | 3579.91 | 1.02 | 70.72 | |||
| 1.01 | 4622.72 | 1.01 | 147.05 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Liu, L.; Chen, S.; Zhang, S.; Liu, L.; Feng, L.; Zhu, J.; Zhang, J.; Zheng, L. Numerical Simulations of the Oscillating Second-Grade Fluid through a Rectangular Cross Duct with Fractional Constitution Relationship. Fractal Fract. 2022, 6, 666. https://doi.org/10.3390/fractalfract6110666
Zhang B, Liu L, Chen S, Zhang S, Liu L, Feng L, Zhu J, Zhang J, Zheng L. Numerical Simulations of the Oscillating Second-Grade Fluid through a Rectangular Cross Duct with Fractional Constitution Relationship. Fractal and Fractional. 2022; 6(11):666. https://doi.org/10.3390/fractalfract6110666
Chicago/Turabian StyleZhang, Bo, Lin Liu, Siyu Chen, Sen Zhang, Lang Liu, Libo Feng, Jing Zhu, Jiangshan Zhang, and Liancun Zheng. 2022. "Numerical Simulations of the Oscillating Second-Grade Fluid through a Rectangular Cross Duct with Fractional Constitution Relationship" Fractal and Fractional 6, no. 11: 666. https://doi.org/10.3390/fractalfract6110666
APA StyleZhang, B., Liu, L., Chen, S., Zhang, S., Liu, L., Feng, L., Zhu, J., Zhang, J., & Zheng, L. (2022). Numerical Simulations of the Oscillating Second-Grade Fluid through a Rectangular Cross Duct with Fractional Constitution Relationship. Fractal and Fractional, 6(11), 666. https://doi.org/10.3390/fractalfract6110666








