A Reliable Approach for Solving Delay Fractional Differential Equations
Abstract
:1. Introduction
2. Basic Definitions and Formulas
3. Method of Solution
4. Theoretical Results
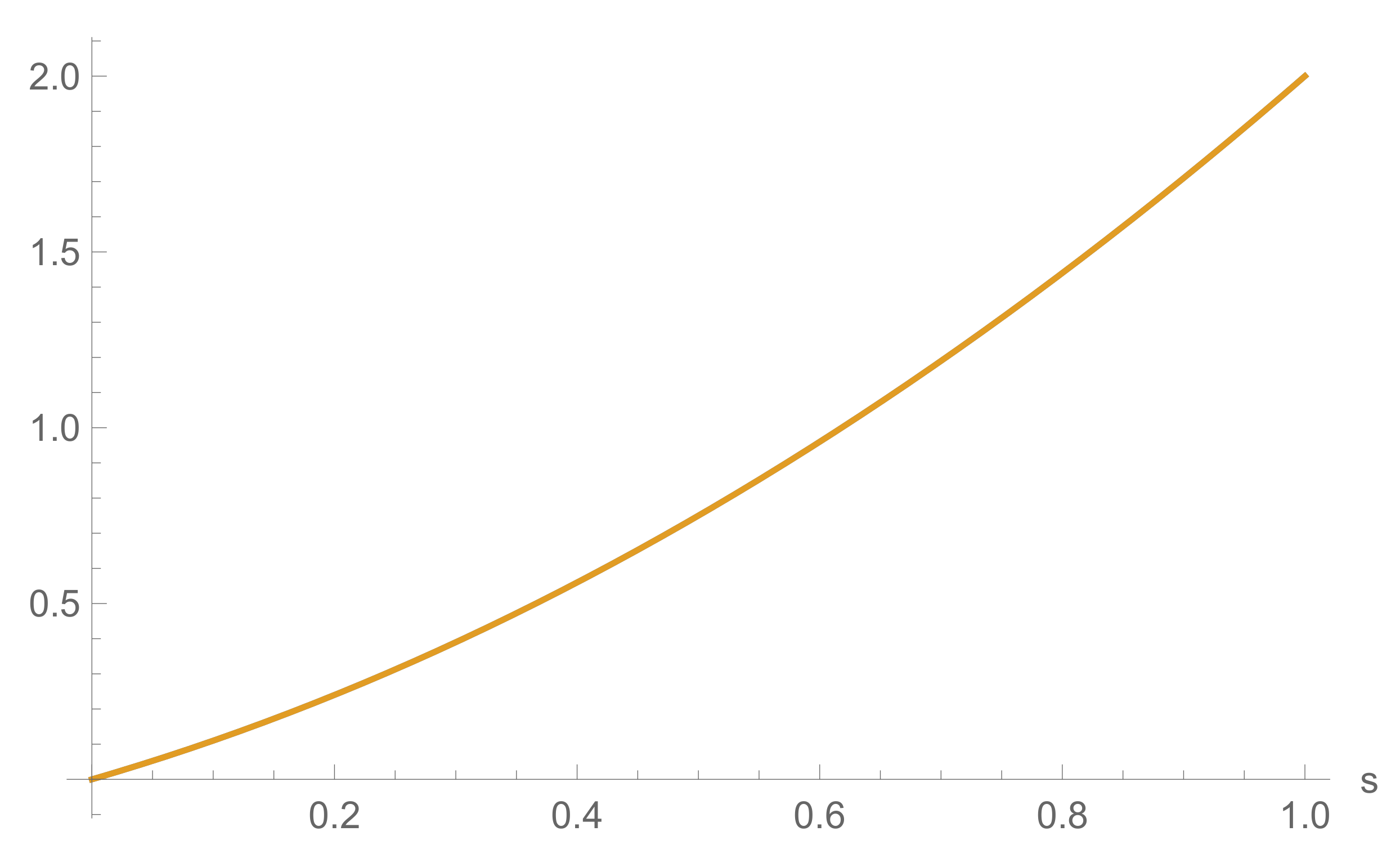
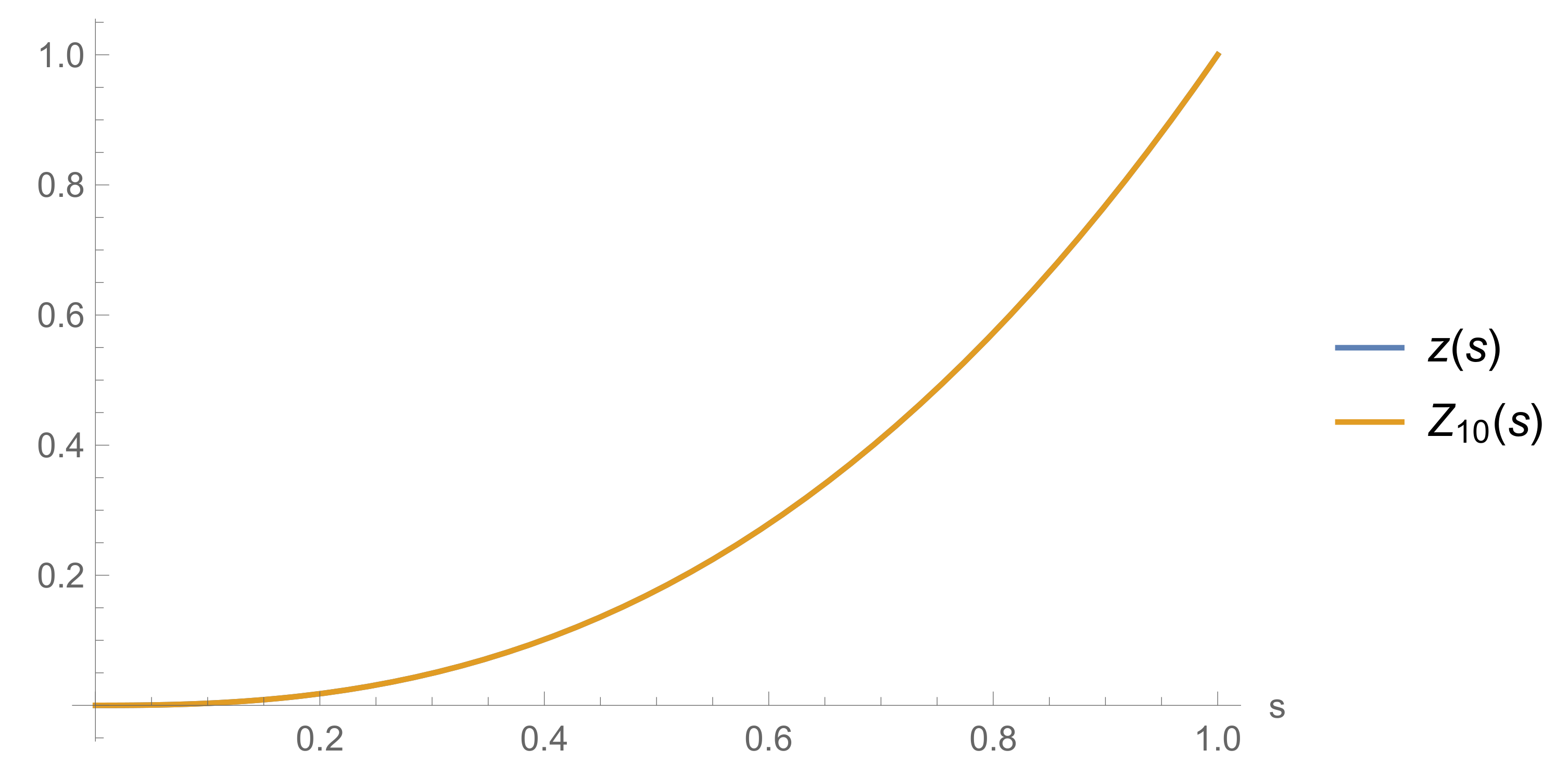
5. Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alshomrani, A.; Ullah, M.; Baleanu, D. Caputo SIR model for COVID-19 under optimized fractional order. Adv. Differ. Equ. 2021, 2021, 185. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Ullah, R.; Baleanu, D. Mathematical analysis of tuberculosis control model using nonsingular kernel type Caputo derivative. Adv. Differ. Equ. 2021, 2021, 26. [Google Scholar] [CrossRef]
- Omay, T.; Baleanu, D. Fractional unit-root tests allowing for a fractional frequency flexible Fourier form trend: Predictability of COVID-19. Adv. Differ. Equ. 2021, 2021, 167. [Google Scholar] [CrossRef] [PubMed]
- Alomari, A.K.; Syam, M.; Anakira, N.R.; Jameel, A.F. Homotopy Sumudu transform method for solving applications in physics. Results Phys. 2020, 18, 103265. [Google Scholar] [CrossRef]
- Chen, Y.; Moore, K.L. Analytical stability bound for a class of delayed fractional-order dynamic systems. Nonlinear Dyn. 2002, 29, 191–200. [Google Scholar] [CrossRef]
- Caglar, H.; Caglar, N.; Ozer, M. B-spline solution of non-linear singular boundary value problems arising in physiology. Chaos Solitons Fractals 2009, 39, 1232–1237. [Google Scholar] [CrossRef]
- Shahmorad, S.; Ostadzad, M.H.; Baleanu, D. A Tau-like numerical method for solving fractional delay integro-differential equations. Appl. Numer. Math. 2020, 151, 322–336. [Google Scholar] [CrossRef]
- Syam, M.; Al-Refai, M. First order delay equations Implicit hybrid method. Alex. Eng. J. 2020, 59, 2677–2681. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Yaseen, M.; Yousaf, A.; Srivastava, R. A cubic B-spline collocation method with new approximation for the numerical treatment of the heat equation with classical and non-classical boundary conditions. Phys. Scr. 2021, 96, 045212. [Google Scholar] [CrossRef]
- Zheng, W.; Huang, R.; Luo, Y.; Chen, Y.; Wang, X.; Chen, Y. A Look-up table based fractional order composite controller synthesis method for the PMSM speed servo system. Fractal Fract. 2022, 6, 47. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Al-Hutami, H.; Ahmad, B. A Langevin-type q-variant system of nonlinear fractional integro-difference equations with nonlocal boundary conditions. Fractal Fract. 2022, 6, 45. [Google Scholar] [CrossRef]
- Reyaz, R.; Mohamad, A.; Lim, Y.; Saqib, M.; Shafie, S. Analytical solution for impact of Caputo-Fabrizio fractional derivative on MHD casson fluid with thermal radiation and chemical reaction effects. Fractal Fract. 2022, 6, 38. [Google Scholar] [CrossRef]
- Sene, N. Analytical solutions of a class of fluids models with the Caputo fractional derivative. Fractal Fract. 2022, 6, 35. [Google Scholar] [CrossRef]
- Zhu, C.G.; Kang, W.S. Numerical solution of Burgers-Fisher equation by cubic B-spline quasi-interpolation. Appl. Math. Comp. 2010, 216, 2679–2686. [Google Scholar] [CrossRef]
- Kashkari, B.; Syam, M. A numerical approach for investigating a special class of fractional Riccati equation. Results Phys. 2000, 17, 103080. [Google Scholar] [CrossRef]
- Abdelhakem, M.; Mahmoud, D.; Baleanu, D.; El-kady, M. Shifted ultraspherical pseudo-Galerkin method for approximating the solutions of some types of ordinary fractional problem. Adv. Differ. Equ. 2021, 2021, 110. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Gómez-Aguilar, J. A novel predictor–corrector scheme for solving variable-order fractional delay differential equations involving operators with Mittag–Leffler kernel. Discret. Contin. Dyn. Syst. Ser. 2020, 13, 561–574. [Google Scholar] [CrossRef] [Green Version]
- Daftardar-Gejji, V.; Sukale, Y.; Bhalekar, S. A new predictor-corrector method for fractional differential equations. Appl. Math. Comput. 2014, 244, 158–182. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving non linear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef] [Green Version]
- Gülsu, M.; Gürbüz, B.; Öztürk, Y.; Sezer, M. Laguerre polynomial approach for solving linear delay difference equations. Appl. Math. Comput. 2011, 217, 6765–6776. [Google Scholar] [CrossRef]
- Gürbüz, B.; Sezer, M. Laguerre polynomial solutions of a class of initial and boundary value problems arising in science and engineering fields. Acta Phys. Pol. 2000, 130, 194–197. [Google Scholar] [CrossRef]
- Gurbuz, B.; Sezerm, M. Laguerre polynomial approach for solving nonlinear Klein-Gordon equations. Malays. J. Math. Sci. 2017, 11, 191–203. [Google Scholar]
- Gurbuz, B.; Sezer, M. Modified operational matrix method for second-order nonlinear ordinary differential equations with quadratic and cubic terms. Int. J. Optim. Control Theor. Appl. 2020, 10, 218–225. [Google Scholar] [CrossRef]
- Kashkari, B.; Syam, M. Fractional-order Legendre operational matrix of fractional integration for solving the Riccati equation with fractional order. Appl. Math. Comput. 2016, 290, 281–291. [Google Scholar] [CrossRef]
- Gorenflo, R.; Luchko, Y. Operational method for solving generalized Abel integral equations of second kind. Integral Transform. Spec. Funct. 1997, 5, 47–58. [Google Scholar] [CrossRef]
- Hadid, S.B.; Luchko, Y.F. An operational method for solving fractional differential equations of an arbitrary real order. Panamer. Math. J. 1996, 6, 57–73. [Google Scholar]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Samko, S.G.; Ross, B. Integration and differentiation to a variable fractional order. Integral Transform. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Samko, S. Fractional integration and differentiation of variable order: An overview. Nonlinear Dyn. 2013, 71, 653–662. [Google Scholar] [CrossRef]
- Naylor, A.W.; Sell, G.R. Linear Operator Theory in Engineering and Science, 2nd ed.; Applied Mathematical Sciences; Springer: New York, NY, USA; Berlin, Germany, 1982; Volume 40. [Google Scholar]


| s | |
|---|---|
| 0 | |
| 0.1 | |
| 0.2 | |
| 0.3 | |
| 0.4 | |
| 0.5 | |
| 0.6 | |
| 0.7 | |
| 0.8 | |
| 0.9 | |
| 1.0 |
| s | |
|---|---|
| 0 | |
| 0.1 | |
| 0.2 | |
| 0.3 | |
| 0.4 | |
| 0.5 | |
| 0.6 | |
| 0.7 | |
| 0.8 | |
| 0.9 | |
| 1.0 |
| s | |
|---|---|
| 0 | |
| 0.1 | |
| 0.2 | |
| 0.3 | |
| 0.4 | |
| 0.5 | |
| 0.6 | |
| 0.7 | |
| 0.8 | |
| 0.9 | |
| 1.0 |
| s | |
|---|---|
| 0 | |
| 0.1 | |
| 0.2 | |
| 0.3 | |
| 0.4 | |
| 0.5 | |
| 0.6 | |
| 0.7 | |
| 0.8 | |
| 0.9 | |
| 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hashim, I.; Sharadga, M.; Syam, M.I.; Al-Refai, M. A Reliable Approach for Solving Delay Fractional Differential Equations. Fractal Fract. 2022, 6, 124. https://doi.org/10.3390/fractalfract6020124
Hashim I, Sharadga M, Syam MI, Al-Refai M. A Reliable Approach for Solving Delay Fractional Differential Equations. Fractal and Fractional. 2022; 6(2):124. https://doi.org/10.3390/fractalfract6020124
Chicago/Turabian StyleHashim, Ishak, Mwaffag Sharadga, Muhammed I. Syam, and Mohammed Al-Refai. 2022. "A Reliable Approach for Solving Delay Fractional Differential Equations" Fractal and Fractional 6, no. 2: 124. https://doi.org/10.3390/fractalfract6020124
APA StyleHashim, I., Sharadga, M., Syam, M. I., & Al-Refai, M. (2022). A Reliable Approach for Solving Delay Fractional Differential Equations. Fractal and Fractional, 6(2), 124. https://doi.org/10.3390/fractalfract6020124









