Consensus of Fractional-Order Double-Integral Multi-Agent System in a Bounded Fluctuating Potential
Abstract
:1. Introduction
2. Model and Consensus Analysis of Double-Integral FOMAS
2.1. Double-Integral FOMAS Model and Its Consensus Conditions
2.1.1. Graph Theory
2.1.2. Double-Integral FOMAS
2.1.3. Consensus Conditions for Double-Integral FOMAS
- (1)
- Category 1:.
- (2)
- Category 2:, and the largest eigenvalue of the Laplacian matrixsatisfies.
- (3)
- Category 3:, and the largest eigenvalue of the Laplacian matrixsatisfies
- (1)
- When , that is or , then has two different eigenvalues ;
- (2)
- When , that is or , then has two identical eigenvalues .
- (3)
- When , that is , then has two different eigenvalues .
2.2. Simulation Verification of Consensus Conditions
- (1)
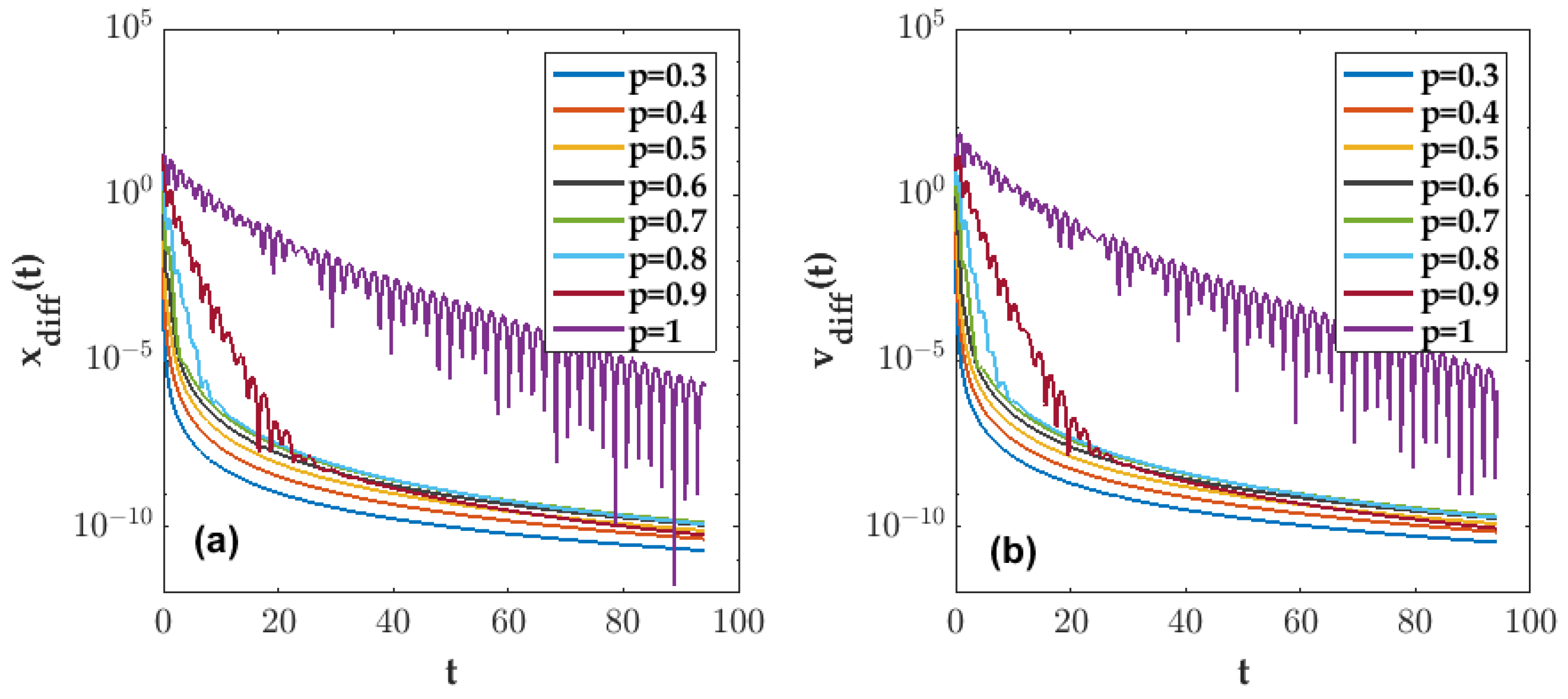
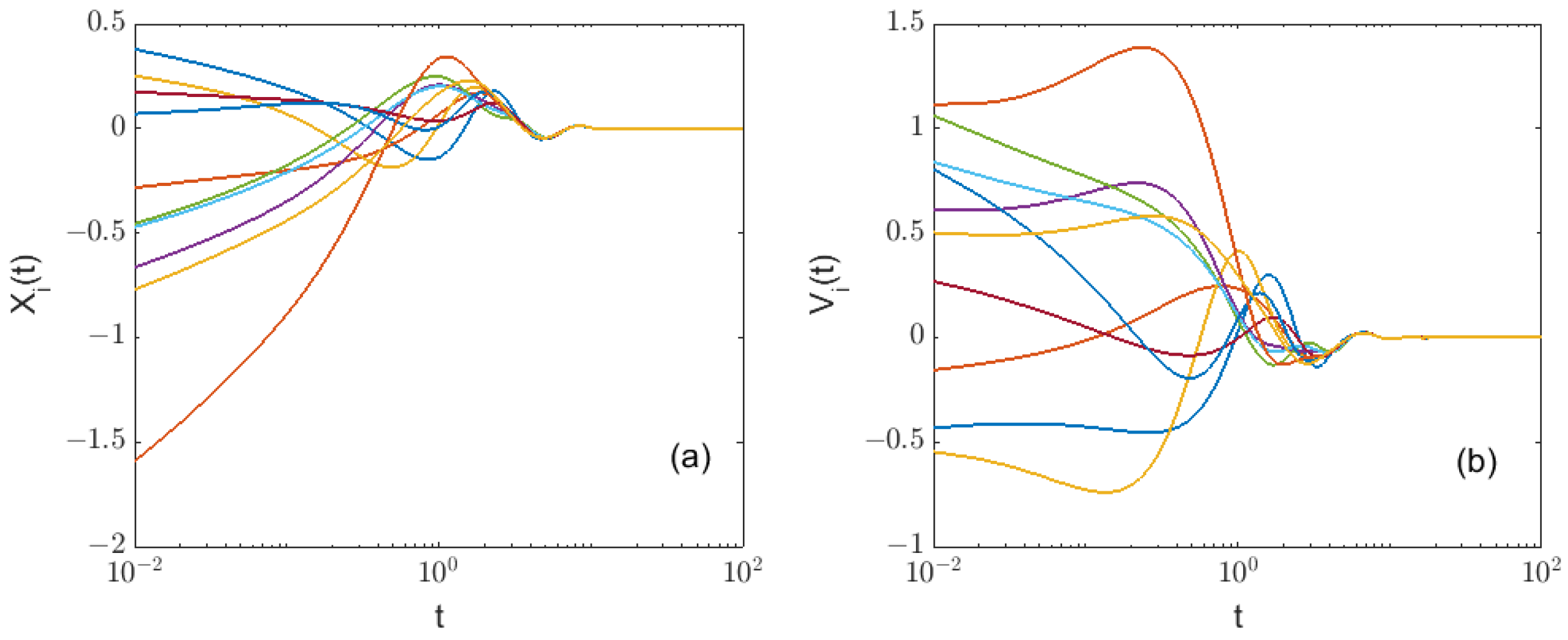
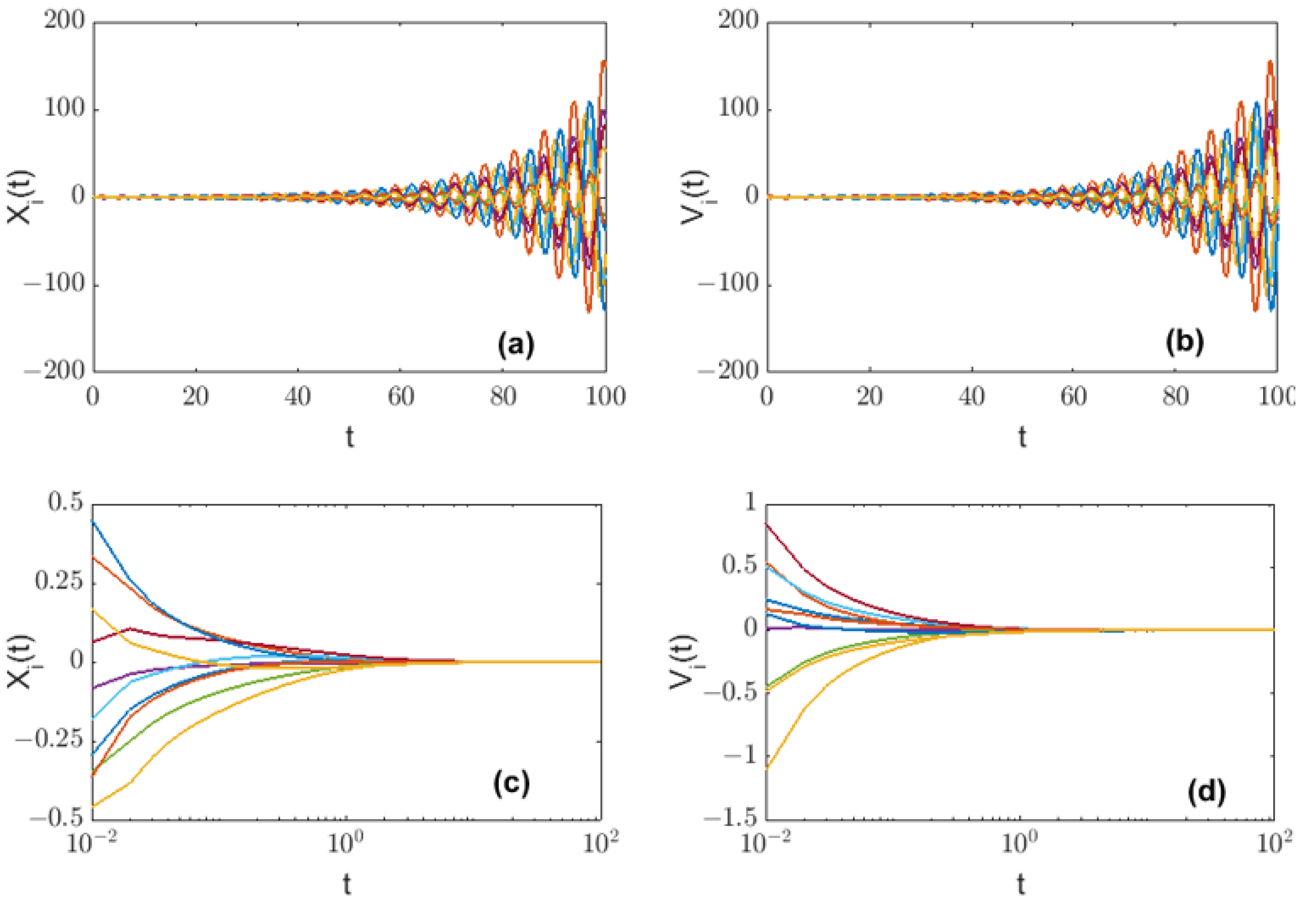
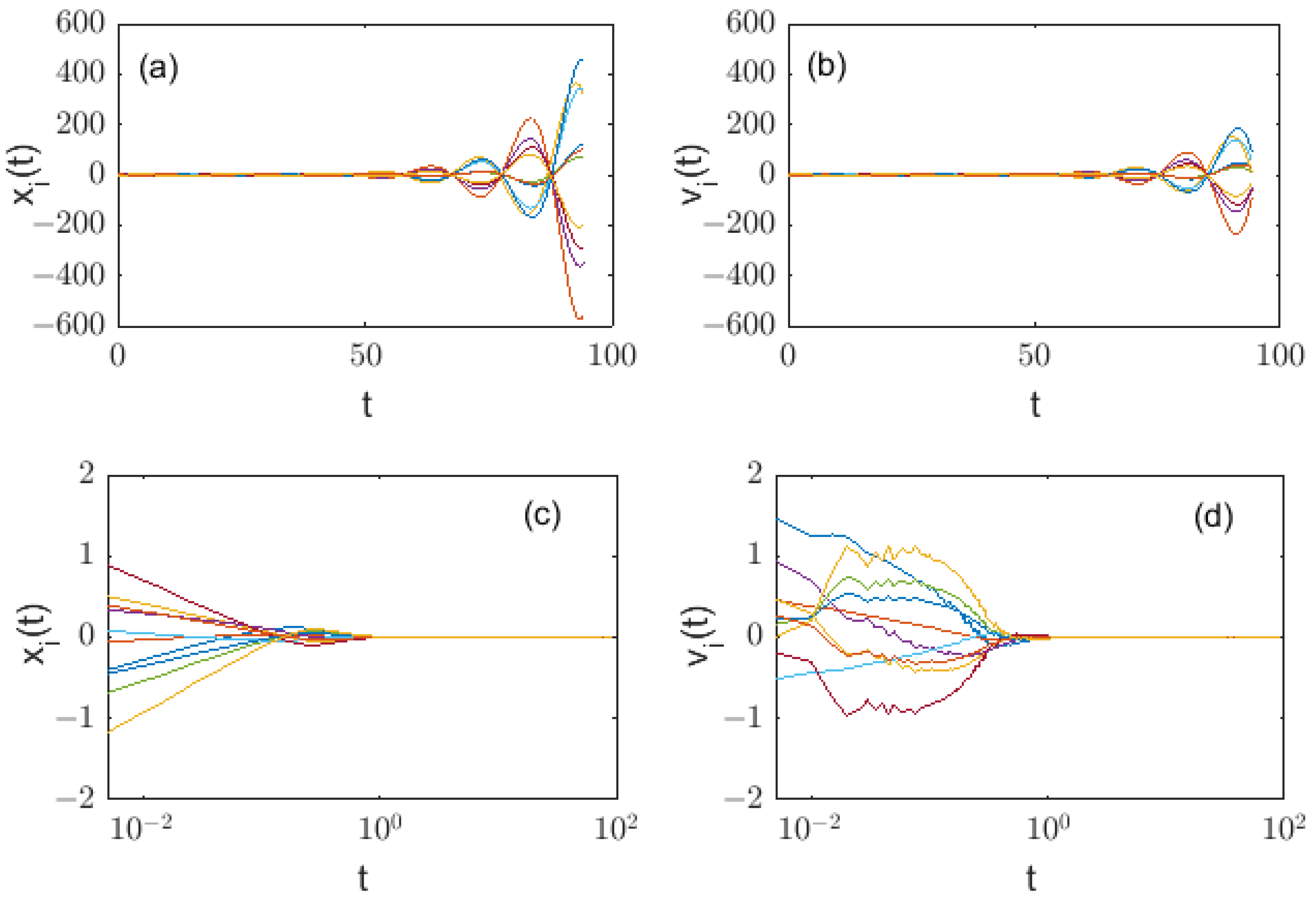
- When the position coupling strength , the velocity coupling strength , and the potential field parameter , Figure 1 shows the time-varying curves of the average position difference function xdiff(t) and average velocity difference function vdiff(t) in Equations (11) and (12) of the FOMAS (3) under different orders. It can be seen that for all fractional orders, the values of the average position difference function and the average velocity difference function gradually decrease as time increases, and converge to a minimum value, indicating that all agents tend to be consistent in terms of position and velocity. In addition, it can be seen that the larger the order, the lower the value of the average position difference function and the average velocity difference function at the same time, indicating that the system achieves synchronization faster.
- (2)
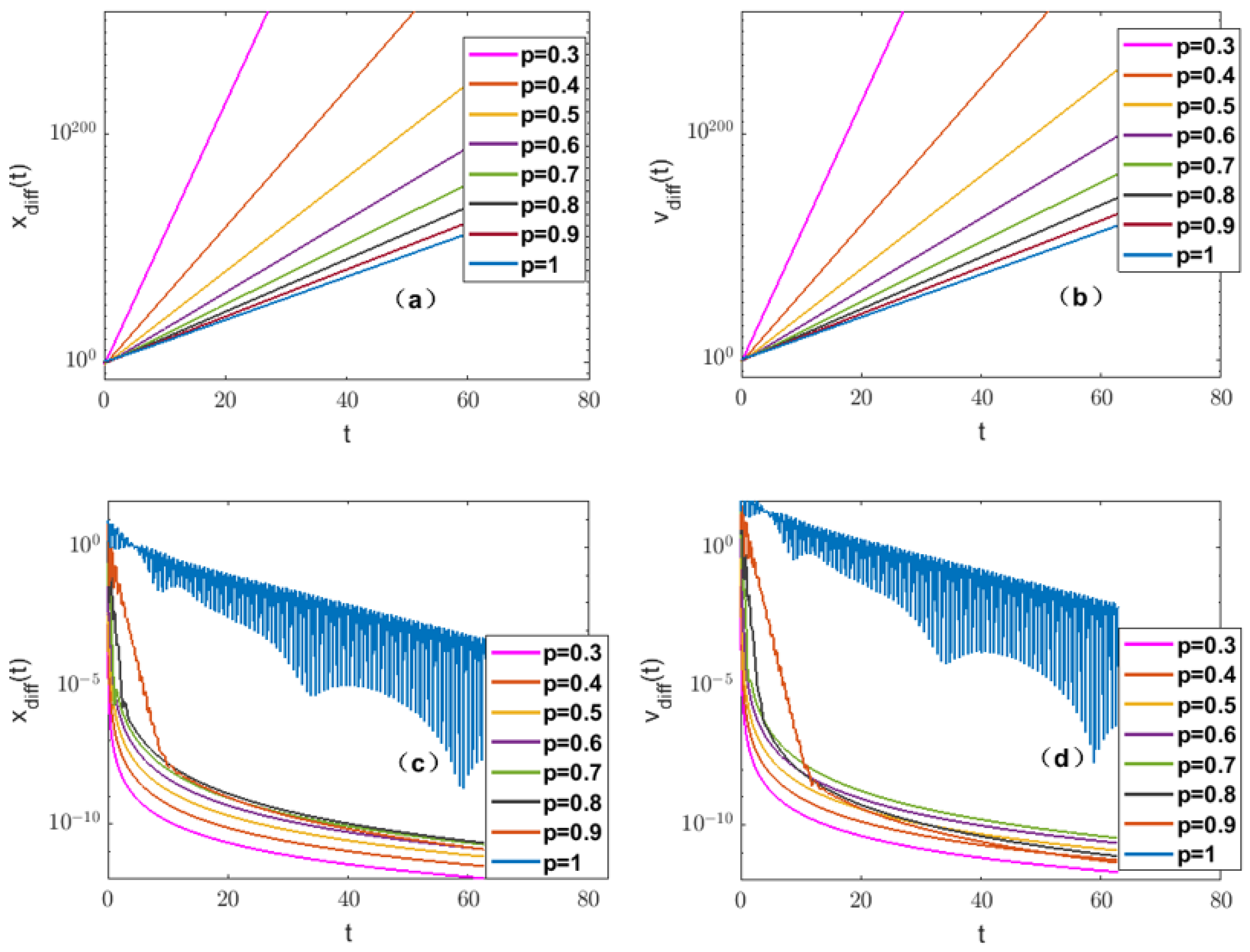
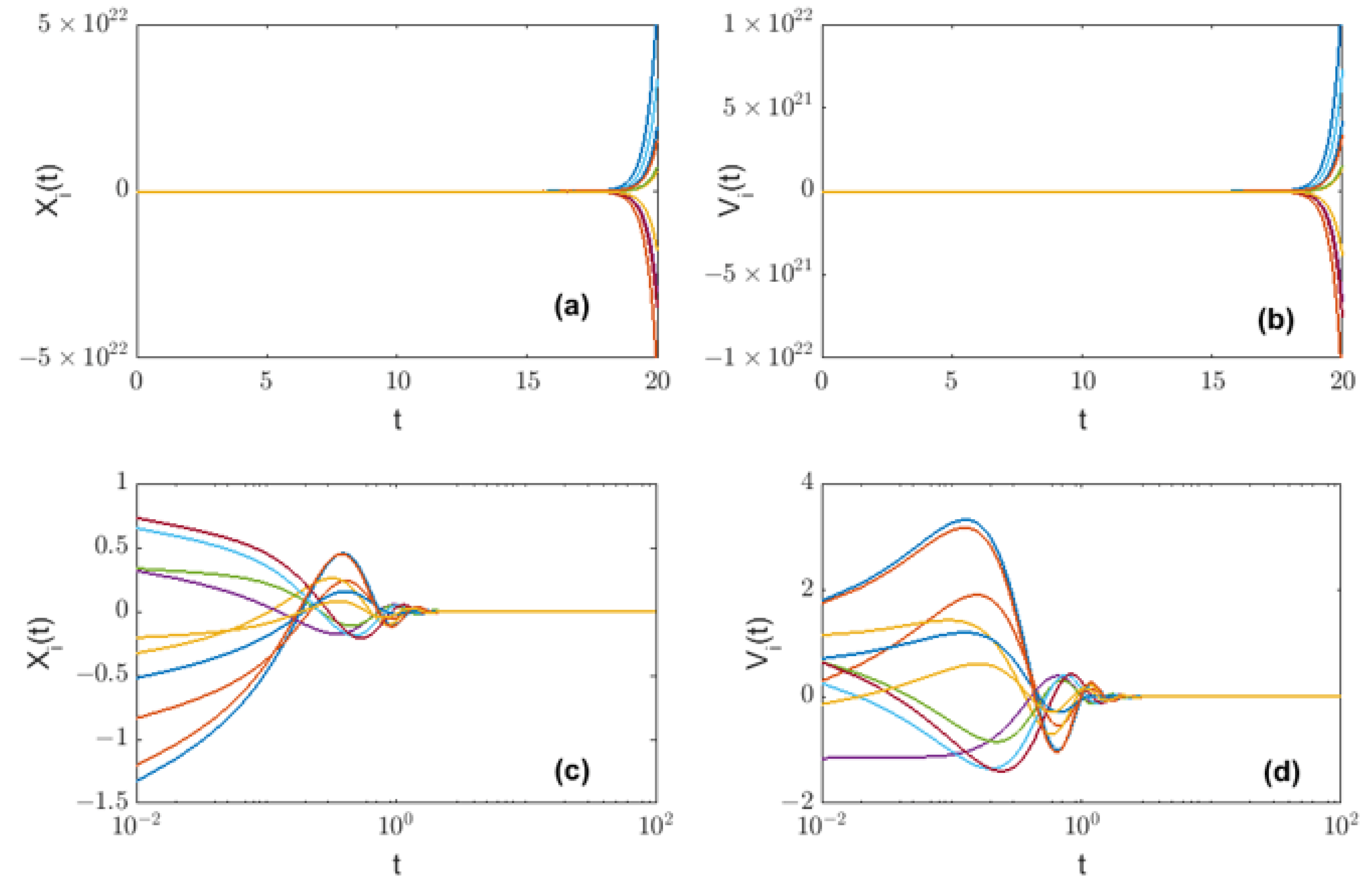
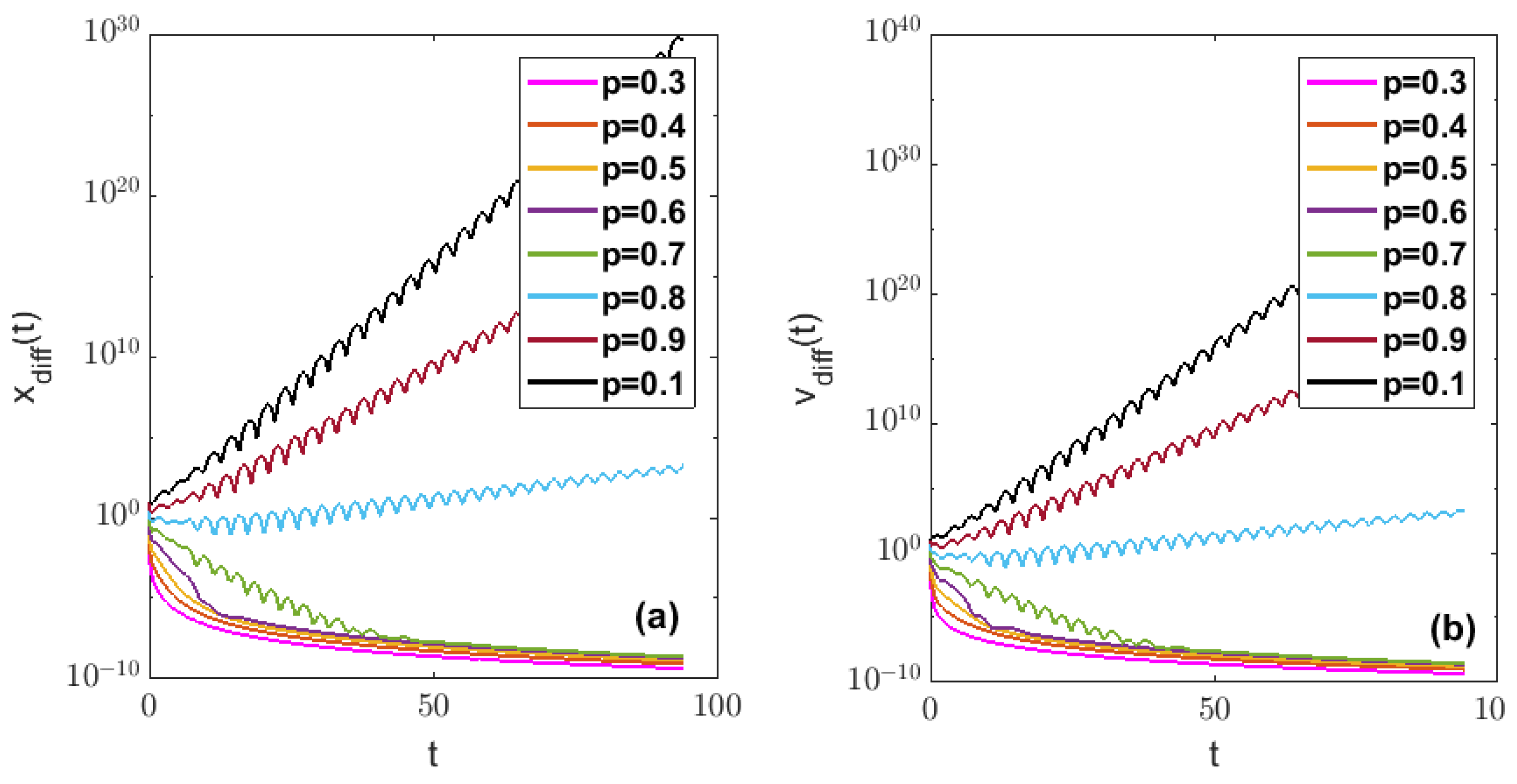
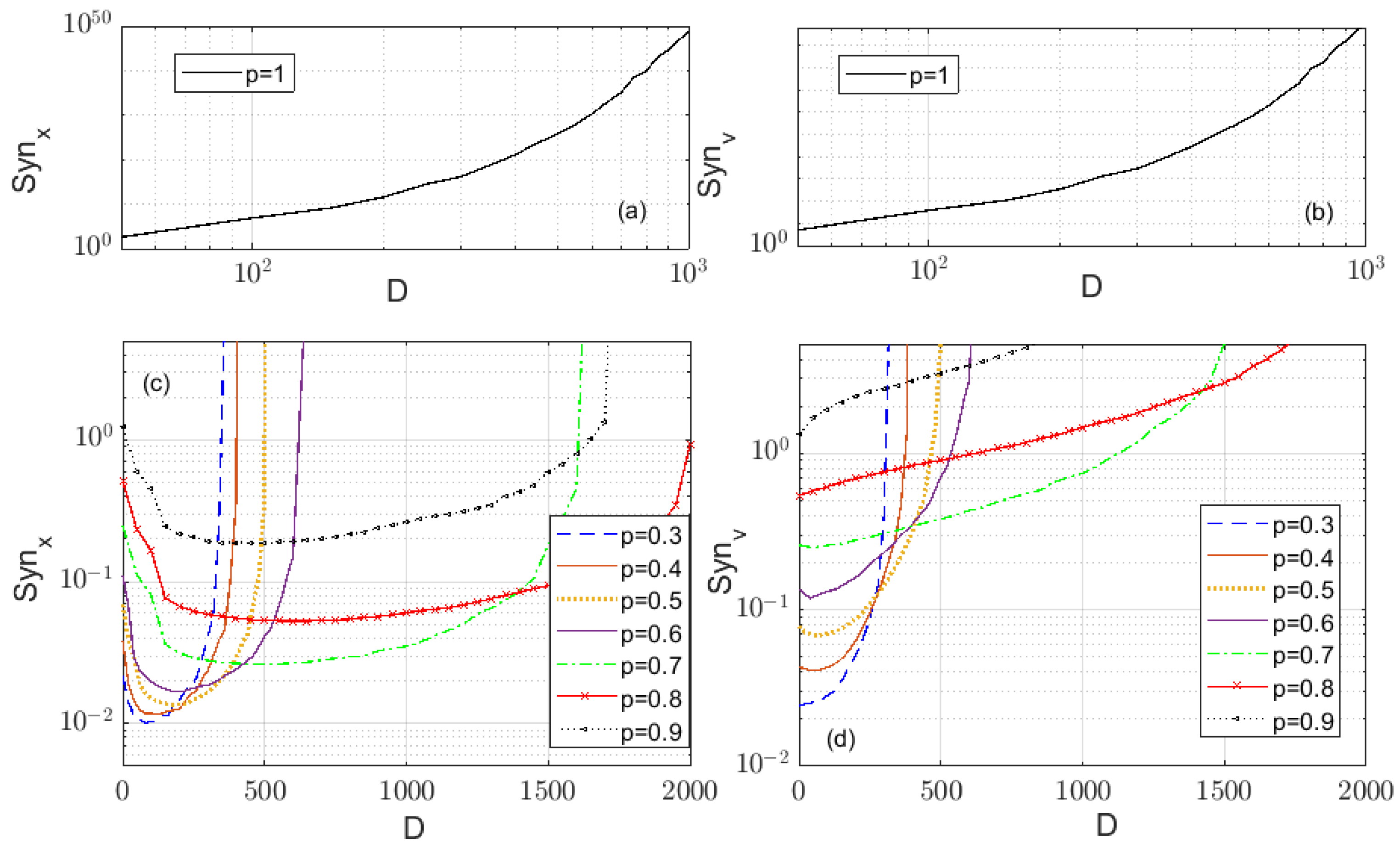
- When the position coupling strength and the velocity coupling strength , Figure 3a–d respectively show the curves of the average position/velocity difference functions of the FOMAS (3) changing with time under different orders. In Figure 3a,b, , and thus , which does not satisfy the consensus conditions in Theorem 1, it can be found that all the curves show a trend of rapid growth to infinity as time increases. In Figure 3c,d, , and thus , which satisfies the consensus conditions in Theorem 1, compared with Figure 3a,b, all curves in Figure 3c,d tend to zero as time increases. At the same time, it can be seen that the larger the order, the lower the average position/velocity difference functions at the same time, and the faster the system achieves consensus.
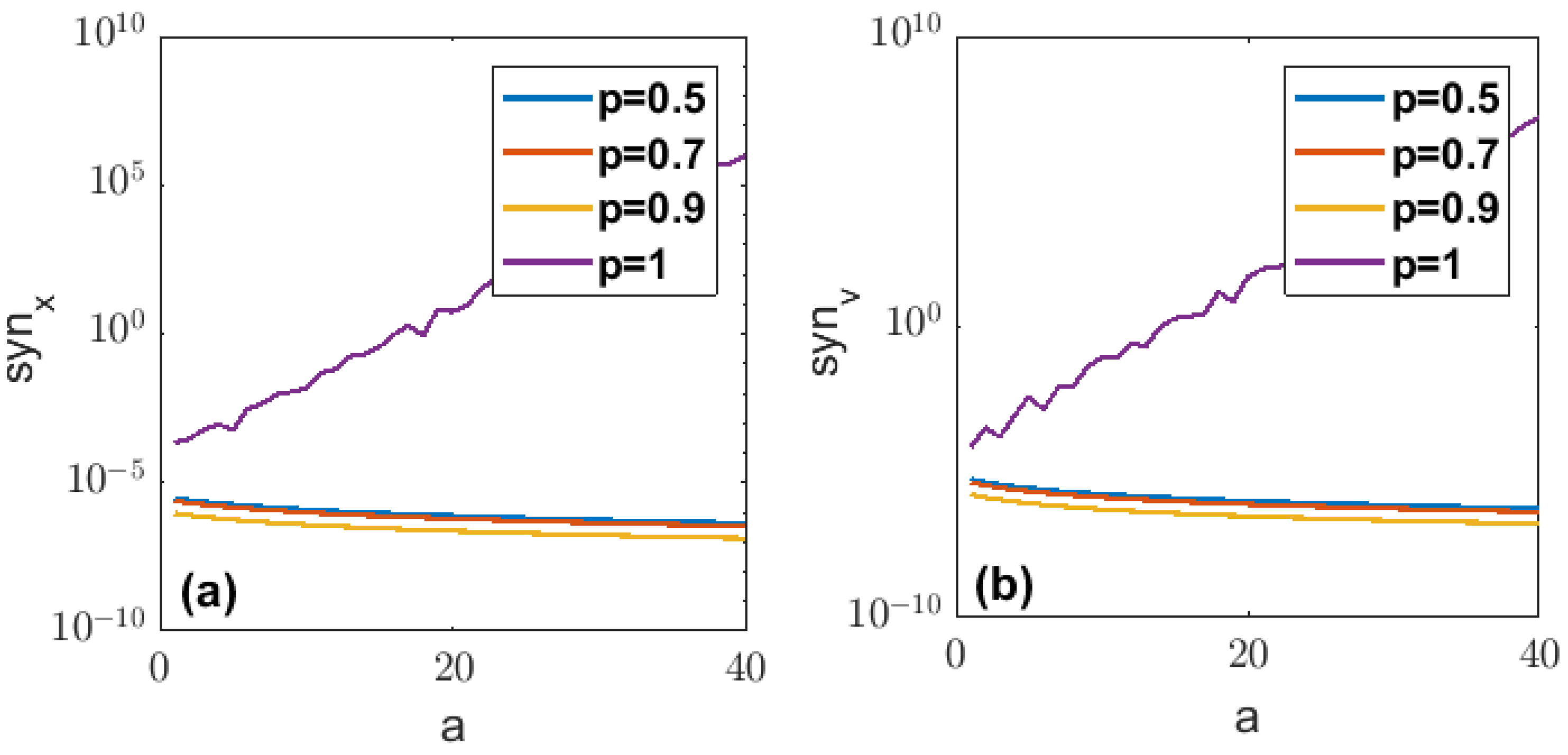
2.3. Influence of Parameters on the Consensus of the Double-Integral FOMAS
- (1)
- Influence of potential parameter a
- (2)
- Influence of position coupling strength c
- (3)
- Influence of velocity coupling strength d
3. Consensus Analysis of Double-Integral FOMAS in a Bounded Fluctuating Potential
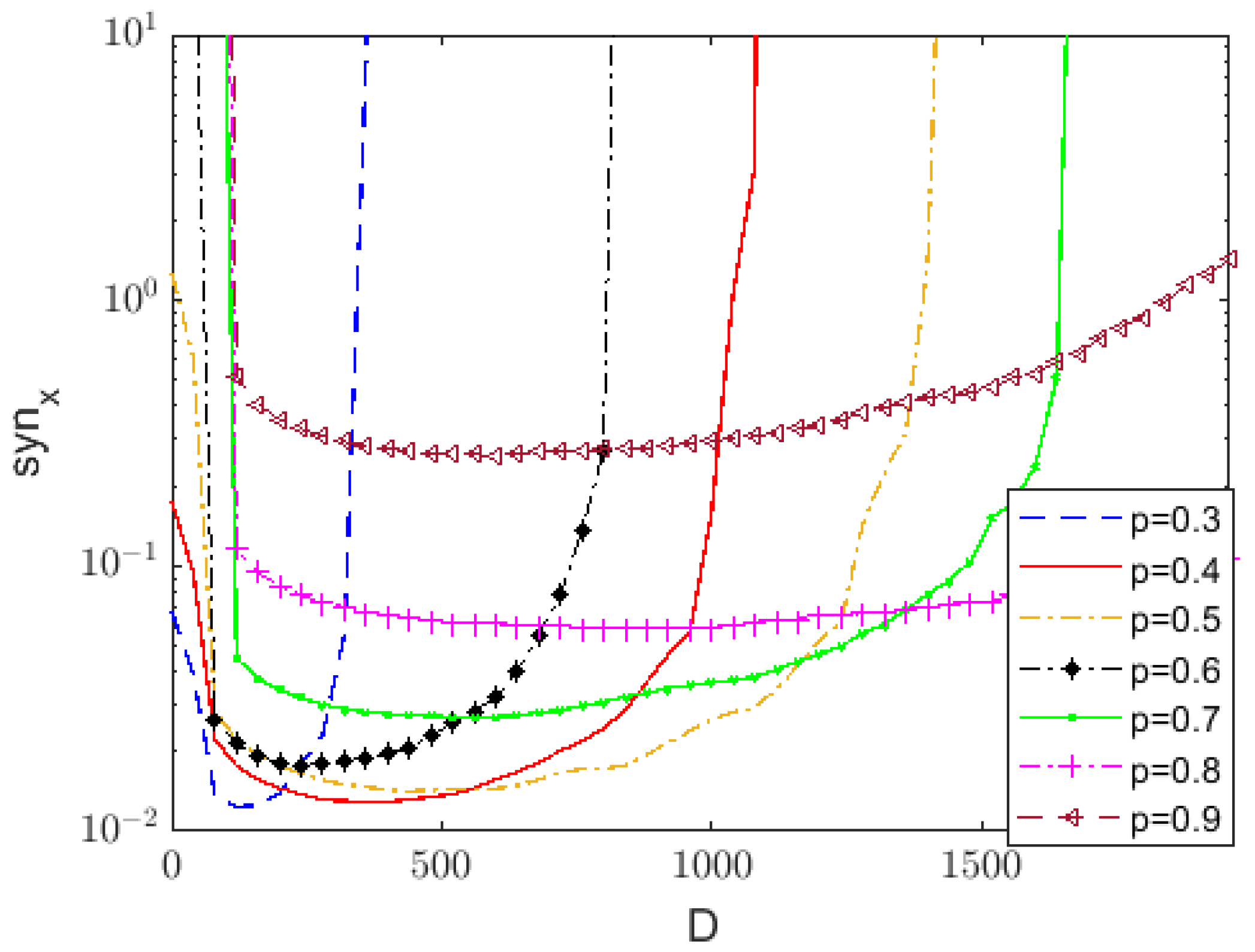
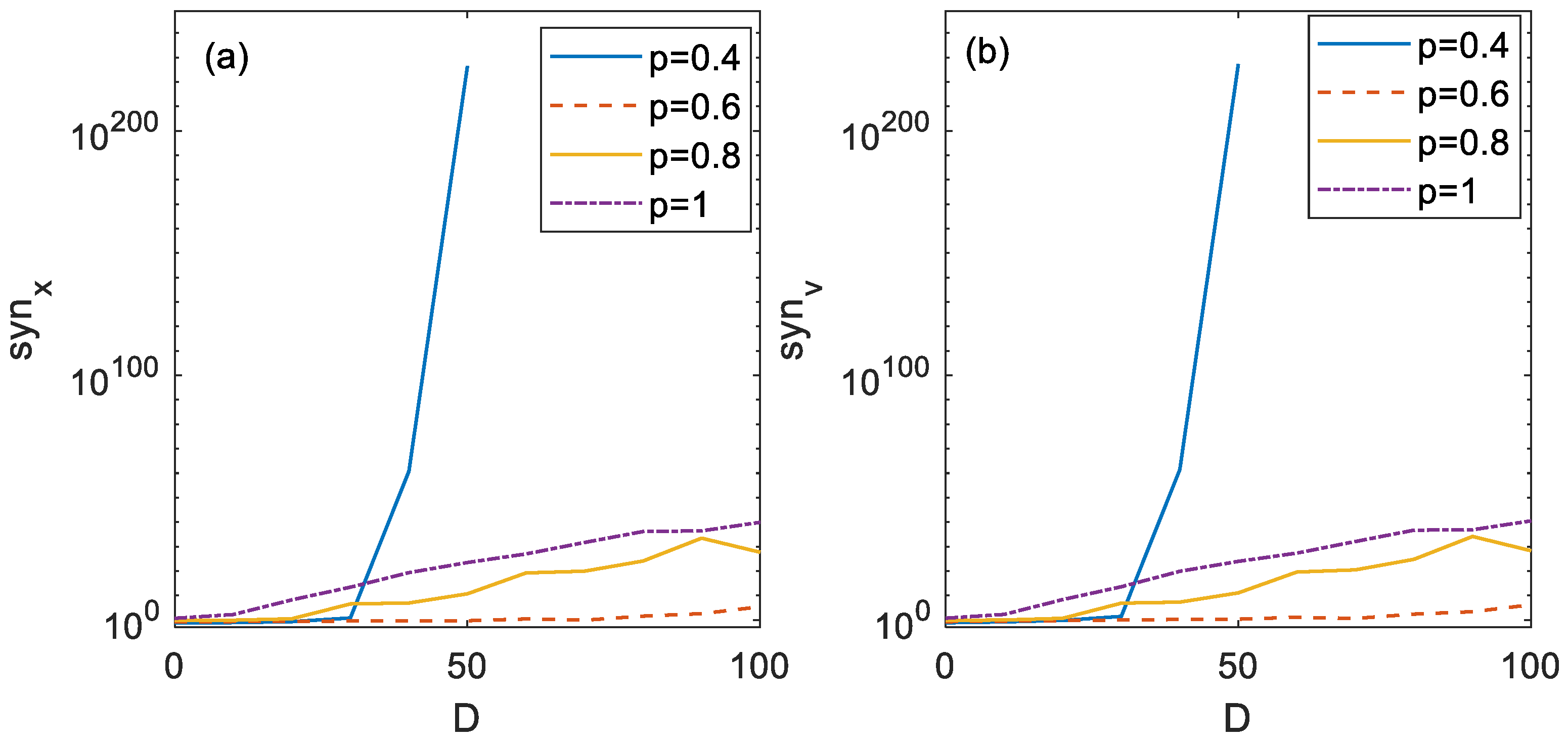
3.1. The Influence of Bounded Noise on System Consensus
3.2. The Influence of Unbounded Noise on System Consensus
4. Conclusions
- (1)
- Several recent papers have discussed the consensus problem of the FOMASs in the absence of noise [23,24,25,26,27,28]. On the one hand, most protocol terms use the relative position information of neighboring agents [24,26], since the relative position state can be obtained more easily through localization methods [27]. In this paper, we consider the protocol term consisting of both the relative position and velocity information of neighboring agents, with the hope of drawing general conclusions from a more general perspective. On the other hand, most of the above literature only gives and verifies the consensus conditions [23,24,25,26,27,28]. In this paper, we not only give the analytical consensus conditions of the presented system in the absence of noise, but also analyze the influences of the system order and other system parameters on the consensus behavior in detail. It is found that the fractional order, coupling strength of the position and velocity, and potential parameters have different effects on the system’s consensus behavior. Moreover, it is easier to achieve position and velocity consensus in the presented FOMAS than in the classical integer-order MAS. That is, the fractional-order system has a larger range of synchronization parameters.
- (2)
- Most specifically, the influences of the system order and other system parameters on the consensus of the presented double-integral FOMASs in the presence of bounded noise are also analyzed in detail. It is found that, due to the synergistic and nonlinear effects of noise and fractional-order systems, common and bounded noise have a promoting effect on the consensus of the presented FOMAS, while it does not promote the consensus of the corresponding integer-order MAS. That is to say, the bounded noise with the appropriate intensity plays an optimization role for the presented FOMAS. It also shows that the fractional-order complex system under the action of noise has richer dynamic characteristics than the integer-order complex system. To our best knowledge, this paper is the first to report the positive effect of noise on the consensus of MASs.
- (3)
- The fractional order and the system parameters (coupling strength and potential parameters) of the presented FOMAS have different effects on the system consensus behavior under the action of noise with different intensities. All of them can change the optimal noise intensity of the system to achieve complete consensus, which also shows that the fractional order, the system parameters, and noise play complementary roles in the complete consensus of the system. When the order and system parameters are controllable, the consensus of the system can be realized by adjusting these parameters; when the order and system parameters are uncontrollable, the double-integral FOMAS can also be synchronized by changing the noise intensity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mainzer, K. Thinking in Complexity: The Complex Dynamics of Matter, Mind and Man-Kind; Springer-Verlag: New York, NY, USA, 1997. [Google Scholar]
- Christen, K. Complexity and Criticality; Fudan University Press: Shanghai, China, 2006. [Google Scholar]
- Yang, L.X.; Jiang, J. Complex dynamical behavior and modified projective synchronization in fractional-order hyper-chaotic complex Lu system. Chaos Soliton Fract. 2015, 78, 267–276. [Google Scholar] [CrossRef]
- Wooldrideg, M. An Introduction to Multi-Agent Systems; Publishing House of Electronics Industry: Beijing, China, 2003. [Google Scholar]
- Zhu, J. Stabilization and synchronization for a heterogeneous multi-agent system via harmonic control. Syst. Control Lett. 2014, 66, 1–7. [Google Scholar] [CrossRef]
- Gambuzza, L.V.; Frasca, M. Distributed control of multi-consensus. IEEE Trans. Autom. Control 2020, 99, 2032–2044. [Google Scholar]
- Mattioni, M. On multiconsensus of multi-agent systems under aperiodic and asynchronous sampling. IEEE Control Syst Lett. 2020, 4, 839–844. [Google Scholar] [CrossRef]
- Panteley, E.; Loría, A. Synchronization and dynamic consensus of heterogeneous networked systems. IEEE Trans. Autom. Control 2017, 62, 3758–3773. [Google Scholar] [CrossRef] [Green Version]
- Mattioni, M.; Monaco, S. Cluster partitioning of heterogeneous multi-agent systems. Automatica 2022, 138, 110136. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Jiang, F.; Xie, D.; Liu, B. Static consensus of second-order multi-agent systems with impulsive algorithm and time-delays. Neurocomputing 2017, 223, 18–25. [Google Scholar] [CrossRef]
- Cacace, F.; Mattioni, M.; Monaco, S.; Ricciardi-Celsi, L. Topology-induced containment for general linear systems on weakly connected digraphs. Automatica 2021, 131, 109734. [Google Scholar] [CrossRef]
- Gambuzza, L.V.; Frasca, M.; Sorrentino, F.; Pecora, L.M.; Boccaletti, S. Controlling symmetries and clustered dynamics of complex networks. IEEE Trans. Netw. Sci. Eng. 2020, 8, 282–293. [Google Scholar] [CrossRef]
- Cristofaro, A.; Mattioni, M. Hybrid consensus for multi-agent systems with time-driven jumps. Nonlinear Anal. Hybrid Syst. 2021, 43, 101113. [Google Scholar] [CrossRef]
- Barkai, G.; Mirkin, L.; Zelazo, D. On Sampled-Data Consensus: Divide and Concur. IEEE Control Syst. Lett. 2021, 6, 343–348. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Ren, W.; Kurths, J.; Zheng, W.X. Distributed higher order consensus protocols multi-agent dynamical systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 1924–1932. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Deng, Z.; Hong, Y. Optimal Output Consensus of High-Order Multiagent Systems With Embedded Technique. IEEE Trans. Cybern. 2018, 49, 1768–1779. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Y.; Wang, J.; Zhang, Y.; Xu, Y. Event-triggered bipartite consensus for high-order multi-agent systems with input saturation. Neurocomputing 2019, 379, 284–295. [Google Scholar] [CrossRef]
- Ni, J.; Wen, C.; Zhao, Y. Fixed-time leader-follower quantized output consensus of high-order multi-agent systems over digraph. Inf. Sci. 2021, 587, 408–434. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Almatroud, A.O. Extreme Multi stability of a Fractional-Order Discrete-Time Neural Network. Fractal Fract. 2021, 5, 202. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Ciancio, A. New Challenges Arising in Engineering Problems with Fractional and Integer Order. Fractal. Fract. 2021, 5, 35. [Google Scholar] [CrossRef]
- Zhu, W.; Li, W.; Zhou, P.; Yang, C. Consensus of fractional-order multi-agent systems with linear models via observer-type protocol. Neurocomputing 2016, 230, 60–65. [Google Scholar] [CrossRef]
- Yu, W.; Li, Y.; Wen, G.; Yu, X.; Cao, J. Observer Design for Tracking Consensus in Second-Order Multi-Agent Systems: Fractional Order Less Than Two. IEEE Trans. Autom. Control 2016, 62, 894–900. [Google Scholar] [CrossRef]
- Yu, Z.; Jiang, H.; Hu, C.; Yu, J. Necessary and Sufficient Conditions for Consensus of Fractional-Order Multiagent Systems via Sampled-Data Control. IEEE Trans. Cybern. 2017, 47, 1892–1901. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Xie, G.; Gao, Y. Consensus of fractional-order double-integrator multi-agent systems. Neurocomputing 2019, 340, 110–124. [Google Scholar] [CrossRef]
- Wang, A.; Liao, X.; Dong, T. Fractional-order follower observer design for tracking consensus in second-order leader multi-agent systems: Periodic sampled-based event-triggered control. J. Frankl. Inst. 2018, 355, 4618–4628. [Google Scholar] [CrossRef]
- Hu, T.; Park, J.H.; He, Z.; Zhang, X.; Zhong, S. State-based event-triggered consensus strategy for Takagi–Sugeno fuzzy fractional-order multiagent systems with switching topologize. ISA Trans. 2021. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Wang, Y.; Hou, Z.-G.; Tan, M.; Cao, Z. Sampled-data based average consensus of second-order integral multi-agent systems: Switching topologies and communication noises. Automatica 2013, 49, 1458–1464. [Google Scholar] [CrossRef]
- Sun, W.; Lü, J.J.; Yu, X.; Chen, S. Second-order consensus of multi-agent systems with noise. IET Control Theory Appl. 2014, 8, 2026–2032. [Google Scholar] [CrossRef]
- Ming, P.; Liu, J.; Tan, S.; Wang, G.; Shang, L.; Jia, C. Consensus stabilization of stochastic multi-agent system with Markovian switching topologies and stochastic communication noise. J. Frankl. Inst. 2015, 352, 3684–3700. [Google Scholar] [CrossRef]
- Chen, J.; Ling, Q. A robust quantized consensus protocol for discrete-time multi-agent systems with additive noise. ISA Trans. 2018, 86, 29–38. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Gong, Y.; Wang, Q. Noise-induced synchronization transitions in neuronal network with delayed electrical or chemical coupling. Eur. Phys. J. B 2014, 87, 198-1–198-6. [Google Scholar] [CrossRef]
- Zhou, C.; Kurths, J.; Hu, B. Array-Enhanced Coherence Resonance: Nontrivial Effects of Heterogeneity and Spatial Independence of Noise. Phys. Rev. Lett. 2001, 87, 98101. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhang, J.; Yuan, Z.; Zhou, T. Noise-induced switches in network systems of the genetic toggle switch. BMC Syst. Biol. 2007, 1, 50. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, X.; Lu, Q.; Kurths, J. Correlated noise induced spatiotemporal coherence resonance in a square lattice network. Phys. A Stat. Mech. Its Appl. 2008, 387, 6679–6685. [Google Scholar] [CrossRef]
- Maritan, A.; Banavar, J.R. Chaos, noise, and synchronization. Phys. Rev. Lett. 1994, 72, 1451. [Google Scholar] [CrossRef]
- Kiss, I.Z.; Zhai, Y.; Hudson, J.L.; Zhou, C.; Kurths, J. Noise enhanced phase synchronization and coherence resonance in sets of chaotic oscillators with weak global coupling. Chaos Interdiscip. J. Nonlinear Sci. 2003, 13, 267–278. [Google Scholar] [CrossRef] [PubMed]
- Lai, L.; Zhang, L.; Yu, T. Collective behaviors in globally coupled harmonic oscillators with fluctuating damping coefficient. Nonlinear Dyn. 2019, 97, 2231–2248. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, L. Noise effect on the signal transmission in an underdamped fractional coupled system. Nonlinear Dyn. 2020, 102, 2077–2102. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Master stability functions for synchronized chaos in arrays of oscillators. In Proceedings of the IEEE International Symposium on Circuits & Systems, Monterey, CA, USA, 31 May–3 June 1998. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Luo, M.; Zhang, L. Consensus of Fractional-Order Double-Integral Multi-Agent System in a Bounded Fluctuating Potential. Fractal Fract. 2022, 6, 147. https://doi.org/10.3390/fractalfract6030147
Chen X, Luo M, Zhang L. Consensus of Fractional-Order Double-Integral Multi-Agent System in a Bounded Fluctuating Potential. Fractal and Fractional. 2022; 6(3):147. https://doi.org/10.3390/fractalfract6030147
Chicago/Turabian StyleChen, Xi, Maokang Luo, and Lu Zhang. 2022. "Consensus of Fractional-Order Double-Integral Multi-Agent System in a Bounded Fluctuating Potential" Fractal and Fractional 6, no. 3: 147. https://doi.org/10.3390/fractalfract6030147
APA StyleChen, X., Luo, M., & Zhang, L. (2022). Consensus of Fractional-Order Double-Integral Multi-Agent System in a Bounded Fluctuating Potential. Fractal and Fractional, 6(3), 147. https://doi.org/10.3390/fractalfract6030147





