1. Introduction
In this paper, we consider the local discontinuous Galerkin (LDG) finite element method for the following time-fractional fourth-order problem with periodic boundary condition
where
,
,
and
are arbitrary constants. Without loss of generality, we assume that
and
; however, we do not require the sign of
to be positive or negative. The source term
and the initial value
are given functions. The term
represents the Caputo fractional derivative of order
(
) with respect to
t, which is [
1,
2],
in which the operator
denotes the partial derivative with respect to
s, and
is the usual gamma function.
Time-fractional partial differential equations with fourth-order spatial derivatives have been widely used in various fields, such as bridge slabs, airplane wings, floor system and window glass (e.g., [
2,
3,
4,
5]). On the assumption that the analytical solution is sufficiently smooth, many numerical methods have been devised for this kind of problem. In [
6], a fully discrete LDG scheme was proposed to solve the time-fractional fourth-order equation and was proven to be stable and convergent with order
, where
k is the degree of piece-wise polynomial, and
and
h are the temporal and spatial stepsizes, respectively.
Soon after, Guo et al. [
7] showed that the order of convergence for the LDG method presented in [
6] can be improved to the optimal order
. Liu et al. [
8] presented a mixed finite element method for the time-fractional fourth-order problem, and the stability as well as the convergence were proven. Zhang and Pu [
9] solved the fourth-order fractional sub-diffusion equation by applying the
-
formula for the time variable and employing a compact operator to approximate the spatial fourth-order derivative. The unconditional stability and convergence were proven using the discrete energy method.
Cui [
10] studied the convergence of a compact finite difference scheme for the time-fractional fourth-order equation. Fei and Huang [
11] analyzed the Galerkin–Legendre spectral method for the distributed-order time-fractional fourth-order partial differential equation. In [
12], a space-time spectral-Galerkin method was presented for the fourth-order time-fractional partial integro-differential equation with a weakly singular kernel.
Note that, in most of the numerical methods mentioned above, the convergence analysis requires that solution
u of problem (
1) be smooth enough with respect to
t, and then the expected accuracy can be achieved. However, from a practical application point of view, this requirement is unrealistic, because the solution
u of a time-fractional differential equation usually exhibits a weak initial singularity, that is,
and /or
blows up as
, although
is continuous on
, see, e.g., [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22]. However, to the authors’ knowledge, there is little discussion on numerical methods and related numerical analysis that take into account the possible initial singularity of time-fractional fourth-order problems (
1).
The main objective of this paper is to study two types of time discretization schemes combined with the LDG method in the spatial direction for solving problem (
1) with an initial singularity. The first scheme is to approximate the Caputo time-fractional derivative with the L1 formula on nonuniform meshes, to discretize the spatial derivative with the LDG method, and then a fully discrete numerical scheme is obtained. With the help of the discrete fractional Gronwall inequality, we show that the scheme is numerically stable and yields the optimal error estimate (i.e.,
th-order accurate in time and
th-order accurate in space when piece-wise polynomials of up to
k are used).
However, no matter how the mesh is divided, the accuracy of this approach in the time direction is at most . In order to construct a numerical scheme with higher accuracy in the time direction, we consider another formula to discretize the Caputo time-fractional derivative, namely the - formula, while, in the spatial direction, we still use the LDG method to approximate it. This method is then shown to be stable and convergent and to achieve second-order accuracy in the time direction.
The rest of the paper is organized as follows. In
Section 2, we introduce some notations, definitions and projections that will be used in the following numerical analysis. Furthermore, the semi-discrete LDG scheme is presented in this section. In
Section 3, a fully discrete numerical scheme based on the L1 formula in the time direction and the LDG method in the spatial direction is proposed for the time-fractional fourth-order Equation (
1), and its stability analysis and error estimate are rigorously discussed. In
Section 4, a higher-order numerical scheme is constructed, and the stability and convergence of the scheme are likewise demonstrated. In
Section 5, numerical examples are provided to illustrate the theoretical statements. The last section includes some concluding remarks.
4. Nonuniform -–LDG Scheme
In the section, based on the LDG method in the spatial direction and
-
approximation in the time direction, we propose a fully discrete numerical scheme (called the nonuniform
-
–LDG scheme for brevity) with high temporal accuracy to solve the time-fractional fourth-order Equation (
1).
4.1. The Fully Discrete Numerical Scheme and Its Stability
For a given finite time , let , be the mesh points, . Denote , and let be the time mesh sizes. For , we set , , and for .
The nonuniform
-
approximation to Caputo’s fractional derivative at
is given by [
28]
where
,
, and for
,
Denote
,
for
, and
. Then, for
, it holds that
Referring to Ref. [
29], we introduce the discrete convolution kernel
,
Moreover, it was proven in [
25] that
where
is a positive constant.
Let
,
,
, and then the weak form of the time-fractional fourth-order Equation (
1) at
is formulated as
where
are test functions;
; the bilinear operators
and
are defined in (
6) and (
9), respectively;
has been given in (
8); and
The LDG method introduced in
Section 2 is used for spatial discretization. Then, the fully discrete nonuniform
-
–LDG approximation scheme for (
1) reads as: find
,
,
,
such that, for all
, it holds that
Below, we study the stability of the nonuniform -–LDG scheme (58). The following lemmas play a key role in proving the stability for the nonuniform meshes.
Lemma 10 ([
25]).
For any finite time and a given nonnegative sequence , assume that there exists a constant Λ
, independent of time-steps, such that . Let and suppose that the grid function satisfieswhere are nonnegative sequences. If the maximum time-step , it holds that, for , Lemma 11 ([
26]).
Suppose . For any function , we have the following inequality Theorem 3. If the graded mesh satisfies the maximum time-step condition , then, for , the solution of the fully discrete nonuniform -–LDG scheme (58) satisfies Proof. Taking the test function
in (
58a) and applying Lemma 2, we obtain
Similar to that in the proof of (
26), we can use the Cauchy–Schwarz inequality to obtain
A combination of Lemma 11 and (
60) leads to
It thus follows from Lemma 10 with
,
,
,
, and
that
provided that the maximum time-step
. The proof is completed. □
4.2. Error Estimate of the Nonuniform -–LDG Scheme
In this section, we study the error analysis of fully discrete nonuniform
-
–LDG scheme (58) for Equation (
1). Assume that the exact solution
of (
1) is sufficiently smooth, i.e.,
Lemma 12 ([
30]).
Suppose . Then, for any function , one haswhereand is the quadratic polynomial that interpolates to at the points , and . Lemma 13 ([
30]).
Suppose that satisfies the condition (62). Then, we have In
Section 3.2, we gave the convergence analysis of the nonuniform L1–LDG scheme, and the same idea can be used for the nonuniform
-
–LDG scheme. However, the proof will be somewhat complicated. Along a similar line, we can easily establish the error equation by subtracting (58) from (57) that, for any
and
,
where
,
, and
are the errors with the decompositions
Here,
and
is the elliptic projection defined in (12).
Theorem 4. Assume that the solution u of the problem (1) satisfies the condition (62) and . Let be the numerical solution of the fully discrete LDG scheme (58). Suppose and the nonuniform mesh satisfies the maximum time-step condition , then for , the following estimate holdswhere C is a positive constant independent of M and h. Proof. Substituting (
64) into (63) and denoting
, we observe that
in which
and
. By the definition (12) of elliptic projection, we have
Then, Equations (
65a)–(
65d) become
Setting
in (
67a) and using Lemma 2, we arrive at
By an analysis similar to that in the proof of (
47), we have that
where
is a positive constant. Employing the definition of operator
and applying (
66c)–(
66d), it is easy to see that
Similar to that in the proof of (
42), we can derive
Then, a simple use of the Cauchy–Schwarz inequality and interpolation property (
14) yields
Combining (
68), (
69) and (
72), we can derive
Thus, if we take
, inequality (
73) reduces to
From interpolation property (
14), we have
Next, we estimate
. When
, since
, there exists a constant
C such that
. When
, by using ([
30], Lemma 9) and (
62), we have
where, in the second step, the estimate
has been applied. As a consequence,
which, together with the case of
, leads to
Then, it follows from Lemmas 12 and 13 that
Substituting (
77) into (
74) and using Lemma 11, we easily obtain
By virtue of Lemma 10 and (
56), it yields that
provided that the maximum time-step
. Finally, we complete the proof of Theorem 4 by combining the above inequality with interpolation property (
14) and the triangle inequality. □
5. Numerical Examples
The purpose of this section is to numerically validate the efficiency of schemes (18) and (58) for solving the time-fractional fourth-order Equation (
1) with initial singularity. All the algorithms were implemented using MATLAB R2016a, and were run in a 3.10 GHz PC with 16 GB RAM and a Windows 10 operating system.
Example 1. Consider the problem (
1)
with , , , , , and the periodic boundary condition in use. In this case, the source termThe analytical solution is given by . This solution displays a weak singularity at . To solve Example 1, we apply the nonuniform L1–LDG scheme (18) with
in computation. The
-norm errors and temporal convergence orders of the numerical solution
for
and different time-steps are listed in
Table 1. The convergence orders of
and
are close to
, which is consistent with the theoretical prediction in Theorem 2. However, the accuracy of
is slightly lower. In
Table 2 and
Table 3, for fixed
and
, we observe that the spatial convergence order for (18) is
, which is in agreement with the theoretical analysis. The numerical solutions of the scheme (18) for different
are given in
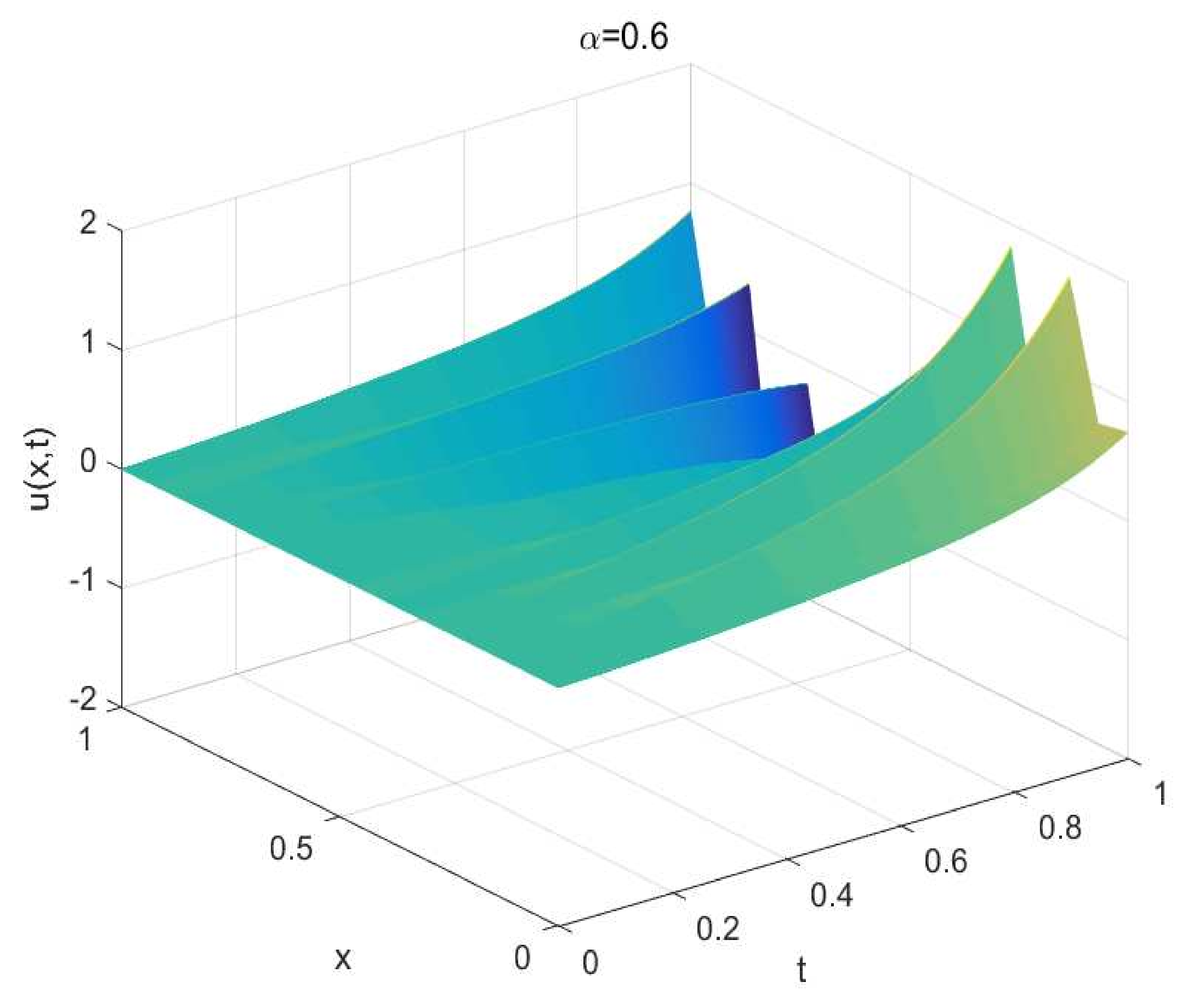
Figure 1,
Figure 2 and
Figure 3.
Figure 4 depicts the
-norm errors versus
N between the numerical solution and the exact solution for different
at
. The graphs show good agreement between the two solutions.
Example 2. The purpose of this example is to investigate the accuracy and efficiency of the proposed nonuniform -–LDG method (57). For simplicity, the equation in Example 1 is still regarded as a test problem, but it is solved by the scheme (57). The -norm errors at time and convergence orders in the temporal direction with different α and r are shown in Table 4, Table 5 and Table 6. The orders of convergence displayed indicate that the order of convergence is , which coincides with Theorem 4. From Table 5 and Table 6, we can also see that the grading parameter yields the temporal optimal second-order accuracy. Then, we refine the spatial step size with a fixed temporal step size . The -norm errors at time and convergence orders in the spatial direction are shown in Table 7. The results imply that the algorithm (57) has an accuracy of in space.