A Visually Secure Image Encryption Based on the Fractional Lorenz System and Compressive Sensing

Abstract

Recently, generating visually secure cipher images by compressive sensing (CS) techniques has drawn much attention among researchers. However, most of these algorithms generate cipher images based on direct bit substitution and the underlying relationship between the hidden and modified data is not considered, which reduces the visual security of cipher images. In addition, performing CS on plain images directly is inefficient, and CS decryption quality is not high enough. Thus, we design a novel cryptosystem by introducing vector quantization (VQ) into CS-based encryption based on a 3D fractional Lorenz chaotic system. In our work, CS compresses only the sparser error matrix generated from the plain and VQ images in the secret generation phase, which improves CS compression performance and the quality of decrypted images. In addition, a smooth function is used in the embedding phase to find the underlying relationship and determine relatively suitable modifiable values for the carrier image. All the secret streams are produced by updating the initial values and control parameters from the fractional chaotic system, and then utilized in CS, diffusion, and embedding. Simulation results demonstrate the effectiveness of the proposed method.

1. Introduction

With the constant advancement of the Internet and image processing technology, a mass of digital images are being generated, transmitted, and stored conveniently. Meanwhile, the data security of these transmitted images is of increasing concern due to an insecure network environment [1,2]. While encryption is considered as an effective technique to secure sensitive images, the intrinsic characteristics of digital images such as bulky data volume, high redundancy, and a strong correlation between adjacent pixels make traditional AES and DES encryption methods inefficient [3]. Therefore, specialized algorithms have been extensively developed, such as fractional chaotic systems [4], quantum computation [5], and compressive sensing (CS) [6,7,8,9].

As of now, fractional Lorenz systems have been widely applied to image encryption. For instance, Wang et al. [10] applied the fractional-order hyper-chaotic Lorenz system to image encryption to improve encryption security. Similarly, to enhance security and efficiency, He et al. [11] performed encryption on plain images using pseudorandom streams generated by the fractional Lorenz system. Badr et al. [12] considered a face image encryption with the fractional-order Lorenz chaotic system to achieve cancellable face recognition. Additionally, fractional chaotic systems have been introduced to CS-based image encryption [13,14,15,16] recently. For instance, to improve encryption security, Yan et al. [13] and Kayalvizhi et al. [14] introduced fractional-order hyper-chaotic systems into image encryption, combining CS and DNA operation. To address the issue that CS reconstruction precision is not high enough, Fan et al. [15] proposed a subdata cipher structure based on 3D fractional logistic systems. The structure verified that the bifurcation diagrams of the 3D fractional system are well-suited for encryption. To reduce CS storage space and computational complexity, Ye et al. [16] designed a color image encryption scheme based on quaternion discrete multifractional transform and CS. The scheme utilizes the chaos-based orders to improve key sensitivity. The above schemes [10,11,12,13,14,15,16] tried to encrypt visible information into meaningless or noiselike content before transmission. Unfortunately, the noiselike appearance over public channels is likely to hint at the presence of a possible cipher, thereby incurring cryptanalysis attacks on suspicious content. As a result, it is always imperative to design secure cryptosystems so that the unauthorized entities cannot differentiate the cipher images by direct visual inspection.

Bao and Zhou [17] first introduced the concept of meaningful image encryption. The plain image was encrypted into a noiselike structure by an existing encryption method, and then transformed by discrete wavelet transform (DWT) to obtain a visually meaningful cipher image. This scheme achieves the transmission of cipher image with minimal suspicion, but the volume of the cipher image is four times larger than that of the plain image, which increases the transmission cost. The work in [18] was a variant of Bao and Zhou’s scheme [17], which reduced the file size of the cipher image and improved the visual security of the decrypted image. The research in [19] was another refinement, which compressed the plain image into a secret image by CS, and then embedded the secret image into the carrier image to form a cipher image. The refinement scheme in [19] is robust, but the embedding is handled by DWT, which is not fully reversible. The schemes in [20,21] resorted to integer discrete transform (IWT) and least-significant bit (LSB) embedding to ensure reversibility. In addition, to reduce the storage space of the CS measurement matrix, Wen et al. [22] and Ping et al. [23] integrated the semitensor product (STP) technique with CS. To have stronger robustness, Zhu et al. [24] used singular value decomposition (SVD) embedding to create the final visually secure cipher images. Unfortunately, the scheme in [24] needs to transmit the unmodified carrier image into the receiver to extract the embedded information. On this basis, a series of meaningful encryption schemes are investigated to improve the visual security of the cipher image or the quality of the decrypted image [25,26,27,28]. However, when CS is directly performed on a plain image [19,20,21,22,24], there are problems of inefficiency and poor quality of the decrypted image [15]. Furthermore, the underlying relationship between the hidden and the modified data is not considered in [19,20,21,22], which reduces the visual security of the cipher image.

To overcome the above shortcomings, we detail a novel and visually secure image encryption scheme that introduces the fractional Lorenz system into CS-based cryptosystem. First, the plain image is partitioned into VQ index blocks and error compensations that are sparse enough to be compressed by CS. Then, the index information and the measurements are diffused by a pseudorandom sequence obtained by the fractional Lorenz system to obtain a noiselike secret image. Next, the secret image is hidden into the carrier image by smooth function embedding [29]. Particularly, the lifting integer wavelet transform (LIWT) is introduced to decompose the carrier image to obtain the integer coefficient matrices, and the invertible coefficient quantization [30] is performed to eliminate the energy loss of the extracted information. Finally, a visually meaningful cipher image is obtained, which is of the same resolution as the plain image and appears visually the same as the carrier image. All cipher streams are obtained by updating the control parameters of the fractional Lorenz system and then used in the generation of CS measurement matrices, diffusion of the combination matrix, and permutation of the cover image.

The remainder of this paper is organized as follows. Preliminaries are introduced in Section 2. The description of our scheme is provided in Section 3. Simulation results and performance analyses are given in Section 4. The conclusion is drawn from the work in Section 5.

2. Preliminaries

2.1. Compressive Sensing

Compressive sensing (CS) asserts that the signal which is sparse or can be sparsely represented can be reconstructed from much lower samples than the conventional Nyquist–Shannon sampling theorem. In CS theory, a redundant sparse signal x of size $n\times 1$ can be sparsely represented through an orthogonal basis $\Psi$ and measured with $m\times n$ measurement matrix $\Phi$, the measured value y of size $m\times 1$ is obtained by

$$y=\Phi x=\Phi \Psi s=\Theta s,$$

(1)

where $\Theta$ and s are the sensing matrix and the transformed coefficient matrix, respectively. The dimensions need to meet the relationship that

$$ck\log \left(\frac{n}{k}\right)\le m\ll n,$$

(2)

where k denotes the number of nonzero elements of the sparse signal, and c is a constant. When requiring to reconstruct x from y, one should solve a nonconvex optimal problem as follows:

$$\begin{array}{ccc}\min {∥s∥}_1& s.t.& \Theta s=y,\end{array}$$

(3)

where $∥·∥$ represents the sum of absolute values of each element in a vector. There are many algorithms to reconstruct x from y, such as orthogonal match pursuit (OMP), basic pursuit (BP), and smoothed $l_0$ norm (SL₀).

2.2. The 3D Fractional Lorenz System

The 3D Lorenz chaotic system has been widely studied as a nonlinear uncertainty system due to its complicated evolution orbits of stretching and folding [31,32]. The system is used to produce the pseudorandom sequences for subsequent encryption and embedding in our work, and its mathematical formula is depicted as follows:

$$\left\{\begin{array}{c}{D}_t^{{\alpha }_1}x\left(t\right)=-\sigma x\left(t\right)+\sigma y\left(t\right)\hfill \\ D_t^{{\alpha }_2}y\left(t\right)=-rx\left(t\right)-y\left(t\right)-x\left(t\right)z\left(t\right)\hfill \\ D_t^{{\alpha }_3}z\left(t\right)=x\left(t\right)y\left(t\right)-bz\left(t\right)\hfill \end{array}\right.$$

(4)

where t represents the time state, ${\alpha }_1={\alpha }_2={\alpha }_3$ are the fractional orders that equal to 0.995, $\sigma$ and r are associated with the Prandtl number and Rayleigh number, respectively, b is the geometric factor, and $\sigma \in [9,10]$, $r\in [25,30]$ and $b\in [2,3]$. For a more detailed mathematical derivation, please refer to the literature [12,32].

2.3. Vector Quantization

Vector quantization (VQ), a lossy data compression technique, is a dimensionality reduction method that attempts to replace high-dimensional data with low-dimensional codeword indexes. It includes three components: codebook generator, VQ encoder, and VQ decoder. The codebook generator uses the LBG clustering algorithm [33] with the image sub-block size $p\times q$ to yield k-dimensional codewords $C{W}_f=\left(c{w}_f^1,c{w}_f^2,\cdots ,c{w}_f^k\right)$ that constitute the codebook $CB$ of size $Num$, where $k=p\times q$ and $1\le f\le Num$. The VQ encoder exploits $CB$ to compress a sized $N_0\times N_0$ image to VQ indexes. It first groups the image into a series of sized $p\times q$ image sub-blocks $SB=[s{b}_1,s{b}_2,\cdots ,s{b}_{{N_0}^2/p/q}]$, and the j-th block content $s{b}_j$ ($1\le j\le {N_0}^2/p/q$) is:

$$s{b}_j=\left(s{b}_j^1,\cdots ,s{b}_j^2,\cdots ,s{b}_j^{2\times q},\cdots ,s{b}_j^{(p-1)\times q+1},\cdots ,s{b}_j^k\right).$$

(5)

For each sub-block, the nearest codeword is found with the smallest minimum Euclidean distance from $SB$. The Euclidean between $C{W}_f$ and $SB$ is defined as

$$D\left(SB,C{W}_f\right)=\sqrt{\sum _{i=1}^k{\left(s{b}_j^i-c{w}_f^i\right)}^2},$$

(6)

where $C{W}_f$ represents the f-th codeword in $CB$, and $c{w}_f^i$ is the i-th component of $C{W}_f$. At the VQ decoder side, one can exploit the trained $CB$ to decode the encoded VQ indexes to reconstruct the original image.

3. The Proposed Scheme

The proposed encryption scheme is introduced in two stages, as shown in Figure 1. In the first stage, the plain image is processed into an index matrix and an error matrix via the VQ encoder and decoder. The error matrix was confused with zigzag and compressed with a CS measurement matrix to obtain the measured values. The resulting values and the index matrix are diffused toobtainher to create an invisible secret image. In the second stage, the secret image is hidden into the carrier image to generate the cipher image. The hiding procedure is implemented by a smooth function to minimize the gap between the hidden and the modified data. Below, we introduce each in the proposed scheme.

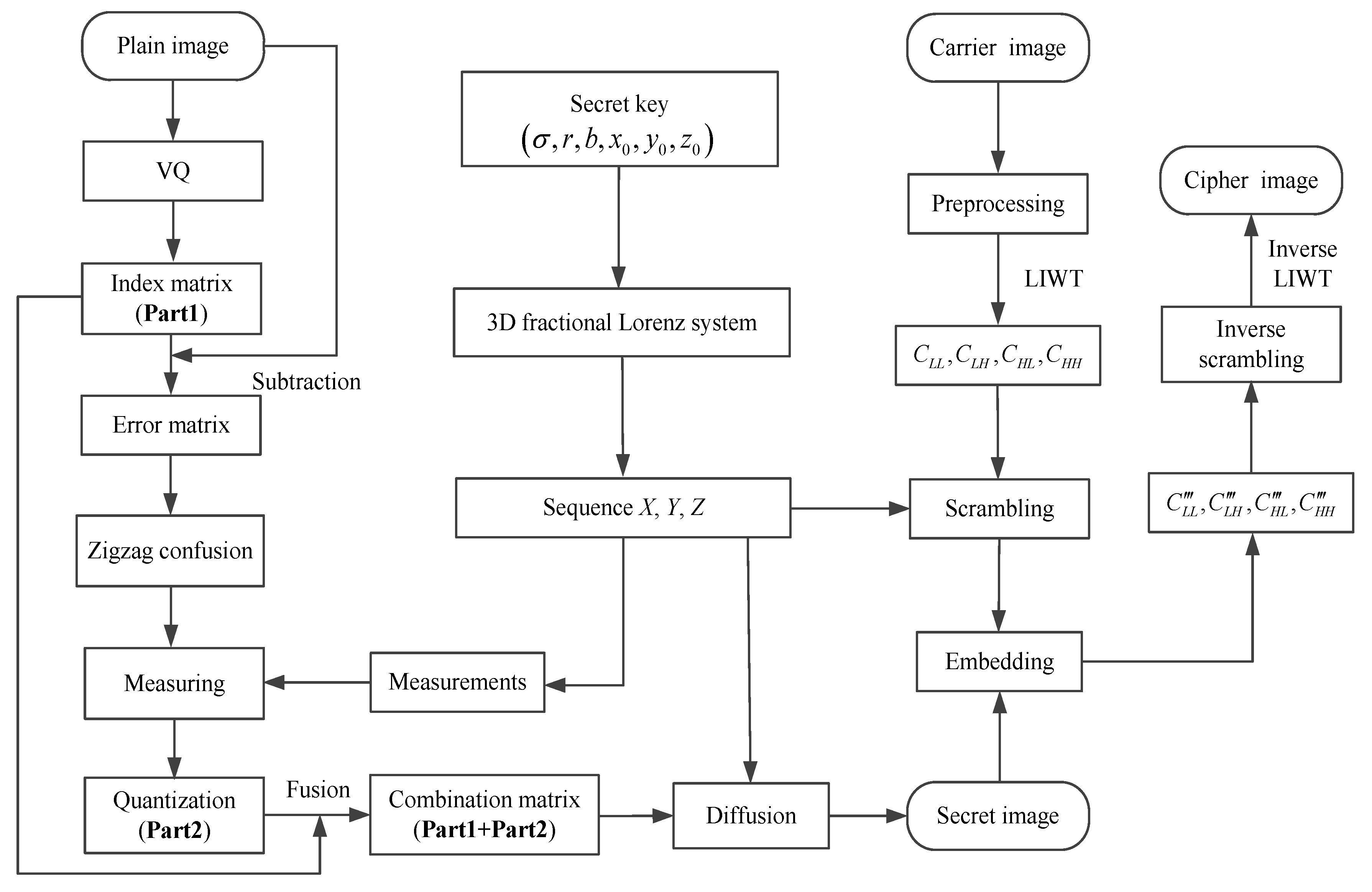
3.1. Encryption Process

The encryption operations begin with the following assumptions: the size of both the plain image $I_o$ and the carrier image $I_{car}$ is $N_0\times N_0$; the plain image $I_o$ is divided into $p\times q$ nonoverlapping sub-blocks $SB=[s{b}_1,s{b}_2,\cdots ,s{b}_{{N_0}^2/p/q}]$, the confused error matrix is sampled by CS in $l\times l$ block-unit way, and the size of the measurement matrix $\Phi$ is $M_b\times l_b$, where $l_b=l\times l$ and $M_b<l_b$.

3.1.1. Generating Index Matrix and Error Matrix Based on VQ

Step 1: Find the best matching codeword for each sub-block $SB$ and assign the corresponding index to the sub-block according to the following equation:

$$s^{j_0}=\underset{f_0}{\arg \min }D\left(S{B}_{j_0}^i,C{W}_{f_0}^i\right),$$

(7)

where $0\le f_0\le Num$, $1\le i\le p\times q$, $1\le j_0\le {N_0}^2/p/q$, and $s^{j_0}$ is the best matching codeword index. All the assigned indexes constitute a vector $s=[s^1,s^2\cdots ,s^{{N_0}^2/p/q}]$ as Part1 shown in Figure 1.

Step 2: Exploit the well-trained codebook to decode the index vector to obtain the reconstructed image $I_{vq}$, and subsequently calculate the error matrix $P_0$ using Equation (8).

$$\begin{array}{c}\begin{array}{c}{P}_0=I_o-I_{vq}.\end{array}\end{array}$$

(8)

Unlike previous studies that directly use CS to compress plain images, we choose the error matrix as input based on the following merits. Firstly, the error matrix has better sparsity than the plain image, and we can find a reasonable explanation from the comparable results in Figure 2a,c. Thus, the error image as CS input fully reflects the sparsity emphasized by CS theory. In this way, there is no need to investigate how to choose a suitable sparse basis. Secondly, the error matrix is used as a complement to the VQ indexes in the reconstruction stage, which helps to improve the quality of the decrypted images.

3.1.2. Generating the Secret Image Based on CS and Zigzag Confusion

Step 1: Calculate the initial values $(x_0,y_0,z_0)$ of the 3D Lorenz system using three external key parameters $k_0$, $k_1$, and $k_2$ that are associated with the original plain $I_o$.

$$\left\{\begin{array}{c}{x}_0=⌊\left(\left(abs\left(k_0\right)-⌊k_0⌋\right)\times {10}^{14}\right)\mathrm{mod}{2}^5⌋+1\hfill \\ y_0=⌊\left(\left(abs\left(k_1\right)-⌊k_1⌋\right)\times {10}^{14}\right)\mathrm{mod}{2}^5⌋+1\hfill \\ z_0=⌊\left(\left(abs\left(k_2\right)-⌊k_2⌋\right)\times {10}^{14}\right)\mathrm{mod}{2}^5⌋+1\hfill \end{array}\right..$$

(9)

Step 2: Generate the following three sequences $K{S}_i$$(i=1,2,\cdots ,{N_0}^2/l/l)$, $K{B}_j$$(j=0,1,$$\cdots ,N_1\times N_2-1)$, where $N_1\times N_2$ is the size of the combination matrix, and  $K{F}_k$$(k=1,2,\cdots ,{N_0}^2/4)$ using $(x_0,y_0,z_0)$, which are used to construct the measurement matrix, diffuse the combination matrix and scramble the coefficients of carrier image, respectively.

Step 3: Scan the error matrix $P_0$ via ziazag order using the given initial value $({\dot{x}}_0,{\dot{y}}_0)$ in advance, where ${\dot{x}}_0$ and ${\dot{y}}_0$ are not greater than $N_0$, to yield the confused errors $e_t$$(t=1,2,\cdots ,{N_0}^2)$.

Step 4: Set a threshold TS to alter the errors $e_t$ to zero if the absolute values are smaller than TS, and then divide the altered errors into nonoverlapping sub-blocks $P_1=[P_{1,1},P_{1,2},\cdots ,P_{1,{N_0}^2/l/l}]$ of block size $l\times l$.

Step 5: Construct the measurement matrix ${\Phi }_i$$(i=1,2,\cdots ,{N_0}^2/l/l)$ according to Algorithm 1. Then, measure each block in $P_1$ by use of ${\Phi }_i$ to produce the measured values $P_2=[P_{2,1},P_{2,2},\cdots ,P_{2,{N_0}^2/l/l}]$. If the sampling rate is $SR$, the length of each block in $P_2$ is $M_b=SR\times l^2=SR\times l_b$.

Algorithm 1: The construction of measurement matrix ${\Phi }_i$.

Input: A distance d, the initial values $(x_0,y_0,z_0)$, and control parameters $(\sigma ,r,b)$. Output: The measurement matrix ${\Phi }_i$$(i\in [1,{N_0}^2/l/l])$. (1):  Iterate the 3D Lorenz system $2i+500+M_b{l}_{b}d$ times with initial values $(x_0,y_0,z_0)$ and control parameters $(\sigma ,r,b)$, abandon the preceding $2i+500$ elements to bypass the transient state, then obtain three chaotic secret code streams $X_i=[x_{i,1},x_{i,2},\cdots ,x_{i,M_b{l}_{b}d}]$, $Y_i=[y_{i,1},y_{i,2},\cdots ,y_{i,M_b{l}_{b}d}]$ and $Z_i=[z_{i,1},z_{i,2},\cdots ,z_{i,M_b{l}_{b}d}]$. (2): Obtain the sequence $K{S}_i=\left[K{S}_{i,1},K{S}_{i,2},\cdots ,K{S}_{i,M_b{l}_{b}d}\right]$ based on $K{S}_i=(X_i+Y_i+Z_i)/3$. (3): Generate the sequence $K{S}_i^{\prime }$ by sampling sequence $K{S}_i$ with interval d as $K{S}_{i,\epsilon }^{\prime }=K{S}_{i,(1+\epsilon d)}$$(\epsilon =0,1,\cdots ,M_b{l}_b-1)$. (4): Obtain a more random sequence $K{S}^{″}$ with $K{S}_{i,\epsilon }^{″}=1-2K{S}_{i,\epsilon }^{\prime }$$(\epsilon =0,1,\cdots ,M_b{l}_b-1)$. (5): Construct the measurement matrix ${\Phi }_i$ according to the following formula: $${\Phi }_i=\sqrt{\frac{2}{M_b}}\left[\begin{array}{cccc}K{S^{″}}_{i,1}& K{S^{″}}_{i,M_b+1}& \cdots & K{S^{″}}_{i,M_b{l}_b-M_b+1}\\ K{S^{″}}_{i,2}& K{S^{″}}_{i,M_b+2}& \cdots & K{S^{″}}_{i,M_b{l}_b-M_b+2}\\ ⋮& ⋮& \ddots & ⋮\\ K{S^{″}}_{i,M_b}& K{S^{″}}_{i,2M_b}& \cdots & K{S^{″}}_{i,M_b{l}_b}\end{array}\right].$$ (10)

Step 6: Quantify all the elements of $P_2$ into a specific range of [0, 255] using the sigmoid map function in Equation (11), and obtain a novel vector $P_3$ as Part2.

$$P_3=round\left(a_1·\left(1+e^{-a_2(P_2-a_3)}\right)\right),$$

(11)

where $round(·)$ denotes rounding the elements to the nearest integer, $a_1=255$, $a_2=\max -\min$, $a_3=(\max +\min )/2$, and max and min are the maximum and minimum elements of $P_2$, respectively.

Step 7: Append all the measurement vector $P_3$ (Part2) to the index vector s (Part1) orderly to obtain the combination matrix $P_4=\left[s,P_{3,1},P_{3,2},\cdots ,P_{3,{N_0}^2/l/l}\right]$, and the size of $P_4$ is

$$N_1\times N_2={N_0}^2/p/q+SR\times {N_0}^2.$$

(12)

Note that all the index values in s are 8 bits long. If the block size and the sampling rate are set to $p\times q=4\times 4$ and $SR=3/16$, respectively, then $N_1\times N_2={N_0}^2/4$.

Step 8: Diffuse the combination matrix $P_4$ [15] with the sequence $K{B}_j$ generated in Step 2, and obtain the secret image $P_5$.

$$P_{5,j}=(P_{4,j}+K{B}_j)mod256\oplus K{B}_j\oplus P_{5,j-1},$$

(13)

where $P_{4,j}$ is the j-th element of the matrix $P_4$, $P_{5,j}$ is the j-th element of the matrix $P_5$, and $j=0,1,\cdots ,N_1\times N_2-1$.

3.1.3. Embedding the Secret Image into the Carrier Image

Step 1: Preprocess the elements of the carrier $I_{car}$ of resolution $N_0\times N_0$ into the range $[8,248]$.

$$I_{car}(i,j)=floor(8+0.9397\times I_{car}(i,j)),$$

(14)

where $i,j\in [1,N_0]$, and $floor(·)$ is a downward rounding function.

Step 2: Perform an LIWT operation on the modified carrier $I_{car}$, and then obtain the coefficient components $C_{LL}$, $C_{LH}$, $C_{HL}$, and $C_{HH}$, with each having the size of $(N_0/2)\times (N_0/2)$.

Step 3: Scramble $C_{LH}$, $C_{HL}$, and $C_{HH}$ with the pseudorandom sequence $KF$ generated in Section 3.1.2, and then obtain the scrambled components $C_{LH}^{\prime }$, $C_{HL}^{\prime }$ and $C_{HH}^{\prime }$.

Step 4: Embed the secret image $P_5$ into the two components $C_{LH}^{\prime }$ and $C_{HL}^{\prime }$ by a smooth function and the component $C_{HH}^{\prime }$ by a direct substitution, and the detailed embedding process is described in Algorithm 2.

Algorithm 2: The embedding process.

Input: The secret image $P_5$ and the scrambled components $C_{LH}^{\prime }$, $C_{HL}^{\prime }$, and $C_{HH}^{\prime }$. Output: The marked coefficient components ${\tilde{C}}_{LH}$, ${\tilde{C}}_{HL}$, and ${\tilde{C}}_{HH}$. (1): Stretch the secret image $P_5$ into a one-dimensional vector $F^{\prime }=[f_1^{\prime },f_2^{\prime },\cdots ,f_{N_1\times N_2}^{\prime }]$, and represent all the elements of the vector $F^{\prime }$ in binary as $b_7{b}_6{b}_5{b}_4{b}_3{b}_2{b}_1{b}_0$, where $b_7$ is the highest bit and $b_0$ is the lowest bit. (2): Quantify the coefficients of $C_{LH}^{\prime }$, $C_{HL}^{\prime }$, and $C_{HH}^{\prime }$ into non-negative integers in a reversible way. $$c_i^{\prime }\mathrm{mod}{N}_t=c_i^{″}=\left\{\begin{array}{cc}{c}_i^{\prime },& c_i\ge 0,\\ c_i^{\prime }+N_t,& others,\end{array}\right.$$ (15) where $1\le i\le {N_0}^2/4$, $N_t$ is a constant value that must satisfy $N_t>2c_i^{\prime }$, $c_i^{\prime }$ is the i-th coefficient value, and $c_i^{″}$ is the quantized non-negative coefficient value. (3): Use the smooth function to embed $b_7{b}_6{b}_5$ and $b_4{b}_3{b}_2$ into the lowest three bits of the components $C_{LH}^{″}$ and $C_{HL}^{″}$, respectively. The embedding process for $C_{LH}^{″}$ is described as the following formula: $$v_i=4\times w_0+2\times w_1+w_2-\mathrm{mod}(c_i^{″},8),$$ (16) $${\tilde{c}}_i=\left\{\begin{array}{ccc}{c}_i^{″}+v_i& if& |v_i|<5,\\ c_i^{″}+v_i+8& if& v_i\le -5,\\ c_i^{″}+v_i-8& if& v_i\ge 5,\end{array}\right.$$ (17) where $w_0$, $w_1$, and $w_2$ are the secret data to be embedded, ${\tilde{c}}_i$ is i-th element value of the marked component ${\tilde{C}}_{LH}$, and $v_i$ is the gap between the value of the secret data which is going to be embedded in $c_i^{″}$ and the value of the three LSBs in $c_i^{″}$. The generation of marked component ${\tilde{C}}_{HL}$ is the same as that of ${\tilde{C}}_{HL}$, so we do not reiterate here. (4): Embed $b_1{b}_0$ into the lowest two bits of $C_{HH}^{″}$ directly and keep other higher bits constant, then obtain the marked coefficient matrix ${\tilde{C}}_{HH}$.

Step 5: Execute the inverse quantization on the marked component ${\tilde{C}}_{LH}$, and obtain $C_{LH}^{‴}$.

$$c_i^{‴}=\left\{\begin{array}{cc}{\tilde{c}}_i,& {\tilde{c}}_i<N_t/2,\\ {\tilde{c}}_i-N_t,& others,\end{array}\right.$$

(18)

where $c_i^{‴}$ is the i-th element value of $C_{LH}^{‴}$. Then, perform the same inverse quantization on the marked components ${\tilde{C}}_{HL}$ and ${\tilde{C}}_{HH}$ to generate $C_{HL}^{‴}$ and $C_{HH}^{‴}$.

Step 6: Perform the inverse scrambling of Step 3 on the components $C_{LH}^{‴}$, $C_{HL}^{‴}$, and $C_{HH}^{‴}$, and apply the inverse LIWT to obtain the final cipher image $I_{ciph}$, which consists of the components $C_{LL}$, $C_{MLH}$, $C_{MHL}$, and $C_{MHH}$.

Essentially, the embedding uses the smooth function to modify the lowest three bits of the carrier coefficients, rather than physically changing these coefficients by direct bit substitution. To be specific, given $c_i^{″}=232={\left(11101000\right)}_2$, $w_0{w}_1{w}_2=\{1,1,1\}$. After direct bit substitution, we can obtain the modified coefficient value ${\tilde{c}}_i=232+7=239={\left(11101111\right)}_2$ with a difference of $|{\tilde{c}}_i-c_i^{″}|=7$. However, when the smooth function in Equation (18) is introduced, we can obtain the modified coefficient value ${\tilde{c}}_i=232+7-8=231={\left(11100111\right)}_2$ with a difference of $|{\tilde{c}}_i-c_i^{″}|=1$. The peak signal-to-noise ratio (PSNR) of the cipher image generated using the smooth function can be improved by 2 dB on average. The detailed process is shown in Algorithm 2.

The quantization process in Algorithm 2 converts the negative coefficients to the corresponding positive coefficients. For better illustration, this process is described in Figure 3. The top half of the figure represents the distribution of unquantized coefficients and the bottom half represents the distribution of quantized coefficients. The inverse quantization can be achieved if and only if $N_t-c_i^{\prime }>c_i^{\prime }$, i.e., $N_t>2c_i^{\prime }$. In this way, the data expansion issue can be addressed and invertibility can be guaranteed.

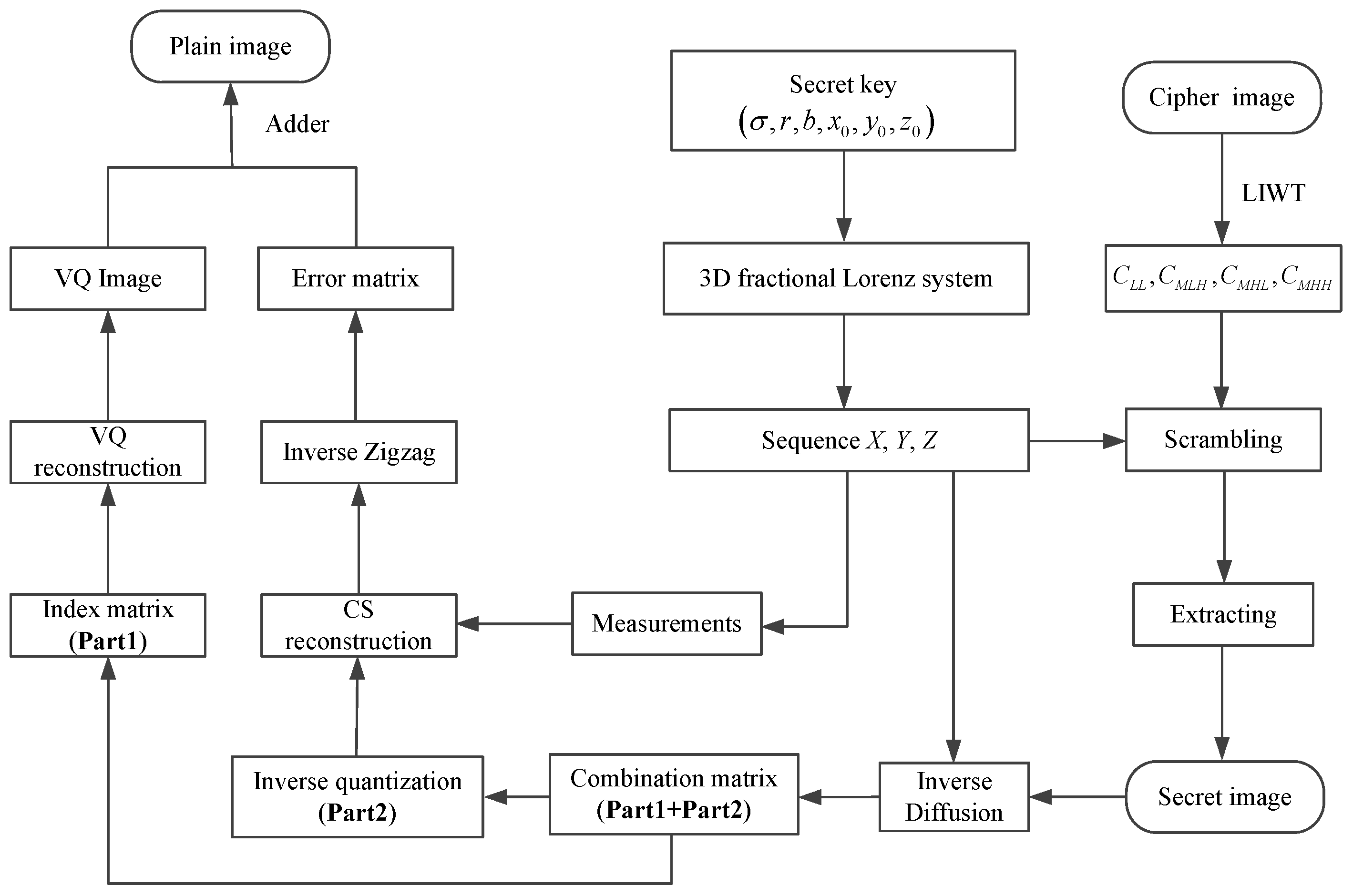
3.2. Decryption Process

The decryption process is the inverse of the encryption process. Figure 4 illustrates the schematic of the process. Firstly, the secret image is extracted from the received cipher image, then the plain image is restored according to the extracted secret image. The LIWT ensures an integer to an integer transform, and the subsequent coefficient quantization operation ensures conversion reversibility.

3.2.1. Extracting the Secret Image from the Cipher Image

Step 1: Apply the LIWT to the cipher image, and then obtain the coefficient components $C_{LL}$, $C_{MLH}$, $C_{MHL}$, and $C_{MHH}$.

Step 2: Scramble $C_{MLH}$, $C_{MHL}$, and $C_{MHH}$ to obtain the components $C_{LH}^{‴}$, $C_{HL}^{‴}$, and $C_{HH}^{‴}$, and quantize them into non-negative integer components $C_{LH}^{″}$, $C_{HL}^{″}$, and $C_{HH}^{″}$.

Step 3: Transform the elements of components $C_{LH}^{″}$, $C_{HL}^{″}$, and $C_{HH}^{″}$ into their binary formats, and pick out the lowest 3 bits from $C_{LH}^{″}$ as $b_7{b}_6{b}_5$, the lowest 3 bits from $C_{HL}^{″}$ as $b_4{b}_3{b}_2$, and the lowest 2 bits from $C_{HH}^{″}$ as $b_1{b}_0$.

Step 4: Recombine the binary bits into 8-bit representation $b_7{b}_6{b}_5{b}_4{b}_3{b}_2{b}_1{b}_0$ and change it to decimal format to obtain the vector $F^{\prime }=[f_1^{\prime },f_2^{\prime },\cdots ,f_{N_1\times N_2}^{\prime }]$, then obtain the secret image $P_5$ by converting $F^{\prime }$ into $N_1$ rows and $N_2$ columns.

3.2.2. Recovering the Plain Image

Step 1: Conduct the inverse diffusion on the extracted secret image $P_5$ to obtain the combination image $P_4$, and then obtain the index vector $s=[s^1,s^2\cdots ,s^{{N_0}^2/p/q}]$ as in Part1 and the measurement vector $P_3=\left[P_{3,1},P_{3,2},\cdots ,P_{3,{N_0}^2/l/l}\right]$ as in Part2.

Step 2: Perform the inverse sigmoid quantization on $P_3$ according to Equation (19), and obtain the measured values $P_2$.

$$P_2=round(\log (a_1·\frac{1}{P_3}-1)/(-a_2)+a_3).$$

(19)

Step 3: Execute the OMP reconstruction algorithm on $P_2$ as the following equation:

$$\begin{array}{ccc}{P}_{1,i}=OMP(P_{2,i},{\Phi }_i),& for& 1\le i\le {N_0}^2/l/l\end{array}.$$

(20)

Step 4: Manipulate the inverse zigzag confusion (IZC) on the recovered sparse error matrix $P_1$ by the following equation:

$$\begin{array}{c}{P}_0=IZC(P_1,{\dot{x}}_0,{\dot{y}}_0).\end{array}$$

(21)

Step 5: Execute the VQ reconstruction algorithm on Part1, and then obtain the lossy VQ reconstruction image $I_{vq}$.

Step 6: Obtain the decrypted image via adding the reconstructed error matrix $P_0$ to the corresponding reconstructed image $I_{vq}$.

$$I_0=Adder(P_0,I_{vq}).$$

(22)

In order to better explain the process of the proposed algorithm, we take a specific $8\times 8$ image matrix as an example to theoretically analyze the effectiveness of the proposed algorithm. Since our algorithm consists of three preliminary parts: the VQ process, the error compression process, and the secret image embedding process, we explain the proposed method from these three aspects. In the VQ encoding process, the input $8\times 8$ image matrix is encoded into 4 codeword indexes, then the lossy VQ image matrix of equal size is generated by the VQ decoding process, and the error matrix e is generated using Equation (8). In the error compression process, a measurement matrix ${\Phi }_{12\times 64}$ of size $12\times 64$ is first generated using the fractional Lorenz system, and then the measured value P of size $12\times 1$ is generated by compressing the error matrix with $P_{12\times 1}={\Phi }_{12\times 64}\times e_{64\times 1}$. On this basis, the combined matrix is obtained, and the percentage is $4/8\times 8+12/\left(8\times 8\right)=1/16+3/16=1/4$ of the input image matrix. In the embedding process, the secret image can be embedded into the coefficient matrices of the carrier image using the smoothing function, which is the usual information hiding process.

4. Simulation and Performance Analyses

In this section, the simulation results of the proposed visual secure encryption algorithm are presented, and performance analyses are elaborated from the aspects of image encryption and decryption results, key sensitivity, histogram and correlation analyses, information entropy analysis, chosen plaintext attack (CPA), noise and data loss attacks, running efficiency analysis, and comparison analysis. All experiments are conducted on a 64-bit Windows 7 PC with 16.0 GB random-access memory (RAM) and Inter(R) Core(TM) i7-4770 CPU @ 3.40 GHz, and the platform is MATLAB R2012b. The sized $256\times 256$ or $512\times 512$ images including Lena, Barbara, Baboon, Jet, Woman, Peppers, Cameraman, and Goldhill are selected as the plain images and carrier images, respectively. In the VQ phase, we utilize a trained codebook with 256 codewords of length 16 to encode and decode the plain images, and the image sub-block size of this process is set as $p\times q=4\times 4$. In the CS phase, the block size of the sampling is set as $l\times l=8\times 8$, and the default sampling rate is $SR=3/16$ and the threshold is TS = 25.

4.1. Simulation Results

In this subsection, we analyze and discuss the encryption and decryption results of the proposed scheme. In addition, the selections of the carrier images and the settings of the threshold TS are essential for the encryption and reconstruction effect. Thus, we also evaluate them in detail in the following contents.

4.1.1. Encryption and Decryption Results

Figure 5 presents the encryption and decryption results. The sized $256\times 256$ Lena, Baboon, Woman, and Cameraman as the plain images, in conjunction with the same-sized Barbara, Jet, Peppers, and Goldhill as the carrier images, are tested successively. As we can observe from the visual perception, the secret images were compressed to a quarter of the corresponding plain images, and their appearances resemble noiselike contents. In addition, the cipher images are obtained that are visually the same as the associated carrier images. Thus, if they are saved and transmitted among other natural images, the underlying attacks are not conscious of them. In another aspect, the reconstructed error matrices and the decoded VQ images are combined to recover the plain images, as displayed in Figure 6. The reconstructed error matrices merely fulfill information compensation to the corresponding decoded VQ images, illustrating that the decrypted images have higher visual quality while maintaining the compression performance.

To analyze the similarities between two images quantitatively, the commonly used PSNR and mean structural similarity (MSSIM) [34], which are based on statistical models for images in the spatial domain, are exploited in this paper. The numerical results with smooth function and without smooth function (i.e., direct bit substitution) are given in

Table 1. PSNR and MSSIM values of simulation results.

Size	Plain Image	Carrier Image	With Smooth Function			Without Smooth Function
			PSNRdec(dB)	PSNRciph(dB)	MSSIMciph	PSNRdec(dB)	PSNRciph(dB)	MSSIMciph
$256\times 256$	Lena	Barbara	32.1670	42.3844	0.9990	32.1670	39.7819	0.9982
	Baboon	Jet	26.4461	42.4317	0.9978	26.4461	39.4862	0.9960
	Woman	Peppers	33.9596	42.4443	0.9983	33.9596	39.7859	0.9970
	Cameraman	Goldhill	29.2672	42.3324	0.9986	29.2672	39.6536	0.9976
$512\times 512$	Lena	Barbara	33.6028	42.3879	0.9985	33.9741	39.6025	0.9974
	Baboon	Jet	23.3306	42.4855	0.9972	23.3306	39.5200	0.9952
	Woman	Peppers	35.4988	42.3948	0.9976	35.4988	39.7142	0.9958
	Cameraman	Goldhill	33.9741	42.3654	0.9981	33.6028	39.7277	0.9968

, where PSNR_dec represents the PSNR value between the plain image and corresponding decrypted image, and PSNR_cip and MSSIM_cip represent the PSNR and MSSIM values between the carrier image and corresponding cipher image, respectively. We can see that when the smooth function is introduced, all PSNR_cip values are greater than 42 dB, and the MSSIM_cip values are larger than 0.9970, which are higher than those generated without the use of the smooth function. After employing the smoothing function, the quality of each cipher image is promoted by more than 2 dB, indicating that the introduced smooth function and the quantization of the coefficient sign exert significant efficacy. Besides, the PSNR_dec values with the sized $512\times 512$ carrier images and plain images are higher than those of the corresponding sized $256\times 256$ images, except for the Baboon texture image. Thus, the image size affects the decryption quality. In conclusion, the results mentioned above indicate that our method produces visually secure cipher images for transmission and offers satisfactory visual quality for both cipher and decrypted images.

4.1.2. Influence of Different Carrier Images on Encryption and Decryption

The LIWT operation converts the carrier pixel values to integer coefficient values and the subsequent quantization operation handles the signs of the generated coefficients in a reversible manner. Thus, these operations do not cause energy loss to the extracted secret image. Additionally, the invertible embedding and extraction processes ensure the integrity of the extracted information. However, the truncation errors from the rounding operation perhaps lead to the loss of error information and further degrade the quality of the decrypted image to some degree. To evaluate the influence of different carrier images on the simulation results, the $256\times 256$ and $512\times 512$ images of Woman are encrypted and then embedded into four different carrier images: Barbara, Jet, Lena, and Goldhill, respectively.

Table 2. PSNR and MSSIM values for different carrier images.

Plain Image	Carrier Image	With Smooth Function			Without Smooth Function
		PSNRdec(dB)	PSNRciph(dB)	MSSIMciph	PSNRdec(dB)	PSNRciph(dB)	MSSIMciph
Woman ($256\times 256$)	Barbara	33.9596	42.3844	0.9990	33.9596	39.7819	0.9982
	Jet	33.7542	42.4317	0.9978	33.7542	39.4862	0.9960
	Lena	33.4563	42.5292	0.9981	33.4563	39.6842	0.9978
	Goldhill	33.6521	42.3324	0.9986	33.6521	39.6536	0.9976
Woman ($512\times 512$)	Barbara	35.4988	42.3879	0.9985	35.4988	39.6025	0.9974
	Jet	35.4356	42.4855	0.9972	35.4356	39.5200	0.9952
	Lena	35.4732	42.4021	0.9977	35.4732	39.7345	0.9961
	Goldhill	35.4381	42.3654	0.9981	35.4381	39.7277	0.9968

lists the calculated PSNR_dec, PSNR_cip, and MSSIM_cip values with and without the smooth function. It can be seen that even when testing different carrier images, the PSNR_dec values are still very similar and vary within a very narrow interval, verifying that different carrier images have little effect on the quality of decrypted images. Moreover, when the smooth function is utilized, all PSNR_cip values are greater than 42 dB, and the MSSIM_cip values are larger than 0.9970, which are greater than the corresponding PSNR_cip and MSSIM_cip values generated without the smooth function. Thus, the introduced smooth function effectively improves the visual security of cipher images.

4.1.3. Influence of Threshold TS on Encryption and Decryption

Here, we also evaluate the influence of threshold TS on the encryption and decryption effect. Firstly, four $256\times 256$ plain images including Woman, Lena, Baboon, and Cameraman are encrypted in turn, and then embedded in four carrier images Barbara, Jet, Peppers, and Goldhill, respectively. The test procedure for the images of size $512\times 512$ is the same. Figure 7 plots the relationship between TS and PSNR. As shown, regardless of the plain image or image size used, the PSNR values initially increase and then gradually decrease as TS increases. The maximum PSNR value fluctuates with the selection of plain image. Moreover, for the same plain image but with different sizes, the maximum PSNR value still varies with the setting of TS. Thus, the threshold TS influences the decryption of the plain image. A reasonable recommendation is to set the threshold TS to 25.

4.2. Performance Analyses

In this section, performance analyses are assessed from key sensitivity analysis, histogram analysis, correlation analysis, information entropy analysis, CPA attack, noise attack, data loss attack, and running efficiency analysis. In what follows, we analyze and discuss them successively.

4.2.1. Key Space and Sensitive Analysis

Key space refers to the total number of different keys used in the encryption algorithm. As described in Equation (9), the initialization processes of three initial values for the fractional Lorenz system depends on three external keys with 17 decimals. Therefore, the total key space is ${10}^{3\times 17}={10}^{51}$, which is enough to resist against a brute-force attack. Key sensitivity is a property that allows a robust encryption design to yield a completely different output by making subtle changes to the keys used. The plain image Woman ($256\times 256$) and the carrier image Peppers ($256\times 256$) (see Figure 5(a3,b3) are subjected to the proposed algorithm with the correct key $(x_0,y_0,z_0)$, and the subtly modified keys $(x_0+{10}^{-15},$$y_0,z_0)$, $(x_0,y_0+{10}^{-15},z_0)$, and $(x_0,y_0,z_0+{10}^{-15})$. The corresponding decrypted images are displayed in Figure 8. As one would expect, when the key is changed subtly, the corresponding decrypted image is noisy and cannot provide any visual information, implying that the decryption process is sensitive to the used keys.

In another aspect, the four keys are utilized to encrypt the same plain image Woman, and the generated secret images and the final cipher images are presented in Figure 9a–d,e–h, respectively. The differential images between the original and modified secret images are shown in Figure 9i–k. As can be observed, minor changes to the keys used can cause significant changes to the secret images. However, the corresponding cipher images are visible and appear identical to each other, which means the cipher images can be transmitted securely over a public channel.

4.2.2. Histogram Analysis

The histogram of an image depicts the probability density distribution of discrete pixel values, plotted on the horizontal axis with 0–255 gray levels and on the vertical axis with the corresponding frequencies. A secure cryptosystem should obtain the secret image with a flat histogram distribution to resist statistic attacks. In this paper, the plain image and the corresponding carrier image are the same as those in Section 4.1.1. The histogram distributions of the secret image, the carrier image, and the cipher image are shown in Figure 10, respectively. As seen, the histograms of the secret images are flat and similar to each other; on the contrary, the histograms of the cipher images are uneven and look the same as the carrier images. Thus, the attacker cannot obtain valuable information from the histogram distributions of the cipher images to recover the plaintext information. This shows that our scheme can provide acceptable visual security without raising suspicion in transmission.

4.2.3. Correlation Analysis

The correlation between adjacent pixels is often used as one of the important criteria to evaluate the security performance of the existing cryptosystems. For natural images, there is strong correlation between adjacent pixels; however, it can be greatly weakened by secure cryptographic cryptosystems. The correlation coefficient (CC) is calculated as

$$C_{xy}=\frac{L_s{\sum }_{i=1}^{L_s}\left(x_i{y}_i\right)-{\sum }_{i=1}^{L_s}{x}_i{\sum }_{i=1}^{L_s}{y}_i}{\sqrt{\left(L_s{\sum }_{i=1}^{L_s}{x}_i^2-{\left({\sum }_{i=1}^{L_s}{x}_i\right)}^2\right)\left(L_s{\sum }_{i=1}^{L_s}{y}_i^2-{\left({\sum }_{i=1}^{L_s}{y}_i\right)}^2\right)}},$$

(23)

where $x_i$ and $y_i$ are the adjacent pixel values, and $L_s$ is the total number of selected pixel pairs. In the experiment, we randomly choose 2000 adjacent pixel pairs in horizontal, vertical, and diagonal directions to calculate the correlation between adjacent pixels. The sized $256\times 256$ images Woman and Peppers are used as the plain image and carrier image, respectively. Figure 11 and

Table 3. Correlation coefficients among adjacent pixels.

Image	Horizontal	Vertical	Diagonal
Plain image	0.9915	0.9935	0.9863
Secret image	0.0287	−0.0056	−0.0536
Carrier image	0.9694	0.9754	0.9435
Cipher image	0.9676	0.9676	0.9305

show the correlation results. We can see that the plain image, carrier image, and cipher image have a strong correlation with correlation coefficients close to 1, and the secret image has weaker correlation with corresponding correlation coefficient close to 0. In addition, the correlation plots in the third column of Figure 11 are similar to those in the fourth column, so it is not easy to distinguish the cipher image from the corresponding carrier image. In short, the correlation of the plain image is effectively broken by the encryption design, and the correlation of the carrier image is well-preserved with the smoothing function embedding.

4.2.4. Information Entropy Analysis

Information entropy is one of the important metrics to evaluate cryptographic security [35,36]. For a meaningful encryption system, the closer the information entropy of the encrypted image is to the carrier image entropy value, the better the encryption effect. The formula of entropy value is as follows:

$$H\left(x\right)=-{\sum }_{i=1}^{N}p\left(x_i\right){\log }_{2}p\left(x_i\right),$$

(24)

where $p\left(x_i\right)$ is the probability of $x_i$.

Table 4. Information entropy results.

Image	Plain Image	Secret Image	Carrier Image	Cipher Image
Baboon	7.1391	7.9896	7.2185	7.1396
Woman	7.2695	7.9895	7.2185	7.1396
Cameraman	7.0477	7.9899	7.2185	7.1398
Jet	6.7059	7.9901	7.2185	7.1399
Peppers	7.5924	7.9890	7.2185	7.1395
Barbara	7.6385	7.9894	7.2185	7.1395

lists the entropy results of different plain images embedded into the same carrier image ’Lena’. From this, it can be obtained that the entropy value of the encrypted image is close to that of the carrier image and the entropy value of the reconstructed image is close to that of the plain image, so the algorithm in this paper can effectively resist the information entropy attack.

4.2.5. Cpa Attack

A known plaintext attack (KPA) refers to a cryptanalytic model in which an attacker tries to reveal key association information with prior knowledge of the plaintext and the corresponding ciphertext. Compared with KPA, CPA is more powerful than KPA in that the attacker can choose any plaintext and generate the corresponding ciphertext to reveal key-related information. If an encryption scheme is resistant to a CPA attack, it is undoubtedly also resistant to a KPA attack. Based on this, a secure image encryption mechanism should be able to resist CPA. In our scheme, although the plain image changes only one bit of information, the generated secret image has obvious differences, which is due to the chaotic initial values of the fractional Lorenz system associated with the plaintext content. Chaos is extremely sensitive to the initial values, and a slightly changed plain image will generate different initial values, thus generating a different pseudorandom sequence and a completely different secret image. Based on the above analysis, the algorithm in this paper can resist a CPA attack.

4.2.6. Noise Attack

The cipher images may be interfered with by noise pollution when stored and transmitted in a public channel. Therefore, in this part, we test the proposed encryption algorithm against noise attacks. The cipher image Peppers is separately polluted by noise intensities 0.00001, 0.0001, 0.0005, 0.001, 0.005, and 0.01, and the noisy cipher images and the corresponding decrypted images are illustrated in Figure 12. As can be seen in Figure 12 and

Table 5. PSNR values under different salt and pepper noise attack.

Image	Noise Intensity
	0.00001	0.0001	0.0005	0.001	0.005	0.01
Woman ($256\times 256$)	41.0635	40.8181	39.2176	34.5001	28.2351	25.4084
Peppers ($256\times 256$)	32.5193	29.3239	28.6176	22.3247	15.9286	14.1350

, when the noisy intensity varies from 0.00001 to 0.01, the PSNR value of the decrypted image Woman decreases accordingly from 32.5193 dB to 14.1350 dB. In addition, one can see that there are several smaller destroyed squares in the decrypted images, which are different from these neighbor pixels. These small squares correspond to those VQ indexes that are damaged in the cipher image. Whereas the pixels located in the destroyed blocks cannot be recovered, these destroyed blocks imply that our method has the ability to detect inconspicuous potential attacks and locate tampering.

4.2.7. Data Loss Attack

To test the robustness against data loss attacks, the cipher image Peppers is assigned 0 by different size squares, and the cipher images and the corresponding decrypted images are shown in Figure 13. The data loss sizes of the cipher images in the first row of Figure 13 are $8\times 8$, $16\times 16$, $32\times 32$, and $64\times 64$, and the images in the second row correspond to the decrypted images. It can be seen from Figure 13(b1–b4) that some indexes in the tampered cipher image are destroyed, which further maps the block content of the decrypted image. In addition,

Table 6. PSNR, MSSIM and CC values of decrypted image for different data loss.

Size of Data Loss	PSNR (dB)	MSSIM	CC
$8\times 8$	28.9935	0.9477	0.9891
$16\times 16$	24.8029	0.8661	0.9714
$32\times 32$	18.6750	0.6018	0.8828
$64\times 64$	14.2427	0.3748	0.6503

lists the PSNR, MSSIM, and CC values of the decrypted images. It can be seen that the PSNR value of the decrypted image decreases gradually as the data loss square of the cipher images increases. Moreover, the PSNR value of the decrypted image decreases from 28.9935 dB to 14.2427 dB. Based on the calculated PSNR, MSSIM, and CC values, it is clear that the proposed encryption algorithm can resist data loss attacks to a certain extent.

4.2.8. Running Efficiency Analysis

Running efficiency is an important metric for encryption performance, especially for testing real-time application scenarios.

Table 7. Encryption time for images of size $256\times 256$ (Unit: s).

Item	Lena	Baboon	Woman	Cameraman	Average
Compression	0.1405	0.1256	0.1200	0.1324	0.1296
Diffusion	0.0057	0.0074	0.0100	0.0062	0.0073
Embedding	16.9714	17.3376	17.8024	16.9080	17.2549
Total	5.7059	5.8235	5.9775	5.6822	5.7973

,

Table 8. Decryption time for images of size $256\times 256$ (Unit: s).

Item	Lena	Baboon	Woman	Cameraman	Average
Extraction	8.5617	8.6331	8.9388	8.6678	8.7004
Inverse-diffusion	0.0049	0.0054	0.0059	0.0052	0.0054
Reconstruction	6.6999	6.8180	7.0726	6.5937	6.7961
Total	5.0888	5.1522	5.3391	5.0889	5.1673

,

Table 9. Encryption time for images of size $512\times 512$ (Unit: s).

Item	Lena	Baboon	Woman	Cameraman	Average
Compression	0.7345	0.7897	0.7124	0.7345	0.7428
Diffusion	0.0106	0.0096	0.0103	0.0100	0.0101
Embedding	69.0720	68.7851	69.6957	70.4789	69.5079
Total	23.2724	23.1948	23.4728	23.7411	23.4203

and

Table 10. Decryption time for images of size $512\times 512$ (Unit: s).

Item	Lena	Baboon	Woman	Cameraman	Average
Extraction	34.5340	35.4738	35.5933	34.6818	35.0707
Inverse-diffusion	0.0089	0.0116	0.0092	0.0089	0.0097
Reconstruction	27.5058	28.4689	27.7533	27.1136	27.7104
Total	20.6829	21.3181	21.1186	20.6014	20.9303

list the encryption time and decryption time for different size images. The size of the carrier image is kept the same as that of the plain image. ’Compression’ denotes the CS compression process, ’Diffusion’ denotes the diffusion process of the measurements and VQ indexes, ’Embedding’ denotes the total process of embedding the secret image into the three coefficient matrices of the carrier image, and ’Reconstruction’ denotes the decryption process of the plain image. It can be seen that the average time consumed for encryption ranges from 5.7973 s to 23.4203 s and for decryption from 5.1673 s to 20.9303 s when the size of the original image changes from $256\times 256$ to $512\times 512$. For the encryption process, the time spent on compression and diffusion is very small, and about all time is spent on smooth function embedding. When the image size is enlarged, more data is needed for embedding, and therefore, more time is consumed. As for the decryption process, the time spent on reconstruction accounts for about $45\%$ of the total time regardless of the image size chosen, while the time spent on the inverse diffusion is almost negligible. Based on the above data analysis, the proposed method is very suitable for the encryption and decryption of small and medium-sized images. When testing larger images, assistance from the cloud is essential, where encryption occurs locally and decryption is performed on the cloud.

4.3. Comparison with the Existing Work

In this subsection, visual security and compression performance of the proposed scheme are discussed and compared with other related schemes successively.

4.3.1. Visual Security

From the aspect of visual security, the appearance of the cipher image is closer to that of the carrier image, and greater visual security is obtained. In the simulation, the plain image and carrier image have the same size, and the volume of the cipher image is equal to that of the carrier image. The PSNR and MSSIM values between the carrier images and cipher images of our scheme and schemes [19,20,24] are given in Table 10. The carrier images and cipher images of all compared schemes have the same pixel resolution, i.e., $256\times 256$. The compression rate of the compared schemes [19,20,24] is fixed to 1/4, which is the same as our scheme, but the difference is that our compression rate consists of two parts: a 1/16 index matrix and a 3/16 error matrix. From the results listed in

Table 11. Comparison of the PSNR and MSSIM values of cipher images.

Plain Image	Carrier Image	PSNR (dB)				MSSIM
		Ref. [19]	Ref. [20]	Ref. [24]	Ours	Ref. [19]	Ref. [20]	Ref. [24]	Ours
Lena	Peppers	18.5136	32.3513	31.7986	42.4468	0.6726	0.9257	0.9903	0.9983
Jet	Baboon	23.3967	37.1058	32.5976	42.2459	0.6991	0.9833	0.9955	0.9989
Girl	Goldhill	28.2318	36.1125	32.0647	42.1456	0.7021	0.9666	0.9942	0.9986
Barbara	Bridge	25.2321	35.5629	31.7397	42.2451	0.7337	0.9783	0.9946	0.9993
Average		23.8436	35.2831	32.0502	42.2709	0.7019	0.9635	0.9937	0.9988

, we can find that the proposed scheme outperforms all the compared schemes in terms of PSNR and SSIM values of the cipher images. The reasons for this are summarized below.

(i): We use the LIWT transform to convert the carrier pixel values to integer coefficient components, and there are no errors in the inverse LIWT transform.

(ii): The quantization operation on the generated coefficients is reversible, which makes it free from energy loss.

(iii): We introduce a smoothing function in the embedding process, which is essential to reduce the numerical differences between the hidden and modified data.

In addition, we also subject the carrier and cipher images of size $512\times 512$ to our algorithm, and compare the PSNR and SSIM values of the decrypted images of the proposed scheme and other schemes [19,20,21]. These results are listed in

Table 12. Comparison of the PSNR values of decrypted images.

Plain Image	Carrier Image		Ref. [19]	Ref. [20]	Ref. [21]	Ours
Barbara ($512\times 512$)	Lena ($512\times 512$)	PSNR (dB)	28.4817	28.4435	28.5534	29.3547
		MSSIM	0.9915	0.8128	0.9932	0.9920
	Bridge ($512\times 512$)	PSNR (dB)	28.1745	28.4435	28.5534	29.7569
		MSSIM	0.9865	0.8128	0.9932	0.9920
	Girl ($512\times 512$)	PSNR (dB)	28.1932	28.4435	28.5534	29.4532
		MSSIM	0.9872	0.8128	0.9932	0.9920
	Peppers ($512\times 512$)	PSNR (dB)	28.2321	28.4435	28.5534	29.5542
		MSSIM	0.9891	0.8128	0.9932	0.9920

. It can be found that the PSNR and MSSIM values in our scheme are larger than the corresponding values in the schemes [19,20], so combining CS and VQ leads to an improvement in the quality of the decrypted images. The PSNR and MSSIM values in the schemes [20,21] are fixed, which means that the decryption results are independent of the carrier image used, indicating that the embedding and extraction processes of both methods is fully reversible. On the other hand, the SSIM values of the scheme in [21] are better than our scheme, while the PSNR values are smaller than ours. Therefore, the scheme in [21] and the proposed scheme have different aspects of advantages and both have better visual security.

4.3.2. Compression Performance

In the rest of the subsection, we further evaluate the compression and encryption performance of the proposed scheme. Specifically, the image Lena of size $256\times 256$ as the plain image is firstly processed by the VQ encoder to generate the index matrix and the error matrix. Then, the generated error matrix is confused and compressed by CS, and the VQ index matrix and the measurements are fused together and encrypted by the diffusion process. The decryption process is the reverse process of encryption, and the final decrypted image is generated by supplementing the reconstructed error matrix to the decoded VQ indexes. The PSNR values of the decrypted images at different compression ratios are calculated and compared with other related schemes in [19,21,24]. All compared methods use the Lena of size $256\times 256$ as the plain image and the OMP algorithm as the CS reconstruction algorithm.

Table 13. Comparison of the PSNR values of decrypted images under different compression ratios.

Plain Image	CR	Ref. [19]	Ref. [21]	Ref. [24]	Ours
Lena	0.25	23.45	26.56	27.95	31.97
($256\times 256$)	0.5	27.64	29.83	32.27	34.01
	0.75	31.25	31.62	35.18	38.76

shows the results. It can be seen that the proposed encryption design achieves more satisfactory compression performance compared with the schemes in [19,21,24].

5. Conclusions

This paper proposes a visually secure image encryption scheme based on a fractional chaotic system and CS technology. In our method, the fractional chaotic system is used to generate the measurement matrix and improve the encryption and embedding effect. Besides, the smooth function and coefficient quantization are used to improve the visual security of the cipher images. Simulation results and performance analyses are performed for images of different sizes to verify the improvements on the visual security of the cipher images and the visual quality of the corresponding decrypted images. The excellent performance proves that the proposed scheme can be an effective solution for protecting digital images from suspicion and attacks during storage and transmission.