FOPI/FOPID Tuning Rule Based on a Fractional Order Model for the Process
Abstract
:1. Introduction
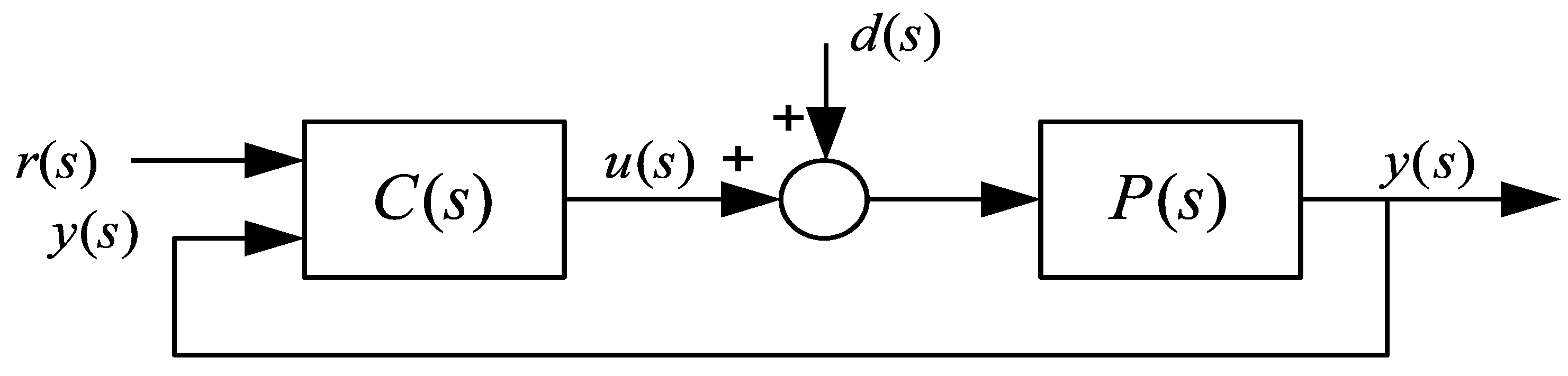
2. Problem Formulation
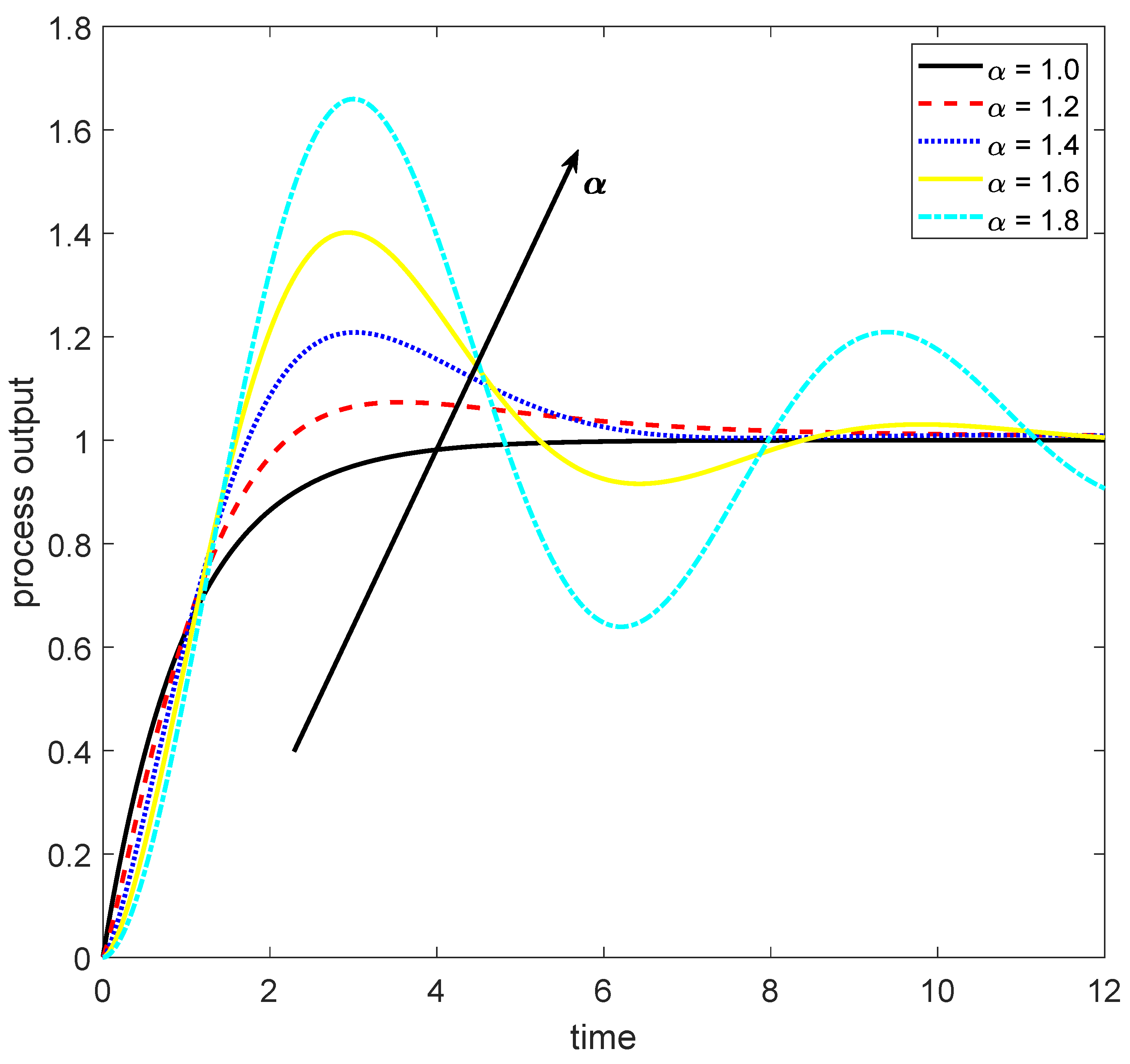
2.1. Controlled Process Model
2.2. FOPI(D) Controller Equation
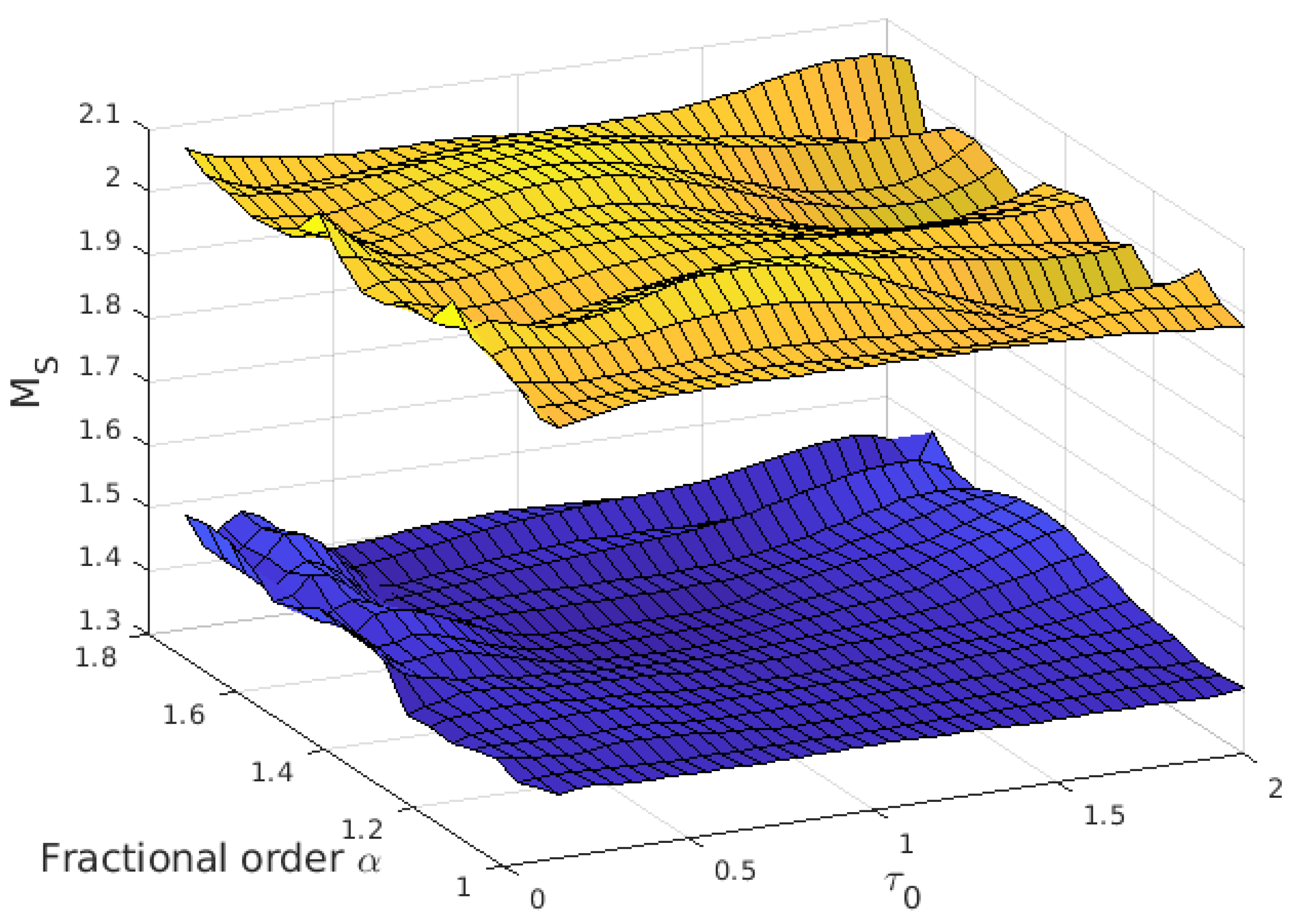
2.3. Performance and Robustness
3. Optimal Tuning
4. Robustness and Performance Analysis for the Tuning Rule
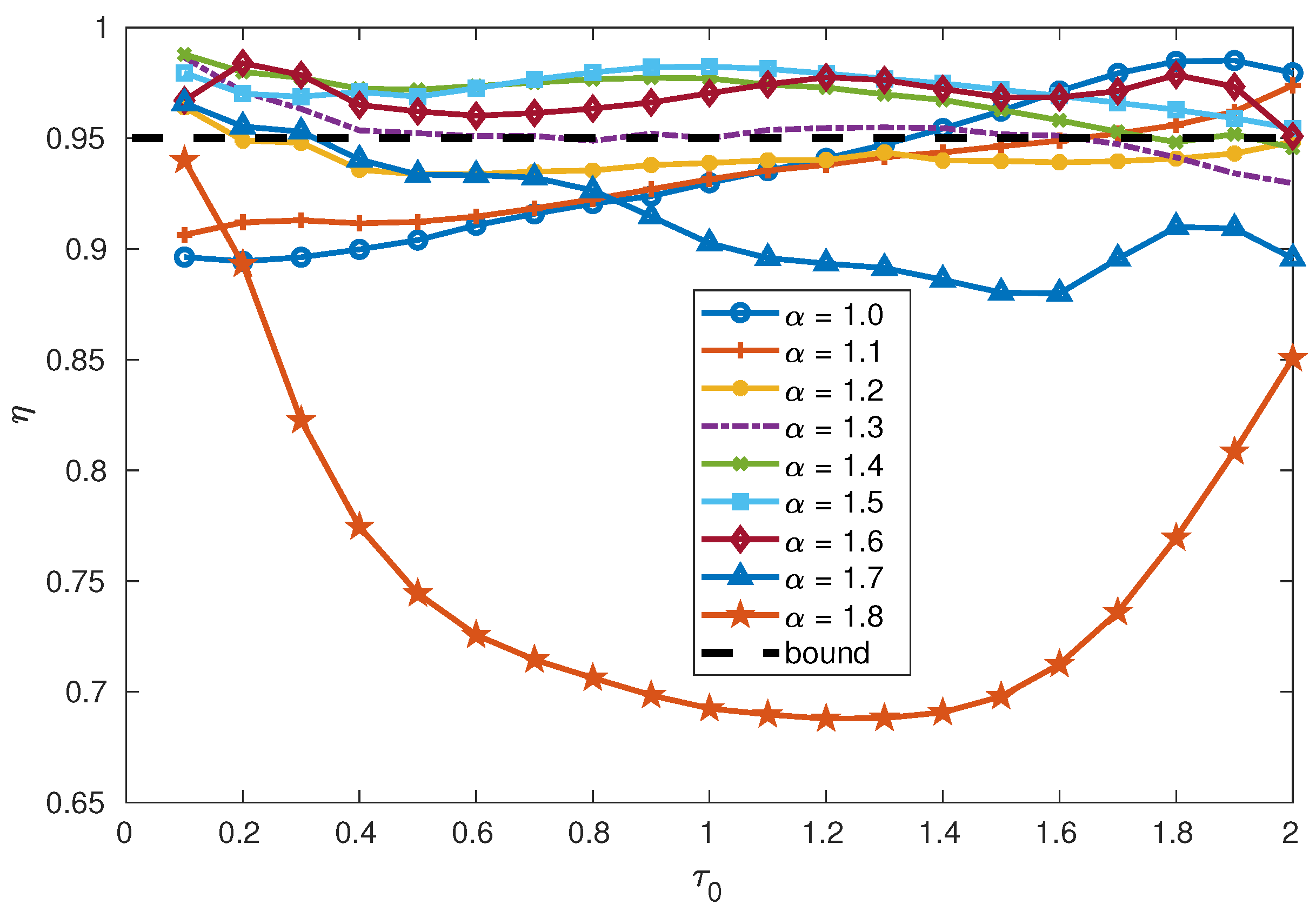
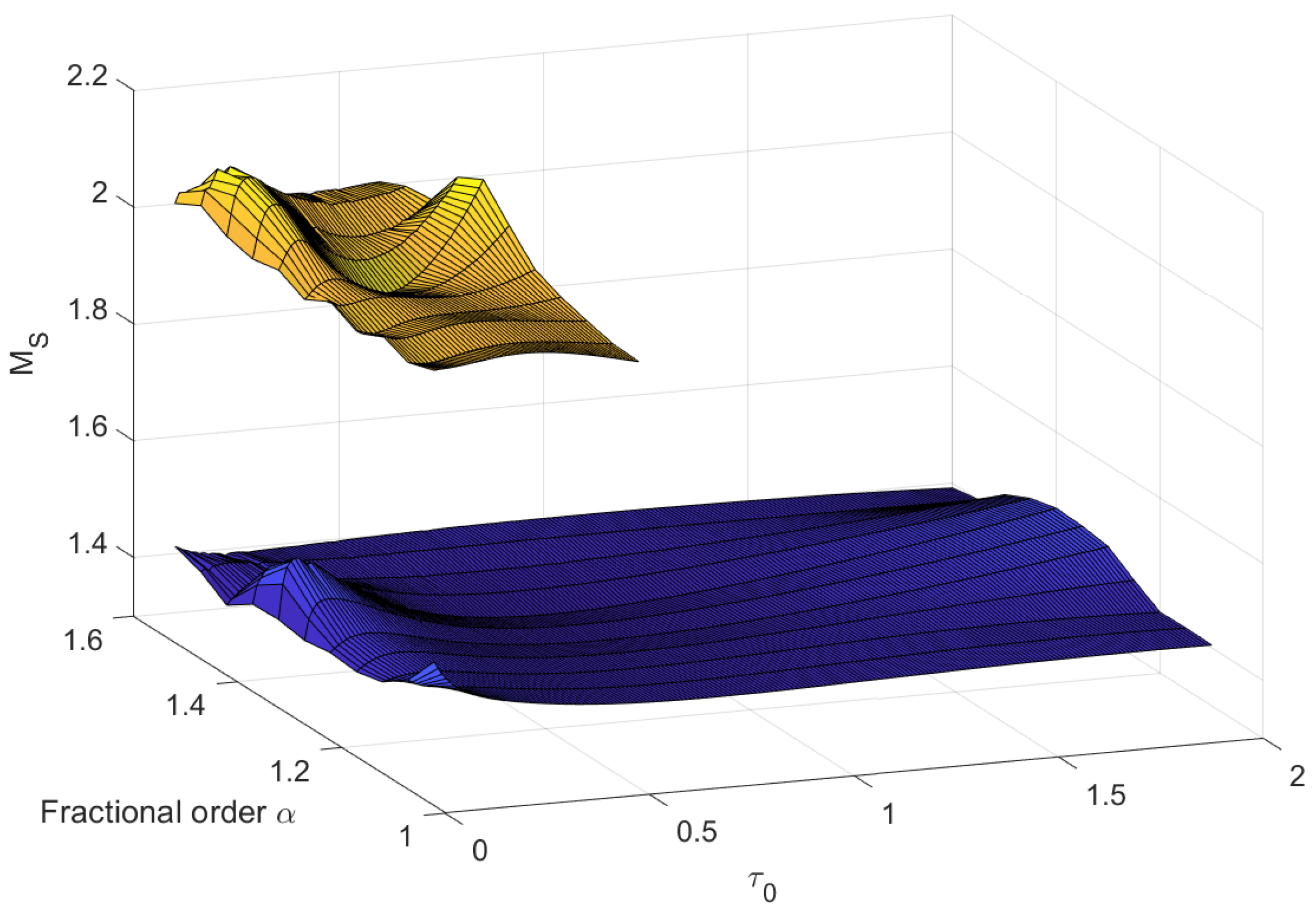
4.1. FOPID Controllers
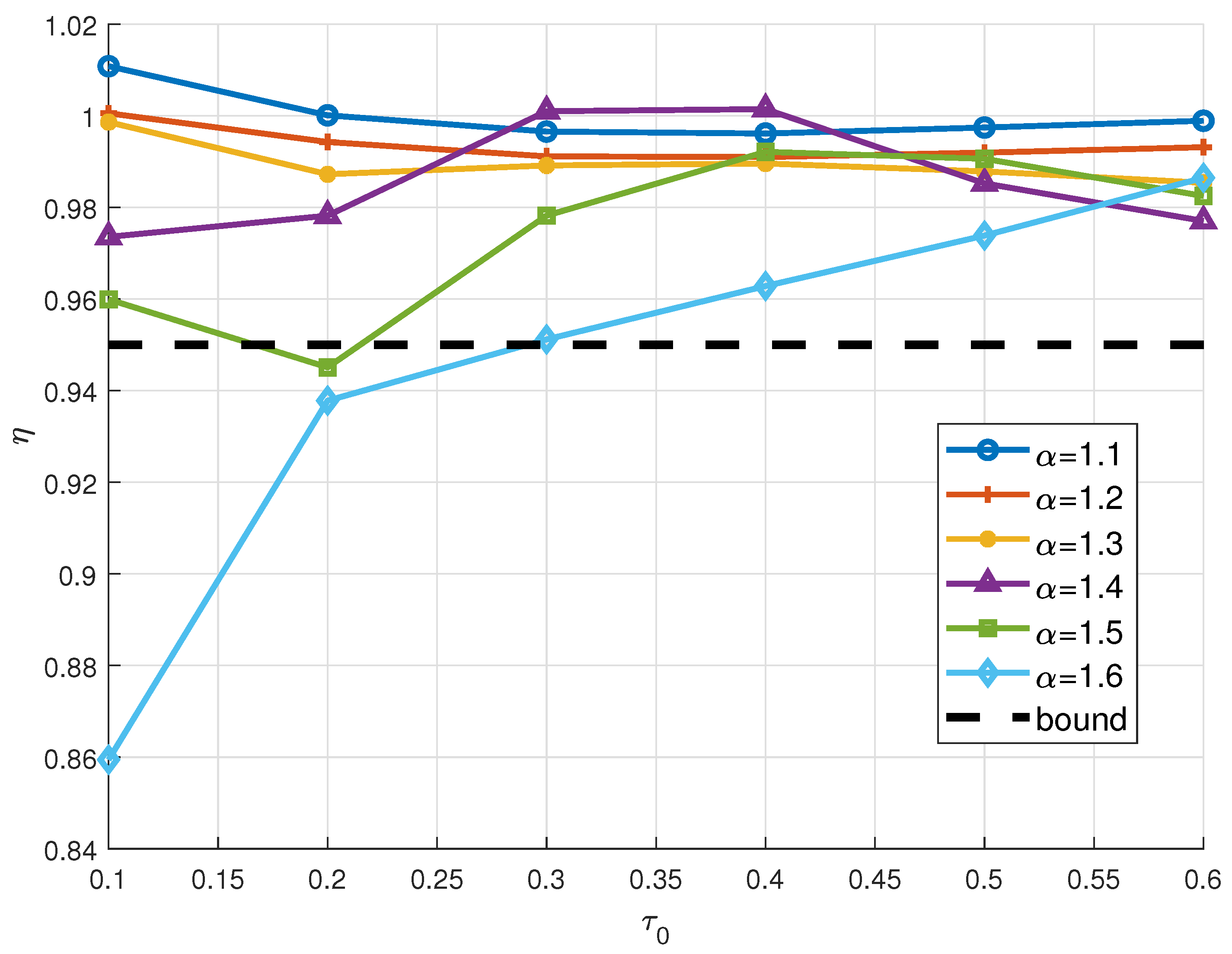
4.2. FOPI Controllers
5. Simulation Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.A.; Hosseinnia, S.H.; Petlenkov, E.; Ates, A.; Cech, M. Towards Industrialization of FOPID Controllers: A Survey on Milestones of Fractional-Order Control and Pathways for Future Developments. IEEE Access 2021, 9, 21016–21042. [Google Scholar] [CrossRef]
- Dastjerdi, A.A.; Vinagre, B.M.; Chen, Y.; HosseinNia, S.H. Linear fractional order controllers; A survey in the frequency domain. Annu. Rev. Control 2019, 47, 51–70. [Google Scholar] [CrossRef]
- Malek, H.; Luo, Y.; Chen, Y. Identification and tuning fractional order proportional integral controllers for time delayed systems with a fractional pole. Mechatronics 2013, 23, 746–754. [Google Scholar] [CrossRef]
- Königsmarková, J.; Čech, M. Robust PI/PID parameter surfaces for a class of fractional-order processes. IFAC-PapersOnLine 2018, 51, 763–768. [Google Scholar] [CrossRef]
- Zhao, C.; Xue, D.; Chen, Y. A fractional order PID tuning algorithm for a class of fractional order plants. In Proceedings of the IEEE International Conference Mechatronics and Automation, Niagara Falls, ON, Canada, 20 July–1 August 2005; Volume 1, pp. 216–221. [Google Scholar] [CrossRef]
- Li, D.; Liu, L.; Jin, Q.; Hirasawa, K. Maximum sensitivity based fractional IMC–PID controller design for non-integer order system with time delay. J. Process Control 2015, 31, 17–29. [Google Scholar] [CrossRef]
- Liu, L.; Pan, F.; Xue, D. Variable-order fuzzy fractional PID controller. ISA Trans. 2015, 55, 227–233. [Google Scholar] [CrossRef]
- Muresan, C.I.; Ionescu, C.M. Generalization of the FOPDT Model for Identification and Control Purposes. Processes 2020, 8, 682. [Google Scholar] [CrossRef]
- Gharab, S.; Feliu-Batlle, V.; Rivas-Perez, R. A Fractional-Order Partially Non-Linear Model of a Laboratory Prototype of Hydraulic Canal System. Entropy 2019, 21, 309. [Google Scholar] [CrossRef]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. Grey Box Identification of Fractional-order System Models from Frequency Domain Data. In Proceedings of the 2018 41st International Conference on Telecommunications and Signal Processing (TSP), Athens, Greece, 4–6 July 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Fahim, S.M.; Ahmed, S.; Imtiaz, S.A. Fractional order model identification using the sinusoidal input. ISA Trans. 2018, 83, 35–41. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.Q. Identification of Linear Fractional Order Systems Using the Relay Feedback Approach. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 3704–3709. [Google Scholar]
- Luo, Y.; Chen, Y.Q. Discussion on: Simple Fractional Order Model Structures and their Applications in Control System Design. Eur. J. Control 2010, 6, 695–699. [Google Scholar]
- Das, S.; Molla, N.; Pan, I. Online Identification of Fractional Order Models with Time Delay: An Experimental Study. In Proceedings of the International Conference on Communication and Industrial Application, Xi’ian, China, 20–21 August 2011; pp. 1–5. [Google Scholar]
- Tavakoli, M.; Haeri, M.; Saleh, M. Simple Fractional Order Model Structures and their Applications in Control System Design. Eur. J. Control 2010, 16, 680–694. [Google Scholar] [CrossRef]
- Wang, H.; He, Q.; Zhao, Z.; Zhang, J. A Design Method of Fractional Order PIλDμ Controller for Higher Order Systems. In Proceedings of the 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015; pp. 272–277. [Google Scholar]
- Das, S.; Pan, I.; Das, S.; Gupta, A. A novel fractional order fuzzy PID controller and its optimal time domain tuning based on integral performance indices. Eng. Appl. Artif. Intell. 2012, 25, 430–442. [Google Scholar] [CrossRef]
- Padula, F.; Visioli, A. Tuning rules for optimal PID and fractional-order PID controllers. J. Process Control 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Campos, D.; Arrieta, O.; Vilanova, R.; Rojas, J. Robust Tuning for 2DoF Fractional-Order PI Controllers Based on Model Reference Approach. In Proceedings of the International Conference on Information Technology & Systems, Dubai, United Arab Emirates, 8–10 November 2022; pp. 687–696. [Google Scholar]
- Maâmar, B.; Rachid, M. IMC-PID-fractional-order-filter controllers design for integer order systems. ISA Trans. 2014, 53, 1620–1628. [Google Scholar] [CrossRef]
- Valério, D.; da Costa, J.S. Tuning of fractional PID controllers with Ziegler–Nichols-type rules. Signal Process. 2006, 86, 2771–2784. [Google Scholar] [CrossRef]
- Arrieta, O.; Urvina, L.; Visioli, A.; Vilanova, R.; Padula, F. Servo/Regulation Intermediate Tuning for Fractional Order PID Controllers. In Proceedings of the IEEE Multi-Conference on Systems and Control, Sydney, NSW, Australia, 21–23 September 2015; pp. 1242–1247. [Google Scholar]
- Beschi, M.; Padula, F.; Visioli, A. Fractional robust PID control of a solar furnace. Control Eng. Pract. 2016, 56, 190–199. [Google Scholar] [CrossRef]
- Beschi, M.; Padula, F.; Visioli, A. The generalized isodamping approach for robust fractional PID controllers design. Int. J. Control 2017, 90, 1157–1164. [Google Scholar] [CrossRef]
- Meneses, H.; Arrieta, O.; Padula, F.; Vilanova, R.; Visioli, A. PI/PID control design based on a fractional-order model for the process. IFAC-PapersOnLine 2019, 52, 976–981. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, C.; Zhou, X.; Zhu, H. Fractional order fuzzy PID optimal control in copper removal process of zinc hydrometallurgy. Hydrometallurgy 2018, 178, 60–76. [Google Scholar] [CrossRef]
- Deniz, F.N.; Yüce, A.; Tan, N.; Atherton, D.P. Tuning of Fractional Order PID Controllers Based on Integral Performance Criteria Using Fourier Series Method. IFAC-PapersOnLine 2017, 50, 8561–8566. [Google Scholar] [CrossRef]
- Chen, Y.; Bhaskaran, T.; Xue, D. Practical Tuning Rule Development for Fractional Order Proportional and Integral Controllers. J. Comput. Nonlinear Dyn. 2008, 3, 021403. [Google Scholar] [CrossRef]
- Grandi, G.L.; Trierweiler, J.O. Tuning of Fractional Order PID Controllers based on the Frequency Response Approximation Method. IFAC-PapersOnLine 2019, 52, 982–987. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F. Frequency-Band Complex Noninteger Differentiator: Characterization and Synthesis. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Visioli, A. Practical PID Control; Springer Verlag Advances in Industrial Control Series; Springer: London, UK, 2006. [Google Scholar]
- Åström, K.; Hägglund, T. Advanced PID Control; ISA—The Instrumentation, Systems, and Automation Society: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Arrieta, O.; Vilanova, R. Performance degradation analysis of Optimal PID settings and Servo/Regulation tradeoff tuning. In Proceedings of the Conference on Systems and Control (CSC07), Marrakech, Morocco, 16–18 May 2007. [Google Scholar]
- Arrieta, O.; Vilanova, R. Servo/Regulation tradeoff tuning of PID controllers with a robustness consideration. In Proceedings of the 46th IEEE Conference on Decision and Control (CDC07), New Orleans, LA, USA, 12–14 December 2007. [Google Scholar]
- Arrieta, O.; Vilanova, R. Performance Degradation analysis of controller tuning modes: Application to an optimal PID tuning. Int. J. Innov. Comput. Inf. Control 2010, 6, 4719–4729. [Google Scholar]
- Arrieta, O.; Vilanova, R.; Rojas, J.D.; Meneses, M. Improved PID controller tuning rules for performance degradation/robustness increase trade-off. Electr. Eng. 2016, 98, 233–243. [Google Scholar] [CrossRef]
- Shinskey, F.G.G. Feedback Controllers for the Process Industries; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Tavazoei, M.S. Notes on integral performance indices in fractional-order control systems. J. Process Control 2010, 20, 285–291. [Google Scholar] [CrossRef]
- Meneses, H.; Guevara, E.; Arrieta, O.; Padula, F.; Vilanova, R.; Visioli, A. Improvement of the Control System Performance based on Fractional-Order PID Controllers and Models with Robustness Considerations. IFAC-PapersOnLine 2018, 51, 551–556. [Google Scholar] [CrossRef]
- Barbosa, R.; Tenreiro Machado, J.; Ferreira, I. Tuning of PID Controllers Based on Bode’s Ideal Transfer Function. Nonlinear Dyn. 2004, 38, 305–321. [Google Scholar] [CrossRef]
- Guevara, E.; Meneses, H.; Arrieta, O.; Vilanova, R.; Visioli, A.; Padula, F. Fractional order model identification: Computational optimization. In Proceedings of the 2015 IEEE 20th Conference on Emerging Technologies Factory Automation (ETFA), Luxembourg, 8–11 September 2015; pp. 1–4. [Google Scholar]
- Alfaro, V.M. Low-Order Models Identification from Process Reaction Curve. Cienc. Tecnol. Costa Rica 2006, 24, 197–216. (In Spanish) [Google Scholar]




| Fractional Model Order | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | |
| = 1.4 | |||||||||
| a | 0.5638 | 0.5653 | 0.5432 | 0.4328 | 0.3650 | 0.3351 | 0.2532 | 0.2378 | 0.1849 |
| a | −0.9893 | −1.0791 | −1.1283 | −1.2442 | −1.2734 | −1.2932 | −1.4021 | −1.3649 | −1.5736 |
| a | 0.1577 | 0.1491 | 0.1554 | 0.2161 | 0.1832 | 0.1343 | 0.1207 | 0.0284 | 0.0013 |
| b | −0.4000 | 0.1654 | 0.1383 | −0.3206 | −0.2715 | −0.2702 | −0.6129 | −0.7134 | 0.0637 |
| b | 1.9196 | −0.5511 | −0.4646 | 1.5184 | 1.4090 | 1.5126 | 2.9236 | 3.4332 | −0.6934 |
| b | −3.2939 | 0.3352 | 0.2729 | −2.6022 | −2.6646 | −2.9467 | −4.5127 | −5.3134 | 2.6015 |
| b | 2.7735 | 0.5874 | 0.4581 | 1.9910 | 2.0294 | 2.0369 | 2.1310 | 2.2545 | −4.2468 |
| b | 0.2315 | 0.7783 | 0.9765 | 0.8235 | 0.8424 | 0.9472 | 1.1278 | 1.2233 | 2.9495 |
| c | −0.0183 | −0.0267 | −0.0041 | 0.0529 | 0.0613 | 0.0813 | 0.0620 | −0.1829 | −0.1222 |
| c | 0.0419 | 0.0705 | 0.0059 | −0.1789 | −0.1725 | −0.2300 | −0.3381 | 0.4952 | 0.5186 |
| c | 0.2780 | 0.3095 | 0.4054 | 0.5958 | 0.6102 | 0.7256 | 1.1030 | 0.7696 | 1.3970 |
| c | −0.0092 | −0.0056 | −0.0044 | −0.0035 | 0.0658 | 0.1053 | 0.0961 | 0.2357 | 0.1155 |
| d | −0.0060 | 0.0229 | 0.0805 | 0.0095 | 0.0647 | 0.0903 | 0.1043 | 0.0827 | 0.0215 |
| d | 0.0277 | −0.0861 | −0.3340 | −0.1421 | −0.3946 | −0.4802 | −0.5093 | −0.4150 | −0.1752 |
| d | −0.0967 | 0.0275 | 0.3543 | 0.3105 | 0.6515 | 0.7309 | 0.7412 | 0.6236 | 0.3322 |
| d | 1.2090 | 1.2080 | 1.1290 | 1.0780 | 0.9217 | 0.9046 | 0.9145 | 0.9566 | 1.1100 |
| Fractional Model Order | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | |
| = 2.0 | |||||||||
| a | 0.9955 | 0.8489 | 0.5728 | 0.5794 | 0.5374 | 0.3551 | 0.2700 | 0.2994 | 0.2658 |
| a | −1.0001 | −1.1607 | −1.3786 | −1.3572 | −1.4250 | −1.6330 | −1.7331 | −1.7088 | −1.7546 |
| a | 0.2899 | 0.3599 | 0.4664 | 0.2440 | 0.1421 | 0.2829 | 0.2587 | 0.1533 | 0.0646 |
| b | −0.4951 | 0.1149 | −0.2805 | −0.1981 | −0.1695 | −0.0510 | −0.0156 | −0.3510 | −0.4147 |
| b | 2.5286 | −0.4875 | 1.4698 | 1.0982 | 0.9569 | 0.2631 | 0.0347 | 1.7148 | 1.9312 |
| b | −4.5373 | 0.4419 | −2.6825 | −2.1250 | −1.9021 | −0.4175 | 0.1649 | −2.6742 | −2.7057 |
| b | 3.7920 | 0.7243 | 2.4579 | 1.8162 | 1.4605 | 0.2979 | −0.4271 | 1.1461 | 0.4894 |
| b | 0.1189 | 0.6500 | 0.4359 | 0.6983 | 0.8765 | 1.1982 | 1.4558 | 1.3167 | 1.7059 |
| c | −0.0322 | −0.0168 | 0.0593 | 0.0413 | 0.1046 | 0.1654 | 0.2576 | 0.0775 | −0.0033 |
| c | 0.0834 | 0.0282 | −0.2785 | −0.2214 | −0.3584 | −0.7399 | −1.1615 | −0.6308 | −0.2688 |
| c | 0.2353 | 0.3495 | 0.7055 | 0.7685 | 1.0178 | 1.4743 | 2.0619 | 1.8940 | 1.8795 |
| c | −0.0063 | −0.0142 | −0.0373 | −0.0171 | −0.0228 | −0.0411 | −0.0693 | −0.0314 | −0.0009 |
| d | 0.0000 | −0.0694 | −0.1143 | 0.0000 | 0.0000 | −0.0637 | −0.0665 | −0.0027 | 0.0089 |
| d | 0.0105 | 0.2257 | 0.4496 | 0.0000 | 0.0000 | 0.2103 | 0.2108 | −0.0069 | −0.0543 |
| d | −0.0872 | −0.2320 | −0.4362 | 0.0000 | 0.0000 | −0.0330 | 0.0234 | 0.2409 | 0.2475 |
| d | 1.2125 | 1.2165 | 1.1699 | 1.0000 | 1.0000 | 0.9900 | 0.9861 | 1.0054 | 1.0287 |
| Fractional Model Order | ||||||
|---|---|---|---|---|---|---|
| 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | |
| = 1.4 | ||||||
| a | 0.1646 | 0.1461 | 0.1132 | 0.06155 | 0.06375 | 0.3025 |
| a | −1.413 | −1.32 | −1.313 | −1.535 | −1.245 | −0.4086 |
| a | 0.1514 | 0.1339 | 0.116 | 0.1153 | 0.07255 | −0.1073 |
| b | 0.08874 | 0.03202 | 0.01904 | 0.06183 | 0.1728 | −0.9853 |
| b | 1.83 | 2.729 | −1.338 | −1.173 | −0.986 | 0.263 |
| b | 0.9161 | 1.016 | 1.017 | 0.8984 | 0.6747 | 2.295 |
| c | 0 | 0 | 0 | 1.8 | 0.003039 | −0.09594 |
| c | 0 | 0 | 0 | −9.306 | −2.057 | 1.694 |
| c | 1.01 | 1.03 | 1.043 | 1.059 | 1.068 | 1.445 |
| Fractional Model Order | ||||||
|---|---|---|---|---|---|---|
| 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | |
| = 2.0 | ||||||
| a | 0.4784 | 0.3539 | 0.1929 | 0.07267 | 0.1209 | 0.1949 |
| a | −1.16 | −1.289 | −1.524 | −1.901 | −1.439 | −1.036 |
| a | 0.2257 | 0.2792 | 0.4144 | 0.504 | 0.227 | 0.2001 |
| b | 1.2 | −0.1899 | 0.4381 | −0.4154 | −1.421 | −1.13 |
| b | 0.3124 | −0.8787 | 0.2076 | 1.891 | 0.5037 | 0.09457 |
| b | 0.1598 | 2.258 | 1.01 | 1.586 | 2.43 | 2.849 |
| c | 0.2798 | −0.04119 | 5.739 | 1.673 | 5.772 | 0.6522 |
| c | 0.002471 | 0.3394 | −1.891 | −3.252 | −3.51 | −0.1015 |
| c | 0.727 | 1.041 | 1.011 | 1.014 | 1.017 | 0.7017 |
| Tuning Rule | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P.&V. SP | 1.4 | 0.34 | 2.96 | 1 | 2.43 | 1.2 | 1.4026 | 10.7959 | 9.1082 | 9.1615 | 19.9041 | 18.2697 |
| P.&V. LD | 1.4 | 0.33 | 2.63 | 1 | 2.53 | 1.2 | 1.4283 | 10.8432 | 8.7614 | 8.9092 | 19.6046 | 17.6706 |
| P.&V. SP | 2.0 | 0.54 | 3.15 | 1 | 2.97 | 1.2 | 2.1195 | 9.4469 | 6.4376 | 6.8593 | 15.8845 | 13.2969 |
| P.&V. LD | 2.0 | 0.59 | 3.07 | 1 | 2.62 | 1.2 | 2.1156 | 9.467 | 6.4112 | 7.266 | 15.8782 | 13.6772 |
| H-F | 1.4 | 0.2352 | 2.43 | 1 | 4.01 | 1.07 | 1.4988 | 12.4727 | 10.4577 | 10.4726 | 22.9304 | 20.9302 |
| H-F | 2.0 | 0.5 | 2.43 | 1 | 4.01 | 1.07 | 2.8553 | 8.9615 | 5.5793 | 7.5733 | 14.5407 | 13.1526 |
| FOMCoRoT | 1.4 | 0.571 | 5.0104 | 1 | 1.9429 | 1.1371 | 1.3983 | 8.9024 | 8.769 | 8.771 | 17.6714 | 17.54 |
| FOMCoRoT | 2.0 | 0.9917 | 5.8036 | 1 | 1.9001 | 1.1353 | 1.9771 | 8.3925 | 5.8549 | 6.459 | 14.2473 | 12.3138 |
| Tuning Rule | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P.&V. SP | 1.4 | 3.8255 | 5.4555 | 1 | 0.2169 | 1.2 | 1.3703 | 1.8059 | 1.4266 | 1.6346 | 3.2325 | 3.0612 |
| P.&V. LD | 1.4 | 2.6563 | 1.2797 | 1 | 0.4811 | 1.1 | 1.3962 | 2.8454 | 0.7184 | 2.3704 | 3.5638 | 3.0887 |
| P.&V. SP | 2.0 | 5.7387 | 5.5095 | 1 | 0.3177 | 1.1 | 1.7828 | 1.4267 | 0.9604 | 1.1408 | 2.3872 | 2.1012 |
| P.&V. LD | 2.0 | 4.0728 | 0.937 | 1 | 0.4811 | 1 | 1.8299 | 1.9595 | 0.3303 | 1.65 | 2.2808 | 1.9803 |
| H-F | 1.4 | 0.2369 | 0.2586 | 1 | 6.8601 | 1.0413 | 1.5003 | 7.1647 | 1.1131 | 1.121 | 8.2778 | 2.2341 |
| H-F | 2.0 | 0.5036 | 0.2586 | 1 | 6.8601 | 1.0413 | 2.8689 | 6.7233 | 0.5238 | 0.5412 | 7.2471 | 1.0649 |
| FOMCoRoT | 1.4 | 7.6136 | 3.8014 | 1 | 0.1514 | 1.2048 | 1.397 | 1.3301 | 0.4993 | 1.1131 | 1.8294 | 1.6124 |
| FOMCoRoT | 2.0 | 13.9519 | 3.3554 | 1 | 0.1277 | 1.2028 | 2.0435 | 1.0017 | 0.2405 | 0.7637 | 1.2422 | 1.0042 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meneses, H.; Arrieta, O.; Padula, F.; Visioli, A.; Vilanova, R. FOPI/FOPID Tuning Rule Based on a Fractional Order Model for the Process. Fractal Fract. 2022, 6, 478. https://doi.org/10.3390/fractalfract6090478
Meneses H, Arrieta O, Padula F, Visioli A, Vilanova R. FOPI/FOPID Tuning Rule Based on a Fractional Order Model for the Process. Fractal and Fractional. 2022; 6(9):478. https://doi.org/10.3390/fractalfract6090478
Chicago/Turabian StyleMeneses, Helber, Orlando Arrieta, Fabrizio Padula, Antonio Visioli, and Ramon Vilanova. 2022. "FOPI/FOPID Tuning Rule Based on a Fractional Order Model for the Process" Fractal and Fractional 6, no. 9: 478. https://doi.org/10.3390/fractalfract6090478
APA StyleMeneses, H., Arrieta, O., Padula, F., Visioli, A., & Vilanova, R. (2022). FOPI/FOPID Tuning Rule Based on a Fractional Order Model for the Process. Fractal and Fractional, 6(9), 478. https://doi.org/10.3390/fractalfract6090478









