Time-Delay Fractional Variable Order Adaptive Synchronization and Anti-Synchronization between Chen and Lorenz Chaotic Systems Using Fractional Order PID Control
Abstract
:1. Introduction
2. Description of the Chen and Lorenz Chaotic Systems
3. Time-Delay Adaptive Synchronization of Chaotic Systems of Fractional Order
4. Time-Delay Adaptive Anti-Synchronization of Fractional Order Chaotic Systems
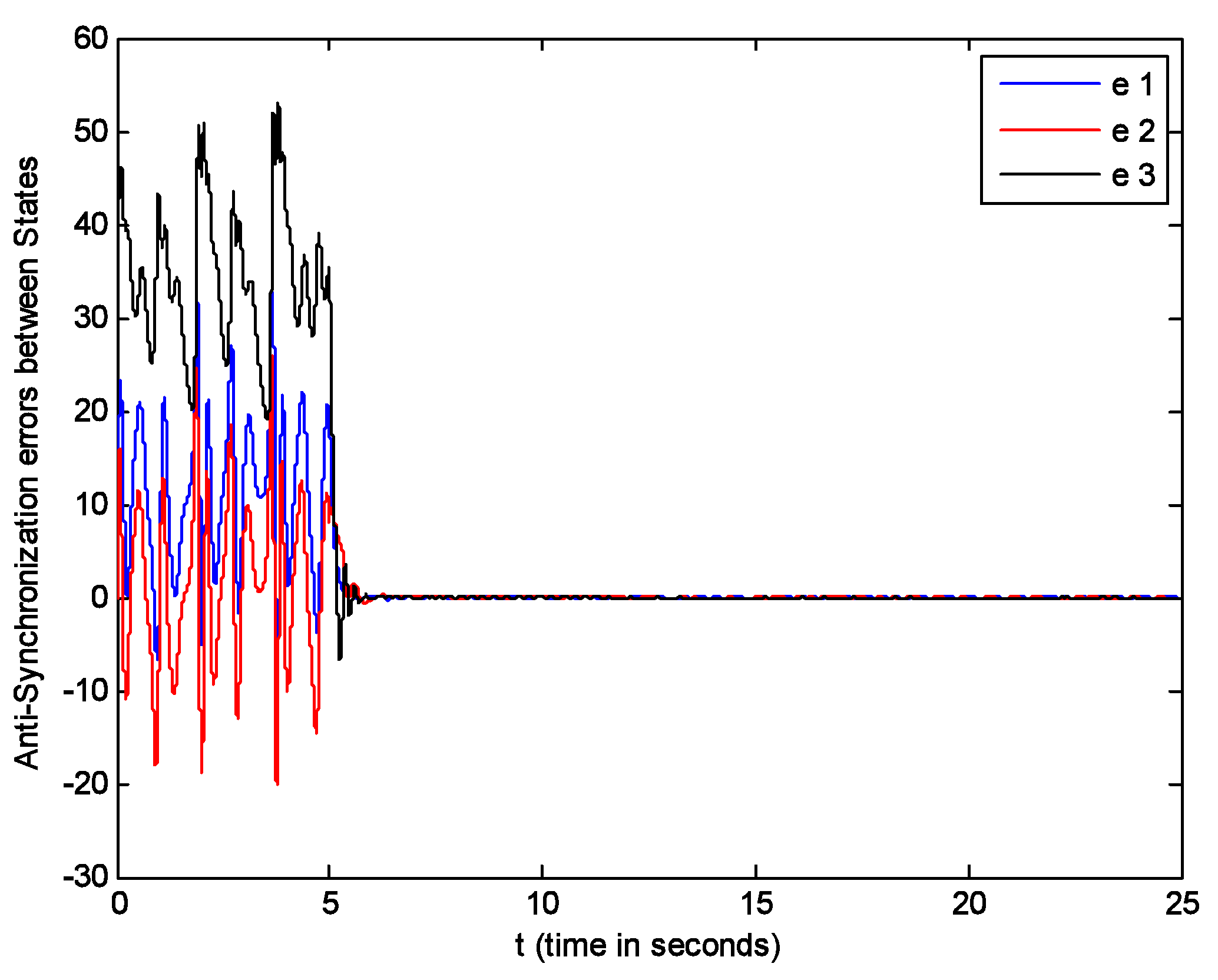
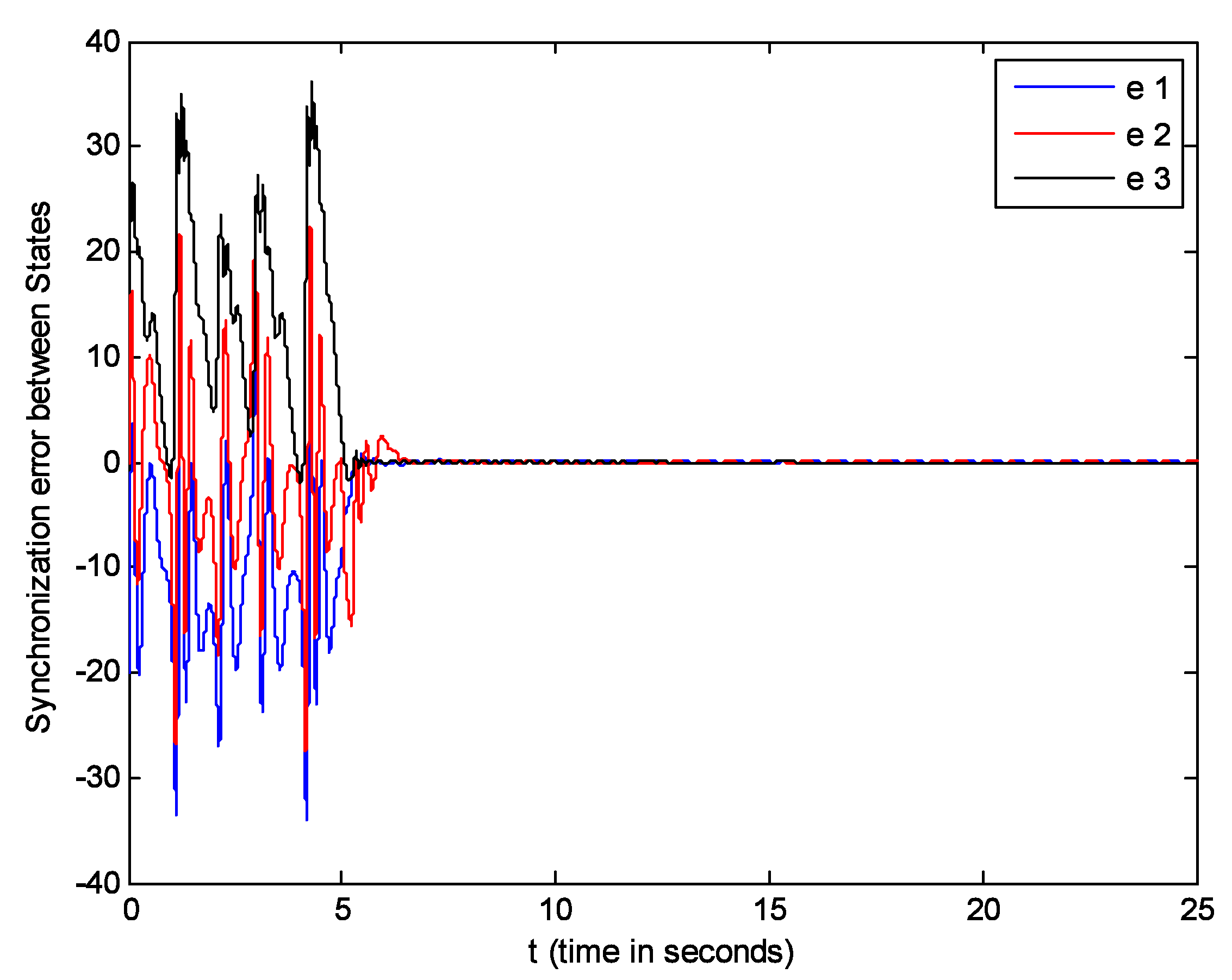
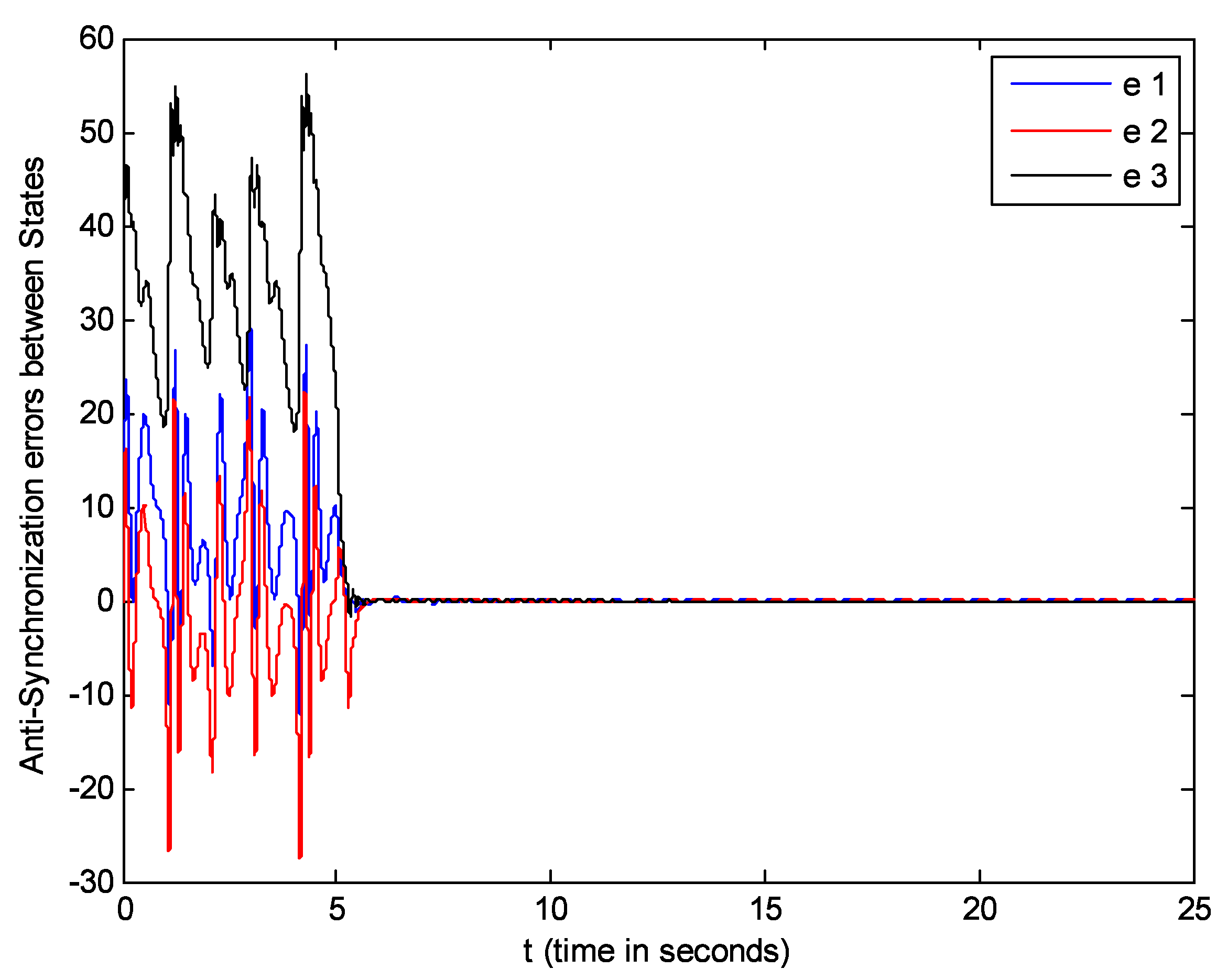
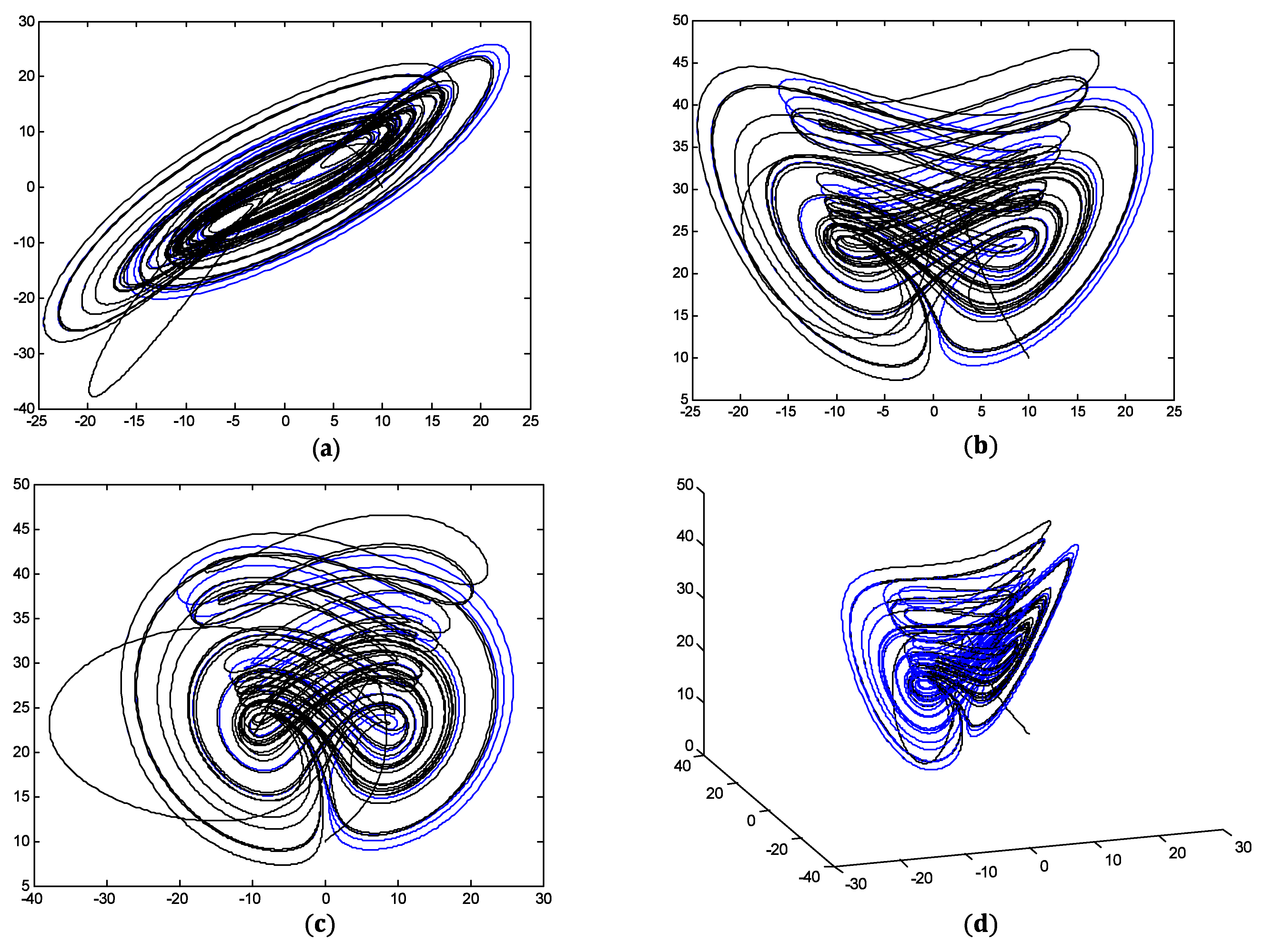
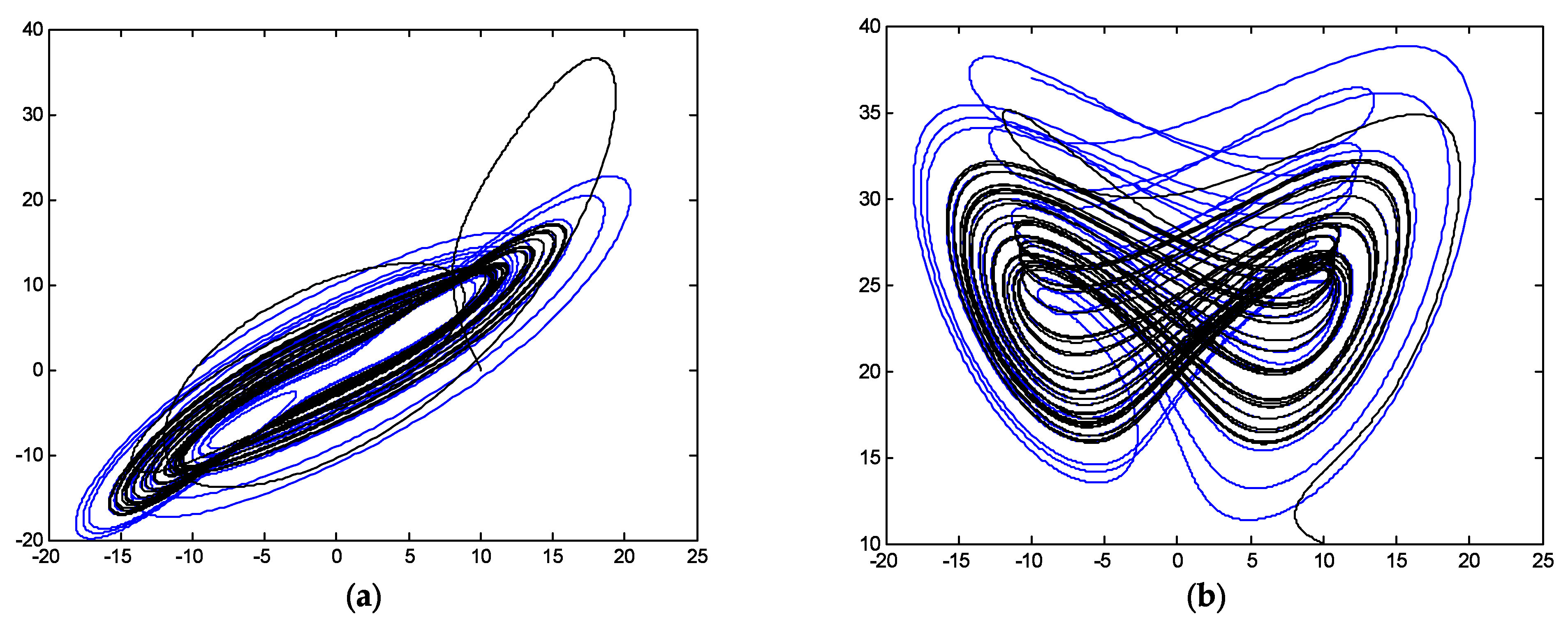
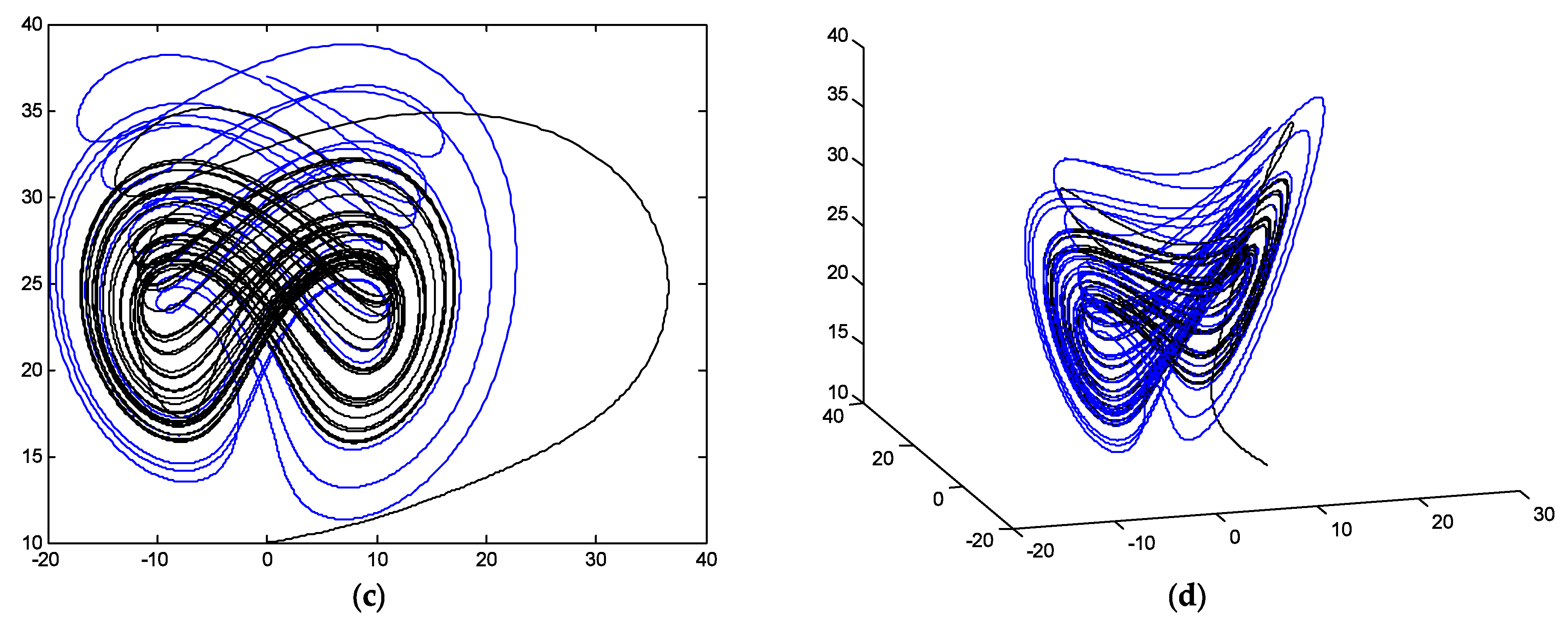
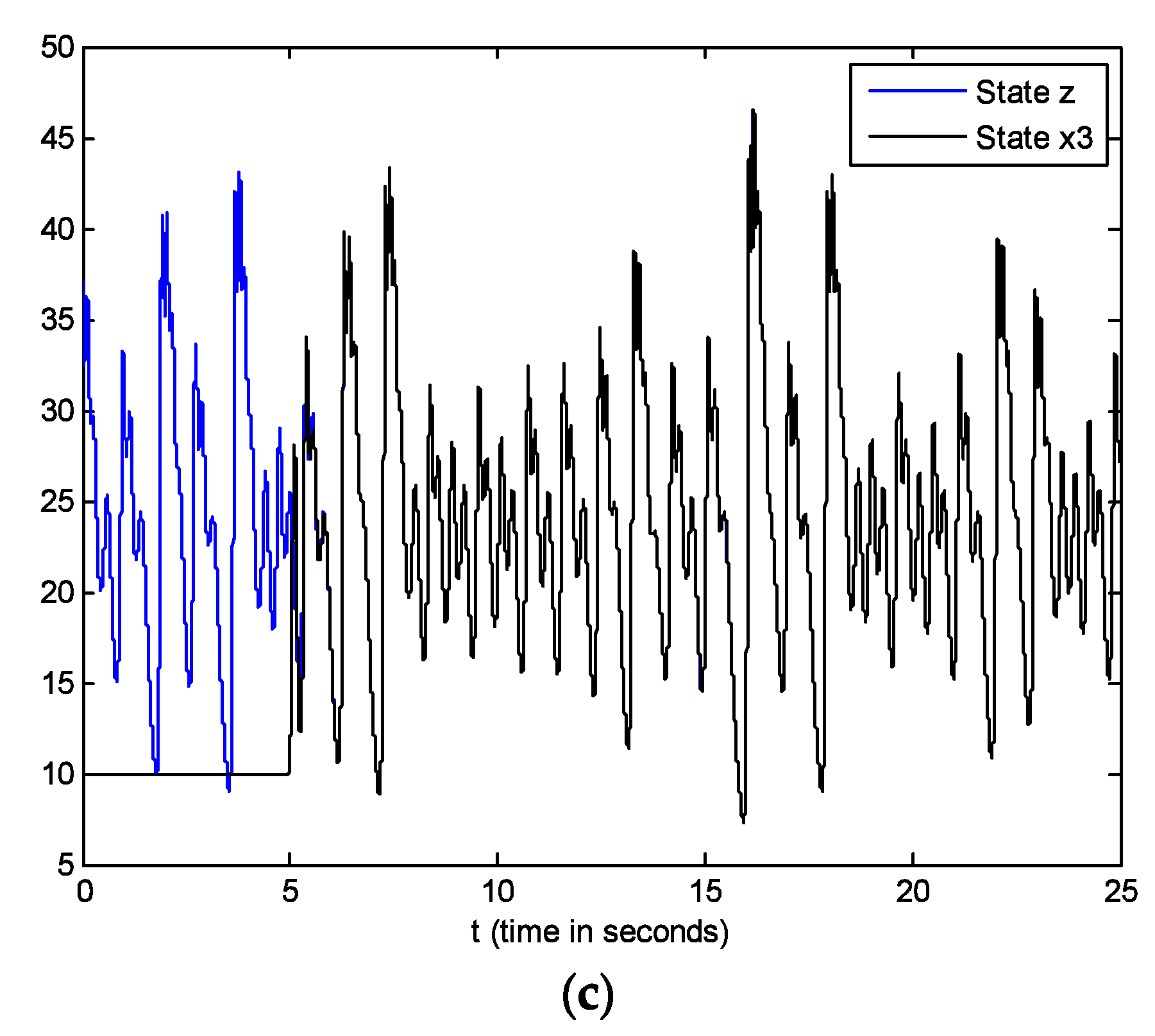
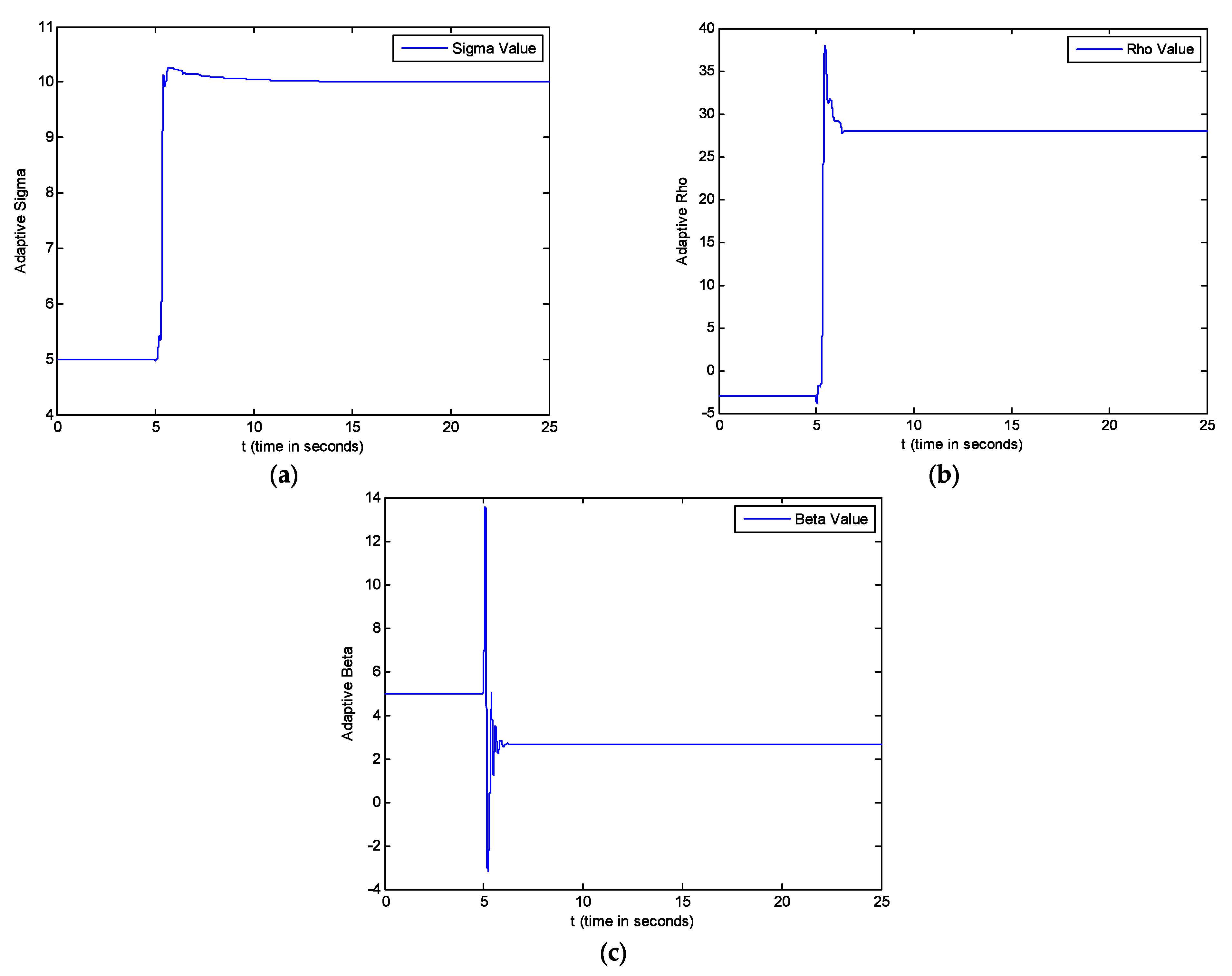
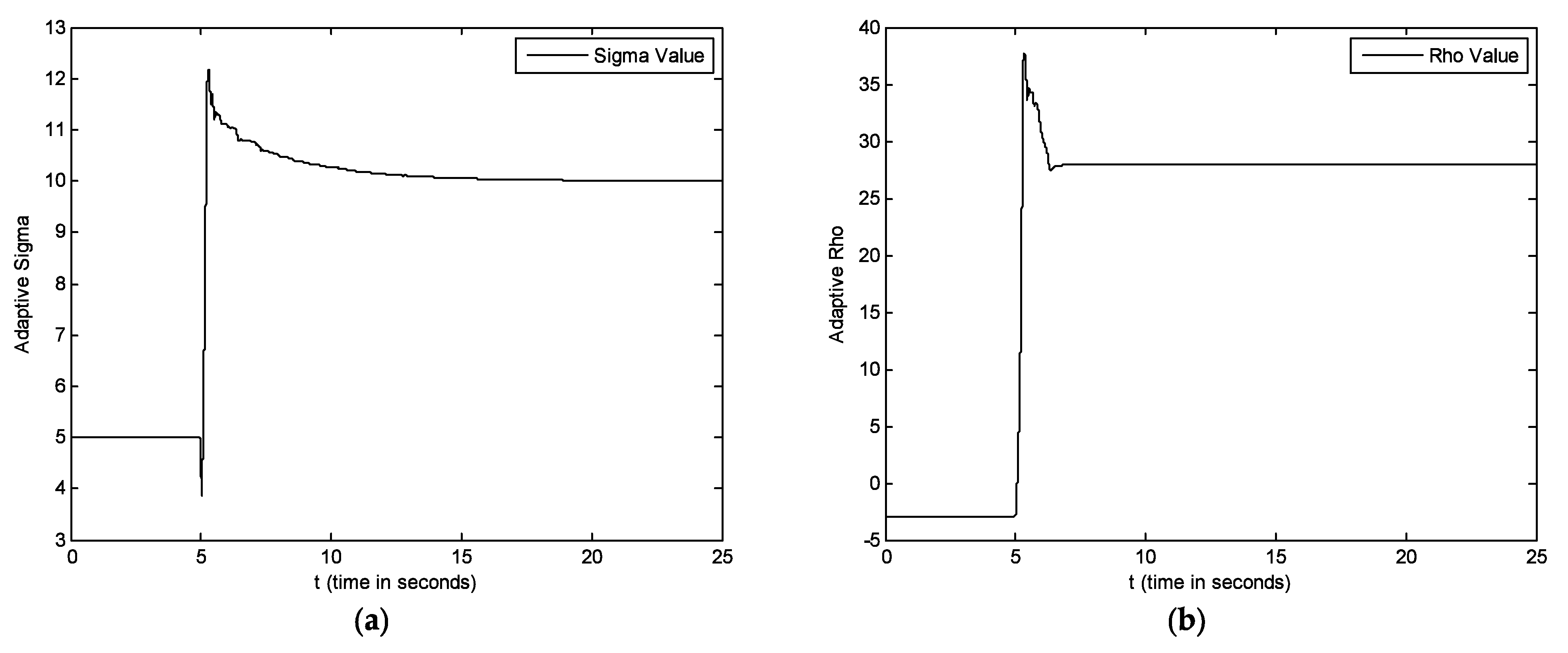
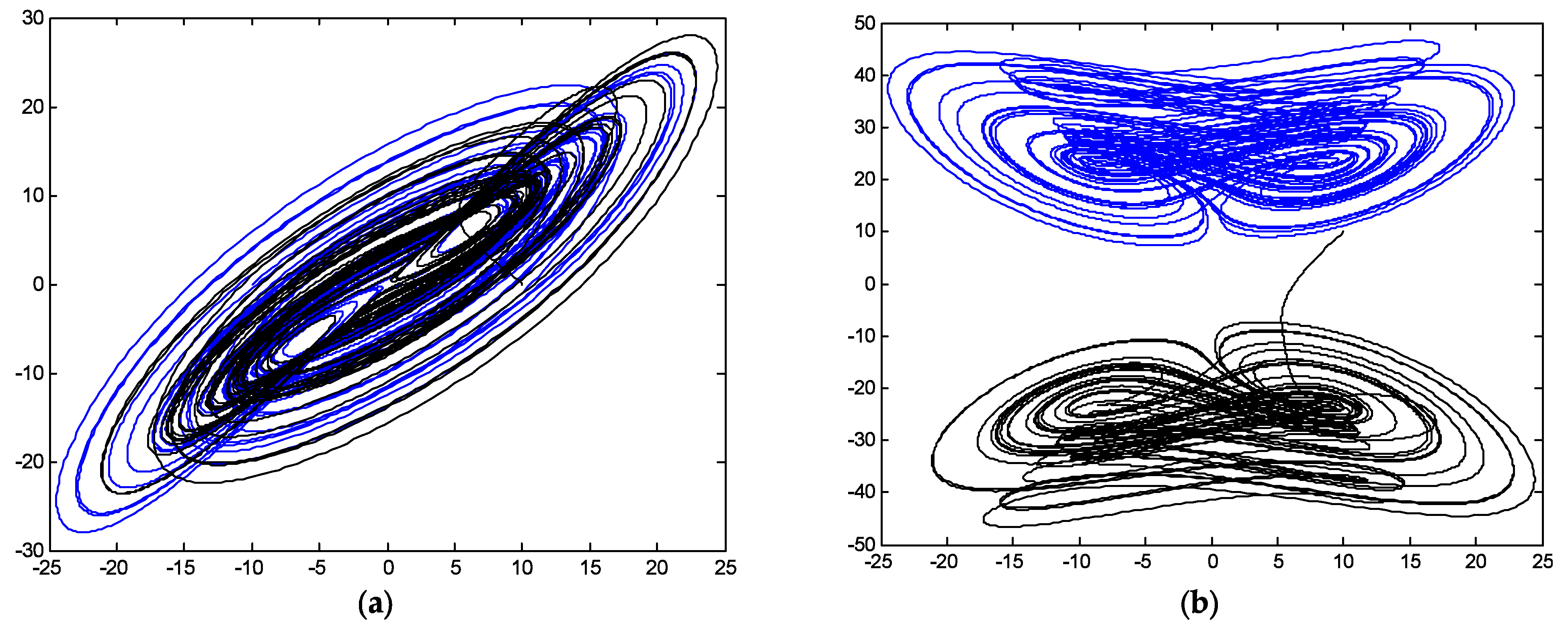
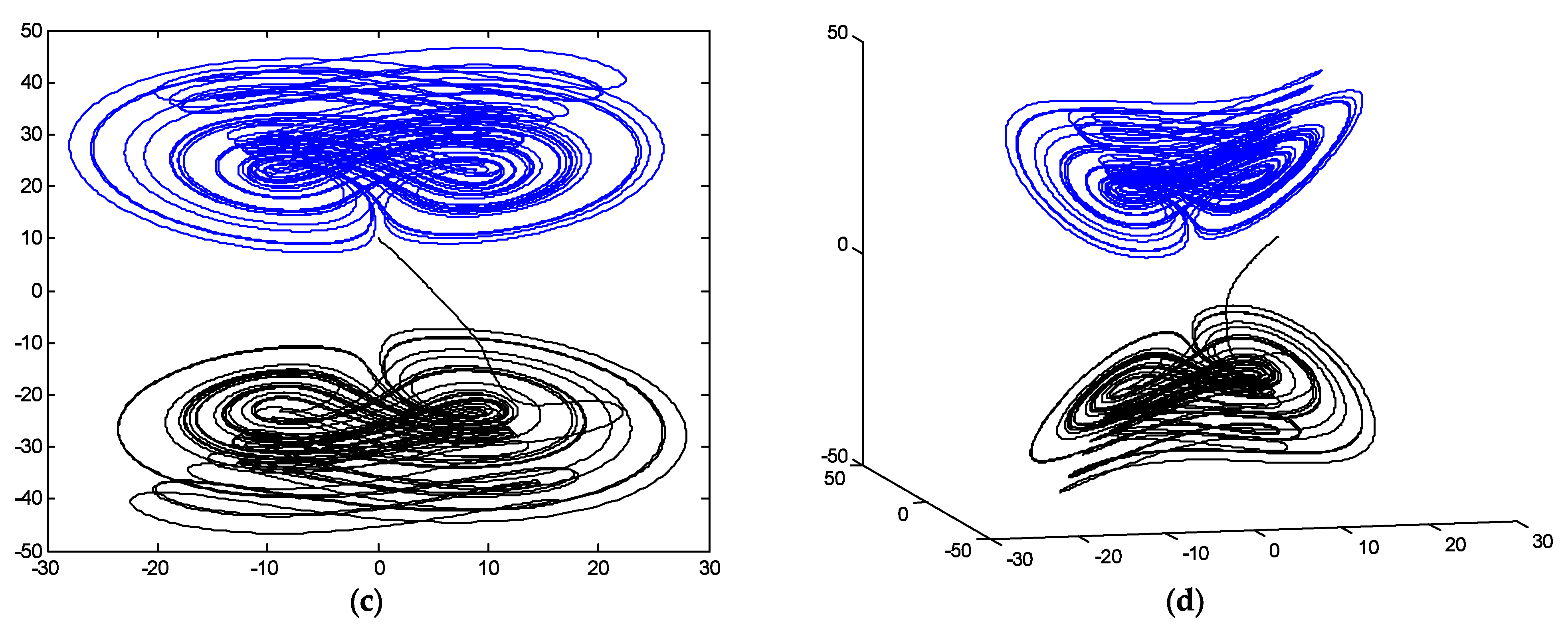
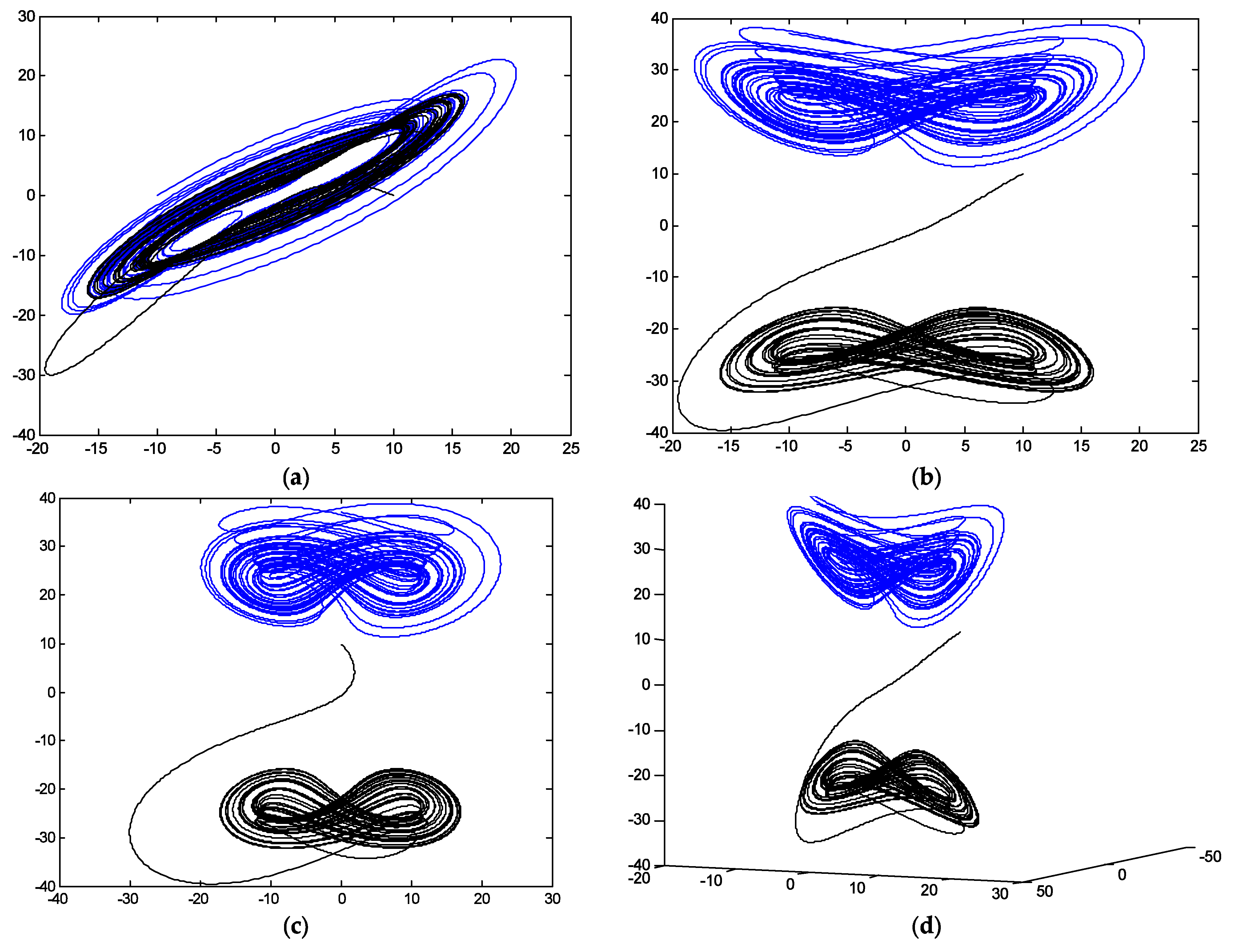
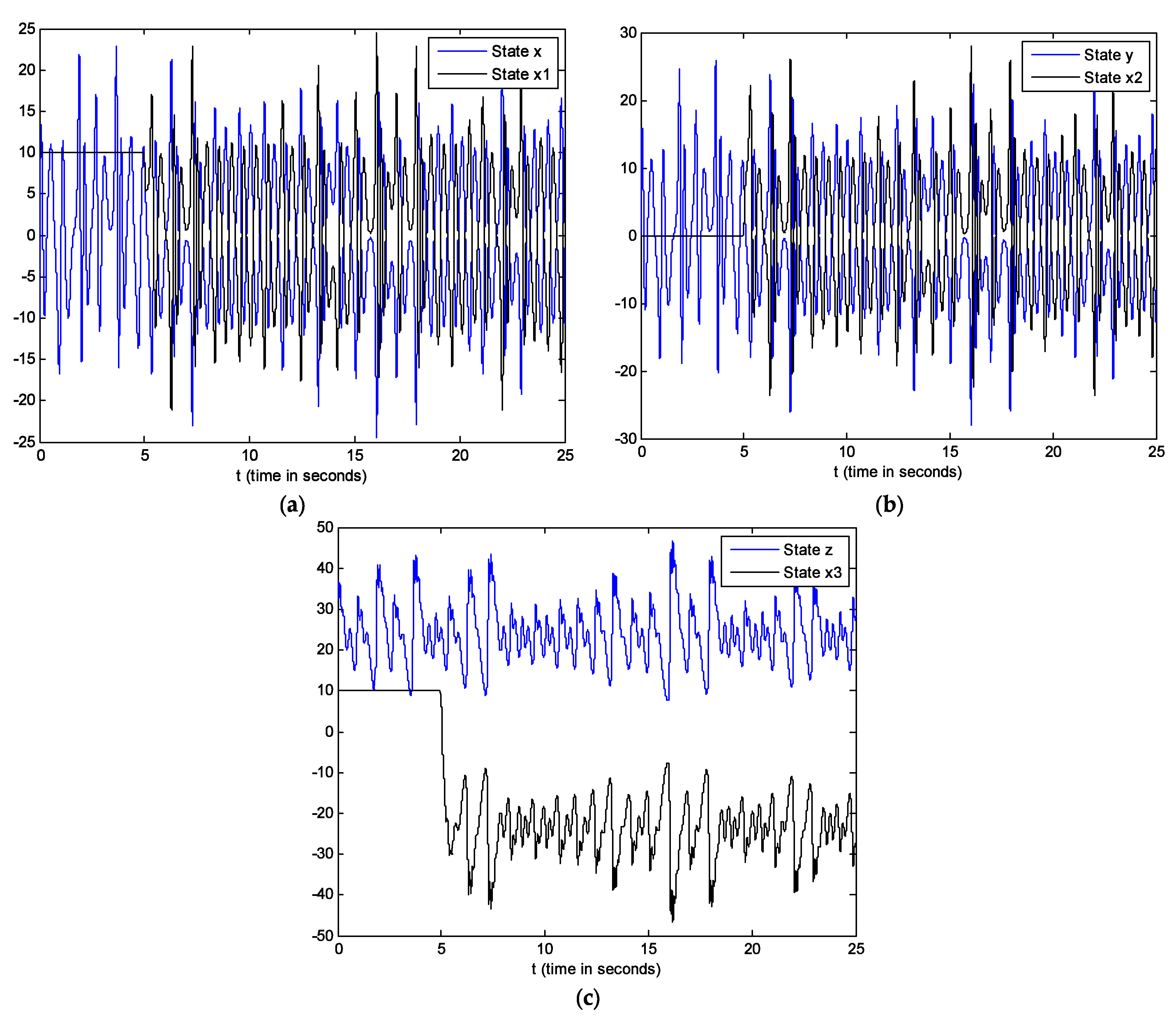
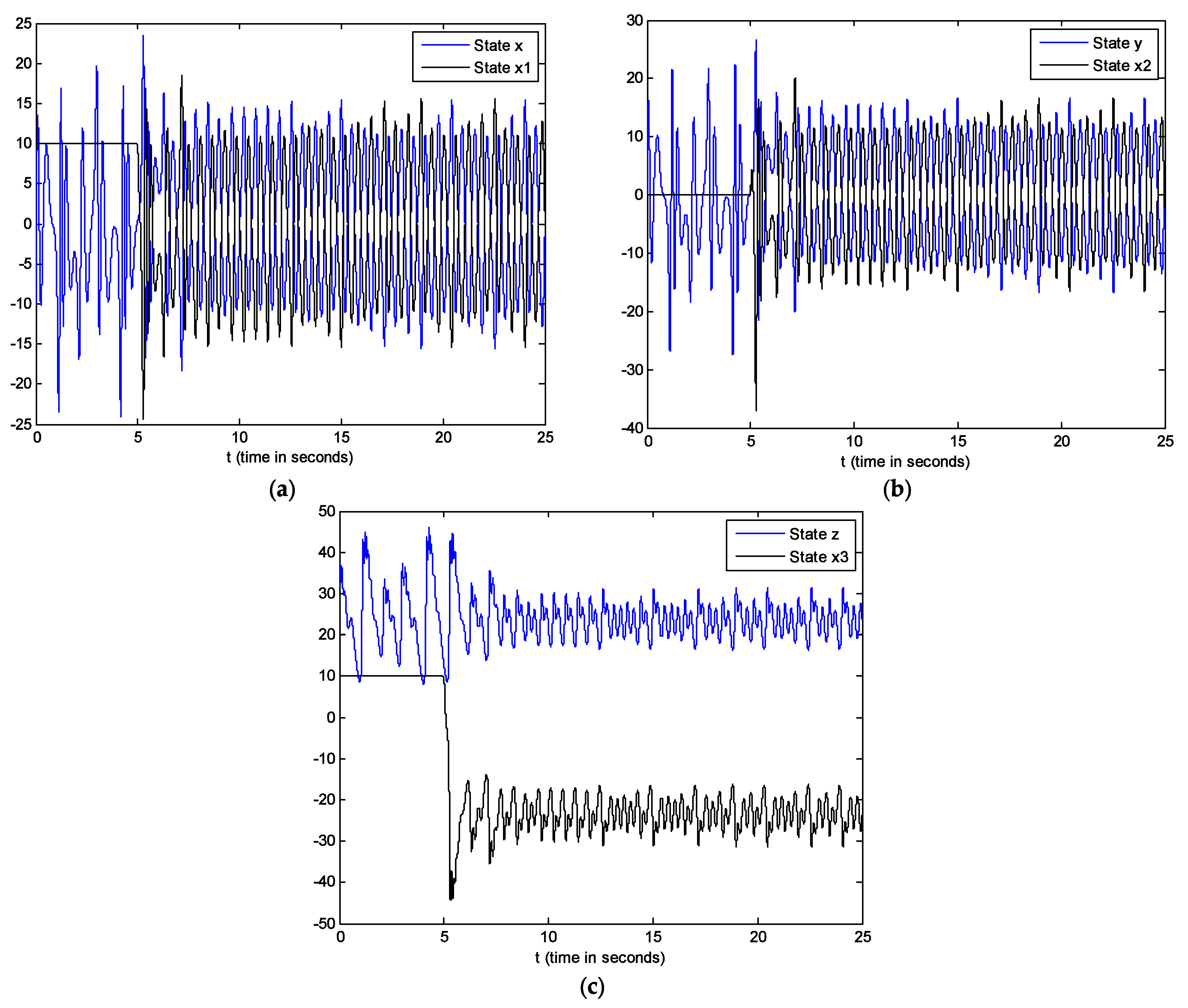
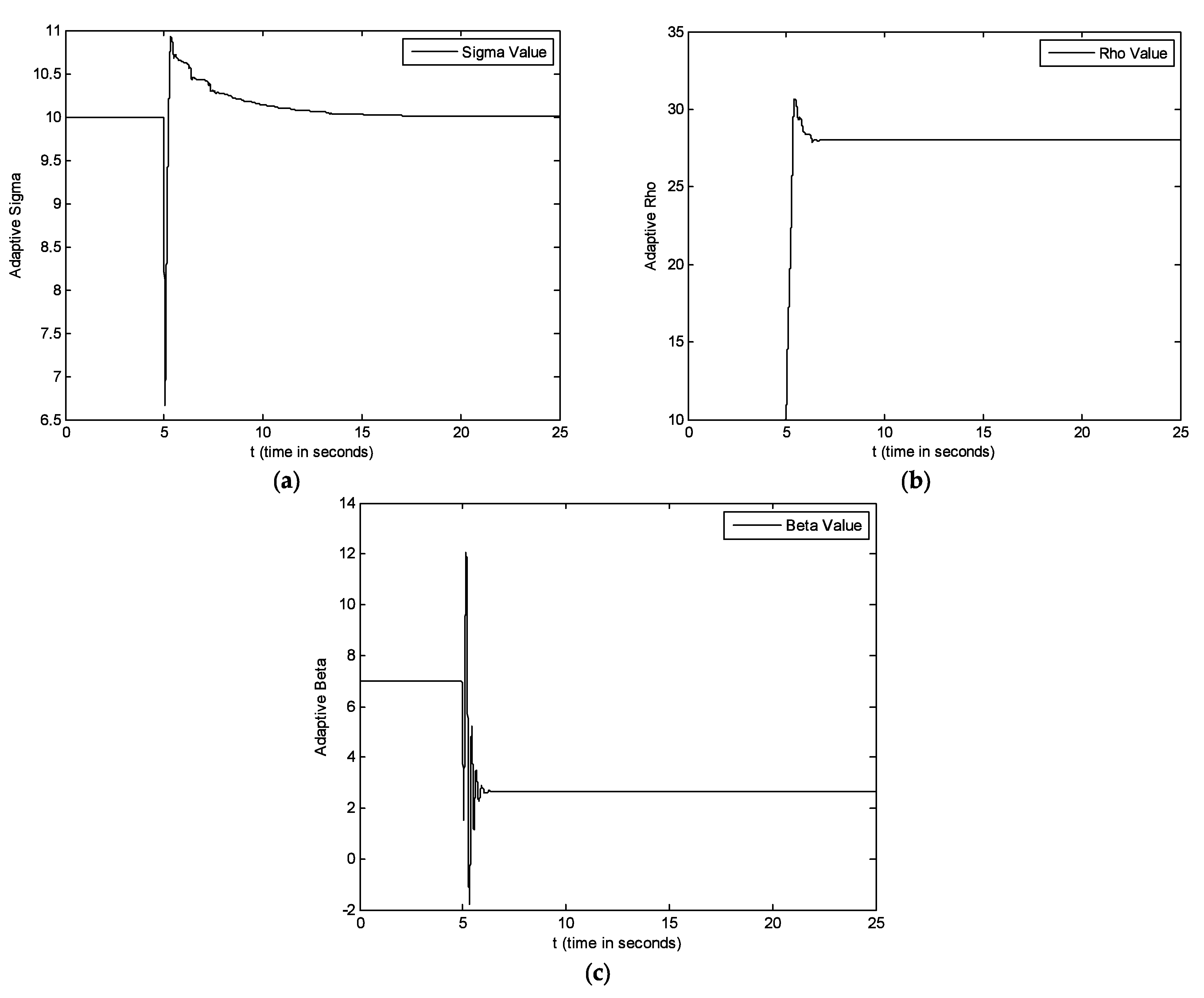
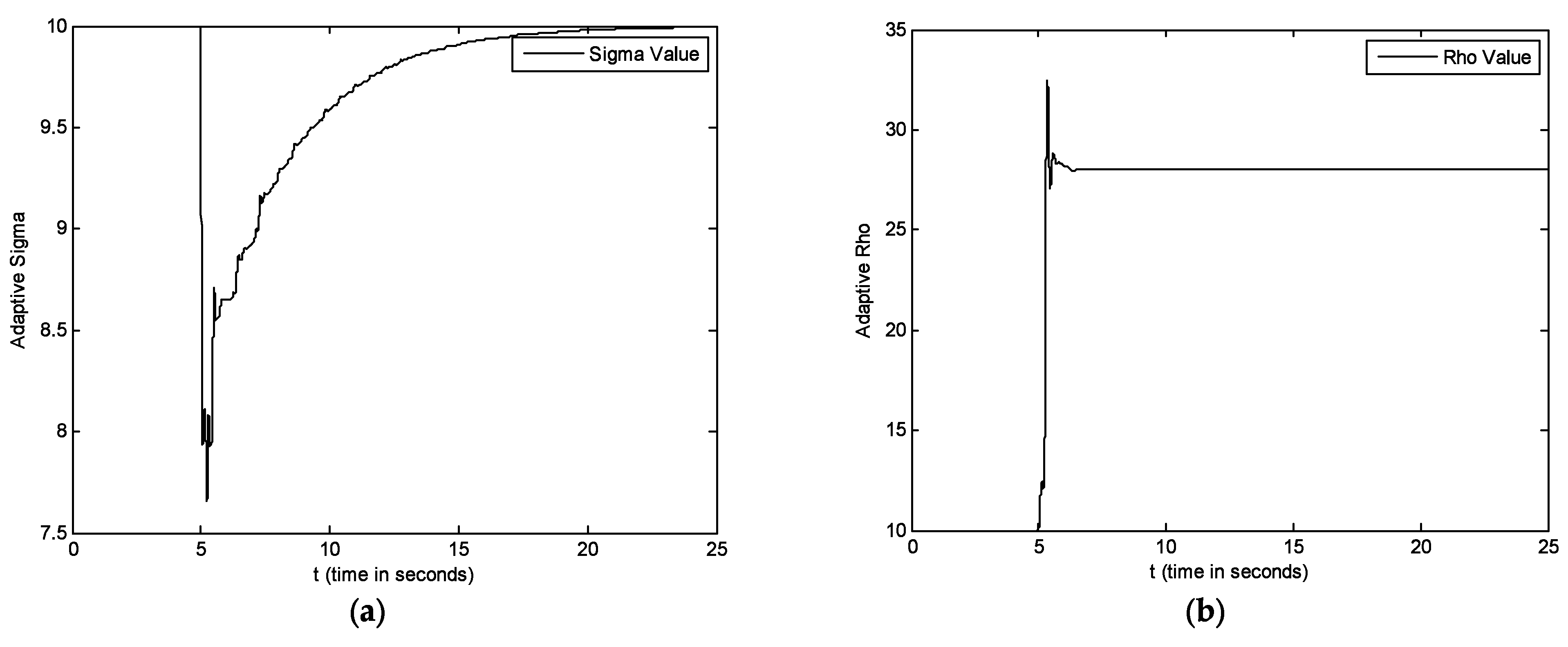
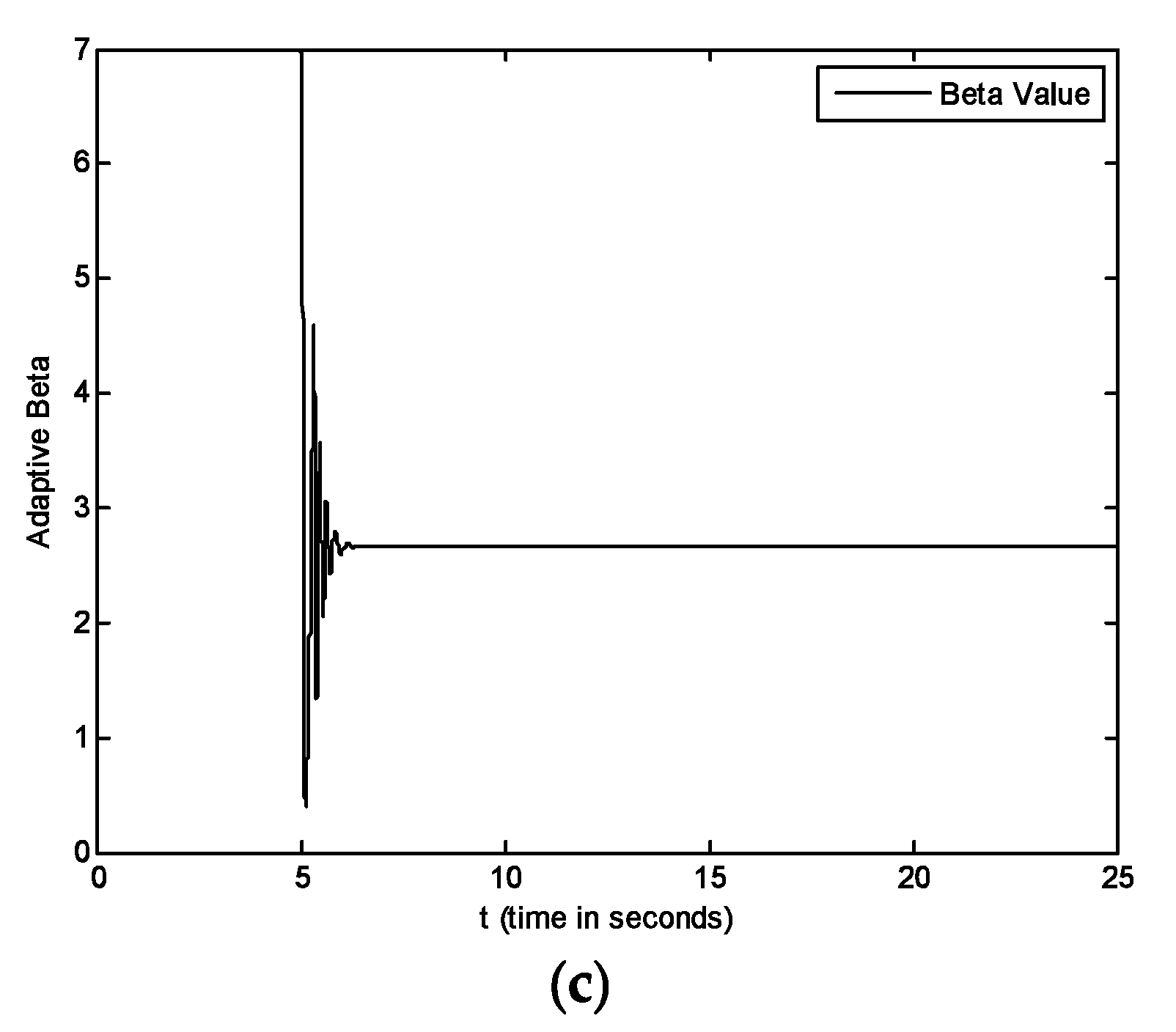
5. Simulations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- García-Sepúlveda, O.; Posadas-Castillo, C.; Cortés-Preciado, A.D.; Platas-Garza, M.A.; Garza-González, E.; Sanchez, A.G.S. Synchronization of fractional-order Lu chaotic oscillators for voice encryption. Rev. Mex. Fısica 2020, 66, 364–371. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Y.; Yang, S. Adaptive Synchronization of Fractional-Order Complex Chaotic system with Unknown Complex Parameters. Entropy 2019, 21, 207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piotr, O.; Piotr, D. Variable, Fractional-Order PID Controller Synthesis Novelty Method; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef]
- Zakia, H.; Mehmet, Y.; Necati, Ö. Numerical solutions and synchronization of a variable-order fractional chaotic system. Math. Model. Numer. Simul. Appl. 2021, 1, 11–23. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, C.; Liu, T. Control of finite-time anti-synchronization for variable-order fractional chaotic systems with unknown parameters. Nonlinear Dyn. 2016, 86, 1967–1980. [Google Scholar] [CrossRef]
- Tavaresa, D.; Almeida, R.; Delfim, F.M. Caputo Derivatives of Fractional Variable Order: Numerical Approximations. Available online: https://www.elsevier.com/open-access/userlicense/1.0/ (accessed on 21 August 2021).
- Yufeng, X.; Zhimin, H. Synchronization of variable-order fractional financial system via active control method. Cent. Eur. J. Phys. 2013, 11, 824–835. [Google Scholar] [CrossRef] [Green Version]
- Hioual1, A.; Ouannas, A. On fractional variable-order neural networks with time-varying external inputs. Innov. J. Math. 2022, 1, 52–65. [Google Scholar] [CrossRef] [PubMed]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef] [Green Version]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald-Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef] [Green Version]
- Mossa Al-sawalha, M.; Alomari, A.K.; Goh, S.M.; Noorani, M.S.M. Active Anti–Synchronization of two Identical and Different Fractional–Order Chaotic Systems. Int. J. Nonlinear Sci. 2011, 11, 267–274. [Google Scholar]
- Perez, P.J.; Perez, J.P.; Perez, P.R.; Flores, H.A. Fractional Order PID Control Law for Trajectory Tracking Using Fractional Order Time-Delay Recurrent Neural Networks for Fractional Order Complex Dynamical Systems. Comput. Sist. 2019, 23, 1583–1591. [Google Scholar] [CrossRef]
- Merrikh-Bayat, F.; Mirebrahimi, N.; Khalili, M.R. Discrete-Time Fractional-Order PID Controller: Definition, Tuning, Digital Realization and Some Applications. Int. J. Control Autom. Syst. 2015, 13, 81–90. [Google Scholar] [CrossRef]
- Sanchez, E.N.; Perez, J.P.; Perez, J. Trajectory Tracking for Delayed Recurrent Neural Networks. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar]
- Ren, L.; Guo, R.; Vincent, U.E. Coexistence of synchronization and anti-synchronization in chaotic systems. Arch. Control Sci. 2016, 26, 69–79. [Google Scholar] [CrossRef]
- Padron, J.P.; Perez, J.P.; Díaz, J.J.P.; Huerta, A.M. Time-Delay Synchronization and Anti-Synchronization of Variable-Order Fractional Discrete-Time Chen–Rossler Chaotic Systems Using Variable-Order Fractional Discrete-Time PID Control. Mathematics 2021, 9, 2149. [Google Scholar] [CrossRef]
- Lassoued, A.; Boubaker, O. Chapter 17: Fractional-Order Hybrid Synchronization for Multiple Hyperchaotic Systems. In Recent Advances in Chaotic Systems and Synchronization, from Theory to Real World Applications Emerging Methodologies and Applications in Modelling; Elsevier: Amsterdam, The Netherlands, 2019; pp. 351–366. [Google Scholar] [CrossRef]
- Chen, L.; Huang, C.; Liu, H.; Xia, Y. Anti-Synchronization of a Class of Chaotic Systems with Application to Lorenz System: A Unified Analysis of the Integer Order and Fractional Order. Mathematics 2019, 7, 559. [Google Scholar] [CrossRef] [Green Version]
- Chaudhary, H.; Khan, A.; Nigar, U.; Kaushik, S.; Sajid, M. An Effective Synchronization Approach to Stability Analysis for Chaotic Generalized Lotka–Volterra Biological Models Using Active and Parameter Identification Methods. Entropy 2022, 24, 529. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Wang, Y.; Zhou, X. Multi-Switching Combination Synchronization of Three Fractional-Order Delayed Systems. Appl. Sci. 2019, 9, 4348; [Google Scholar] [CrossRef] [Green Version]
- Jahanzaib, L.S.; Trikha, P.; Matoog, R.T.; Muhammad, S.; Al-Ghamdi, A.; Higazy, M.; Matoog, S.M.; Ahmed, A.-G.; Mahmoud, H. Dual Penta-Compound Combination Anti-Synchronization with Analysis and Application to a Novel Fractional Chaotic System. Fractal Fract. 2021, 5, 264. [Google Scholar] [CrossRef]
- Pan, W.; Li, T.; Wang, Y. The Multi-Switching Sliding Mode Combination Synchronization of Fractional Order Non-Identical Chaotic System with Stochastic Disturbances and Unknown Parameters. Fractal Fract. 2022, 6, 102. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Padron, J.P.; Perez, J.P.; Diaz, J.J.P.; Astengo-Noguez, C. Time-Delay Fractional Variable Order Adaptive Synchronization and Anti-Synchronization between Chen and Lorenz Chaotic Systems Using Fractional Order PID Control. Fractal Fract. 2023, 7, 4. https://doi.org/10.3390/fractalfract7010004
Padron JP, Perez JP, Diaz JJP, Astengo-Noguez C. Time-Delay Fractional Variable Order Adaptive Synchronization and Anti-Synchronization between Chen and Lorenz Chaotic Systems Using Fractional Order PID Control. Fractal and Fractional. 2023; 7(1):4. https://doi.org/10.3390/fractalfract7010004
Chicago/Turabian StylePadron, Joel Perez, Jose P. Perez, Jose Javier Perez Diaz, and Carlos Astengo-Noguez. 2023. "Time-Delay Fractional Variable Order Adaptive Synchronization and Anti-Synchronization between Chen and Lorenz Chaotic Systems Using Fractional Order PID Control" Fractal and Fractional 7, no. 1: 4. https://doi.org/10.3390/fractalfract7010004
APA StylePadron, J. P., Perez, J. P., Diaz, J. J. P., & Astengo-Noguez, C. (2023). Time-Delay Fractional Variable Order Adaptive Synchronization and Anti-Synchronization between Chen and Lorenz Chaotic Systems Using Fractional Order PID Control. Fractal and Fractional, 7(1), 4. https://doi.org/10.3390/fractalfract7010004





