Abstract
In the study of heat transfer in tree-like branching network, neither the heat convection caused by fluid flow in the tree-like branching network nor the asymmetric structure of the tree-like branching network can be ignored. In this work, we assume the porous media is embedded with a tree-like branching network that are characterized by damaged pipes. We investigated the effects of surface roughness on heat conduction and heat convection in the porous media embedded with the damaged tree-like branching network based on the fractal features of tree-like branching networks and the basic theory of thermodynamics. The proposed model for thermal conductivity can be expressed as a function of micro-structural parameters of the composite, such as the relative roughness, the ratio of thermal conductivity of the wall to that of the fluid in the micro-channel, the diameter ratio, the length ratio, the branching level, the number of damaged channels, the total number of branching levels, and the main tube porosity of the porous media. The effects of the micro-structural parameters of the model on its effective thermal conductivity have been analyzed in detail. It is believed that the joint expression of heat conduction and heat convection could enrich and develop the physical study of heat transport in porous media.
1. Introduction
The tree-like branching network is widely found in nature, such as plant trunks and leaves, river basins, biological tissues and organs, and in engineering fields, such as the world wide web, the internet, microelectronic chip cooling system, petroleum exploration and production engineering [1,2,3,4,5]; these have self-similar fractal characteristic. Therefore, it is important to study heat transport in tree-like branching networks. In 1926, after summarizing the previous research results, Murray [6] proposed the famous Murray law: In the biological bifurcation network, the third power of the parent tube radius should be equal to the sum of the third power of each sub-tube radius. The theory provides experimental data and theoretical research for the optimal relationship between the diameters of parent branches and sub-branches in tree bifurcation networks. After that, many scholars have used fractal theory to explore the heat transfer mechanism in tree-like branching networks [7,8,9,10]. For example, by establishing a tree-like branching network model to simulate fluid flow, Pence [11] explored the heat transfer characteristics between the fractal-like flow and the parallel-flow network. Alharbi et al. [12] studied the three-dimensional tree-like branching network application in a microelectronic cooling system using the computational fluid dynamics method. They found that the tree-like branching network structure can improve heat dissipation efficiency by reducing the pressure drop of the radiator. By comparing the traditional parallel pipeline with the rectangular tree-like branching network, Chen and Cheng [13] explored the differences between the traditional parallel pipeline and rectangular tree-like branching network in the process of thermal convection. They found that the rectangular tree-like branching network had a larger transmission capacity than the traditional parallel pipeline, leading to a significant increase in the heat dissipation performance of pipes. Yu and Li [14] studied the effective thermal conductivity of composites embedded with a tree-like branching network. It was found that the effective thermal conductivity of the composites embedded with a tree-like branching network would vary with the ratio of the thermal conductivity of each component.
Significantly, although much research on heat conduction in tree-like branching networks has been progressively carried out, the heat convection caused by the fluid flow in this network and the influence of the rough surfaces of the pores on the heat transport is still under-studied. On the one hand, the heat convection between the wall and the fluid is widely distributed in each branch layer of the porous media in the heat transport process of the tree-like branching network [15]. The flow of fluid in porous media will change the temperature difference of each branch layer. If the fluid flow in porous media is not considered during calculation of the effective thermal conductivity of porous media, the calculated effective thermal conductivity will be inaccurate. Peng et al. [16] found that heat convection plays a leading role in the heat transfer process when there is a temperature difference between each branch wall and the fluid by establishing the thermal conductivity coefficient model of heat convection. By measuring the thermal conductivity of dead and living snakes respectively, Liang et al. [17] found that the thermal conductivity of living snakes was significantly more extensive than that of the dead ones. Valvano et al. [18] studied the thermal conductivity of rat liver and found that blood flow could significantly improve the thermal conductivity of the liver. On the other hand, the influence of the rough surfaces of the pores on heat transport can also not be ignored. At present, some researchers [19,20,21] have concluded that the roughness of the capillary surfaces will significantly impact the heat conduction of porous media. Kandlikar et al. [22] studied the influence mechanism of roughness on heat transfer in the small diameter range. Shen et al. [23] studied laminar heat transfer in microchannels with rough surfaces based on fractal theory. Xiao et al. [24] proposed an effective thermal conductivity model with a micro-scale effect. Several investigators [25,26,27] have studied the effects of surface roughness on other aspects, such as gas diffusion in a tree-like branching network. Therefore, the influence of roughness should be considered in studies of the heat transport of a damaged tree-like branching network. Based on the above two aspects, Xia et al. [28] respectively studied heat conduction and heat convection in tree-like branching networks with rough surfaces and established the corresponding fractal model.
However, the above briefly reviewed works were only involved in symmetric tree-like branching networks without involving the asymmetry structure of the network. For different structures, there will be great differences in their internal heat transport. Recently, some scholars have also studied the heat transport of materials with different structure using numerical simulations [29,30] or theoretical models [31,32,33]. For example, by using the second law of thermodynamics and Catteneo–Christov dual theory, Eswaramoorthi et al. [34] established an equation considering energy and concentration to analyze the heat transport process through heat consumption/generation. Therefore, it is very important to study the asymmetric tree-like branching network structure. It is a common phenomenon that a branch layer of the tree-like branching network is damaged, such as leaf vein damage, cardiovascular and cerebrovascular blockage, and obstructive pulmonary disease [35]. Therefore, it is of great significance to study the heat transfer in the damaged tree-like branching network. As a result, construction of a model that considers rough surfaces of a damaged tree-like branching network and that includes both heat conduction and convection turns out to be essential for related studies and becomes the concentration of our work. To explore the influence of asymmetric structure and the heat convection caused by fluid flow on the heat transport in the tree-like branching network, we consider the construction of the damaged tree-like branching network as shown in Figure 1a,b. Then, the thermal conductivity model of porous media embedded with a damaged tree-like branching network considering the influence of roughness is presented based on the theory of fractals and the self-similar fractal characteristic of tree-like branching network. In this work, the influence of heat convection between fluid and wall and the rough surfaces of the pores on the effective thermal conductivity of tree-like branching networks will be our main research object. We systematically analyzed the effect of micro-structural parameters of porous media on the dimensionless thermal conductivity of this model by fractal scaling law. The results can correctly reveal the heat transfer mechanism of tree-like branching networks with rough surfaces and provide a theoretical basis for applying tree-like branching networks.
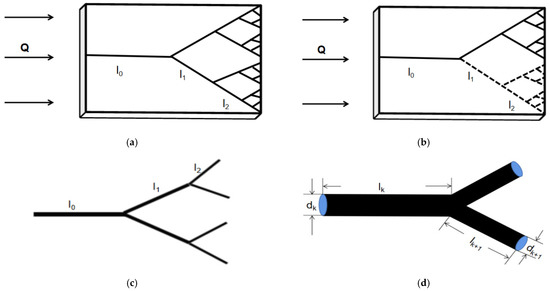
Figure 1.
(a) Schematic of porous media embedded with an undamaged tree-like branching network; (b) Schematic of porous media embedded with a damaged tree-like branching network; (c) Schematic diagram of the tree-like branching network; (d) Schematic diagram of an intermediate branching level structure.
2. Fractal Characteristics of Tree-like Branching Network with Rough Surface
Tree-like branching networks are continuously generated by the main pipe through simple bifurcation rules. The main pipe in the tree-like branching network divides into two or more sub-pipes according to a certain bifurcation angle, and then each sub-pipe divides into a new sub-pipe with the same branch angle. Finally, by repeating this process, a complete tree-like branch network is formed. As shown in Figure 1c, the main pipe only divides into two sub-pipes and each sub-pipe divides into two new sub-pipes. It is a typical branching fractal network, and we also call it a dichotomous branching network. In the present work, we assume that each branch of the tree-like network is a cylindrical tube whose wall thickness can be ignored. The maximum network bifurcation number is m, and each tube of the network bifurcates into N tubes at the next level. (The meaning of all symbols is given in Nomenclature). As shown in Figure 1d, and are respectively used to represent the diameter and length of the kth branching level (k = 0, 1, 2, 3, …, m). Murray et al. [6] found that there is an optimum ratio between the diameter of the main pipe and that of two sub pipes is dk+1/dk = 2−1/3 in a dichotomous branching network. This relationship is also an expression of Murray’s law. On this basis, Bejan [36] found that for a fixed total flow, the optimal diameter ratio is and , respectively, by studying the tree-like branching networks with T-shaped and Y-shaped structures. Although both Murray and Bajan have explored the optimal proportion of the tree-like branching network, they have not clarified the relationship between the heat transfer properties and geometric characteristics of the network structure. Therefore we use a more general model to study the heat transfer characteristics in the tree-like branching network.
To describe the geometric structure of a tree-like branching network, we introduce two essential scale factors to stand for the length and diameter ratio of adjacent two-stage bifurcation [37]:
where and is the length of the kth branching level and diameter of the kth branching level. Thus, we have:
where and are the length and diameter of the 0th branching level, respectively.
In this work, we will introduce the rough surfaces into the tree-like branching network for considering the effect of roughness on effective thermal conductivity in the tree-like branching network. We assume that the rough elements are a set of conical elements with a constant ratio of height to bottom diameter, As shown in Figure 2, which can be expressed as [38,39]:
where is the height of the cone and is bottom circle diameter of the cone.
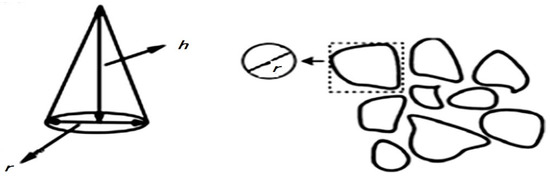
Figure 2.
Rough element classical model and basic morphology of rough element in pores [38].
The bottom diameter distribution of the rough elements satisfies the fractal scaling law [38,39]:
where is the maximum bottom diameter of rough elements. is the fractal dimension of the rough surfaces in the porous media, and its range is . It can be determined by [38,39]:
where is Euclidean dimension, is the ratio of the total bottom area of all cone units to the surface area in the unit pore and is the ratio of the minimum bottom circle diameter to the maximum bottom diameter of the cones. By taking the derivative of in Equation (6), it can be found that the number of rough elements in the infinitesimal range from to is:
To quantify the role of surface roughness of capillaries, the effective average roughness height of the kth branching level in the tree-like branching network, , can be given by [38,39]:
where is the maximum height of the cone at the 0th branching level. The maximum height of the conical elements at distinct branching levels is also assumed to satisfy the proportional relationship between the diameters due to a tree-like branching network. Therefore, the maximum height of the cone in the kth branching level, , can be written as [40]:
So, the relative roughness, , of the kth branching level in the tree-like branching network can be defined as the ratio of the average roughness height to the radius of the kth channel [38]:
3. The Thermal Conductivity Model of Porous Media with Rough Surfaces
3.1. Heat Conduction
In this section, the effective thermal conductivity model of heat conduction of porous media is derived. We assume that one channel of the kth branching level of a network has been destroyed, but the other part of the network has not failed. As shown in Figure 3, when the network structure is destroyed, the tree-like branching network will become asymmetric. The thermal transport characteristics of the tree-like branching network will be different from those of the undamaged normal network.
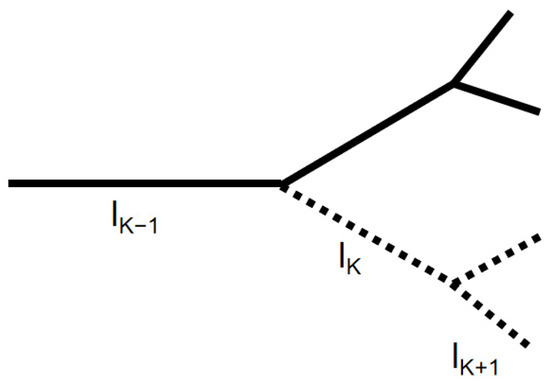
Figure 3.
Schematic diagram of damaged structure.
According to the Fourier’s law and the thermal-electrical analogy technique, the thermal resistance of a single channel of the kth level channel with smooth surfaces, , can be modified as:
where is the cross-sectional area of branching channels, and is the thermal conductivity of the fluid part. So, the thermal resistance of a single channel in the kth level channel with rough surfaces, , can be written as [40]:
Then, we can obtain the total thermal resistance of the undamaged tree-like branching network with rough surfaces, , as follows:
Next, we assume that tubes in the kth branching level are completely destroyed. So, the thermal resistance of the damaged tree-like branching network of the kth branching level can be expressed as [35]:
Then, the thermal resistance of the damaged tree-like branching network of the (k+1)th branching level is obtained as [35]:
where is the branching number of the tree-like branching network. Similarly, the thermal resistance of the damaged tree-like branching network of the (k+j)th branching level is obtained as [35]:
Then, based on Equations (14) and (17), the thermal resistance of the undamaged part of the damaged tree-like branching network before the kth branching level, , can be modified as:
The thermal resistance of the damaged part of the damaged tree-like branching network, , can be modified as:
With the aid of Equations (18) and (19), the total thermal resistance of the damaged tree-like branching network, , can be calculated as:
where . Then, the equivalent length of the damaged tree-like branching network, , can be written as [35]:
The total volume of the damaged tree-like branching network, , can be expressed as [35]:
where Z2 = , where is the volume of the single pipe in ith branching level. In this work, we suppose that the damaged tree-like branching network is equivalent to an ideal model with only a single channel under constant volume. The thermal conductivity of the equivalent single channel is defined as the effective thermal conductivity of the network. With the help of Equations (21) and (22), the effective cross-sectional area of the damaged tree-like branching network, , is:
The cross-sectional area of the main pipe of the damaged tree-like branching network, , is:
We assume that the porosity of the cross-section of the media is and according to the definition of porosity, the area of the entire cross-section of the media, , is:
Accordingly, the equivalent porosity of porous media embedded with the damaged tree-like branching network, , is:
According to the Fourier’s law and the series parallel model, the effective thermal conductivity of porous media embedded with a damaged tree-like branching structure can be composed of the damaged tree-like branching network part and the media matrix part, which can be described as:
where is the effective thermal conductivity of the media matrix part, is the effective thermal conductivity of the damaged tree-like branching network part and is the thermal resistance of the media matrix. It can be written as:
where is the thermal conductivity of the media matrix. Inserting Equations (20), (21), (25), (26) and (28) into Equation (27), the effective thermal conductivity of heat conduction of porous media embedded with a damaged tree-like branching structure, , can be defined as:
3.2. Heat Convection
In the previous section, we only considered the heat conduction of the tree-like branching network, ignoring the heat convection between the fluid and the wall. However, the heat convection between the fluid and the wall cannot be ignored. So, this section mainly derives the effective thermal conductivity of heat convection .
According to Fourier’s law, the thermal conductivity of heat convection caused by fluid flow, , is [28]:
where is the flow of the heat convection of the whole tree-like branching network with rough surfaces, is the heat convection area of the whole tree-like branching network with rough surfaces, is the thickness of the thermal boundary layer of thermal convection caused by fluid flow is mainly related to the characteristics of the fluid, is temperature difference.
It can be seen from Equation (30) that the thermal conductivity of heat convection caused by fluid flow is jointly determined by the flow of the heat convection , the heat convection area and the temperature difference in this damaged tree-like branching network. Therefore, the derivation of and in this model will be introduced in detail below.
According to Newton’s cooling formula, the flow of the heat convection of a single main pipe with rough surfaces, , can be written as:
where is the coefficient of heat convection of a single main pipe with rough surfaces, and is the heat convection area of the single main pipe with rough surfaces. It consists of the heat convection area of all the rough elements in the fractal elements in a single main pipe and the area of the smooth part without rough elements coverage in a single main pipe . That is to say, the heat convection area of a single main pipe with rough surfaces, , can be expressed as [28]:
According to Equation (6), the bottom diameter distribution of the rough elements satisfies the fractal scaling law, hence the total bottom area of all rough elements in a fractal set unit, , is [39]:
where is porosity of rough element distribution.
Since all the rough elements have the same height diameter ratio, the heat convection area of all the rough elements in the fractal elements in a single main pipe, , can be expressed as [28]:
Accordingly, the area of the smooth part without rough elements coverage in a single main pipe, , is [28]:
Inserting Equations (34) and (35) into Equation (32), the heat convection area of a single main pipe with rough surfaces can be defined as:
Chen and Cheng [13] assumed that the flow through the tree-like branching network of each channel is laminar and fully developed, and the Nusselt number of each level remains constant. Therefore, the coefficient of heat convection, , can be expressed as [13]:
where is the characteristic length of the pipe equal to the diameter of the pipe, is the Nusselt number which means the ratio of heat convection to heat conduction. Therefore, the heat convection coefficient of the th branching level of the tree-like branching network, , can be obtained as [13]:
where is the heat convection coefficient of the single main pipe of the tree-like branching network. Thus, the coefficient of heat convection of a single main pipe with rough surfaces, , can be written as [28]:
where is the effective average roughness height of a single main pipe of the tree-like branching network.
Inserting Equations (36) and (39) into Equation (31), the flow of the heat convection of a single main pipe with rough surfaces, , can be written as [28]:
Similarly, the flow of the heat convective of the same main pipe with smooth surface, , is [28]:
where is the heat convection area of a single main pipe of the tree-like branching network with smooth surfaces, which can be determined by:
Chen and Cheng [13] also assumed that the temperature difference between the different levels of tree-like branching networks is constant. Then, by means of Equations (38), (41) and (42), the flow of the heat convection of the undamaged part of the damaged tree-like branching network with smooth surfaces before the kth branching level, , can be modified as:
where is the heat convection area of the th branching level in the tree-like branching network with smooth surfaces.
Likely, the flow of the heat convection of the damaged part of the damaged tree-like branching network with smooth surfaces, , can be modified as:
With the aid of Equations (43) and (44), the flow of the heat convection of the whole damaged tree-like branching network with smooth surfaces, , can be calculated as:
In this model, the micro-channels at all levels have the same relative roughness for the tree-like branching network with rough surfaces. Imitating the work of Xia et al. [28], we also assume that the length ratio and the diameter ratio of the tree-like branching network with rough surfaces are equal to those of smooth surfaces. Therefore, the derivation of Equation (45) is also applicable to the tree-like branching network with rough surfaces. Then, the flow of the heat convection of the whole tree-like branching network with rough surfaces, , is:
Similarly, the heat convection area of the whole tree-like branching network with rough surfaces, , is:
Inserting Equations (46) and (47) into Equation (30), the thermal conductivity of heat convection caused by fluid flow, , is:
where .
3.3. Joint Expression of the Thermal Conductivity of Heat Conduction and Heat Convection
In Section 3.1 and Section 3.2, we derived the thermal convection of heat conduction and heat convection in this porous medium model. In this paper, we assume that the heat transfer in the tree-like branching network is composed of these two common parts. That is to say, the effective thermal conductivity of porous media embedded with a damaged tree-like branching network, , be expressed as:
where is the thermal conductivity of heat convection of porous media embedded with a damaged tree-like branching network.
With respect to Equations (29), (48) and (49), the thermal conductivity of porous media embedded with a damaged tree-like branching network can be written as:
The dimensionless thermal conductivity of porous media embedded with a damaged tree-like branching network is defined by , and it can be expressed as:
It can be noted from Equations (50) and (51) that the thermal conductivity of porous media embedded with a damaged tree-like branching network is an explicit function of the porosity , the thermal conductivity of porous media matrix , the thermal conductivity of fluid , the relative roughness , structural parameters of tree-like branching network () and the characteristics of the fluid. This fractal model takes into account the influence of heat convection in porous media embedded with a damaged tree-like branching network. This model can better represent the effective thermal conductivity of porous media with a damaged tree-like branching network. Therefore, the model is more reasonable and can reveal the heat transfer characteristics and mechanism of porous media with damaged tree-like branching networks.
4. Results and Discussion
Figure 4 shows the dimensionless thermal conductivity versus the diameter ratio for different length ratios for different numbers of damaged channels based on Equation (51). It is found from the figure that the dimensionless effective conductivity decreases with the increase of the diameter ratio, and it decreases with the increase of the number of damaged channels. This result can be explained by the fact that the channel number will decrease with the increase of damaged channels. The decrease of channels will lead to a decrease of the effective cross-sectional area and the heat convection area, so the dimensionless effective conductivity decreases with the increase of the number of damaged channels. When the channels are seriously damaged, the heat transport in porous media is basically completed by the heat conduction of matrix part, so its dimensionless thermal conductivity is low.
Figure 4.
The dimensionless thermal conductivity versus and at , , , = 0.01, m, , m.
Figure 5 compares the dimensionless thermal conductivity versus the total number of branching levels for different numbers of damaged channels. The figure indicates that dimensionless thermal conductivity rises along with an increase in the total number of branching levels. This is because with the increase of bifurcation times, the heat convection area of the branching network pipeline will increase, increasing thermal conductivity. We also find from Figure 5 that dimensionless thermal conductivity decreases with the increase of the number of damaged channels. This is the same as the conclusion in Figure 4.
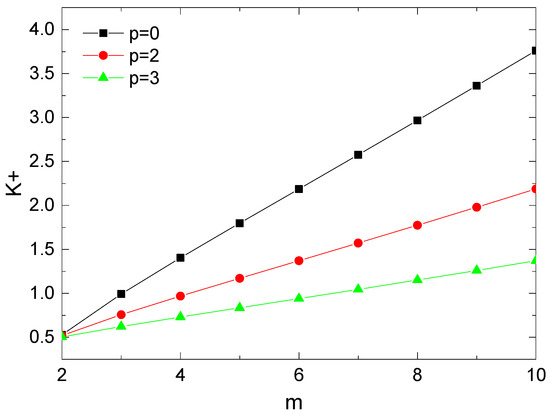
Figure 5.
The dimensionless thermal conductivity versus and at , , , = 0.01, m, , m.
Figure 6 presents the dimensionless thermal conductivity versus the branching number for different total numbers of branching levels. We can find from the figure that the dimensionless conductivity increases with the increase of the branching number and the total number of branching levels. It is worth noting that the change of the dimensionless thermal conductivity with the branching number is relatively gentle when the branching number N is equal to 3, but the change rate becomes higher and higher when the total number of branching levels m gradually increases. With the increase of the branching number, the thermal resistance of the tree-like branching network structure will increase rapidly.
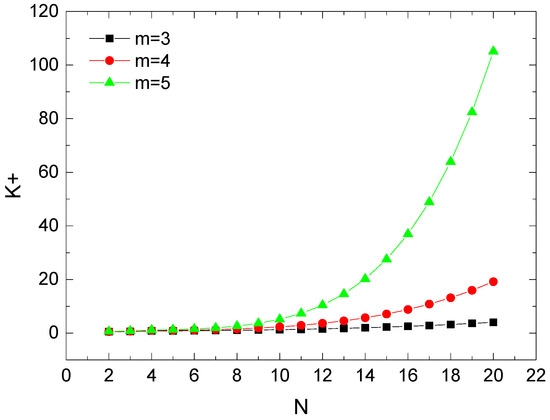
Figure 6.
The dimensionless thermal conductivity versus and at , , , = 0.01, m, , m.
Figure 7 shows the effective thermal conductivity, the thermal conductivity of the damaged tree-like branching network part, the thermal conductivity of the media part, and the heat convection thermal conductivity versus the main tube porosity of porous media for different relative roughness. It is found that the effective thermal conductivity increases with the increase of the main tube porosity of porous media, and the damaged tree-like branching network part thermal conductivity decreases with the increases of the main tube porosity. The thermal conductivity caused by heat convection is not affected by the main tube porosity of porous media. The matrix partial thermal conductivity increases with the increase of the main tube porosity. The change in the overall effective thermal conductivity of the final media is determined by the combination of the three factors. Under the conditions shown in the figure, the matrix partial thermal conductivity plays a dominant role. Compared with the same smooth media, the effective thermal conductivity of the porous media considering the influence of roughness is larger.
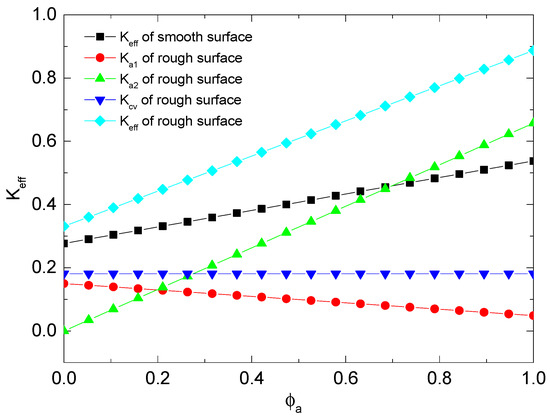
Figure 7.
The thermal conductivity versus at , , , m, , m.
Figure 8 plots the effect of the relative roughness on the effective thermal conductivity, the thermal conductivity of the damaged tree-like branching network part, the thermal conductivity of the media part, and the heat convection thermal conductivity. We can see that the larger relative roughness corresponds to the higher effective thermal conductivity. It is also found that the increase of the thermal conductivity of the damaged tree-like branching network part and the thermal conductivity of the media part is relatively gentle, but the thermal conductivity caused by heat convection increases rapidly with the increase of relative roughness within a certain range. We also found that the overall effective thermal conductivity curve of the media also has a similar trend. It shows that under this condition, the main effect of the rough wall on the heat transfer in the microchannel in the porous media is reflected in the enhancement of heat convection, which is more significant than the effect of heat conduction.
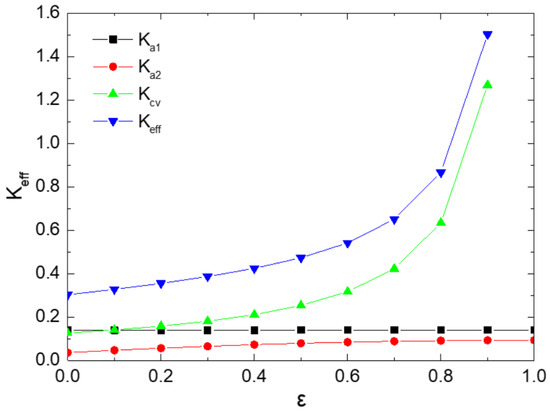
Figure 8.
The thermal conductivity versus at , , ,, m, , m.
The effect of the ratio of thermal conductivity of the wall to that of the fluid for different relative roughness on the dimensionless conductivity is analyzed in Figure 9. We can conclude from Figure 9 that the higher the ratio of thermal conductivity of the wall to that of the fluid, the higher the dimensionless effective thermal conductivity. This can be explained as the cross-sectional area and heat convection area of the media part is larger than those of the damaged tree-like branching network part, which has a greater impact on the thermal conductivity of the whole porous media.
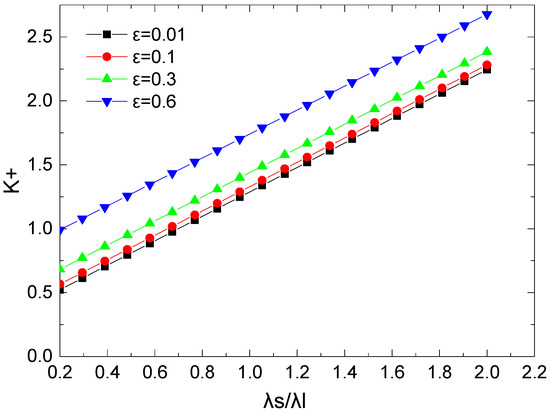
Figure 9.
The dimensionless thermal conductivity versus and at , , , m, , m.
Figure 10 shows the dimensionless thermal conductivity, the dimensionless thermal conductivity of the damaged tree-like branching network part, the dimensionless thermal conductivity of the media part, and the dimensionless heat convection thermal conductivity versus the diameter ratio of porous media embedded with an undamaged tree-like branching network. In the figure, , and represent the dimensionless thermal conductivity of the media part, the dimensionless thermal conductivity of the damaged tree-like branching network part and the dimensionless heat convection thermal conductivity, respectively. It is found that the dimensionless thermal conductivity of the media part is almost unaffected by the diameter ratio. The dimensionless thermal conductivity of the damaged tree-like branching network part slight increases with the increase of the diameter ratio of porous media and the dimensionless thermal conductivity caused by heat convection reduces along with an increase in the diameter ratio. Under the conditions shown in the figure, the heat convection plays a dominant role. The change in the overall dimensionless thermal conductivity of the final media is determined by the combination of the three factors, which is similar to the conclusion in Figure 8. Interestingly, we find that when is around 0.42, the dimensionless thermal conductivity of the damaged tree-like branching network part will increases slightly. We guess that there is a critical diameter ratio in the network for heat conduction which is similar to the conclusion of the optimal diameter ratio mentioned in the research of Miao et al. [24].
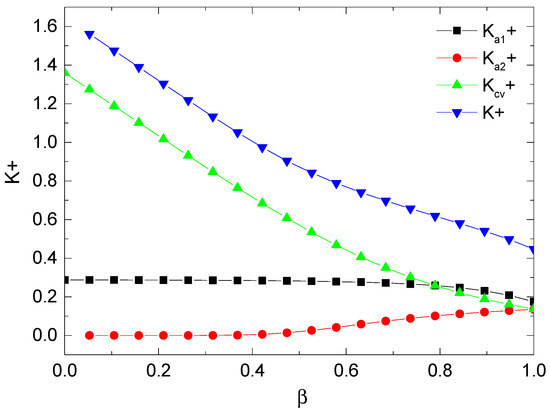
Figure 10.
The dimensionless thermal conductivity versus at , , , , =0.01, m, , m.
5. Conclusions
In this paper, a new thermal conductivity model embedded with a damaged tree-like branching network considering the influence of roughness is established based on the theory of thermoelectric simulation and the characteristics of damaged tree-like branching networks. In this work, we not only established the joint expression of heat conduction and heat convection but also considered the damage of the tree-like branching network. It is found that the length ratio and the number of damaged channels of a damaged tree-like branching network have a significant impact on the dimensionless thermal conductivity. It decreases with the increase of length ratio, number of damaged tubes and total bifurcation layers. It is also found that relative roughness is an important parameter for heat conduction in porous media with damaged tree-like branching networks. The dimensionless thermal conductivity of the tree-like branching network increases with the increase of heat convection area because of the existence of internal rough elements. Compared with the previous thermal conductivity models, this model could manifest more heat transfer mechanisms than empirical correlations, but it cannot fully reveal the complexity of porous media only by considering a single damaged tree-like branching network. The proposed model can enrich and develop understanding of the mechanism of heat transport in porous media, and can guide the development and improvement of heat transport devices in the engineering field. In real life, there are many tree-like branching networks, so our next work will be devoted to further explore the heat transfer in a damaged tree-like branching network.
Author Contributions
Conceptualization, Y.S. and Q.Z.; Methodology, L.R. and Q.Z.; Validation, Q.Z.; Formal analysis, Y.S., X.G., X.M., R.C., S.R. and Q.Z.; Investigation, H.Y., H.W., L.Z. and Q.Z.; Resources, Q.Z.; Data curation, Y.S. and Q.Z.; Writing—original draft, Y.S. and Q.Z.; Writing—review & editing, Q.Z.; Visualization, Q.Z.; Supervision, Q.Z.; Project administration, Q.Z.; Funding acquisition, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant No. 11972266 [Qian Zheng], Knowledge Innovation Program of Wuhan-Basic Research under Grant No. 2022010801010248 [Qian Zheng], Research Project of Hubei Provincial Department of Education under Grant No. T2022016 [Qian Zheng] and No. Q20211708 [Xiuya Guo], the Natural Science Foundation of Hubei Province under Grant No. 2020CFB384 [Huili Wang].
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbols | Description | ||
| m | total numbers of branching levels | the effective cross-sectional area | |
| the branching number of the tree-like branching network | the cross-sectional area of the main pipe of the damaged tree-like branching network | ||
| the length of the kth branching level | the area of the entire cross-section of the media | ||
| the diameter of the kth branching level | the equivalent porosity of porous media embedded with the damaged tree-like branching network | ||
| the length ratio | the effective thermal conductivity of porous media | ||
| the diameter ratio | the effective thermal conductivity of the media matrix part | ||
| the ratio of height to bottom diameter | the effective thermal conductivity of the damaged tree-like branching network part | ||
| the height of the cone | the thermal resistance of the media matrix | ||
| bottom circle diameter of the cone | the thermal conductivity of heat convection caused by fluid flow | ||
| the total number of rough elements | the flow of the heat convection of the whole tree-like branching network with rough surfaces | ||
| fractal dimension | the heat convection area of the whole tree-like branching network with rough surfaces | ||
| Euclidean dimension | temperature difference | ||
| the ratio of the total bottom area of all cone units to the surface area in the unit pore | the thickness of the thermal boundary layer of thermal convection caused by fluid flow is mainly related to the characteristics of the fluid | ||
| the ratio of the minimum bottom circle diameter to the maximum bottom diameter of the cones | the coefficient of heat convection | ||
| the maximum height of the cone at the 0th branching level | the heat convection area of a single main pipe with rough surfaces | ||
| the relative roughness | the heat convection area of all the rough elements in the fractal elements in a single main pipe | ||
| the thermal resistance of a single channel with smooth surfaces | the area of the smooth part without rough elements coverage in a single main pipe | ||
| the thermal resistance of a single channel in the kth level channel with rough surfaces | the total bottom area of all rough elements in a fractal set unit | ||
| the cross-sectional area of branching channels | the flow of the heat convection of a single main pipe with rough surfaces | ||
| the thermal conductivity of the fluid part | the flow of the heat convective of the same main pipe with smooth surface | ||
| the thermal conductivity of the media matrix | the Nusselt number | ||
| the thermal resistance of the undamaged part | the heat convection area of a single main pipe of the tree-like branching network with smooth surfaces | ||
| the thermal resistance of the damaged part | the flow of the heat convection of the undamaged part of the damaged tree-like branching network with smooth surfaces before the kth branching level | ||
| that the porosity of the cross-section of the media | the flow of the heat convection of the damaged part of the damaged tree-like branching network with smooth surfaces | ||
| the total thermal resistance of the damaged tree-like branching network | the flow of the heat convection of the whole damaged tree-like branching network with smooth surfaces | ||
| the equivalent length of the damaged tree-like branching network | the effective thermal conductivity of porous media embedded with a damaged tree-like branching network | ||
| V | the total volume of the damaged tree-like branching network | The dimensionless thermal conductivity |
References
- Mao, N.; Ye, J.; Quan, Z.Z.; Zhang, H.N.; Wu, D.Q.; Qin, X.H.; Wang, R.W.; Yu, J.Y. Tree-like structure driven water transfer in 1D fiber assemblies for Functional Moisture-Wicking Fabrics. Mater. Des. 2020, 186, 108305. [Google Scholar] [CrossRef]
- Liang, M.; Fu, C.; Xiao, B.; Luo, L.; Wang, Z. A fractal study for the effective electrolyte diffusion through charged porous media. Int. J. Heat Mass Transf. 2019, 137, 365–371. [Google Scholar] [CrossRef]
- Jing, D.L.; He, L.; Wang, X.M. Optimization analysis of fractal tree-like microchannel network for electroviscous flow to realize minimum hydraulic resistance. Int. J. Heat Mass Transf. 2018, 125, 749–775. [Google Scholar] [CrossRef]
- Long, G.B.; Xu, G.S. The effects of perforation erosion on practical hydraulic-fracturing applications. SPE J. 2017, 22, 645–659. [Google Scholar] [CrossRef]
- Jia, J.L.; Sang, S.X.; Cao, L.W.; Liu, S.Q. Characteristics of CO2/supercritical CO2 adsorption-induced swelling to anthracite: An experimental study. Fuel 2018, 216, 639–647. [Google Scholar]
- Murry, C.D. The physiological principle of minimum work applied to the angel of branching of arteries. J. Gen. Physiol. 1926, 9, 835–841. [Google Scholar] [CrossRef]
- Long, G.B.; Liu, Y.J.; Xu, W.R.; Zhou, P.; Zhou, J.Q.; Xu, G.S.; Xiao, B.Q. Analysis of crack problems in multilayered elastic medium by a consecutive stiffness method. Mathematics 2022, 10, 4403. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W H Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Liang, M.C.; Liu, Y.M.; Xiao, B.Q.; Yang, S.S.; Wang, Z.K. An analytical model for the transverse permeability of gas diffusion layer with electrical double layer effects in proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Wang, F.Y.; Cheng, H. A fractal permeability model for 2D complex tortuous fractured porous media. J. Pet. Sci. Eng. 2020, 188, 106938. [Google Scholar] [CrossRef]
- Pence, D. The simplicity of fractal-like flow networks for effective heat and mass transport. Exp. Therm. Fluid Sci. 2009, 34, 474–486. [Google Scholar] [CrossRef]
- Alharbi, A.Y.; Pence, D.V.; Cullion, R.N. Thermal characteristics of microscale fractal-like branching channels. J. Heat Transf. 2004, 126, 744–752. [Google Scholar] [CrossRef]
- Chen, Y.P.; Cheng, P. Heat transfer and pressure drop in fractal tree-like microchannel nets. Int. J. Mass Transf. 2002, 45, 2643–2648. [Google Scholar] [CrossRef]
- Li, Y.; Yu, B.M. Study of the starting pressure gradient in branching network. Sci. China Technol. Sci. 2010, 53, 2397–2403. [Google Scholar] [CrossRef]
- Jain, R.K. Grantham Blood flow and heat transfer in Waler 256 mammary carcinoma. J. Natl. Cancer Inst. 1979, 62, 927–933. [Google Scholar]
- Peng, Y.; Zhu, X.G.; Cao, B.; Luo, Y.Q.; Zhou, W.J. Heat transfer and permeability of the tree-like branching networks. Int. J. Heat Mass Transf. 2019, 129, 801–811. [Google Scholar] [CrossRef]
- Liang, X.G.; Ge, X.S.; Zhang, Y.P. A convenient method of measuring the thermal conductivity of biological tissue. Phys. Med. Biol. 1991, 36, 1599. [Google Scholar] [CrossRef]
- Valvano, J.W.; Allen, J.T.; Bowman, H.F. The simultaneous measurement of thermal conductivity, thermal diffusivity, and perfusion in small volumes of tissue. J. Biomech. Eng. 1984, 106, 192–197. [Google Scholar] [CrossRef]
- Xiao, B.Q.; Liu, Y.H.; Chen, H.X.; Chen, X.B.; Long, G.B. A novel fractal solution for laminar flow resistance in roughened cylindrical microchannels. Fractals 2020, 28, 2050097. [Google Scholar] [CrossRef]
- Xiao, B.Q.; Huang, Q.W.; Chen, H.X.; Chen, X.B.; Long, G.B. A fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals 2021, 29, 2150017. [Google Scholar] [CrossRef]
- Yang, S.S. Fractal study on the heat transfer characteristics in the rough microchannels. Fractals 2021, 29, 21501188. [Google Scholar] [CrossRef]
- Satish, G.K.; Shailesh, J.S.; Tian, S.R. Effect of surface roughness on heat transfer and fluid flow characteristics at low Reynolds numbers in small diameter tube. Heat Transf. Eng. 2003, 24, 4–16. [Google Scholar]
- Shen, S.; Xu, J.L.; Zhou, J.J. Flow and heat transfer in microchannels with rough wall surface. Energy Convers. Manag. 2006, 47, 1125–1131. [Google Scholar] [CrossRef]
- Xiao, B.Q. A fractal model for predicting the effective thermal conductivity of roughened porous media with microscale conductivity. Fractals 2021, 29, 2150114. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, H.L.; Guo, X.Y. Research on the effect of surface roughness on gas diffusion coefficient of porous media embedded with a fractal-like tree network. Fractals 2021, 29, 2150195. [Google Scholar] [CrossRef]
- Xiao, B.Q.; Wang, P.L.; Wu, J.S. A Novel fractal model for gas diffusion coefficient in dry porous media embedded with a damaged tree-like branching network. Fractals 2022, 30, 2250150. [Google Scholar] [CrossRef]
- Xiao, B.Q.; Wang, W.; Zhang, X.; Long, G.B.; Fan, J.T.; Chen, H.X.; Deng, L. A novel fractal solution for permeability and Kozeny-Carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 2019, 349, 92–98. [Google Scholar] [CrossRef]
- Xia, Y.L.; Zheng, S.; Yang, S.S.; Yi, S. Analysis on effective thermal conductivity model of porous media with rough fractal-like tree network. J. Cent. China Norm. Univ. 2022, 2, 255–261. [Google Scholar]
- Qureshi, M.Z.A.; Faisal, M.; Raza, Q.; Ali, B.; Botmart, T.; Shah, N.A. Morphological nanolayer impact on hybrid nanofluids flow due to dispersion of polymer/CNT matrix nanocomposite material. AIMS Math. 2023, 8, 633–656. [Google Scholar] [CrossRef]
- Sajjan, K.; Shah, N.A.; Ahammad, N.A.; Raju, C.S.K.; Kumar, M.D.; Weera, W. Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. AIMS Math. 2022, 7, 18416–18449. [Google Scholar] [CrossRef]
- Rauf, A.; Shah, N.A.; Mushtaq, A.; Botmart, T. Heat transport and magnetohydrodynamic hybrid micropolar ferrofluid flow over a non-linearly stretching sheet. AIMS Math. 2023, 8, 164–193. [Google Scholar] [CrossRef]
- Oreyeni, T.; Shah, N.A.; Popoola, A.O.; Elzahar, E.R.; Yook, S.J. The significance of exponential space-based heat generation and variable thermophysical properties on the dynamics of Casson fluid over a stratified surface with non-uniform thickness. Waves Random Complex Media 2022, 32, 1–19. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, H.L.; Jiang, J.; Xu, C. Fractal analysis of surface roughness effects on gas diffusion in porous nanofibers. Fractals 2020, 28, 2050125. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Loganathan, K.; Faisal, M.; Botmart, T.; Shah, N.A. Analytical and numerical investigation of Darcy-Forchheimer flow of a nonlinear-radiative non-Newtonian fluid over a Riga plate with entropy optimization. Ain. Shams Eng. J. 2022, 101887. [Google Scholar] [CrossRef]
- Miao, T.J.; Chen, A.M.; Xu, Y.; Yang, S.S.; Yu, B.M. Optimal structure of damaged tree-like branching networks for the equivalent thermal conductivity. Therm. Sci. 2016, 102, 89–99. [Google Scholar] [CrossRef]
- Bejan, A. The Constructal Law of Organization in Nature: Tree-Shaped Flows and Body Size. J. Exp. Biol. 2005, 208, 1677–1686. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Yu, B.M.; Yun, M.J.; Zou, M.Q. Heat conduction in fractal tree-like branched networks. Int. J. Heat Mass Transf. 2006, 49, 3746–3751. [Google Scholar] [CrossRef]
- Yang, S.S.; Liang, M.C.; Yu, B.M.; Zou, M.Q. Permeability model for fractal porous media with rough surfaces. Microfluid. Nanofluid. 2014, 18, 1085–1093. [Google Scholar] [CrossRef]
- Yang, S.S.; Yu, B.M.; Zou, M.Q.; Liang, M.C. A fractal analysis of laminar flow resistance in roughened microchannels. Int. J. Heat Mass Transf. 2014, 77, 208–217. [Google Scholar] [CrossRef]
- Yang, S.S.; Fu, H.H.; Yu, B.M. Fractal analysis of flow resistance in tree-like branching net-works with roughened microchannels. Fractals 2017, 25, 1750008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).