Fractional-Order PID Controller Based on Immune Feedback Mechanism for Time-Delay Systems
Abstract
:1. Introduction
2. Fractional-Order PID Controller
2.1. Fractional-Order PID Control
2.2. Integer-Order Approximations
2.3. Oustaloup’s Recursive Approximation
3. Immune Feedback Mechanism
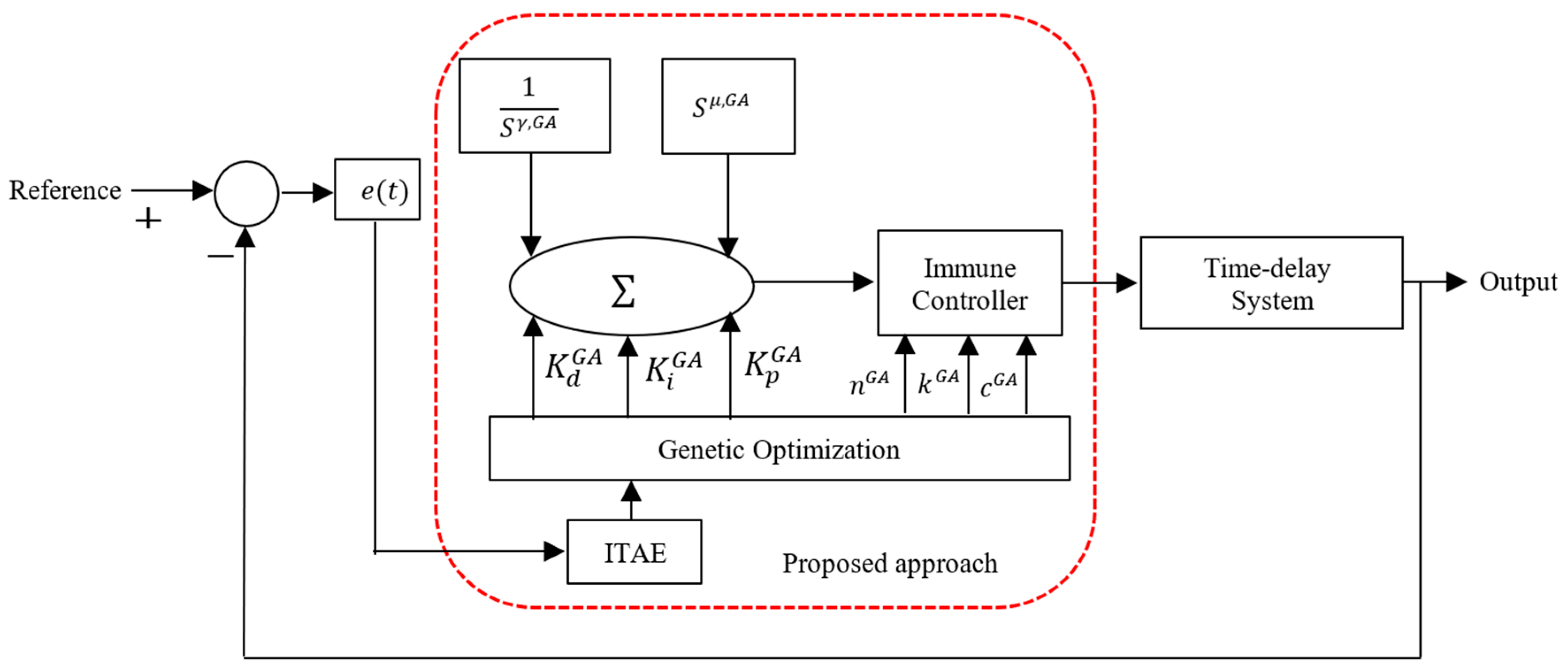
4. Design of Fractional-Order PID Controller Based on Immune Feedback Mechanism
4.1. Principle
4.2. Tuning
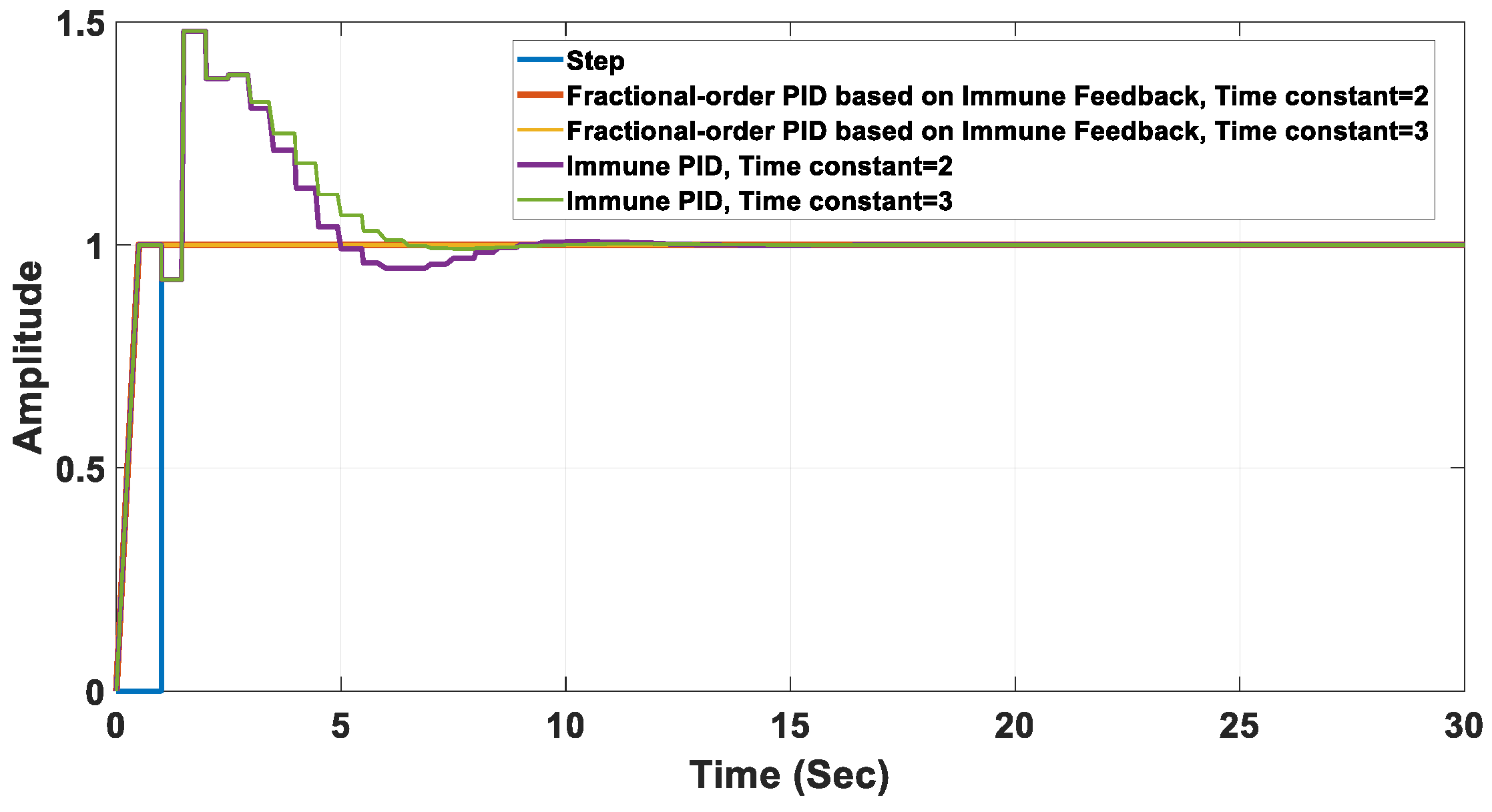
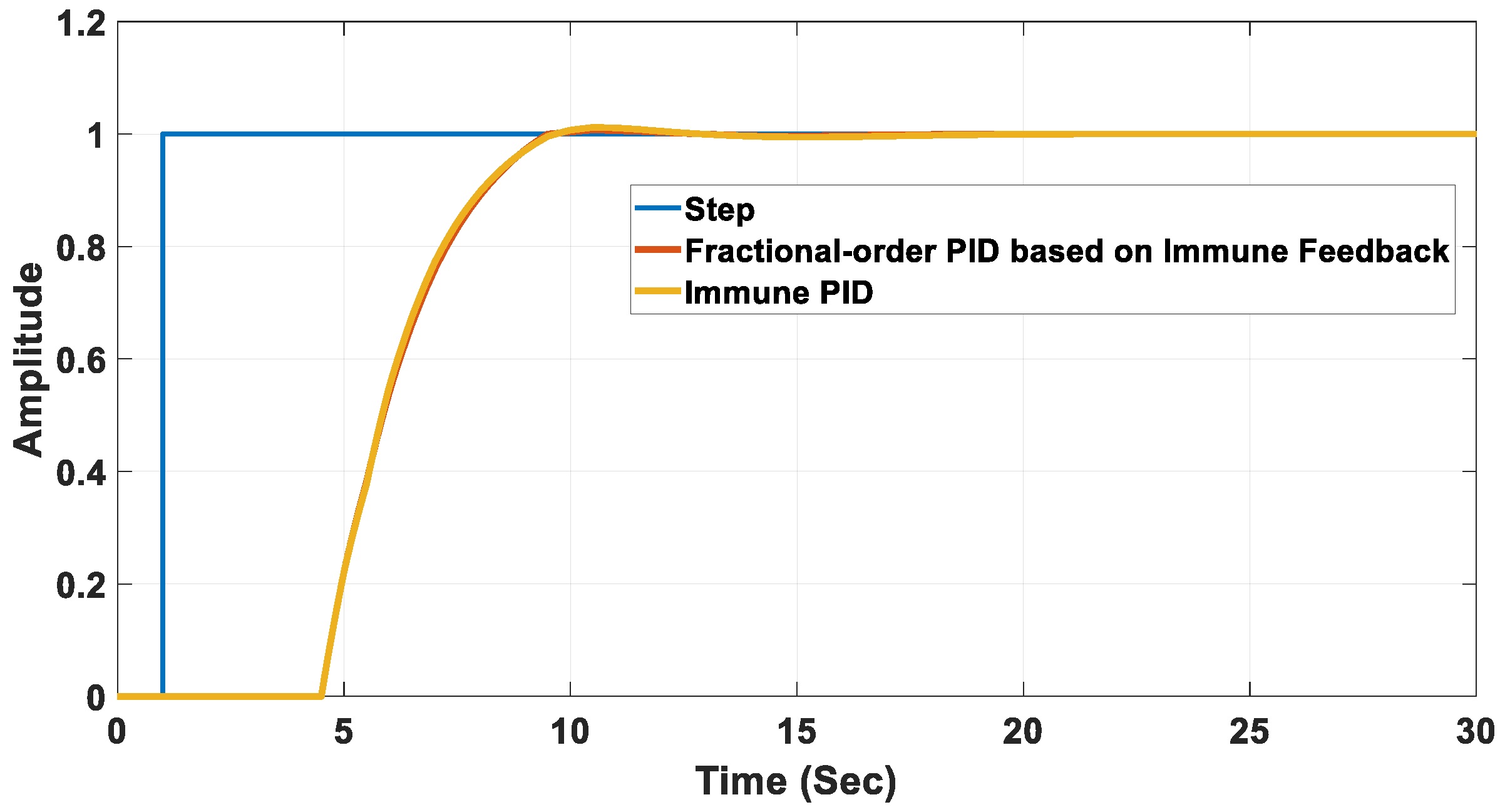
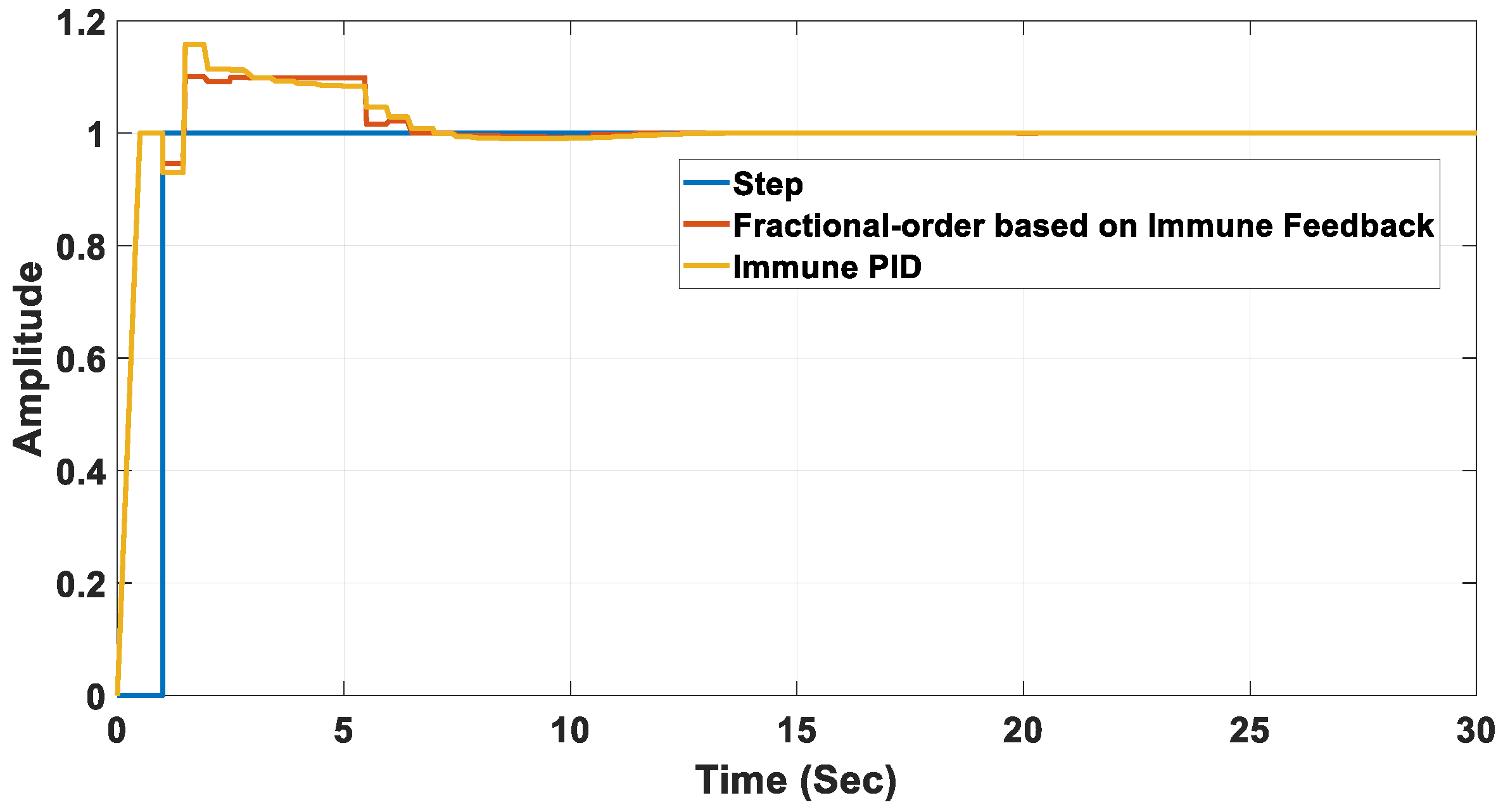
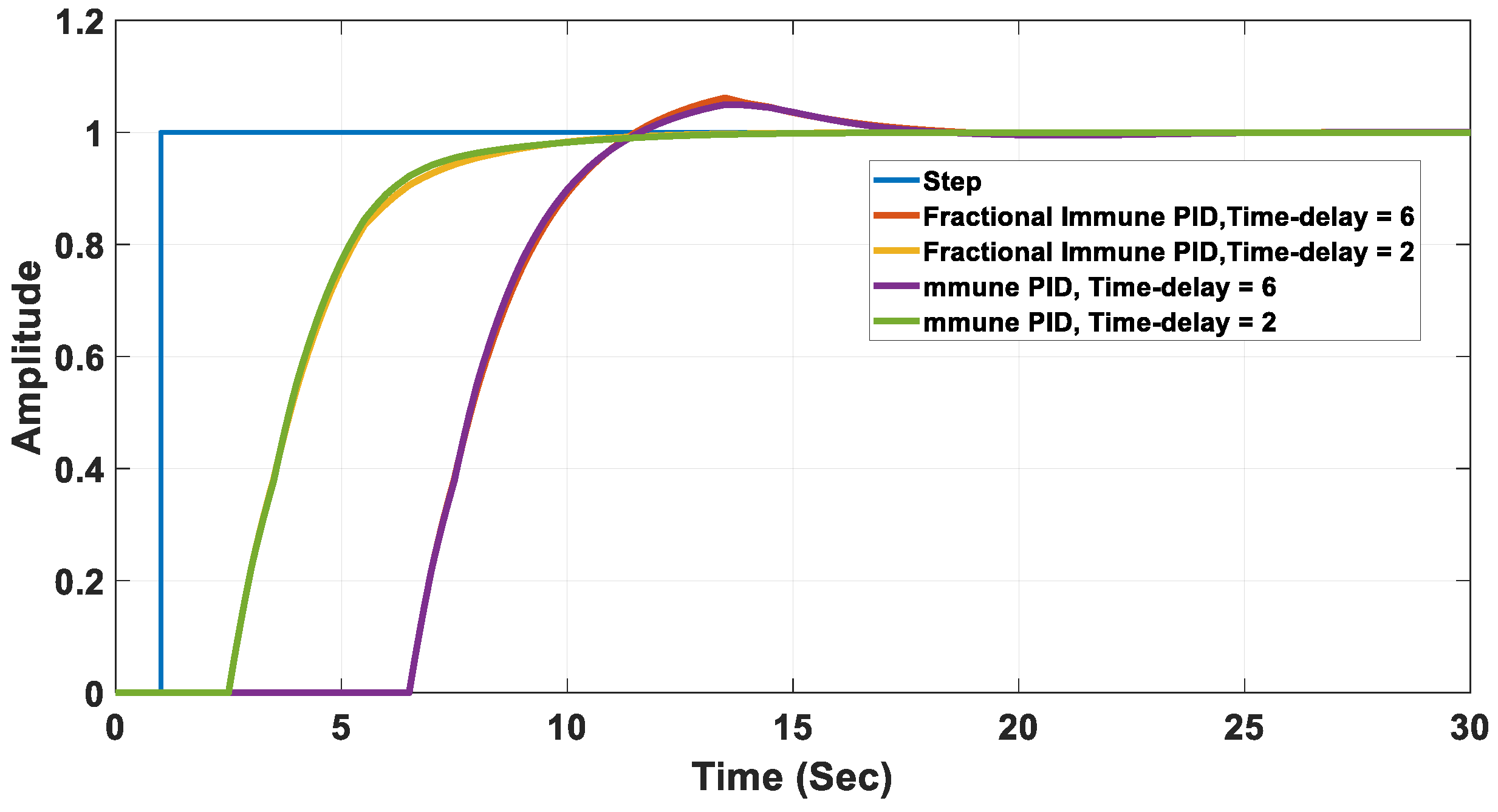
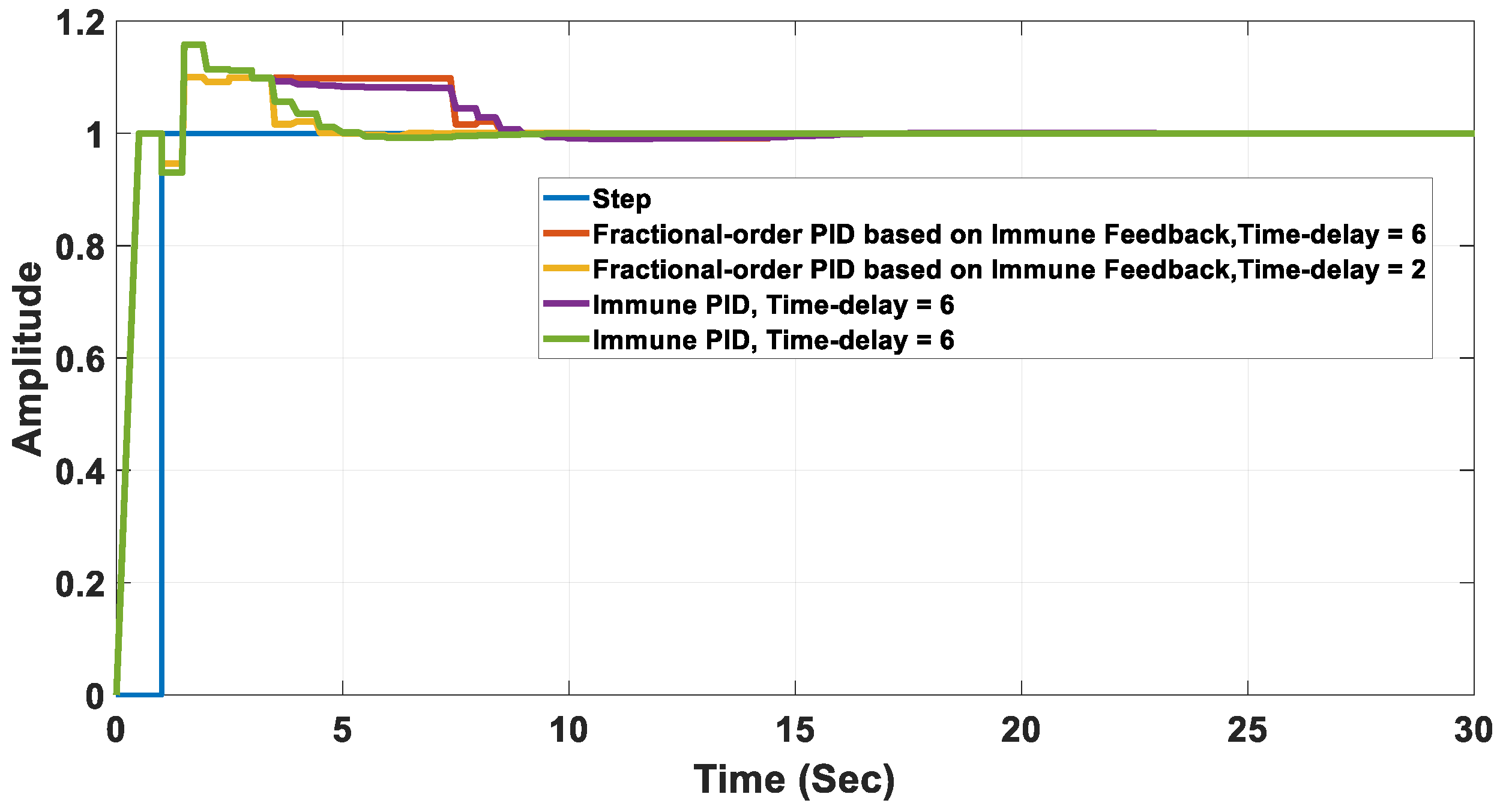
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hagglund, T.; Astrom, K.J. PID Controllers: Theory, Design, and Tuning, 2nd ed.; International Society of Automation: Durham, NC, USA, 1995; ISBN 978-1-55617-516-9. [Google Scholar]
- Martins, F.G. Tuning PID Controllers Using the ITAE Criterion. Int. J. Eng. Educ. 2005, 21, 867. [Google Scholar]
- Baleanu, D.; Luo, A.C.J.; Machado, J.A.T. Fractional Dynamics and Control; Springer: New York, NY, USA, 2012; ISBN 9781461404576. [Google Scholar]
- Chen, Y.; Petráš, I.; Xue, D. Fractional Order Control—A Tutorial; Fractional Order Control—A Tutorial. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009. [Google Scholar]
- Tepljakov, A. Fractional-Order Modeling and Control of Dynamic Systems; Springer Theses; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-52949-3. [Google Scholar]
- Podlubny, I. Fractional-Order Systems and PIλDμ-Controllers. IEEE Trans. Autom. Control. 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Dulǎu, M.; Gligor, A.; Dulǎu, T.M. Fractional Order Controllers Versus Integer Order Controllers. Procedia Eng. 2017, 181, 538–545. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; ISBN 978-1-84996-334-3. [Google Scholar]
- Valério, D.; Sá da Costa, J. An Introduction to Fractional Control; Institution of Engineering and Technology: Harts, WV, USA, 2012; ISBN 9781849195461. [Google Scholar]
- Bingi, K.; Ibrahim, R.; Karsiti, M.N.; Hassan, S.M.; Harindran, V.R. Fractional-Order Systems and PID Controllers; Studies in Systems, Decision and Control; Springer International Publishing: Cham, Switzerland, 2020; Volume 264, ISBN 978-3-030-33933-3. [Google Scholar]
- Padula, F.; Visioli, A. Advances in Robust Fractional Control; Springer International Publishing: Cham, Switzerland, 2015; ISBN 9783319109305. [Google Scholar]
- Padula, F.; Visioli, A. Tuning Rules for Optimal PID and Fractional-Order PID Controllers. J. Process. Control. 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Padhee, S.; Gautam, A.K.; Singh, Y.; Kaur, G. A Novel Evolutionary Tuning Method for Fractional Order PID Controller. Int. J. Soft Comput. Eng. (IJSCE) 2011, 1, 1–9. [Google Scholar]
- Monje, C.A.; Vinagre, B.M.; Feliu, V.; Chen, Y.Q. Tuning and Auto-Tuning of Fractional Order Controllers for Industry Applications. Control. Eng. Pract. 2008, 16, 798–812. [Google Scholar] [CrossRef] [Green Version]
- Valério, D.; da Costa, J.S. Tuning of Fractional PID Controllers with Ziegler–Nichols-Type Rules. Signal Process. 2006, 86, 2771–2784. [Google Scholar] [CrossRef]
- Muresan, C.I.; Birs, I.; Ionescu, C.; Dulf, E.H.; de Keyser, R. A Review of Recent Developments in Autotuning Methods for Fractional-Order Controllers. Fractal Fract. 2022, 6, 37. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Intelligent Fractional Order Systems and Control; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2013; Volume 438, ISBN 978-3-642-31548-0. [Google Scholar]
- Bingül, Z.A.F.E.R.; Karahan, O. Fractional PID Controllers Tuned by Evolutionary Algorithms for Robot Trajectory Control. Turk. J. Electr. Eng. Comput. Sci. 2012, 20, 1123–1136. [Google Scholar] [CrossRef]
- Duarte Valério. Available online: http://web.ist.utl.pt/duarte.valerio/ninteger/ninteger.htm (accessed on 26 October 2022).
- Tepljakov, A.; Petlenkov, E.; Belikov, J. FOMCON: A MATLAB Toolbox for Fractional-Order System Identification and Control. Int. J. Microelectron. Comput. Sci. 2011, 2, 51–62. [Google Scholar]
- Takahashi, K.; Yamada, T. Application of an Immune Feedback Mechanism to Control Systems. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 1998, 41, 184–191. [Google Scholar] [CrossRef] [Green Version]
- Dasgupta, D. Artificial Immune Systems and Their Applications; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Tiwari, S.; Kaur, G.; Singh, H. Analysis of Fuzzy PID and Immune PID Controller for Three Tank Liquid Level Control. Int. J. Soft Comput. Eng. (IJSCE) 2011, 1, 185–189. [Google Scholar]
- Fridman, E. Introduction to Time-Delay Systems; Systems & Control: Foundations & Applications; Springer International Publishing: Cham, Switzerland, 2014; ISBN 978-3-319-09392-5. [Google Scholar]
- Silva, G.J.; Datta, A.; Bhattachaiyya, S.P. PID Controllers for Time-Delay Systems; Birkhäuser: Boston, MA, USA, 2005. [Google Scholar]
- Witrant, E.; Fridman, E.; Sename, O.; Dugard, L. Recent Results on Time-Delay Systems; Witrant, E., Fridman, E., Sename, O., Dugard, L., Eds.; Advances in Delays and Dynamics; Springer International Publishing: Cham, Switzerland, 2016; Volume 5, ISBN 978-3-319-26367-0. [Google Scholar]
- Boudjehem, B.; Boudjehem, D. Fractional Order Controller Design for Desired Response. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2012, 227, 243–251. [Google Scholar] [CrossRef]
- Abdulwahhab, O.W. Design of a Complex Fractional Order PID Controller for a First Order Plus Time Delay System. ISA Trans. 2020, 99, 154–158. [Google Scholar] [CrossRef] [PubMed]
- Pop, C.I.; Ionescu, C.; de Keyser, R.; Dulf, E.H.; Pop, C.I.; Dulf, E.H.; Ionescu, C.; de Keyser, R. Robustness Evaluation of Fractional Order Control for Varying Time Delay Processes. Signal Image Video Process. 2012, 6, 453–461. [Google Scholar] [CrossRef]
- Gopinath, R. Design of Fractional Order Controllers for First Order Plus Time Delay Systems. Int. J. Comput. Appl. 2013, 975, 8887. [Google Scholar]
- Birs, I.; Muresan, C.; Nascu, I.; Ionescu, C. A Survey of Recent Advances in Fractional Order Control for Time Delay Systems. IEEE Access 2019, 7, 30951–30965. [Google Scholar] [CrossRef]
- Yüce, A.; Tan, N.; Atherton, D.P. Fractional Order PI Controller Design for Time Delay Systems. IFAC-Pap. 2016, 49, 94–99. [Google Scholar] [CrossRef]
- Sadalla, T.; Horla, D.; Giernacki, W.; Kozierski, P. Influence of Time Delay on Fractional-Order PI-Controlled System for a Second-Order Oscillatory Plant Model with Time Delay. Arch. Electr. Eng. 2017, 66, 693–704. [Google Scholar] [CrossRef] [Green Version]
- Jajarmi, A.; Baleanu, D. Suboptimal Control of Fractional-Order Dynamic Systems with Delay Argument. J. Vib. Control. 2017, 24, 2430–2446. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Y. Stabilizing and Robust Fractional Order PI Controller Synthesis for First Order plus Time Delay Systems. Automatica 2012, 48, 2159–2167. [Google Scholar] [CrossRef]
- Moghaddam, T.V.; Bigdeli, N.; Afshar, K. Tuning a Fractional Order PID Controller with Lead Compensator in Frequency Domain. Int. J. Electr. Inf. Eng. 2011, 5, 366–371. [Google Scholar] [CrossRef]
- Sadati, S.J.; Ranjbar Noei, A.; Ghaderi, R. Fractional-Order Control of a Nonlinear Time-Delay System: Case Study in Oxygen Regulation in the Heart-Lung Machine. J. Control. Sci. Eng. 2012, 2012, 14. [Google Scholar] [CrossRef] [Green Version]
- Narang, A.; Shah, S.L.; Chen, T. Tuning of Fractional PI Controllers for Fractional Order System Models with and without Time Delays. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; IEEE Xplore. IEEE Conference Publication: Manhattan, NY, USA, 2010. [Google Scholar]
- Ranganayakulu, R.; Uday Bhaskar Babu, G.; Seshagiri Rao, A. Fractional Filter IMC-PID Controller Design for Second Order plus Time Delay Processes. Cogent Eng. 2017, 4, 1366888. [Google Scholar] [CrossRef]
- Muresan, C.I.; Dutta, A.; Dulf, E.H.; Pinar, Z.; Maxim, A.; Ionescu, C.M. Tuning Algorithms for Fractional Order Internal Model Controllers for Time Delay Processes. Int. J. Control. 2015, 89, 579–593. [Google Scholar] [CrossRef]
- Lanusse, P.; Oustaloup, A. Control of Time-Delay Systems Using Robust Fractional-Order Control and Robust Smith Predictor Based Control. In Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference—DETC2005, Brooklyn, NY, USA, 3–6 August 2008; pp. 1475–1483. [Google Scholar] [CrossRef]
- Feliu-Batlle, V.; Rivas Pérez, R.; Castillo García, F.J.; Sanchez Rodriguez, L. Smith Predictor Based Robust Fractional Order Control: Application to Water Distribution in a Main Irrigation Canal Pool. J. Process. Control. 2009, 19, 506–519. [Google Scholar] [CrossRef]
- Safaei, M.; Tavakoli, S. Smith Predictor Based Fractional-Order Control Design for Time-Delay Integer-Order Systems. Int. J. Dyn. Control. 2018, 6, 179–187. [Google Scholar] [CrossRef]
- Bhamre, P.K.; Kadu, C.B. Design of a Smith Predictor Based Fractional Order PID Controller for a Coupled Tank System. In Proceedings of the International Conference on Automatic Control and Dynamic Optimization Techniques, ICACDOT 2016, Pune, India, 9–10 September 2016; pp. 705–708. [Google Scholar] [CrossRef]
- Liu, F.; Li, F.; Xiao, D. The Design of Fuzzy PID Controller for Networked Systems with Random Time Delay. Int. J. Grid Distrib. Comput. 2016, 9, 117–124. [Google Scholar] [CrossRef]
- Jesus, I.S.; Barbosa, R.S. Smith-Fuzzy Fractional Control of Systems with Time Delay. AEU—Int. J. Electron. Commun. 2017, 78, 54–63. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, Q.; Wang, Z.; Shao, X.; Wen, X. Sliding Mode Control Based On SVM for Fractional Order Time-Delay System. In Proceedings of the International Conference on Control and Automation (ICCA 2016), Kathmandu, Nepal, 1–3 June 2016. [Google Scholar] [CrossRef]
- Yousefi, M.; Binazadeh, T. Delay-Independent Sliding Mode Control of Time-Delay Linear Fractional Order Systems. Trans. Inst. Meas. Control. 2016, 40, 1212–1222. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-Band Complex Noninteger Differentiator: Characterization and Synthesis. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Xue, D.; Zhao, C.; Chen, Y.Q. A Modified Approximation Method of Fractional Order System. In Proceedings of the 2006 International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 1043–1048. [Google Scholar] [CrossRef]
- Deniz, F.N.; Alagoz, B.B.; Tan, N.; Koseoglu, M. Revisiting Four Approximation Methods for Fractional Order Transfer Function Implementations: Stability Preservation, Time and Frequency Response Matching Analyses. Annu. Rev. Control. 2020, 49, 239–257. [Google Scholar] [CrossRef]
- El-Khazali, R.; Batiha, I.M.; Momani, S. Approximation of Fractional-Order Operators. In Springer Proceedings in Mathematics and Statistics; Springer: Berlin/Heidelberg, Germany, 2019; Volume 303, pp. 121–151. [Google Scholar] [CrossRef]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. Application of New-Ton’s Method to Analog and Digital Realization of Fractional-Order Controllers. Int. J. Microelectron. Comput. Sci. 2013, 3, 45–52. [Google Scholar]
- Colín-Cervantes, J.D.; Sánchez-López, C.; Ochoa-Montiel, R.; Torres-Muñoz, D.; Hernández-Mejía, C.M.; Sánchez-Gaspariano, L.A.; González-Hernández, H.G. Rational Approximations of Arbitrary Order: A Survey. Fractal Fract. 2021, 5, 267. [Google Scholar] [CrossRef]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.A.; Hassan Hosseinnia, S.; Petlenkov, E.; Ates, A.; Cech, M. Towards Industrialization of FOPID Controllers: A Survey on Milestones of Fractional-Order Control and Pathways for Future Developments. IEEE Access 2021, 9, 21016–21042. [Google Scholar] [CrossRef]
- Xue, D.; Chen, Y.; Atherton, D.P. Linear Feedback Control: Analysis and Design with MATLAB; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; ISBN 978-0-898716-38-2. [Google Scholar]
- Wang, W.; Gao, X.Z.; Wang, C. A New Immune PID Controller Based on Immune Tuning. In Proceedings of the International Conference on Intelligent Computing, Qingdao, China, 21–24 August 2007; pp. 1337–1346. [Google Scholar] [CrossRef]







| Immune System | Control System |
|---|---|
| The k generation reproduction of antigens and antibodies. | The sampling time of discrete system. |
| is the antigen concentration of generation. | is the difference between setpoint value and output value at the sampling time. |
| is the B cell concentration of the k generation. | is the output value of controller at the sampling instant. |
| Symbol | Interpretation in the Immune System |
|---|---|
| Amount of antigens at the kth generation | |
| Output from stimulated by the antigens | |
| Effect of on B cells | |
| Total stimulation of B cells | |
| Stimulation factor | |
| Suppression factor | |
| Stabilization factor | |
| The effect of the reaction of B cells and the antigens |
| 1.7152 | 0.5848 | 1.2576 |
| 401.5 | 65.1 | 0.016 | 0.48 | 0.06 |
| 9.77 × 10−5 | 0.0001 | 20.47 |
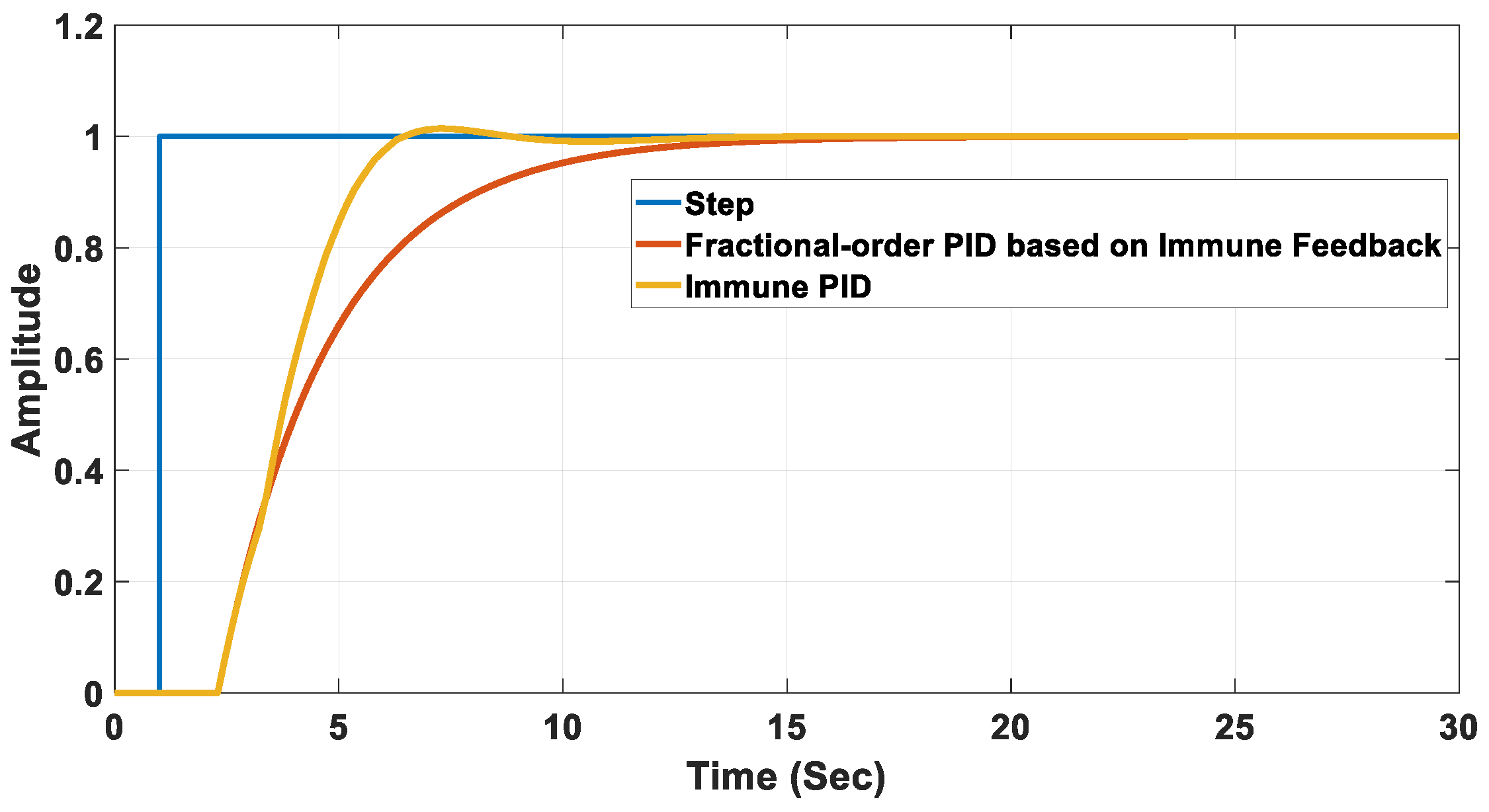
| Controller Used | Peak (%) | Settling Time (s) | Rise Time (s) | Steady State Error (%) |
|---|---|---|---|---|
| Immune PID | 1.4 | 5.7 | 2.76 | 1 |
| FOPID based on IFM | No overshoot | 9.8 | 5.44 | 0 |
| 1.8257 | 0.0079346 | 3.1803 | 0.066297 | 0.99368 |
| 0.257 | 4.427 | 0.093956 |
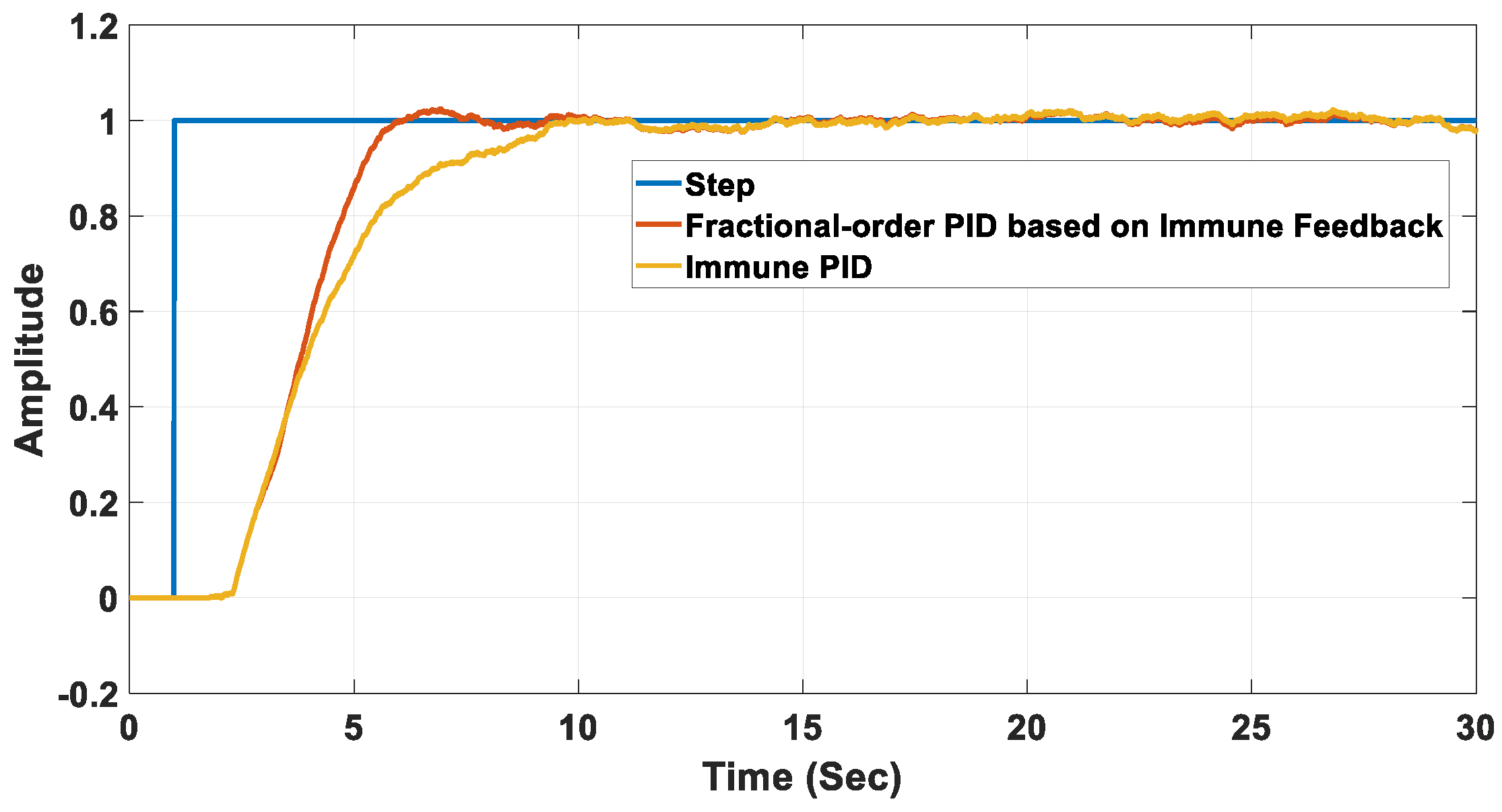
| Controller Used | Peak (%) | Settling Time (s) | Rise Time (s) | Steady State Error (%) |
|---|---|---|---|---|
| Immune PID | No overshoot | 8.6 | 8.0 | 0 |
| FOPID based on IFM | No overshoot | 8.6 | 8.0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makhbouche, A.; Boudjehem, B.; Birs, I.; Muresan, C.I. Fractional-Order PID Controller Based on Immune Feedback Mechanism for Time-Delay Systems. Fractal Fract. 2023, 7, 53. https://doi.org/10.3390/fractalfract7010053
Makhbouche A, Boudjehem B, Birs I, Muresan CI. Fractional-Order PID Controller Based on Immune Feedback Mechanism for Time-Delay Systems. Fractal and Fractional. 2023; 7(1):53. https://doi.org/10.3390/fractalfract7010053
Chicago/Turabian StyleMakhbouche, Adel, Badreddine Boudjehem, Isabela Birs, and Cristina I. Muresan. 2023. "Fractional-Order PID Controller Based on Immune Feedback Mechanism for Time-Delay Systems" Fractal and Fractional 7, no. 1: 53. https://doi.org/10.3390/fractalfract7010053
APA StyleMakhbouche, A., Boudjehem, B., Birs, I., & Muresan, C. I. (2023). Fractional-Order PID Controller Based on Immune Feedback Mechanism for Time-Delay Systems. Fractal and Fractional, 7(1), 53. https://doi.org/10.3390/fractalfract7010053









