Abstract
Fractals are essential in representing the natural environment due to their important characteristic of self similarity. The dynamical behavior of fractals mostly depends on escape criteria using different iterative techniques. In this article, we establish an escape criteria using DK-iteration as well as complex sine function and complex exponential function . We use this to analyze the dynamical behavior of specific fractals namely Julia set and Mandelbrot set. This is achieved by generalizing the existing algorithms, which led to the visualization of beautiful fractals for and 4. Moreover, the image generation time in seconds using different values of input parameters is also computed.
1. Introduction
Fractals are common in nature because they adequately describe: tree branches, leaf patterns, lightning, electricity, clouds, crystals, rivers, and so on. Fractals play an important role in surveying or examining various natural or living frameworks, such as microorganism culture. Fractals are also used in liquid mechanics to determine and comprehend violent streams. Fractal geometries are important in the design of modern telecommunications systems, particularly antennas, for reasons such as smaller size, improved gain, and efficiency when operating in multi-frequency bands [1]. In addition, computational architectural design, radar frameworks, and engineering models fall into the areas in which fractal theory is widely used [2]. Cryptography [3], image compression [4], as well as encryption [5] are also common applications. Using these facts as inspiration, the authors establish an escape criteria for generating fractals of complex functions using the DK-iterative scheme. Thus, before presenting the findings of our research, it’s indeed necessary that we review and understand some fundamental terms in the subsequent paragraphs.
A fractal can be characterized as “a mathematical figure whose every point shows the same similarity as the entirety” or “an extremely irregular shape for which any appropriate focused part is like another larger or more modest part when amplified or diminished”. The word “fractal” is a Latin word that means broken or fractured. This terminology was first used by B. Mandelbrot [6] and later on he became famous as the “father of fractal geometry”. In the beginning of 20th century, P. Fatou and G. Julia tried to find the progressive estimate of where but they were unable to draw the graph of the proposed function. In 1985, B. Mandelbrot started work on this and successfully sketched the graph of complex function . He defined Mandelbrot set by changing the values of complex parameter b and variable x [7]. M-sets for where and are elaborated in [8]. The images like J-set and M-set using rational and transcendental complex functions are discussed in [9]. Later on anti J-sets and anti M-sets were defined by Crow et al. [10], and they generated graphs of where which are tri-corns.
Fixed point theory is playing an important role in the generation of fractals using different iterative schemes. For instance, implicit iterations with s-convexity are mainly discussed in [11,12,13,14,15]. Biological images and their characteristics are presented in [16,17,18,19]. Moreover, J-sets and M-sets of transcendental complex functions using diverse iterations are visualized by the authors of [20,21]. Fractals with high dimensions are elaborated in [22,23,24]. Specific fractals of general nature have been also created by applying diverse iterative techniques like Mann [25], Ishikawa [26], Noor [27], S and CR [28,29] iterations. Hence, the behavior of these fractals is discussed in [30,31,32,33,34,35] as well. In this research article, we use DK-iteration to generate the J-sets and M-sets using complex sine as well as exponential functions, where .
The rest of the article is as follows. Some basic definition of M-set, J-set and some iterative schemes are explained in Section 2. We prove main results in Section 3. Section 4 presents algorithms and examples of fractals (i.e., J-sets and M-sets). We conclude these results by highlighting future applications in Section 5.
2. Basic Definitions and Preliminaries
This section contains basic notions and terms required for this research.
Definition 1.
(J-set [36]): A set containing the end points of the following
forms a basic J-set, where τ is a polynomial having degree 2 or greater than 2 with domain and range consisting of complex numbers, . Moreover, the set itself is named as filled J-set.
Definition 2.
(M-Set [7]): M-set is a well-defined collection of connected J-sets and following to [37], we have
Moreover, zero is chosen as an initial point because it is a unique critical point.
Definition 3.
(Noor Iteration [38]) Let and be a complex mapping then Noor iterative scheme is defined as
where and
Definition 4.
(DK-iteration [39]) For any , Dogan and Karakaya introduced a new three step iteration (i.e., DK-iteration), which is defined as
where and
3. Main Results
Escape criterion is an important tool to generate complex fractals. In this section, we present results for complex sine and exponential function via DK-iteration. Since DK-iteration have three steps, one can easily notice that depends on , depends on and depends on for all . So, for we assume , and throughout this article.
3.1. Escape Criterion of DK-Iteration for Sine Function
Let be a complex sine function, then the Maclaurin expansion for sine function is
where satisfying the bound and similarly,
where satisfying the bound and consequently,
where satisfying the bound
Theorem 1.
Assume that be the sequence of iterates defined in (4) and , where be a complex sine function with , and . Then , as .
Proof.
By making use of the given information and fixing , and , the initial step of DK-iteration can be written as
Next, by using (5), and the given fact we obtain
Now, we consider the second step of DK-iteration
Hence, by using (7), and , we obtain
Now for final step of DK-iterative scheme, we have
Hence, by neglecting , and using (6) and (7), we obtain successively
Continuing in this way, for , we have
next, for , we have
and so on, iterating upto the general term we get
Since and therefore, as □
Corollary 1.
For some , assume that
then there exits a positive number such that
and therefore, as
3.2. Escape Criterion of DK-Iteration for Exponential Function
Let us expand as a Maclaurin series as follows
where such that
Similarly,
where such that
Continuing in this way, we have
where such that
Theorem 2.
Assume that be the sequence of iterates defined in (4) and , where m≥ 2, be a complex exponential function with , and . Then , as .
Proof.
Since and , and then the initial step of DK-iteration is
By using (8) and the given fact that we obtain the criteria
Now, for the second step of DK-iteration we have,
Hence, by making use of (10) and we have
Now for the final step of DK-iteration we have
Taking , then neglecting , and using (9) and (10), respectively, we have
Continuing in this way, for , we have
and for , we have
and so on iterating upto the general term we get
Since and therefore, as □
Corollary 2.
For some , assume that
then there exits a positive number such that
and then as
4. Applications in Fractals
This section presents fractals (i.e., J-sets and M-sets) using DK-iterative scheme. Mainly, the fractals are generated by following a criterion to execute images by an algorithm. There are some popular algorithms to generate the fractals:
- Distance Estimator [40],
- Potential Function Algorithm [41]
- Escape Criteria [42].
From the above listed methods, escape criterion is used here in the following Algorithms 1 and 2 to create the J-sets and M-sets in graphs. We use Mathematica 9.0 in computer “Intel(R) Core(TM) i7-7500U CPU @ 2.70 GHz 2.90 GHz” to obtain our desire results. In this section we use abbreviation DKIS for DK-iterative scheme.
4.1. Julia Set
J-set is a set of points for which the orbit of as . So, here we discuss some J-sets of functions using DK-iteration. Maximum number of iterations are considered 30 (i.e., ) and in Algorithm 1.
| Algorithm 1: Geometry of J-Set |
 |
Example 1.
J-sets for are generated here with the following inputs
 Figure 1. J-set for via DKIS. The image execution time is s.
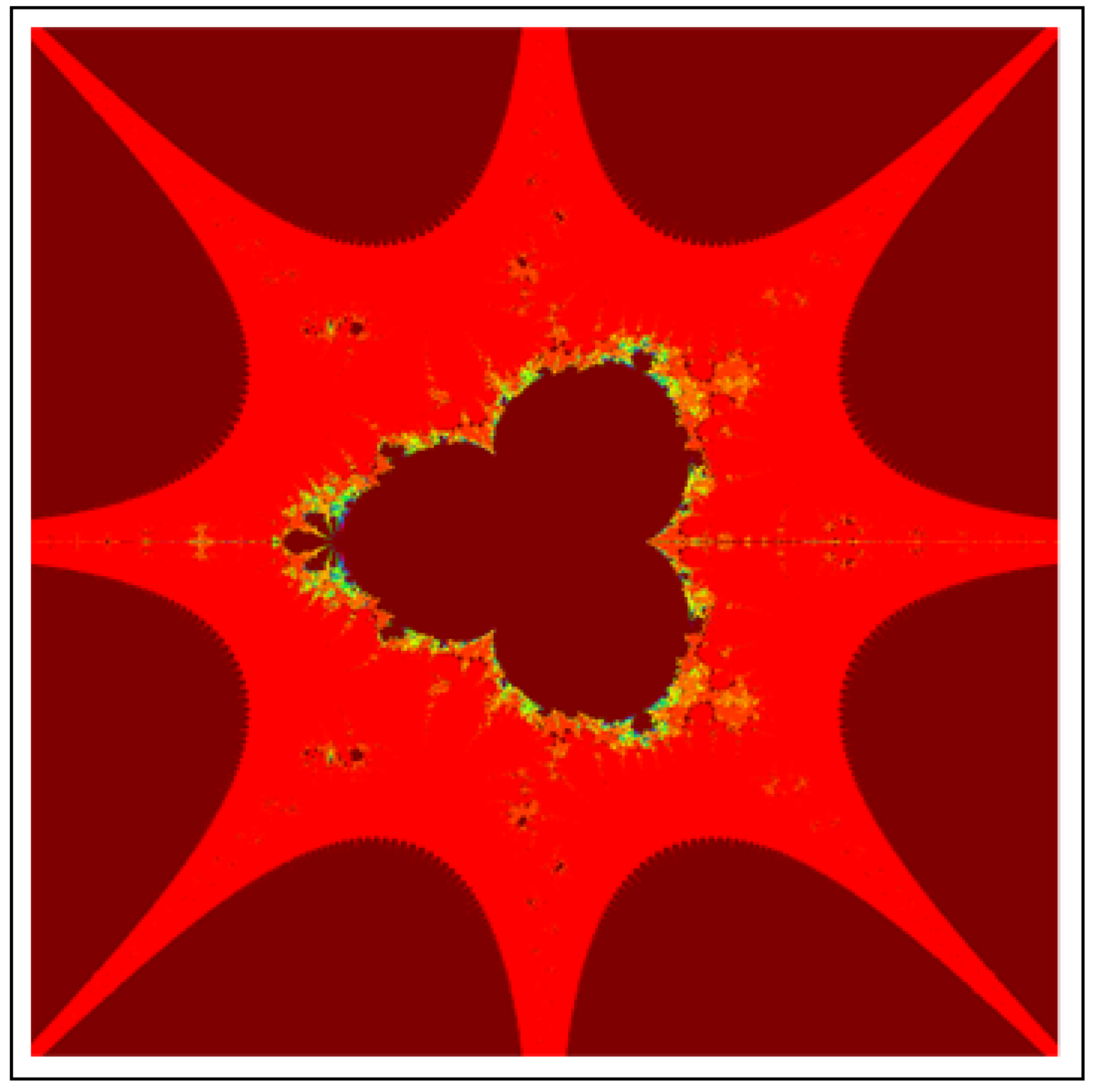
Figure 1. J-set for via DKIS. The image execution time is s.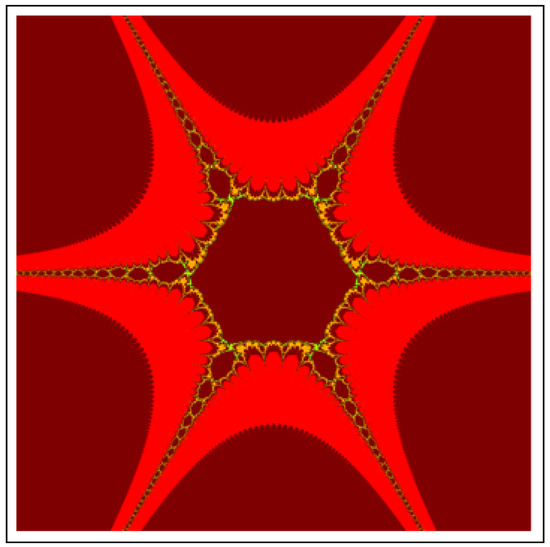 Figure 2. J-set for via DKIS. The image execution time is s.
Figure 2. J-set for via DKIS. The image execution time is s. Figure 3. J-set for via DKIS. The image execution time is s.
Figure 3. J-set for via DKIS. The image execution time is s. Figure 4. J-set for via DKIS. The image execution time is s.
Figure 4. J-set for via DKIS. The image execution time is s.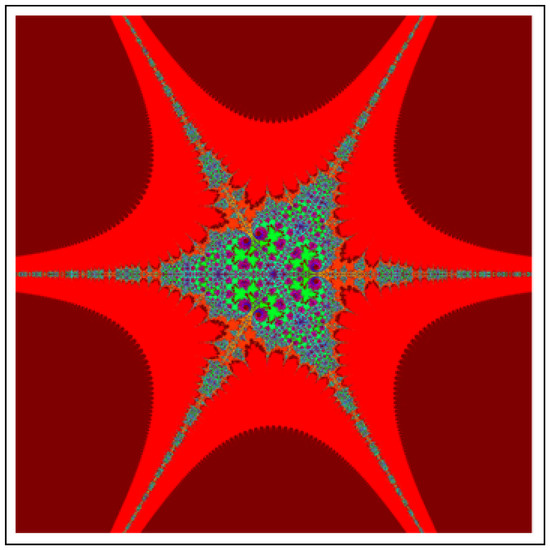 Figure 5. J-set for via DKIS. The image execution time is s.
Figure 5. J-set for via DKIS. The image execution time is s. Figure 6. J-set for via DKIS. The image execution time is s.
Figure 6. J-set for via DKIS. The image execution time is s. Figure 7. J-set for via DKIS. The image execution time is s.
Figure 7. J-set for via DKIS. The image execution time is s. Figure 8. J-set for via DKIS. The image execution time is 1077 s.
Figure 8. J-set for via DKIS. The image execution time is 1077 s. Figure 9. J-set for via DKIS. The image execution time is s.
Figure 9. J-set for via DKIS. The image execution time is s.
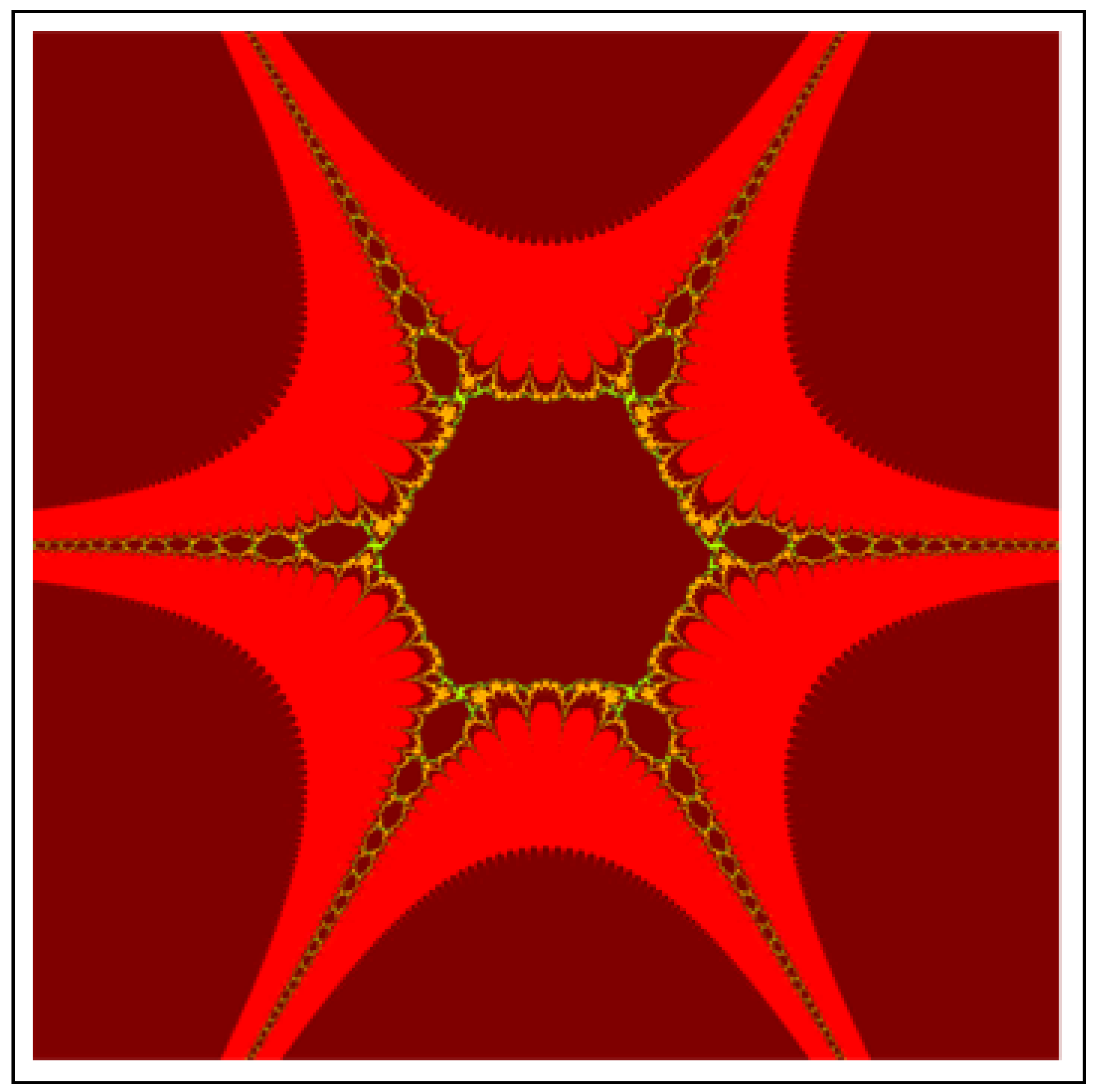
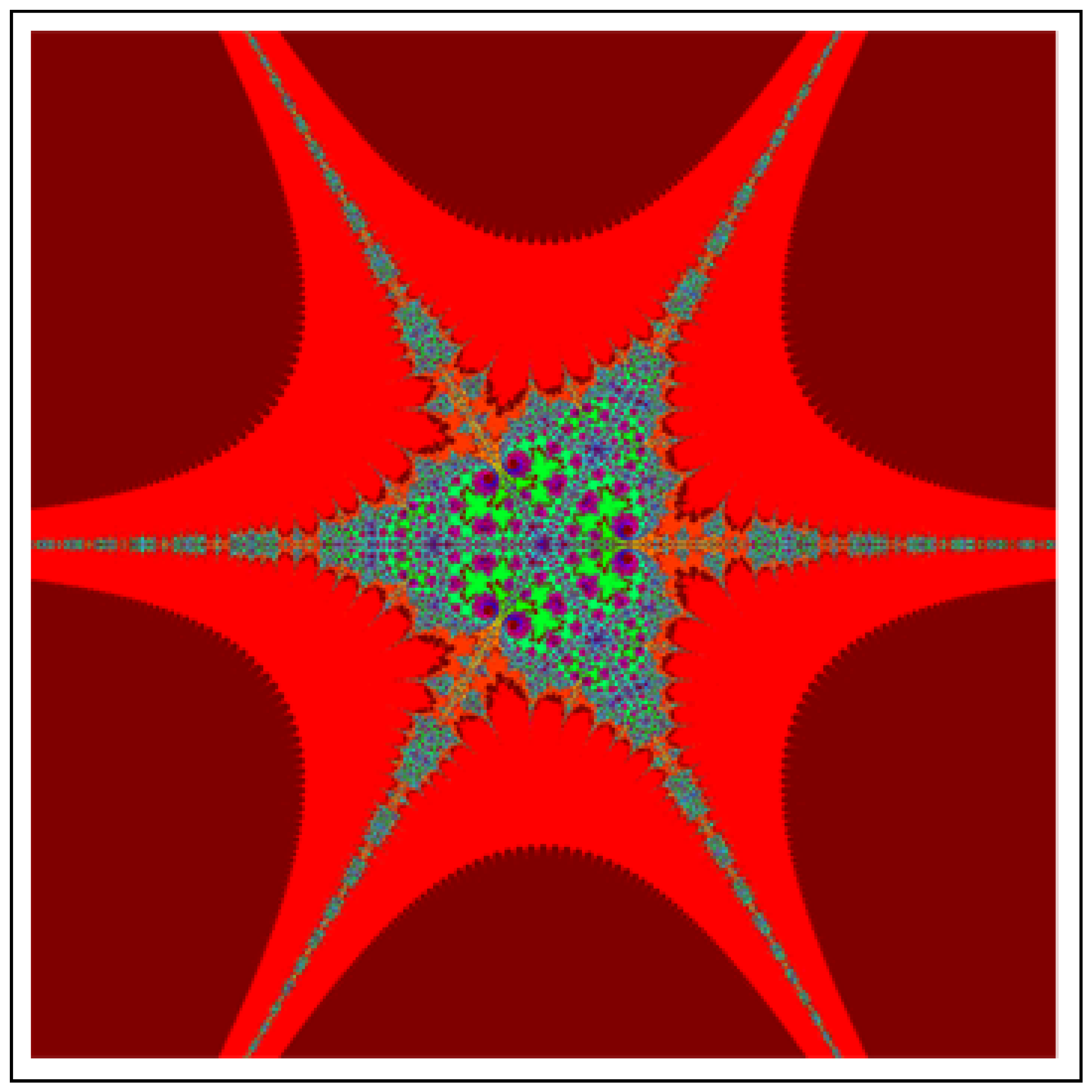
All J-sets for have 4 attractors appears on main body of each. From 4 attractors, two are symmetrical to x-axis and other two are symmetrical to y-axis. Furthermore, each attractor has an angle , where K represents the position of each attractor form standard or initial attractor. For , Images of J-sets have 6 attractors. All six attractors have an angle and two of them have symmetry about x-axis. The J-sets for have 8 attractors and each have an angle . We observe that in the image of all J-sets, each attractor have infinite many lashes. All figures look similar to each other but have difference in Julia points.
Example 2.
J-sets for are generated here with the following inputs
 Figure 10. J-set for via DKIS. The image execution time is s.
Figure 10. J-set for via DKIS. The image execution time is s. Figure 11. J-set for via DKIS. The image execution time is s.
Figure 11. J-set for via DKIS. The image execution time is s. Figure 12. J-set for via DKIS. The image execution time is s.
Figure 12. J-set for via DKIS. The image execution time is s. Figure 13. J-set for via DKIS. The image execution time is s.
Figure 13. J-set for via DKIS. The image execution time is s. Figure 14. J-set for via DKIS. The image execution time is s.
Figure 14. J-set for via DKIS. The image execution time is s. Figure 15. J-set for via DKIS. The image execution time is s.
Figure 15. J-set for via DKIS. The image execution time is s. Figure 16. J-set for via DKIS. The image execution time is s.
Figure 16. J-set for via DKIS. The image execution time is s. Figure 17. J-set for via DKIS. The image execution time is s.
Figure 17. J-set for via DKIS. The image execution time is s.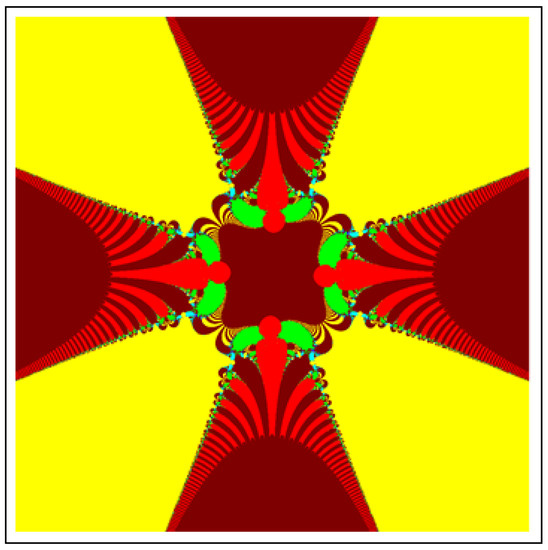 Figure 18. J-set for via DKIS. The image execution time is s.
Figure 18. J-set for via DKIS. The image execution time is s.
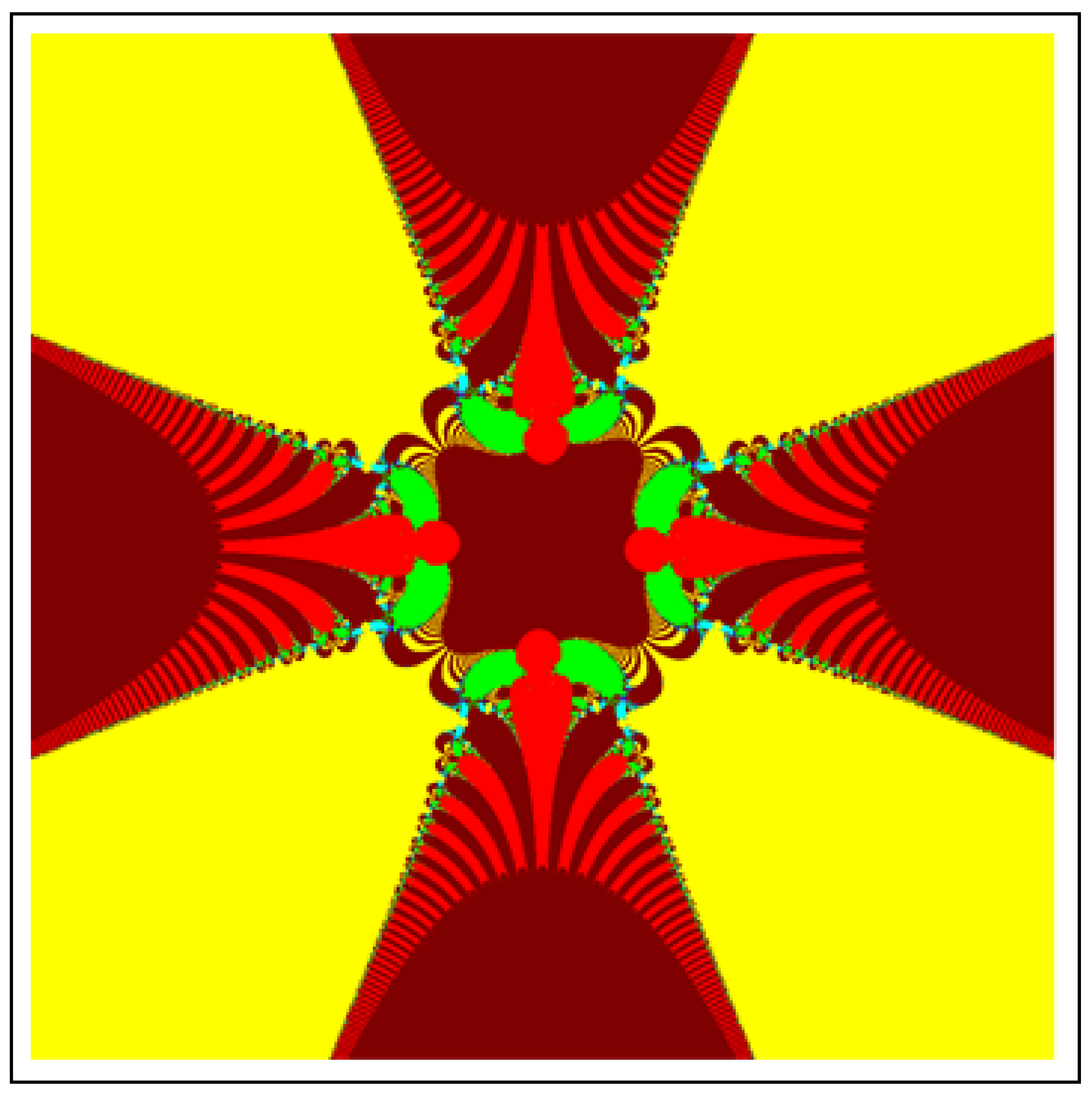
All J-sets for have two bunches of lashes. The size of lashes gradually decrease from the center of the bunch. The angle between two bunches is . The images for and have three and four bunches, respectively. We notice that for , the angle between every two bunches is and for , the angle is .
4.2. Mandelbrot Set
Here we discuss some M-sets for the function and at different m in the orbit of proposed iteration. We have generated M-sets for via DK-iteration. In all graphs we set the value of L as 30 (i.e., Fixed number of iterations) and in Algorithm 2.
| Algorithm 2: Geometry of M-Set |
 |
Example 3.
M-sets for are generated here with the following inputs:
 Figure 19. M-set for via DKIS. The image execution time is s.
Figure 19. M-set for via DKIS. The image execution time is s. Figure 20. M-set for via DKIS. The image execution time is s.
Figure 20. M-set for via DKIS. The image execution time is s. Figure 21. M-set for via DKIS. The image execution time is s.
Figure 21. M-set for via DKIS. The image execution time is s. Figure 22. M-set for via DKIS. The image execution time is s.
Figure 22. M-set for via DKIS. The image execution time is s. Figure 23. M-set for via DKIS. The image execution time is s.
Figure 23. M-set for via DKIS. The image execution time is s. Figure 24. M-set for via DKIS. The image execution time is s.
Figure 24. M-set for via DKIS. The image execution time is s.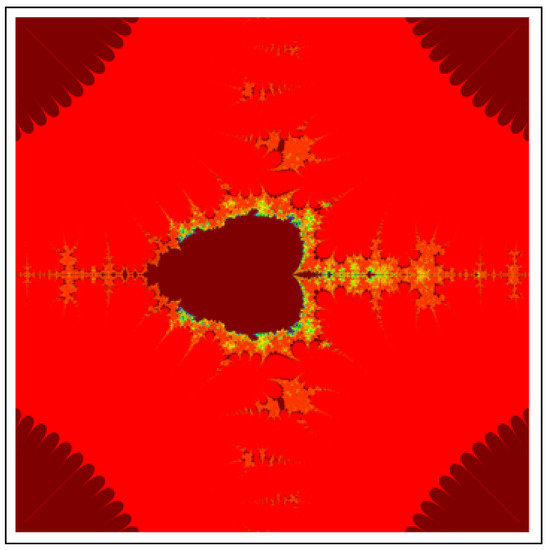 Figure 25. M-set for via DKIS. The image execution time is s.
Figure 25. M-set for via DKIS. The image execution time is s. Figure 26. M-set for via DKIS. The image execution time is s.
Figure 26. M-set for via DKIS. The image execution time is s.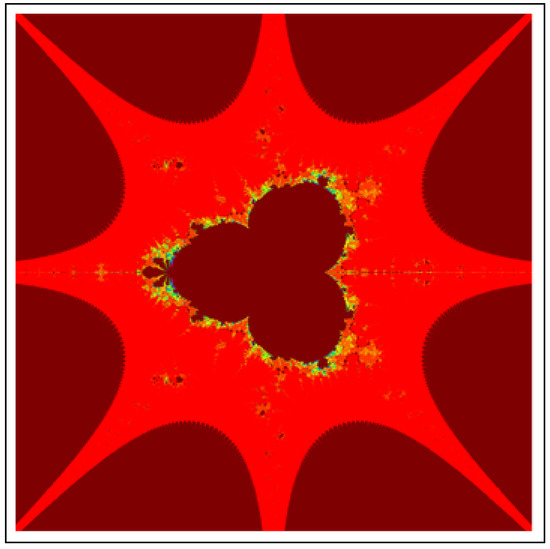 Figure 27. M-set for via DKIS. The image execution time is s.
Figure 27. M-set for via DKIS. The image execution time is s.
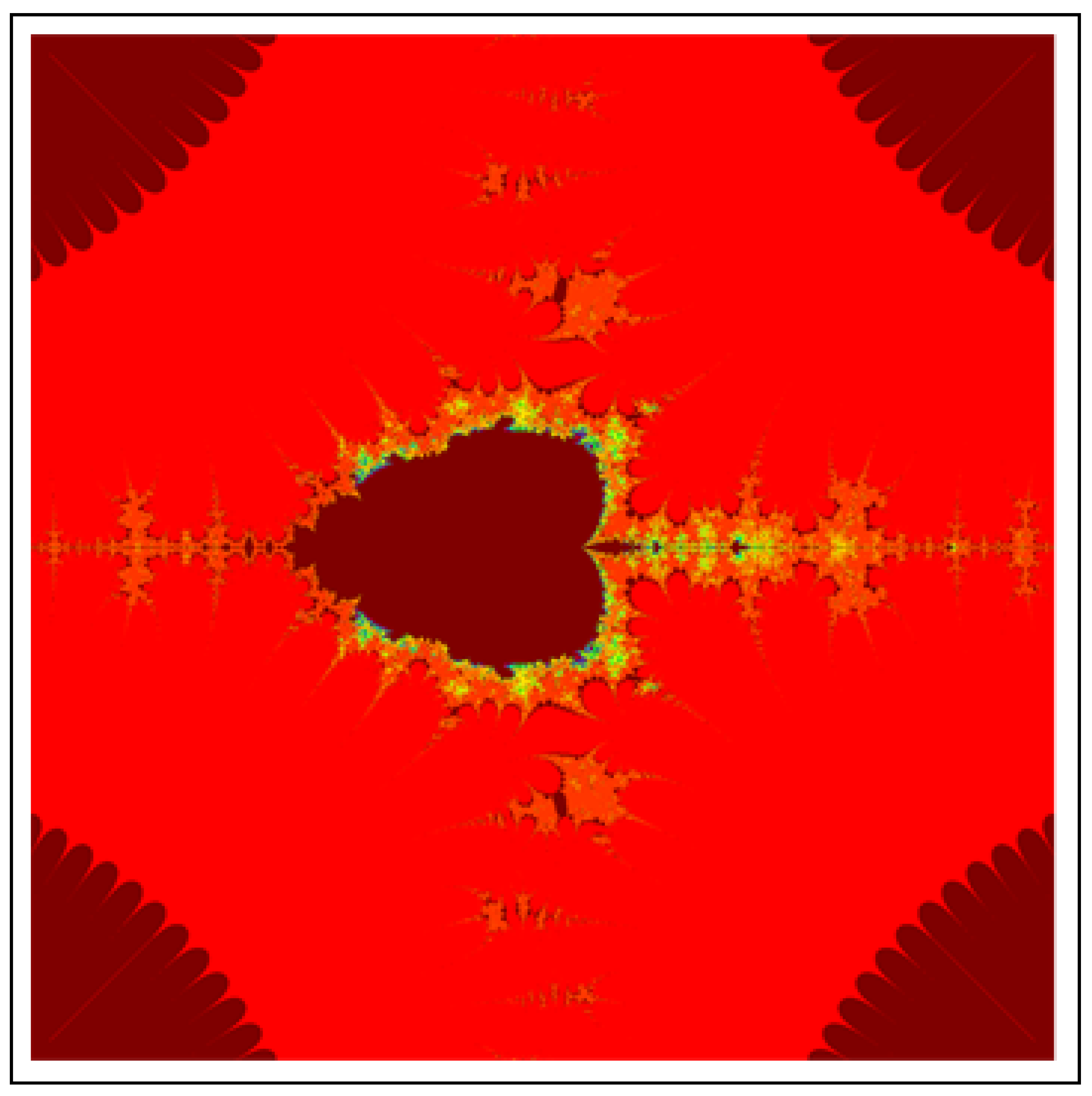
All M-sets for have 4 attractors on their main bodies and a classical quadratic Mandelbrot set at their centers. From 4 attractors, two are symmetrical to x-axis and other two are symmetrical to y-axis. For , Images of M-sets have 6 attractors and a classical cubic Mandelbrot set at their centers. All six attractors have an angle and two of them have symmetry about x-axis. The M-sets for have 8 attractors and a bi-quadratic classical Mandelbrot set at their centers. The angle of attractor from the initial attractor. Moreover, here we also observe that in the images of all M-sets, attractors have infinite many lashes.
Example 4.
M-sets for are generated here with the following inputs:
 Figure 28. M-set for via DKIS. The image execution time is s.
Figure 28. M-set for via DKIS. The image execution time is s. Figure 29. M-set for via DKIS. The image execution time is s.
Figure 29. M-set for via DKIS. The image execution time is s. Figure 30. M-set for via DKIS. The image execution time is s.
Figure 30. M-set for via DKIS. The image execution time is s. Figure 31. M-set for via DKIS. The image execution time is s.
Figure 31. M-set for via DKIS. The image execution time is s. Figure 32. M-set for via DKIS. The image execution time is s.
Figure 32. M-set for via DKIS. The image execution time is s. Figure 33. M-set for via DKIS. The image execution time is s.
Figure 33. M-set for via DKIS. The image execution time is s. Figure 34. M-set for via DKIS. The image execution time is s.
Figure 34. M-set for via DKIS. The image execution time is s. Figure 35. M-set for via DKIS. The image execution time is s.
Figure 35. M-set for via DKIS. The image execution time is s. Figure 36. M-set for via DKIS. The image execution time is s.
Figure 36. M-set for via DKIS. The image execution time is s.
All M-sets for have two bunches of lashes and two junctions of quadratic Mandelbrot sets. In each Junction infinite many large bulbs of quadratic Mandelbrot sets emerge on the main body. On the other hand, each lash of bunches is attract towards the Mandel-bulb of the junctions of quadratic Mandelbrot sets. The images for and have three and four bunches along with three and four junctions (i.e., Junctions of cubic and bi-quadratic Mandelbrot sets), respectively.
5. Conclusions
Escape criteria is proved by considering the complex sine, as well as exponential, functions using DK-iteration. These results are implemented in Algorithms 1 and 2 to visualize the Jsets and M-sets in DK-orbit. We discussed the generated Quadratic, Cubic, Bi-quadratic, J-sets and M-sets with detailed explanation. We observed that the attractors of J-sets for originated from the center with an angle of where K represented the positions of attractors from the initial attractor and same argument for M-sets with an extra characteristic that image of M-sets contains m type of Mandelbrot set at center for every m. We also observed that J and M-sets for had m bunches of lashes and each M-set had junctions of m Mandelbrot sets between the bunches. Furthermore, we calculated the image execution time in seconds that showed, for any change in inputs the images had different execution time.
We hope that these findings are useful to study different types of fractals which were mentioned initially. The results of this paper can also be used in cloth industry for designing and printing purposes.
Author Contributions
Conceptualization, A.T. and M.T.; Data curation, M.A. (Muhammad Azhar), M.A. (Muhammad Arshad) and F.L.; Formal analysis, A.T., M.A. (Muhammad Azhar), M.A. (Muhammad Arshad) and F.L.; Investigation, A.T. and M.T.; Methodology, A.T., M.T. and M.A. (Muhammad Azhar); Project administration, M.A. (Muhammad Azhar); Resources, F.L.; Supervision, M.A. (Muhammad Arshad); Validation, F.L.; Writing—review & editing, M.T. and M.A. (Muhammad Arshad). All authors have read and agreed to the published version of the manuscript.
Funding
No specific external funding has been received for this article.
Data Availability Statement
The research is theoretical in nature. As a result, no data were used.
Acknowledgments
The authors extend their appreciation to the deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through project number (IFP-2020-123).
Conflicts of Interest
The authors declare that they have no competing interest.
References
- Kharbanda, M.; Bajaj, N. An exploration of fractal art in fashion design. In Proceedings of the 2013 International Conference on Communication and Signal Processing, Melmaruvathur, India, 3–5 April 2013; pp. 226–230. [Google Scholar]
- Cohen, N. Fractal antenna applications in wireless telecommunications. In Proceedings of the Professional Program Proceedings. Electronic Industries Forum of New England, Boston, MA, USA, 6–8 May 1997; pp. 43–49. [Google Scholar]
- Zhang, X.; Wang, L.; Zhou, Z.; Niu, Y. A chaos-based image encryption technique utilizing Hilbert curves and H-Fractals. IEEE Access 2019, 7, 74734–74746. [Google Scholar] [CrossRef]
- Fisher, Y. Fractal image compression. Fractals 1984, 2, 347–361. [Google Scholar] [CrossRef]
- Kumar, S. Public key cryptographic system using Mandelbrot sets. In Proceedings of the MILCOM 2006-2006 IEEE Military Communications Conference, Washington, DC, USA, 23–25 October 2006; pp. 1–5. [Google Scholar]
- Barnsley, M. Fractals Everywhere; Academic: Boston, MA, USA, 1993. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry Nature; Freeman: New York, NY, USA, 1982; Volume 2. [Google Scholar]
- Lakhtakia, A.; Varadan, W.; Messier, R.; Varadan, V.K. On the symmetries of the Julia sets for the process zp + c. J. Phys. A Math. Gen. 1987, 20, 3533–3535. [Google Scholar] [CrossRef]
- Blanchard, P.; Devaney, R.L.; Garijo, A.; Russell, E.D. A generalized version of the Mcmullen domain. Int. J. Bifurc. Chaos 2008, 8, 2309–2318. [Google Scholar] [CrossRef]
- Crowe, W.D.; Hasson, R.; Rippon, P.J.; Strain-Clark, P.E.D. On the structure of the Mandelbar set. Nonlinearity 1989, 2, 541. [Google Scholar] [CrossRef]
- Nazeer, W.; Kang, S.M.; Tanveer, M.; Shahid, A.A. Fixed point results in the generation of Julia and Mandelbrot sets. J. Inequalities Appl. 2015, 2015, 298. [Google Scholar] [CrossRef]
- Kwun, Y.C.; Tanveer, M.; Nazeer, W.; Abbas, M.; Kang, S.M. Fractal generation in modified Jungck–S orbit. IEEE Access 2019, 7, 35060–35071. [Google Scholar] [CrossRef]
- Kwun, Y.C.; Tanveer, M.; Nazeer, W.; Gdawiec, K.; Kang, S.M. Mandelbrot and Julia sets via Jungck-CR iteration with s-convexity. IEEE Access 2019, 7, 12167–12176. [Google Scholar] [CrossRef]
- Li, D.; Tanveer, M.; Nazeer, W.; Guo, X. Boundaries of filled Julia sets in generalized Jungck-Mann orbit. IEEE Access 2019, 7, 76859–76867. [Google Scholar] [CrossRef]
- Li, X.; Tanveer, M.; Abbas, M.; Ahmad, M.; Kwun, Y.C.; Liu, J. Fixed point results for fractal generation in extended Jungck-SP orbit. IEEE Access 2019, 7, 160472–160481. [Google Scholar] [CrossRef]
- Pickover, C.A. Biomorphs: Computer displays of biological forms generated from mathematical feedback loops. Comput. Graph. Forum 1986, 5, 313–316. [Google Scholar] [CrossRef]
- Gdawiec, K.; Kotarski, W.; Lisowska, A. Biomorphs via modified iterations. J. Nonlinear Sci. Appl. 2016, 9, 2305–2315. [Google Scholar] [CrossRef]
- Sanz, R.A. Biomorphs with memory. Int. J. Parallel Emergent Distrib. Syst. 2018, 33, 1–11. [Google Scholar] [CrossRef]
- Busse, A.J.; Janowicz, M.W.; Ochnio, L.; Ashbourn, J.M.A. Pickover biomorphs and non-standard complex numbers. Chaos Solitons Fractals 2018, 113, 46–52. [Google Scholar] [CrossRef]
- Qi, H.; Tanveer, M.; Nazeer, W.; Chu, Y. Fixed Point Results for Fractal Generation of Complex Polynomials Involving Sine Function via Non-Standard Iterations. IEEE Access 2020, 8, 154301–154317. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Tanveer, M.; Azhar, M.; Nazeer, W.; Qureshi, S. A Four Step Feedback Iteration and Its Applications in Fractals. Fractal Fract. 2022, 6, 662. [Google Scholar] [CrossRef]
- Kim, T. Quaternion Julia set shape optimization. Comput. Graph. Forum 2015, 34, 167–176. [Google Scholar] [CrossRef]
- Drakopoulos, V.; Mimikou, N.; Theoharis, T. An overview of parallel visualisation methods for mandelbrot and Julia sets. Comput. Graph. 2003, 27, 635–646. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, L.; Xu, R.; Kong, R. An image encryption algorithm utilizing Julia sets and Hilbert curves. PLoS ONE 2014, 9, e84655. [Google Scholar] [CrossRef]
- Rani, M.; Agarwal, R. Effect of stochastic noise on superior Julia sets. J. Math. Imag. Vis. 2010, 36, 63. [Google Scholar] [CrossRef]
- Prasad, B.; Katiyar, K. Fractals via Ishikawa iteration. In Proceedings of the International Conference on Logic, Information, Control and Computation, Gandhigram, India, 25–27 February 2011; pp. 197–203. [Google Scholar]
- Ashish, M.R.; Chugh, R. Julia sets and mandelbrot sets in Noor orbit. Appl. Math. Comput. 2014, 228, 615–631. [Google Scholar] [CrossRef]
- Kang, S.M.; Rafiq, A.; Latif, A.; Shahid, A.A.; Kwun, Y.C. Tricorns and Multi-corns of S-iteration scheme. J. Funct. Spaces 2015, 2015, 417167. [Google Scholar]
- Chugh, R.; Kumar, V.; Kumar, S. Strong convergence of a new three step iterative scheme in Banach spaces. Amer. J. Comput. Math. 2012, 2, 345. [Google Scholar] [CrossRef]
- Tassaddiq, A. General escape criteria for the generation of fractals in extended Jungck–Noor orbit. Math. Comput. Simul. 2022, 196, 1–14. [Google Scholar] [CrossRef]
- Tanveer, M.; Ahmed, I.; Raza, A.; Nawaz, S.; Lv, Y.P. New escape conditions with general complex polynomial for fractals via new fixed point iteration. AIMS Math. 2021, 6, 5563–5580. [Google Scholar] [CrossRef]
- Li, D.; Shahid, A.A.; Tassaddiq, A.; Khan, A.; Guo, X.; Ahmad, M. CR iteration in generation of antifractals with s-convexity. IEEE Access 2020, 8, 61621–61630. [Google Scholar] [CrossRef]
- Tanveer, M.; Nazeer, W.; Gdawiec, K. New Escape Criteria for Complex Fractals Generation in Jungck-CR Orbit. Indian J. Pure Appl. Math. 2020, 51, 1285–1303. [Google Scholar] [CrossRef]
- Zou, C.; Shahid, A.; Tassaddiq, A.; Khan, A.; Ahmad, M. Mandelbrot sets and Julia sets in Picard–Mann orbit. IEEE Access 2020, 8, 64411–64421. [Google Scholar] [CrossRef]
- Goyal, K.; Prasad, B. Dynamics of iterative schemes for quadratic polynomial. Proc. AIP Conf. 2001, 9, 149–153. [Google Scholar]
- Devaney, R. A First Course in Chaotic Dynamical Systems: Theory and Experiment; Addison-Wesley: New York, NY, USA, 1992. [Google Scholar]
- Liu, X.; Zhu, Z.; Wang, G.; Zhu, W. Composed accelerated escape time algorithm to construct the general mandelbrot sets. Fractals 2001, 9, 149–153. [Google Scholar] [CrossRef]
- Noor, M.A. New approximation schemes for general variational inequalities. J. Math. Anal. Appl. 2000, 51, 217–229. [Google Scholar] [CrossRef]
- Dogan, K.; Karakaya, V. A study in the fixed point theory for a new iterative scheme and a class of generalized mappings. Creat. Math. Inform. 2018, 27, 151–160. [Google Scholar] [CrossRef]
- Strotov, V.V.; Smirnov, S.A.; Korepanov, S.E.; Cherpalkin, A.V. Object distance estimation algorithm for real-time fpga-based stereoscopic vision system. High-Perform. Comput. Geosci. Remote Sens. 2018, 10792, 71–78. [Google Scholar]
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots, in Autonomous Robot Vehicles; Springer: Berlin/Heidelberg, Germany, 1986; pp. 396–404. [Google Scholar]
- Barrallo, J.; Jones, D.M. Coloring algorithms for dynamical systems in the complex plane. In Visual Mathematics; Mathematical Institute SASA: Belgrade, Serbia, 1999; Volume 1. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).