Modeling and Initialization of Nonlinear and Chaotic Fractional Order Systems Based on the Infinite State Representation

Abstract

Based on the infinite state representation, any linear or nonlinear fractional order differential system can be modelized by a finite-dimension set of integer order differential equations. Consequently, the recurrent issue of the Caputo derivative initialization disappears since the initial conditions of the fractional order system are those of its distributed integer order differential system, as proven by the numerical simulations presented in the paper. Moreover, this technique applies directly to fractional-order chaotic systems, like the Chen system. The true interest of the fractional order approach is to multiply the number of equations to increase the complexity of the chaotic original system, which is essential for the confidentiality of coded communications. Moreover, the sensitivity to initial conditions of this augmented system generalizes the Lorenz approach. Determining the Lyapunov exponents by an experimental technique and with the G.S. spectrum algorithm provides proof of the validity of the infinite state representation approach.

1. Introduction

Nonlinear differential and distributed systems are used to model real-world physical processes. The study of nonlinear models is a fundamental topic that has stimulated intense research works reported in classical textbooks [1,2,3]. A particular class of these nonlinear systems corresponds to chaotic systems, which have received important attention since the works of Lorenz [4] and their use for coded and secured communications [5,6]. Initial conditions represent a fundamental topic in system theory [7], but they exhibit a crucial importance for chaotic systems because of their high sensitivity to infinitely small variations of their initial conditions [8], a sensitivity which had already been intuited by Poincaré [9].

The study of integer order chaotic systems is now a well-established theory, with numerous journal papers and books (e.g., [10,11,12]). Fractional calculus researchers have considered the generalization of this theory with the use of fractional derivatives: one can cite the fractional Chua system [13], the survey book on nonlinear and chaotic systems [14], and, for example, the recent research works related in [15]. Knowing that the complexity of chaotic systems is an essential feature to ensure the security of coded communications [16,17], introducing fractional order in the derivatives has been interpreted as a convenient way to increase complexity and security.

However, to our knowledge, fractional calculus researchers have not investigated the fundamental notion of sensitivity to initial conditions since this notion has not been mastered, even in the linear case. The research work presented in this paper intends to emphasize the initialization concept in the nonlinear and chaotic fractional cases, thanks to the infinite state representation, an original approach that has proved its efficiency in the linear case [18].

Fractional order systems, either linear or nonlinear, are characterized by a long memory behavior corresponding to fractional derivatives’ non-locality [19]. Unfortunately, the usual definition of fractional initial conditions is related to the Caputo derivative [20,21,22] and is interpreted as x(0), which is in contradiction with the long memory feature since x(0) is a local initial value.

Many research works on linear system initialization (e.g., the dependence on pre-histories [23], the error linked to the Caputo derivative [24], the necessity of true physical initial conditions [25], the correction of initialization with past history [26], the estimation of exact initial conditions [27], the aberration phenomenon due to the use of the Caputo derivative [28], and the non-objectivity due to the Caputo partial derivative [29]) have proven that the initial conditions related to the Caputo derivative definition are unable to predict the future behavior of fractional systems, which is the main objective of system theory.

However, two approaches have emerged to provide a satisfactory solution to this basic problem:

• The history function technique of Lorenzo and Hartley [30], which is an input/output approach that avoids the definition of state variables;
• The infinite state representation of Trigeassou and Maamri [31], which is directly related to an infinite dimension distributed state variable and permits us to take into account the long memory phenomenon.

It has been proven in the linear case that these techniques are equivalent [32]. However, although the history function technique is a good approach to analyzing fractional order problems, such as the misuse of the Caputo derivative, it does not permit the prediction of dynamical transients like the infinite state technique (see, e.g., volume 2 of [18]). Moreover, the input/output approach does not apply in the nonlinear case. On the contrary, the infinite state approach does not suffer from the same limitation, thanks to its distributed state variable. It is perfectly suited to the modeling, the initialization, and the stability of fractional order nonlinear systems, as reported in [18] (e.g., the Lyapunov stability analysis of the van der Pol oscillator, volume 2, chapter 10).

The infinite state technique relies essentially on the Riemann–Liouville integrator and, more specifically, on its infinite dimension modal model. As it has been proven previously [33], integrating fractional differential systems does not require using a specific derivative like the Caputo one. The integration of fractional systems, either linear or nonlinear, is a straightforward generalization of the integer order case [34].

The system state is, in fact, the state of the integrator, i.e., of the fractional integrator; the essential difference to the integer order case is that the system state is infinite-dimensional due to the specificity of the fractional integrator. This methodology [18,31,35] has already been applied to the modeling of fractional linear differential systems. Since a fractional integrator is associated with every fractional derivative, with no constraint on the different fractional orders, the consequence is that a nonlinear system is modeled by the association of an infinite dimension linear part (due to the fractional integrators) and of a nonlinear one (due to the nonlinear system characteristic). Practically, a fractional integrator is approximated by a finite-dimension modal model [35]. Consequently, a large dimension set of nonlinear integer-order differential systems models a nonlinear fractional-order system.

The objective of this paper is two-fold: to generalize the initialization technique developed in the linear case to fractional nonlinear systems and to define an original approach to the modeling of chaotic fractional order systems based on the infinite state representation. The first part of the paper (Section 3 and Section 4) is dedicated to the modeling of fractional nonlinear systems with the infinite state technique and its application to a simple nonlinear system, which permits the definition of the large dimension distributed state variable and, as a consequence, to demonstrate the dependence of system dynamical behaviors on the initial conditions of the equivalent nonlinear integer order system. The second part (Section 5 and Section 6) is related to the application of this technique to a fractional-order chaotic system. The direct consequence is to increase the complexity of the chaotic system since each component is equivalent to a large dimension nonlinear integer order differential system. The other consequence is the sensitivity of the fractional order chaotic system to a large dimension set of initial conditions, which the determination of the corresponding set of Lyapunov exponents will quantify.

The paper is composed of seven sections. The fractional integrator and its distributed infinite dimension modal model are introduced in Section 2. In Section 3, a general technique for the modeling of nonlinear fractional order differential systems is presented. A finite dimension approximation is proposed for modeling an elementary nonlinear system in Section 4, and its initialization based on a distributed state variable is analyzed via numerical simulation. This technique is applied to the modeling and the initialization of the Chen fractional chaotic system in Section 5. The initialization sensitivity of the Chen system is investigated, and the determination of the Lyapunov exponents is presented in Section 6. Finally, the concluding remarks in Section 7 summarize this presentation.

2. Materials and Methods: The Fractional Integrator

2.1. Riemann–Liouville Integration

The Riemann–Liouville integral $x(t)$, or fractional integral, of a function $v(t)$ is defined as [21]

$$x(t) = {}_{0}I_t^n\left(v(t)\right) = {\displaystyle \underset{0}{\overset{t}{\int }} \frac{{\left(t - \tau \right)}^{n-1}}{\Gamma (n)}} v(\tau ) d\tau n >0$$

(1)

where $\Gamma (n)$ is the gamma function.

The fractional integral is, in fact, a convolution integral, characterized by the impulse response, or Kernel, $h_n(t)$ such as

$$h_n(t) = \frac{t^{n-1}}{\Gamma (n)}$$

(2)

Using the Laplace transform, we obtain

$$\frac{1}{s^n} = L \left\{ h_n(t) \right\}$$

(3)

where $\frac{1}{s^n}$ corresponds to the fractional order integration operator.

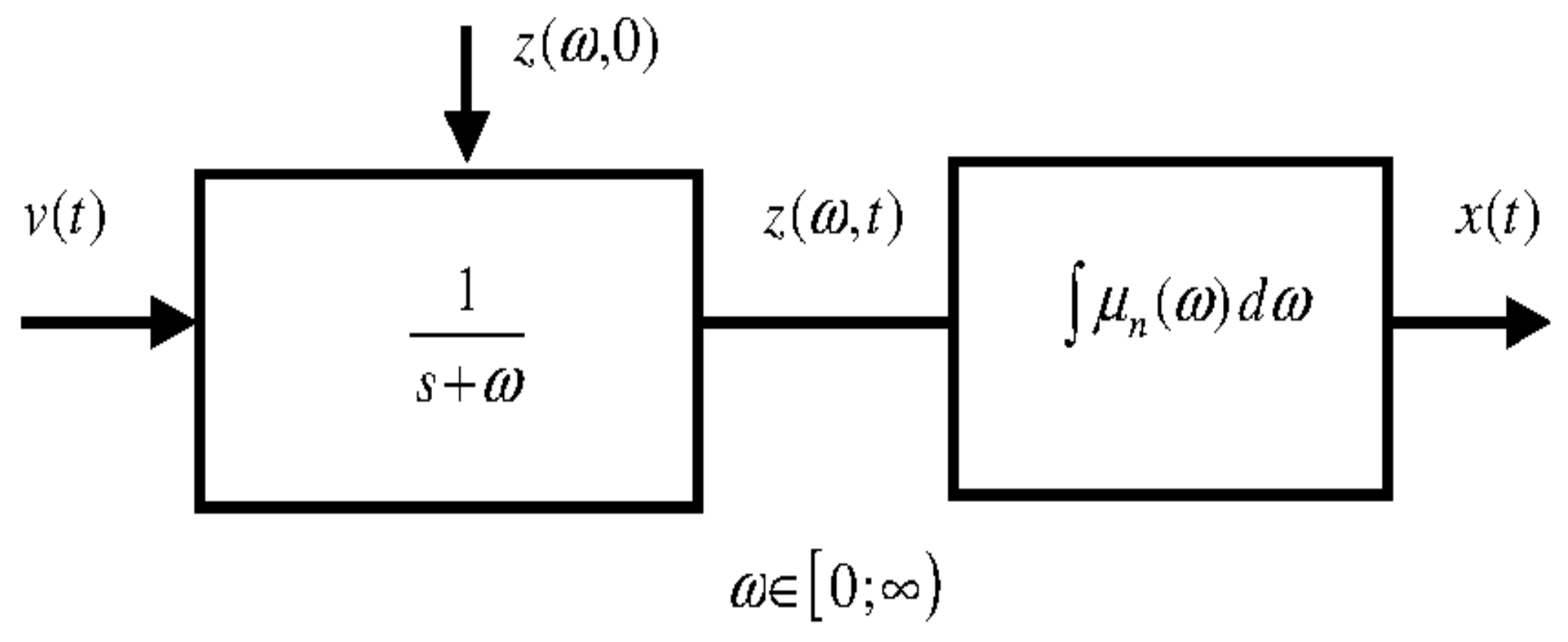
2.2. The Distributed Fractional Integrator Model

Another expression of $h_n(t)$ is derived from the inverse Laplace transform of $\frac{1}{s^n}$ [18,36,37] for $0<n<1$, which leads to

$$h_n(t) = {\displaystyle \underset{0}{\overset{\infty }{\int }} {\mu }_n}(\omega ) e^{- \omega t}d\omega$$

(4)

Ordinary Laplace transform results in

$${\mu }_n(\omega ) = \frac{\sin (n\pi )}{\pi } {\omega }^{- n}$$

(5)

where ${\mu }_n(\omega )$ is the weighting function of the modal model of $\frac{1}{s^n}$.

$$\frac{1}{s^n} = {\displaystyle \underset{0}{\overset{\infty }{\int }} {\mu }_n}(\omega ) \frac{1}{s + \omega } d\omega 0<n <1$$

(6)

Consequently, the fractional integrator output $x(t)$ for any input $v(t)$ is the solution of the frequency-distributed integer order model:

$$\{\begin{array}{c} \frac{\partial z(\omega ,t)}{\partial t} = - \omega z(\omega ,t) + v(t) \omega \in \left[0 , \infty \right)\\ x(t) = {\displaystyle \underset{0}{\overset{\infty }{\int }} {\mu }_n(\omega ) z(\omega ,t) d\omega }\\ {\mu }_n(\omega ) = \frac{\sin (n\pi )}{\pi } {\omega }^{-n}\end{array} 0<n <1$$

(7)

Figure 1 displays the graphic representation of Equation (7).

This graph shows that the fractional integrator output is the weighted sum of the frequency-distributed variables $z(\omega ,t)$, where each variable is the output of a first-order system $\frac{1}{s + \omega }$ with input $v(t)$ and the initial condition $z(\omega ,0)$.

It also exhibits that the fractional integrator is composed of an infinity of modes $\omega$, ranging from $0$ to $\infty$, whereas the integer order integrator corresponds to only one mode localized at $\omega = 0$.

The integrator output $x(t)$, which is only the weighted sum of all the distributed state variables, $z(\omega ,t)$ is called a pseudo-state variable.

2.3. Transients of the Fractional Integrator [35]

Consider the Laplace transform of (7):

$$\{\begin{array}{c}s Z(\omega ,s) - z(\omega ,0) = - \omega Z(\omega ,s) + V(s)\\ X(s)= {\displaystyle \underset{0}{\overset{\infty }{\int }} {\mu }_n(\omega ) Z(\omega ,s) d\omega }\end{array} \omega \in \left[ 0 , \infty \right)$$

(8)

where $z(\omega ,0)$ is the initial value of $z(\omega ,t)$ at $t = 0$

(8) and then (6) lead to:

$$X(s) = {\displaystyle \underset{0}{\overset{\infty }{\int }} {\mu }_n(\omega ) \frac{z(\omega ,0)}{s + \omega }} d\omega + \frac{1}{s^n} V(s)$$

(9)

So, we can write in the time domain:

$$x(t) = {\displaystyle \underset{0}{\overset{\infty }{\int }} {\mu }_n(\omega ) z(\omega ,0) e^{- \omega t} d\omega + {}_{0}I_t^n}(v(t) )$$

(10)

where

• ${\displaystyle \underset{0}{\overset{\infty }{\int }} {\mu }_n(\omega ) z(\omega ,0) e^{- \omega t} d\omega }$ is the free response of the fractional integrator initialized by the distributed initial conditions $z(\omega ,0) \forall \omega \in \left[ 0 , \infty \right)$;
• $I_t^n\left(v(t)\right)$ is the forced response of the fractional integrator caused by the input $v(t)$.

This means that the definition (1) is an input/output relation, which does not consider the initial conditions $z(\omega ,0)$ of the fractional integrator, i.e., its behavior for $t\in \left(-\infty ,0\right]$.

Since (7) is an integer order differential system, it has to verify the fundamental law of linear systems [7]:

system response = free response + forced response.

2.4. The Finite Dimension Approximation

The infinite dimension model and, more particularly, fractional order models have aroused critics [38] because they refer to infinitely slow and fast modes. Obviously, physical systems are not characterized by infinite memory or infinitely fast transients.

In fact, the interest of model (7) is essentially theoretical; it is used to derive proofs for the exact representation of fractional order models, such as initialization issues [33].

Practically, the model (7) is approximated by a finite number of modes ${\omega }_j$ inside a frequency band $\left\{ {\omega }_{\min } , {\omega }_{\max }\right\}$, which permits limiting the long memory to a realistic value and eliminating too fast transients. Moreover, an integer order integrator is added to this approximation in order to respect the integrator’s behavior at $\omega = 0$. This technique is an indirect discretization, based on the frequency response of $\frac{1}{s^n}$, inspired by Oustaloup’s synthesis method [39].

Consequently, the finite dimension approximation of model (7) is composed of $J$ cells on the interval $\left\{ {\omega }_{\min } , {\omega }_{\max }\right\}$, associated with an integer order integrator at $\omega = 0$.

So, the global approximation (11) is composed of $J + 1$ cells (or modes), which act in parallel:

$$\{\begin{array}{c}\frac{d{z}_j(t)}{dt} = - {\omega }_j z_j(t) +v(t) j = 0 to J\\ x(t) = {\displaystyle \sum _{j=0}^J c_j z_j(t)}\end{array}$$

(11)

Refer to Appendix A for practical information.

3. Modeling of a Fractional Order Nonlinear System

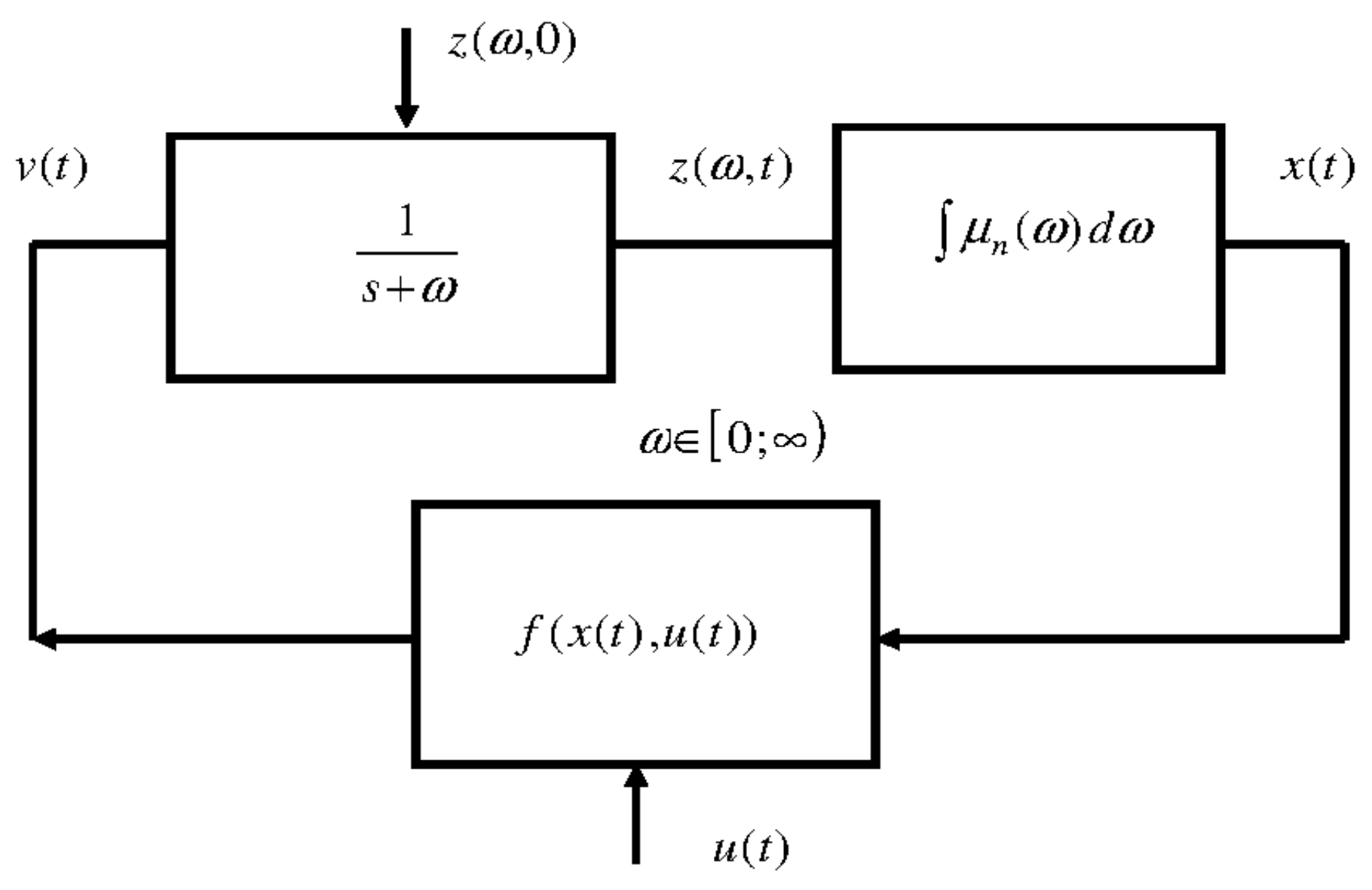
3.1. Elementary Nonlinear System

Consider the elementary fractional order system

$$D^n\left(x(t)\right) = f\left( x(t),u(t)\right) 0 <n <1$$

(12)

and the fractional integrator of order $n$ associated with $D^n\left(x(t)\right)$.

The usual approach to integrating (12) is to explicitly use the Caputo or Riemann–Liouville derivatives with their inappropriate initial conditions [21,22].

On the contrary, with the infinite state representation, the differential equation is transformed into an equivalent integral equation [33]:

$$x(t) = I_t^n\left( D^n\left(x(t)\right)\right) = I_t^n\left( f\left(x(t),u(t)\right)\right)$$

(13)

Then, using the distributed modal model of $\frac{1}{s^n}$ (Equation (7) and according to the principle of infinite state representation [18,33]), Equation (13) is equivalent to:

$$\{\begin{array}{c}\frac{\partial z(\omega ,t)}{\partial t} = - \omega z(\omega ,t) + f\left(x(t),u(t)\right) \omega \in \left[0,\infty \right)\\ x(t) = {\displaystyle \underset{0}{\overset{\infty }{\int }} {\mu }_n(\omega ) z(\omega ,t) d\omega }\\ {\mu }_n(\omega ) = \frac{\sin (n\pi )}{\pi } {\omega }^{-n}\end{array} 0<n <1$$

(14)

which is an infinite dimension integer order differential system [40] with the distributed initial condition $z(\omega ,0), \omega \in \left[0, \infty \right)$. This distributed system is represented in Figure 2. This integer order differential system can be integrated with Picard’s method [34] without reference to any fractional derivative.

Notice that the nonlinear system is a closed-loop system composed of two parts:

• A linear one, corresponding to the integer order distributed model of the fractional integrator;
• A nonlinear one corresponding to the function $f\left(x(t),u(t)\right)$.

3.2. General Case: Fractional Order Nonlinear System

Let us consider the $N$ derivatives of nonlinear FDS:

$$D^{\underset{\_}{n}}\left(\underset{\_}{x}(t)\right) = \underset{\_}{F}\left(\underset{\_}{x}(t),u(t)\right) \dim (\underset{\_}{x}(t)) = N$$

(15)

with

$$\begin{array}{l}{\underset{\_}{n}}^T = \left[ n_1 \dots n_i \dots n_N\right]\\ 0 < n_{i } \le 1 \forall i = 1 to N\\ \underset{\_}{x}{(t)}^T = \left[ x_1(t) \dots x_i(t) \dots x_N(t) \right]\\ {\underset{\_}{F}}^T\left( \underset{\_}{x}(t),u(t)\right) = \left[ f_1(\underset{\_}{x},u) \dots f_i(\underset{\_}{x},u) \dots f_N(\underset{\_}{x},u) \right]\end{array}$$

Consequently, the nonlinear system (12) is equivalent to the infinite dimension integer order differential system:

$$\{\begin{array}{c}\frac{\partial \underset{\_}{z}(\omega ,t)}{\partial t} = - \omega \underset{\_}{z}(\omega ,t) + \underset{\_}{F}\left(\underset{\_}{x}(t),u(t)\right) \omega \in \left[0,\infty \right)\\ \underset{\_}{x}(t) = {\displaystyle \underset{0}{\overset{\infty }{\int }} \left[ {\mu }_{\underset{\_}{n}}(\omega )\right] \underset{\_}{z}(\omega ,t) d\omega }\\ \left[ {\mu }_{\underset{\_}{n}}(\omega )\right] = \left[\begin{array}{ccc}{\mu }_{n_1}(\omega )& & 0\\ & {\mu }_{n_i}(\omega )& \\ 0& & {\mu }_{n_N}(\omega )\end{array}\right]\end{array} 0<n <1$$

(16)

where ${\underset{\_}{z}}^T(\omega ,t) = \left[ z_1(\omega ,t) \dots z_i(\omega ,t) \dots z_N(\omega ,t)\right]$ represents the state variables of the FDS and ${\underset{\_}{z}}^T(\omega ,0) ; \omega \in \left[ 0 , \infty \right)$ its distributed initial conditions.

Remark 1.

Notice that no particular hypothesis is required for the different fractional orders, i.e., the proposed modeling technique applies either to commensurate or non-commensurate order systems. Moreover, if $n_i = 1$, then $z_i(\omega ,t) = x_i(t)$, i.e., the i^th distributed model reduces to the integer order integrator $\frac{1}{s}$.

4. Finite Dimension Modeling and Initialization of an Elementary Nonlinear System

4.1. Finite Dimension Modeling

Consider the elementary nonlinear system (12)

$$D^n\left(x(t)\right) = f\left(x(t),u(t) \right) 0 < n < 1$$

where

$$f\left( x(t),u(t) \right) = a x^3(t) + b x(t) + u(t) a > 0 b < 0$$

(17)

Whereas many properties of a linear fractional order system can be analyzed and predicted using the infinite dimension model of the fractional integrator [18], it is necessary to use a finite dimension approximation of this model in order to obtain insight into the dynamics of the nonlinear system such as the stability analysis by Lyapunov method, e.g., thanks to the definition of a new Lyapunov function [41], its application to the control of nonlinear systems [42], the stability analysis of nonlinear systems with fractional damping [43], and the influence of initialization on the stability of a nonlinear system [44].

Using the finite dimension approximation (11), we can write

$$\{\begin{array}{c}\frac{d{z}_j(t)}{dt} = - {\omega }_j z_j(t) +a{x}^3(t) + b x(t) + u(t) j=0 \mathit{to} J\\ x(t) = {\displaystyle \sum _{j=0}^J c_j z_j(t)}\end{array}$$

(18)

This differential system is an integer order nonlinear system of dimension $J+1$, with the initial conditions $\left\{z_j(0) , j = 0 to J \right\}$. Its numerical simulation permits the investigation of its dynamical behavior and its initialization.

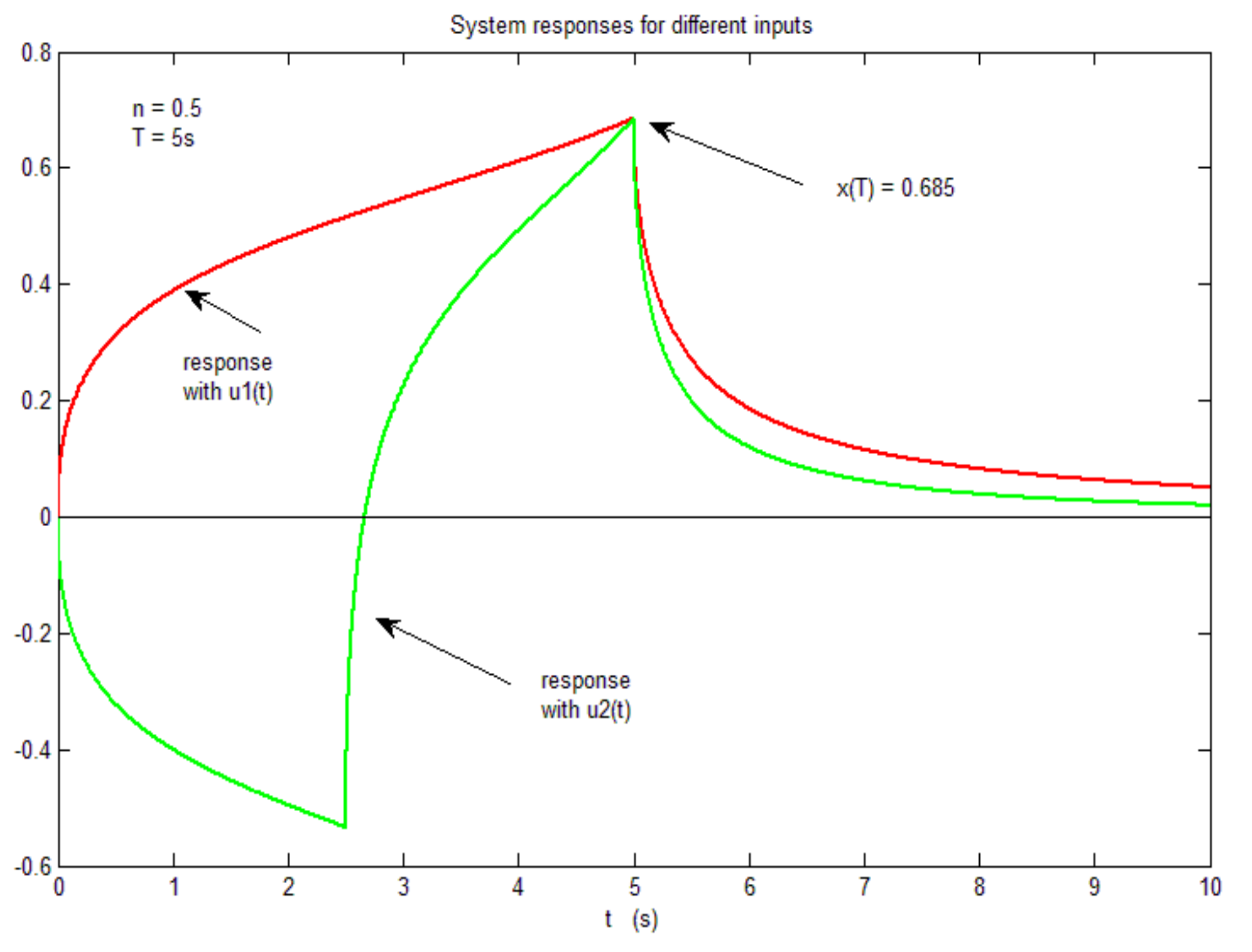
4.2. Simulation and Initialization of the Nonlinear System

System (18) is simulated with the following parameters (refer to [35] for more details on the simulation technique).

$$a = 1 , b= -1 , J = 20 , T_e = {10}^{-3} , {\omega }_{\min } = {10}^{-3} , {\omega }_{\max } = {10}^3$$

At $t = 0$, the system is at rest, i.e., $\left\{z_j(0) = 0 , j = 0 to J\right\}$.

Two different step inputs, $u_1(t)$ and $u_2(t)$, are applied and are chosen such as at $t = T = 5 s$, we obtain the same value $x(T)$. After successive trial and error simulations, we impose:

$$\begin{gathered} u_1(t) = \{\begin{array}{c} U for 0 < t < T\\ 0 for t > T\end{array} \\ {u}_2(t) = \{\begin{array}{c}{U}_1 for 0 < t < \frac{T}{2}\\ U_2 for \frac{T}{2} < t < T\\ 0 for t > T\end{array} \end{gathered}$$

(19)

with $T=5 s ,U=0.632, U_1=-0.648, U_2=0.842$.

The usual approach to the numerical simulation of linear and nonlinear fractional systems is based on the Grünwald–Letnikov (G.L.) derivative [14], in particular on the G.L. integrator, see chapter 3, volume 1 of [18]. Thus, we have compared this technique to the infinite state one. Of course, it would have been possible to use other numerical simulation techniques like those proposed in [21,22]. However, since our objective is to focus on system initialization, these techniques, which rely explicitly on the Caputo derivative and its initial conditions, are inappropriate for this comparison. On the contrary, the G.L. simulation technique provides an explicit initial condition, even if it suffers from its large dimension.

Since the corresponding graphs are very close, we have only represented the infinite state graphs in Figure 3 and evaluated the corresponding simulation errors with the absolute error criterion:

$$J_u = \frac{{\displaystyle \sum _{i=0}^K \left| x_{GL}(i) - x_{IS}(i) \right|}}{K + 1}$$

with

$$K = \frac{2 T}{T_e} = {10}^4$$

(20)

So, the values of the criterion $J_{u1} = 0.560 {10}^{-3}$ and $J_{u2} = 0.153 {10}^{-3}$ demonstrate that the two simulation techniques provide equivalent results.

In fact, the objective of the two inputs is to obtain for $t > T$ two free responses $x(t)$ starting from the same initial value $x(T)$ but with different past histories $0 < t < T$ (see Figure 3). Obviously, the initial values $\left\{z_j(0) , j = 0 to J \right\}$ are different between the two cases (see Figure 4). This simulation shows that for the same initial value, $x(T)$, the two free responses are different (see Figure 3), that is to say that $x(T)$, as in the FDS linear case [35,45], is not sufficient to predict the future of a fractional differential nonlinear system. This is a supplementary proof of the inability of Caputo’s initial conditions (i.e., $x(0)$) to characterize the initial state of a fractional system, either linear or nonlinear.

It is important to notice that the system state at $t = T$ with the G.L. technique is composed of the past values of $x(t)$, for $t \in \left[ 0 , T \right]$. The obvious drawback is that the system state becomes too large as $T$ increases. In order to overcome it, Podlubny has proposed the short memory principle [21], which is, however, the origin of a static error (see chapter 3, volume 1 of [18]).

Consequently, the finite dimension state of the infinite state (I.S.) technique provides a not-too-large internal system state without static error, thanks to the supplementary mode at $\omega = 0$.

Remark 2.

The graphs in Figure 4 represent the amplitude distribution of the modes $z_j(T)$. Notice that input $u_2(t)$generates larger amplitudes at high frequencies than input $u_1(t)$.

Remark 3.

Due to the higher frequency distribution of its internal state variables, notice that the decrease in the response initialized by input 2 is faster than the other one.

4.3. Concluding Remark

Linear and nonlinear fractional order systems are characterized by two complementary representations:

• A compact one like (12 or 15) related to the pseudo-state variables $x(t)$ (with specific mathematical tools like the Mittag–Leffler function and the G.L. simulation technique), praised by a majority of fractional researchers with an explicit reference to the Caputo derivative, which is not adapted to a true state space formalism, particularly to solve initialization problems;
• A frequency distributed one, like (14 or 16), characterized by an infinite dimension set of integer order differential equations, where the distributed state variable $z(\omega ,t)$ is adapted to conventional state space formalism, allowing the solution of initialization problems with the usual mathematical tools of system theory.

In fact, the critics related to the infinite dimension of (14 or 16) are easily avoided using a finite dimension approximation corresponding to a non-singular kernel, allowing the treatment of realistic long memory processes. Moreover, thanks to this approximation, the definition of a distributed state variable $z_j(t)$ is particularly obvious since each state variable corresponds to a mode ${\omega }_j$ in such a way that the initialization problem is nothing else than that of a conventional integer order system, contrary to the “mysterious” initialization of the compact representation.

5. Modeling and Initialization of a Fractional Chaotic System

5.1. Introduction

In his famous paper [4], Lorenz demonstrated that chaos could be generated by a set of three nonlinear equations, which was a simplification of a meteo process. This paper is analyzed in the book [12], which presents a comprehensive interpretation of the chaos phenomenon with simplified mathematics. On the contrary, many papers [10,11] have presented complex mathematical proofs for the existence of the chaotic attractor. Since our paper is intended to propose a novel approach to fractional chaos, we will use a presentation based on numerical simulations with an approach similar to [12].

Since the early 90s, researchers of fractional calculus have converted integer-order chaotic systems into fractional ones simply by replacing ordinary and fractional derivatives with appropriate fractional orders to generate chaos. The book of Petras [14] presents an interesting survey of these results. The Lorenz system can be converted into a fractional system with an order equal to 0.995; in fact, very close to 1. The Chen system, a modified version of the Lorenz system [46,47,48], seems more representative since the fractional order has to be superior to 0.824. Although we have investigated many of the chaotic systems of [14], for this first presentation, we have concentrated on the Chen system with an order equal to 0.9.

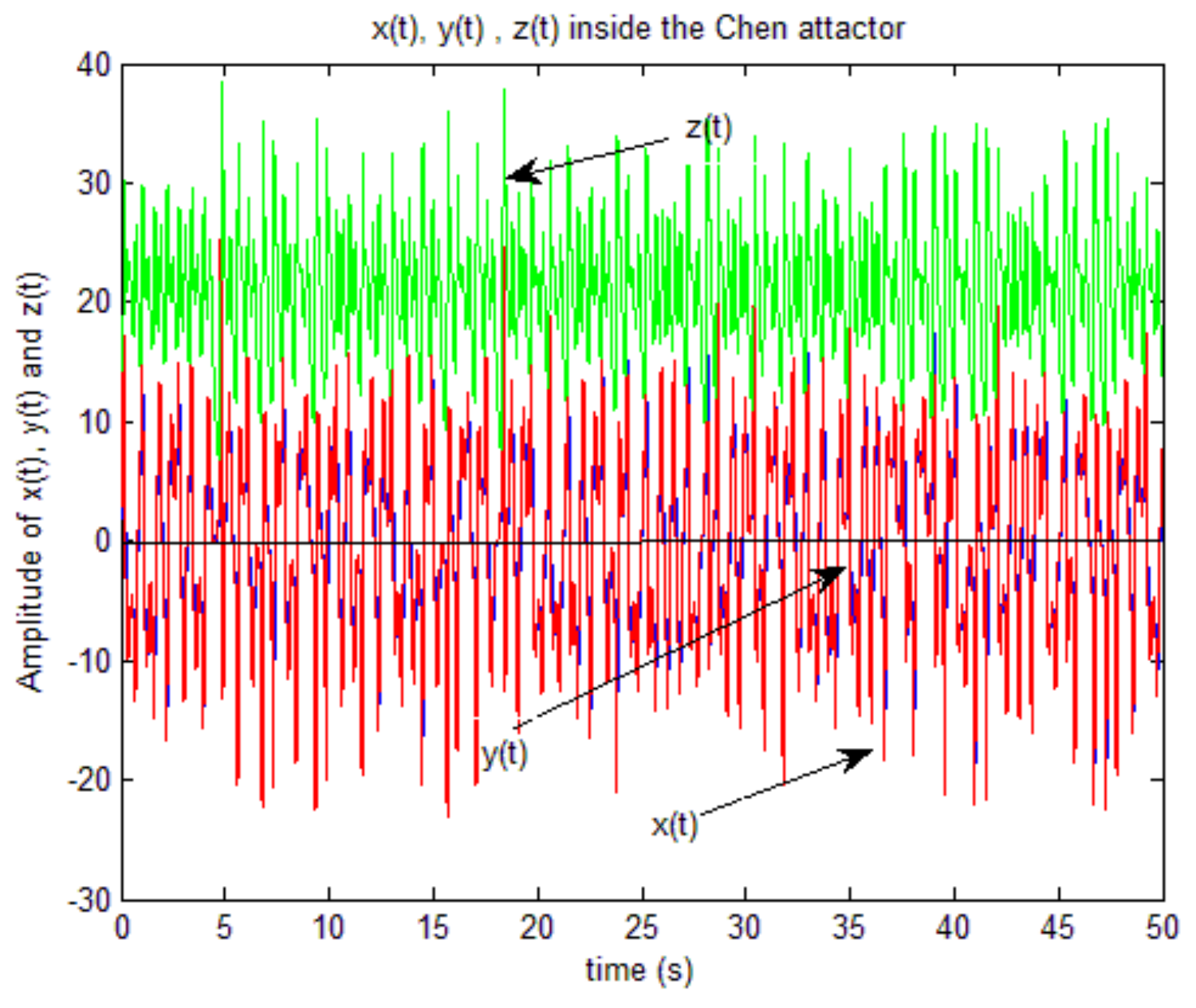
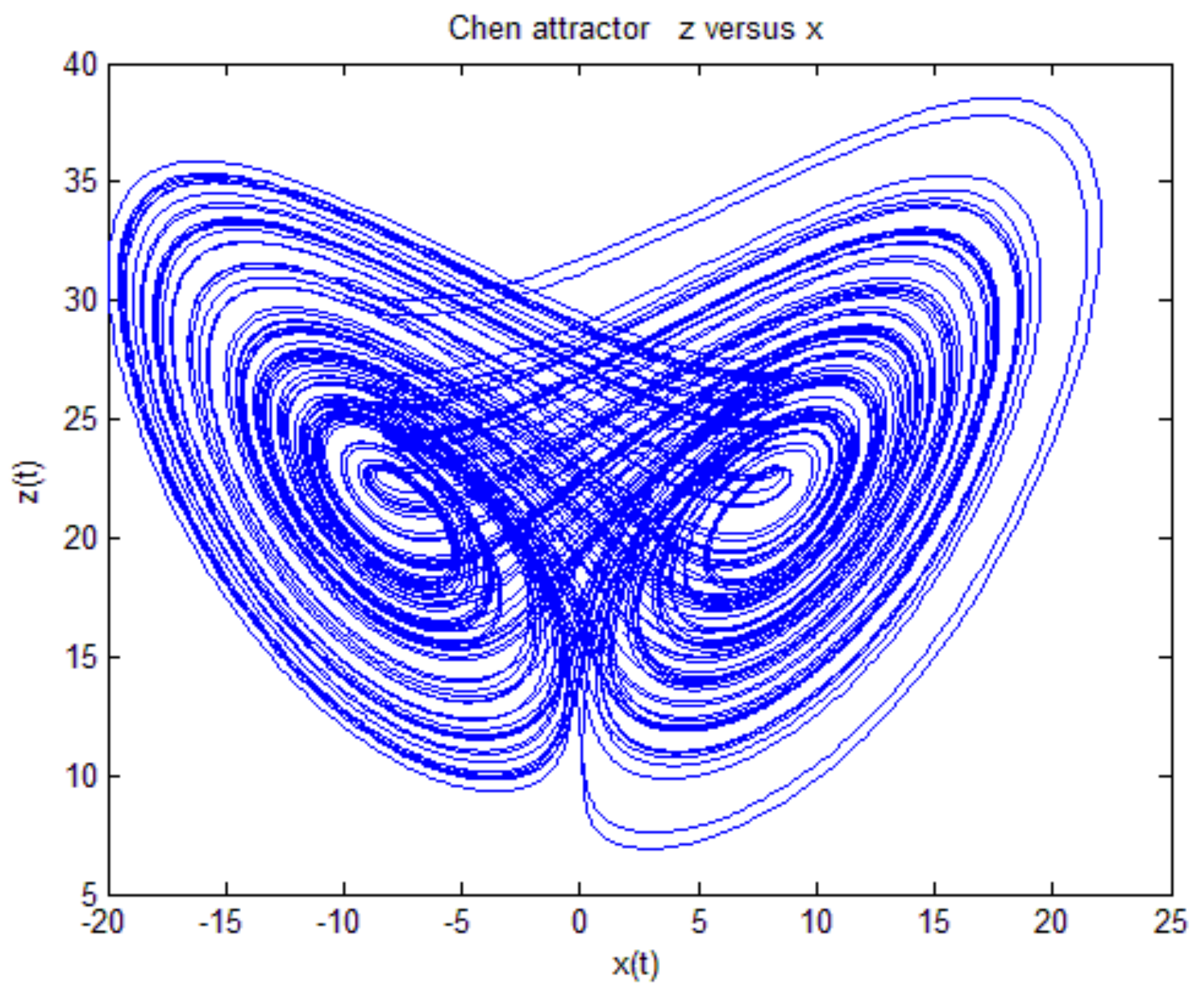
5.2. Modeling of the Chen System

Using fractional derivatives with $n = 0.9$, the integer order Chen system becomes:

$$\{\begin{array}{c}{D}^n\left(x(t)\right) = a (y - x)\\ D^n\left(y(t)\right) = (c-a) x- x z + cy\\ D^n\left(z(t)\right) = x y - b z\end{array}$$

(21)

Using the infinite state representation presented previously with the finite approximation (11), system (21) is converted into a large order integer dimension chaotic system:

$$\{\begin{array}{c}\{\begin{array}{c}\frac{d{Z}_{x,j}(t)}{dt} = -{\omega }_j z_{x,j}(t) + a (y-x) j = 0 to J\\ x(t) = {\displaystyle \sum _{j=0}^J c_j z_{x,j}(t)}\end{array}\\ \{\begin{array}{c}\frac{d{z}_{y,j}(t)}{dt} = -{\omega }_j z_{y,j}(t) + (c-a) x - x z + c y j = 0 to J\\ y(t) = {\displaystyle \sum _{j=0}^J c_j z_{y,j}(t)}\end{array}\\ \{\begin{array}{c}\frac{d{z}_{z,j}(t)}{dt} = -{\omega }_j z_{z,j}(t) + x y - b z j = 0 to J\\ z(t) = {\displaystyle \sum _{j=0}^J c_j z_{z,j}(t)}\end{array}\end{array}$$

(22)

We notice immediately the interest in fractional chaos. The fractional order introduces a new degree of complexity compared to the original integer order system. However, the infinite state representation introduces a more important degree of complexity since the fractional order is at the origin of an equivalent large dimension $3 (J + 1)$ set of integer order nonlinear equations, whose parameter $c_j$ is also dependent on the fractional order through the weighting function ${\mu }_n(\omega )$ and the finite approximation on the interval $\left\{{\omega }_{\min } ; {\omega }_{\max }\right\}$.

Moreover, it would be possible to introduce three different fractional orders $\left\{ n_1 , n_2 , n_3 \right\}$; thus, the resulting increase in complexity would be able to provide much more secure coded communications.

For a comprehensive presentation of this new approach, we have limited this presentation to a commensurate order system with the same fixed number of $J + 1$ cells for each equation.

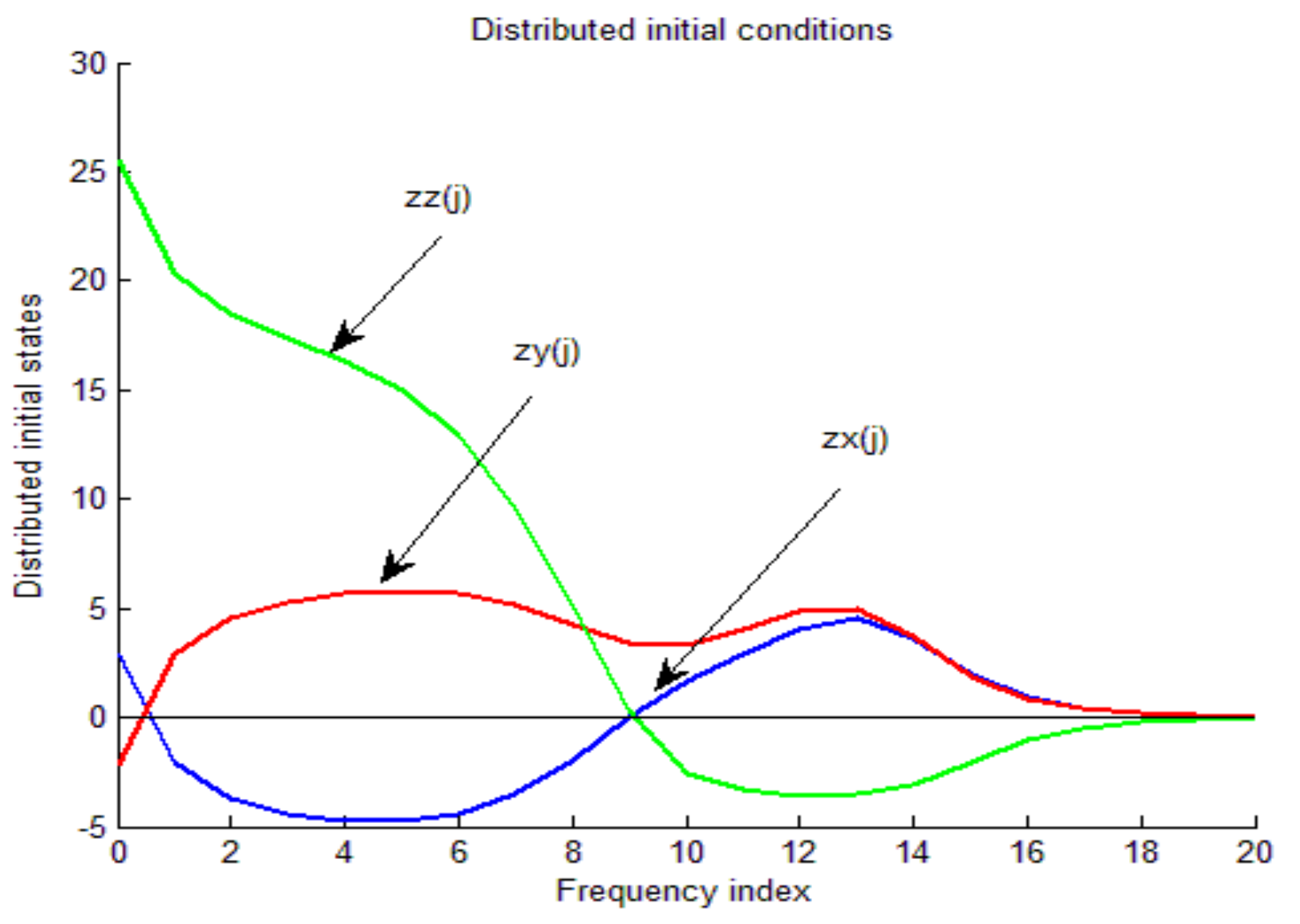
5.3. Simulation and Initialization of the Chen System

The system (22) is simulated with the following parameters:

$$\begin{array}{l}a = 35 b = 3 c = 28 n = 0.9\\ {\omega }_{\min } = {10}^{-3} {\omega }_{\max } = {10}^3 \\ J = 20 T_{e } = {10}^{-3}\end{array}$$

In the first step, it is necessary to arbitrarily initialize the $3 (J + 1)$ differential system:

$$\{\begin{array}{c}{z}_{x,j}(0) = \frac{10}{j+1}\\ z_{y,j}(0) = - \frac{10}{j+1}\\ z_{z,j}(0) = \frac{10}{j+1}\end{array} j = 0 to J$$

With these initial values, after a transient, $\left\{ x(t) y(t) z(t) \right\}$ are in the attractor. So, at $T = 5 s$, we collect the corresponding distributions $\left\{ z_{x,j}(T) z_{y,j}(T) z_{z,j}(T) \right\}$, which will be used as initial values for a second simulation. These distributions are plotted in Figure 5.

Then, we can start the second simulation, which provides the graphs of $\left\{ x(t) y(t) z(t) \right\}$ in Figure 6. The attractor is plotted in Figure 7 and Figure 8 with a final time equal to $50 s$.

6. Quantification of Initialization Sensitivity

6.1. Experimental Approach

Since most chaotic fractional research deals with the Caputo derivative and its pseudo-initial conditions $\left\{ x(0) y(0) z(0) \right\}$, sensitivity to initial conditions has not been investigated, though it represents an essential feature of chaos called the butterfly effect [8].

However, with the initial conditions depicted in Figure 5, it is straightforward to test this sensitivity to an infinitely small variation of one of the components of $\left\{ z_{x,j}(0) z_{y,j}(0) z_{z,j}(0) \right\}$. Notice that in the integer order case, we can test only one component among $3$ [12], whereas in the distributed fractional order case, we can modify only one component among $3 (J+1)$!

For example, we have modified $z_{x,j}(0)$ for $j = 0$ with ${\delta }_x = {10}^{-10}$, and we have represented the graph of ${\delta }_j(t) = z_{x,j}(t) - {\overline{z}}_{x,j}(t)$ with a logarithmic scale, where ${\overline{z}}_{x,j}(t)$ represents $z_{x,j}(t)$ with its initial condition disturbed by ${\delta }_x$.

We have reproduced the same experiment with two other values of $j$, i.e., $j = 4$ and $j = 9$.

The three graphs are represented in Figure 9.

Since each of these graphs exhibits a pseudo-linear growth between $0$ and $10 s$ (which corresponds to an exponential divergence; see Equations (24) and (25)), we have drawn a straight line in this zone whose slope is approximately equal to $2.6$.

For $t > 10 s$, ${\delta }_j(t)$ has joined the attractor, and it does not increase anymore, so there is a kind of saturation (see [12] p. 329).

We have also performed the same experiment with the pseudo-state variable

$$x(t) = {\displaystyle \sum _{j=0}^J c_j z_{x,j}(t)}$$

and we obtained an equivalent graph (Figure 10) with the same slope of the pseudo-linear zone.

This is an obvious result since $x(t)$ is a linear combination of the graphs $z_{x,j}(t)$ presenting the same exponential divergence.

Let us define

$${\delta }_j(t) = z_{x,j}(t) - {\overline{z}}_{x,j}(t)$$

(23)

The difference ${\delta }_j(t)$ is caused by the elementary disturbance ${\delta }_j(0)$ of the initial condition $z_{x,j}(0)$. According to well-known results on initial conditions sensitivity [12], the graphs $z_{x,j}(t)$ and ${\overline{z}}_{x,j}(t)$ diverge exponentially.

So, we can write

$$\Vert {\delta }_j(t) \Vert = \Vert {\delta }_j(0) \Vert e^{\lambda t}$$

(24)

where $\lambda$ is called a Lyapunov exponent.

Since

$$\lambda t = \ln \frac{\Vert {\delta }_j(t) \Vert }{\Vert {\delta }_j(0) \Vert }$$

(25)

the slope of the pseudo-linear part of the previous graphs is equal to $\lambda$.

From Figure 9 and Figure 10, we read off a Lyapunov exponent $\lambda = 2.6$ for the fractional Chen system.

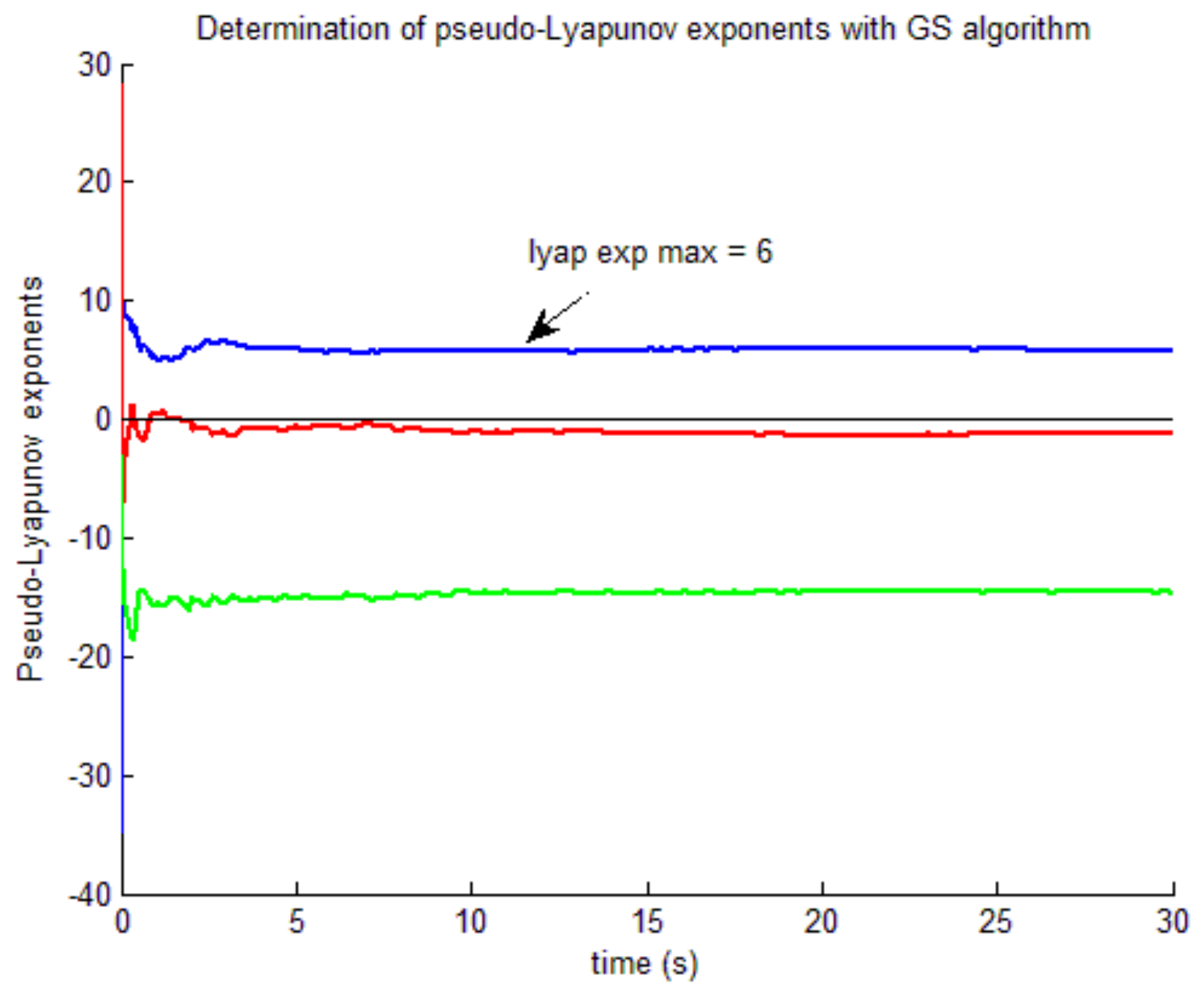
6.2. Determination of Lyapunov Exponents with the G.S. Spectrum Algorithm

Theoretically [49], the number of Lyapunov exponents equals the number of nonlinear chaotic system equations.

So, we have three Lyapunov exponents for a conventional integer-order chaotic system. However, with the infinite state representation, the Chen fractional system has been converted into a $3 (J + 1)$ dimension integer-order chaotic system, and consequently, we have to consider $3 (J + 1)$ Lyapunov exponents.

It is essential to notice that the exponential divergence of the initialization sensitivity graphs we observed previously is caused by the largest exponential exponent, i.e., by the positive Lyapunov exponent.

We have empirically determined the largest exponent. However, is it possible to determine all these Lyapunov exponents in practice?

The solution is provided by the G.S. spectrum algorithm [49] (see Appendix B).

For this, we have to formulate the Jacobian of the nonlinear system $\left[ J_{\underset{\_}{Z}} \right]$

where

$$\underset{\_}{Z} = \left[\begin{array}{c}{\underset{\_}{z}}_x\\ {\underset{\_}{z}}_y\\ {\underset{\_}{z}}_z\end{array}\right]$$

with

$$\dim \underset{\_}{Z} = 3 (J + 1)$$

and to compute the eigenvalues of $\left[I\right] + \left[ J_{\underset{\_}{Z}}(i)\right] T_e$ at each iteration.

We have applied this algorithm to the Chen system initialized via the distributed initial conditions of Figure 5, and we have only represented three Lyapunov exponents for $j=1,j=5, \mathrm{a}\mathrm{n}\mathrm{d} j=10$ (Figure 11). The 10 first Lyapunov exponents are displayed in

Table 1. The 10 first Lyapunov exponents derived from the GS spectrum algorithm.

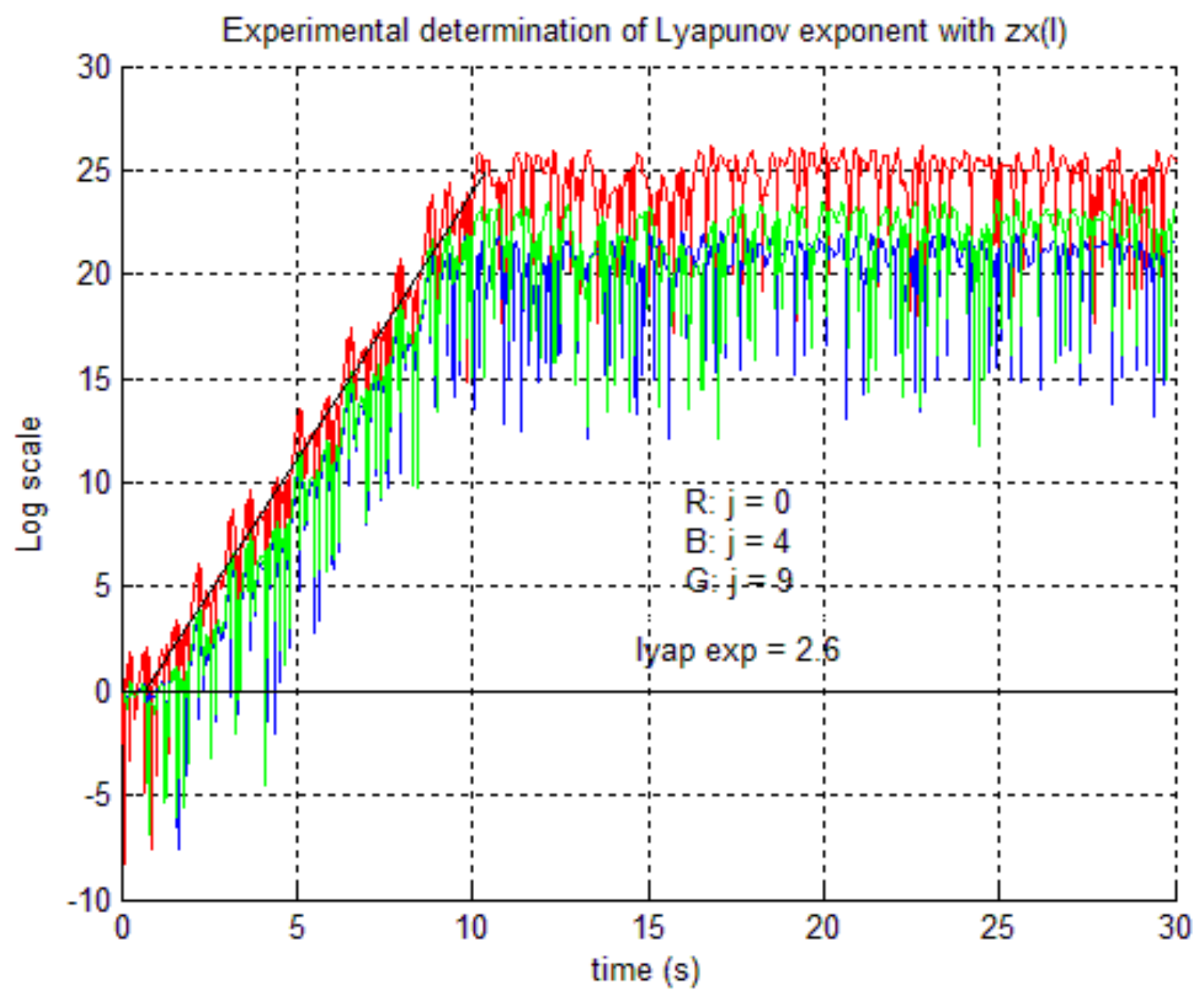
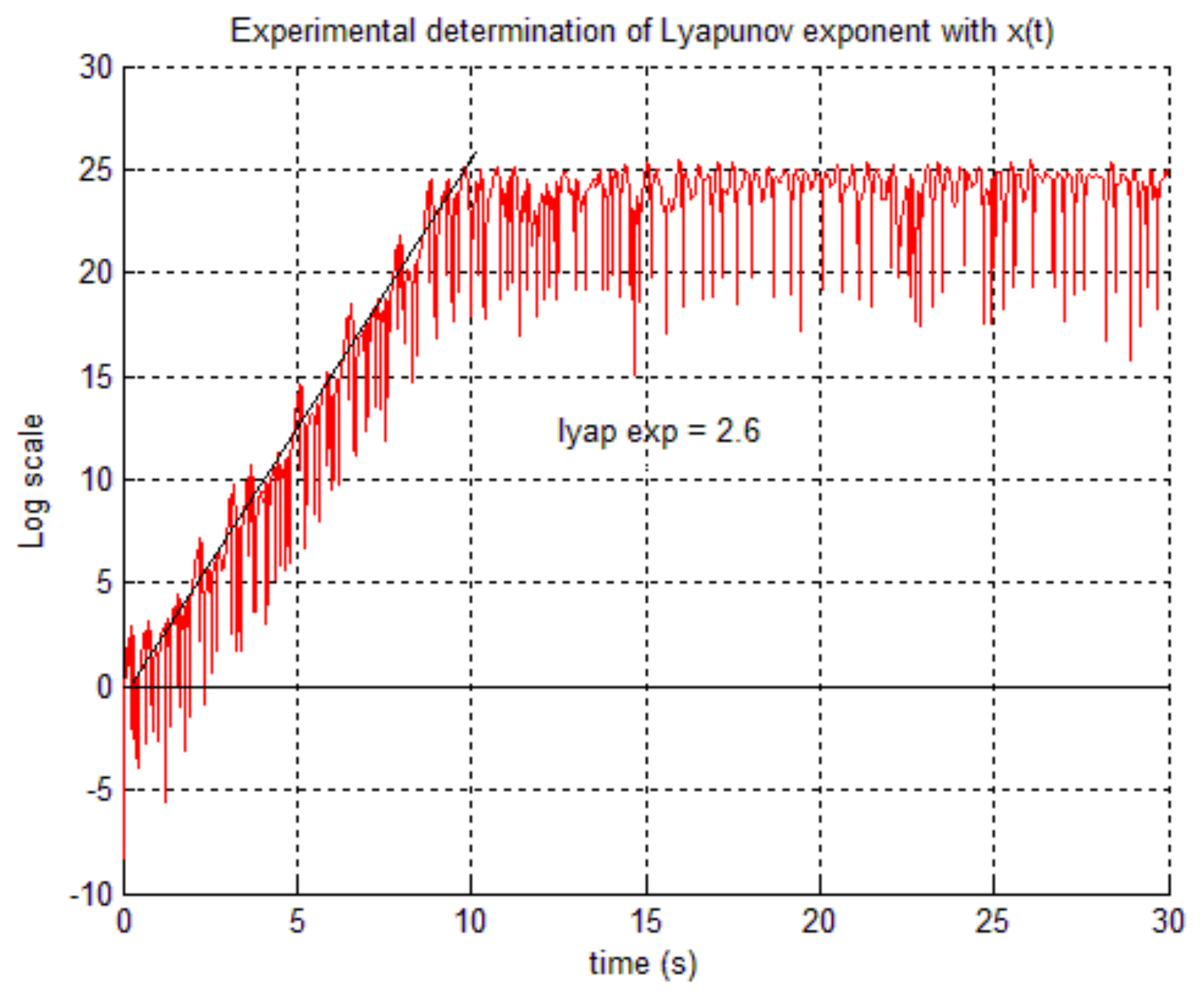
i	1	2	3	4	5	6	7	8	9	10
lyap exp	2.6831	−0.0025	−0.0038	−0.0065	−0.0119	−0.0228	−0.0443	−0.0873	−0.1726	−0.3421

.

As we observe on this graph, there is only one positive Lyapunov exponent, which is equal to $\lambda \approx 2.7$ corresponding to the determination of the previous empirical value.

In fact, it would be possible to apply this algorithm to the pseudo-state values with $\dim \underset{\_}{\lambda } = 3$.

If we proceed using $\left\{ x(t), y(t), z(t) \right\}$, we obtain the pseudo-Lyapunov exponents represented in Figure 12.

We obtain ${\lambda }_{\max } = 6$, which obviously does not correspond to the Lyapunov exponent of the pseudo-state variable $x(t)$ calculated previously.

6.3. Concluding Remark

Initialization is a fundamental topic of system theory, particularly chaos theory, where the sensitivity to initial conditions is an essential feature known as the butterfly effect. The initialization of fractional order systems has remained unsolved for many years due to the lack of appropriate initial conditions. Fortunately, the infinite state representation, which transforms the original fractional system into an equivalent large-dimension set of ordinary differential equations, provides an efficient solution to the previous problem, as demonstrated in Section 4.

The application of this methodology to fractional-order chaotic systems is a promising approach, as demonstrated in Section 5 and Section 6. More particularly, the sensitivity to initial conditions has been interpreted and generalized thanks to the usual tools of system theory. Fractional Lyapunov exponents have been derived using the G.S. spectrum algorithm so they can characterize this sensitivity, which we call the fractional butterfly effect.

7. Conclusions

Thanks to the infinite state representation, the fractional-order chaotic Chen system has been transformed into a finite dimension set of integer-order differential equations that can be analyzed via the usual mathematical tools of system theory. This introductory example will deserve more rigorous mathematical developments, like theoretical proofs related to the existence of the attractor of the transformed system and the generalization of this approach to other chaotic fractional order systems. However, an obvious and promising domain of investigation will concern the synchronization of distributed chaotic systems induced via the infinite state representation and their application to more secure communications thanks to the increase in system complexity.