An Efficient Approach to Solving the Fractional SIR Epidemic Model with the Atangana–Baleanu–Caputo Fractional Operator

Abstract

In this article, we study the fractional SIR epidemic model with the Atangana–Baleanu–Caputo fractional operator. We explore the properties and applicability of the ZZ transformation on the Atangana–Baleanu–Caputo fractional operator as the ZZ transform of the Atangana–Baleanu–Caputo fractional derivative. This study is an application of two power methods. We obtain a special solution with the homotopy perturbation method (HPM) combined with the ZZ transformation scheme; then we present the problem and study the existence of the solution, and also we apply this new method to solving the fractional SIR epidemic with the ABC operator. The solutions show up as infinite series. The behavior of the numerical solutions of this model, represented by series of the evolution in the time fractional epidemic, is compared with the Adomian decomposition method and the Laplace–Adomian decomposition method. The results showed an increase in the number of immunized persons compared to the results obtained via those two methods.

1. Introduction

Fractional calculus plays a fundamental role in modeling many problems in fluid mechanics, acoustics and electromagnetism, as well as studying some phenomena of dynamic systems [1,2,3,4,5]. Fractal calculus is very effective, for example, in dealing with phenomena in hierarchical or porous media [6]. In the study just cited, J-H He touched on the basic concept of the fractal gradient of temperature to reveal the basic properties of calculus and then the fractal velocity and the derivative of the fractal material were introduced to derive the laws of fluid mechanics and thermal conductivity in fractal space. Many studies use different fractional operators to describe certain phenomena in physics, engineering and biology [7,8,9]. For example, in [10], He et al. present the definition of a new fractional derivative by demonstrating its application in explaining the excellent thermal protection of polar bear hair so that the fractal porosity of its internal structure makes the polar bear mathematically adapted to live in the harsh Arctic region. Recently, many classifications of fractional operators have been proposed, for example, Caputo, Riemann–Liouville, Caputo–Fabrizio, Atangana–Baleanu–Caputo fractional operators, to accurately and successfully study and describe complex phenomena in science and engineering [11,12].

In the recent past, definitions of fractional derivatives based on nonsingular kernels, like the Atangana–Baleanu fractional derivative, were also provided. Additionally, some models of dissipative events cannot be fully characterized by a single fractional operator, which highlights the significance of fractional derivatives with nonsingular kernels. Material heterogeneities and some structures or media with varying scales can be depicted using the Atangana–Baleanu operator. The new kernel’s nonlocality enables a better representation of memory within structures and media with various scales. Additionally, we may state that this derivative can play a particular role in the investigation of some materials’ macroscopic behavior in relation to nonlocal exchanges, which are crucial for characterizing a material’s properties. Therefore, the Atangana–Baleanu–Caputo fractional derivative is the most general fractional operator based on the Mittag–Leffler function, which is more suitable for describing real-world complex problems [13].

In [14], the authors take the advantages of the Atangana–Baleanu partial integral operator and the Bessel functions, some differential dependency results were extracted and the work was developed for the case of the analytical functions specified on the open unit disk. The applications of the Atangana–Baleanu fractional integral were considered in recent studies related to geometric function theory to obtain interesting differential subordinations, etc.; see [15,16,17,18].

These complex problems have been studied in the literature, and are divided into linear and nonlinear, as they have aroused the interest of many researchers who study their behavior in terms of solvability, uniqueness and the stability of their solutions, especially nonlinearity [19,20,21]. Due to the complexities of nonlinear phenomena in searching for their solutions by modeling them into ordinary or fractional differential equations, they do not always contain accurate analytical solutions. Because of this difficulty, researchers have focused their attention on developing several numerical methods to find an approximate solution. There are many techniques employed to search for the numerical solution of the linear or nonlinear fractional differential equations, integral equations and the linear or nonlinear systems of fractional differential equations. Since the integral transformations, such as the Laplace transform, Sumudu transform, and so on, could not solve the nonlinear types, we therefore note that many mathematicians have studied the methods of solving nonlinear differential equations or nonlinear fractional differential systems. Among these methods, we cite a more effective method called the homotopy perturbation method (HPM) [22,23] and a modified Laplace transform to solve some nonlinear differential equations such as the case of the ZZ transform. This integral transform generalizes a few well-known transformations that are connected to other well-known transformations. To obtain the natural transformation, divide the ZZ transformation by the adjusted variable. The ZZ transform can be used to address problems without switching to a new frequency domain and to provide new, iterative results since it has the ability to preserve the scale and the unity, and the ZZ transform is useful for solving fractional differential equations with variable coefficients [24,25,26].

Thus, we find that some researchers are working on a combination of analytical or semi-analytical methods with certain integral transformations [27,28,29,30]. The HPM method involves dividing the solution domain into sub-domains and transforming the FPDEs into a set of algebraic equations. These equations are then solved by using other numerical methods. The solution is then transformed back to the original domain and the solution is obtained by combining the solutions from each sub-domain.

The homotopy perturbation method has been coupled with the ZZ transform (HPZZTM) to facilitate the process of solving ordinary differential equations and partial derivatives of integer order or fractional order [31]. This combination has also been applied to solve systems of nonlinear partial differential equations of fractional order. This method combines the advantages of both the HPM and the ZZ Transform methods [23].

The aim of this work is to investigate the properties of the ZZ transformation on the Atangana–Baleanu–Caputo fractional derivative; consequently, we combined it with the homotopy perturbation method and applied this new technique to the linear and nonlinear general fractional differential non-homogeneous equations, especially to the following fractional SIR epidemic model with the Atangana–Baleanu–Caputo fractional operator:

$$\left\{\begin{array}{c}{}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mathcal{S}(⊺)=-\beta \mathcal{S}(⊺)\mathcal{I}(⊺),\mathcal{S}\left(0\right)=N_1\hfill \\ {}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mathcal{I}(⊺)=\beta \mathcal{S}(⊺)\mathcal{I}(⊺)-\gamma \mathcal{I}(⊺),\mathcal{I}\left(0\right)=N_2\hfill \\ {}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\Re (⊺)=\gamma \mathcal{I}(⊺),\Re \left(0\right)=N_3\hfill \end{array}\right.$$

(1)

Many studies have been tried to resolve the SIR epidemic model of integer order; in [32], by using the homotopy analysis method; in [33], an exact solution was suggested via the homotopy perturbation method; and the differential transform method in [34]. Recently, A. Qazza and R. Saadeh presented the solution of the fractional SIR epidemic model with a Caputo fractional derivative by using the Laplace residual-power-series method in [35].

This epidemic mathematical model is known as the Susceptible-Infected-Recovered model (SIR) ([36,37]). Concerning the SIR model, it is assumed that in the presence of Infectious Disease A, a fixed population size can be divided into three groups, that is, ($\mathcal{S}$), (I) and (R), respectively. Specifically, the compartments used in the McKendrick–Kermack design are defined as follows [38]:

(a) Compartment ($\mathcal{S}$) (susceptible) includes persons of the total population not yet infected by the disease at time ⊺, or those who are susceptible to the disease. The number of persons in that compartment corresponds to $\mathcal{S}(⊺)$.

(b) Compartment ($\mathcal{I}$) (infected) is composed of persons who have been infected by the epidemic disease and who may transmit the disease to those in the sensitive category. The number of persons in that compartment corresponds to $\mathcal{I}(⊺)$.

(c) Compartment (ℜ) (recovered) is composed of individuals who have been infected during outbreaks and have fully recovered. The number of persons in that compartment corresponds to $\Re (⊺)$. They cannot be infected again and they are unable to pass the disease on to others.

The paper is organized as follows: In Section 2, we present some basic tools in the form of definitions, properties of the fractional calculus and ZZ transform. In Section 3, we introduce the main results of the homotopy perturbation method coupled with the ZZ transform to the general nonlinear fractional differential equations. In Section 4, we apply this method to the fractional SIR epidemic model with the Atangana–Baleanu–Caputo fractional operator. In Section 5, we show the numerical results and discussion. Finally, we conclude our research in the final section.

2. Basic Definitions

Definition 1.

Let $\mu \in H^1(0,I)$, $I>0$, $0\le \sigma <1$; then, the Atangana–Baleanu fractional derivative in the Caputo sense [13,39] is given as:

$${}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mu (⊺)=\frac{\Phi \left(\sigma \right)}{1-\sigma }{\int }_0^{⊺}{\mu }^{\prime }\left(s\right)E_{\sigma }\left[\frac{\sigma }{\sigma -1}{(⊺-s)}^{\sigma }\right]ds.$$

(2)

where the kernel $E_{\sigma }$ is the Mittag–Leffler function of one parameter and $\Phi \left(\sigma \right)$ is a normalization function such that $\Phi \left(0\right)=\Phi \left(1\right)=1$ [40].

Definition 2.

The fractional integral of order σ of a new fractional derivative is defined by:

$${}_0^{\mathcal{AB}}{I}_{⊺}^0\mu (⊺)=\frac{1-\sigma }{\Phi \left(\sigma \right)}\mu (⊺)+\frac{\sigma }{\Phi \left(\sigma \right)\Gamma \left(\sigma \right)}{\int }_0^{⊺}\mu \left(y\right){(⊺-y)}^{\sigma -1}dy.$$

(3)

Here $\Gamma (.)$ is the Euler Gamma function.

2.1. Definitions and Properties of the ZZ Transform

We give some basic definitions and properties of the ZZ transform (see [24,25]).

Throughout, set

$$\mathcal{A}=\{\mu (⊺):\exists M>0,\lambda >0,\mid \mu (⊺)\mid \le M{e}^{\lambda ⊺},if⊺\ge 0\},$$

and suppose that $\mu (⊺)$ is an integrable function defined on the set $\mathcal{A}$.

Definition 3.

Let $\mu (⊺)$ be a function defined for all $⊺\ge 0$. The ZZ transform of $\mu (⊺)$ is the function $F(\vartheta ,\xi )$ defined by

$$\mathcal{Z}\left[\mu (⊺)\right]=F(\vartheta ,\xi )=\xi {\int }_0^{\infty }\mu (\vartheta ⊺)e^{-\xi ⊺}d⊺.$$

(4)

The integral transform (4) exists for all $\frac{\xi }{\vartheta }>\lambda$.

2.1.1. Some Properties of the ZZ Transform

Theorem 1.

The ZZ transform of the $n^{th}$ derivative of $\mu (⊺)$ is given by

$$\mathcal{Z}\left[{\mu }^{\left(n\right)}(⊺)\right](\xi ,\vartheta )={\left(\frac{\xi }{\vartheta }\right)}^n\mathcal{Z}\left[\mu (⊺)\right]-\sum _{k=0}^{n-1}{\left(\frac{\xi }{\vartheta }\right)}^{n-k}{\mu }^{\left(k\right)}\left(0\right),\frac{\xi }{\vartheta }>0,\forall n\in \mathbb{N}.$$

(5)

Theorem 2.

The ZZ transform of convolution of functions $\mu (⊺)$ and $\phi (⊺)$

$$\mathcal{Z}[\mu \ast \phi ]=\mathcal{Z}\left[\mu \right].\mathcal{Z}\left[\phi \right].$$

(6)

Moreover,

$${\mathcal{Z}}^{-1}[\mu .\phi ]={\mathcal{Z}}^{-1}\left[\mu \right]\ast {\mathcal{Z}}^{-1}\left[\phi \right].$$

(7)

Proof. 

We have

$$\mu \ast \phi ={\int }_0^{\infty }\mu \left(x\right)\phi (⊺-x)dx.$$

Using the ZZ transform and the Leibniz theorem, we obtain

$$\mathcal{Z}[\mu \ast \phi ]=\mathcal{Z}\left[{\int }_0^{\infty }\mu \left(x\right)\phi (⊺-x)dx\right]=\xi {\int }_0^{\infty }\left[{\int }_0^{\infty }\mu \left(x\right)\phi (⊺-x)dx\right]e^{-\xi ⊺}dx,$$

By setting $y=⊺-x$, we obtain

$$\begin{array}{cc}\hfill \mathcal{Z}[\mu \ast \phi ]& {\displaystyle =\xi {\int }_0^{\infty }\mu \left(x\right)e^{-\xi x}\left[{\int }_0^{\infty }\phi \left(y\right)e^{-\xi y}dy\right]dx}\hfill \\ & {\displaystyle =\xi {\int }_0^{\infty }\mu \left(x\right)e^{-\xi x}dx.\mathcal{Z}\left[\phi \right]}\hfill \\ & =\mathcal{Z}\left[\mu \right].\mathcal{Z}\left[\phi \right].\hfill \end{array}$$

Furthermore, the convolution of the inverse transform is

$$\mathcal{Z}[{\mathcal{Z}}^{-1}\left(\mu \right)\ast {\mathcal{Z}}^{-1}\left(\phi \right)]=\mu .\phi .$$

Hence,

$${\mathcal{Z}}^{-1}[\mu .\phi ]={\mathcal{Z}}^{-1}\left(\mu \right)\ast {\mathcal{Z}}^{-1}\left(\phi \right).$$

□

2.1.2. ZZ Transform of Several Elementary Functions

In this following table, we will give the transformation of some elementary functions by the ZZ Transform.

$\mu (⊺)$	$\mathcal{Z}\left[\mu (⊺)\right]$
ine 1	1
ine ⊺	$\frac{\vartheta }{\xi }$
ine ${⊺}^n$	$n!\frac{{\vartheta }^n}{{\xi }^n}$,$n=0,1,2,\dots$
ine ${⊺}^{\sigma }$	$\Gamma (\sigma +1)\frac{{\vartheta }^{\sigma }}{{\xi }^{\sigma }},$$\sigma ⩾0.$

Lemma 1.

Let $0<n<1$ and $\lambda \in \mathbb{R}$ such that $\frac{\xi }{\vartheta }<{\left|\lambda \right|}^{\frac{1}{n}}$; then,

$$\mathcal{Z}\left[{⊺}^{\sigma -1}{E}_{n,\sigma }^{\gamma }(\lambda .{⊺}^n)(\xi ,\vartheta )\right]={\left(\frac{\vartheta }{\xi }\right)}^{\alpha }.{(1-\lambda {\left(\frac{\vartheta }{\xi }\right)}^n)}^{-\gamma },\frac{\xi }{\vartheta }>0.$$

(8)

Proof. 

We have

$$\mathcal{Z}\left[{⊺}^{\sigma -1}{E}_{n,\sigma }^{\gamma }(\lambda .{⊺}^n)(\xi ,\vartheta )\right]=\frac{\xi }{\vartheta }{\int }_0^{\infty }{⊺}^{\sigma -1}{E}_{n,\sigma }^{\gamma }(\lambda .{⊺}^n)e^{-\frac{\xi }{\vartheta }}d⊺$$

$$=\frac{\xi }{\vartheta }{\int }_0^{\infty }{⊺}^{\sigma -1}\sum _{k=0}^{\infty }\frac{\gamma k}{\Gamma (nk+\sigma )}.\frac{{\left(\lambda {⊺}^n\right)}^k}{k!}{e}^{-\frac{\xi }{\vartheta }}d⊺$$

$$=\sum _{k=0}^{\infty }\frac{\gamma k}{\Gamma (nk+\sigma )}.\frac{{\lambda }^k}{k!}\frac{\xi }{\vartheta }{\int }_0^{\infty }{⊺}^{nk+\sigma -1}{e}^{-\frac{\xi }{\vartheta }}d⊺$$

$$=\sum _{k=0}^{\infty }\frac{\gamma k}{\Gamma (nk+\sigma )}.\frac{{\lambda }^k}{k!}\frac{\xi }{\vartheta }\mathcal{Z}\left[{⊺}^{nk+\sigma -1}\right]$$

$$=\sum _{k=0}^{\infty }\frac{\gamma k}{\Gamma (nk+\sigma )}.\frac{{\lambda }^k}{k!}\frac{\xi }{\vartheta }\Gamma (nk+\sigma ){\left(\frac{\vartheta }{\xi }\right)}^{nk+\gamma }$$

$$={\left(\frac{\vartheta }{\xi }\right)}^{\sigma }.\sum _{k=0}^{\infty }\frac{\gamma k}{k!}{\left[\lambda {\left(\frac{\vartheta }{\xi }\right)}^n\right]}^k.$$

Since $\frac{\xi }{\vartheta }<{\left|\lambda \right|}^{\frac{1}{n}}$, the result is that

$$\mathcal{Z}\left[{⊺}^{\sigma -1}{E}_{n,\sigma }^{\gamma }(\lambda .{⊺}^n)(\xi ,\vartheta )\right]={\left(\frac{\vartheta }{\xi }\right)}^{\sigma }.{(1-\lambda {\left(\frac{\vartheta }{\xi }\right)}^n)}^{-\gamma }.$$

□

Corollary 1.

In the same way as in the last Lemma 1, we obtained the ZZ transform of the function $E_n\left(\lambda {⊺}^n\right)$ as:

$${\displaystyle \mathcal{Z}\left[E_n\left(\lambda {⊺}^n\right)\right](\xi ,\vartheta )=\left(\frac{\vartheta }{\xi }\right)(\frac{{\left(\frac{\xi }{\vartheta }\right)}^n}{{\left(\frac{\xi }{\vartheta }\right)}^n-\lambda }),}$$

(9)

and the ZZ transform of the function ${⊺}^{\sigma -1}{E}_n\left(\lambda {⊺}^n\right)$ as:

$${\displaystyle \mathcal{Z}\left[{⊺}^{\sigma -1}{E}_n\left(\lambda {⊺}^n\right)\right](\xi ,\vartheta )=\frac{{\left(\frac{\xi }{\vartheta }\right)}^{n-\sigma }}{{\left(\frac{\xi }{\vartheta }\right)}^n-\lambda }.}$$

(10)

Theorem 3.

The ZZ transform of the Atangana–Baleanu–Caputo fractional derivative ${}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }$ is defined as:

$$\mathcal{Z}{[}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mu (⊺)](\vartheta ,\xi )=\frac{\Phi \left(\sigma \right)}{1-\sigma }\frac{\mathcal{Z}\left[\mu (⊺)\right]{\left(\frac{\xi }{\vartheta }\right)}^{\sigma }-{\left(\frac{\xi }{\vartheta }\right)}^{\sigma -1}\mu \left(0\right)}{{\left(\frac{\xi }{\vartheta }\right)}^{\sigma }+\frac{\sigma }{1-\sigma }}.$$

(11)

Proof. 

We have

$${\int }_0^{⊺}{\mu }^{\prime }\left(x\right)E_{\sigma }\left[\frac{\sigma }{\sigma -1}{(⊺-x)}^{\sigma }\right]dx={\mu }^{\prime }(⊺)\ast E_{\sigma }\left[\frac{\sigma }{\sigma -1}{⊺}^{\sigma }\right],$$

(12)

then one has

$$\mathcal{Z}{[}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mu (⊺)](\vartheta ,\xi )=\mathcal{Z}\left[\frac{\Phi \left(\sigma \right)}{1-\sigma }{\int }_0^{⊺}{\mu }^{\prime }\left(x\right)E_{\sigma }\left(\frac{\sigma }{\sigma -1}{(⊺-x)}^{\sigma }\right)dx\right]$$

(13)

$$=\frac{\Phi \left(\sigma \right)}{1-\sigma }\mathcal{Z}\left[{\mu }^{\prime }(⊺)\ast E_{\sigma }\left(\frac{\sigma }{\sigma -1}{⊺}^{\sigma }\right)\right]$$

$$=\frac{\Phi \left(\sigma \right)}{1-\sigma }\mathcal{Z}\left[{\mu }^{\prime }(⊺)\right].\mathcal{Z}\left[E_{\sigma }\left(\frac{\sigma }{\sigma -1}{⊺}^{\sigma }\right)\right].$$

By using (5) and applying the result found in Corollary 1, we have

$$\begin{array}{cc}\mathcal{Z}{[}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mu (⊺)](\vartheta ,\xi )\hfill & =\frac{\Phi \left(\sigma \right)}{1-\sigma }[\frac{\xi }{\vartheta }\mathcal{Z}\left[\mu (⊺)\right]-\mu \left(0\right)]\frac{\vartheta }{\xi }\frac{{\left(\frac{\xi }{\vartheta }\right)}^{\sigma }}{{\left(\frac{\xi }{\vartheta }\right)}^{\sigma }-\frac{\sigma }{\sigma -1}}\hfill \\ \hfill & =\frac{\Phi \left(\sigma \right)}{1-\sigma }\frac{\mathcal{Z}\left[\mu (⊺)\right]{\left(\frac{\xi }{\vartheta }\right)}^{\sigma }-{\left(\frac{\xi }{\vartheta }\right)}^{\sigma -1}\mu \left(0\right)}{{\left(\frac{\xi }{\vartheta }\right)}^{\sigma }+\frac{\sigma }{1-\sigma }}.\hfill \end{array}$$

(14)

□

3. Implementation of HPZZTM to the General Nonlinear Fractional Differential Equations

We present the basic idea of the homotopy perturbation ZZ transform method, so we consider the following general nonlinear fractional partial differential non-homogeneous equation

$${}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mu (x,⊺)+R\mu (x,⊺)+N\mu (x,⊺)=g(x,⊺),$$

(15)

with the initial terms

$$\mu (x,0)=h\left(x\right)and{\mu }_{⊺}(x,0)=f\left(x\right),$$

(16)

where R is the differential linear operator, N is the nonlinear operator and $g(x,⊺)$ is the source terms.

When we apply the ZZ transformation on either side of (15), we obtain

$$\mathcal{Z}{[}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mu (x,⊺)]+\mathcal{Z}\left[R\mu (x,⊺)\right]+\mathcal{Z}\left[N\mu (x,⊺)\right]=\mathcal{Z}\left[g(x,⊺)\right].$$

(17)

Using this transformation’s differentiating characteristic, we have

$${\displaystyle \mathcal{Z}\left[\mu (x,⊺)\right]=h\left(x\right)+\frac{\vartheta }{s}f\left(x\right)-\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}[g(x,⊺)-R\mu (x,⊺)-N\mu (x,⊺)].}$$

(18)

Consider the reverse ZZ transformation on each side of (18) and then according to (16), we obtain

$$\mu (x,⊺)=G(x,⊺)-{\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}[R\mu (x,⊺)+N\mu (x,⊺)]}\right],$$

(19)

where the terms $G(x,⊺)$ are the non-homogeneous terms and the previously established conditions. Now, we apply the perturbation technique ([22,41]). We express the solution with this technique as a power series in $\rho$, as shown below

$$\mu (x,⊺)=\sum _{n=0}^{\infty }{\rho }^n{\mu }_n(x,⊺).$$

(20)

We break down the nonlinear term into

$$N\mu (x,⊺)=\sum _{n=0}^{\infty }{\rho }^n{H}_n\left(\mu \right),$$

(21)

where $H_n$ are the polynomials of He [23], which are calculated with the following formulas

$$H_n({\mu }_0,...,{\mu }_n)=\frac{1}{n!}\frac{{\partial }^n}{\partial {\rho }^n}{\left[N\left(\sum _{i=0}^{\infty }{\rho }^i{\mu }_i\right)\right]}_{\rho =0},n=0,1,2,3,\cdots$$

(22)

By substituting (20) and (21) into Equation (19), we obtain

$$\sum _{n=0}^{\infty }{\rho }^n{\mu }_n=G(x,⊺)-\left({\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}\left[R\sum _{n=0}^{\infty }{\rho }^n{\mu }_n+\sum _{n=0}^{\infty }{\rho }^n{H}_n\left(\mu \right)\right]}\right]\right),$$

(23)

This is a coupling of the homotopy perturbation method and the ZZ transform (HPZZTM).

Now, by matching both sides of Equation (23) with respect to the power of $\rho$, we obtain the following first terms of the solution

$$\begin{array}{c}{\rho }^0:{\mu }_0(x,⊺)=G(x,⊺),\hfill \\ {\rho }^1:{\mu }_1(x,⊺)=-{\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}\left[R{\mu }_0(x,⊺)+H_0\left(\mu \right)\right]}\right],\hfill \\ {\rho }^2:{\mu }_2(x,⊺)=-{\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}\left[R{\mu }_1(x,⊺)+H_1\left(\mu \right)\right]}\right],\hfill \\ {\rho }^3:{\mu }_3(x,⊺)=-{\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}\left[R{\mu }_2(x,⊺)+H_2\left(\mu \right)\right]}\right],\hfill \\ ⋮\hfill \end{array}$$

(24)

Finally, the approximate solution is calculated by

$$\mu (x,⊺)={\mu }_0(x,⊺)+{\mu }_1(x,⊺)+{\mu }_2(x,⊺)+{\mu }_3(x,⊺)+\cdots$$

In [42,43], it has been established that this series converges.

4. Study the Epidemic Model with Atangana–Baleanu–Caputo Fractional Derivative

4.1. Presentation of the Problem

The problem of the spread of a disease in a supposed population of constant size during the period of the epidemic is examined in [44].

At time ⊺, suppose the population consists of $\mathcal{S}(⊺)$ susceptible population: the population not infected to date and subject to the infection.

$\mathcal{I}(⊺)$ represent the infected population: those who have the disease and are still at large.

$\Re (⊺)$ represents the recovered population: those who have recovered and have therefore become immune.

Suppose there is a constant rate between $\mathcal{S}(⊺)$ and $\Re (⊺)$ which causes the transmission. Then, over time $\delta ⊺$, $\delta \mathcal{S}$ become infectious, or

$$\delta \mathcal{S}=-\beta \mathcal{S}\mathcal{I}\delta ⊺,\beta >0.$$

If $\gamma >0$ is the isolation rate of the current infected population, then

$$\delta \mathcal{S}=\beta \mathcal{S}\mathcal{I}\delta ⊺-\gamma \mathcal{I}\delta ⊺.$$

The number of new isolated population $\delta \Re$ is given by

$$\delta \Re =\gamma \mathcal{I}\delta ⊺.$$

Now $\delta ⊺\to 0$, then the following system determines the progress of the disease:

$$\left\{\begin{array}{c}{}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mathcal{S}(⊺)=-\beta \mathcal{S}(⊺)\mathcal{I}(⊺),\mathcal{S}\left(0\right)=N_1\hfill \\ {}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mathcal{I}(⊺)=\beta \mathcal{S}(⊺)\mathcal{I}(⊺)-\gamma \mathcal{I}(⊺),\mathcal{I}\left(0\right)=N_2\hfill \\ {}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\Re (⊺)=\gamma \mathcal{I}(⊺),\Re \left(0\right)=N_3\hfill \end{array}\right..$$

(25)

4.2. The Existence of the Solution

We define these operators:

$$\left\{\begin{array}{c}{f}_1(⊺,\Omega (⊺))=-\beta \mathcal{S}(⊺)\mathcal{I}(⊺)\hfill \\ f_2(⊺,\Omega (⊺))=\beta \mathcal{S}(⊺)\mathcal{I}(⊺)-\gamma \mathcal{I}(⊺)\hfill \\ f_3(⊺,\Omega (⊺))=\gamma \mathcal{I}(⊺)\hfill \end{array}\right.,$$

(26)

and the matrix form of the system (25) is

$${}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\Omega (⊺)=F(⊺,\Omega (⊺)),\Omega \left(0\right)={\Omega }_0,$$

(27)

where $\Omega (⊺)=(\mathcal{S}(⊺),\mathcal{I}(⊺),\mathcal{R}(⊺)),{\Omega }_0(\mathcal{S}\left(0\right),\mathcal{I}\left(0\right),\mathcal{R}\left(0\right))$ and $F(⊺,\Omega (⊺))=(f_1(⊺,\Omega (⊺)),$ $f_2(⊺,\Omega (⊺)), f_3(⊺,\Omega (⊺))).$

Lemma 2.

The function F is Lipschitz continuous on $[0,T]\times B({\Omega }_0,q)$, with

$$[0,T]\times B({\Omega }_0,q)=\{(⊺,\Omega (⊺))\in [0,T]\times {\mathbb{R}}_{+}^3,\underset{⊺\in [0,T]}{sup}\parallel \Omega (⊺)-{\Omega }_0{\parallel }_1\le q\},$$

so there exists a constant $L\in {\mathbb{R}}_{+},\forall (⊺,{\Omega }_1(⊺)),(⊺,{\Omega }_2(⊺))\in [0,T]\times B({\Omega }_0,q)$ and

$$\parallel F(⊺,{\Omega }_1(⊺))-F(⊺,{\Omega }_2(⊺)){\parallel }_1\le L{\parallel {\Omega }_1(⊺)-{\Omega }_2(⊺)\parallel }_1,$$

(28)

with ${\parallel \Omega (⊺)\parallel }_1={\sum }_{i=1}^3\left|{\Omega }_i(⊺)\right|$ being the Manhattan norm.

Proof. 

We shall prove that the function F satisfies the Lipschitz condition in the second argument $\Omega$.

$$\begin{array}{cc}\parallel F(⊺,{\Omega }_1(⊺))-F(⊺,{\Omega }_2(⊺)){\parallel }_1\hfill & =|f_1(⊺,{\Omega }_1(⊺))-f_1(⊺,{\Omega }_2(⊺))|+|f_2(⊺,{\Omega }_1(⊺))-f_2(⊺,{\Omega }_2(⊺))|\hfill \\ \hfill & +|f_3(⊺,{\Omega }_1(⊺))-f_3(⊺,{\Omega }_2(⊺))|\hfill \\ \hfill & =|-\beta {\mathcal{S}}_1(⊺){\mathcal{I}}_1(⊺)+\beta {\mathcal{S}}_2(⊺){\mathcal{I}}_2(⊺)|+|\beta {\mathcal{S}}_1(⊺){\mathcal{I}}_1(⊺)-\gamma {\mathcal{I}}_1(⊺)\hfill \\ \hfill & -\beta {\mathcal{S}}_2(⊺){\mathcal{I}}_2(⊺)+\gamma {\mathcal{I}}_2(⊺)|+|\gamma {\mathcal{I}}_1(⊺)-\gamma {\mathcal{I}}_2(⊺)|,\hfill \end{array}$$

(29)

and we have

$$\begin{array}{cc}|-\beta {\mathcal{S}}_1(⊺){\mathcal{I}}_1(⊺)+\beta {\mathcal{S}}_2(⊺){\mathcal{I}}_2(⊺)|\hfill & =\beta |{\mathcal{S}}_1(⊺){\mathcal{I}}_1(⊺)-{\mathcal{S}}_1(⊺){\mathcal{I}}_2(⊺)+{\mathcal{S}}_1(⊺){\mathcal{I}}_2(⊺)-{\mathcal{S}}_2(⊺){\mathcal{I}}_2(⊺)|\hfill \\ \hfill & \le \beta |{\mathcal{S}}_1(⊺)\left|\right|{\mathcal{I}}_1(⊺)-{\mathcal{I}}_2(⊺)|+\beta |{\mathcal{I}}_2(⊺)\left|\right|{\mathcal{S}}_1(⊺)-{\mathcal{S}}_2(⊺)|.\hfill \end{array}$$

(30)

In the same way, we can prove that

$$\begin{array}{cc}|\beta {\mathcal{S}}_1(⊺){\mathcal{I}}_1(⊺)-\gamma {\mathcal{I}}_1(⊺)-\beta {\mathcal{S}}_2(⊺){\mathcal{I}}_2(⊺)+\gamma {\mathcal{I}}_2(⊺)\left|\right|\hfill & \le \beta |{\mathcal{S}}_1(⊺)\left|\right|{\mathcal{I}}_1(⊺)-{\mathcal{I}}_2(⊺)|+\beta |{\mathcal{I}}_2(⊺)\left|\right|{\mathcal{S}}_1(⊺)-{\mathcal{S}}_2(⊺)|\hfill \\ \hfill & +\gamma |{\mathcal{I}}_1(⊺)-{\mathcal{I}}_2(⊺)|.\hfill \end{array}$$

(31)

Then

$$\begin{array}{cc}\parallel F(⊺,{\Omega }_1(⊺))-F(⊺,{\Omega }_2(⊺)){\parallel }_1\hfill & \le 2\beta |{\mathcal{I}}_2(⊺)\left|\right|{\mathcal{S}}_1(⊺)-{\mathcal{S}}_2(⊺)|+2\beta |{\mathcal{S}}_1(⊺)\left|\right|{\mathcal{I}}_1(⊺)-{\mathcal{I}}_2(⊺)|\hfill \\ \hfill & +2\gamma |{\mathcal{I}}_1(⊺)-{\mathcal{I}}_2(⊺)|\hfill \\ \hfill & \le \left(2\beta (q+\mathcal{I}\left(0\right))\right|{\mathcal{S}}_1(⊺)-{\mathcal{S}}_2(⊺)|+(2\beta (q+\mathcal{S}\left(0\right))+2\gamma )|{\mathcal{I}}_1(⊺)-{\mathcal{I}}_2(⊺)|\hfill \\ \hfill & \le L\parallel {\Omega }_1(⊺)-{\Omega }_2{(⊺)\parallel }_1,\hfill \end{array}$$

(32)

where

$$L=max\left\{\right(2\beta (q+\mathcal{I}(0\left)\right),\left(2\beta \right(q+\mathcal{S}\left(0\right))+2\gamma )\}.$$

□

4.3. The Solution by Applying This Approach

First, we apply the ZZ transform to two sides of (25) with the use of its property

$$\left\{\begin{array}{c}\mathcal{Z}{[}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mathcal{S}(⊺)]=-\beta \mathcal{Z}\left[\mathcal{S}(⊺)\mathcal{I}(⊺)\right]\hfill \\ \mathcal{Z}{[}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\mathcal{I}(⊺)]=\beta \mathcal{Z}\left[\mathcal{S}(⊺)\mathcal{I}(⊺)\right]-\gamma \mathcal{Z}\left[\mathcal{I}(⊺)\right]\hfill \\ \mathcal{Z}{[}_0^{\mathcal{ABC}}{D}_{⊺}^{\sigma }\Re (⊺)]=\gamma \mathcal{Z}\left[\mathcal{I}(⊺)\right]\hfill \end{array}\right..$$

(33)

$$\left\{\begin{array}{c}{\displaystyle \mathcal{Z}\left[\mathcal{S}(⊺)\right]=\mathcal{S}\left(0\right)-\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\beta \mathcal{Z}\left[\mathcal{S}(⊺)\mathcal{I}(⊺)\right]}\hfill \\ {\displaystyle \mathcal{Z}\left[\mathcal{I}(⊺)\right]=\mathcal{I}\left(0\right)-\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)(\beta \mathcal{Z}\left[\mathcal{S}(⊺)\mathcal{I}(⊺)\right]-\gamma \mathcal{Z}\left[\mathcal{I}(⊺)\right])}\hfill \\ {\displaystyle \mathcal{Z}[\Re (⊺)]=\Re \left(0\right)-\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\gamma \mathcal{Z}\left[\mathcal{I}(⊺)\right]}\hfill \end{array}\right..$$

(34)

In the second, we take the inverse ZZ transform for both sides of (33) and using the initial conditions, we have

$$\left\{\begin{array}{c}\mathcal{S}(⊺)=N_1-\beta {\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\alpha }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}\left[\mathcal{S}(⊺)\mathcal{I}(⊺)\right]}\right]\hfill \\ \mathcal{I}(⊺)=N_2+{\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\alpha }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\beta \mathcal{Z}\left[\mathcal{S}(⊺)\mathcal{I}(⊺)\right]-\gamma \mathcal{Z}\left[\mathcal{I}(⊺)\right]}\right]\hfill \\ \Re (⊺)=N_3+\gamma {\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}\left[\mathcal{I}(⊺)\right]}\right]\hfill \end{array}\right..$$

(35)

Now, we represent the solutions as the following infinite series

$$\mathcal{S}(⊺)=\sum _{n=0}^{\infty }{\rho }^n{\mathcal{S}}_n(⊺),\mathcal{I}(⊺)=\sum _{n=0}^{\infty }{\rho }^n{\mathcal{I}}_n(⊺)\Re (⊺)=\sum _{n=0}^{\infty }{\rho }^n{\Re }_n(⊺),$$

(36)

and the nonlinear terms as

$$\sum _{n=0}^{\infty }{\rho }^n{H}_n=\mathcal{S}.\mathcal{I}$$

(37)

By substituting (36) and (37) with (35), we obtain

$$\left\{\begin{array}{c}\sum _{n=0}^{\infty }{\rho }^n{\mathcal{S}}_n(⊺)=N_1-\rho \beta {\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}\left[\sum _{n=0}^{\infty }{\rho }^n{H}_n\right]}\right]\hfill \\ \sum _{n=0}^{\infty }{\rho }^n{\mathcal{I}}_n(⊺)=N_2+\rho \beta {\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}\left[\sum _{n=0}^{\infty }{\rho }^n{H}_n\right]}\right]\hfill \\ -\rho \gamma {\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}\left[\sum _{n=0}^{\infty }{\rho }^n{\mathcal{I}}_n(⊺)\right]}\right]\hfill \\ \sum _{n=0}^{\infty }{\rho }^n{\Re }_n(⊺)=N_3+\rho \gamma {\mathcal{Z}}^{-1}\left[{\displaystyle \left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}{\left(\frac{\vartheta }{\xi }\right)}^{\sigma }\right)\mathcal{Z}\left[\sum _{n=0}^{\infty }{\rho }^n{\mathcal{I}}_n(⊺)\right]}\right]\hfill \end{array}\right..$$

(38)

The first elements of He’s polynomials are provided by

$$\begin{array}{c}{H}_0=N_1{N}_2,\hfill \\ {\displaystyle H_1=[(\beta N_1{N}_2-\gamma N_2)N_1-\beta N_1{N}_2^2]\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}\frac{{⊺}^{\sigma }}{\Gamma (\sigma +1)}\right),}\hfill \\ {\displaystyle H_2=\left[N_1{N}_2({\beta }^2{N}_1^2-3{\beta }^2{N}_1{N}_2-2\beta \gamma N_1+3\beta \gamma N_2)\right]\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}\frac{{⊺}^{2\sigma }}{\Gamma (2\sigma +1)}\right),}\hfill \\ ⋮\hfill \end{array}$$

(39)

Using (39) and comparing the two sides of (38), we obtain

$$\begin{array}{c}{\mathcal{S}}_0(⊺)=N_1,\hfill \\ {\displaystyle {\mathcal{S}}_1(⊺)=-\beta N_1{N}_2\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}\frac{{⊺}^{\sigma }}{\Gamma (\sigma +1)}\right),}\hfill \\ {\displaystyle {\mathcal{S}}_2(⊺)=-\beta N_1{N}_2(\beta N_1-\gamma -\beta N_2)\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}\frac{{⊺}^{2\sigma }}{\Gamma (2\sigma +1)}\right),}\hfill \\ {\displaystyle {\mathcal{S}}_3(⊺)=-\beta N_1{N}_2({\beta }^2{N}_1^2+{\beta }^2{N}_2^2-2\beta \gamma N_1-4{\beta }^2{N}_1{N}_2+3\beta \gamma N_2+{\gamma }^2)\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}\frac{{⊺}^{3\sigma }}{\Gamma (3\sigma +1)}\right),}\hfill \\ ⋮\hfill \end{array}$$

(40)

And

$$\begin{array}{c}{\mathcal{I}}_0(⊺)=N_2,\hfill \\ {\displaystyle {\mathcal{I}}_1(⊺)=(\beta N_1{N}_2-\gamma N_2)\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}\frac{{⊺}^{\sigma }}{\Gamma (\sigma +1)}\right),}\hfill \\ {\displaystyle {\mathcal{I}}_2(⊺)=N_2({\beta }^2{N}_1^2-2\beta \gamma N_1-{\beta }^2{N}_1{N}_2+{\gamma }^2)\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}\frac{{⊺}^{2\sigma }}{\Gamma (2\sigma +1)}\right),}\hfill \\ {\mathcal{I}}_3(⊺)=N_2({\beta }^3{N}_1^3+{\beta }^3{N}_1{N}_2^2-3{\beta }^2\gamma N_1^2-4{\beta }^3{N}_1^2{N}_2^2+4{\beta }^2\gamma N_1{N}_2\hfill \\ {\displaystyle +3\beta {\gamma }^2{N}_1-{\gamma }^3)\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}\frac{{⊺}^{3\sigma }}{\Gamma (3\sigma +1)}\right),}\hfill \\ ⋮\hfill \end{array}$$

(41)

Also

$$\begin{array}{c}{\Re }_0(⊺)=N_3,\hfill \\ {\displaystyle {\Re }_1(⊺)=\gamma N_2\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}\frac{{⊺}^{\sigma }}{\Gamma (\sigma +1)}\right),}\hfill \\ {\displaystyle {\Re }_2(⊺)=\gamma (\beta N_1{N}_2-\gamma N_2)\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}\frac{{⊺}^{2\sigma }}{\Gamma (2\sigma +1)}\right),}\hfill \\ {\displaystyle {\Re }_3(⊺)=\gamma N_2({\beta }^2{N}_1^2-2\beta \gamma N_1-{\beta }^2{N}_1{N}_2+{\gamma }^2)\left(\frac{1-\sigma }{\Phi \left(\sigma \right)}+\frac{\sigma }{\Phi \left(\sigma \right)}\frac{{⊺}^{3\sigma }}{\Gamma (3\sigma +1)}\right).}\hfill \\ ⋮\hfill \end{array}$$

(42)

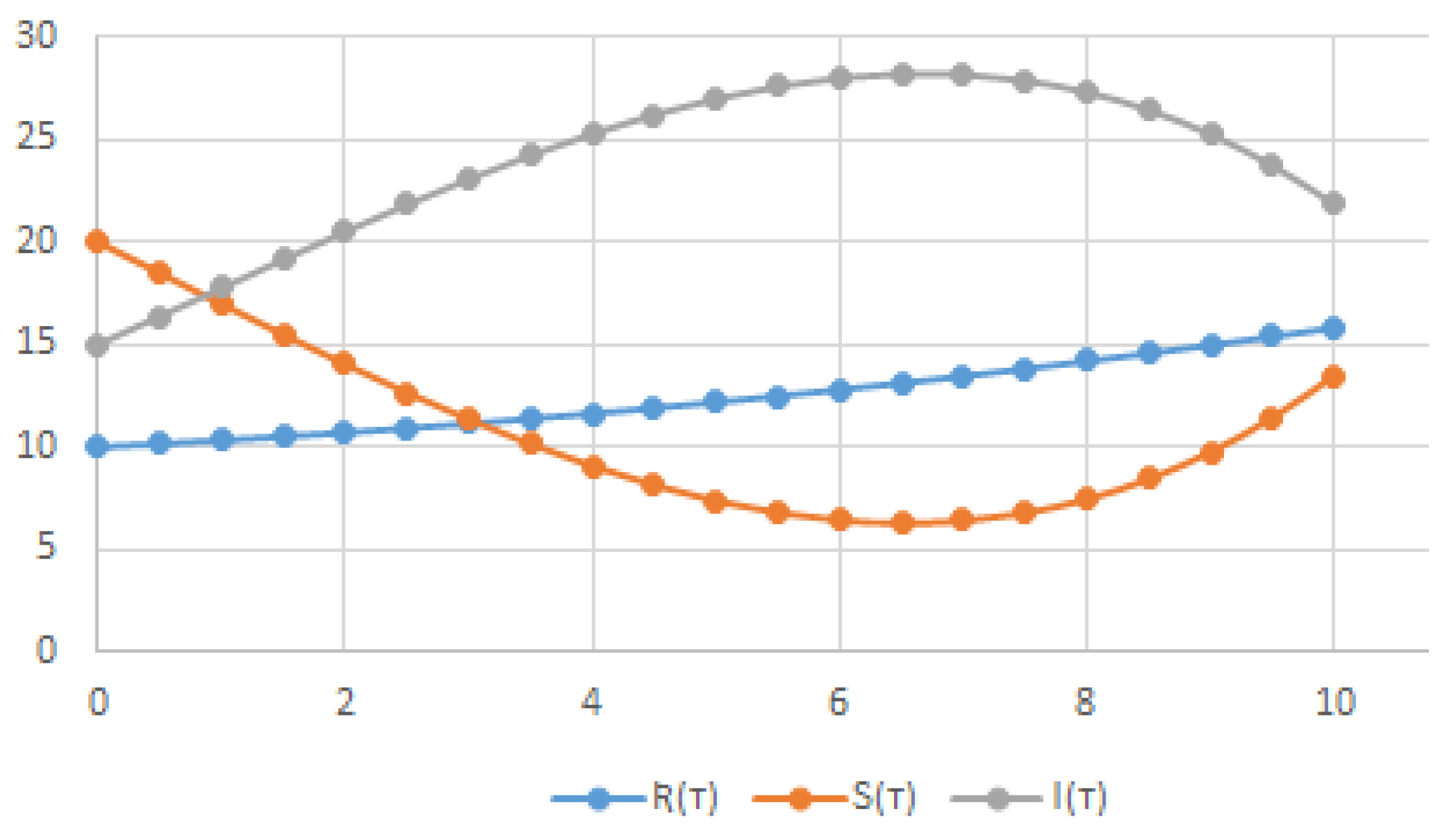
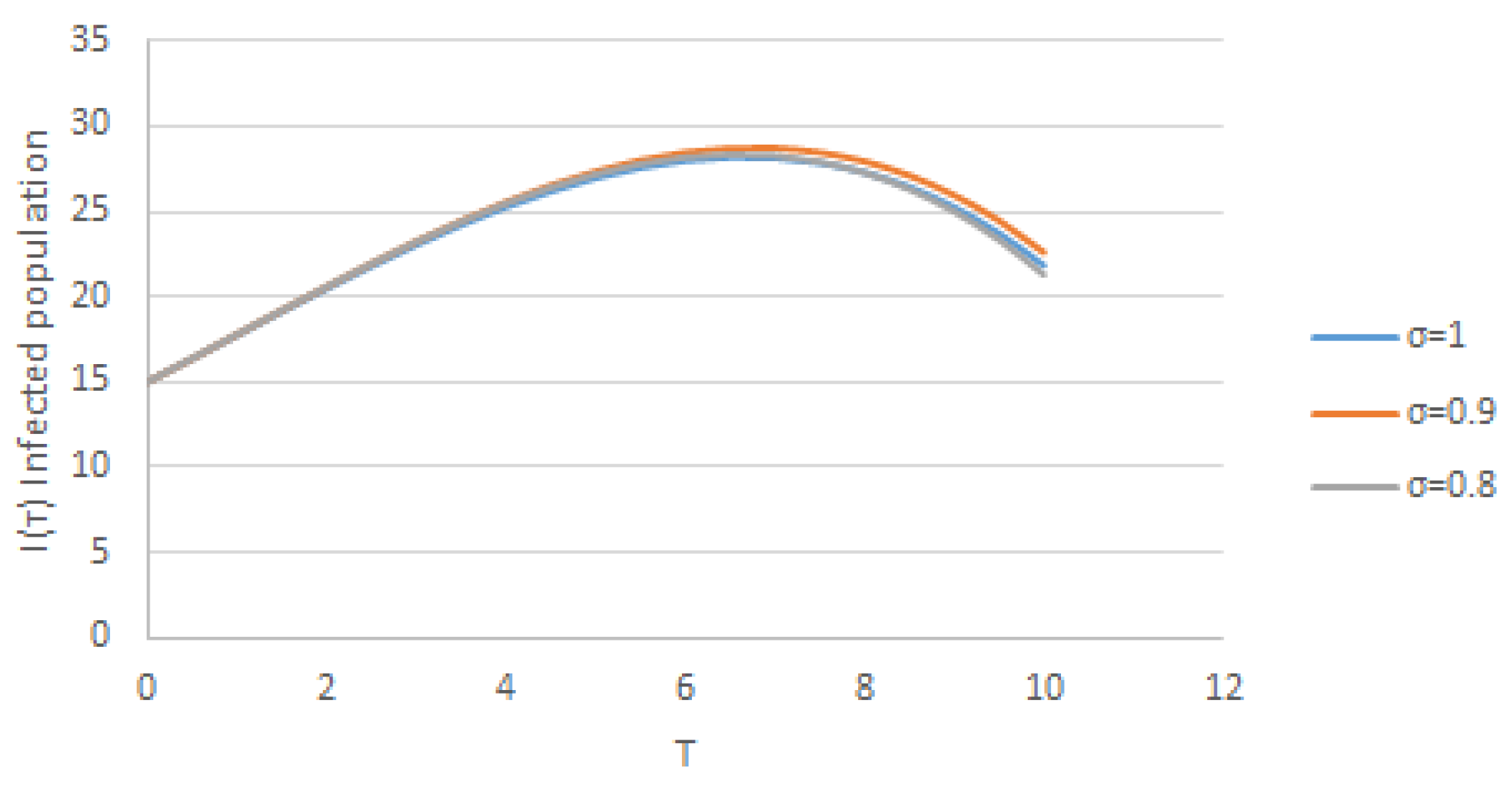
5. Numerical Results and Discussion

For the comparison with the results of Biazar [45,46], we consider the following values:

$\sigma =1$;

$N_1=20$ Initial population of $\mathcal{S}(⊺)$, who are susceptible;

$N_2=15$ Initial population of $\mathcal{I}(⊺)$, who are infected;

$N_3=10$ Initial population of $\Re (⊺)$, who are recovered;

$\beta =0.01$ Rate of change from susceptible population to infected population;

$\gamma =0.02$ Rate of change from infected population to recovered population.

The three-term approximations for $\mathcal{S}(⊺)$, $\mathcal{I}(⊺)$ and $\Re (⊺)$ are calculated and presented below.

$$\begin{array}{c}\mathcal{S}(⊺)=20-3⊺-0.045{⊺}^2+0.0280{⊺}^3\cdots ,\hfill \\ \mathcal{I}(⊺)=15+2.7⊺+0.08{⊺}^2-0.02817{⊺}^3\cdots ,\hfill \\ \Re (⊺)=10+0.3⊺+0.027{⊺}^2+0.00012{⊺}^3\cdots \hfill \end{array}$$

(43)

These results (43) are illustrated in Figure 1; as shown in the graphs, the number of infected persons increases and then is followed by a decrease in the number of susceptible people during the period of the epidemic; during this time of epidemic, the number of people immunized increases compared to the results of the number of immune population obtained via the Adomian decomposition method and the Laplace–Adomian decomposition method (see graphs 1, 2 and 3 of [45] and the graphs 1 and 2 and the table of [46]). Comparing the results obtained via HPZZTM with those obtained via ADM in [45] and L-ADM in [46] shows that the results of the three-term approximations of HPZZTM are the same as the results of the three-term approximations of ADM and L-ADM. Hence, we conclude that this method has proven successful in this epidemic model (Figure 2, Figure 3 and Figure 4).

6. Conclusions

The study presented in this paper is an investigation of the properties of the ZZ transform with respect to the Atangana–Baleanu–Caputo fractional operator; additionally, we combined the homotopy perturbation method with the ZZ integral transform, which is called the homotopy perturbation ZZ transform method (HPZZTM). This method was also used to solve the linear and nonlinear general fractional differential non-homogeneous equations, especially the fractional SIR epidemic model with the Atangana–Baleanu–Caputo fractional operator. Therefore, this new method is easy to apply to reach the desired results, as illustrated with the help of the presented model through the results obtained; it was also compared with the Adomian decomposition method and the Laplace–Adomian decomposition method. The HPZZTM method has proven its effectiveness and potential in solving these types of equations and it enabled us to obtain the exact solution in a faster way than the classical methods such as ADM and L-ADM presented in [45,46]; this is what the results showed as the number of immunized persons increased compared to the results obtained via these two methods. The ease of use and the strength of this method in achieving a solution is evidence of its speed in solving the example presented in this work or other linear or nonlinear problems.