The Formative Factors of a Rock Burst Based on Energy Calculations and the Experimental Verification of Butterfly-Shaped Plastic Zones
Abstract
:1. Introduction
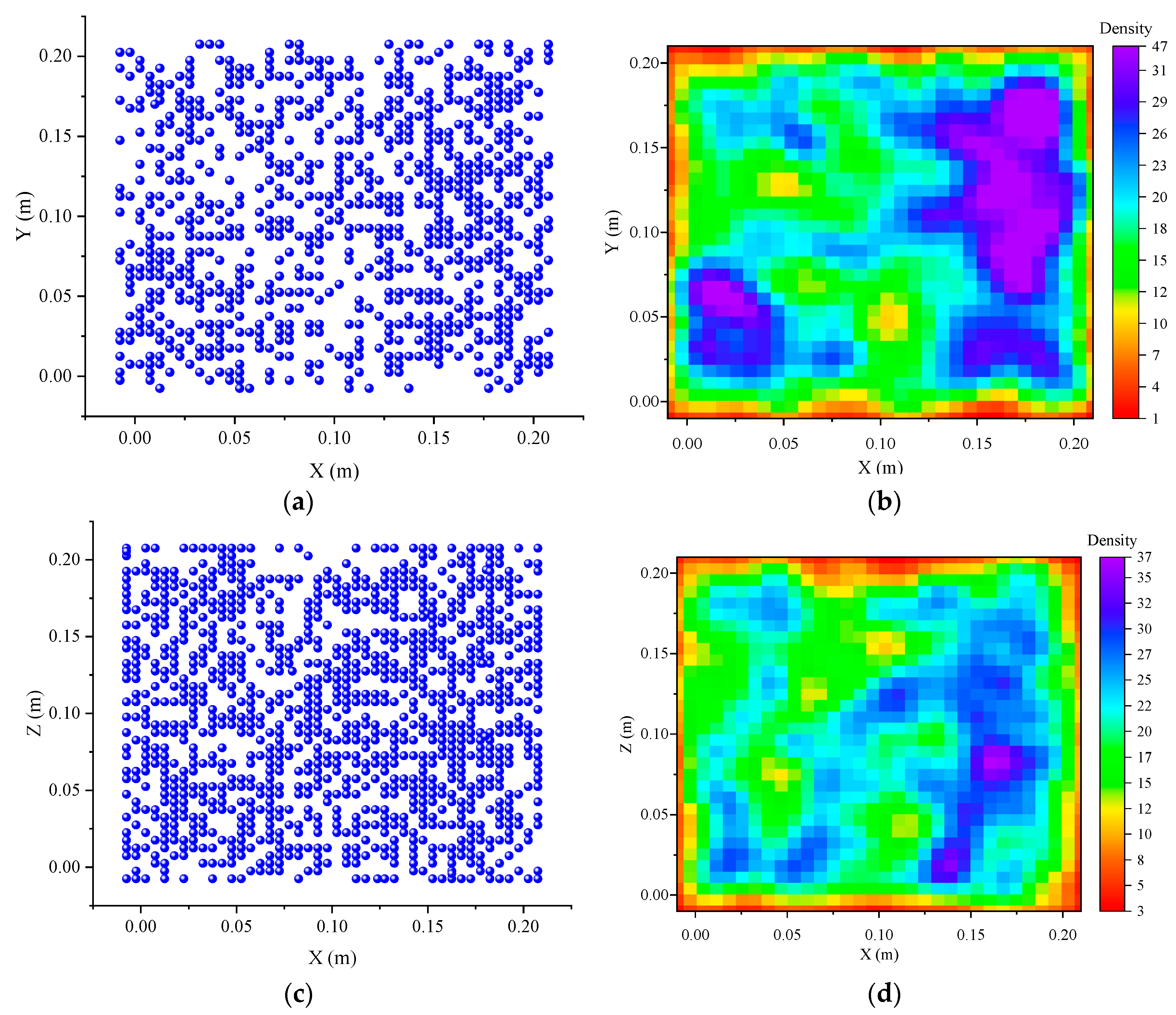
2. Numerical Methodology
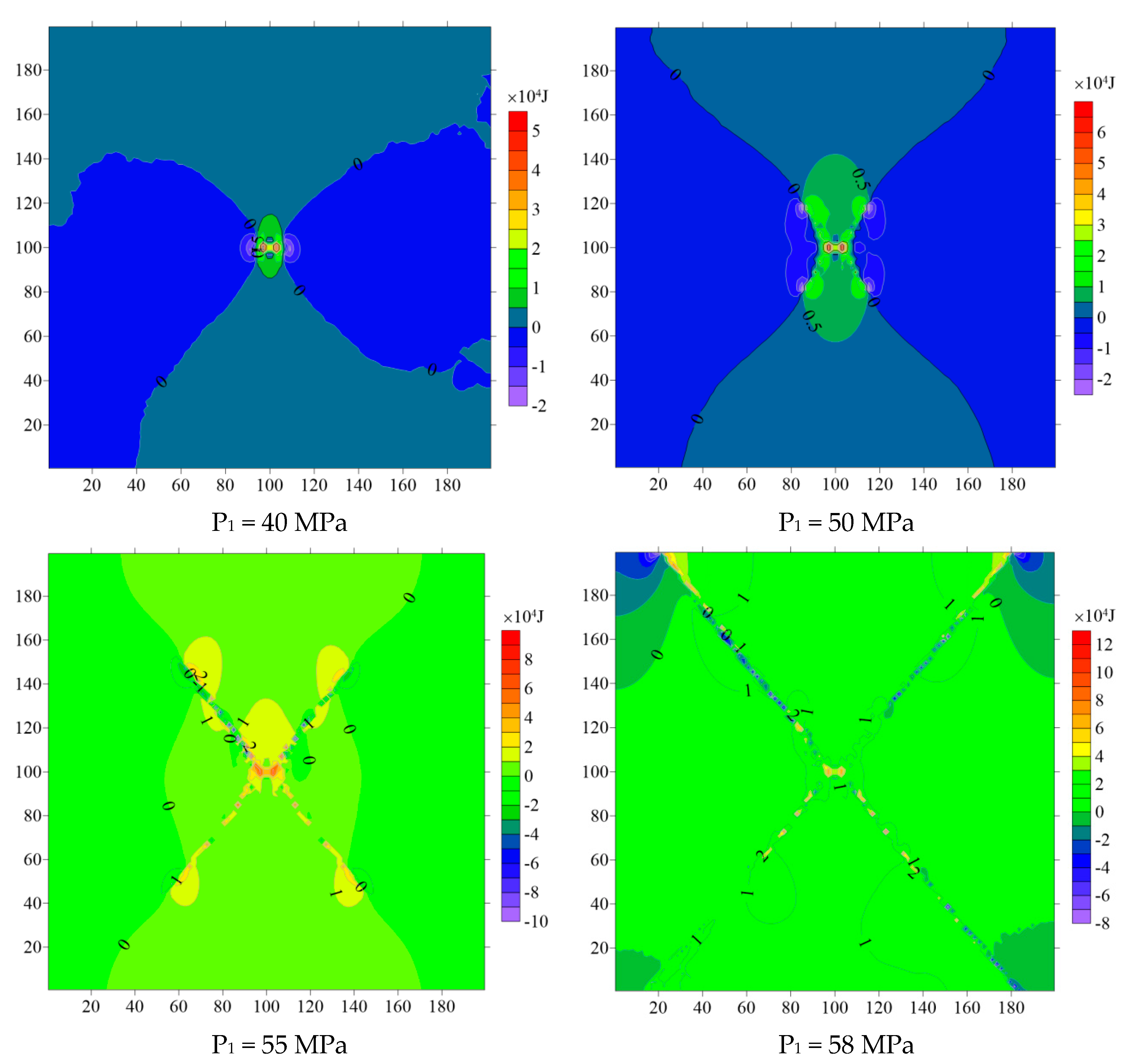
3. Results
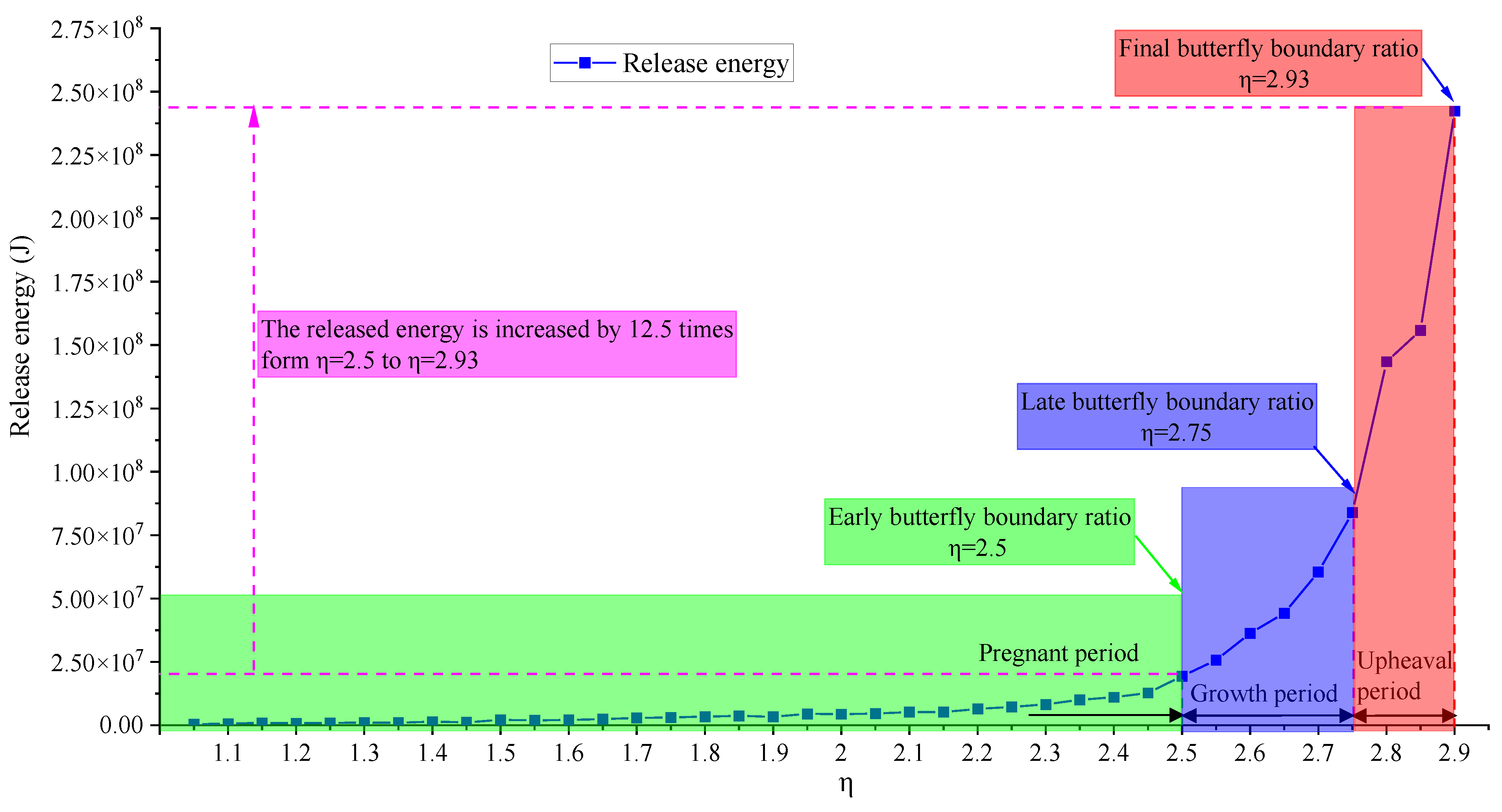
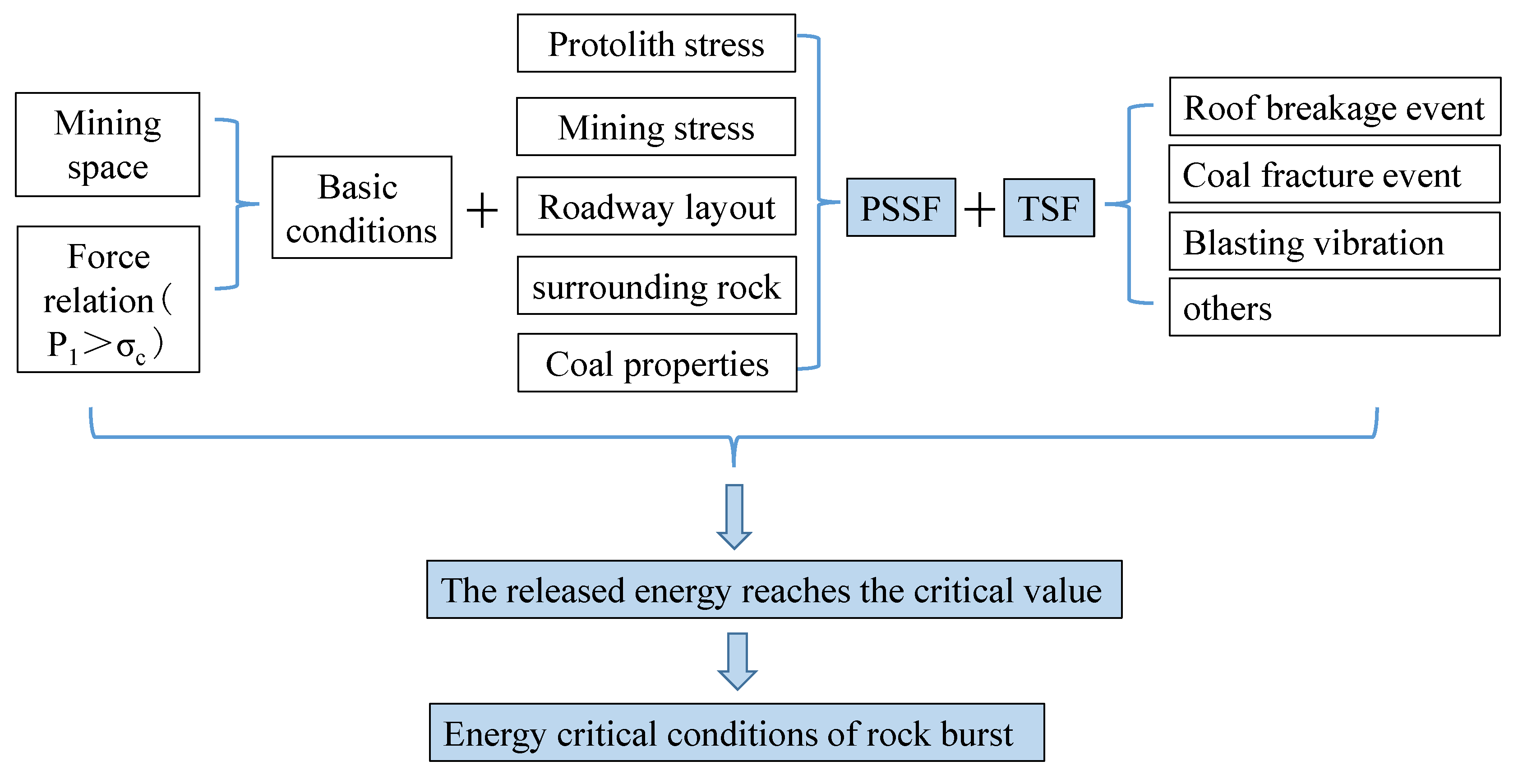
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, J.H.; Jiang, Q.H.; Zhang, Q.B.; Zhao, J. Dynamic stress adjustment and rock damage during blasting excavation in a deep-buried circular tunnel. Tunn. Undergr. Space Technol. 2018, 71, 591–604. [Google Scholar] [CrossRef]
- Feng, X.-T.; Liu, J.; Chen, B.; Xiao, Y.; Feng, G.; Zhang, F. Monitoring, Warning, and Control of Rockburst in Deep Metal Mines. Engineering 2017, 3, 538–545. [Google Scholar] [CrossRef]
- Mark, C. Coal bursts in the deep longwall mines of the United States. Int. J. Coal Sci. Technol. 2016, 3, 1–9. [Google Scholar] [CrossRef]
- Mark, C. Coal bursts that occur during development: A rock mechanics enigma. Int. J. Min. Sci. Technol. 2018, 28, 35–42. [Google Scholar] [CrossRef]
- Zhang, Q.B.; He, L.; Zhu, W.S. Displacement measurement techniques and numerical verification in 3D geomechanical model tests of an underground cavern group. Tunn. Undergr. Space Technol. 2016, 56, 54–64. [Google Scholar] [CrossRef]
- Zhang, W.; Qu, X.; Li, C.; Xu, X.; Zhang, S.; Jin, G.; Wang, Y. Fracture analysis of multi-hard roofs based on microseismic monitoring and control techniques for induced rock burst: A case study. Arab. J. Geosci. 2019, 12, 784. [Google Scholar] [CrossRef]
- Carri, A.; Valletta, A.; Cavalca, E.; Savi, R.; Segalini, A. Advantages of IoT-Based Geotechnical Monitoring Systems Integrating Automatic Procedures for Data Acquisition and Elaboration. Sensors 2021, 21, 2249. [Google Scholar] [CrossRef]
- Valletta, A.; Carri, A.; Savi, R.; Segalini, A. Algorithms for the Near-Real Time Identification and Classification of Landslide Events Detected by Automatic Monitoring Tools. In International Scientific Conference Environmental Challenges in Civil Engineering; Springer International Publishing: Cham, Switzerland, 2022; pp. 74–84. [Google Scholar]
- Drusa, M.; Kais, L.; Dubovan, J.; Markovic, M.; Bahleda, F.; Mecar, M. Measurement of Axial Strain of Geogrid by Optical Sensors. Sensors 2021, 21, 6404. [Google Scholar] [CrossRef]
- Rybak, J.; Khayrutdinov, M.M.; Kuziev, D.A.; Kongar-Syuryun, C.B.; Babyr, N.V. Prediction of the geomechanical state of the rock mass when mining salt deposits with stowing. J. Min. Inst. 2022, 253, 61–70. [Google Scholar] [CrossRef]
- Liu, J.K.; Luan, H.J.; Zhang, Y.C.; Sakaguchi, O.; Jiang, Y.J. Prediction of unconfined compressive strength ahead of tunnel face using measurement-while-drilling data based on hybrid genetic algorithm. Geomech. Eng. 2020, 22, 81–95. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, W.; Wu, Z.; Li, J.; Shen, Y.; Zhang, G. Microseismic Signals in Heading Face of Tengdong Coal Mine and Their Application for Rock Burst Monitoring. Shock Vib. 2021, 2021, 6650446. [Google Scholar] [CrossRef]
- Zhang, W.; Huo, T.; Li, C.; Wang, C.; Qu, X.; Xin, C.; Berardengo, M. Characteristics of Valuable Microseismic Events in Heading Face of an Underground Coal Mine Using Microseismic System. Shock Vib. 2021, 2021, 6683238. [Google Scholar] [CrossRef]
- Shen, P.; Tang, H.; Zhang, B.; Ning, Y.; He, C. Investigation on the fracture and mechanical behaviors of simulated transversely isotropic rock made of two interbedded materials. Eng. Geol. 2021, 286, 106058. [Google Scholar] [CrossRef]
- Cook, N.G.W.; Hoek, E.; Pretorius, J.P.; Ortlepp, W.D.; Salamon, M.D.G. Rock mechanics applied to the study of rock burst. J. S. Afr. Inst. Min. Metall. 1966, 66, 435–528. [Google Scholar]
- Bieniawski, Z.T.; Denkhaus, H.G.; Vogler, U. Failure of fractured rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1969, 6, 323–330. [Google Scholar] [CrossRef]
- Brady, B.H.G.; Bnown, E.T. Rock Mechonics for Underground Mining; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Bieniawski, Z.T. Mechanism of brittle of rocks. Part I, II and III. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1967, 4, 395–406. [Google Scholar] [CrossRef]
- Pan, Y. Disturbance response instability theory of rockburst in coal mine. J. China Coal Soc. 2018, 43, 2091–2098. [Google Scholar]
- Gao, F.; Stead, D.; Kang, H. Simulation of roof shear failure in coal mine roadways using an innovative UDEC Trigon approach. Comput. Geotech. 2014, 61, 33–41. [Google Scholar] [CrossRef]
- Li, Y. Mechanism of rock burst and its preliminary application. J. China Inst. Min. 1985, 3, 37–43. [Google Scholar]
- Pan, J. Theory of rockburst start up and its complete technology system. J. China Coal Soc. 2019, 44, 173–182. [Google Scholar]
- Zhao, Z.; Ma, N.; Guo, X.; Zhao, X.; Xia, Y.; Ma, Z. Mechanism conjecture of butterfly rock burst in coal seam roadway. J. China Coal Soc. 2016, 11, 2689–2697. [Google Scholar]
- Ma, N.; Guo, X.; Zhao, Z.; Zhao, X.; Liu, H. Occurrence mechanisms and judging criterion on circular tunnel butterfly rock burst in homogeneous medium. J. China Coal Soc. 2016, 11, 2679–2688. [Google Scholar]
- Jiang, L.; Kong, P.; Zhang, P.; Shu, J.; Wang, Q.; Chen, L.; Wu, Q. Dynamic Analysis of the Rock Burst Potential of a Longwall Panel Intersecting with a Fault. Rock Mech. Rock Eng. 2019, 53, 1737–1754. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, L.; Jiang, J.; Zheng, P.; Li, W. Strata Behaviors and Rock Burst–Inducing Mechanism under the Coupling Effect of a Hard, Thick Stratum and a Normal Fault. Int. J. Geomech. 2018, 18, 04017135. [Google Scholar] [CrossRef]
- He, H.; Dou, L.; Gong, S.; Zhou, P.; Xue, Z. Rock burst rules induced by cracking of overlying key stratum. Chin. J. Geotech. Eng. 2010, 32, 1260–1265. [Google Scholar]
- Lu, C.-P.; Liu, G.-J.; Liu, Y.; Zhang, N.; Xue, J.-H.; Zhang, L. Microseismic multi-parameter characteristics of rockburst hazard induced by hard roof fall and high stress concentration. Int. J. Rock Mech. Min. Sci. 2015, 76, 18–32. [Google Scholar] [CrossRef]
- Xie, J.; Xu, J.; Wang, F. Mining-induced stress distribution of the working face in a kilometer-deep coal mine—A case study in Tangshan coal mine. J. Geophys. Eng. 2018, 15, 2060–2070. [Google Scholar] [CrossRef]
- Cao, A.; Dou, L.; Cai, W.; Gong, S.; Liu, S.; Zhao, Y. Tomographic imaging of high seismic activities in underground island longwall face. Arab. J. Geosci. 2016, 9, 232. [Google Scholar] [CrossRef]
- Lu, C.-P.; Dou, L.-M.; Zhang, N.; Xue, J.-H.; Wang, X.-N.; Liu, H.; Zhang, J.-W. Microseismic frequency-spectrum evolutionary rule of rockburst triggered by roof fall. Int. J. Rock Mech. Min. Sci. 2013, 64, 6–16. [Google Scholar] [CrossRef]
- Xie, H.; Ju, Y.; Li, L. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles. Chin. J. Rock Mech. Eng. 2005, 24, 3003–3010. [Google Scholar]
- Kong, P.; Jiang, L.; Shu, J.; Sainoki, A.; Wang, Q. Effect of Fracture Heterogeneity on Rock Mass Stability in a Highly Heterogeneous Underground Roadway. Rock Mech. Rock Eng. 2019, 52, 4547–4564. [Google Scholar] [CrossRef]
- Zhu, S.; Jiang, F.; Wang, X.; Jiang, Y.; Ning, T.; Sun, S. Energy accumulation characteristics and rockburst mechanism of surrounding rock at heading face of extra-thick coal seam. Chin. J. Geotech. Eng. 2019, 41, 2071–2078. [Google Scholar]
- Hao, S.; Huilin, Z.; Guansheng, Q.; Wei, L.; Mingjun, W. Preparation and CO2 adsorption properties of TEPA-functionalized multi-level porous particles based on solid waste. Colloids Surf. A Physicochem. Eng. Asp. 2022, 653, 130004. [Google Scholar]
- Liu, H.; Guo, L.; Zhao, X. Expansionary Evolution Characteristics of Plastic Zone in Rock and Coal Mass Ahead of Excavation Face and the Mechanism of Coal and Gas Outburst. Energies 2020, 13, 984. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, Z.; Gao, X.; Wu, X.; Ma, N. Analytical solutions for characteristic radii of circular roadway surrounding rock plastic zone and their application. Int. J. Min. Sci. Technol. 2019, 29, 263–272. [Google Scholar] [CrossRef]
- Gao, F.; Kang, H.; Yang, L. An Experimental Investigation into the Strainburst Process Under Quasi-static Loading. Rock Mech. Rock Eng. 2020, 53, 5617–5629. [Google Scholar] [CrossRef]
- Wu, Y.; Gao, F.; Chen, J.; He, J. Experimental Study on the Performance of Rock Bolts in Coal Burst-Prone Mines. Rock Mech. Rock Eng. 2019, 52, 3959–3970. [Google Scholar] [CrossRef]
- Gao, F.; Kaiser, P.K.; Stead, D.; Eberhardt, E.; Elmo, D. Strainburst phenomena and numerical simulation of self-initiated brittle rock failure. Int. J. Rock Mech. Min. Sci. 2019, 116, 52–63. [Google Scholar] [CrossRef]
- Gao, F.; Kang, H.; Li, J. Numerical simulation of fault-slip rockbursts using the distinct element method. Tunn. Undergr. Space Technol. 2021, 110, 103805. [Google Scholar] [CrossRef]
- Haitjema, H. Occam’s Razor. Ground Water 2019, 57, 349. [Google Scholar] [CrossRef]
- Hsiung, S.M.; Blake, W.; Chowdhury, A.H.; Williams, T.J. Effects of mining-induced seismic events on a deep underground mine. Pageoph 1994, 139, 741–762. [Google Scholar] [CrossRef]
- Xie, L.X.; Yang, S.Q.; Gu, J.C.; Zhang, Q.B.; Lu, W.B.; Jing, H.W.; Wang, Z.L. JHR constitutive model for rock under dynamic loads. Comput. Geotech. 2019, 108, 161–172. [Google Scholar] [CrossRef]
- Zhu, F.; Zhao, J. Peridynamic modelling of blasting induced rock fractures. J. Mech. Phys. Solids 2021, 153, 104469. [Google Scholar] [CrossRef]
- Gibowicz, S.J.; Kijko, A. An Introduction to Mining Seismology; Earthquake Publish House: San Diego, CA, USA, 1998. [Google Scholar]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Chen, M.; Zhao, J. Analysis of damage mechanisms and optimization of cut blasting design under high in-situ stresses. Tunn. Undergr. Space Technol. 2017, 66, 19–33. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, J.; Liang, W. Pattern transitions of localized deformation in high-porosity sandstones: Insights from multiscale analysis. Comput. Geotech. 2020, 126, 103733. [Google Scholar] [CrossRef]
- Li, X.; Li, X.-F.; Zhang, Q.-B.; Zhao, J. A numerical study of spalling and related rockburst under dynamic disturbance using a particle-based numerical manifold method (PNMM). Tunn. Undergr. Space Technol. 2018, 81, 438–449. [Google Scholar] [CrossRef]
- Zhao, T.-b.; Guo, W.-y.; Tan, Y.-l.; Lu, C.-p.; Wang, C.-w. Case histories of rock bursts under complicated geological conditions. Bull. Eng. Geol. Environ. 2017, 77, 1529–1545. [Google Scholar] [CrossRef]
- Guo, W.; Gu, Q.; Tan, Y.; Hu, S. Case Studies of Rock Bursts in Tectonic Areas with Facies Change. Energies 2019, 12, 1330. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, H.; Zhang, B.; Lian, Z.; Yang, L.; Liu, T. Investigating the Characteristic of Weak Magnetic Stress Internal Detection Signals of Long-Distance Oil and Gas Pipeline Under Demagnetization Effect. IEEE Trans. Instrum. Meas. 2021, 70, 6011013. [Google Scholar] [CrossRef]
- Herbut, A.; Rybak, J.; Brząkała, W. On a Sensor Placement Methodology for Monitoring the Vibrations of Horizontally Excited Ground. Sensors 2020, 20, 1938. [Google Scholar] [CrossRef]
- He, S.H.; Goudarzy, M.; Ding, Z.; Sun, Y.F. Strength, Deformation, and Particle Breakage Behavior of Calcareous Sand: Role of Anisotropic Consolidation. J. Geotech. Geoenviron. Eng. 2023, 149, 17. [Google Scholar] [CrossRef]
- Sun, Y.F.; Sumelka, W.; He, S.H.; Gao, Y.F. Enhanced Fractional Model for Soil-Structure Interface Considering 3D Stress State and Fabric Effect. J. Eng. Mech. 2022, 148, 16. [Google Scholar] [CrossRef]
- Kong, B.; Dai, C.-X.; Hu, H.; Xia, J.; He, S.-H. The Fractal Characteristics of Soft Soil under Cyclic Loading Based on SEM. Fractal Fract. 2022, 6, 423. [Google Scholar] [CrossRef]
- He, S.-H.; Ding, Z.; Sun, Y.; Chen, W.-Y.; Xia, T.-D. Cumulative deformations and particle breakage in calcareous sand subjected to drained high-cyclic loading: Experimental investigation. Soil Dyn. Earthq. Eng. 2022, 161, 107417. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, M.-B.; Zhang, X.; Wei, X.-J. Theoretical analysis on the deformation of existing tunnel caused by under-crossing of large-diameter slurry shield considering construction factors. Tunn. Undergr. Space Technol. 2023, 133, 104913. [Google Scholar] [CrossRef]
- Wang, R.; Ding, Z.; Zhang, Y.; Xu, Y. Self-healing of high-performance engineered cementitious materials with crystalline admixture in the seawater environment. J. Build. Eng. 2023, 63, 105472. [Google Scholar] [CrossRef]
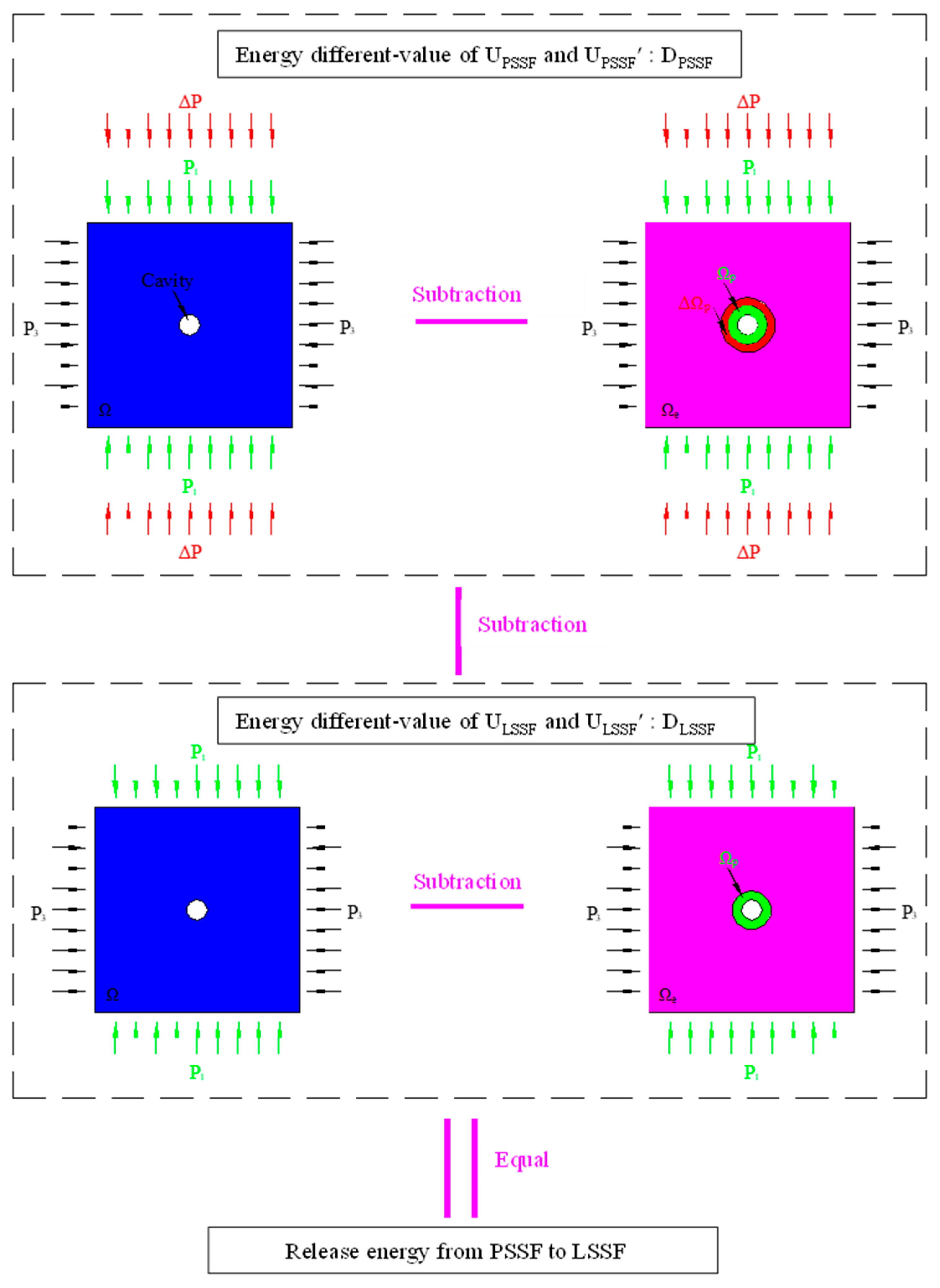
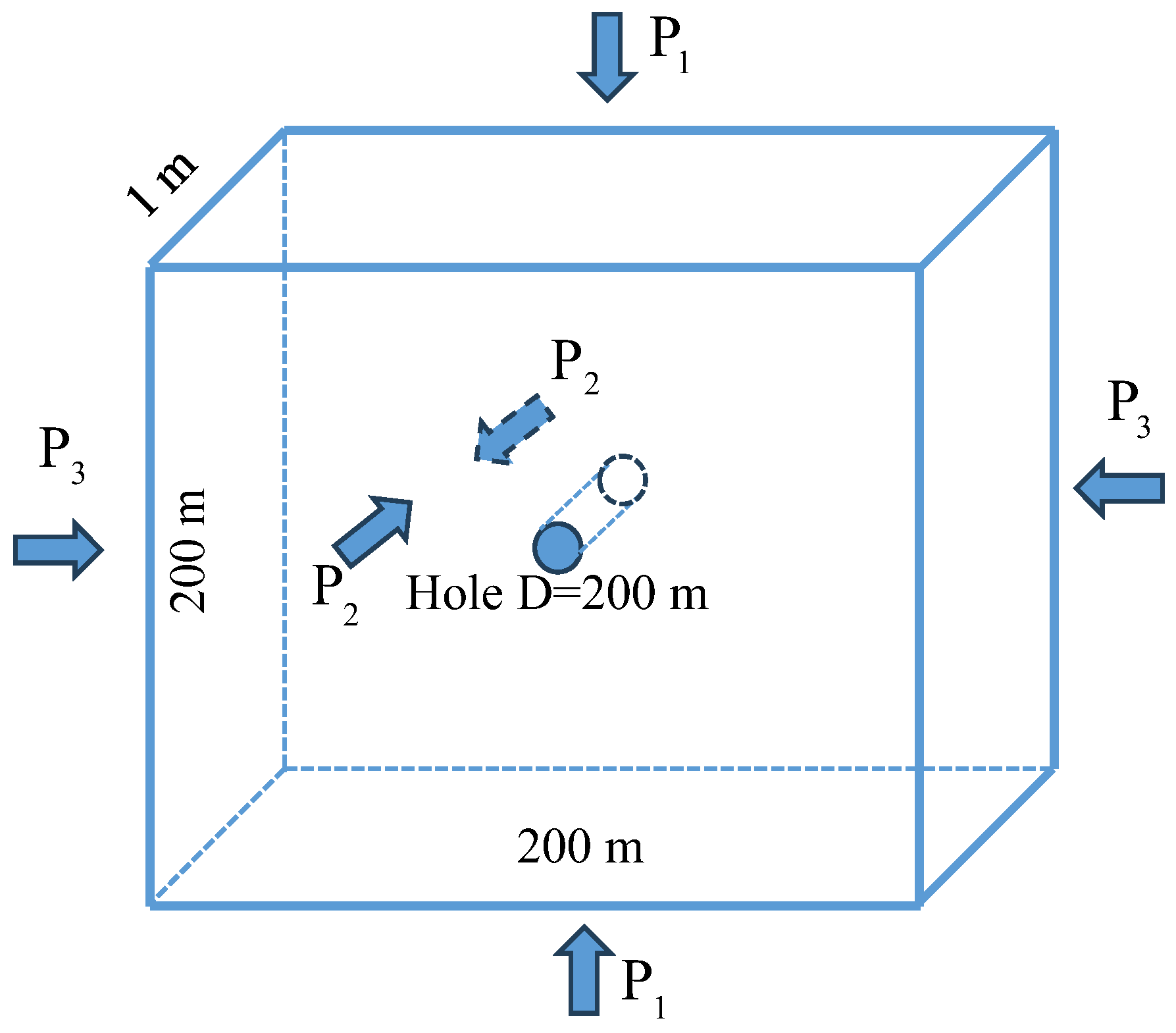
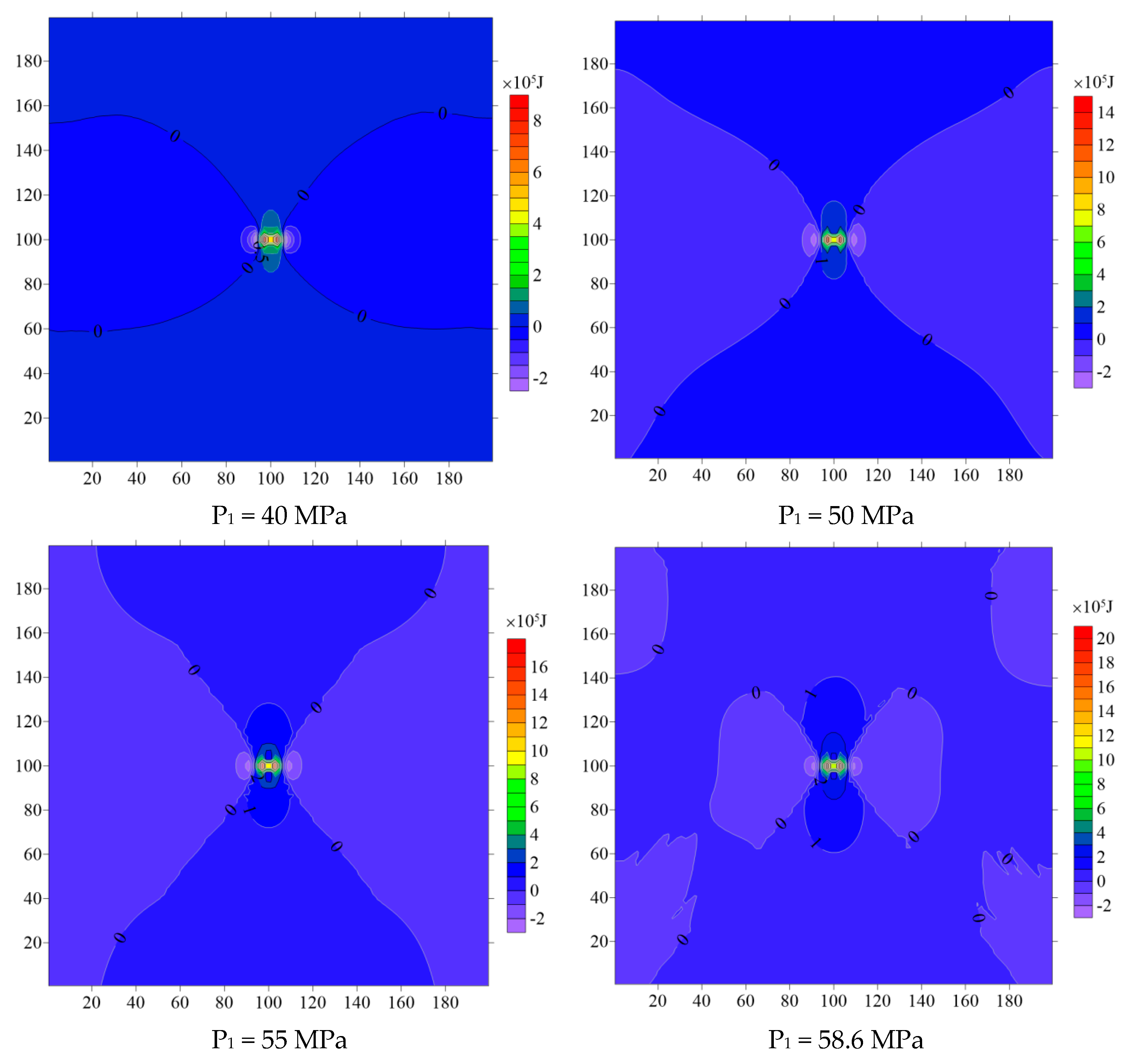
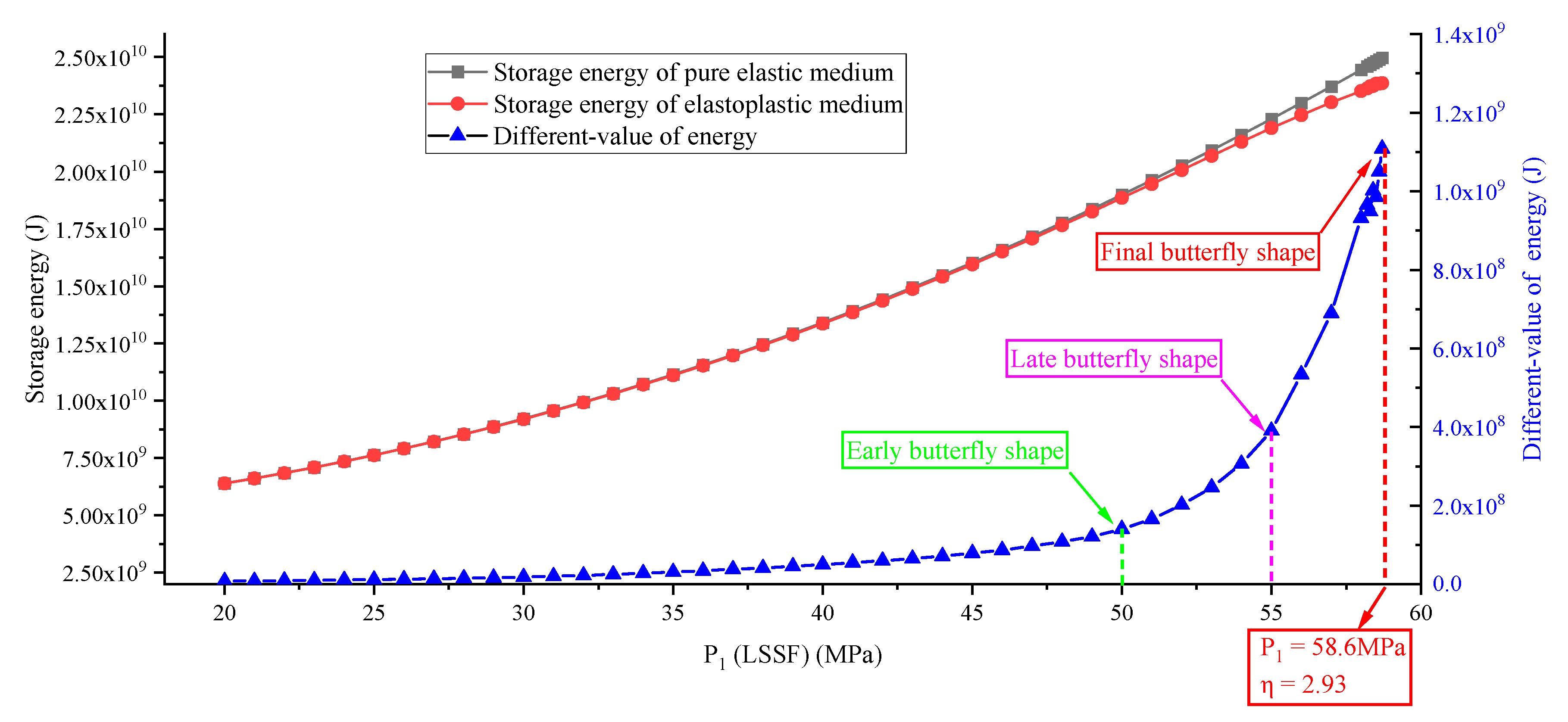




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Feng, J.; Ren, J.; Ma, J.; Shi, J.; Zhang, J. The Formative Factors of a Rock Burst Based on Energy Calculations and the Experimental Verification of Butterfly-Shaped Plastic Zones. Fractal Fract. 2023, 7, 829. https://doi.org/10.3390/fractalfract7110829
Zhang W, Feng J, Ren J, Ma J, Shi J, Zhang J. The Formative Factors of a Rock Burst Based on Energy Calculations and the Experimental Verification of Butterfly-Shaped Plastic Zones. Fractal and Fractional. 2023; 7(11):829. https://doi.org/10.3390/fractalfract7110829
Chicago/Turabian StyleZhang, Wenlong, Jicheng Feng, Jianju Ren, Ji Ma, Jianjun Shi, and Junfeng Zhang. 2023. "The Formative Factors of a Rock Burst Based on Energy Calculations and the Experimental Verification of Butterfly-Shaped Plastic Zones" Fractal and Fractional 7, no. 11: 829. https://doi.org/10.3390/fractalfract7110829
APA StyleZhang, W., Feng, J., Ren, J., Ma, J., Shi, J., & Zhang, J. (2023). The Formative Factors of a Rock Burst Based on Energy Calculations and the Experimental Verification of Butterfly-Shaped Plastic Zones. Fractal and Fractional, 7(11), 829. https://doi.org/10.3390/fractalfract7110829







