A Class of Fractional Stochastic Differential Equations with a Soft Wall
Abstract
:1. Introduction
2. Main Results
- (A)
- Linear growth of f for any and any
- (B)
- Lipschitz continuity of fin space: for any and
- (C)
- Hölder continuity in time: there exists such that for any and any
- (D)
- Function D is strictly monotonic and surjective.
- (E)
- Constant exists, such that
3. Remarks on the Condition (E)
4. Proofs of Theorems
4.1. Proof of Theorems 1 and 2
4.2. Proof of Theorems 4 and 5
5. Example: Fractional Pearson Diffusion Process with Soft Wall
6. Modelling: Fractional Vasicek Process
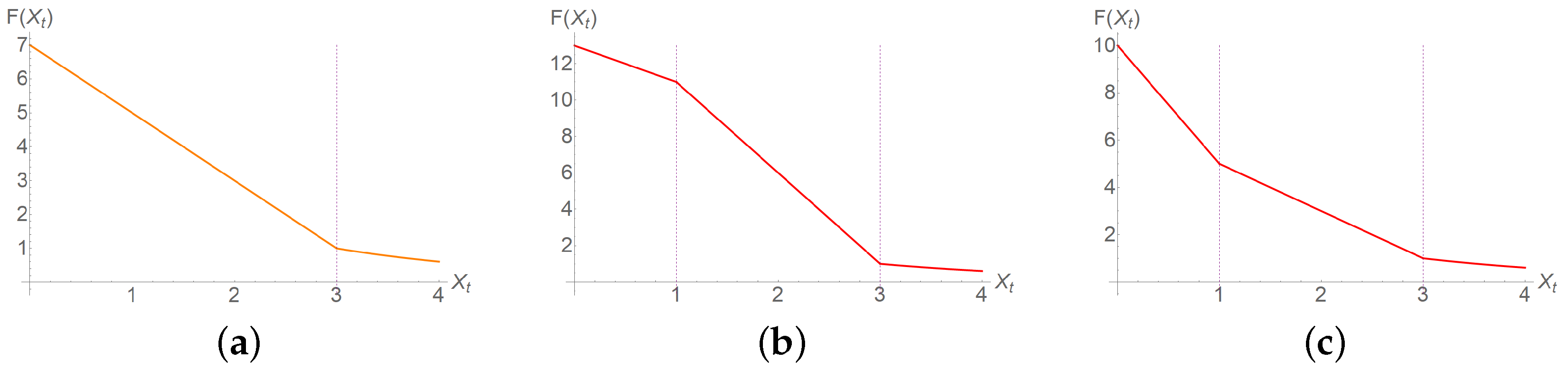
6.1. Profile of Soft-Wall Resistant Force
6.2. Process Trajectories Simulation under Soft-Wall conditions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Estimation of Hurst Parameter
Appendix B. Supplementary Results
Appendix B.1. Limit Results on fBm
Appendix B.2. Hölder Continuous Paths
Appendix B.3. Pathwise Integration
Appendix B.4. Gronwall’s lemma
References
- Nualart, D.; Ouknine, Y. Regularization of differential equations by fractional noise. Stoch. Process Their Appl. 2002, 102, 103–116. [Google Scholar] [CrossRef] [Green Version]
- Nualart, D.; Rǎşcanu, A. Differential equations driven by fractional Brownian motion. Collect. Math. 2002, 53, 55–81. [Google Scholar]
- Xu, L.; Luo, J. Stochastic differential equations driven by fractional Brownian motion. Stat. Probab. Lett. 2018, 142, 102–108. [Google Scholar] [CrossRef]
- Fuliński, A. Fractional Brownian Motions. Acta Phys. Pol. B 2020, 51, 1097–1129. [Google Scholar] [CrossRef]
- Capasso, V.; Wieczorek, R. A hybrid stochastic model of retinal angiogenesis. Math. Methods Appl. Sci. 2020, 43, 10578–10592. [Google Scholar] [CrossRef]
- Vojta, T.; Halladay, S.; Skinner, S.; Janušonis, S.; Guggenberger, T.; Metzler, R. Reflected fractional Brownian motion in one and higher dimensions. Phys. Rev. E 2020, 102, 032108. [Google Scholar] [CrossRef] [PubMed]
- Duncan, T.; Nualart, D. Existence of strong solutions and uniqueness in law for stochastic differential equations driven by fractional Brownian motion. Stoch. Dyn. 2009, 9, 423–435. [Google Scholar] [CrossRef]
- Guerra, J.; Nualart, D. Stochastic differential equations driven by fractional Brownian motion and standard Brownian motion. Stoch. Anal. Appl. 2008, 26, 1053–1075. [Google Scholar] [CrossRef] [Green Version]
- Kubilius, K. The existence and uniqueness of the solution of an integral equation driven by a p-semimartingale of special type. Stoch. Process. Appl. 2002, 98, 289–315. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zhan, W.; Xu, L. Stochastic differential equations with time-dependent coefficients driven by fractional Brownian motion. Phys. A 2019, 530, 121565. [Google Scholar] [CrossRef]
- Mishura, Y.; Shevchenko, G. Mixed stochastic differential equations with long-range dependence: Existence, uniqueness and convergence of solutions. Comput. Math. Appl. 2012, 64, 3217–3227. [Google Scholar] [CrossRef]
- Pei, B.; Xu, Y. On the non-Lipschitz stochastic differential equations driven by fractional Brownian motion. Adv. Differ. Equ. 2016, 194. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, J.L.; Erraoui, M.; Essaky, E.H. Mixed Stochastic Differential Equations: Existence and Uniqueness Result. J. Theor. Probab. 2018, 31, 1119–1141. [Google Scholar] [CrossRef] [Green Version]
- Vojta, T.; Wada, A.H.O. Fractional Brownian motion with a reflecting wall. Phys. Rev. E 2018, 97, 020102. [Google Scholar]
- Leonenko, G.M.; Phillips, T.N. High-order approximation of Pearson diffusion processes. J. Comput. Appl. Math. 2012, 236, 2853–2868. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Ying, L.; Pei, X. Parameter estimation for Vasicek model driven by a general Gaussian noise. Commun. Stat.-Theory Methods 2021, 1–17. [Google Scholar] [CrossRef]
- Kubilius, K.; Mishura, Y.; Ralchenko, K. Parameter Estimation in Fractional Diffusion Models; Bocconi & Springer Series; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Holte, J.M. Discrete Gronwall lemma and applications. In Proceedings of the MAA North Central Section Meeting at UND, Grand Forks, ND, USA, 24 October 2009. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubilius, K.; Medžiūnas, A. A Class of Fractional Stochastic Differential Equations with a Soft Wall. Fractal Fract. 2023, 7, 110. https://doi.org/10.3390/fractalfract7020110
Kubilius K, Medžiūnas A. A Class of Fractional Stochastic Differential Equations with a Soft Wall. Fractal and Fractional. 2023; 7(2):110. https://doi.org/10.3390/fractalfract7020110
Chicago/Turabian StyleKubilius, Kęstutis, and Aidas Medžiūnas. 2023. "A Class of Fractional Stochastic Differential Equations with a Soft Wall" Fractal and Fractional 7, no. 2: 110. https://doi.org/10.3390/fractalfract7020110
APA StyleKubilius, K., & Medžiūnas, A. (2023). A Class of Fractional Stochastic Differential Equations with a Soft Wall. Fractal and Fractional, 7(2), 110. https://doi.org/10.3390/fractalfract7020110












