Abstract
In this article, we investigate novel optical solitons solutions for the Lakshmanan–Porsezian–Daniel (LPD) equation, along with group velocity dispersion and spatio-temporal dispersion, via three altered analytical techniques. A variety of bright, singular, dark, periodic singular, and kink solitons solutions are constructed via the Kudryashov method, the generalized tanh method and the Sardar-subequation method. The dynamical behavior of the extracted solutions is demonstrated in graphical form such as 3D plots, 2D plots, and contour plots. The originality of the obtained solutions is recognized by comparison with each other and solutions previously stated in the literature for the LPD model, which displays the efficiency of the methods under consideration.
1. Introduction
Nonlinear evolution equations (NLEEs) have become more significant because many physical phenomena are demonstrated in nonlinear nature. The study of NLEEs is a main field of research in physics, mathematics, optics, biology, engineering, and other areas of natural sciences. A differential model is considered one of the best sources to examine the characteristics of physical phenomena thoroughly. The LPD equation is one of the well-known nonlinear partial differential equations to study physical phenomena. In many research problems, the application of nonlinear models has great interest for mathematical modeling. The LPD equation has the capability to perform the dynamics of optical solitons similarly to the Schrödinger equation [1,2]. The LPD equation defines the communication of solitons using different waveguides. Many mathematicians and researchers have worked on the LPD equation using different mathematical techniques, for instance, the undetermined coefficients method [3], extended trial equation method [4], semi-inverse variational principle [5], etc. In the current study, we examined the dynamics of solitons along with group velocity dispersion (GVD) and spatio-temporal dispersion (STD). Recently, many analytical schemes have been established to find the solutions of NLEEs, such as the modified exp-function scheme [6], extended tanh function scheme [7], variational iteration method [8], first integral method [9], Hirota’s direct method [10], new extended generalized Kudryashov method [11], improved subequation scheme [12], modified -expansion approach [13], fractional reduced differential transform scheme [14], Sine–Gordon expansion approach [15], extended modified mapping scheme [16], iterative approach [17], extended trial equation method [18], simplest equation method [19], F-expansion approach [20], ansatz scheme [21], modified Kudryashov scheme [22], homoseparation analysis scheme [23], extended mapping method [24], modified simple equation method [25], modified extended mapping method [26], reduced differential transform approach [27], extended direct algebraic approach [28], functional variable method [29], improved F-expansion method and improved auxiliary method [30], new extended direct algebraic method [31], Ricatti mapping method [32], generalized Ricatti mapping method [33], the -model expansion method [34], and many more. In this paper, a novel variety of optical soliton solutions of the LPD equation are fabricated using three well-known analytical techniques, named the Kudryashov method [35], the generalized tanh method [36], and the Sardar-subequation method [37]. A novel variety of solitons solutions is obtained using these techniques. Many researchers have resolved various models utilizing these methods, and motivating solutions have been added in the literature. Moreover, nonlinear fractional differential equations also have been utilized to demonstrate real phenomena in physical and natural sciences. Consequently, numerous explanations of fractional derivatives, for instance, beta-derivative and truncated M-fractional [38], as well as the Atangana–Baleanu fractional-operator with Mittag-Leffler kernel [39].
This article is sketched as follows: The LPD equation is stated in the “Governing Model” section. The proposed methods and applications on the LPD equation are explained in the section titled “Description and Application of Methods”. Graphical interpretations of some selected results are stated in the “Graphical Explanation” section. The “Comparison with Other Methods” section offers a comparison with some other schemes. Final comments are deliberated in the “Results and Discussion” section. The “Conclusions” section comprises the final comments.
2. Governing Model
A nonlinear LPD equation with GVD and STD [3] is given as
where, indicates the complex function, while x and t are the independent variables indicating the space and time, individually. The first term denotes the temporal evolution of the soliton, l and m are GVD and STD, singly. ℜ denotes the real function, and it is necessary to keep its evenness . is an i-times continuous differential function when the complex place C is preserved as 2D linear space , as
where and denote the fourth-order dispersion and two-photon absorption, accordingly. While , , , and represent the terms of dispersion.
Mathematical Analysis
We use the following wave transformations to examine Equation (1):
where indicates pulse profile and
where, , , and indicate phase components of soliton, frequency of soliton, and velocity of soliton, respectively, while and are phase constant and wave number. Inserting Equations (3) and (4) into Equation (1), the obtained appearance can be separated into real and imaginary portions. This yields a real portion, as
while the imaginary part yields
In view of this, Equations (5) and (6) are independent linearly and, keeping the coefficients equal to zero, obtain outcomes as follows:
and speed of soliton is
whenever .
The Kerr law of nonlinearity has the fact that the light wave in the fiber come across the nonlinear replies when there exists an external force on the optical field; therefore, . So, Equation (12) becomes
Using the transformation , Equation (13) becomes
3. Description and Application of the Methods
3.1. The Kudryashov Method
Suppose a PDE in (1), using wave transformations (3) and (4) into (1), then ODE is attained as in (14). We take up that (14) has a solution, such as
here, are constants and
which satisfies the nonlinear differential equation given as
Inserting Equation (15) into Equation (14), we found a set of equations by comparing the coefficients of to zero.
Application of the Kudryashov Method
By KM, consider Equation (14) having a solution such as
where and are constants. Substituting Equation (18) into Equation (14) yields a set of equations on the corresponding coefficients of to zero. By solving the set of equations, novel sets of solutions for Equation (1) are achieved.
- SET: 1
The exact solution for (1) is given by
- SET 2:
The exact solution for (1) is given by
3.2. The Generalized Tanh Method
Suppose a PDE in (1); using wave transformations (3) and (4) into (1), then ODE is attained as in (14). We take up that (14) has a solution such as
here, are constants and
Using the balance principle on (14), the value of ℵ can be determine. Inserting (25) into (14) along with (26) yields a set of equations; resolving it, we attain the solutions that accept (14), like this
- CASE 1: If , then
- CASE 2: If , then
- CASE 3: If , then
Application of the Generalized Tanh Method
Putting (32) along with (26) into (14) attains a polynomial of . We attain a system of equations by comparing the alike powers of to zero; in the solution, we obtain
- SET 1
- CASE 1: If , then
- CASE 2: If , then
- CASE 3: If , then
- SET 2
- CASE 1: If , then
- CASE 2: If , then
- CASE 3: If , then
3.3. The Sardar-Subequation Method
Suppose a PDE in (1); using wave transformations (3) and (4) into (1), then ODE is attained as in (14). We take up that (14) has a solution such as
where are constants.
where A and C are constants and (46) yields sets of solutions as
- CASE 1: When and , then
- CASE 2: When and , then
- CASE 3: When and , then
- CASE 4: When and , then
Application of the SSM
In order to find the solitons solutions of LPD, the SSM is applied on (14). The balance rule on (14) yields , so (45) reduces to
where , are constants. Replacing the (47) into (14) obtains the set of equations in and n. By solving the system, we yield
- CASE 1: When and , then
- CASE 2: When and , then
- CASE 3: When and , then
- CASE 4: When and , then
4. Graphical Explanation
In this section, some selected solutions are sketched in the form of 2D, 3D, and contour plots. An abundance of optical soliton solutions are retrieved in the shape of rational, exponential, trigonometric, and hyperbolic function solutions. To recognize the original phenomena of the governing model, some solutions are plotted properly. An abundance of solitons are obtained by allocating the proper values to the involved parameters. The acquired solutions comprise singular, kink, periodic singular, dark–bright, and bright solitons. Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 represent kink soliton, singular soliton, periodic singular soliton, singular dark soliton, bright soliton, dark soliton, and dark–bright soliton, respectively, of the solutions given in Equations (21), (35), (37), (40), (41), (49), (53), (55), and (62).

Figure 1.
(A) 3D graph of kink soliton of (21) using , , , , , . (A-1) 2D plot and (A-2) contour plot of (21).
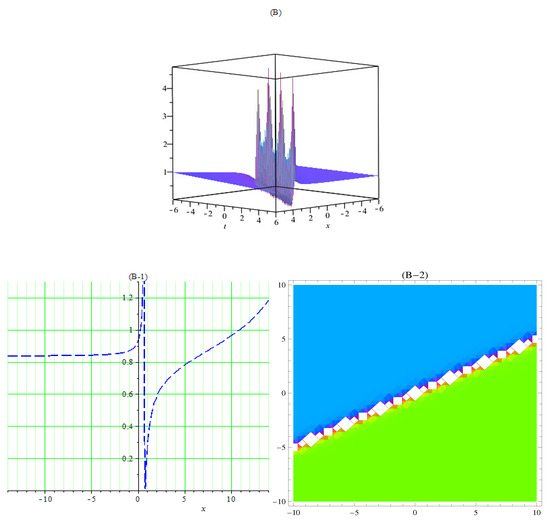
Figure 2.
(B) 3D graph of singular soliton of (35) using , , , , , . (B-1) 2D plot and (B-2) contour plot of (35).
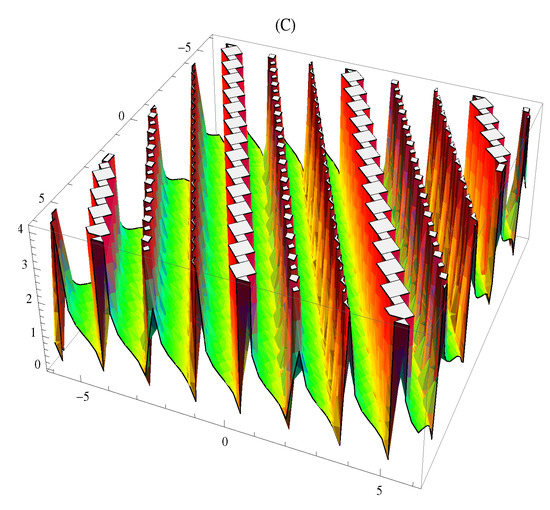
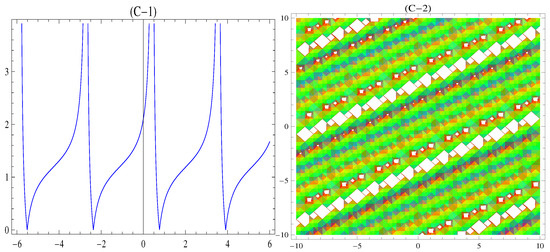
Figure 3.
(C) 3D graph of periodic–singular of (37) with , , , , , . (C-1) 2D plot and (C-2) contour plot of (37).
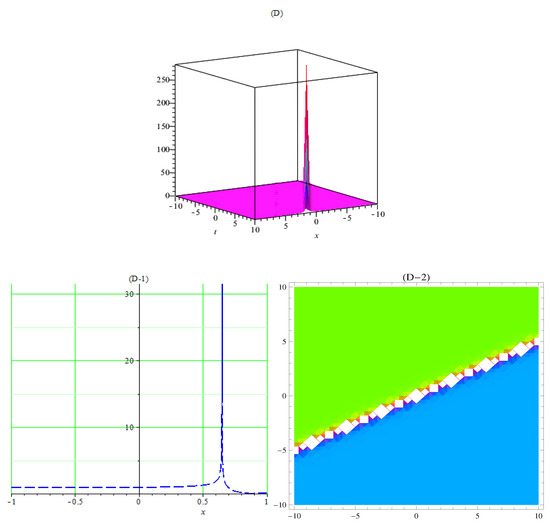
Figure 4.
(D) 3D graph of singular soliton of (40) using , , , , , . (D-1) 2D plot and (D-2) contour plot of (40).
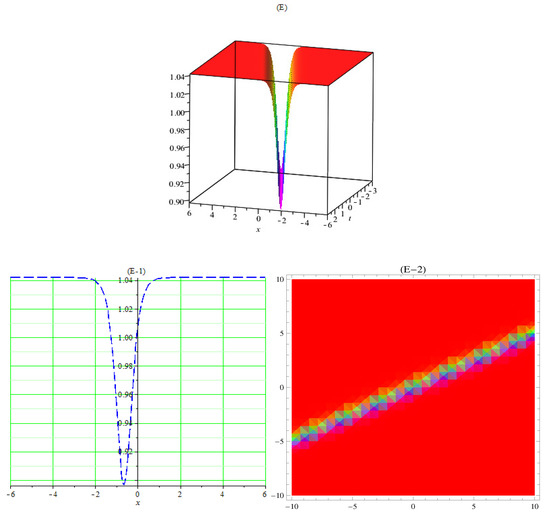
Figure 5.
(E) 3D graph of dark soliton of (41) using , , , , , . (E-1) 2D plot and (E-2) contour plot of (41).
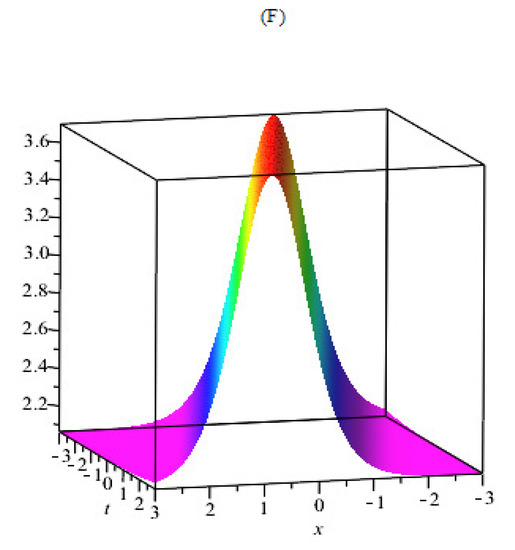

Figure 6.
(F) 3D graph of bright soliton of (49) using , , , , , , . (F-1) 2D plot and (F-2) contour plot of (49).
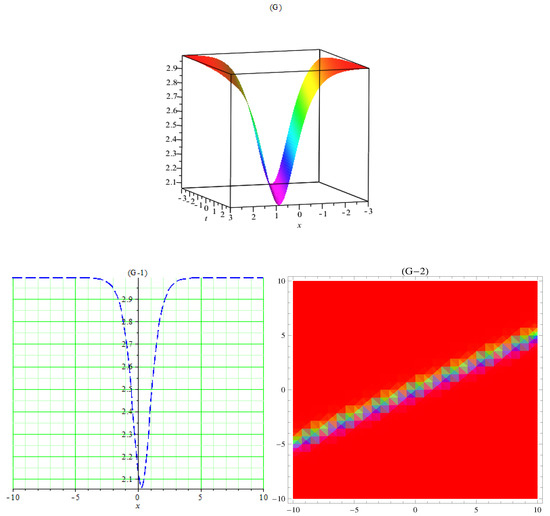
Figure 7.
(G) 3D graph of dark soliton of (53) using , , , , , , . (G-1) 2D plot and (G-2) contour plot of (53).
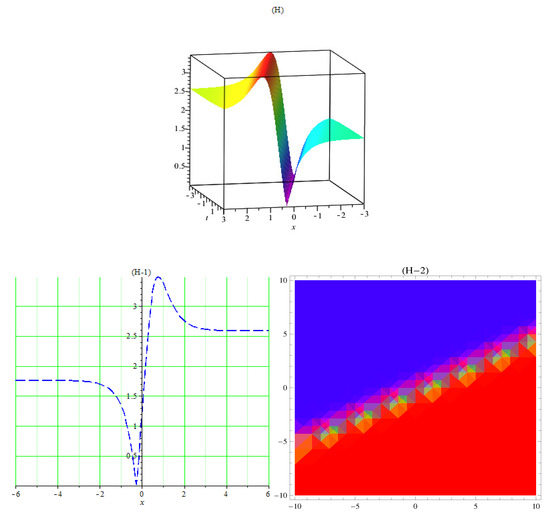
Figure 8.
(H) 3D graph of dark–bright (55) with , , , , , , . (H-1) 2D plot and (H-2) contour plot of (55).

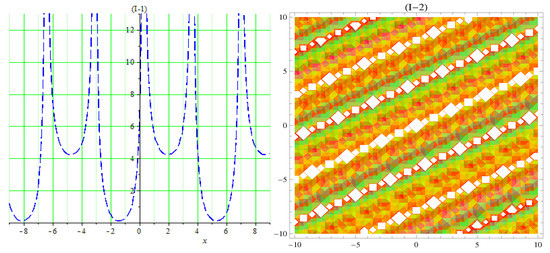
Figure 9.
(I) 3D graph of periodic–singular soliton of (62) with , , , , , , . (I-1) 2D plot and (I-2) contour plot of (62).
5. Comparison with Other Methods
In this study, we observed that the Kudryashov method gave only a single solution in one set, which is kink soliton, the tanh method provided three families and five solutions in the shape of singular, dark, and periodic singular solitons, while the Sardar-subequation method offered four families with fourteen solutions. From this observation, we conclude that the Sardar-subequation method is extra worthwhile and appreciated, owing to the abundant diversity of optical solitons solutions achieved. The attained solitons solutions show that the Sardar-subequation method gives more solutions than the Kudryashov method and tanh method. Moreover, the Sardar-subequation method is compared with some other methods, such as [30], semi-inverse variational method [5], extended trial equation method [6], modified simple equation method [15], and simple equation method [29], as [30] covered kink solitons, [5] stated bright solitons, [6] observed singular and dark solitons, [15] offered dark singular solitons, and [29] extracted bright dark solitons only.
6. Results and Discussion
In this study, the LPD equation with the Kerr law of nonlinearity is solved by renowned analytical techniques, i.e., the Kudryashov method, the generalized tanh method, and the Sardar-subequation method, to construct a diversity of optical solitons solutions. After applying these methods, some selected solutions are demonstrated, such as bright dark, singular, and periodic singular soliton solutions. To understand the physical profiles of waves, 2D, 3D, and contour plots are deliberated. The calculations are made with the help of Mathematical software.
In Figure 1A, the 3D plot, Figure 1A-1, the 2D plot, and Figure 1A-2, the contour plot of of Equation (21) are solved by the Kudryashov method, which demonstrates the behavior of a kink soliton by using the suitable values of the parameters. In Figure 2B, the 3D plot, Figure 2B-1, the 2D plot, and Figure 2B-2, the contour plot of of Equation (35) are solved by the tanh method; this gives us a singular soliton solution by using the suitable values of the parameters. In Figure 3C, the 3D plot, Figure 3C-1, the 2D plot, and Figure 3C-2, the contour plot of of Equation (37) are solved by the tanh method; this gives us a periodic singular soliton solution by using the suitable values of the parameters. In Figure 4D, the 3D plot, Figure 4D-1, the 2D plot, and Figure 4D-2, the contour plot of of Equation (40) are solved by the tanh method; this gives us a singular soliton solution by using the suitable values of the parameters. In Figure 5E, the 3D plot, Figure 5E-1, the 2D plot, and Figure 5E-2, the contour plot of of Equation (41) are solved by the tanh method; this gives us a dark soliton solution by using the suitable values of the parameters. In Figure 6F, the 3D plot, Figure 6F-1, the 2D plot, and Figure 6F-2, the contour plot of of Equation (49) are solved by the Sardar-subequation method; this gives us a bright soliton solution by using the suitable values of the parameters. In Figure 7G, the 3D plot, Figure 7G-1, the 2D plot, and Figure 7G-2, the contour plot of of Equation (53) are solved by the Sardar-subequation method; this gives us a dark soliton solution by using the suitable values of the parameters. In Figure 8A, the 3D plot, Figure 8H-1, the 2D plot, and Figure 8H-2, the contour plot of of Equation (55) are solved by the Sardar-subequation method; this gives us a combined dark–bright soliton solution by using the suitable values of the parameters. In Figure 9I, the 3D plot, Figure 9I-1, the 2D plot, and Figure 9I-2, the contour plot of of Equation (62) are solved by the Sardar-subequation method; this gives us a periodic singular soliton solution by using the suitable values of the parameters.
Remark: From the above discussion, we conclude that the Sardar-subeaquation method is more beneficial and generalized than the Kudryashov method and tanh method. It is beneficial that the methods under consideration are utilized on the LPD equation for the first time to the best of our knowledge. The obtained solutions of this article are novel, unique, and not stated anywhere else in the literature. Thus, understandings validate that the techniques under discussion are meaningful for the analytical study of various other NLPDEs in optics and various other natural sciences.
7. Conclusions
This study retrieved a variety of optical solitons solutions, such as periodic, kink, singular, dark–bright, and periodic–singular, of the LPD model by using the Kudryashov method, tanh method, and the Sardar-subequation method. In this paper, the Kudryashov method gave just a single solution in one set, the tanh method gave three cases with five solutions, and the Sardar-subequation method gave four families with fourteen solutions. We sketched 3D, 2D, and contour graphs of some selected solutions. By comparison, we observed that the Sardar-subequation method is a more suitable and general analytical technique than the Kudryashov method and tanh method. It was also observed that the Kudryashov method just gives a kink soliton solution, and the tanh method provides singular, periodic–singular, and dark solitons, while the Sardar-subequation method gives dark, singular, bright, combined dark–bright, and periodic–singular solitons solutions. The present novel solutions may support recognizing the dynamic behavior of various optical and other physical systems.
Author Contributions
Conceptualization, M.I.A.; Methodology, N.U.; Software, N.U.; Validation, M.Y.A.; Investigation, N.U.; Resources, M.Y.A.; Writing—original draft, N.U.; Writing—review & editing, M.I.A.; Visualization M.I.A.; Supervision, M.I.A.; Project administration, M.Y.A. and S.M.E.; Funding acquisition, S.M.E. All authors have read and agreed to the published version of the manuscript.
Funding
The authors have not disclosed any funding.
Data Availability Statement
The data used to support the findings of this study are included within the article.
Acknowledgments
Naeem Ullah and Muhammad Asjad Imran are greatly obliged and thankful to the University of Management and Technology Lahore, Pakistan for facilitating and supporting the research work.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- Al Qarni, A.A.; Ebaid, A.; Alshaery, A.A.; Bakodah, H.O.; Biswas, A.; Khan, S.; Ekici, M.; Zhou, Q.; Moshokoa, S.P. Optical solitons for Lakshmanan-Porsezian-Daniel model by Riccati equation approach. Optik 2019, 182, 922–929. [Google Scholar] [CrossRef]
- Manafian, J.; Foroutan, M.; Guzali, A. Applications of the ETEM for obtaining optical soliton solutions for the Lakshmanan-Porsezian-Daniel model. Eur. Phys. J. Plus 2017, 132, 1–22. [Google Scholar] [CrossRef]
- Vega-Guzman, J.; Alqahtani, R.T.; Zhou, Q.; Mahmood, M.F.; Moshokoa, S.P.; Ullah, M.Z.; Biswas, A.; Belic, M. Optical solitons for lakshmanan-porsezian-daniel model with spatio-temporal dispersion using the method of undetermined coefficients. Optik 2017, 144, 115–123. [Google Scholar] [CrossRef]
- Biswas, A.; Ekici, M.; Sonmezoglu, A.; Triki, H.; Majid, F.B.; Zhou, Q.; Moshokoa, S.P.; Mirzazadeh, M.; Belic, M. Optical solitons with Lakshmanan-Porsezian-Daniel model using a couple of integration schemes. Optik 2018, 158, 705–711. [Google Scholar] [CrossRef]
- Alqahtani, R.T.; Babatin, M.M.; Biswas, A. Bright optical solitons for LakshmananPorsezian-Daniel model by semi-inverse variational principle. Optik 2018, 154, 109–114. [Google Scholar] [CrossRef]
- Bekir, A.; Boz, A. Exact solutions for nonlinear evolution equations using exp-function method. Phys. Lett. A 2008, 372, 1619–1625. [Google Scholar] [CrossRef]
- Zahran, E.H.M.; Khater, M.M.A. Modified extended tanh-function method and its applications to the Bogoyavlenskii equation. Appl. Math. Model. 2016, 40, 1769–1775. [Google Scholar] [CrossRef]
- Nadeem, M.; Li, F.; Ahmad, H. Modified Laplace variational iteration method for solving fourth-order parabolic partial differential equation with variable coefficients. Comput. Math. Appl. 2019, 78, 2052–2062. [Google Scholar] [CrossRef]
- Faraz, N.; Sadaf, M.; Akram, G.; Zainab, I.; Khan, Y. Effects of fractional order time derivative on the solitary wave dynamics of the generalized ZK-Burgers equation. Results Phys. 2021, 25, 104217. [Google Scholar] [CrossRef]
- Arnous, A.H.; Biswas, A.; Ekici, M.; Alzahrani, A.K.; Belic, M. Optical solitons and conservation laws of Kudryashov’s equation with improved modified extended tanh-function. Optik 2020, 225, 165406. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Shohib, R.M.A.; Alngar, M.E.M. New extended generalized Kudryashov method for solving three nonlinear partial differential equations. Nonlinear Anal. Model. Control 2020, 25, 598–617. [Google Scholar] [CrossRef]
- Karaagac, B. New exact solutions for some fractional order differential equations via improved sub-equation method. Discret. Dyn. Syst.-Ser. S 2019, 12, 447–454. [Google Scholar] [CrossRef]
- Sonmezoglu, A. Exact solutions for some fractional differential equations. Adv. Math. Phys. 2015, 2015, 567842. [Google Scholar] [CrossRef]
- Iqbal, M.; Seadawy, A.R.; Lu, D. Construction of solitary wave solutions to the nonlinear modified Kortewegede Vries dynamical equation in unmagnetized plasma via mathematical methods. Mod. Phys. Lett. A 2018, 33, 1850183. [Google Scholar] [CrossRef]
- Saleh, R.; Kassem, M.; Mabrouk, S.M. Exact solutions of nonlinear fractional order partial differential equations via singular manifold method. Chin. J. Phys. 2019, 61, 290–300. [Google Scholar] [CrossRef]
- Martineza, H.Y.; Aguilarb, J.F.G.; Baleanu, D. Beta-derivative and sub-equation method applied to the optical solitons in medium with parabolic law nonlinearity and higher order dispersion. Optik 2018, 155, 357–365. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A.R.; Ali, A. Dispersive traveling wave solutions of the equal-width and modified equal-width equations via mathematical methods and its applications. Results Phys. 2018, 9, 313–320. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Manafian, J. New soliton solution to the longitudinal wave equation in a magneto-electro-elastic circular rod. Results Phys. 2018, 8, 1158–1167. [Google Scholar] [CrossRef]
- Helal, M.A.; Seadawy, A.R.; Zekry, M.H. Stability analysis of solitary wave solutions for the fourth-order nonlinear Boussinesq water wave equation. Appl. Math. Comput. 2014, 232, 1094–1103. [Google Scholar] [CrossRef]
- Seadawy, A.R.; El-Rashidy, K. Dispersive solitary wave solutions of Kadomtsev-Petviashvili and modified Kadomtsev-Petviashvili dynamical equations in unmagnetized dust plasma. Results Phys. 2018, 8, 1216–1222. [Google Scholar] [CrossRef]
- Shi, D.; Zhang, Y. Diversity of exact solutions to the conformable space-time fractional mew equation. Appl. Math. Lett. 2020, 99, 105994. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A.R.; Ali, A. Applications of exact traveling wave solutions of modified Liouville and the symmetric regularized long wave equations via two new techniques. Results Phys. 2018, 9, 1403–1410. [Google Scholar] [CrossRef]
- Zuriqat, M. Exact solution for the fractional partial differential equation by homo separation analysis method. Afriqa Mat. 2019, 30, 1133–1143. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.; Lu, D. Elliptic function and solitary wave solutions of the higher-order nonlinear Schrödinger dynamical equation with fourth-order dispersion and cubic-quintic nonlinearity and its stability. Eur. Phys. J. Plus 2017, 132, 371. [Google Scholar] [CrossRef]
- Arnous, A.H.; Seadawy, A.R.; Alqahtani, R.T.; Biswas, A. Optical solitons with complex ginzburg-landau equation by modified simple equation method. Optik 2017, 144, 475–480. [Google Scholar] [CrossRef]
- Abdullah; Seadawy, A.R.; Wang, J. Mathematical methods and solitary wave solutions of three-dimensional Zakharov-Kuznetsov-Burgers equation in dusty plasma and its applications. Results Phys. 2017, 7, 4269–4277. [Google Scholar] [CrossRef]
- Owyed, S.; Abdou, M.A.; Abdel-Atyb, A.H.; Nekhili, W.A.R. Numerical and approximate solutions for coupled time fractional nonlinear evolutions equations via reduced differential transform method. Chaos Solitons Fractals 2019, 217, 109474. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Lu, D.; Yue, C. Travelling wave solutions of the generalized nonlinear fifth-order kdv water wave equations and its stability. J. Taibah Univ. Sci. 2017, 11, 623–633. [Google Scholar] [CrossRef]
- Nasreen, N.; Seadawy, A.R.; Lu, D. Optical soliton and elliptic functions solutions of Sasa-satsuma dynamical equation and its applications. Appl. Math.-A J. Chin. Univ. 2021, 36, 229–242. [Google Scholar]
- Seadawy, A.R.; Lu, D.; Nasreen, N. Construction of solitary wave solutions of some nonlinear dynamical system arising in nonlinear water wave models. Indian J. Phys. 2020, 94, 1785–1794. [Google Scholar] [CrossRef]
- Nasreen, N.; Seadawy, A.R.; Lu, D. Study of modulation instability analysis and optical soliton solutions of higher-order dispersive nonlinear Schrodinger equation with dual-power law nonlinearity. Mod. Phys. Lett. B 2019, 33, 1950309. [Google Scholar] [CrossRef]
- Nasreen, N.; Seadawy, A.R.; Lu, D.; Albarakati, W.A. Dispersive solitary wave and soliton solutions of the gernalized third ordernonlinear Schrödinger dynamical equation by modified analytical method. Results Phys. 2019, 15, 102641. [Google Scholar] [CrossRef]
- Cenesiz, Y.; Tasbozan, O.; Kurt, A. Functional variable method for conformable fractional modified kdv-zkequation and Maccari system. Tbilisi Math J. 2017, 10, 117–125. [Google Scholar] [CrossRef]
- Asjad, M.I.; Faridi, W.A.; Alahazmi, S.E.; Hussain, A. The modulation instability analysis and generalized fractional propagating patterns of the Peyrard-Bishop DNA dynamical equation. Opt. Quantum Electron. 2023, 55, 232. [Google Scholar] [CrossRef]
- Rehman, H.U.; Ullah, N.; Imran, M.A. Highly dispersive optical solitons using Kudryashov’s method. Optik 2019, 199, 163349. [Google Scholar] [CrossRef]
- Ullah, N.; Rehman, H.U.; Imran, M.A.; Abdeljawad, T. Highly dispersive optical solitons with cubic law and cubic-quintic-septic law nonlinearities. Results Phys. 2020, 103021. [Google Scholar] [CrossRef]
- Imran, M.A.; Ullah, N.; Rehman, H.U.; Baleanu, D. Optical solitons for conformable space-time fractional non-linear model. J. Math. Comput. Sci. 2022, 27, 28–41. [Google Scholar]
- Faridi, W.A.; Imran, M.A.; Jhangeer, A.; Yusuf, A.; Sulaiman, T.A. The weakly non linear waves propagation for Kelvin–Helmholtz instability in the magnetohydrodynamics fow impelled by fractional theory. Opt. Quantum Electron. 2023, 55, 172. [Google Scholar] [CrossRef]
- Majid, S.Z.; Faridi, W.A.; Asjad, M.I.; Abd El-Rahman, M.; Eldin, S.M. Explicit Soliton Structure Formation for the Riemann Wave Equation and a Sensitive Demonstration. Fractal Fract. 2023, 7, 102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).