Abstract
In a famous architectural discussion, Colin Rowe links the geometric properties of two sixteenth century villas by Andrea Palladio and two twentieth century villas by the architect Le Corbusier. Rowe observed that different structural systems produced heightened geometric complexity in cross sections through Palladio’s villas and in Le Corbusier’s plans. Rowe also described a particular type of geometric scaling in portions of the four villas which he partially explains as a type of mathematical ‘natural beauty’ akin to the golden ratio and Fibonacci sequence. In his writings, Rowe refers to several geometric properties that encapsulate complex, scaled structures, but he lacked a mathematical system to rigorously describe and test his ideas. The present paper utilises the box-counting method for calculating fractal dimensions to analyse 100 images, consisting of architectural plans, sections, and elevations of the four villas and two Fibonacci sequences, to test Rowe’s ideas. Ultimately, the results of this research do not support the majority of Rowe’s claims about geometric complexity in the villas of Palladio and Le Corbusier, but they do provide insights into Rowe’s discussion of geometric scaling and the properties of four famous houses.
1. Introduction
Fractal dimension analysis continues to be widely used in architectural research as a means of illuminating a range for geometric properties of buildings [1,2,3,4,5]. Architectural researchers have also developed discipline-specific methodological refinements [6] and application types to address questions about perceptions of spaces and forms and correspondence with neurophysiological responses [7,8,9,10]. Many applications of fractal dimension analysis in architecture are also automated or integrated into design software [11,12]. However, because the research questions which are important in architecture are often qualitative and contingent, research applying fractal dimensions to architecture tends to use a combination of mathematical data (often small sets) and basic statistical analysis to support qualitative discussion and debate. Such an approach is used in this paper to investigate one aspect of Colin Rowe’s complex comparison of Neo-Classical and Modernist architecture.
Colin Rowe was one of the twentieth century’s most significant architectural scholars. In his most famous work, The Mathematics of the Ideal Villa [13], he offered a unexpected argument comparing two villas by Italian architect Andrea Palladio and two by Swiss–French architect Le Corbusier. While both architects are known for their freestanding, geometrically derived designs, upon initial examination, their works appear to have little in common. Palladio’s sixteenth century Italian villas are strongly symmetrical, with tightly controlled proportions, whereas Le Corbusier’s twentieth century villas are abstract, free-form, or asymmetrical. Despite what appear to be obvious differences between these works, Rowe revealed a range of previously unrecognised similarities, starting with the same rhythmic pattern in their planning structures (the geometry of the grids of columns that run through the villas to create a stable structure). Rowe develops this observation to demonstrate that these structural systems and building materials intrinsically lead to diverse architectural expressions, while retaining a common underlying geometric language. For example, Palladio’s architecture, as catalogued in his I Quattro Libri Dell’architettura (The Four Books of Architecture) [14], relied on a planar grid of load-bearing masonry walls, supporting vaulted or domed structures, leading to the creation of cellular rooms with restricted dimensions in the horizontal plane but more freedom in their vertical expression. In contrast, Rowe notes that Le Corbusier utilised the ‘dom-ino’ system of construction—comprising reinforced concrete floor plates supported by a slender grid of columns—providing for unrestricted architectural expression in the horizontal plane (the floor plan) at the cost of significant limitations to creativity in the vertical plane (the cross sections). Thereafter, Rowe offers a series of observations about patterns in the vertical complexity of Palladio (that is, in the cross-sectional properties of these villas) and in the horizontal complexity of Le Corbusier (that is, in planning of rooms or spaces in these villas). However, these claims, and his explanation for the architectural and mathematical patterns they rely upon, have never been critically tested.
One of the reasons Rowe’s arguments have never been tested is that his descriptions of the geometry of these villas merge both poetic and mathematical interpretations. For example, Rowe proposes that both Palladio’s and Le Corbusier’s designs ‘share a common standard, a mathematical one, defined by Wren as “natural beauty”’ [13] (p. 102). For Rowe, natural beauty is about both geometric proportion and scaling, and he claims it is seen in different parts of Palladio’s and Le Corbusier’s villas. Rowe then suggests that this natural beauty is akin to that of the golden section, which relies on nesting of similar proportions, wherein a larger geometry can be scaled down to neatly fit into a smaller one. Rowe further highlights how, in these nested geometric systems, “elaborations in detail of the dominant schema [are] complicated by its interplay with a subsidiary system” [13] (p. 103). This is a different type of reference to the scaling of a larger geometric system into a smaller one. Throughout his descriptions of the two architect’s works, it appears that Rowe is seeking a language and a system of mathematics that could comprehensively encapsulate their diverse levels of geometric complexity. He even suggests that this un-named pattern could be thought of as a “symbiosis of systems” [15] (p. 13) in the villas, another reference to a recurring, scaled set of interconnected geometries.
In the 1940s, when Rowe wrote The Mathematics of the Ideal Villa, he did not have access to a method that could encapsulate complex geometric patterns across scales. This lack of a mathematical system, and an associated method for measuring these properties, has meant that this is one part of Rowe’s theory that has not been tested. A catalyst for the present paper is the observation that Rowe’s description has parallels to fractal geometry [16], and that fractal dimensions could be used to examine some of his ideas about complexity. Because Rowe was unaware of fractals and his descriptions are imprecise (merging references to mathematics with ones from philosophy and art), the present paper cannot prove or disprove his argument, but it can illuminate possible readings of his intentions. By measuring the fractal dimensions of elevations, plans, and cross sections from the four villas Rowe described, this paper develops a detailed reading of the mathematical similarities and differences of the two architect’s works.
The four cases examined in this paper are Palladio’s villas Malcontenta (also known as the Villa Foscari) and Rotonda and Le Corbusier’s villas Stein (also known as ‘Garches’), and Savoye. The following sections examine Rowe’s discussion of planar complexity and mathematical proportions in these works and develops two main hypotheses based on this discussion. Thereafter, the paper introduces a method for measuring fractal dimensions in architecture, along with the methodological variables used to ensure an accurate and repeatable analysis. Finally, the results are reported, and their implications are discussed in terms of the formal hypotheses and Rowe’s legacy.
1.1. Rowe’s Arguments about Palladio and Le Corbusier
Andrea Palladio (1508–1580) holds a pre-eminent position in architectural history. Much of his fame can be traced to the publication of I Quattro Libri Dell’architettura [14,17], a richly illustrated and widely translated treatise that documents both the classical architecture of ancient Rome, and Palladio’s own classically inspired works. Palladio’s work has since been heralded for its rigorous geometric proportions and clarity [18], and the term ‘Palladian’ has become synonymous with the Neo-Classical style, being the revival of classical Roman or Greek architecture. Probably his most famous works are his two freestanding villas, Malcontenta (circa 1560) and Rotonda (circa 1592) (Figure 1). In contrast, Le Corbusier (1887–1965) was a pioneer of modernism, a movement inspired by the types of emerging technology found in automobiles, aircraft, and ships, and is famous for white, unadorned, geometric architecture. In attempting to develop an aesthetic that reflected his society and era, Le Corbusier developed five architectural strategies that coalesced into a machine a habiter—a machine for living [19]. One of these strategies was the use of reinforced concrete slabs supported by slender columns. This system, which Le Corbusier referred to as ‘dom-ino’ construction, allowed him a previously unattainable level of freedom to shape the planning of rooms in any way he desired, including having extensive windows. Two of his most well-known houses are the 1927 Villa Stein and the 1931 Villa Savoye (Figure 2).

Figure 1.
Perspective views of Palladio’s Villa Malcontenta (left) and Villa Rotonda (right).

Figure 2.
Perspective views of Le Corbusier’s Villa Stein (left) and Villa Savoye (right).
Colin Rowe (1920–1999) was a British-born, American-naturalised architectural scholar and teacher who influenced a generation of designers and researchers. While he wrote several major works in his career [20,21,22], his most famous essay, later revised and expanded, was The Mathematics of the Ideal Villa. Rowe’s starting point for this work was the observation, later revealed as a ‘strawman’ (a proposition which has been set up to be rejected, and replaced by another), that Palladio and Le Corbusier both used a similar ‘nine-square’ structural grid to arrange their plans. The architectural expression of this structural grid differs, however, because of the technology available at the time; stone for Palladio and concrete for Le Corbusier. Palladio’s heavy stone structure restricts his planning of rooms, but provides relative freedom for their heights, or cross sections. In contrast, Le Corbusier’s concrete structure does the reverse; the grid of thin columns frees his planning of rooms, but the horizontal floor plates restrict variations to the cross section. This observation is the catalyst for Rowe to propose a series of increasingly rich and complex geometric relationships between the four villas.
Rowe observes that “Palladio’s structural system makes it almost necessary to repeat the same plan on every level of the building” [13] (p. 101), whereas Le Corbusier’s structure provides a more “flexible arrangement” [13] (p. 101) for every level of the plan (Figure 3). In contrast, Palladio is free to use “vertical extension into arch and vault, diagonal roof line and parapet [to vary] the geometric asperities of his cube” [13] (p. 103), which is something Le Corbusier at “Garches is unable to allow himself” [13] (p. 103). Emphasising this distinction, for Rowe, the planning of Palladio’s Villa Malcontenta—“a cruciform hall with, symmetrically disposed about it, two suites of three rooms each and two staircases” [13] (p. 6),—is an arrangement of refined simplicity. Ultimately, Palladio “sought complete clarity of plan, the most lucid organization of conventional elements based on symmetry as the most memorable form of order, and mathematics as the supreme sanction in the world of external forms” [13] (p. 103). In contrast, in Le Corbusier’s Villa Stein, “there is nothing so readily describable” [15] (p. 6). Le Corbusier’s planning includes a Z-shaped space containing asymmetrical stairs, a floor void, a penetrating terrace, a dining room, a library, and a fragmented cross axis.

Figure 3.
Cutaway plan views of Palladio’s Villa Malcontenta (left) and Le Corbusier’s Villa Stein (right).
Rowe eloquently summarises the affordances and limitations of Palladio’s and Le Corbusier’s structural systems with the now-famous statement: “free section is replaced by free plan, paralysed plan by paralysed section; and the limitations in both cases are equally severe; as though the solid wall structure had been turned on its side, the former complexities of section and subtleties of elevation are now transferred to plan” [13] (p. 103). Another way to understand this proposition is that the greater vertical freedom afforded to Palladio results in a greater level of complexity in his cross sections when compared to his plans, whereas the opposite is true for Le Corbusier. Furthermore, these characteristics have impacts on the villas’ elevations. Where Palladio’s elevations directly reflect their underlying cross sections, coupled with the limited window openings afforded by stone construction, Le Corbusier’s façades are unhindered by structural concerns. This means that the complexity of Le Corbusier’s plans may result in increased complexity in elevations, particularly at the front and rear. The situation is, however, a little different for the more famous pair of villas in Rowe’s discussion, which Rowe describes as having a more genial effect due to the architects diffusing their treatment of the facades through all four elevations, effectively reducing the intensity of their impact. In summary, Rowe’s arguments about the complexity of plans, sections, and elevations can all potentially be investigated by measuring and comparing the fractal dimensions of the four villas.
1.2. Scale-Free Self-Similarity and Relationship to the Golden Ratio
The rationale for using fractal dimensions to investigate Rowe’s geometric ‘symbiosis of systems’ at least partially reflects his discussion of a range of proportional scales (harmonic numbers, golden ratios, Fibonacci sequences, etc.). Rowe even makes explicit reference to architect Christopher Wren’s argument that natural beauty is derived from the geometric equality and proportions of ‘regular shapes’, such as the square and circle, which he promoted as the most beautiful, followed by the parallelogram and oval, that share a common basis in self-similarity over multiple scales. While golden ratios and proportional systems of this type are, at best, ‘trivial fractals’, Rowe did not have any alternative language to define the phenomenon of distributed geometric complexity that he was observing.
In describing the villas Stein and Malcontenta as “blocks of corresponding volume, each measuring eight units in length, by five and a half in breadth, by five in height” [13] (p. 101), Rowe conceives of each villa, excluding roof treatments, as having identical scale-free proportions. Some of these proportions, Rowe suggests, evoke the golden ratio, or approximations of the Fibonacci sequence. Thus, a length of eight units and a height of five units might reflect an architectural application of the Fibonacci sequence, and Rowe’s identification of the 2:1:2:1:2 rhythm of the structural bays in these villas may represent the first numbers of the sequence (1:2). However, even if this argument is accepted prima facie, in the sections and facades of these buildings, a depth of five-and-a-half units and a height of five units does not align with this sequence, and the rhythm of structural bays in both villas is different (Figure 4).

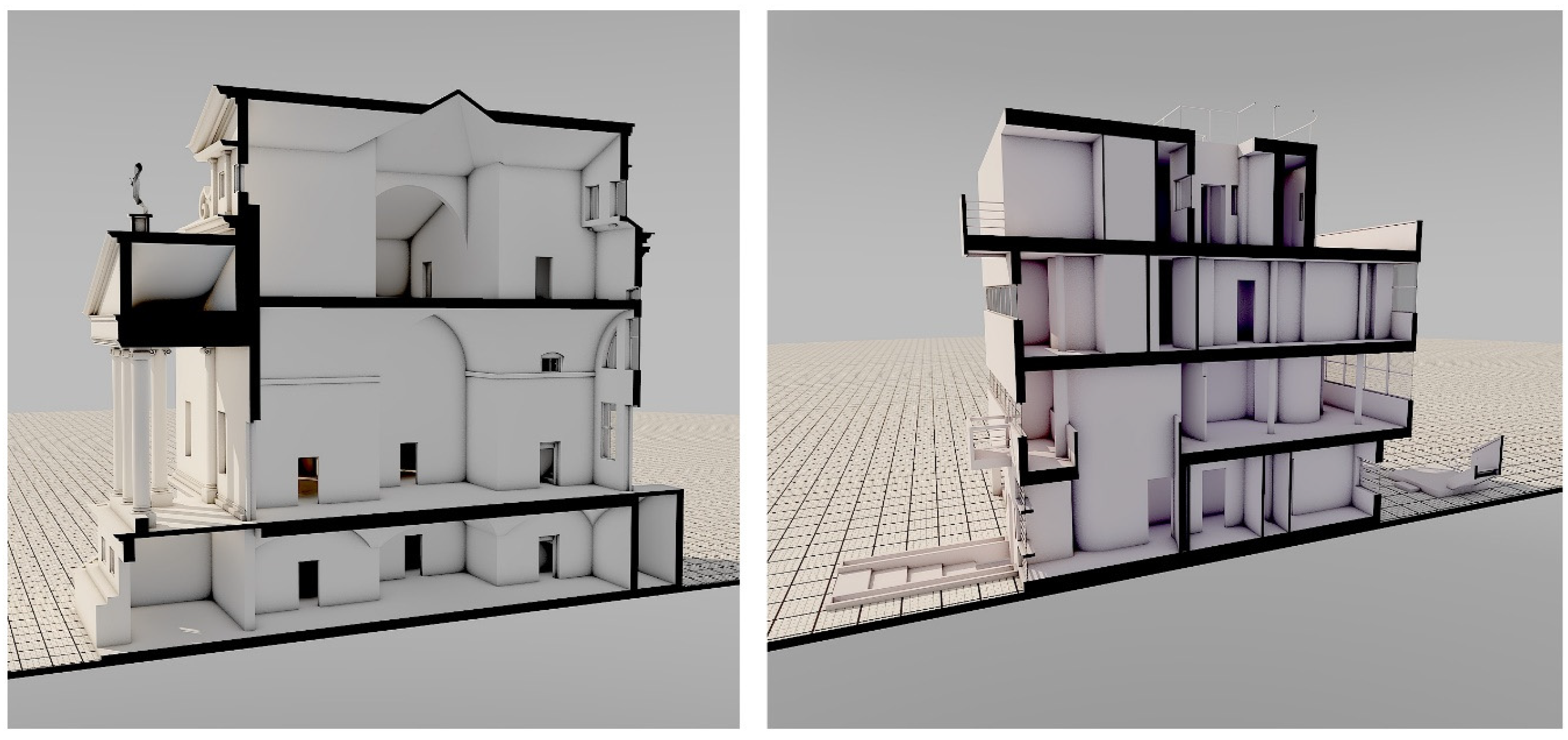
Figure 4.
Cutaway cross section through Palladio’s Villa Malcontenta (left) and Le Corbusier’s Villa Stein (right).
In Palladio’s villa floor plans, Rowe observes that “the rooms comprising the suites of three can be read as a progression from a 3:4 to 2:3 relationship. They are numbered 12:16, 16:16, and 16:24.” [13] (p. 103). Here, the ratios 1:1 (16:16) and 2:3 fall within the Fibonacci sequence, while the ratio 3:4 does not; however, the ratio 4:3 is a harmonic proportion that was revered at Palladio’s time, whereas the 1:1 and 2:3 ratios were not. Once again, Rowe does not address the extent to which the partial presence of a golden ratio appears in Palladio’s villas, although it should be noted that all three room–ratio dimensions are among those that Palladio identified as being particularly meritorious in I Quattro Libri Dell’architettura. While Rowe’s focus on room dimensions in the Villa Malcontenta only partially conforms to approximations of the golden ratio, the existence of proportional, harmonic, and golden ratios in Palladio’s plans has been the subject of significant debate [23,24,25,26]. Palladio demonstrated the geometric construction of the geometric mean, the arithmetic mean, and the harmonic mean [27], proposing these values as room heights, and it has been demonstrated that room heights in the Villa Rotonda closely approximate the values of the arithmetic mean [25].
One issue with identifying harmonic and golden ratios within Palladio’s architecture arises from discrepancies between the built works and the drawings of them published in I Quattro Libri Dell’architettura, with the latter being considered idealised versions that are unconstrained by the realities of a site [23]. Despite this, researchers have shown that only 54% of room dimensions in I Quattro Libri Dell’architettura conform to harmonic numbers [28]. There are, however, several Palladian designs where most rooms have harmonic dimensions, including the two Rowe chose as examples (Villa Malcontenta = 71%, Villa Rotonda = 66%).
In a later revision of The Mathematics of the Ideal Villa, Rowe was eager to dismiss issues arising from approximations of the golden ratio and differences between Palladio’s built works and their idealised drawings. “[I]f the ratio of 3:5 = 5:8 is only [Rowe states] an approximation to that of the golden section, and if the ideal measurement of Palladio’s rooms does not concur with what is their actual size, this is to be expected and it should not be considered useful to enlarge upon these inconsistencies” [15] (p. 11). Nevertheless, Rowe does suggest that approximations of the golden ratio in the form of a Fibonacci sequence are most likely to be present in the front and rear facades of the Villa Stein, followed by the plans of the Villa Malcontenta. However, as researchers have observed, anyone seeking superficial evidence of the golden ratio is likely to find it, regardless of whether or not the designer intended it [29]. An alternative approach to examining proportional systems across multiple scales in a building would involve measuring the fractal dimensions of their plans, sections, and elevations and comparing these with the fractal dimensions of the proportional systems; for example, the golden ratio or the Fibonacci sequence.
2. Research Hypotheses
2.1. Hypothesis 1
In The Mathematics of the Ideal Villa, Rowe differentiates between the architecture of Palladio and Le Corbusier through a discussion of the structural systems and their geometric implications. The first hypothesis is about Rowe’s claims about the differences in complexity of the plans and cross sections of the four villas. In addition, Rowe suggests that the complexity should be more pronounced in Palladio’s Villa Malcontenta and Le Corbusier’s Villa Stein than in the Villa Rotonda and Villa Savoye, respectively. As such, the first hypothesis has three parts:
H1.1.
In Palladio’s villas Malcontenta and Rotonda, the mean D of the cross sections in each will be greater than that of the plans of each.
H1.2.
In Le Corbusier’s villas Stein and Savoye, the mean D of the plans in each will be greater than that of the cross sections of each.
H1.3.
The mean D values of plans and elevations of the villas Malcontenta and Stein will exceed the equivalent for the villas Rotonda and Savoye, respectively.
It is notable that Rowe does not directly comment on the relationship between complexity in Palladio’s villas and in Le Corbusier’s, perhaps suggesting that there will not necessarily be one. The results developed for this paper are also used to discuss this omission.
2.2. Hypothesis 2
In The Mathematics of the Ideal Villa, Rowe refers to ratios associated with ‘natural beauty’, the most common being harmonic numbers and the Fibonacci sequence. One of Rowe’s suggestions is that an approximation of the golden ratio in the form of a Fibonacci sequence of rectangles is most likely to be present in the front and rear facades of the Villa Stein, followed by the plans of the Villa Malcontenta. This can be framed as two hypotheses.
H2.1.
The fractal dimensions of the front and rear facades of Le Corbusier’s Villa Stein will be closer to the fractal dimension of the Fibonacci sequence of rectangles than any of the other six elevations of Le Corbusier’s villas.
H2.2.
The fractal dimension of the piano nobile (main floor) of Palladio’s Villa Malcontenta will be closer to the fractal dimension of the Fibonacci sequence of rectangles than the plans of the Villa Rotonda.
For the purposes of testing, the Fibonacci sequence of rectangles is defined as the first fourteen scales of a Fibonacci spiral. The number of iterations (n = 10) reflects the software’s capacity to develop a statistically reliable result.
3. Measuring Fractal Dimensions in Architecture
Fractal Dimensions and Applications in Architectural Research
In architectural scholarship, fractal analysis is a common method for quantifying the “the relative density and diversity of geometric information in an image” [1] (p. 3). While this field of research does present alternative means of quantitatively measuring complexity, few of these approaches are as broadly useful and offer methods that minimise qualitative interpretations of data prior to generating quantitative measures. For example, previous research has used two-dimensional isovist analysis to calculate complexity in architectural plans, and, in theory, this method may also be applied to architectural sections [10]. However, this approach is incapable of evaluating the facades, or elevations, of buildings. Other analytical methods that can be used to evaluate formal complexity include the use of shape grammars; however, this approach relies on the researcher developing a qualitative or speculative interpretation of the design that is formally codified as a shape grammar, and this grammar can then be used to calculate the complexity of the design [30]. Other approaches such as those based on thermodynamics are also capable of producing quantitative measures of complexity but once again rely on qualitative assessments to generate quantitative data [31].
A fractal is a fraction of a dimension, and, in the case of a two dimensional architectural representation of a building, fractal analysis will reveal a result between 1 and 2, where a lower result indicates low complexity and a higher result indicates greater complexity [32,33]. One simple definition of fractal geometry is “a visual image some features of which repeat at many different scales” [7] (p. 164). An important distinction to make between architectural drawings and pure fractals, such as the Koch Snowflake, is that the pure fractal may contain an infinite number of iterations of scale-free self-similarity whereas architectural representations are limited by various media constraints, such as line thicknesses and image sizes.
There are multiple methods for determining the fractal dimension (D) of an image. Mandelbrot proposed several alternative approaches, with one, the box-counting method, being refined through multiple variations [1,16]. Furthermore, assessments of the different methods have revealed that, for the majority of fractal analysis subjects—say, in which D occupies a range of 1.2 through 1.8—box-counting is often the most useful and accurate [34,35]. While the box-counting method is well known, a brief description is provided here of how it works.
The process for determining the fractal dimension of an image using the box-counting method relies on overlaying grids of multiple scales to assess the density of information in the image. This process operates by overlaying the image with a grid and recording the number of boxes that contain information (N(S1)), then overlaying the image with a smaller scale grid, and again recording the number of boxes that contain information (N(S2)). The information density recorded by each grid is then compared using a log–log plot of the number of boxes containing information (log[N(S#)]) versus the size of each grid (log[1/S#]). The slope of the least-squares regression line of the log–log plot is the fractal dimension of the image and, for a comparison of two grids, can be calculated as:
To improve the accuracy of the results, the box-counting process must be undertaken through multiple iterations, using grids of different sizes. Several methodological variants have also been shown to shape the accuracy of the measurement, such as the scaling coefficient between grid sizes [1]. The box-counting theorem for multiple iterations is expressed as:
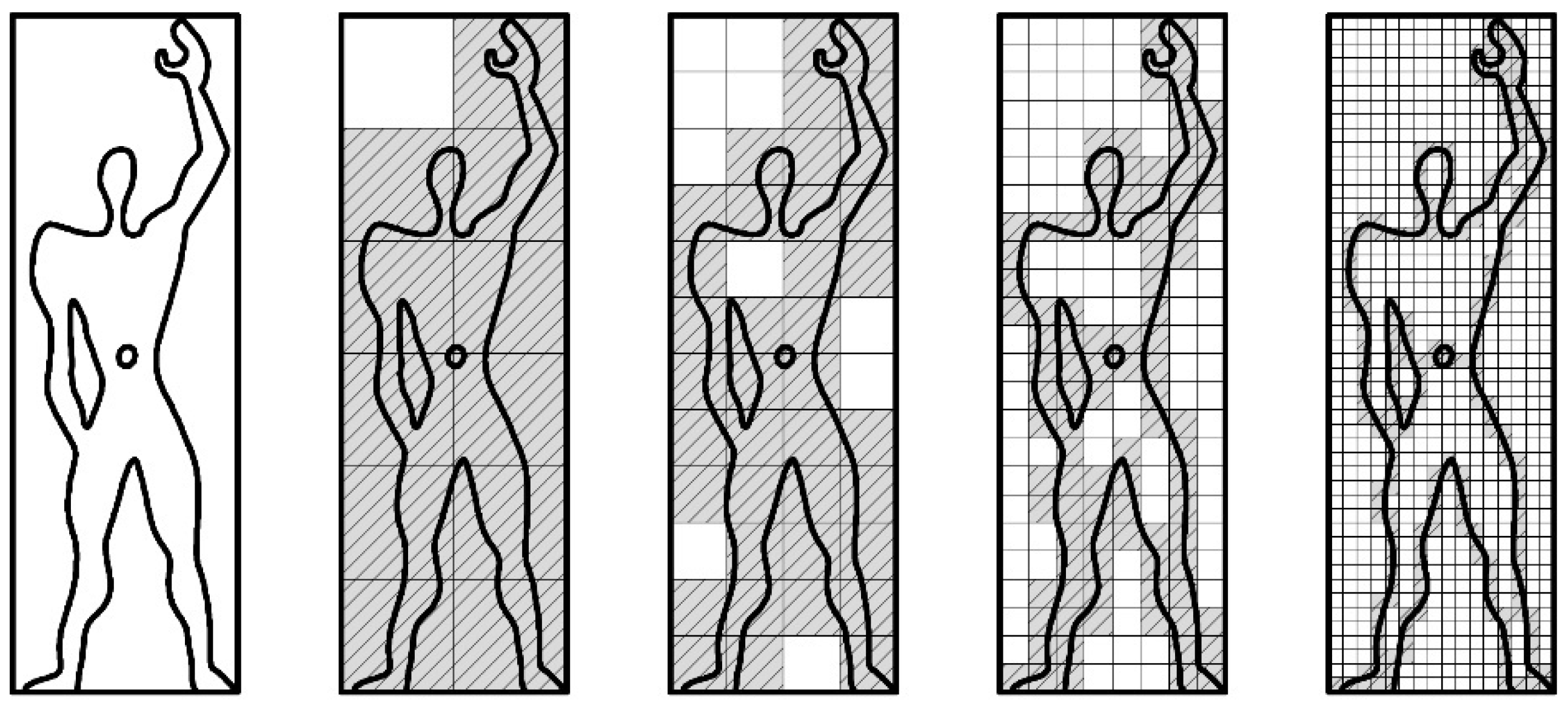
Applying the box-counting method to Le Corbusier’s Modulor (Figure 5), a stylised depiction of the human form based on the golden ratio and Fibonacci numbers, reveals that the fractal dimension (D) is 1.4428 when using just four different grids. In the first grid of 2 by 6 boxes, information is recorded in 11 boxes; the second grid of 4 by 12 boxes records information in 38 boxes, the third grid of 8 by 24 boxes records information in 97 boxes, and the final grid of 16 by 48 boxes records information in 221 boxes. A log–log plot of these results reveals a regression line with a slope of y = 3.0148x − 21.3040 and linear correlation of R2 = 0.9995. Of course, an analysis of a simple image consisting of only three iterations is unlikely to produce an accurate result. For this reason, most researchers use software packages to develop results, one example of which is Image J software [36] employing the FracLac plug-in [37]. Using this software, Le Corbusier’s Modulor Man has a D value of 1.1207, a result befitting a simple line image.
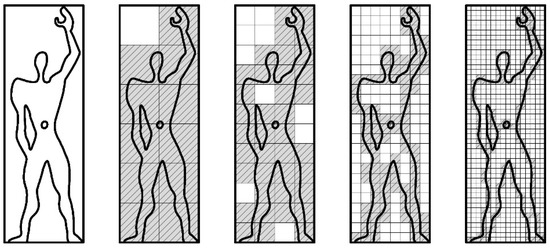
Figure 5.
Four stages of box-counting for Le Corbusier’s Modulor with hatching to indicate grids that contain information.
The history of architectural interest in fractal geometry dates to 1978, not long after the first English translation of Mandelbrot’s work [38]. The first applications of the box-counting method to architectural and urban cases were typically published in the 1990s [39] (Bovill 1996). In these early works, researchers often employed manual variations of the method (drawn by hand) to develop estimates of D for the elevations of buildings or for urban plans. These applications, however, tended to rely on only two or three scales of comparison, undermining their accuracy, and there were no accepted image and representation standards, leading to lack of repeatability [40,41,42,43]. Contemporary researchers are more aware of the need to explicitly state methodological considerations and image standards, and analyses are now typically undertaken using specialised software that increases reliability and accuracy while reducing errors [6,11,12,44,45].
In past research, the complexity properties of several hundred buildings have been measured with fractal dimensions, and, in some cases, comparisons constructed between buildings, cities, and natural forms [4]. Le Corbusier’s domestic architecture has been the subject of fractal dimension analysis on multiple occasions. The elevations of the Villa Savoye have, for example, been measured and compared in several studies [6,42,46,47]. In contrast, Palladio’s works have not formally been investigated using fractal analysis, although there are studies which examine the classical Greek and Roman orders (types of column capitals), as well as associated classical porticos and entries, which have connections to Palladian architecture [47,48]. Previous applications of fractal analysis to 625 plans and elevations of 85 houses by 13 architects, including Le Corbusier, in a range of different styles indicates that the fractal dimension of architectural elevations fall within a range of 1.2183 > D >1.5906, with a mean of D = 1.4148, and plans fall within a range of 1.2427 > D > 1.4955, with a mean value of D = 1.3645 [1]. However, this past analysis does not incorporate architectural section drawings.
The standard architectural application of fractal dimension analysis is a two-dimensional line drawing of a plan (a top-down view created using a horizontal cut through the building), elevation (a side view of the building), or cross section (a side view of a cut, typically vertically through the building, to expose the heights of spaces inside). Perspective images are only rarely used, because the angle of viewing changes the amount of geometry visible in an image. In contrast, orthographic drawings such as plans and elevations, which do not replicate the way humans visually experience the world, provide a more consistent and repeatable subject of analysis [8,46,49]. Most architectural analysis also relies on binary black and white images, which typically omit surface textures of the buildings being analysed. While this is the most repeatable approach, it does not depict the building in the way in which we experience the world [9]. Methodological variations, such as the differential box-counting approach, are compatible with non-binary images but also require strict control of variables such as the direction and volume of illumination affecting the surface of the building [1]. For these reasons, it is important to acknowledge that there are architectural features and properties that contribute to the perceived complexity of a building but are omitted from a fractal analysis because they undermine capacity for validation or comparative studies. Despite these limitations, the box-counting method has been used in research that has demonstrated links between fractal dimensions and human perceptions or environmental preferences when considering aspects of the built environment [50,51].
4. Research Methodology
The method applied in this paper to test the hypotheses consists of three stages: (1) preparation of images for measuring (villa plans, sections, elevations, and the Fibonacci sequence of rectangles); (2) application of the box-counting method to these images using software; and (3) extracting derived measures, typically mean results for plans, sections, and elevations, to test the hypotheses.
4.1. Stage 1: Image Preparation
The plans, sections, and elevations analysed in this research were extracted from digital 3D models of the villas. The images depict the ‘third level of detail’ which is commonly used in the fractal analysis of buildings. The ‘third level’ depicts the building outline, all major forms (the primary modulation or shaping of the design), and secondary forms such as basic mullions in windows which are visible at a scale of 1:100. The images are all binary (black and white), use a line thickness of one pixel, and have a resolution of 300dpi, and the content of the image (the plan, elevation, or section) is surrounded by a border of white space equal to 25% of the length of the shorter side. These properties produce images of different sizes, with plans ranging between 1976 × 2116 and 8689 × 8689 pixels, sections ranging between 2652 × 1141 and 7220 × 4284 pixels, and elevations ranging between 2796 × 1578 and 7220 × 4284 pixels. These properties also replicate or exceed the recommended minimum standards previously identified for achieving accurate fractal dimension results for architecture [1].
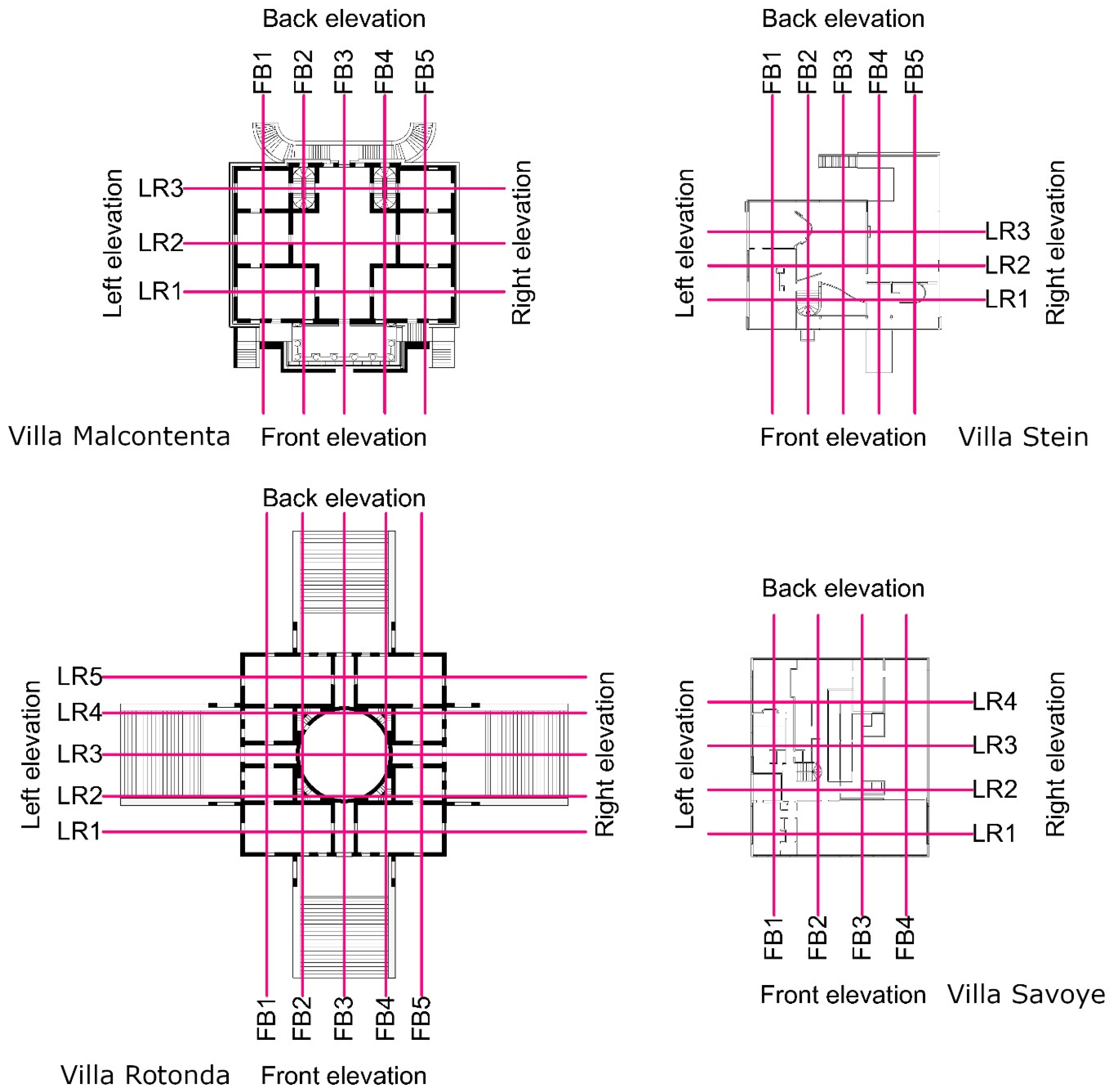
A plan is a horizontally oriented slice through a building, a section is a vertically oriented slice through a building, and both plans and sections are prepared with ‘unrestricted’ view depths. Architectural drawings with unrestricted view depth will show architectural features ‘beyond’ the plane slicing through the building. A plan with an unrestricted view depth will display architectural features of the floors and lower storeys that are not obscured by architectural elements closer to the cutting plane. Similarly, a section with an unrestricted view depth will display windows, doors, and other architectural features in the background that are not obscured by closer elements. The plans of the villas are constructed at a height of 1.2 m above the floor. Architectural sections are rarely studied using fractal analysis, and, in the present research, each section is extracted through a plane located along the centreline of the structural bays, such that, in the case of Palladio’s villas, the section cuts through the highest point of vaulted and domed ceilings (Figure 6). Each villa has a ‘front’ elevation that contains the main formal entrance, an opposite ‘back’ elevation, and, when viewed from the front of the villa, a ‘left’ and ‘right’ elevation. Each section cutting plane is numbered commencing from the front and left elevations and includes coding to indicate the orientation of the cutting plane, location of cutting plane, and direction of view. Thus, for example, section ‘FB 1L’ is a section cutting from the front to the back (FB) of the villa, located on the first cutting plane (1), and looking toward the left elevation (L).

Figure 6.
Location map for cross section planes through each villa.
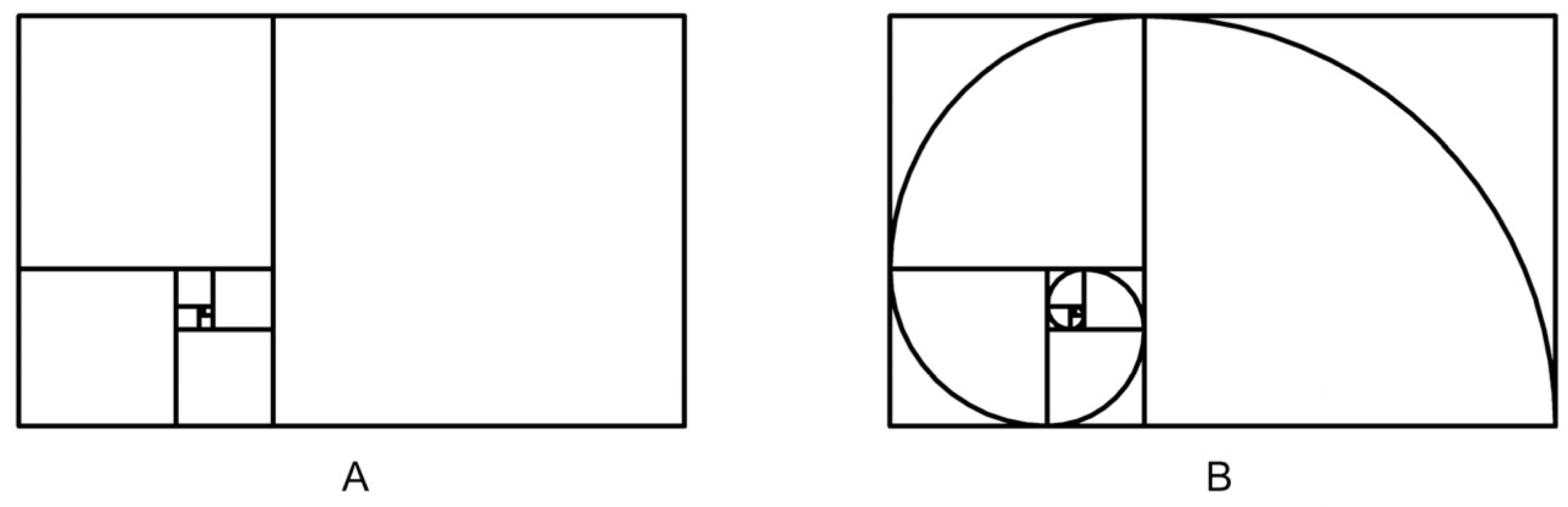
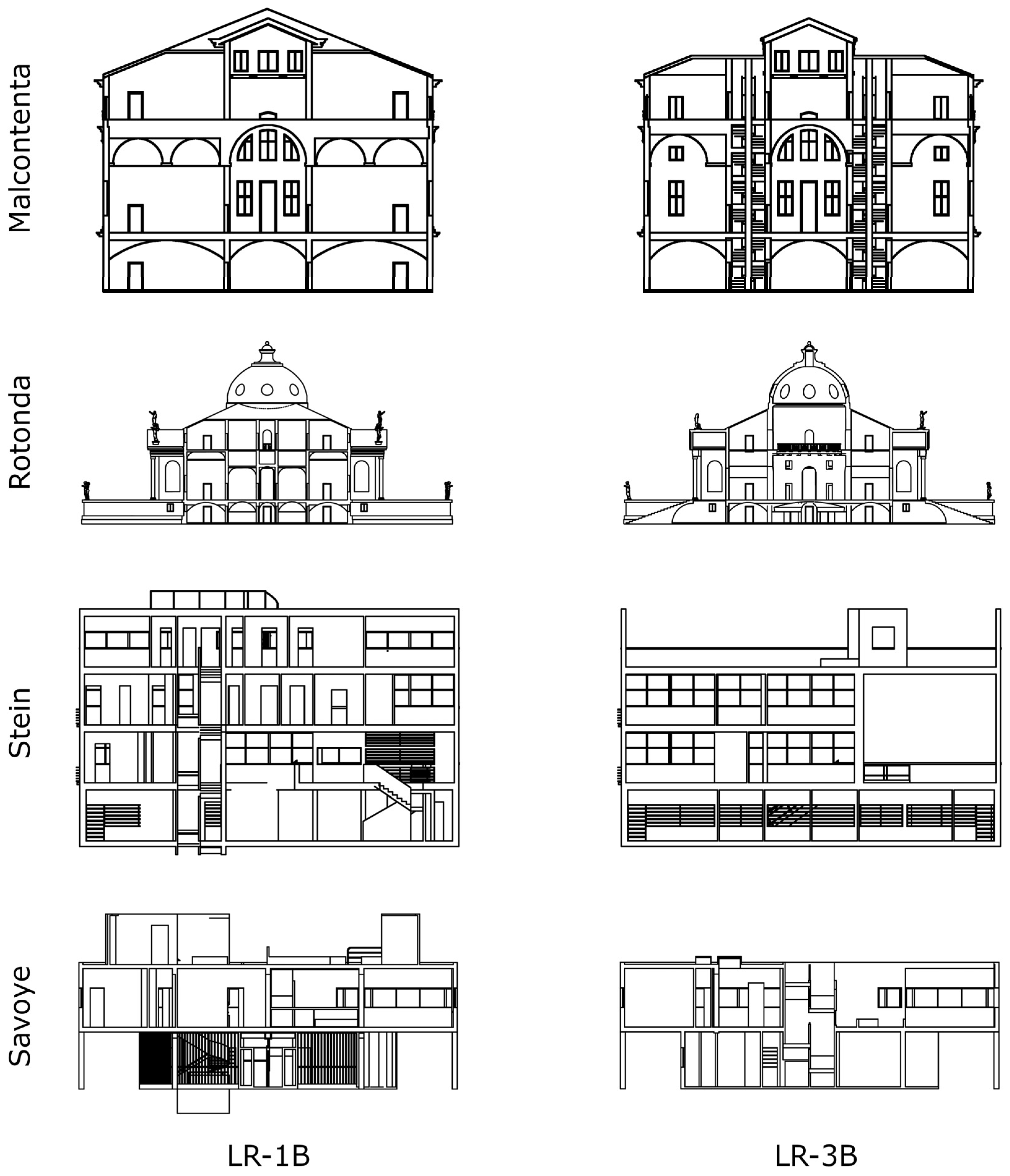
The architectural models from which the drawings are developed for this paper are derived from published sources. The models of Le Corbusier’s villas are developed from Le Corbusier: Houses [52] which is a common source for computational analysis of these works. The models of Palladio’s villas are based primarily on the architect’s own illustrations published in I Quattro Libri Dell’architettura [14]. As noted previously, these are typically understood as ‘idealised’ versions of each villa, and they differ from the constructed versions in many ways. For the present research, wherever possible, Palladio’s illustrations form the basis of the models being analysed. If, however, there is insufficient information in the drawings in I Quattro Libri Dell’architettura to construct a full model, additional information is sourced from the constructed works. One example of a difference between the idealised and constructed versions of the same works is seen at the rear of the Villa Malcontenta. Palladio’s illustrations show elaborate external stairs (which are included in the model used in the present research), whereas these are absent in the constructed villa. A less significant difference is that the constructed version of the Villa Rotonda includes several small chimneys that are absent from Palladio’s illustrations and are excluded from the analysed drawings. The arrangement of internal stairs of the Villa Malcontenta is not completely clear in the idealised version, and so has been modelled to reflect the constructed version. The statues in the analysed drawings of both of Palladio’s villas are generic models with a similar level of formal complexity to the statues in the illustrations and constructed designs. The representation of a Fibonacci spiral is constructed to 10 iterations by drawing boxes corresponding to the size of each of the first 11 numbers (Figure 7). As a point of reference, the same Fibonacci sequence of boxes, modified to include 11 quarter-circle arcs forming a spiral, is also analysed, but does not contribute to the results of this research. In total, 100 images (16 elevations, 14 floor plans, 68 sections (Figure 8), and 2 representations of the Fibonacci sequence) were produced and their D values were measured in a consistent way.

Figure 7.
(A) Fibonacci sequence of boxes through 10 iterations and (B) the sequence with quarter arcs forming a spiral. To support legibility, line thicknesses are increased compared to the analysed images.

Figure 8.
Example sections LR-1B and LR-3B through each villa; note that villas are not shown to the same scale and line thicknesses are increased compared to the analysed images.
4.2. Stage 2: Computational Analysis
The fractal dimension of each image is calculated using Image J software v.1.53k [36] with the FracLac plug-in v.2015SEP090313a9330 [37]. The initial grid dimension is set at 25% of the length of the shorter side of the image, and the final grid dimensions is set at 10 pixels. The grid scaling coefficient for the analysis is 1.4142:1 (an approximation of √2:1). These settings align to best practice in the architecture field for achieving an accurate and replicable fractal dimension result [1]. One minor departure from the standard architectural method involves the starting position of the first grid. In the past, architectural analyses used a grid with an origin point at the top left corner of the image. In contrast, Image J software with the FracLac plug-in allows users to run multiple analyses on the same image with the results being provided both individually and as a mean value. The current research develops four analyses per image, one each with the grid origin point located at a corner of the image, and reports the mean values of these four analyses. This effectively negates the need for a single origin point for the grid and produces more robust outcomes.
4.3. Stage 3: Extracting Derived Measures
The final methodological stage simply calculates averages and standard deviations and Student’s t-tests of the results to allow, for example, a comparison of the average fractal dimension of all four elevations of a villa.
4.4. Limitations
One limitation of the analytical method is that it uses the standard ‘third level’ of architectural representation, which means the fractal dimension is of the building outline, major geometry, and secondary geometry, but excludes the texture of materials. This has no impact on measurements derived from Le Corbusier’s architecture, but some of the elevations of Palladio’s villas feature rusticated stonework and some of the interiors were designed to have murals, both of which could increase the volume of geometry measured in elevations and the unrestricted sections. While this could reduce the fractal dimension measurement, the inclusion of material texture is rare in architectural scholarship and previous research includes findings that architectural features such as “trim and ornament contribute more to an impression of detail than does texture” [53] (p. 95). A further limitation is simply that architecture is not fractal, in the sense that there is no defined Iterated Function System (IFS) generating it. Architecture does, however, have a distribution of geometry across a range of scales, which allows its fractal dimensions to be calculated and compared.
5. Results
5.1. Elevations
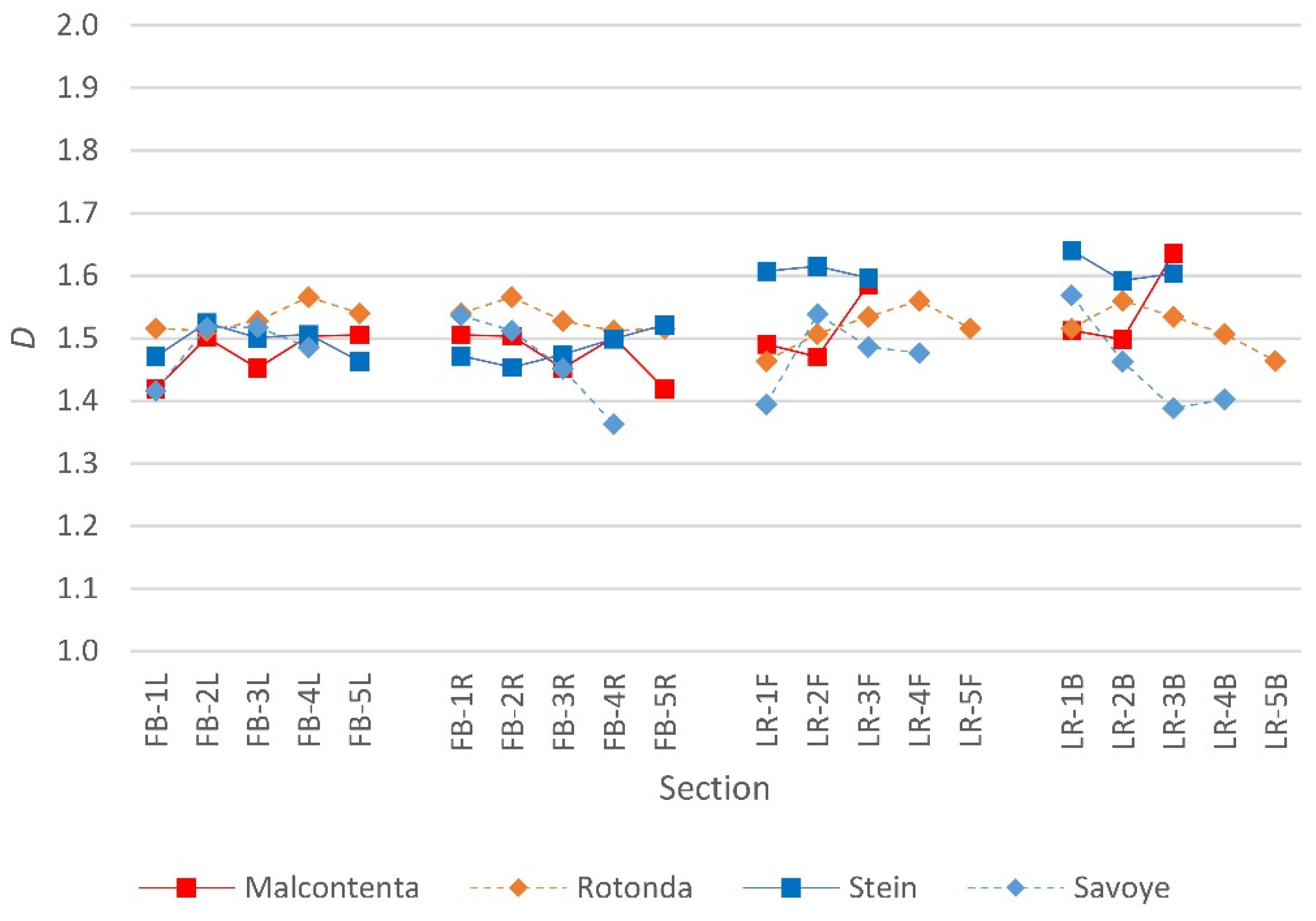
Fractal analysis in architectural research has traditionally focussed on elevation and plan drawings. The elevations of the Villa Rotonda produce the most consistent D values (see Table 1), largely due to the high level of symmetry in the design. The front and rear facades are essentially identical (D = 1.5855), as are the left and right facades (D = 1.5927). Furthermore, the difference between front/rear and left/right elevations is limited to the presence or absence of two windows and two wall niches.

Table 1.
D values of elevations.
In the remaining villas, the rear elevations have greater complexity. It might usually be expected that the front elevation would be foremost in the architect’s mind and receive a greater level of formal modulation or detailing, often to “address the visitor”, provide surveillance, or signal a point of entry or arrival [54,55]. This expectation is, however, arguably invalid in the specific cases of the Villas Malcontenta and Savoye. Both designs were also intended to be approached from the rear, the Villa Malcontenta occasionally receiving visitors arriving by barge via the canal behind the house, and at the Villa Savoye the visitor could be chauffeured down a long, sweeping driveway that passes under the rear façade and encircles the building to deposit visitors at the ‘front’ door. Indeed, arriving at the Villa Savoye through this procedure played a significant role in shaping the ground floor, the façade of which is curved in such a way as to allow a vehicle to circle the building. At the Villa Stein, the presence of a greater number of window mullions and roof-level architectural features which are largely hidden from the front of the building may be a contributing factor to the rear elevation having greater complexity than the front elevation.
5.2. Floor Plans
The villas have between three and five floor plans, with the Villa Stein having five levels including a roof terrace, whereas the villas Malcontenta and Rotonda contain three floor levels and the Villa Savoye has three floor levels, including a roof terrace. For this reason, the Villa Stein provides two additional data points compared to the remaining villas. The Palladian villas and the Villa Stein each have extensive external stairs providing access to the first floor and these stairs are visible on all floor plans. The Villa Rotonda has the most extensive external stairs, followed by the Villa Malcontenta, and it is likely that the presence of these stairs on all floor plans contributes to the higher fractal dimensions of these designs. Thus, the Villa Rotonda has the highest mean (D = 1.6091), followed by the Villa Malcontenta (D = 1.5256) and the Villa Stein (D = 1.3943), while the Villa Savoye develops the lowest visual complexity (D = 1.2961) in Table 2.

Table 2.
D values of floor plans.
5.3. Sections
The D values for sections highlight the symmetry of Palladio’s designs (Table 3). The Villa Malcontenta is symmetrical about a central front-to-rear axis and this is reflected in the results of the sections (Figure 9), which contrast to left-to-right sections that demonstrate higher visual complexity at the rear of the building. This higher complexity likely arises from these sections cutting through two sets of symmetrically arranged staircases, which increase the geometric information in the images compared to other restricted depth sections through the villa. The Villa Rotonda is similarly symmetrical in two axes (mean D = 1.5243 and SD = 0.0283), and this is also demonstrated in the results for the front-to-back and left-to-right sections. The most prominent discrepancy in sectional data is found in the Villa Savoye (mean D = 1.4736 and SD = 0.0625), where, for example, one section (FB-4R, D = 1.3626) cuts through the living room and level one terrace and is oriented toward a large wall with a wide horizonal opening, having relatively reduced complexity. As constructed, this opening provides extensive views of the surrounding terrain, a factor which is not recorded using this methodology. The same section line oriented in the opposite direction (FB-4L, D = 1.4853) captures significantly more visual complexity through the inclusion of the ramp leading from the ground to the first floor.

Table 3.
D values of sections.

Figure 9.
D values of sections.
6. Discussion
Rowe’s The Mathematics of the Ideal Villa discusses mathematical similarities and differences in the villas of Palladio and Le Corbusier that had not previously been observed, and later proposes that these observations should be rigorously tested. The current research fulfils a portion of this request by examining two hypotheses derived from Rowe’s writing.
6.1. Hypothesis 1
H1.1 states that in Palladio’s villas Malcontenta and Rotonda, the mean D of the cross sections in each will be greater than that of the plans of each. The mean D of the sections through Palladio’s Villa Malcontenta (D = 1.4973) is lower than the mean D of its plans (D = 1.5256). Similarly, the fractal dimensions of the sections through the Villa Rotonda (M = 1.5243, SD = 0.0283) are significantly lower, t(14.616) = -4.989, p < 0.001), than the D values of its plans (M = 1.6091, SD = 0.0546).
H1.2 states that in Le Corbusier’s villas Stein and Savoye, the mean D of the plans in each will be greater than that of the cross sections of each. Unexpectedly, the D values of the floor plans in the villas Stein and Savoye (M = 1.3943 and M = 1.2961, respectively) are significantly lower than the sections in the villas Stein and Savoye (M = 1.5337 and M = 1.4736, respectively). As summarised in Table 4, the D results do not support H1.1 and H1.2.

Table 4.
t-test results for H1.1 and H1.2.
H1.3 argues that the average result of the mean fractal dimensions of the plans and elevations of the villas Malcontenta and Stein, will exceed the equivalent for the villas Rotonda and Savoye, respectively. This hypothesis is partly supported by Le Corbusier’s villas through the pairing of the villas Stein and Savoye, but is unsupported by Palladio’s villas through the pairing of the villas Malcontenta and Rotonda (Table 5). Specifically, the fractal dimensions of the plans of the Villa Stein (M = 1.3943, SD = 0.0419), compared to those of the Villa Savoye (M = 1.2961, SD = 0.0804), are significantly higher, t(14.659) = 3.925, p < 0.001. However, this hypothesis is rejected by the other results in Table 5. Beyond the given hypotheses, interestingly, the fractal dimensions of the two Palladian villas’ plans (M = 1.5674, SD = 0.0693), compared to Le Corbusier’s designs (M = 1.3575, SD = 0.0755), are significantly higher, t(51.76) = 10.791, p < 0.001. The D values of the two Palladian villas’ elevations (M = 1.5691, SD = 0.0574), compared to Le Corbusier’s ones (M = 1.4590, SD = 0.0724), are also significantly higher, t(58.926) = 6.739, p < 0.001. There are, however, no differences in the fractal dimensions of sections, which may result from the particular cutting planes chosen, rather than their embedded complexities.

Table 5.
t-test results for H1.3.
6.2. Hypothesis 2
This second hypothesis focuses on Rowe’s discussion of the proportions and scaling of the golden section, approximated by the Fibonacci spiral, having informed the designs of Le Corbusier’s elevations and Palladio’s plans. A graphical representation of the first ten iterations (11 squares, numbers 1 through 89) of a Fibonacci sequence has a D of 1.0760, and for completeness, the same series of boxes with 11 quarter circles forming a spiral produces a D of 1.1663.
H2.1 anticipates that the D values of the front and rear facades of Le Corbusier’s Villa Stein are closer to the D value of the Fibonacci sequence of rectangles than any of the other six elevations of Le Corbusier’s villas. The front elevation of the Villa Stein is measured as D = 1.4733, which is 37% higher than for the Fibonacci sequence (D = 1.0760), and the rear elevation (D = 1.5897) is 47% higher, which is also the furthest of Le Corbusier’s elevations from the Fibonacci sequence. Therefore, Hypothesis 2.1 is not supported by these results.
H2.2 maintains that the D values of the piano nobile of Palladio’s Villa Malcontenta will be closer to the D of the Fibonacci spiral (D = 1.0760) than the plans of the Villa Rotonda. The piano nobile of the Villa Rotonda (D = 1.6591) exceeds the fractal dimension of the piano nobile of the Villa Malcontenta (D = 1.5701) and does not support the hypothesis.
6.3. Discussion
It should be acknowledged that there are several potential reasons why the results developed for the present research are largely unsupportive of the hypotheses. First, it is possible that Rowe’s argument is simply incorrect about these particular propositions. For example, while in theory Le Corbusier’s plans should be less constrained than his sections, in practice this doesn’t necessarily appear to be the case. Similarly, in theory Palladio’s sections should be freer than his plans to pursue complex spatial volumes, but in practice this isn’t true either. Second, it is possible that, despite Rowe’s many references to scaling geometry, complexity, and nested proportions, his ‘symbiosis of systems’ may be incompatible with fractal geometry. Rowe’s arguments may have been referring to something completely different, perhaps a designer’s sense of a type of deeper geometric order that can be perceived in the decisions the architects make, but which is not present in the walls, floors, and roofs of the four villas.
A further factor complicating this result is that Rowe never states whether he is referring to Palladio’s villas as they were built or the idealised versions in I Quattro Libri Dell’architettura. As noted previously, there are some differences between the two, including the elaborate external staircases on the rear façade of the Villa Malcontenta. Images in The Mathematics of the Ideal Villa also do not show those external stairs, leading to the possibility that Rowe was taking about the built version, but using modified illustrations of the idealised. Perhaps being aware of this, Rowe warns that “it should not be considered useful to enlarge upon these inconsistencies” [15] p. 11. It is possible that he is discussing a hybrid amalgam that incorporates the aspects of both versions that are most convenient to his narrative. Because of this, future research may benefit from repeating the current method using survey drawings of the constructed versions of Palladio’s villas
As a point of discussion, it is useful to consider the position of the present results within the context of other architectural works. Previous research has analysed plans and elevations of 85 domestic buildings by a range of 20th century architects and practices and reported average values for plans and elevations (D = 1.3645 and D = 1.4148 respectively) [1]. The mean fractal dimensions for all plans (D = 1.4553) and all sections (D = 1.5691) place the Palladian villas analysed in this paper within 8% and 11%, respectively, of the mean values of this broader study. These results identify that Palladio’s plans are most similar in terms of formal complexity to the Textile block houses of Frank Lloyd Wright, and Palladio’s elevations are most similar to the plans of Wright’s Prairie and Textile block houses. Wright’s prairie architecture is renowned for elevations consisting of relatively simple geometric compositions, but which exhibit a high level of architectural detail, bearing some formal parallels to the rectangular prisms that Rowe identifies as the basis of Palladio’s designs and which are then enhanced with detailed gabled porticos, bands of masonry, and window detailing. Wright is also famous for a planning strategy that commenced by laying out regular gridlines spaced at one-foot intervals, then positioning walls on multiples of the grid’s basic unit, which also bears similarity to many of Palladio’s villas being designed with room sizes based around multiples of the Vicentine foot that suggest an underlying regularly spaced grid.
7. Conclusions
The analysis in the current research makes a contribution to fulfilling Rowe’s request that his ideas be tested rigorously, and, like previous attempts [56], the current research finds only partial evidence to support Rowe’s propositions. At face value, the results developed in this paper do not support H1.1 or H1.2 but do support H1.3. In addition, Hypothesis H2.1 and H2.2 are not supported by the analysis.
While Rowe never directly compares the complexity of Palladio’s and Le Corbusier’s villas, it is notable that, when considering the mean results for all plans and elevations, those for Malcontenta (D = 1.5373) and Rotonda (D = 1.5991) are notably higher than the equivalent results for the villas Stein (D = 1.4304) and Savoye (D = 1.3847), even though all four villas are regarded as relatively pure, freestanding geometric forms. Despite the apparent asymmetry and complexity of Le Corbusier’s abstract, geometric compositions, Palladio’s supposedly pure ‘temples’ are more visually complex. It is interesting to speculate that Rowe may have intuitively grasped that this realisation would not support his argument, potentially explaining the obvious omission of any commentary on this topic. It is also possible that this unexpected result is an instance where human perceptions [50] tend to read symmetrical forms as less complex than asymmetrical ones. Future research could revisit the hypotheses proposed in this paper from a more perceptual and neurophysiological perspective, using eye-tracking as an alternative means of testing assumptions about the way people read the geometry of a building.
Author Contributions
Conceptualization, M.J.D. and M.J.O.; methodology, M.J.D.; formal analysis, M.J.D. and J.H.L. and M.J.O.; investigation, M.J.D.; resources, M.J.D.; writing, review and editing, M.J.D., J.H.L. and M.J.O.; visualization, M.J.D.; project administration, M.J.D., J.H.L. and M.J.O.; funding acquisition, J.H.L. and M.J.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Australian Research Council, grant number DP 220101598.
Data Availability Statement
The data presented in this article is available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ostwald, M.J.; Vaughan, J. The Fractal Dimension of Architecture; Birkhauser: Basel, Switzerland; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Driscoll, J.C. Fractal Patterns as Fitness Criteria in Genetic Algorithms Applied as a Design Tool in Architecture. Nexus Netwirk J. 2021, 23, 21–37. [Google Scholar] [CrossRef]
- An, W.; Wang, C.; Zhang, H.; Bi, Z. Measuring the Formal Complexity of Architectural Curved Surfaces Based on 3D Box-Counting Dimension. Nexus Netwirk J. 2022, 24, 753–766. [Google Scholar] [CrossRef]
- Vaughan, J.; Ostwald, M.J. Examining the Position of Wright’s Fallingwater in the Context of His Larger Body of Work: An Analysis Using Fractal Dimensions. Fractal Fract. 2022, 6, 187. [Google Scholar] [CrossRef]
- Lee, J.H.; Ostwald, M.J. The ‘visual attractiveness’ of architectural facades: Measuring visual complexity and attractive strength in architecture. Archit. Sci. Rev. 2023, 66, 42–52. [Google Scholar] [CrossRef]
- Ostwald, M.J. The fractal analysis of architecture: Calibrating the box-counting method using scaling coefficient and grid disposition variables. Environ. Plan. B Plan. Des. 2013, 40, 644–663. [Google Scholar] [CrossRef]
- Stamps, A.E., III. Fractals, skylines, nature and beauty. Landsc. Urban Plan. 2002, 60, 163–184. [Google Scholar] [CrossRef]
- Vaughan, J.; Ostwald, M.J. Quantifying the Changing Visual Experience of Architecture: Combining Movement with Visual Complexity. In Across: Architectural Research Throught to Practice: 48th International Conference of the Architectural Science Association (ANZAScA); Madeo, F., Schnabel, M.A., Eds.; The Architectural Science Association; Genoa Universtiy Press: Genoa, Italy, 2014; pp. 557–568. [Google Scholar]
- Lee, J.; Ostwald, M. Fractal Dimension Calculation and Visual Attention Simulation: Assessing the Visual Character of an Architectural Façade. Buildings 2021, 11, 163. [Google Scholar] [CrossRef]
- Ostwald, M.J.; Dawes, M.J. The Mathematics of the Modernist Villa; Williams, K., Ed.; Birkhäuser: Cham, Switzerland, 2018. [Google Scholar]
- Lorenz, W.E. Estimating the Fractal Dimension of Architecture: Using Two Measurement Methods Implemented in AutoCAD by VBA. In Proceedings of the Digital Physicality, eCAADe 2012, Prague, Czech Republic, 12–14 September 2012; pp. 505–513. [Google Scholar]
- Lorenz, W.E. Fractal geometry of architecture: Implementation of the box-counting method in a CAD-software, in Computation: The New Realm of Architectural Design. In Proceedings of the eCAADe 2009, Istanbul, Turkey, 16–19 September 2009; pp. 697–704. [Google Scholar]
- Rowe, C. The Mathematics of the Ideal Villa. Archit. Rev. 1947, 100–104. [Google Scholar]
- Palladio, A. The Architecture of A. Palladio in Four Books; 1715 Translation ed.; Giacamo Lioni: London, UK, 1715. [Google Scholar]
- Rowe, C.; Slutzky, R. The Mathematics of the Ideal Villa and Other Essays; MIT Press: Cambridge, MA, USA, 1976; p. 240. [Google Scholar]
- Mandelbrot, B.B. Les Objets Fractals: Forme, Hasard et Dimension; Flammarion: Paris, France, 1975. [Google Scholar]
- Kruft, H.-W. A History of Architectural Theory: From Vitruvius to the Present; Zwemmer: London, UK; Princeton Architectural Press: New York, NY, USA, 1994. [Google Scholar]
- Wittkower, R. Architectural Principles in the Age of Humanism, 4th ed.; St. Martins’s Press: London, UK; New York, NY, USA, 1988. [Google Scholar]
- Stewart, D.E.; Corbusier, L. Towards a New Architecture; Rodker: London, UK, 1931. [Google Scholar]
- Rowe, C.; Koetter, F. Collage City; MIT Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Rowe, C. As I Was Saying: Recollections and Miscellaneous Essays; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Rowe, C. The Architecture of Good Intentions: Towards a Possible Retrospect; Academy: London, UK, 1994. [Google Scholar]
- Fletcher, R. Palladio’s Villa Emo: The Golden Proportion Hypothesis Defended. Nexus Netwirk J. 2001, 3, 105–112. [Google Scholar] [CrossRef]
- March, L. Palladio’s Villa Emo: The Golden Proportion Hypothesis Rebutted. Nexus Netwirk J. 2001, 3, 85–104. [Google Scholar] [CrossRef]
- Mitrovic, B.; Djordjević, I. Palladio’s Theory of Proportions and the Second Book of the Quattro Libri dell’Architettura. J. Soc. Archit. Hist. 1990, 49, 279–292. [Google Scholar]
- Tikhonova, O. New Approach to Proportional Analysis of Palladio’s Designs in Book II with Particular Attention to Loggias. Nexus Netw. J. 2019, 21, 359–381. [Google Scholar] [CrossRef]
- Wassel, S.R. The Mathematics of Palladio’s Villas: Workshop ’98. Nexus Netwirk J. 1998, 1, 121–128. [Google Scholar] [CrossRef]
- Howard, D.; Longair, M. Harmonic Proportion and Palladio’s Quattro Libri. J. Soc. Archit. Hist. 1982, 41, 116–143. [Google Scholar] [CrossRef]
- Fischler, R. The early relationship of Le Corbusier to the ‘golden number’. Environ. Plan. B 1979, 6, 95–103. [Google Scholar] [CrossRef]
- Stiny, G.; Gips, J. An evaluation of Palladian plans. Environ. Plan. B Plan. Des. 1978, 5, 199–206. [Google Scholar] [CrossRef]
- Salingaros, N.A. Life and Complexity in Architecture From a Thermodynamic Analogy. Phys. Essays 1997, 10, 165–173. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature, Updated and Augmented; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Voss, R.F. Characterization and Measurement of Random Fractals. Phys. Scr. 1986, T13, 27–32. [Google Scholar] [CrossRef]
- Avestas, P.; Matsopoulos, G.; Nikita, K. Applications of fractal theory on medical data processing. In Advanced Infrastructures for Future Healthcare; Marsh, A., Grndinetti, L., Kauranne, T., Eds.; IOS Press: Amsterdam, The Netherlands, 2000; pp. 425–441. [Google Scholar]
- Li, J.; Du, Q.; Sun, C. An improved box counting method for image fractal dimension estimation. Pattern Recognit. 2009, 42, 2460–2469. [Google Scholar] [CrossRef]
- Rasband, W. ImageJ 1997–2018; National Institute of Health: Bethesda, MD, USA, 2018. [Google Scholar]
- Karperien, A. FracLac for Image J 1999–2013; National Institute of Health: Bethesda, MD, USA, 2013. [Google Scholar]
- Ostwald, M.J. “Fractal architecture”:Late twentieth century connections between architecture and fractal geometry. Nexus Netwirk J. 2001, 3, 73–84. [Google Scholar] [CrossRef]
- Batty, M. Longley, Fractal Cities: A Geometry of Form and Function; Academic Press: San Deigo, CA, USA, 1994. [Google Scholar]
- Bechhoefer, W.; Appleby, M. Fractals, Music and Vernacular Architecture: An Ex-periment in Contextual Design. Crit. Methodol. Study Tradit. Environ. 1997, 97, 1–33. [Google Scholar]
- Cagdas, G.; Gozubuyuk, G.; Ediz, O. Fractal Based Generative Design for Harmony Between Old and New. In Generative Art 2005, Proceedings of the 8th Generative Art Conference; Soddu, C., Ed.; Domus Argenia: Serramanna, Italy, 2005. [Google Scholar]
- Wen, K.-C.; Kao, Y.-N. An Analytic Study of Architectural Design Style by Frac-tal Dimension Method. In Proceedings of the 22nd International Symposium on Automation and Robotics in Construction, Ferrara, Italy, 11–14 September 2005. [Google Scholar]
- Burkle-Elizondo, G.; Valdez-Cepeda, R.D. Fractal analysis of Mesoamerican pyr-amids. Nonlinear Dyn. Psychol. Life Sci. 2006, 10, 105–122. [Google Scholar]
- Cooper, J.C.; Oskrochi, R. Fractal Analysis of Street Vistas: A Potential Tool for Assessing Levels of Visual Variety in Everyday Street Scenes. Environ. Plan. B Plan. Des. 2008, 35, 349–363. [Google Scholar] [CrossRef]
- Ostwald, M.J.; Vaughan, J. Limits and Errors Optimising Image Pre-Processing Standards for Architectural Fractal Analysis. ArS Archit. Sci. 2013, 7, 1–19. [Google Scholar]
- Bovill, C. Fractal Geometry in Architecture and Design; Design science collection; Birkhäuser: Boston, MA, USA, 1996. [Google Scholar]
- Lorenz, W.E. Fractals and fractal architecture. In Faculty of Architecture and Spatial Planning; Vienna University of Technology: Vienna, Australia, 2003. [Google Scholar]
- Capo, D. The Fractal Nature of the Architectural Orders. Nexus Network J. 2004, 6, 30–40. [Google Scholar] [CrossRef]
- Ostwald, M.J.; Tucker, C. Reconsidering Bovill’s Method for Determining the Fractal Geometry of Architecture. In Proceedings of the 41st Annual Conference of the Architectural Science Association ANZAScA, Melbourne, Australia, 14–16 November 2007; pp. 182–190. [Google Scholar]
- Stamps, A.E. Psychology and the Aesthetics of the Built Environment; Kluwer Academic: Boston, MA, USA, 2000. [Google Scholar]
- Ostwald, M.J.; Vaughan, J.; Chalup, S.K. Data-cluster analysis of correlations be-tween façade complexity and orientation in Modernist architecture. In Proceedings of the 43rd Annual Conference of the Architectural Science Association, ANZAScA2009, Launceston, Australia, 25–27 November 2009; pp. 729–736. [Google Scholar]
- Ando, T. Le Corbusier: Houses; Toto: Kitakyushu, Japan, 2001; p. 416. [Google Scholar]
- Stamps, A.E., III. Architectural detail, Van der Laan septaves and pixel counts. Des. Stud. 1999, 20, 83–97. [Google Scholar] [CrossRef]
- Ching, F. Architecture: Form, Space and Order; John Wiley and Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Moore, C.; Allen, G.; Lyndon, D. The Place of Houses; Holt, Rinehart and Watson: New York, NY, USA, 1974. [Google Scholar]
- Dawes, M.J.; Lee, J.H.; Ostwald, M.J. Intelligibility and cellularity in the villas of Palladio and Le Corbusier: Examining Rowe’s observations. Int. J. Archit. Res. 2021. ahead of print. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).