Generalized Criteria for Admissibility of Singular Fractional Order Systems
Abstract
:1. Introduction
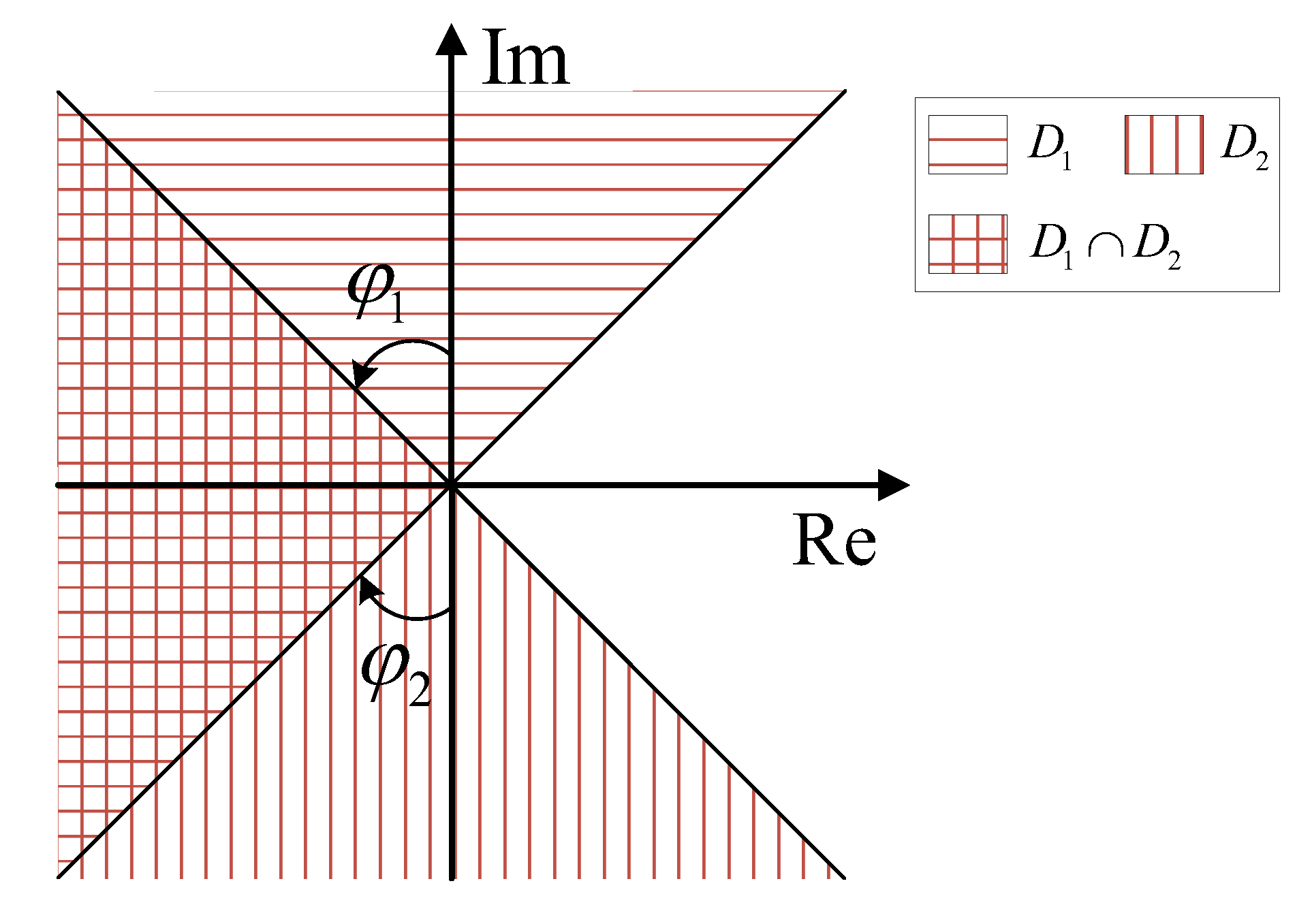
- An LMI region and a GLMI region are appiled to study the stability region of FOSs in the case of , leading to a unified criterion for the stability of FOSs, which can only be discussed and studied separately in most existing results because of the different convexity in the case of and . Furthermore, since this method is applicable to larger fractional intervals, it is more advantageous than the existing results when investigating systems with varying fractional orders.
- Based on isomorphic mapping and congruent transform to deal with the unified criteria for stability with complex decision variables, the new approach to stability analysis of FOSs with is derived, which contains the least decision variables and does not involve a complex matrix. This avoids the problem that the existing results need to solve the complex variables directly, which is difficult to solve by using the LMI toolbox.
- The new way to analyze the admissibility for FOSs with eliminates the equality constraints, avoids the non-strict LMIs and has the form of strict LMIs, so it offers an easier method to solve the decision variables than the existing literature. In addition, this method only involves a few real decision variables, so it can be directly used to design the controller without additional conditions and has no conservatism.
2. Problem Statement and Preliminaries
2.1. System Description
2.2. Definitions and Lemmas
3. Main Results
3.1. Stability of FOSs
3.2. Admissibility of SFOSs
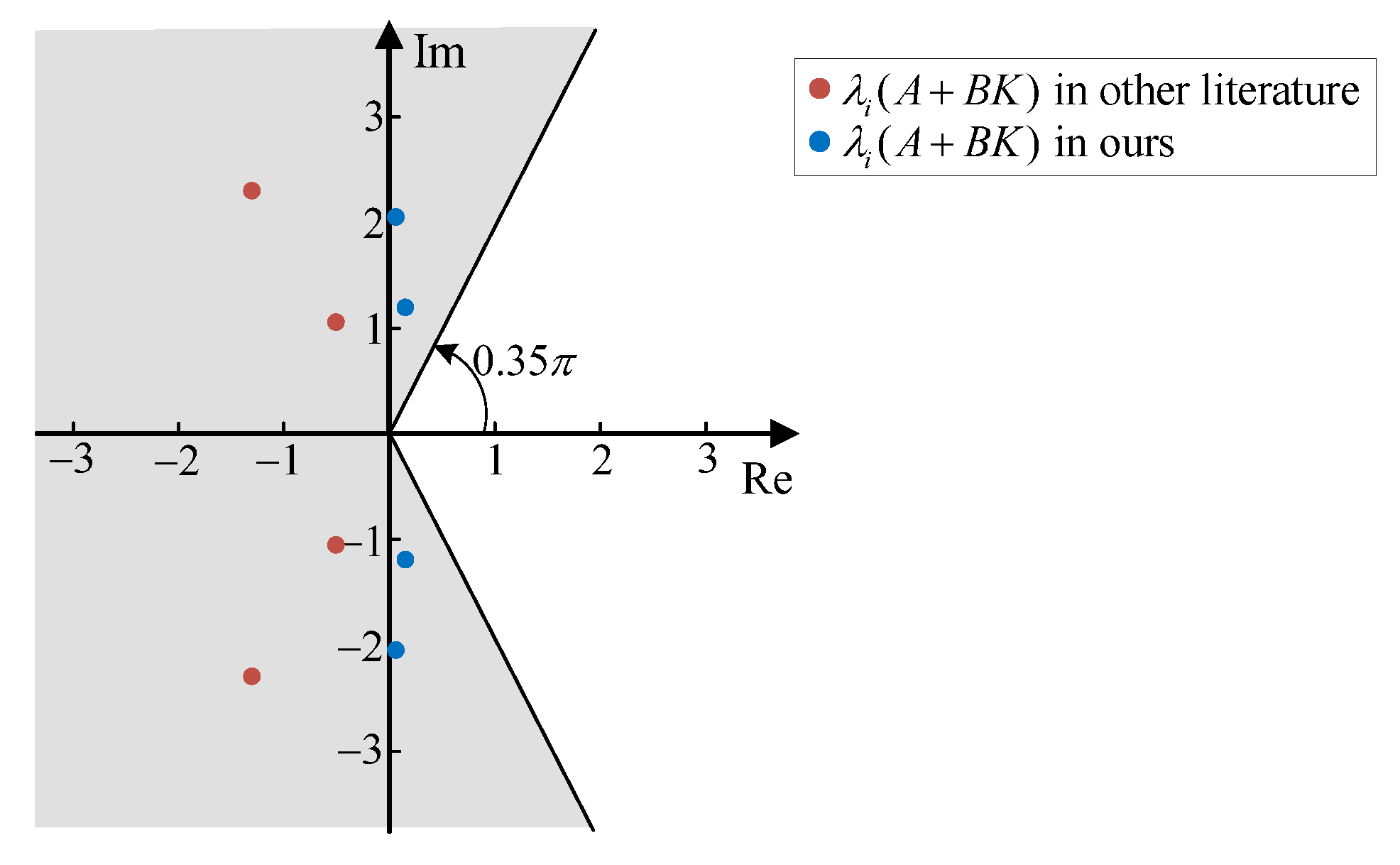
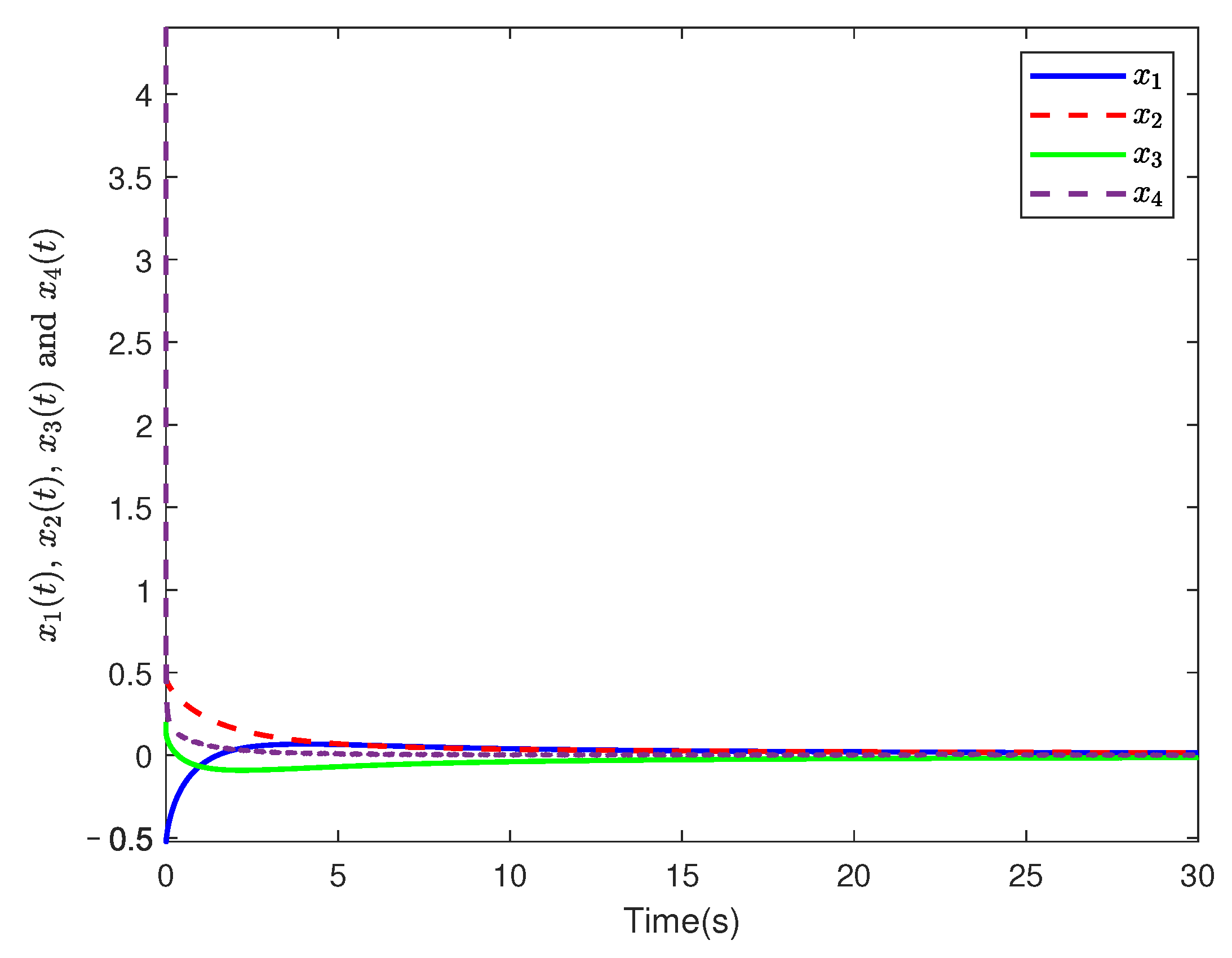
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- Listing 1: The partial code for solving LMIs in Theorem 8
- n = size (A,1);
- nK = size (B,2);
- m = rank (E);
- setlmis ([]);
- [X,m1,sX] = lmivar (1,[n 1]);
- [Y,m2,sY] = lmivar (3,skewdec(size(A),m1));
- [Z,~,sZ] = lmivar (2,[nK n]);
- [Q,~,sQ] = lmivar (2,[m,n]);
- [P1,~,sP1] = lmivar(3,[sX − floor (alpha − 1) ∗sY; floor (alpha − 1) ∗ sY sX]);
- [P2,~,sP2] = lmivar( 3,[sX floor (alpha − 1) ∗ sY;−floor (alpha − 1) ∗ sY sX]);
- [barQ,~,sbarQ] = lmivar (3,[sQ zeros(m,n); zeros (m,n) sQ]);
- [barZ,~,sbarZ] = lmivar (3,[sZ zeros(nK,n); zeros(nK,n) sZ]);
- lmiterm ([−1 1 1 P1],1,1)
- lmiterm ([−2 1 1 P2],1,1)
- lmiterm ([3 1 1 P1], kron(theta, A), barE’,’s’)
- lmiterm ([3 1 1 barQ], kron(theta, A) ∗ barS1,1,’s’)
- lmiterm ([3 1 1 P2], ceil(1 − alpha) ∗ kron(theta’, A), barE’,’s’)
- lmiterm ([3 1 1 barQ], ceil(1 − alpha) ∗ kron(theta’, A) ∗ barS,1,’s’)
- lmiterm ([3 1 1 barZ], ceil(alpha − 1) ∗ kron(theta, B), 1, ’s’)
- lmiterm([3 1 1 barZ], ceil(1 − alpha) ∗ kron(eye(2), B), 1, ’s’)
References
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Moghadam, R.A.; Ebrahimi, S. Design and analysis of a trsional mode MEMS disk resonator for RF applications. J. Multidiscip. Eng. Sci. Technol. 2021, 8, 14300–14303. [Google Scholar]
- Montazeri-Gh, M.; Mahmoodi-K, M. Optimized predictive energy management of plug-in hybrid electric vehicle based on traffic condition. J. Clean. Prod. 2016, 139, 935–948. [Google Scholar] [CrossRef]
- Özköse, F.; Yavuz, M.; Şenel, M.T.; Habbireeh, R. Fractional order modelling of omicron SARS-CoV-2 variant containing heart attack effect using real data from the United Kingdom. Chaos Soliton. Fract. 2022, 157, 111954. [Google Scholar] [CrossRef]
- Zeb, A.; Kumar, P.; Erturk, V.S.; Sitthiwirattham, T. A new study on two different vaccinated fractional-order COVID-19 models via numerical algorithms. J. King Saud. Univ. Sci. 2022, 34, 101914. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, J.X.; Zhang, X. Injected infrared and visible image fusion via L1 decomposition model and guided filtering. IEEE Trans. Comput. Imaging. 2022, 8, 162–173. [Google Scholar] [CrossRef]
- Matignon, D. Stability results on fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Jin, W. Cognitive radio spectrum allocation based on IOT and genetic algorithm. J. Commerc. Biotechnol. 2022, 27. [Google Scholar] [CrossRef]
- Norouzi, A.; Golmohammadi, A. Developing a framework for analytical hierarchy process in the hesitant fuzzy environment for group decision making (case study: Business process prioritization in Markazi electricity power distribution company). Fuzzy Syst. Appl. 2022, 5, 231–267. [Google Scholar]
- Farges, C.; Moze, M.; Sabatier, J. Pseudo-state feedback stabilisation of commensurate fractional order systems. Automatica 2010, 46, 1730–1734. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. A note on the stability of fractional order systems. Math. Comput. Simulat. 2009, 79, 1566–1576. [Google Scholar] [CrossRef]
- Sabatier, J.; Moze, M.; Farges, C. LMI stability conditions for fractional order systems. Comupt. Math. Appl. 2010, 59, 1594–1609. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Ahn, H.; Podlubny, I. Robust stability check of fractional order linear time invariant systems with interval uncertainties. Signal. Proc. 2006, 86, 2611–2618. [Google Scholar] [CrossRef]
- Lu, J.G.; Chen, Y.Q. Robust stability and stabilization of fractional order interval systems with the fractional order α: The 0<α<1 case. IEEE Trans. Automat. Control 2010, 55, 152–158. [Google Scholar] [CrossRef]
- Chilali, M.; Gahinet, P. H∞ design with pole placement constraints: An LMI approach. IEEE Trans. Automat. Control 1996, 41, 358–367. [Google Scholar] [CrossRef]
- Anderson, B.; Bose, N.; Jury, E. A simple test for zeros of a complex polynomial in a sector. IEEE Trans. Automat. Control 1974, 19, 437–438. [Google Scholar] [CrossRef]
- Xu, J. Study on Some Problems in Analysis and Control of Fractional-Order Systems. Master’s Thesis, Shanghai JiaoTong University, Shanghai, China, 2009. [Google Scholar]
- Zhang, X.F.; Lin, C.; Chen, Y.Q.; Boutat, D. A unified framework of stability theorems for LTI fractional order systems with 0<α<2. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3237–3241. [Google Scholar] [CrossRef]
- Xu, S.; Lam, J. Control and Filtering of Singular Systems; Springer: Berlin, Germany, 2006. [Google Scholar] [CrossRef]
- N’Doye, I.; Darouach, M.; Zasadzinski, M.; Radhy, N.E. Robust stabilization of uncertain descriptor fractional-order systems. Automatica 2013, 49, 1907–1913. [Google Scholar] [CrossRef]
- Yu, Y.; Jiao, Z.; Sun, C.Y. Sufficient and necessary condition of admissibility for fractional-order singular system. Acta Autom. Sin. 2013, 39, 2160–2164. [Google Scholar] [CrossRef]
- Marir, S.; Chadli, M.; Bouagada, D. A novel approach of admissibility for singular linear continuous-time fractional-order systems. Int. J. Control Autom. 2017, 15, 959–964. [Google Scholar] [CrossRef]
- Zhang, X.F.; Chen, Y.Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0<α<1 case. ISA Trans. 2018, 82, 42–50. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Meng, B.; Wang, Z. On sliding mode control for singular fractional-order systems with matched external disturbances. Fractal Fract. 2022, 6, 366. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhang, J.X.; Huang, W.K.; Shi, P. Non-fragile sliding mode observer based fault estimation for interval type-2 fuzzy singular fractional order systems. Int. J. Sysi. Sci. 2023, 1–20. [Google Scholar] [CrossRef]
- Marir, S.; Chadli, M.D.; Bouagada, D. New admissibility conditions for singular linear continuous-time fractional-order systems. J. Franklin Inst. 2017, 354, 752–766. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Lu, J.G.; Ma, Y.D. Time domain solution analysis and novel admissibility conditions of singular fractional-order systems. IEEE Trans. Circuits Syst. I-Regul. Pap. 2020, 68, 842–855. [Google Scholar] [CrossRef]
- Zhang, X.F.; Yan, Y.Q. Admissibility of fractional order descriptor systems based on complex variables: An LMI approach. Fractal Fract. 2020, 4, 8. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Zhang, X.F.; Boutat, D.; Shi, P. Quadratic admissibility for a class of LTI uncertain singular fractional-order systems with 0< α< 2. Fractal Fract. 2022, 7, 1. [Google Scholar] [CrossRef]
- Danca, M.F. On the stability domain of a class of linear systems of fractional order. Fractal Fract. 2022, 7, 49. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Low-complexity tracking control of strict-feedback systems with unknown control directions. IEEE Trans. Automat. Contr. 2019, 64, 5175–5182. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Fuzzy adaptive output feedback control of uncertain nonlinear systems with prescribed performance. IEEE Trans. Cybern. 2018, 48, 1342–1354. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Fault-tolerant output-constrained control of unknown Euler-Lagrange systems with prescribed tracking accuracy. Automatica 2020, 111, 108606. [Google Scholar] [CrossRef]
- Ahmad, M.; Zada, A.; Ghaderi, M.; George, R.; Rezapour, S. On the existence and stability of a neutral stochastic fractional differential system. Fractal Fract. 2022, 6, 203. [Google Scholar] [CrossRef]
- Bosche, J.; Bachelier, O.; Mehdi, D. An approach for robust matrix root-clustering analysis in a union of regions. IMA J. Math. Control Inf. 2005, 22, 227–239. [Google Scholar] [CrossRef]
- Lu, J.G.; Chen, G.Y. Robust stability and stabilization of fractional order interval systems: An LMI approach. IEEE Trans. Automat. Control 2009, 54, 1294–1299. [Google Scholar] [CrossRef]
- Iwasaki, T.; Hara, S. Generalized KYP lemma: Unified frequency domain inequalities with design applications. IEEE Trans. Automat. Control 2005, 50, 41–59. [Google Scholar] [CrossRef]

| Ref. | Range | Var. Kind | FOS or SFOS | Nonconservative Stabilization | As a Special Case of Ours | Unified |
|---|---|---|---|---|---|---|
| [11] | Complex | FOS | No | Th. 1 | N/A | |
| [12] | Real | FOS | No | N/A | N/A | |
| [11] | Real | FOS | Yes | Th. 5 | N/A | |
| [15] | Real | FOS | No | Th. 3 | N/A | |
| [19] | Real | FOS | Yes | N/A | No | |
| [27] | Real | SFOS | Yes | Th. 5 | N/A | |
| [24] | Real | SFOS | Yes | Th. 7 | N/A | |
| [26] | Real | SFOS | Yes | N/A | No | |
| [30] | Real | SFOS | Yes | N/A | No | |
| Ours (Th. 5) | Real | FOS | Yes | N/A | Yes | |
| Ours (Th. 7) | Real | SFOS | Yes | N/A | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhang, J.-X.; Zhang, X. Generalized Criteria for Admissibility of Singular Fractional Order Systems. Fractal Fract. 2023, 7, 363. https://doi.org/10.3390/fractalfract7050363
Zhang L, Zhang J-X, Zhang X. Generalized Criteria for Admissibility of Singular Fractional Order Systems. Fractal and Fractional. 2023; 7(5):363. https://doi.org/10.3390/fractalfract7050363
Chicago/Turabian StyleZhang, Longxin, Jin-Xi Zhang, and Xuefeng Zhang. 2023. "Generalized Criteria for Admissibility of Singular Fractional Order Systems" Fractal and Fractional 7, no. 5: 363. https://doi.org/10.3390/fractalfract7050363
APA StyleZhang, L., Zhang, J.-X., & Zhang, X. (2023). Generalized Criteria for Admissibility of Singular Fractional Order Systems. Fractal and Fractional, 7(5), 363. https://doi.org/10.3390/fractalfract7050363








