Exact Solutions and Cosmological Constraints in Fractional Cosmology
Abstract
1. Introduction
2. Fractional Action Integral
2.1. Some Fractional Derivatives
2.2. Frational Action-like Variational Problems
2.3. Applications to Cosmology
2.4. Some Cosmological Solutions
2.5. Model with Cold Dark Matter
2.6. Interpretation of the Fractional Term as a Dark Energy Source
3. Exact Solutions
3.1. First Exact Solution
3.2. Second Exact Solution
3.3. General Solution
3.4. Asymptotic Analysis
3.5. Approximated Analytical Solution
3.6. Discussion
- .
- .
- .
- .
- if .
- . In this case, the equation of state for radiation is recovered for .
- .
- .
- if .
- if .
- .
- .
- .
- .
- .
- if .
- if .
- if .
4. Cosmological Constraints
4.1. Observational Hubble Parameter Data
4.2. Type Ia Supernovae Data
4.3. Joint Analysis and Theoretical Hubble Parameter Integration
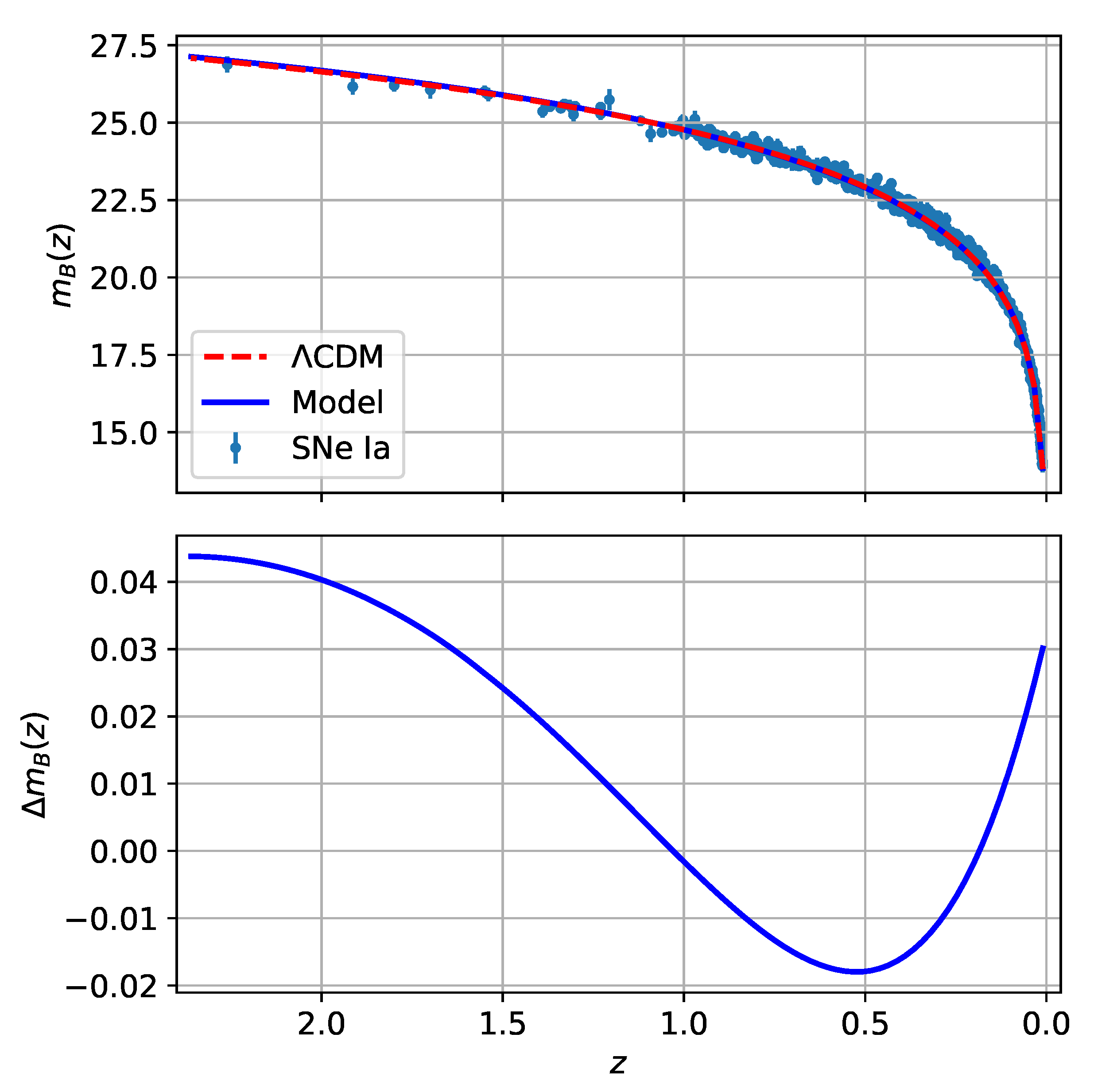
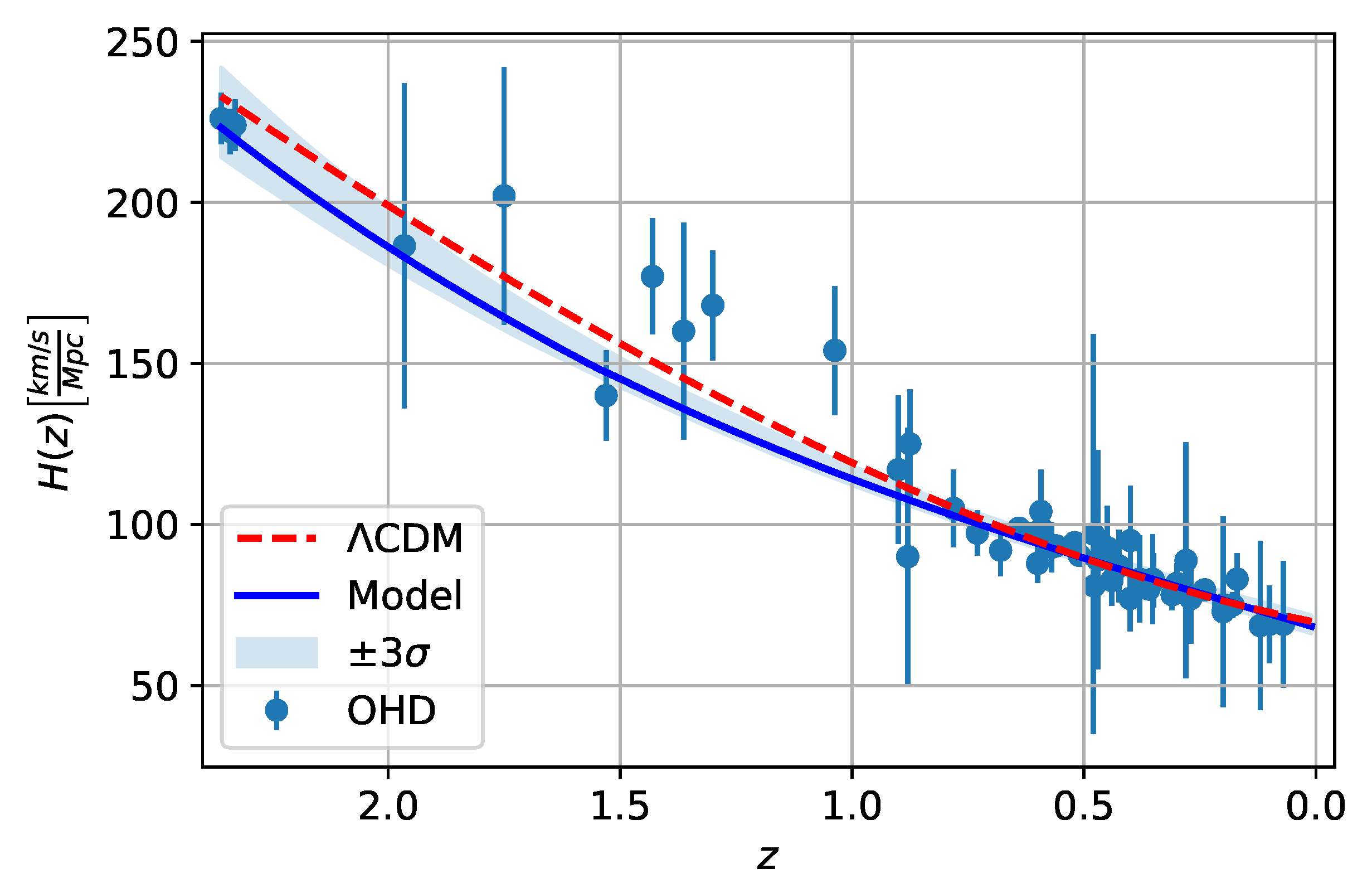
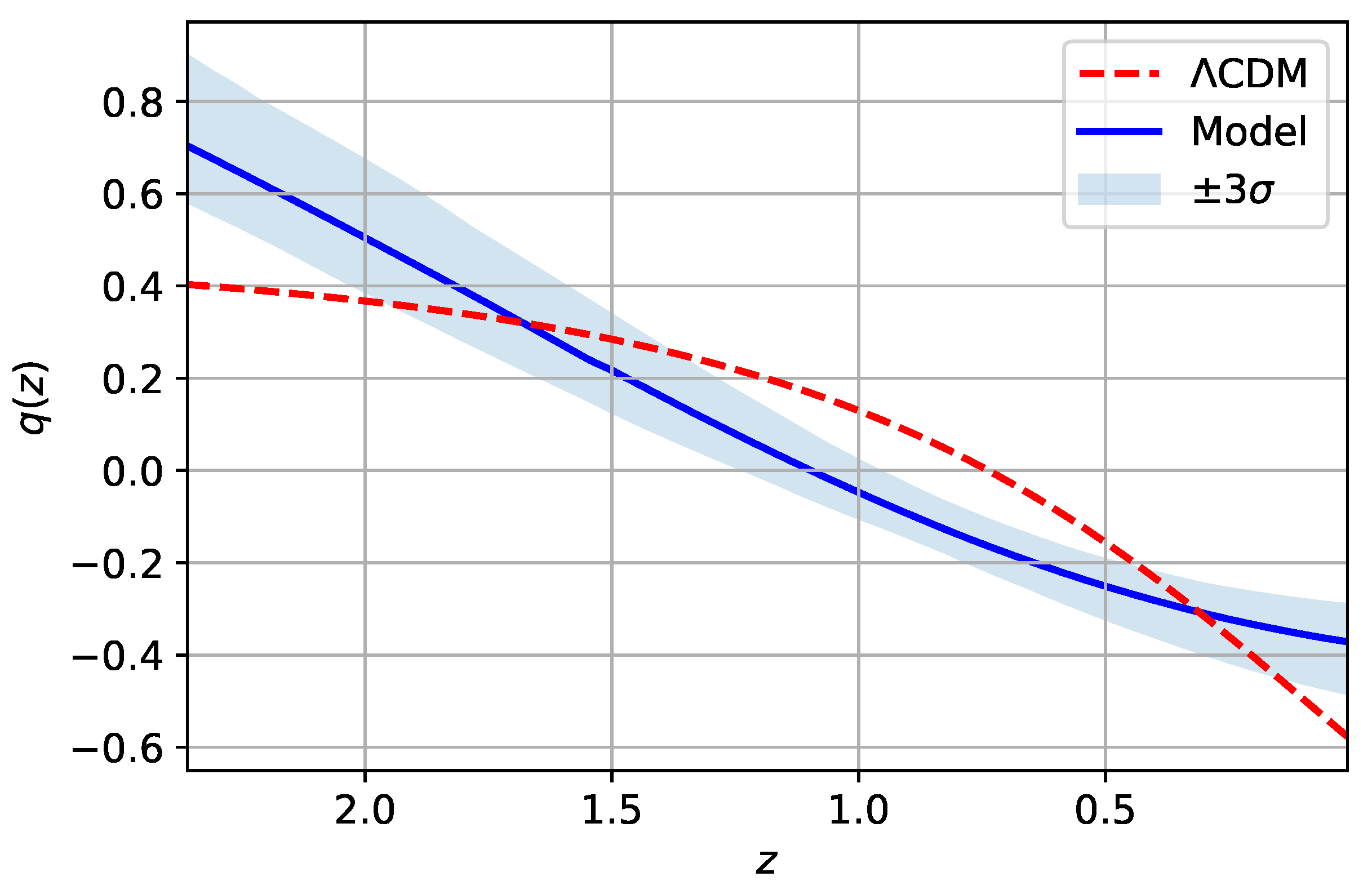
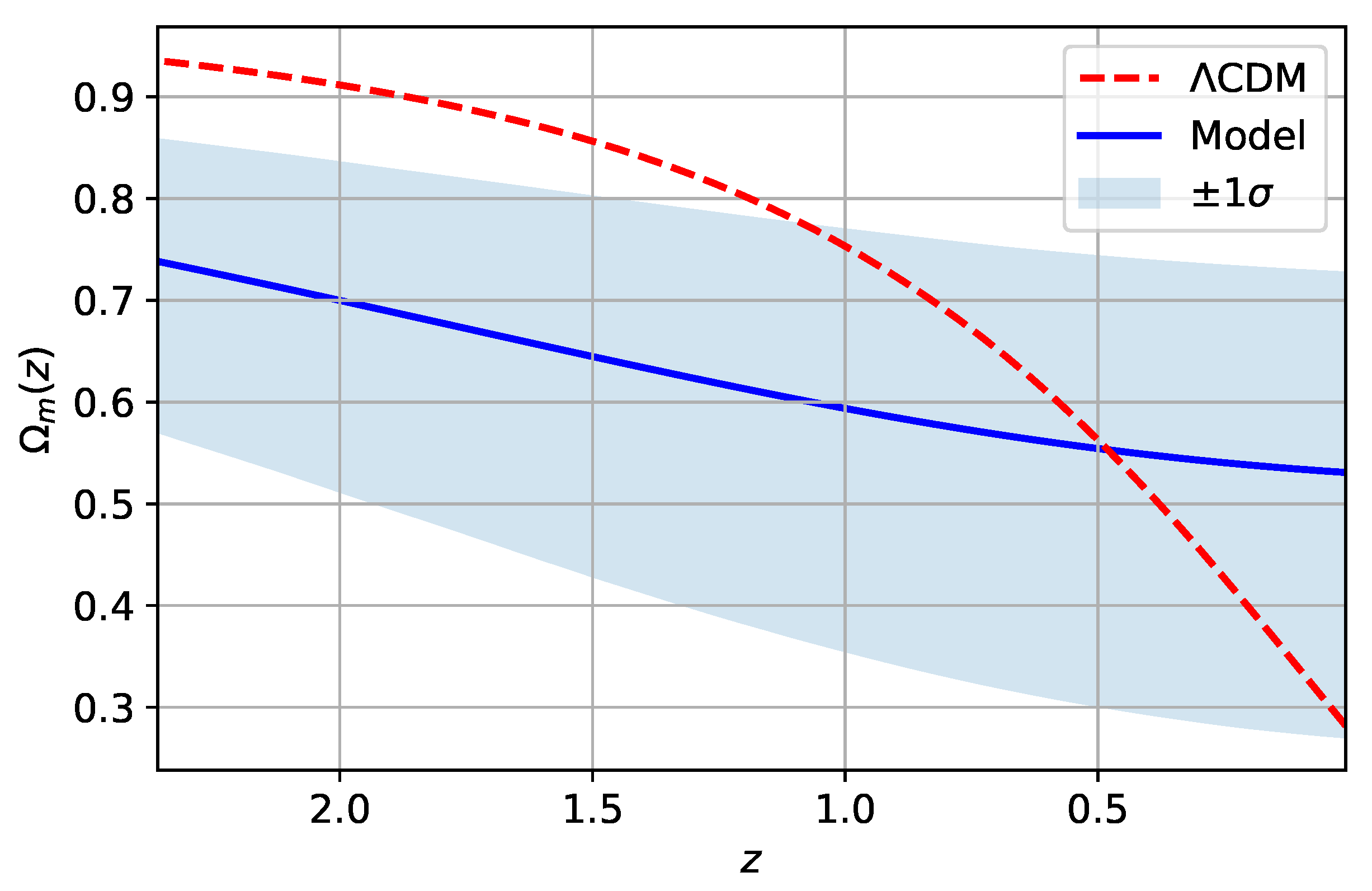
4.4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Advances in Industrial Control; Springer: London, UK, 2010. [Google Scholar]
- Tarasov, V.E. Review of Some Promising Fractional Physical Models. Int. J. Mod. Phys. B 2013, 27, 13300053. [Google Scholar] [CrossRef]
- Bandyopadhyay, B.; Kamal, S. Stabilization and Control of Fractional Order Systems: A Sliding Mode Approach; Lecture Notes in Electrical Engineering; Springer International Publishing: New York, NY, USA, 2014. [Google Scholar]
- Padula, F.; Visioli, A. Advances in Robust Fractional Control; Springer International Publishing: New York, NY, USA, 2014. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction For Physicists, 2nd ed.; World Scientific Publishing Company: Singapore, 2014. [Google Scholar]
- Tarasov, V.E. Applications in Physics, Part A; De Gruyter Reference; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Klafter, J.; Lim, S.C.; Metzler, R. Fractional Dynamics: Recent Advances; World Scientific: Singapore, 2012. [Google Scholar]
- Malinowska, A.B.; Odzijewicz, T.; Torres, D.F.M. Advanced Methods in the Fractional Calculus of Variations; Springer Briefs in Applied Sciences and Technology; Springer International Publishing: New York, NY, USA, 2015. [Google Scholar]
- Lorenzo, C.F.; Hartley, T.T. The Fractional Trigonometry: With Applications to Fractional Differential Equations and Science; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- West, B.J. Fractional Calculus and the Future of Science. Entropy 2021, 23, 1566. [Google Scholar] [CrossRef] [PubMed]
- Calcagni, G. Quantum field theory, gravity and cosmology in a fractal universe. JHEP 2010, 03, 120. [Google Scholar] [CrossRef]
- Calcagni, G. Fractal universe and quantum gravity. Phys. Rev. Lett. 2010, 104, 251301. [Google Scholar] [CrossRef]
- Lim, S.C. Fractional derivative quantum fields at positive temperature. Phys. A 2006, 363, 269–281. [Google Scholar] [CrossRef]
- Lim, S.C.; Eab, C.H. Fractional quantum fields. In Volume 5 Applications in Physics, Part B; Tarasov, V.E., Ed.; De Gruyter: Berlin, Germany, 2019; pp. 237–256. [Google Scholar] [CrossRef]
- Moniz, P.V.; Jalalzadeh, S. Challenging Routes in Quantum Cosmology; World Scientific Publishing: Singapore, 2020. [Google Scholar] [CrossRef]
- Moniz, P.V.; Jalalzadeh, S. From Fractional Quantum Mechanics to Quantum Cosmology: An Overture. Mathematics 2020, 8, 313. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Jalalzadeh, S.; Moniz, P.V. Broadening quantum cosmology with a fractional whirl. Mod. Phys. Lett. A 2021, 36, 2140005. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; da Silva, F.R.; Moniz, P.V. Prospecting black hole thermodynamics with fractional quantum mechanics. Eur. Phys. J. C 2021, 81, 632. [Google Scholar] [CrossRef]
- Rami, E.N.A. Fractional dynamics, fractional weak bosons masses and physics beyond the standard model. Chaos Solitons Fractals 2009, 41, 2262–2270. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Fractional Lagrangian Formulation of General Relativity and Emergence of Complex, Spinorial and Noncommutative Gravity. Int. J. Geom. Methods Mod. Phys. 2009, 6, 25–76. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Modifications at Large Distances From Fractional and Fractal Arguments. Fractals 2010, 18, 185–190. [Google Scholar] [CrossRef]
- El-Nabulsi, A.R. The fractional white dwarf hydrodynamical nonlinear differential equation and emergence of quark stars. Appl. Math. Comput. 2011, 218, 2837–2849. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Glaeske-Kilbas-Saigo fractional integration and fractional Dixmier trace. Acta Math. Vietnam. 2012, 37, 149–160. [Google Scholar]
- El-Nabulsi, R.A.; Wu, C.G. Fractional Complexified Field Theory from Saxena-Kumbhat Fractional Integral, Fractional Derivative of Order (α,β) and Dynamical Fractional Integral Exponent. Afr. Diaspora J. Math. New Ser. 2012, 13, 45–61. [Google Scholar]
- El-Nabulsi, R.A. Fractional derivatives generalization of Einstein`s field equations. Indian J. Phys. 2013, 87, 195–200. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Fractional elliptic operator of order 2/3 from Glaeske-Kilbas-Saigo fractional integral transform. Funct. Anal. Approx. Comput 2015, 7, 29–33. [Google Scholar]
- El-Nabulsi, R.A. A Cosmology Governed by a Fractional Differential Equation and the Generalized Kilbas-Saigo-Mittag–Leffler Function. Int. J. Theor. Phys. 2016, 55, 625–635. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Finite two-point space without quantization on noncommutative space from a generalized fractional integral operator. Complex Anal. Oper. Theory 2018, 12, 1609–1616. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. On generalized fractional spin, fractional angular momentum, fractional momentum operators in quantum mechanics. Few-Body Syst. 2020, 61, 25. [Google Scholar] [CrossRef]
- Roberts, M.D. Fractional Derivative Cosmology. SOP Trans. Theor. Phys. 2014, 1, 310. [Google Scholar] [CrossRef]
- Vacaru, S.I. New Classes of Off-Diagonal Cosmological Solutions in Einstein Gravity. Int. J. Theor. Phys. 2010, 49, 2753–2776. [Google Scholar] [CrossRef]
- Vacaru, S.I. Fractional Nonholonomic Ricci Flows. Chaos Solitons Fractals 2012, 45, 1266–1276. [Google Scholar] [CrossRef]
- Vacaru, S.I. Fractional Dynamics from Einstein Gravity, General Solutions, and Black Holes. Int. J. Theor. Phys. 2012, 51, 1338–1359. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Cosmological Models with Fractional Derivatives and Fractional Action Functional. Commun. Theor. Phys. 2011, 56, 389–396. [Google Scholar] [CrossRef]
- Jamil, M.; Momeni, D.; Rashid, M.A. Fractional Action Cosmology with Power Law Weight Function. J. Phys. Conf. Ser. 2012, 354, 012008. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Cosmic Evolution in Fractional Action Cosmology. Discontinuity Nonlinearity Complex 2013, 2, 115–123. [Google Scholar] [CrossRef]
- Debnath, U.; Jamil, M.; Chattopadhyay, S. Fractional Action Cosmology: Emergent, Logamediate, Intermediate, Power Law Scenarios of the Universe and Generalized Second Law of Thermodynamics. Int. J. Theor. Phys. 2012, 51, 812–837. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Gravitons in fractional action cosmology. Int. J. Theor. Phys. 2012, 51, 3978–3992. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Non-minimal coupling in fractional action cosmology. Indian J. Phys. 2013, 87, 835–840. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Nonstandard fractional exponential Lagrangians, fractional geodesic equation, complex general relativity, and discrete gravity. Can. J. Phys. 2013, 91, 618–622. [Google Scholar] [CrossRef]
- Debnath, U.; Chattopadhyay, S.; Jamil, M. Fractional action cosmology: Some dark energy models in emergent, logamediate, and intermediate scenarios of the universe. J. Theor. Appl. Phys. 2013, 7, 25. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Fractional Einstein–Hilbert Action Cosmology. Mod. Phys. Lett. A 2013, 28, 1350056. [Google Scholar] [CrossRef]
- Calcagni, G. Multi-scale gravity and cosmology. J. Cosmol. Astropart. Phys. 2013, 12, 041. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Testing Fractional Action Cosmology. Eur. Phys. J. Plus 2016, 131, 256. [Google Scholar] [CrossRef]
- Rami, E.N.A. Fractional action oscillating phantom cosmology with conformal coupling. Eur. Phys. J. Plus 2015, 130, 102. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Implications of the Ornstein-Uhlenbeck-like fractional differential equation in cosmology. Rev. Mex. Fis. 2016, 62, 240. [Google Scholar]
- Calcagni, G.; Kuroyanagi, S.; Tsujikawa, S. Cosmic microwave background and inflation in multi-fractional spacetimes. J. Cosmol. Astropart. Phys. 2016, 8, 39. [Google Scholar] [CrossRef]
- Calcagni, G. Multifractional theories: An unconventional review. J. High Energy Phys. 2017, 3, 138, Erratum in J. High Energy Phys. 2017, 6, 20. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Fractional Action Cosmology with Variable Order Parameter. Int. J. Theor. Phys. 2017, 56, 1159–1182. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Wormholes in fractional action cosmology. Can. J. Phys. 2017, 95, 605–609. [Google Scholar] [CrossRef]
- Calcagni, G. Complex dimensions and their observability. Phys. Rev. D 2017, 96, 046001. [Google Scholar] [CrossRef]
- Calcagni, G.; Kuroyanagi, S.; Marsat, S.; Sakellariadou, M.; Tamanini, N.; Tasinato, G. Quantum gravity and gravitational-wave astronomy. J. Cosmol. Astropart. Phys. 2019, 10, 012. [Google Scholar] [CrossRef]
- Calcagni, G.; Kuroyanagi, S. Stochastic gravitational-wave background in quantum gravity. J. Cosmol. Astropart. Phys. 2021, 3, 19. [Google Scholar] [CrossRef]
- Calcagni, G.; De Felice, A. Dark energy in multifractional spacetimes. Phys. Rev. D 2020, 102, 103529. [Google Scholar] [CrossRef]
- Calcagni, G. Multifractional theories: An updated review. Mod. Phys. Lett. A 2021, 36, 2140006. [Google Scholar] [CrossRef]
- Calcagni, G. Classical and quantum gravity with fractional operators. Class. Quant. Grav. 2021, 38, 165005, Erratum in Class. Quant. Grav. 2021, 38, 169601. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Fractional-order derivatives in cosmological models of accelerated expansion. Mod. Phys. Lett. A 2021, 36, 2130014. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; Costa, E.W.O.; Moniz, P.V. de Sitter fractional quantum cosmology. Phys. Rev. D 2022, 105, L121901. [Google Scholar] [CrossRef]
- Landim, R.G. Fractional dark energy: Phantom behavior and negative absolute temperature. Phys. Rev. D 2021, 104, 103508. [Google Scholar] [CrossRef]
- Landim, R.G. Fractional dark energy. Phys. Rev. D 2021, 103, 083511. [Google Scholar] [CrossRef]
- García-Aspeitia, M.A.; Fernandez-Anaya, G.; Hernández-Almada, A.; Leon, G.; Magaña, J. Cosmology under the fractional calculus approach. Mon. Not. R. Astron. Soc. 2022, 517, 4813–4826. [Google Scholar] [CrossRef]
- Micolta-Riascos, B.; Millano, A.D.; Leon, G.; Erices, C.; Paliathanasis, A. Revisiting Fractional Cosmology. Fractal Fract. 2023, 7, 149. [Google Scholar] [CrossRef]
- Hernández-Almada, A.; Leon, G.; Magaña, J.; García-Aspeitia, M.A.; Motta, V. Generalized Emergent Dark Energy: Observational Hubble data constraints and stability analysis. Mon. Not. R. Astron. Soc. 2020, 497, 1590–1602. [Google Scholar] [CrossRef]
- Leon, G.; Magaña, J.; Hernández-Almada, A.; García-Aspeitia, M.A.; Verdugo, T.; Motta, V. Barrow Entropy Cosmology: An observational approach with a hint of stability analysis. J. Cosmol. Astropart. Phys. 2021, 12, 032. [Google Scholar] [CrossRef]
- Hernández-Almada, A.; Leon, G.; Magaña, J.; García-Aspeitia, M.A.; Motta, V.; Saridakis, E.N.; Yesmakhanova, K.; Millano, A.D. Observational constraints and dynamical analysis of Kaniadakis horizon-entropy cosmology. Mon. Not. R. Astron. Soc. 2022, 512, 5122–5134. [Google Scholar] [CrossRef]
- Hernández-Almada, A.; Leon, G.; Magaña, J.; García-Aspeitia, M.A.; Motta, V.; Saridakis, E.N.; Yesmakhanova, K. Kaniadakis-holographic dark energy: Observational constraints and global dynamics. Mon. Not. R. Astron. Soc. 2022, 511, 4147–4158. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z∼0.45: Direct evidence of the epoch of cosmic re-acceleration. J. Cosmol. Astropart. Phys. 2016, 5, 14. [Google Scholar] [CrossRef]
- Valcin, D.; Jimenez, R.; Verde, L.; Bernal, J.L.; Wandelt, B.D. The age of the Universe with globular clusters: Reducing systematic uncertainties. J. Cosmol. Astropart. Phys. 2021, 2021, 17. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Carroll, S.M.; Press, W.H.; Turner, E.L. The Cosmological constant. Ann. Rev. Astron. Astrophys. 1992, 30, 499–542. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A.A. The Case for a positive cosmological Lambda term. Int. J. Mod. Phys. D 2000, 9, 373–444. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant: The Weight of the vacuum. Phys. Rept. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Velten, H.E.S.; vom Marttens, R.F.; Zimdahl, W. Aspects of the cosmological “coincidence problem”. Eur. Phys. J. C 2014, 74, 3160. [Google Scholar] [CrossRef]
- Sadjadi, H.M.; Alimohammadi, M. Cosmological coincidence problem in interactive dark energy models. Phys. Rev. D 2006, 74, 103007. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.M.; Steinhardt, P.J. Quintessence, cosmic coincidence, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 896–899. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; An, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—a review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Basilakos, S.; Leon, G.; Papagiannopoulos, G.; Saridakis, E.N. Dynamical system analysis at background and perturbation levels: Quintessence in severe disadvantage comparing to ΛCDM. Phys. Rev. D 2019, 100, 043524. [Google Scholar] [CrossRef]
- Alho, A.; Uggla, C.; Wainwright, J. Perturbations of the Lambda-CDM model in a dynamical systems perspective. J. Cosmol. Astropart. Phys. 2019, 9, 45. [Google Scholar] [CrossRef]
- Wald, R.M. Asymptotic behavior of homogeneous cosmological models in the presence of a positive cosmological constant. Phys. Rev. D 1983, 28, 2118. [Google Scholar] [CrossRef]
- Kitada, Y.; Maeda, K.I. Cosmic no-hair theorem in homogeneous spacetimes. Vistas Astron. 1993, 37, 461–464. [Google Scholar] [CrossRef]
- Barrow, J.D.; Stein-Schabes, J. Inhomogeneous cosmologies with cosmological constant. Phys. Lett. A 1984, 103, 315–317. [Google Scholar] [CrossRef]
- Maeda, K.I. Recent topics on the inflationary universe: Cosmic no hair conjecture. In Proceedings of the 2nd Workshop on Elementary Particle Picture of the Universe, Tsukuba, Japan, 4–6 February 1988; pp. 51–64. [Google Scholar]
- Cotsakis, S.; Flessas, G. Generalized cosmic no hair theorems. Phys. Lett. B 1993, 319, 69–73. [Google Scholar] [CrossRef]
- Capozziello, S.; De Ritis, R. Cosmic no-hair theorem in anisotropic, nonminimally coupled cosmologies. Int. J. Mod. Phys. D 1996, 5, 209–215. [Google Scholar] [CrossRef]
- Bruni, M.; Mena, F.C.; Tavakol, R.K. Cosmic no hair: Nonlinear asymptotic stability of de Sitter universe. Class. Quant. Grav. 2002, 19, L23–L29. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Higher Education Press: Beijing, China, 2013. [Google Scholar]
- El-Nabulsi, R.A. Fractional unstable Euclidean universe. Electron. J. Theor. Phys. 2005, 2, 1–11. [Google Scholar]
- El-Nabulsi, R.A. Accelerated universe dominated by holographic dark energy, supergravity inflationary potential. Rom. J. Phys. 2007, 52, 163–170. [Google Scholar]
- El-Nabulsi, R.A. Cosmology with a fractional action principle. Rom. Rep. Phys. 2007, 59, 763–771. [Google Scholar]
- El-Nabulsi, R.A. Increasing effective gravitational constant in fractional ADD brane cosmology. Electron. J. Theor. Phys. 2008, 5, 103–106. [Google Scholar]
- Frederico, G.S.; Torres, D. Necessary Optimality Conditions for Fractional Action-like Problems with Intrinsic and Observer Times. WSEAS Trans. Math. 2008, 7, 6–11. [Google Scholar]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 2010. [Google Scholar]
- Carroll, S.M. Spacetime and Geometry; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Carroll, S.; Carroll, S.M. Spacetime and Geometry: An Introduction to General Relativity; Addison Wesley: Boston, MA, USA, 2004. [Google Scholar]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Magaña, J.; Amante, M.H.; Garcia-Aspeitia, M.A.; Motta, V. The Cardassian expansion revisited: Constraints from updated Hubble parameter measurements and type Ia supernova data. Mon. Not. R. Astron. Soc. 2018, 476, 1036. [Google Scholar] [CrossRef]
- Goodman, J.; Weare, J. Ensemble samplers with affine invariance. Commun. Appl. Math. Comput. Sci. 2010, 5, 65–80. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Conley, A.; Meierjurgen Farr, W.; Hogg, D.W.; Lang, D.; Marshall, P.; Price-Whelan, A.; Sanders, J.; Zuntz, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Tripp, R. A two-parameter luminosity correction for Type IA supernovae. Astron. Astrophys. 1998, 331, 815. [Google Scholar]
- Kessler, R.; Scolnic, D. Correcting Type Ia Supernova Distances for Selection Biases and Contamination in Photometrically Identified Samples. Astrophys. J. 2017, 836, 56. [Google Scholar] [CrossRef]
- Lazkoz, R.; Nesseris, S.; Perivolaropoulos, L. Exploring cosmological expansion parametrizations with the gold SnIa data set. J. Cosmol. Astropart. Phys. 2005, 2005, 010. [Google Scholar] [CrossRef]
- Krishnan, C.; Ó Colgáin, E.; Sheikh-Jabbari, M.M.; Yang, T. Running Hubble tension and a H0 diagnostic. Phys. Rev. D 2021, 103. [Google Scholar] [CrossRef]



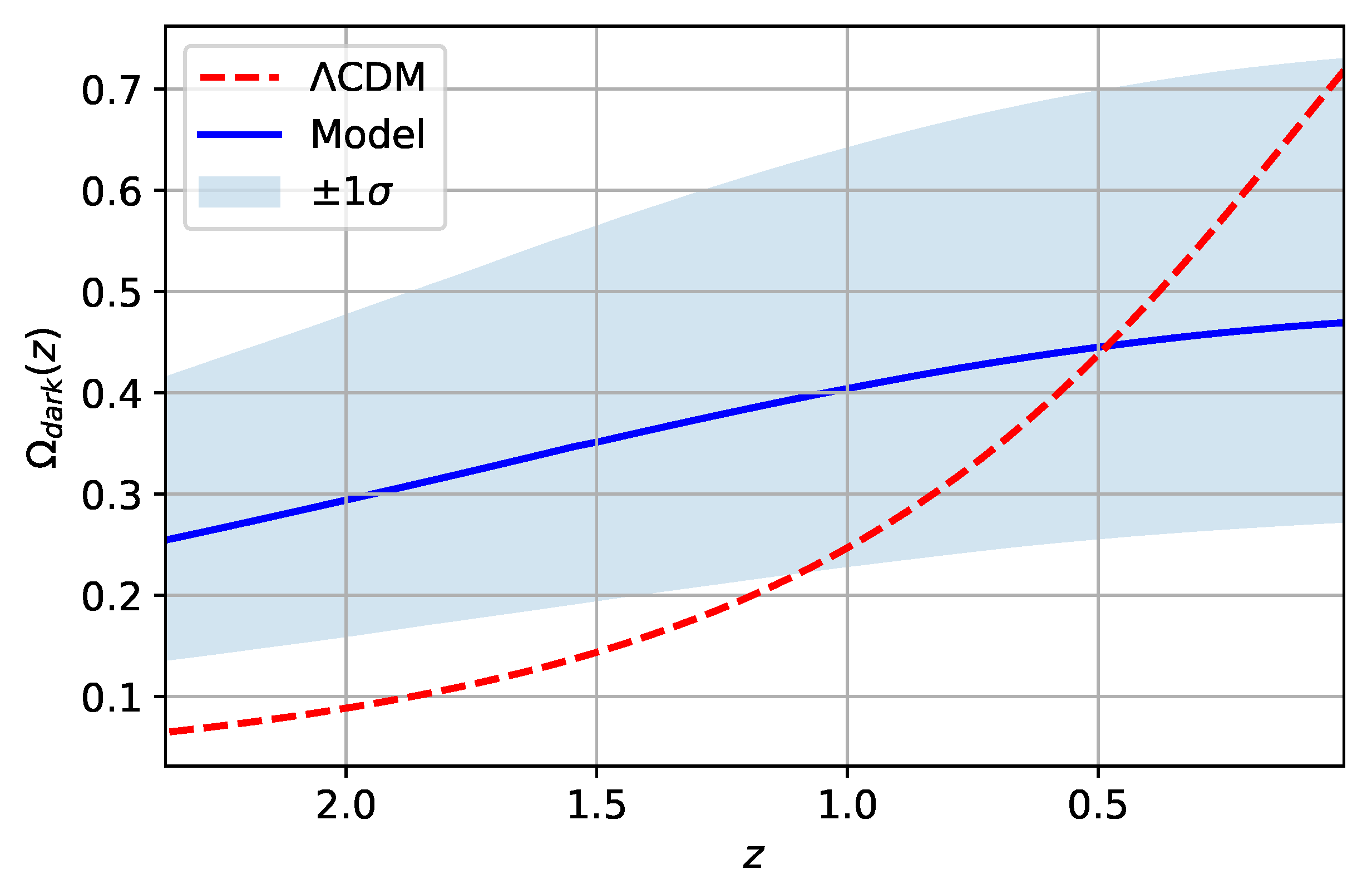
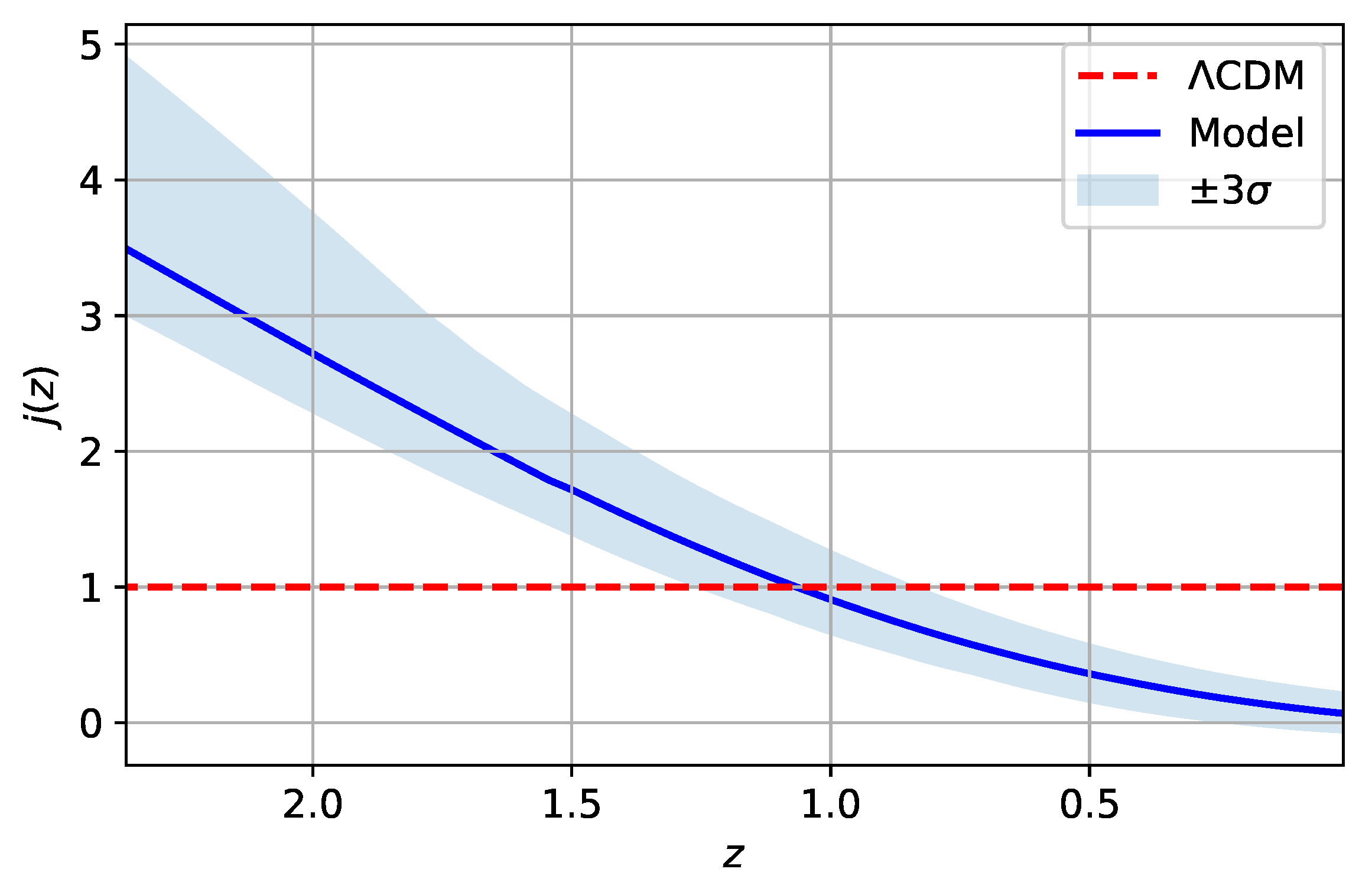
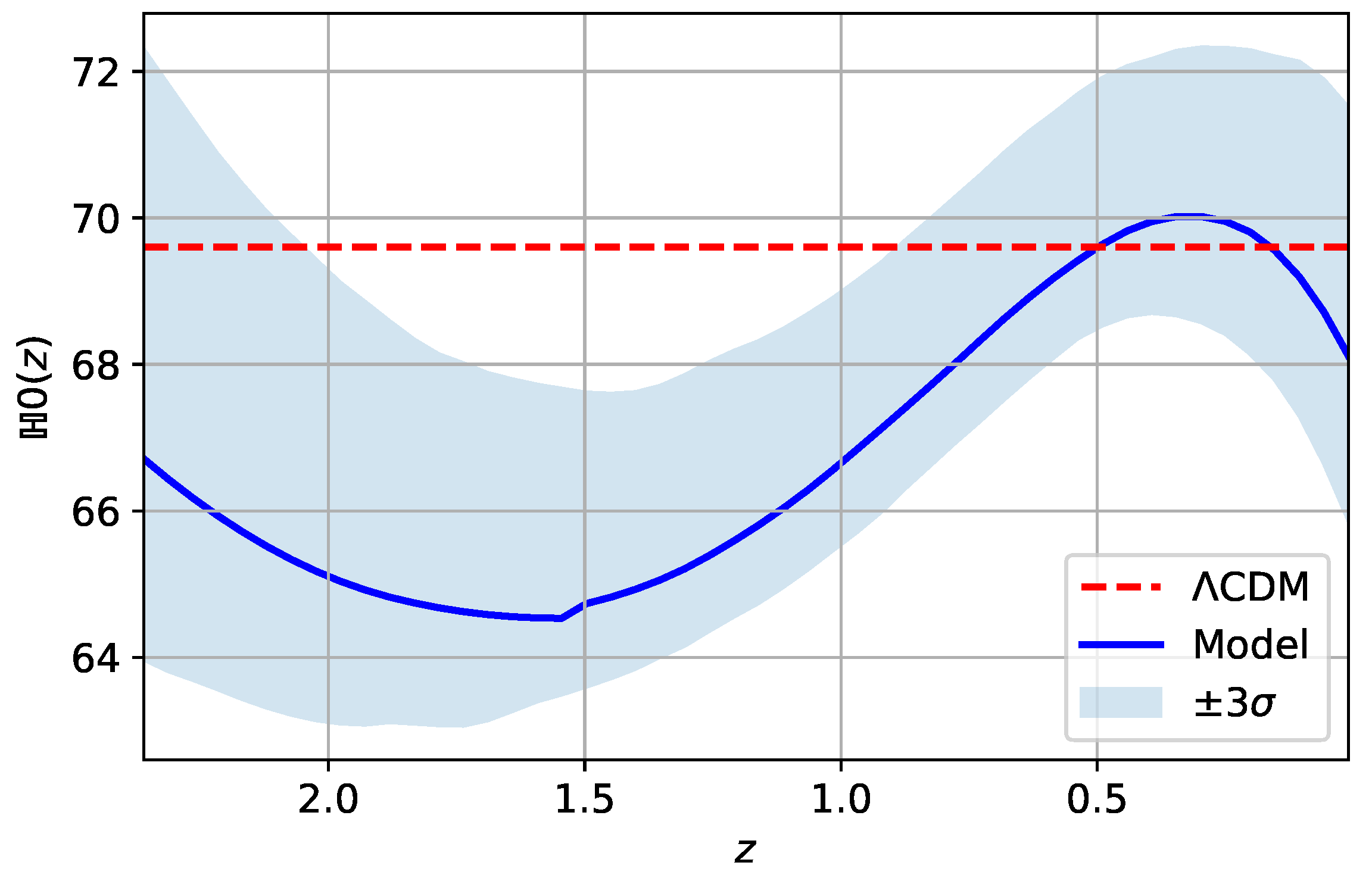
| Label | H | q | Acceleration? | Stability | Scale Factor | |
|---|---|---|---|---|---|---|
| 0 | Accelerated () | Sink () | Power law | |||
| Decelerated () | Source () | |||||
| Saddle () |
| Data | Total Steps | MAF | ||||
|---|---|---|---|---|---|---|
| CDM model | ||||||
| SNe Ia | 1300 | ⋯ | ⋯ | |||
| OHD | 950 | ⋯ | ⋯ | |||
| SNe Ia + OHD | 850 | ⋯ | ⋯ | |||
| Fractional cosmological model | ||||||
| SNe Ia | 5250 | ⋯ | ||||
| OHD | 3150 | ⋯ | ||||
| SNe Ia + OHD | 1900 | ⋯ | ||||
| Data | Best-Fit Values | ||||
|---|---|---|---|---|---|
| CDM model | |||||
| SNe Ia | ⋯ | ⋯ | |||
| OHD | ⋯ | ⋯ | |||
| SNe Ia + OHD | ⋯ | ⋯ | |||
| Fractional cosmological model | |||||
| SNe Ia | ⋯ | ||||
| OHD | ⋯ | ||||
| SNe Ia + OHD | ⋯ | ||||
| Prior | ||
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, E.; Leon, G.; Fernandez-Anaya, G. Exact Solutions and Cosmological Constraints in Fractional Cosmology. Fractal Fract. 2023, 7, 368. https://doi.org/10.3390/fractalfract7050368
González E, Leon G, Fernandez-Anaya G. Exact Solutions and Cosmological Constraints in Fractional Cosmology. Fractal and Fractional. 2023; 7(5):368. https://doi.org/10.3390/fractalfract7050368
Chicago/Turabian StyleGonzález, Esteban, Genly Leon, and Guillermo Fernandez-Anaya. 2023. "Exact Solutions and Cosmological Constraints in Fractional Cosmology" Fractal and Fractional 7, no. 5: 368. https://doi.org/10.3390/fractalfract7050368
APA StyleGonzález, E., Leon, G., & Fernandez-Anaya, G. (2023). Exact Solutions and Cosmological Constraints in Fractional Cosmology. Fractal and Fractional, 7(5), 368. https://doi.org/10.3390/fractalfract7050368








