Dynamics of Age-Structure Smoking Models with Government Intervention Coverage under Fractal-Fractional Order Derivatives
Abstract
1. Introduction
2. Preliminaries
3. Model Formulation
4. Dynamics of the Model
5. Existence and Uniqueness Results
6. Hyers–Ulam (HU) Stability Results
7. Numerical Scheme
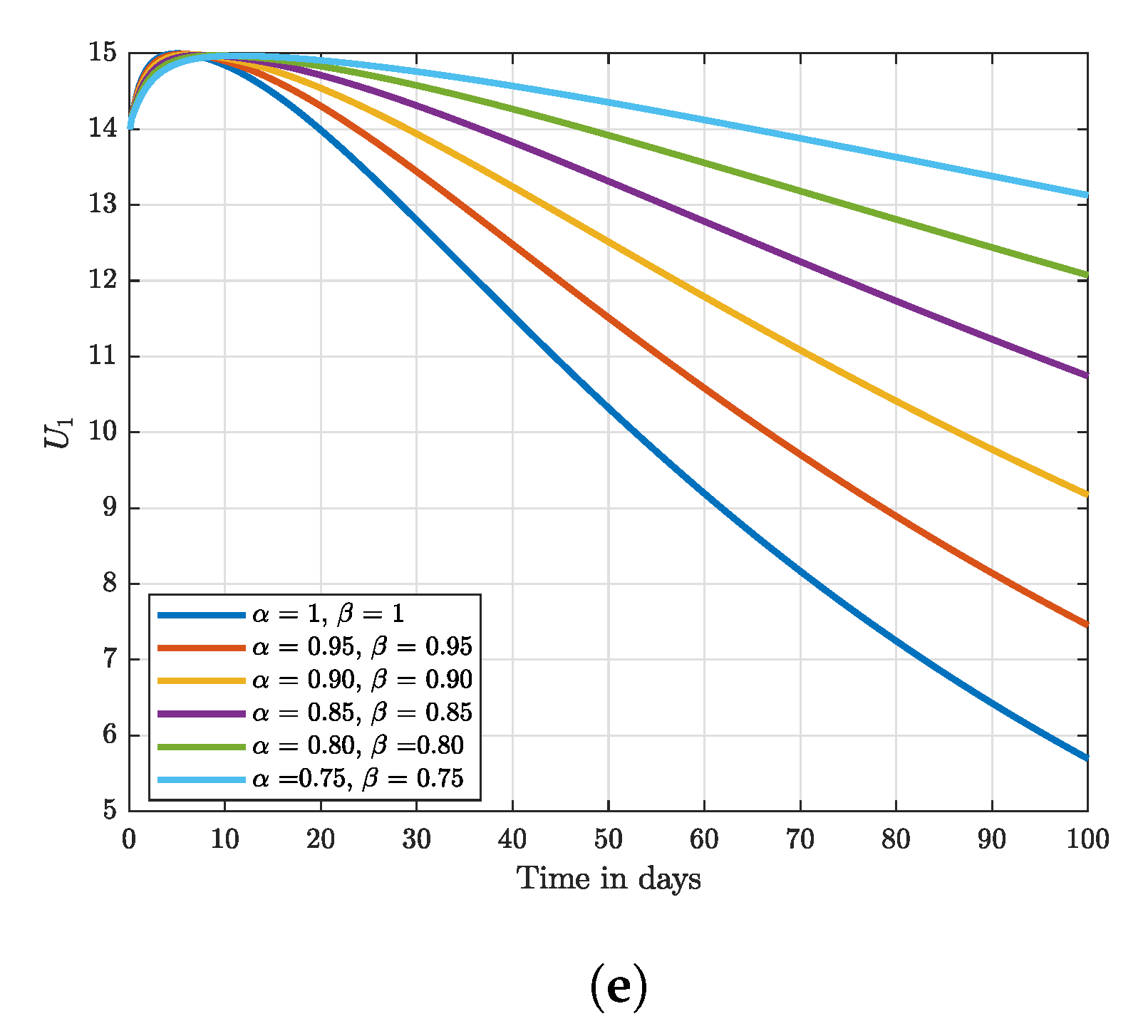
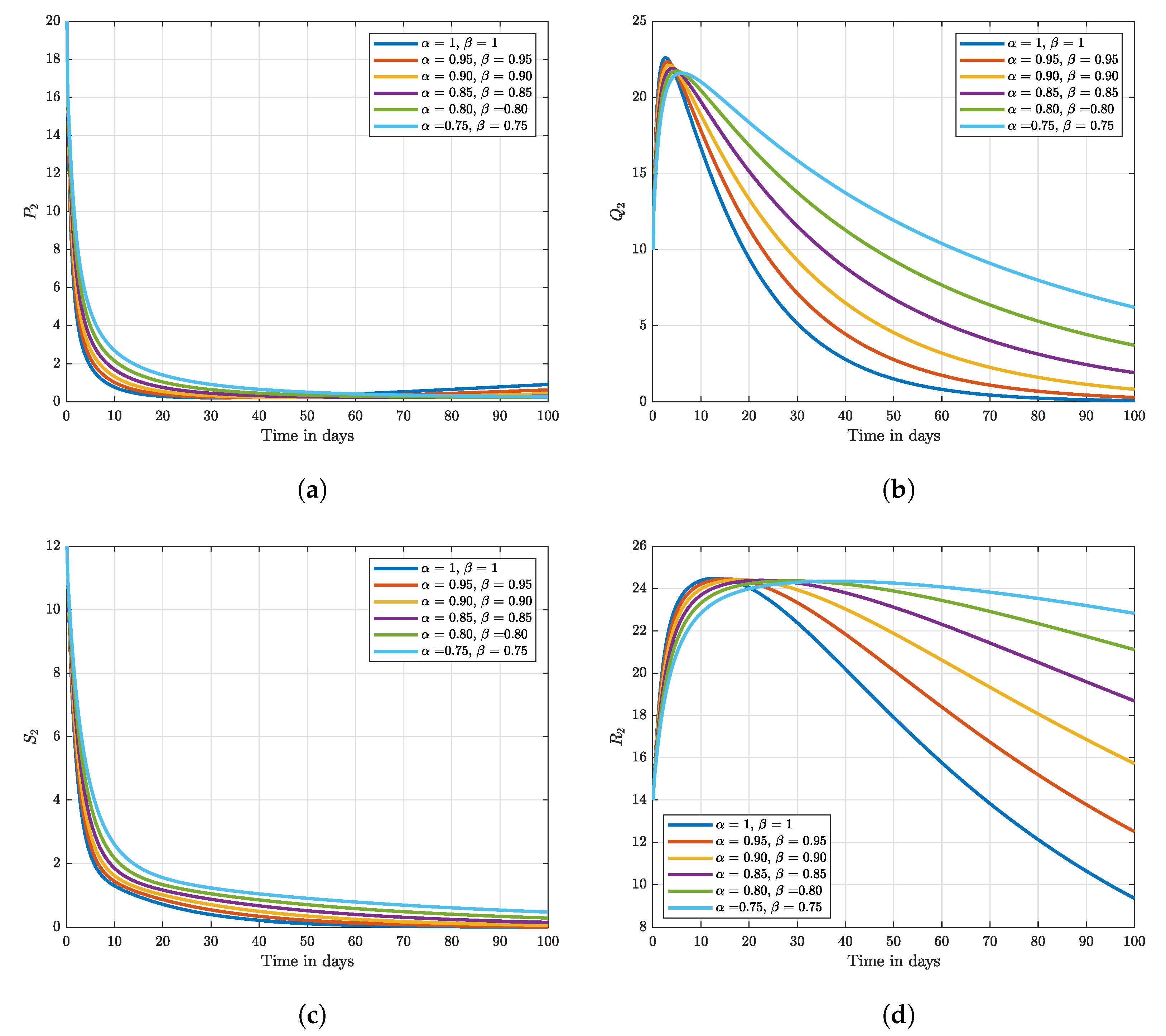
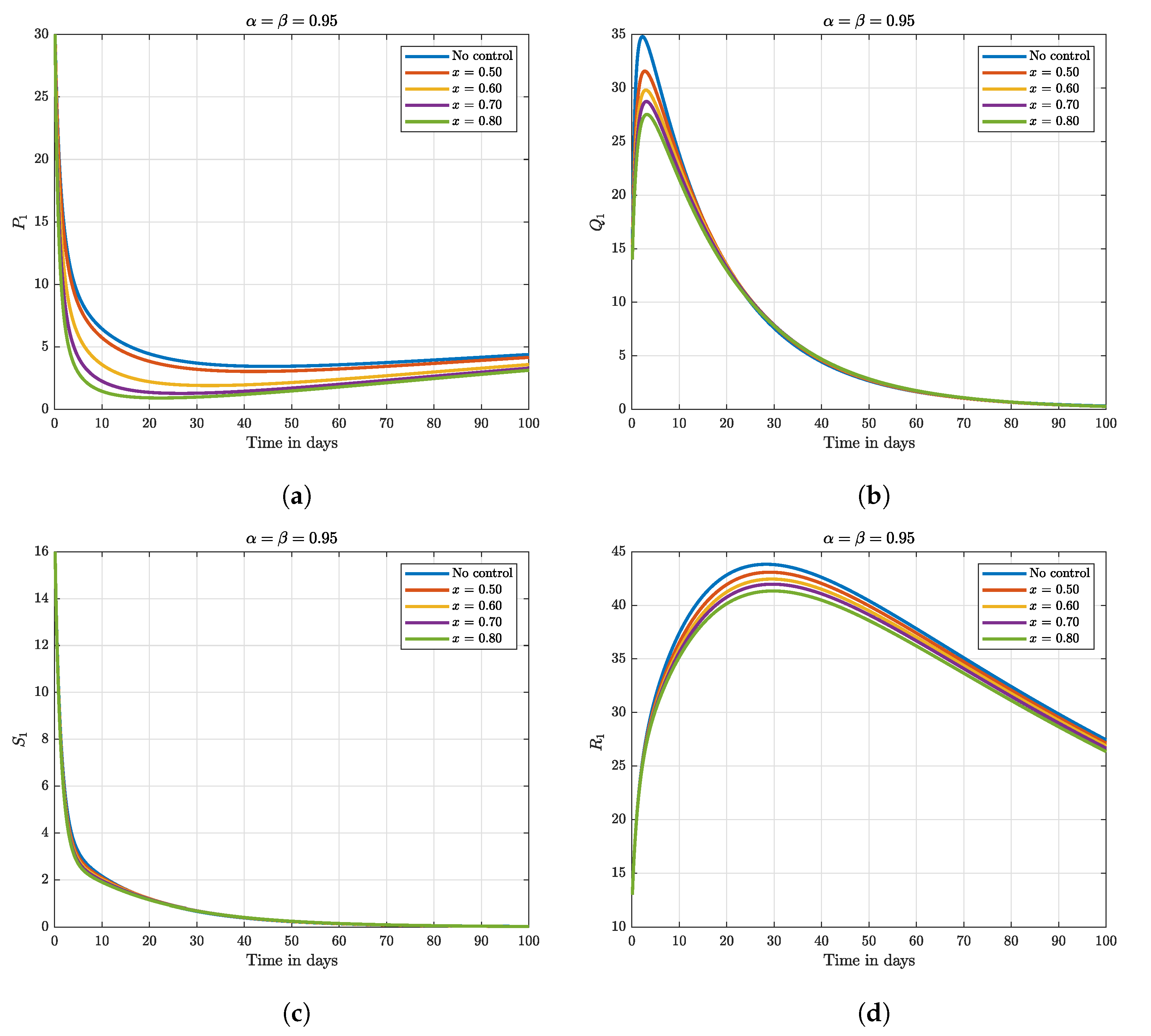
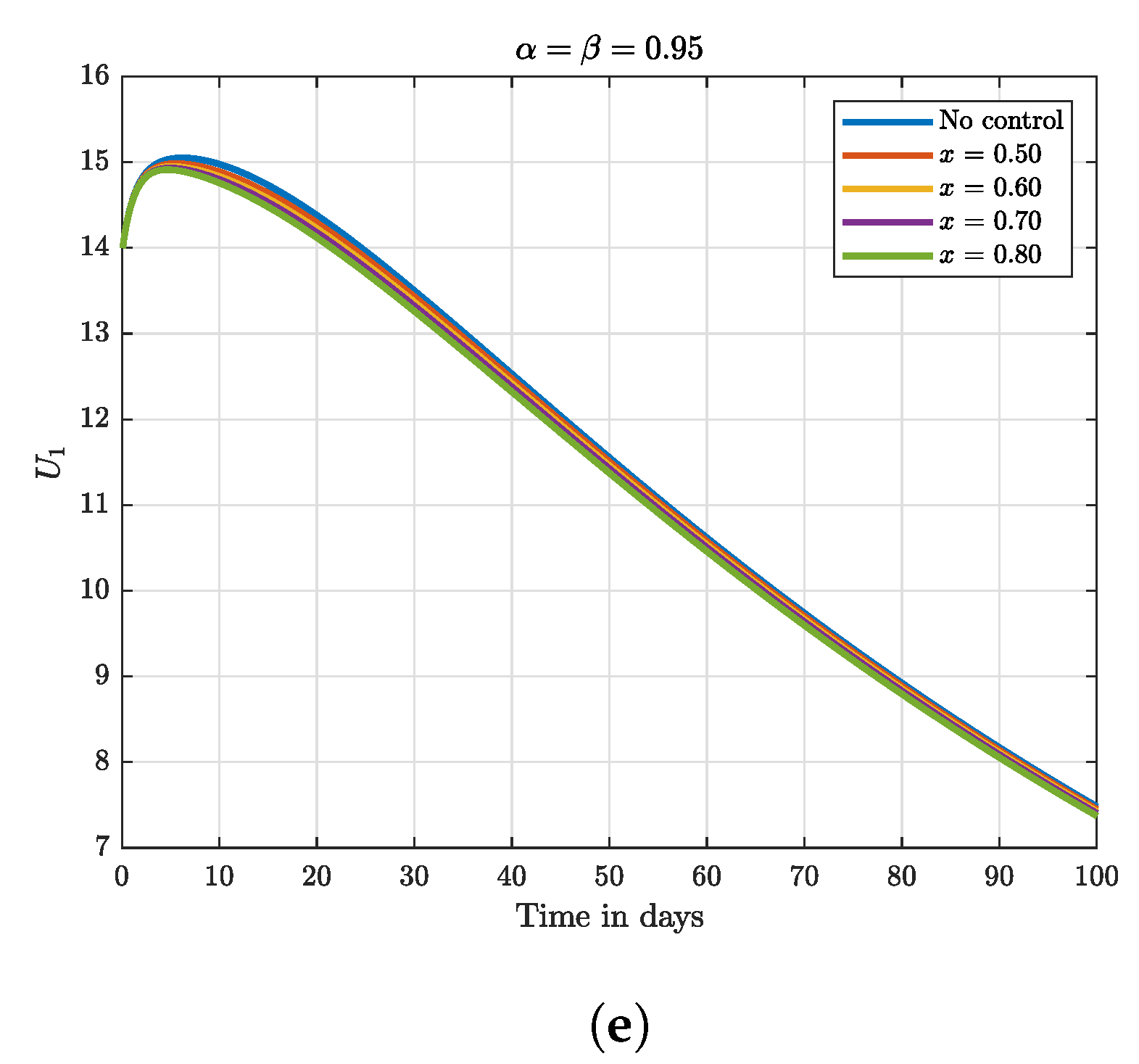
8. Numerical Results and Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Health Organization Tobacco Report. Fact-Sheets about Tobacco. 2021. Available online: https://www.who.int/news-room/fact-sheets/detail/tobacco (accessed on 11 December 2022).
- World Health Organization Tobacco Report. Tobacco in the Western Pacific. 2021. Available online: https://www.who.int/westernpacific/health-topics/tobacco (accessed on 11 December 2022).
- Aslam, M.; Murtaza, R.; Abdeljawad, T.; Rahman, G.U.; Khan, A.; Khan, H.; Gulzar, H. A fractional order HIV/AIDS epidemic model with Mittag-Leffler kernel. Adv. Differ. Equ. 2021, 2021, 107. [Google Scholar] [CrossRef]
- Sher, M.; Shah, K.; Khan, Z.A.; Khan, H.; Khan, A. Computational and theoretical modeling of the transmission dynamics of novel COVID-19 under Mittag-Leffler Power Law. Alex. Eng. J. 2020, 59, 3133–3147. [Google Scholar] [CrossRef]
- Chukwu, W.; Nyabadza, F. A mathematical model and optimal control for Listeriosis disease from ready-to-eat food products. medRxiv 2020. [Google Scholar] [CrossRef]
- Osman, S.; Makinde, O.D.A. Mathematical model for co-infection of listeriosis and anthrax diseases. Int. J. Math. Math. Sci. 2018, 2018, 1725671. [Google Scholar] [CrossRef]
- Sardar, T.; Rana, S.; Bhattacharya, S.; Al-Khaled, K.; Chattopadhyay, J. A generic model for a single strain mosquito-transmitted disease with memory on the host and the vector. Math. Biosci. 2015, 263, 18–38. [Google Scholar] [CrossRef]
- Mensah, J.A.; Dontwi, I.K.; Bonyah, E. Stability analysis of Zika-malaria co-infection model for malaria endemic region. J. Adv. Math. Comput. Sci. 2018, 26, 1–22. [Google Scholar] [CrossRef]
- Peter, O.J.; Yusuf, A.; Ojo, M.M. A Mathematical Model Analysis of Meningitis with Treatment and Vaccination in Fractional Derivatives. Int. J. Appl. Comput. Math. 2022, 8, 117. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Mohammad, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative. Chaos Solit. Fract. 2020, 134, 109705. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Okyere, E.; Yankson, E.; Opoku, A.A.; Adom-Konadu, A.; Acheampong, E.; Arthur, Y.D. Non-fractional and fractional mathematical analysis and simulations for Q fever. Chaos Solitons Fractals 2022, 156, 111821. [Google Scholar] [CrossRef]
- Castillo-Garsow, C.; Jordan-Salivia, G.; Rodriguez-Herrera, A. Mathematical Models for the Dynamics of Tobacco Use, Recovery, and Replase; Technical Report BU-1505-M; Cornell University: Ithaca, NY, USA, 2000. [Google Scholar]
- Zaman, G. Qualitative Behavior of Giving up Smoking Models. Bull. Malays. Math. Sci. Soc. 2011, 34, 403–415. [Google Scholar]
- Zaman, G. Optimal Campaign in the Smoking Dynamics. Comput. Math. Methods Med. 2011, 2011, 163834. [Google Scholar] [CrossRef]
- Abdullah, M.; Ahmad, A.; Raza, N.; Farman, M.; Ahmad, M. Approximate Solution and Analysis of Smoking Epidemic Model with Caputo Fractional Derivatives. Int. J. Appl. Comput. Math. 2018, 4, 112. [Google Scholar] [CrossRef]
- Khan, S.A.; Shah, K.; Zaman, G.; Jarad, F. Existence theory and numerical solutions to smoking model under Caputo-Fabrizio fractional derivative. Chaos 2019, 29, 013128. [Google Scholar] [CrossRef]
- Bonyah, E.; Yavuz, M.; Baleanu, D.; Kumar, S. A robust study on the listeriosis disease by adopting fractal-fractional operators. Alex. Eng. J. 2022, 61, 2016–2028. [Google Scholar] [CrossRef]
- Ahmad, Z.; Bonanomi, G.; di Serafino, D.; Giannino, F. Transmission dynamics and sensitivity analysis of pine wilt disease with asymptomatic carriers via fractal-fractional differential operator of Mit-tag-Leffler kernel. Appl. Numer. Math. 2023, 185, 446–465. [Google Scholar] [CrossRef]
- Malik, A.; Alkholief, M.; Aldakheel, F.M.; Ali Khan, A.; Ahmad, Z.; Kamal, W.; Khalil Gatasheh, M.; Alshamsan, A. Sensitivity analysis of COVID-19 with quarantine and vaccination: A fractal-fractional model. Alex. Eng. J. 2022, 61, 8859–8874. [Google Scholar] [CrossRef]
- Addai, E.; Zhang, L.; Asamoah, J.K.K.; Preko, A.K.; Arthur, Y.D. Fractal–fractional age-structure study of omicron SARS-CoV-2 variant transmission dynamics. Partial. Differ. Equ. Appl. Math. 2022, 6, 100455. [Google Scholar] [CrossRef]
- Addai, E.; Zhang, L.; Ackora-Prah, J.; Gordon, J.F.; Asamoah, J.K.K.; Essel, J.F. Fractal-fractional order dynamics and nu-merical simulations of a Zika epidemic model with insecticide-treated nets. Phys. A 2022, 603, 127809. [Google Scholar] [CrossRef]
- Addai, E.; Zhang, L.; Asamoah, J.K.; Essel, J.F. A fractional order age-specific smoke epidemic model. Appl. Math. Model. 2023, 119, 99–118. [Google Scholar] [CrossRef]
- Atangana, A.; Owolabi, K.M. New numerical approach for fractional differential equations. Math. Model Nat. Phenom 2018, 13, 3. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.M.A.; El-Saka, H.A. Equilibrium points, stability and numerical solutions of fractional-order predator–prey and rabies models. J. Math. Anal. Appl. 2007, 325, 542–553. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M. “Smoking”. 2013. Available online: https://ourworldindata.org/smoking (accessed on 11 December 2022).
- Atangana, A.; Araz, S.I. New Numerical Scheme with Newton Polynomial: Theory, Methods, and Applications; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]




| Variables | Description |
|---|---|
| Total population size for Group 1 and Group 2 | |
| Potential smokers for Group 1 and Group 2 | |
| Occasional smokers for Group 1 and Group 2 | |
| Smokers for Group 1 and Group 2 | |
| Smokers who temporarily quit smoking for Group 1 and Group 2 | |
| Smokers who permanently quit smoking for Group 1 and Group 2 | |
| Parameters | Description |
| Recruitment rate of Group 1 | |
| Recruitment rate of Group 2 | |
| Effective contact rate between and | |
| Effective contact rate between and | |
| Natural death rate for Group 1 and Group 2 | |
| The rate at which occasional smokers become regular smokers for Group 1 and Group 2, | |
| The rate of quitting smoking for both Group 1 and Group 2 | |
| The contact rate between smokers and temporary quitters who revert back to smoking | |
| The fraction of smokers who temporary quit smoking (at the rate ) | |
| The fraction of smokers who temporary quit smoking (at the rate ) | |
| The remaining fraction of smokers who permanently quit smoking |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Addai, E.; Adeniji, A.; Peter, O.J.; Agbaje, J.O.; Oshinubi, K. Dynamics of Age-Structure Smoking Models with Government Intervention Coverage under Fractal-Fractional Order Derivatives. Fractal Fract. 2023, 7, 370. https://doi.org/10.3390/fractalfract7050370
Addai E, Adeniji A, Peter OJ, Agbaje JO, Oshinubi K. Dynamics of Age-Structure Smoking Models with Government Intervention Coverage under Fractal-Fractional Order Derivatives. Fractal and Fractional. 2023; 7(5):370. https://doi.org/10.3390/fractalfract7050370
Chicago/Turabian StyleAddai, Emmanuel, Adejimi Adeniji, Olumuyiwa J. Peter, Janet O. Agbaje, and Kayode Oshinubi. 2023. "Dynamics of Age-Structure Smoking Models with Government Intervention Coverage under Fractal-Fractional Order Derivatives" Fractal and Fractional 7, no. 5: 370. https://doi.org/10.3390/fractalfract7050370
APA StyleAddai, E., Adeniji, A., Peter, O. J., Agbaje, J. O., & Oshinubi, K. (2023). Dynamics of Age-Structure Smoking Models with Government Intervention Coverage under Fractal-Fractional Order Derivatives. Fractal and Fractional, 7(5), 370. https://doi.org/10.3390/fractalfract7050370









