A Sufficient and Necessary Condition for the Power-Exponential Function ${\left(1+\frac{1}{x}\right)}^{\alpha x}$ to Be a Bernstein Function and Related nth Derivatives ^†

Abstract

In the paper, the authors find a sufficient and necessary condition for the power-exponential function ${\left(1+\frac{1}{x}\right)}^{\alpha x}$ to be a Bernstein function, derive closed-form formulas for the nth derivatives of the power-exponential functions ${\left(1+\frac{1}{x}\right)}^{\alpha x}$ and ${(1+x)}^{\alpha /x}$, and present a closed-form formula of the partial Bell polynomials $B_{n,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))$ for $n\ge k\ge 0$, where ${\mathcal{H}}_k\left(x\right)={\int }_0^{\infty }\frac{{\mathrm{e}}^u-1-u}{{\mathrm{e}}^u}{u}^{k-1}{\mathrm{e}}^{-xu}\mathrm{d}u$ for $k\ge 0$ are completely monotonic on $(0,\infty )$.

1. Motivations

Let $I\subseteq \mathbb{R}$ be a finite or infinite interval. Recall from [1] (Chapter XIII) and [2] (Chapter IV) that a real-valued function $f\left(x\right)$ defined on $I\subseteq \mathbb{R}$ is said to be completely monotonic on I if and only if ${(-1)}^k{f}^{\left(k\right)}\left(x\right)\ge 0$ is valid for all $k\ge 0$ and $x\in I$. The interval $I\subseteq \mathbb{R}$ is called the completely monotonic interval of $f\left(x\right)$. A non-negative-valued function $f\left(x\right)$ on an interval I is called (see the paper [3]) (Chapter 3) a Bernstein function if its first derivative $f^{\prime }\left(x\right)$ is completely monotonic on I.

In the paper [4], the authors reviewed, discussed, and presented closed-form formulas for the nth derivative of the power-exponential function $x^x$ for $x>0$. One of the main results in the paper [4] is Theorem 1, in which the formula

$${\left(x^x\right)}^{\left(n\right)}=n!x^{x-n}\sum _{k=0}^n{x}^k\sum _{j=0}^k\left[\sum _{q=0}^{n-k}\frac{s(q+j,j)}{(q+j)!}\left(\genfrac{}{}{0pt}{}{j}{n-k-q}\right)\right]\frac{{(lnx)}^{k-j}}{(k-j)!},n\ge 0$$

was established, where $s(n,k)$ denotes the Stirling numbers of the first kind, which can be analytically generated [5] (p. 20, (1.30)) by

$$\frac{{[ln(1+x)]}^k}{k!}=\sum _{n=k}^{\infty }s(n,k)\frac{x^n}{n!},\left|x\right|<1;$$

see also the monographs [6,7]. For more information on the nth derivative of the function $x^{ax}$, please refer to [8] (pp. 139–140, Example), [9] (p. 8), and the papers [10,11,12].

In this paper, for alternatively demonstrating that, if and only if $0<\alpha \le {\alpha }^{*}\in (2,3)$, the function

$$h_{\alpha }\left(x\right)={\left(1+\frac{1}{x}\right)}^{\alpha x},\alpha \in \mathbb{R},x>0$$

(1)

is a Bernstein function on $(0,\infty )$, see the papers [13,14,15,16], we will compute the nth derivative of the power-exponential function $h_{\alpha }\left(x\right)$ using several approaches.

Why do we consider the power-exponential function $h_{\alpha }\left(x\right)$ and determine the largest number ${\alpha }^{*}\in (2,3)$ such that $h_{\alpha }\left(x\right)$ is a Bernstein function on $(0,\infty )$ for $0<\alpha \le {\alpha }^{*}$? What applications of this necessary and sufficient condition has? Ones can find explicit answers to these two questions in the papers [13,14,15,17,18] and closely related references therein.

Another reason why we will consider the function $h_{\alpha }\left(x\right)$ is that writing out the general formula for the nth derivatives of power-exponential functions, such as $x^{\alpha x}$, ${\left(1+\frac{1}{x}\right)}^{\alpha x}$, and ${(1+x)}^{\alpha /x}$ is, although elementary, also difficult.

2. Preliminaries

In [19] (p. 412, Definition 11.2) and [8] (p. 134, Theorem A), the partial Bell polynomials $B_{n,k}(x_1,x_2,\cdots ,x_{n-k+1})$ in the variables $x_1,x_2,\cdots ,x_{n-k+1}$ of degree k are defined for $n\ge k\ge 0$ by

$$B_{n,k}(x_1,x_2,\cdots ,x_{n-k+1})=\sum _{\begin{array}{c}{k}_j\ge 0\mathrm{for}1\le j\le n-k+1,\\ {\sum }_{j=1}^{n-k+1}j{k}_j=n,\\ {\sum }_{j=1}^{n-k+1}{k}_j=k\end{array}}\frac{n!}{{\prod }_{j=1}^{n-k+1}{k}_j!}\prod _{j=1}^{n-k+1}{\left(\frac{x_j}{j!}\right)}^{k_j}.$$

(2)

In particular, the special values $B_{0,0}\left(x_1\right)=1$ and $B_{n,0}(x_1,x_2,\cdots ,x_{n+1})=0$ for $n\ge 1$ are useful. The famous Faà di Bruno formula can be described in terms of the partial Bell polynomials $B_{n,k}$ by

$$\frac{{\mathrm{d}}^n}{\mathrm{d}{x}^n}f\circ g\left(x\right)=\sum _{k=0}^n{f}^{\left(k\right)}\left(g\left(x\right)\right)B_{n,k}\left(g^{\prime }\left(x\right),g^{″}\left(x\right),\cdots ,g^{(n-k+1)}\left(x\right)\right).$$

(3)

The partial Bell polynomials $B_{n,k}$ satisfy the identities

$$\begin{array}{c}{B}_{n,k}\left(\alpha \beta x_1,\alpha {\beta }^2{x}_2,\cdots ,\alpha {\beta }^{n-k+1}{x}_{n-k+1}\right)={\alpha }^k{\beta }^n{B}_{n,k}(x_1,x_2,\cdots ,x_{n-k+1}),\end{array}$$

(4)

$$\begin{array}{c}{B}_{n,k}\left(x_1,x_2,\cdots ,x_{n-k+1}\right)=\sum _{\ell =0}^k\left(\genfrac{}{}{0pt}{}{n}{\ell }\right)x_1^{\ell }{B}_{n-\ell ,k-\ell }\left(0,x_2,\cdots ,x_{n-k+1}\right),\end{array}$$

(5)

and

$$\begin{array}{c}{B}_{n,k}(x_1+y_1,x_2+y_2,\cdots ,x_{n-k+1}+y_{n-k+1})\hfill \\ \hfill =\sum _{r+s=k}\sum _{\ell +m=n}\left(\genfrac{}{}{0pt}{}{n}{\ell }\right)B_{\ell ,r}(x_1,x_2,\cdots ,x_{\ell -r+1})B_{m,s}(y_1,y_2,\cdots ,y_{m-s+1}).\end{array}$$

(6)

These three identities can be found in [19] (pp. 412, 420) and [8] (pp. 135–137).

In [20] (Theorem 1.1), the closed-form formula

$$B_{n,k}(0,1!,2!,\cdots ,(n-k)!)={(-1)}^{n-k}\left(\genfrac{}{}{0pt}{}{n}{k}\right)\sum _{m=0}^k{(-1)}^m\frac{\left(\genfrac{}{}{0pt}{}{k}{m}\right)}{\left(\genfrac{}{}{0pt}{}{n-m}{n-k}\right)}s(n-m,k-m)$$

(7)

for $n\ge k\ge 0$ was presented. Since

$$B_{n,k}\left(\frac{x_2}{2},\frac{x_3}{3},\cdots ,\frac{x_{n-k+2}}{n-k+2}\right)=\frac{n!}{(n+k)!}{B}_{n+k,k}(0,x_2,\cdots ,x_{n+1})$$

(8)

for $n\ge k\ge 0$, Formula (7) is equivalent to

$$B_{n,k}\left(\frac{1!}{2},\frac{2!}{3},\cdots ,\frac{(n-k+1)!}{n-k+2}\right)={(-1)}^{n-k}\frac{1}{k!}\sum _{m=0}^k{(-1)}^m\frac{\left(\genfrac{}{}{0pt}{}{k}{m}\right)}{\left(\genfrac{}{}{0pt}{}{n+m}{m}\right)}s(n+m,m)$$

(9)

for $n\ge k\ge 0$. Formula (8) can be found in [8] (p. 136), while Formula (9) can be found in [20] (Theorem 1.1).

In [4] (Lemma 1), it was established that

$$\begin{array}{c}{B}_{n,k}(0,0!,1!,2!,\cdots ,(n-k-2)!,(n-k-1)!)\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={(-1)}^{n-k}n!\sum _{j=0}^k\frac{{(-1)}^j}{(k-j)!}\sum _{\ell =0}^{n-k}\frac{s(\ell +j,j)}{(\ell +j)!}\left(\genfrac{}{}{0pt}{}{j}{n-k-\ell }\right)\end{array}$$

(10)

for $n\ge k\ge 0$. In [8] (p. 135, Theorem B) and [20] (Theorem 1.1), we can find the identity

$$B_{n,k}(1!,2!,\cdots ,(n-k+1)!)=\left(\genfrac{}{}{0pt}{}{n-1}{k-1}\right)\frac{n!}{k!}=L(n,k)$$

(11)

for $n\ge k\ge 0$, where $L(n,k)$ is called the Lah numbers in combinatorial number theory (see [6,21] (pp. 43–44)).

A family of polynomials $P_n\left(x\right)$ of degree $n\ge 0$ is said to be of binomial type if it satisfies the binomial identity

$$P_n(x+y)=\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)P_k\left(x\right)P_{n-k}\left(y\right).$$

Let

$$p_n\left(\alpha \right)=\sum _{k=0}^n{B}_{n,k}(x_1,x_2,\cdots ,x_{n-k+1}){\alpha }^k,n\ge 0.$$

Then the family of polynomials $p_n\left(\alpha \right)$ of degree $n\ge 0$ is of binomial type, that is,

$$p_n(\alpha +\beta )=\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)p_k\left(\alpha \right)p_{n-k}\left(\beta \right),n\ge 0,$$

(12)

and

$$p_n^{\prime }\left(0\right)=x_n,n\ge 1.$$

These results can be found in [22,23] (p. 83).

3. A Sufficient and Necessary Condition

In this section, we discuss the nth derivative of the power-exponential function $h_{\alpha }\left(x\right)$ and present a sufficient and necessary condition for $h_{\alpha }\left(x\right)$ to be a Bernstein function on the infinite interval $(0,\infty )$.

Theorem 1. 

For $\alpha \in \mathbb{R}$ and $x>0$, the nth derivative of the power-exponential function $h_{\alpha }\left(x\right)={\left(1+\frac{1}{x}\right)}^{\alpha x}$ can be computed using

$$h_{\alpha }^{\left(n\right)}\left(x\right)={(-1)}^n{h}_{\alpha }\left(x\right)\sum _{k=0}^n{(-1)}^k{\alpha }^k{B}_{n,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right)),$$

(13)

where $n\ge 0$ is an integer and the functions

$${\mathcal{H}}_k\left(x\right)={\int }_0^{\infty }\frac{{\mathrm{e}}^u-1-u}{{\mathrm{e}}^u}{u}^{k-1}{\mathrm{e}}^{-xu}\mathrm{d}u,k\ge 0$$

(14)

are completely monotonic on $(0,\infty )$.

Proof. 

Let $H_{\alpha }\left(x\right)=ln{h}_{\alpha }\left(x\right)$. Then direct computation gives

$$H_{\alpha }^{\prime }\left(x\right)=\alpha \left[ln\left(1+\frac{1}{x}\right)-\frac{1}{1+x}\right]=\alpha {\mathcal{H}}_0\left(x\right)$$

and

$$H_{\alpha }^{(k+1)}\left(x\right)={(-1)}^k\alpha \left[\frac{(k-1)!}{x^k}-\frac{(k-1)!}{{(1+x)}^k}-\frac{k!}{{(1+x)}^{k+1}}\right]={(-1)}^k\alpha {\mathcal{H}}_k\left(x\right)$$

for $k\ge 1$, where we used the integral representation

$$ln\frac{b}{a}={\int }_0^{\infty }\frac{{\mathrm{e}}^{-au}-{\mathrm{e}}^{-bu}}{u}\mathrm{d}u$$

in [24] (p. 230, 5.1.32) and the formula

$$\mathrm{\Gamma }\left(z\right)=w^z{\int }_0^{\infty }{u}^{z-1}{\mathrm{e}}^{-wu}\mathrm{d}u,\Re \left(z\right),\Re \left(w\right)>0$$

(15)

in [24] (p. 255, Entry 6.1.1).

By virtue of the Faà di Bruno Formula (3) and the identity (4), we arrive at

$$\begin{array}{cc}\hfill h_{\alpha }^{\left(n\right)}\left(x\right)& =\frac{{\mathrm{d}}^n{\mathrm{e}}^{H_{\alpha }\left(x\right)}}{\mathrm{d}{x}^n}=\sum _{k=0}^n{\mathrm{e}}^{H_{\alpha }\left(x\right)}{B}_{n,k}\left(H_{\alpha }^{\prime }\left(x\right),H_{\alpha }^{″}\left(x\right),\cdots ,H_{\alpha }^{(n-k+1)}\left(x\right)\right)\hfill \\ \hfill & ={(-1)}^n{h}_{\alpha }\left(x\right)\sum _{k=0}^n{(-1)}^k{\alpha }^k{B}_{n,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))\hfill \end{array}$$

for $n\ge 0$. From the integral representation (14), we can easily see that all the functions ${\mathcal{H}}_k\left(x\right)$ for $k\ge 0$ are completely monotonic on $(0,\infty )$. In conclusion, we acquire the Formula (13). The proof of Theorem 1 is complete. □

Remark 1. 

It is clear that

$${\mathcal{H}}_k^{\prime }\left(x\right)=-{\int }_0^{\infty }\frac{{\mathrm{e}}^u-1-u}{{\mathrm{e}}^u}{u}^k{\mathrm{e}}^{-xu}\mathrm{d}u=-{\mathcal{H}}_{k+1}\left(x\right),k\ge 0.$$

Since the functions ${\mathcal{H}}_k\left(x\right)$ for $k\ge 0$ are completely monotonic on $(0,\infty )$, the product of finitely many completely monotonic functions is a completely monotonic function on the intersection of their completely monotonic intervals, considering definition (2), we conclude that the functions

$$B_{n,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))>0,n\ge k\ge 1$$

are completely monotonic on $(0,\infty )$.

Theorem 2. 

For $\alpha ,\beta \in \mathbb{R}$ and $x>0$, the derivatives of the power-exponential function $h_{\alpha }\left(x\right)={\left(1+\frac{1}{x}\right)}^{\alpha x}$ satisfy the identity

$$h_{\alpha +\beta }^{\left(n\right)}\left(x\right)=\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)h_{\alpha }^{\left(k\right)}\left(x\right)h_{\beta }^{(n-k)}\left(x\right),n\ge 0.$$

(16)

In other words, the nth derivative $h_{\alpha }^{\left(n\right)}\left(x\right)$ for $n\ge 0$ is of binomial type.

Proof. 

Based on Formula (13) in Theorem 1, let

$$p_n\left(\alpha \right)={(-1)}^n\frac{h_{\alpha }^{\left(n\right)}\left(x\right)}{h_{\alpha }\left(x\right)}=\sum _{k=0}^n{B}_{n,k}\left(-{\mathcal{H}}_0\left(x\right),-{\mathcal{H}}_1\left(x\right),\cdots ,-{\mathcal{H}}_{n-k}\left(x\right)\right){\alpha }^k$$

for $n\ge 0$. Making use of Equation (12), we obtain

$${(-1)}^n\frac{h_{\alpha +\beta }^{\left(n\right)}\left(x\right)}{h_{\alpha +\beta }\left(x\right)}=\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right){(-1)}^k\frac{h_{\alpha }^{\left(k\right)}\left(x\right)}{h_{\alpha }\left(x\right)}{(-1)}^{n-k}\frac{h_{\beta }^{(n-k)}\left(x\right)}{h_{\beta }\left(x\right)},n\ge 0,$$

which can be simplified as (16). □

Theorem 3. 

There exists a positive constant ${\alpha }^{*}$ such that, if and only if $0<\alpha \le {\alpha }^{*}$, the power-exponential function $h_{\alpha }\left(x\right)={\left(1+\frac{1}{x}\right)}^{\alpha x}$ is a Bernstein function on $(0,\infty )$.

Proof. 

It is easy to see that $h_{\alpha }\left(x\right)$ for $\alpha \in \mathbb{R}$ is positive on $(0,\infty )$. Hence, to prove that $h_{\alpha }\left(x\right)$ is a Bernstein function on $(0,\infty )$, it is sufficient to show

$$\begin{array}{cc}\hfill {(-1)}^n{\left[h_{\alpha }^{\prime }\left(x\right)\right]}^{\left(n\right)}& ={(-1)}^n{h}_{\alpha }^{(n+1)}\left(x\right)\hfill \\ \hfill & =-h_{\alpha }\left(x\right)\sum _{k=1}^{n+1}{(-1)}^k{\alpha }^k{B}_{n+1,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k+1}\left(x\right))\hfill \\ \hfill & >0\hfill \end{array}$$

for $n\ge 0$. Therefore, it is sufficient to demonstrate

$$\alpha \sum _{k=0}^n{(-1)}^k{\alpha }^k{B}_{n+1,k+1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))>0$$

(17)

on $(0,\infty )$ for all $n\ge 0$ and a part of $\alpha \in \mathbb{R}$.

Descartes’ rule of signs [25] (p. 22) states that:

• If the nonzero terms of a single-variable polynomial with real coefficients are ordered by descending variable exponent, then the number of positive zeros of the polynomial is either equal to the number of sign changes between consecutive (nonzero) coefficients or is less than it by an even number. A zero of multiplicity k is counted as k zeros.
• The number of negative zeros is the number of sign changes after multiplying the coefficients of odd-power terms by $-1$, or fewer than it by an even number.

Applying this rule to the polynomials

$$P_{n,x}\left(\alpha \right)=\sum _{k=0}^n{(-1)}^k{\alpha }^k{B}_{n+1,k+1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))$$

(18)

of the variable $\alpha$ for $n\ge 0$ and $x>0$ reveals that,

• when $n=0$, the polynomial $P_{0,x}\left(\alpha \right)=B_{1,1}\left({\mathcal{H}}_0\left(x\right)\right)={\mathcal{H}}_0\left(x\right)>0$ has no any zero;
• when $n\ge 1$, the polynomial $P_{n,x}\left(\alpha \right)$ has no any negative zero;
• when $n\ge 1$, the polynomial $P_{n,x}\left(\alpha \right)$ has at most n positive zeros or has positive zeros of an even number less than n, or has no positive zero.

For convenience, we denote the set of all positive zeros of the polynomial $P_{n,x}\left(\alpha \right)$ for $n\ge 0$ by $Z_n\left(x\right)$ in $x\in (0,\infty )$. It is clear that $Z_0\left(x\right)=\varnothing$ in $x\in (0,\infty )$. Since

$$P_{1,x}\left(\alpha \right)=B_{2,1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right))-\alpha B_{2,2}\left({\mathcal{H}}_0\left(x\right)\right)={\mathcal{H}}_1\left(x\right)-\alpha {\mathcal{H}}_0^2\left(x\right)$$

has a positive zero $\frac{{\mathcal{H}}_1\left(x\right)}{{\mathcal{H}}_0^2\left(x\right)}$, the set $Z_1\left(x\right)=\left\{\frac{{\mathcal{H}}_1\left(x\right)}{{\mathcal{H}}_0^2\left(x\right)}\right\}$ in $x\in (0,\infty )$. Since

$$P_{n,x}\left(0\right)=B_{n+1,1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_n\left(x\right))={\mathcal{H}}_n\left(x\right)>0,n\ge 0,$$

(19)

if for some positive integer n the set $Z_n\left(x\right)=\varnothing$ in $x\in (0,\infty )$, then the polynomial $P_{n,x}\left(\alpha \right)$ is positive for all $x,\alpha \in (0,\infty )$, and then ${(-1)}^n{\left[h_{\alpha }^{\prime }\left(x\right)\right]}^{\left(n\right)}>0$ is valid for all $x,\alpha \in (0,\infty )$; if for some positive integer n the set $Z_n\left(x\right)\ne \varnothing$ in $x\in (0,\infty )$, then the polynomial $P_{n,x}\left(\alpha \right)$ is positive for those numbers $\alpha$, which are located on the open interval between 0 and the smallest element in $Z_n\left(x\right)$ in $x\in (0,\infty )$, and then ${(-1)}^n{\left[h_{\alpha }^{\prime }\left(x\right)\right]}^{\left(n\right)}>0$ is valid in $x\in (0,\infty )$ for those numbers $\alpha$ which locate on the open interval between 0 and the smallest element in $Z_n\left(x\right)$ in $x\in (0,\infty )$.

Denote

$$Z\left(x\right)=\bigcup _{n=0}^{\infty }{Z}_n\left(x\right),x\in (0,\infty ).$$

Then the union set $Z\left(x\right)$ in $x\in (0,\infty )$ has at least one element. Accordingly, the number

$${\alpha }^{*}=\underset{x\in (0,\infty )}{inf}Z\left(x\right)$$

is defined and significant. From the complete monotonicity of the function ${\mathcal{H}}_n\left(x\right)$ on $(0,\infty )$ and the positivity of $P_{n,x}\left(0\right)$ in (19), we conclude that the number ${\alpha }^{*}$ is positive. Consequently, if and only if $\alpha \in (0,{\alpha }^{*})$, the inequalities ${(-1)}^n{\left[h_{\alpha }^{\prime }\left(x\right)\right]}^{\left(n\right)}>0$ are valid in $x\in (0,\infty )$ for all integers $n\ge 0$, and the power-exponential function $h_{\alpha }\left(x\right)$ is a Bernstein function on $(0,\infty )$. □

Remark 2. 

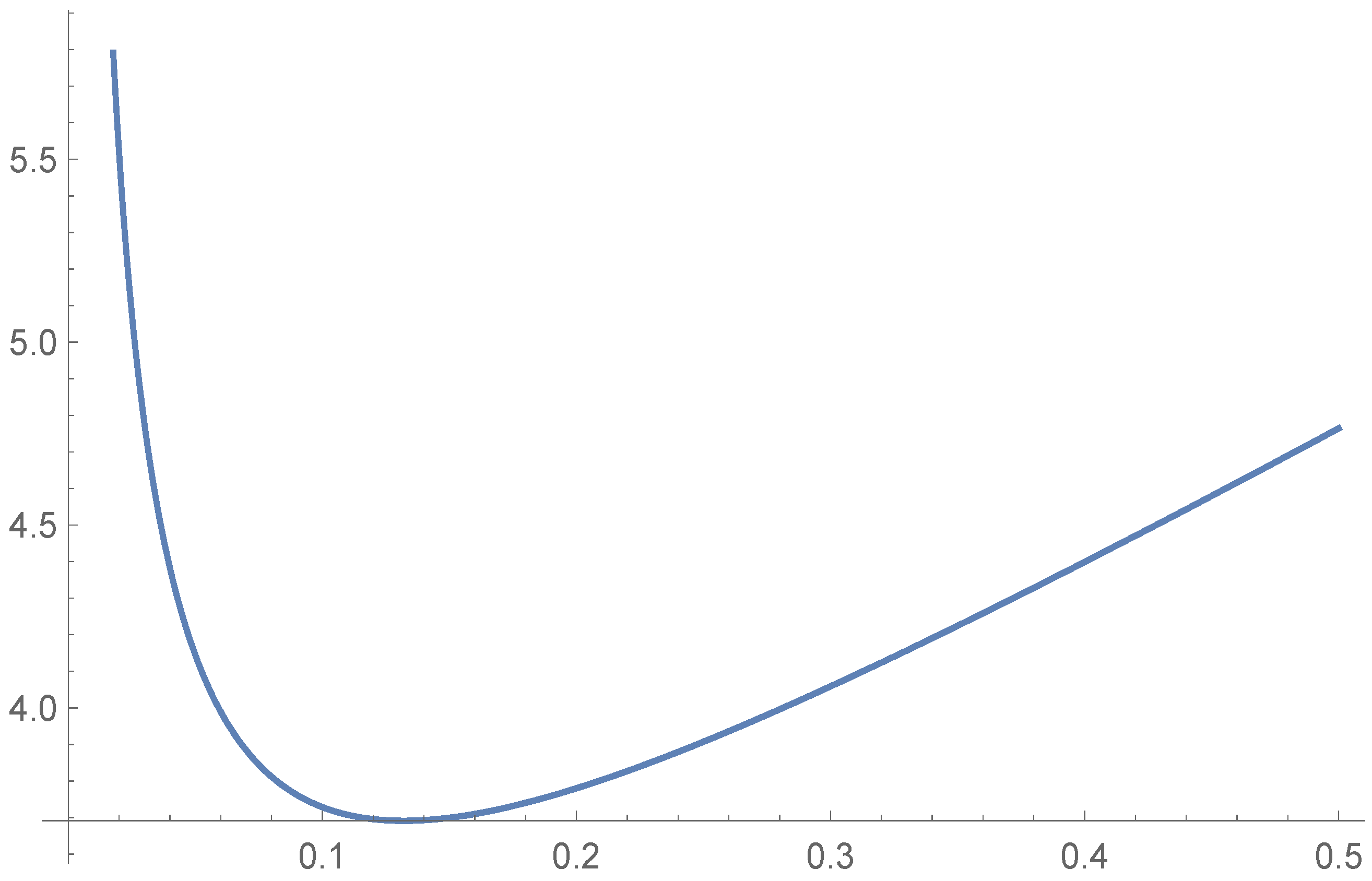
When $n=1$, the inequality (17) is equivalent to

$$B_{2,1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right))-\alpha B_{2,2}\left({\mathcal{H}}_0\left(x\right)\right)>0,x\in (0,\infty ),$$

which can be rewritten as

$$0<\alpha <\frac{B_{2,1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right))}{B_{2,2}\left({\mathcal{H}}_0\left(x\right)\right)}=\frac{{\mathcal{H}}_1\left(x\right)}{{\mathcal{H}}_0^2\left(x\right)}=\frac{1}{x{\left[1+(x+1)ln\frac{x}{1+x}\right]}^2}\triangleq G_1\left(x\right)$$

(20)

for $x\in (0,\infty )$. Using the softwareWolfram Mathematica 12, we can plot the graph of the function $G_1\left(x\right)$ for $x\in \left(0,\frac{1}{2}\right)$. The graph is shown in Figure 1. This implies that ${\alpha }^{*}<3.7\cdots$

Figure 1. The graph of the function $G_1\left(x\right)$ for $x\in \left(0,\frac{1}{2}\right)$.

Remark 3. 

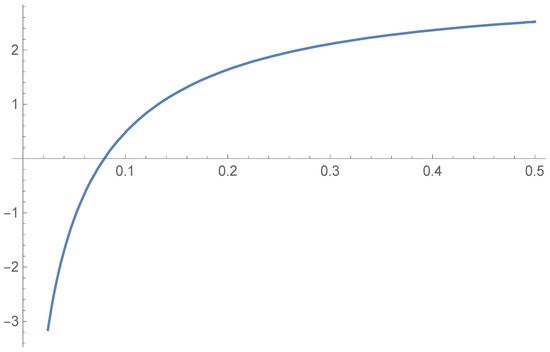
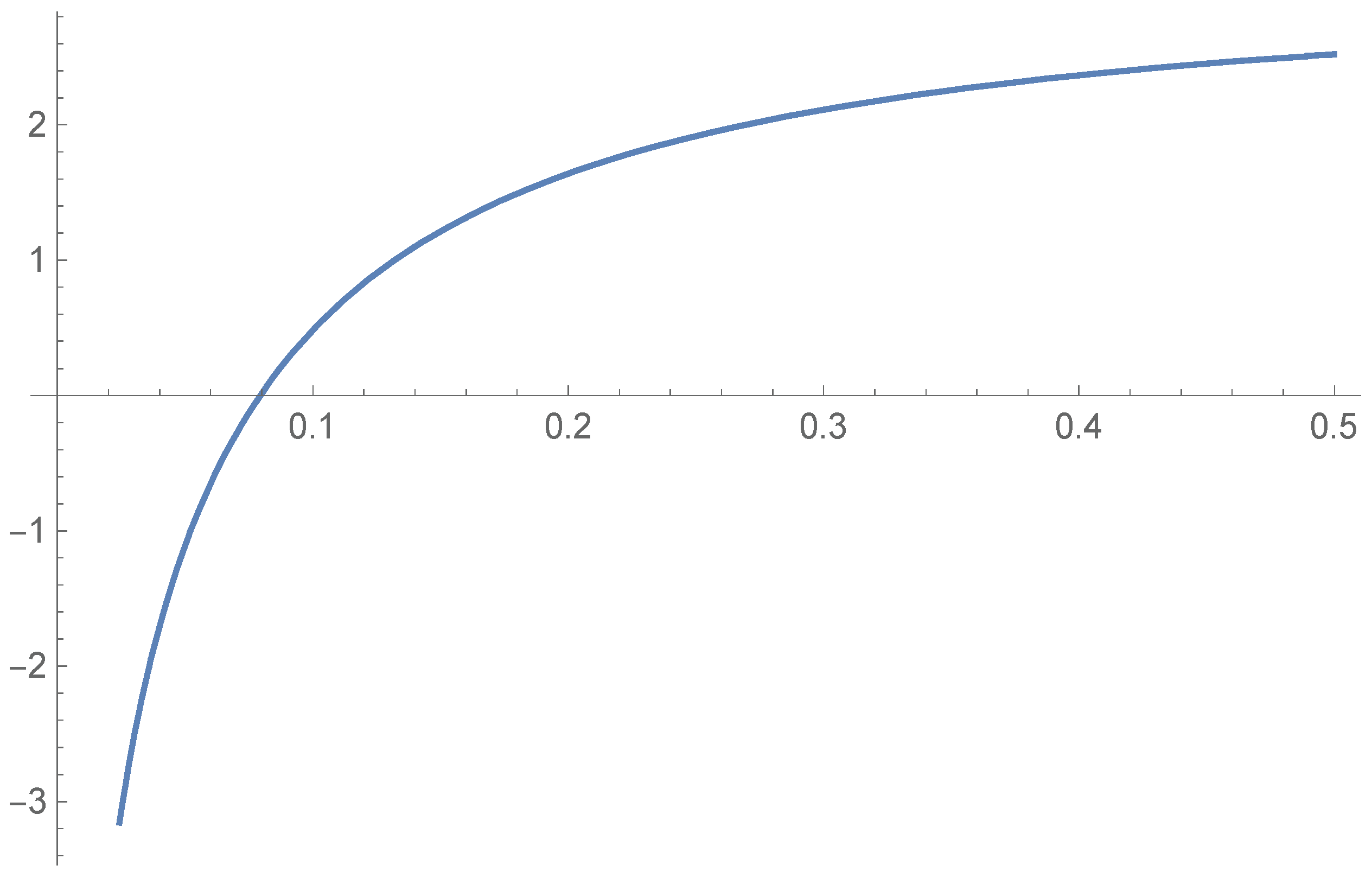
When $n=2$, the inequality (17) can be rearranged as

$$B_{3,1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),{\mathcal{H}}_2\left(x\right))-\alpha B_{3,2}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right))+{\alpha }^2{B}_{3,3}\left({\mathcal{H}}_0\left(x\right)\right)>0,$$

whose discriminant is

$$\begin{array}{cc}\hfill & {\left[B_{3,2}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right))\right]}^2-4B_{3,1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),{\mathcal{H}}_2\left(x\right))B_{3,3}\left({\mathcal{H}}_0\left(x\right)\right)\hfill \\ \hfill & ={\mathcal{H}}_0^2\left(x\right)\left[9{\mathcal{H}}_1^2\left(x\right)-4{\mathcal{H}}_0\left(x\right){\mathcal{H}}_2\left(x\right)\right]\hfill \\ \hfill & ={\mathcal{H}}_0^2\left(x\right)\frac{4\left(3x^2+4x+1\right)lnx-4\left(3x^2+4x+1\right)ln(x+1)+12x+13}{x^2{(x+1)}^4}\hfill \\ \hfill & \triangleq {\mathcal{H}}_0^2\left(x\right)\frac{G_2\left(x\right)}{x^2{(x+1)}^4},x\in (0,\infty ).\hfill \end{array}$$

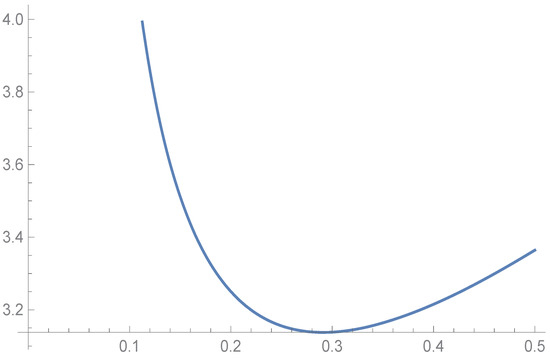
The graph of $G_2\left(x\right)$, plotted using the softwareWolfram Mathematica 12, on the interval $\left(0,\frac{1}{2}\right)$ is shown in Figure 2. This means the function $G_2\left(x\right)$ has a zero $x_0\in (0.06,0.1)$. When $x\in (0,x_0)$, the polynomial $P_{2,x}\left(\alpha \right)$ has no positive zero, that is, the positivity $P_{2,x}\left(\alpha \right)>0$ is valid for all $\alpha >0$ and for $x\in (0,x_0)$; when $x\in (x_0,\infty )$, the polynomial $P_{2,x}\left(\alpha \right)$ of the variable α has two positive zeros

$$\frac{3{\mathcal{H}}_1\left(x\right)\mp \sqrt{9{\mathcal{H}}_1^2\left(x\right)-4{\mathcal{H}}_0\left(x\right){\mathcal{H}}_2\left(x\right)}}{2{\mathcal{H}}_0^2\left(x\right)}.$$

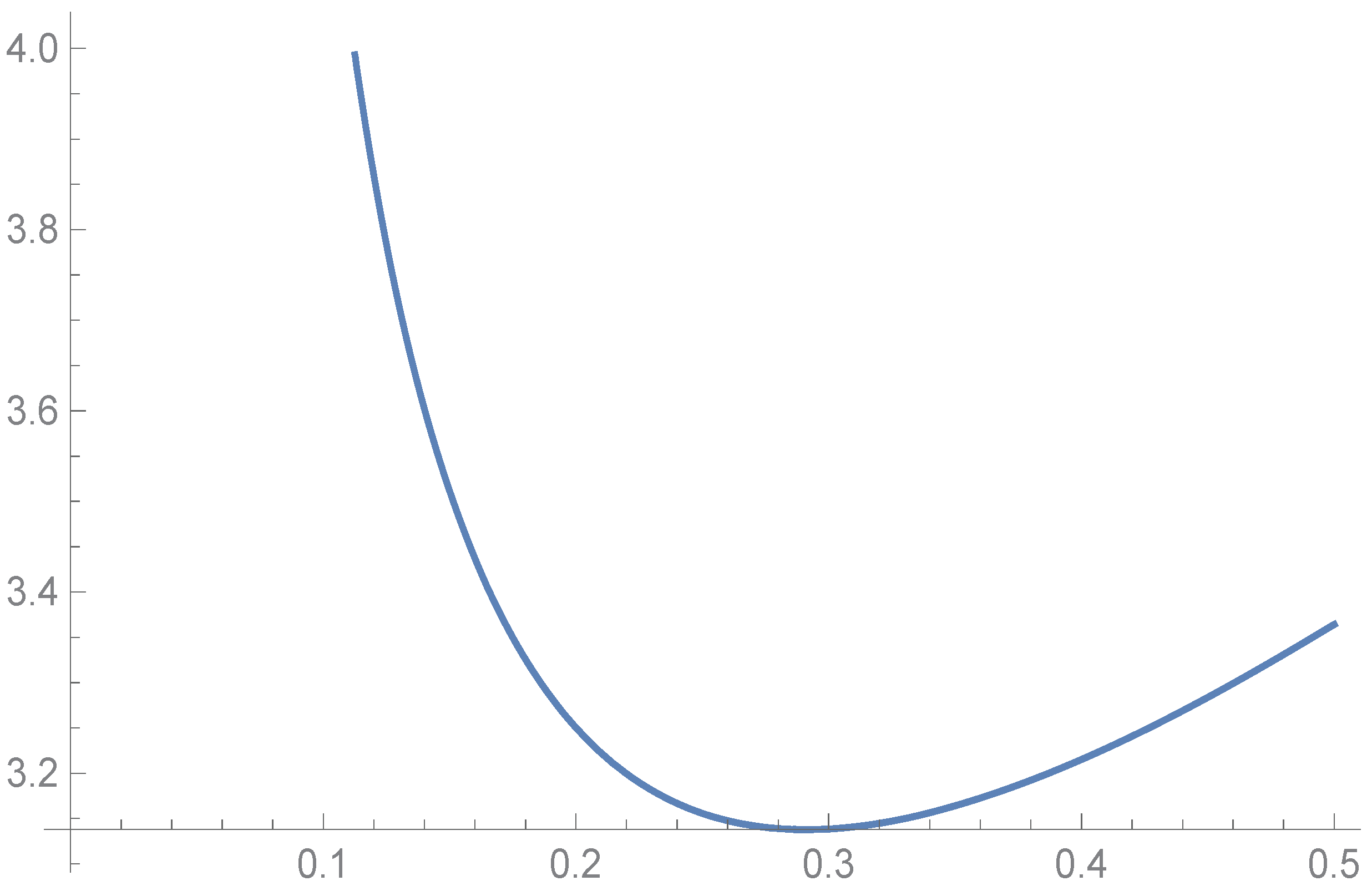
Consequently, we take

$$Z_2\left(x\right)=\left\{\frac{3{\mathcal{H}}_1\left(x\right)\mp \sqrt{9{\mathcal{H}}_1^2\left(x\right)-4{\mathcal{H}}_0\left(x\right){\mathcal{H}}_2\left(x\right)}}{2{\mathcal{H}}_0^2\left(x\right)},x\ge x_0\right\}$$

in $x\in (0,\infty )$. The graph of the function

$$G_3\left(x\right)=\frac{3{\mathcal{H}}_1\left(x\right)-\sqrt{9{\mathcal{H}}_1^2\left(x\right)-4{\mathcal{H}}_0\left(x\right){\mathcal{H}}_2\left(x\right)}}{2{\mathcal{H}}_0^2\left(x\right)},$$

plotted using the software Wolfram Mathematica 12, on the interval $\left(x_0,\frac{1}{2}\right)$ is shown in Figure 3. This implies that ${\alpha }^{*}<3.1\cdots$

Figure 2. The graph of the function $G_2\left(x\right)$ for $x\in \left(0,\frac{1}{2}\right)$.

Figure 3. The graph of the function $G_3\left(x\right)$ for $x\in \left(x_0,\frac{1}{2}\right)$.

Remark 4. 

When $n=3$, the inequality (17) can be concretely written as

$$\begin{array}{c}{P}_{3,x}\left(\alpha \right)=-{\left(ln\frac{1+x}{x}-\frac{1}{1+x}\right)}^4{\alpha }^3+\frac{6}{x{(x+1)}^2}{\left(ln\frac{1+x}{x}-\frac{1}{1+x}\right)}^2{\alpha }^2\hfill \\ \hfill -\frac{4\left(3x^2+4x+1\right)ln\frac{1+x}{x}-12x-1}{x^2{(x+1)}^4}\alpha +\frac{2\left(6x^2+4x+1\right)}{x^3{(x+1)}^4}>0\end{array}$$

for $x>0$. This implies that the polynomial $P_{3,x}\left(\alpha \right)$ of the variable α has at least one positive zero; that is, the set $Z_3\left(x\right)$ in $x\in (0,\infty )$ is not empty.

Remark 5. 

For given $n\ge 1$, if $Z_n\left(x\right)$ in $x\in (0,\infty )$ is not empty, then all the positive zeros of the polynomial $P_{n,x}\left(\alpha \right)$ are bounded using

$$\begin{array}{c}{U}_n\left(x\right)=min\{max\left\{1,\sum _{k=0}^{n-1}\frac{B_{n+1,k+1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))}{B_{n+1,n+1}\left({\mathcal{H}}_0\left(x\right)\right)}\right\},\hfill \\ 1+max\{\frac{B_{n+1,n}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right))}{B_{n+1,n+1}\left({\mathcal{H}}_0\left(x\right)\right)},\frac{B_{n+1,n-1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),{\mathcal{H}}_2\left(x\right))}{B_{n+1,n+1}\left({\mathcal{H}}_0\left(x\right)\right)},\cdots ,\\ \hfill \frac{B_{n+1,k+1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))}{B_{n+1,n+1}\left({\mathcal{H}}_0\left(x\right)\right)},\cdots ,\frac{B_{n+1,1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_n\left(x\right))}{B_{n+1,n+1}\left({\mathcal{H}}_0\left(x\right)\right)}\left\}\right\}.\end{array}$$

In particular,

$$\begin{array}{c}{U}_1\left(x\right)=min\left\{max\left\{1,\frac{B_{2,1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right))}{B_{2,2}\left({\mathcal{H}}_0\left(x\right)\right)}\right\},1+max\left\{\frac{B_{2,1}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right))}{B_{2,2}\left({\mathcal{H}}_0\left(x\right)\right)}\right\}\right\}\\ =min\left\{max\left\{1,\frac{{\mathcal{H}}_1\left(x\right)}{{\mathcal{H}}_0^2\left(x\right)}\right\},1+\frac{{\mathcal{H}}_1\left(x\right)}{{\mathcal{H}}_0^2\left(x\right)}\right\}=max\left\{1,\frac{{\mathcal{H}}_1\left(x\right)}{{\mathcal{H}}_0^2\left(x\right)}\right\}=\frac{{\mathcal{H}}_1\left(x\right)}{{\mathcal{H}}_0^2\left(x\right)}\end{array}$$

for $x\in (0,\infty )$, which coincides with the result in (20).

Remark 6. 

In [16], it was established numerically that ${\alpha }^{*}=2.2\cdots$ See also the paper [14].

4. A Closed-Form Formula of the nth Derivative of ${\left(1+\frac{1}{x}\right)}^{\alpha x}$

In this section, we present an alternative formula for the nth derivative of the power-exponential function $h_{\alpha }\left(x\right)={\left(1+\frac{1}{x}\right)}^{\alpha x}$.

Theorem 4. 

For $n\ge 0$, the nth derivative of the function $h_{\alpha }\left(x\right)={\left(1+\frac{1}{x}\right)}^{\alpha x}$ for $\alpha \in \mathbb{R}$ can be computed using

$$\begin{array}{cc}\hfill \frac{h_{\alpha }^{\left(n\right)}\left(x\right)}{h_{\alpha }\left(x\right)}& =\frac{n!}{{(1+x)}^n}\sum _{k=0}^n\frac{{⟨-\alpha ⟩}_{n-k}}{(n-k)!}\sum _{j=0}^k{\left(1+\frac{1}{x}\right)}^j\hfill \\ \hfill & \times \left\{\sum _{\ell =0}^j{(-1)}^{\ell }{\alpha }^{\ell }{x}^{\ell }\sum _{p=0}^{\ell }\left[\sum _{q=0}^{j-\ell }\frac{s(q+p,p)}{(q+p)!}\left(\genfrac{}{}{0pt}{}{p}{j-\ell -q}\right)\right]\frac{{(lnx)}^{\ell -p}}{(\ell -p)!}\right\}\hfill \\ \hfill & \times \left\{\sum _{\ell =0}^{k-j}{\alpha }^{\ell }{(1+x)}^{\ell }\sum _{p=0}^{\ell }\left[\sum _{q=0}^{k-j-\ell }\frac{s(q+p,p)}{(q+p)!}\left(\genfrac{}{}{0pt}{}{p}{k-j-\ell -q}\right)\right]\frac{{[ln(1+x)]}^{\ell -p}}{(\ell -p)!}\right\},\hfill \end{array}$$

(21)

where $s(q+p,p)$ denotes the Stirling numbers of the first kind and

$${⟨z⟩}_n=\prod _{k=0}^{n-1}(z-k)=\left\{\begin{array}{cc}z(z-1)\cdots (z-n+1),\hfill & n\ge 1\hfill \\ 1,\hfill & n=0\hfill \end{array}\right.$$

stands for the falling factorial of the number $z\in \mathbb{C}$.

Proof. 

The function $h_{\alpha }\left(x\right)$ in (1) can be rewritten as

$$h_{\alpha }\left(x\right)={(1+x)}^{\alpha (1+x)}{x}^{-\alpha x}{(1+x)}^{-\alpha },\alpha \in \mathbb{R},x\ne 0.$$

In [4] (Theorem 3), it was obtained that

$$\begin{array}{c}{\left[{(1+x)}^{\alpha (1+x)}\right]}^{\left(n\right)}=n!{(1+x)}^{\alpha (1+x)-n}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \sum _{k=0}^n{\alpha }^k{(1+x)}^k\sum _{j=0}^k\left[\sum _{q=0}^{n-k}\frac{s(q+j,j)}{(q+j)!}\left(\genfrac{}{}{0pt}{}{j}{n-k-q}\right)\right]\frac{{[ln(1+x)]}^{k-j}}{(k-j)!}.\hfill \end{array}$$

(22)

Replacing $1+x$ with x in (22) yields

$${\left(x^{\alpha x}\right)}^{\left(n\right)}=n!x^{\alpha x-n}\sum _{k=0}^n{\alpha }^k{x}^k\sum _{j=0}^k\left[\sum _{q=0}^{n-k}\frac{s(q+j,j)}{(q+j)!}\left(\genfrac{}{}{0pt}{}{j}{n-k-q}\right)\right]\frac{{(lnx)}^{k-j}}{(k-j)!}.$$

(23)

See also [8] (pp. 139–140, Example), [9] (p. 8), and the papers [10,11,12]. Therefore, making use of Formulas (22) and (23), we obtain

$${\left(x^{-\alpha x}\right)}^{\left(j\right)}=\frac{j!}{x^{\alpha x+j}}\sum _{\ell =0}^j{(-1)}^{\ell }{\alpha }^{\ell }{x}^{\ell }\sum _{p=0}^{\ell }\left[\sum _{q=0}^{j-\ell }\frac{s(q+p,p)}{(q+p)!}\left(\genfrac{}{}{0pt}{}{p}{j-\ell -q}\right)\right]\frac{{(lnx)}^{\ell -p}}{(\ell -p)!}$$

and

$$\begin{array}{c}{\left[{(1+x)}^{\alpha (1+x)}\right]}^{(k-j)}=(k-j)!{(1+x)}^{\alpha (1+x)-(k-j)}\sum _{\ell =0}^{k-j}{\alpha }^{\ell }{(1+x)}^{\ell }\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \sum _{p=0}^{\ell }\left[\sum _{q=0}^{k-j-\ell }\frac{s(q+p,p)}{(q+p)!}\left(\genfrac{}{}{0pt}{}{p}{k-j-\ell -q}\right)\right]\frac{{[ln(1+x)]}^{\ell -p}}{(\ell -p)!}.\end{array}$$

Consequently, we arrive at

$$\begin{array}{cc}\hfill h_{\alpha }^{\left(n\right)}\left(x\right)& =\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right){\left[x^{-\alpha x}{(1+x)}^{\alpha (1+x)}\right]}^{\left(k\right)}{\left[{(1+x)}^{-\alpha }\right]}^{(n-k)}\hfill \\ \hfill & =\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{⟨-\alpha ⟩}_{n-k}}{{(1+x)}^{\alpha +(n-k)}}\sum _{j=0}^k\left(\genfrac{}{}{0pt}{}{k}{j}\right){\left(x^{-\alpha x}\right)}^{\left(j\right)}{\left[{(1+x)}^{\alpha (1+x)}\right]}^{(k-j)}\hfill \\ \hfill & =\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{⟨-\alpha ⟩}_{n-k}}{{(1+x)}^{\alpha +(n-k)}}\sum _{j=0}^k\left(\genfrac{}{}{0pt}{}{k}{j}\right)\frac{j!}{x^{\alpha x+j}}(k-j)!{(1+x)}^{\alpha (1+x)-(k-j)}\hfill \\ \hfill & \times \left\{\sum _{\ell =0}^j{(-1)}^{\ell }{\alpha }^{\ell }{x}^{\ell }\sum _{p=0}^{\ell }\left[\sum _{q=0}^{j-\ell }\frac{s(q+p,p)}{(q+p)!}\left(\genfrac{}{}{0pt}{}{p}{j-\ell -q}\right)\right]\frac{{(lnx)}^{\ell -p}}{(\ell -p)!}\right\}\hfill \\ \hfill & \times \sum _{\ell =0}^{k-j}{\alpha }^{\ell }{(1+x)}^{\ell }\sum _{p=0}^{\ell }\left[\sum _{q=0}^{k-j-\ell }\frac{s(q+p,p)}{(q+p)!}\left(\genfrac{}{}{0pt}{}{p}{k-j-\ell -q}\right)\right]\frac{{[ln(1+x)]}^{\ell -p}}{(\ell -p)!}\hfill \\ \hfill & =h_{\alpha }\left(x\right)\frac{n!}{{(1+x)}^n}\sum _{k=0}^n\frac{{⟨-\alpha ⟩}_{n-k}}{(n-k)!}\sum _{j=0}^k{\left(1+\frac{1}{x}\right)}^j\hfill \\ \hfill & \times \left\{\sum _{\ell =0}^j{(-1)}^{\ell }{\alpha }^{\ell }{x}^{\ell }\sum _{p=0}^{\ell }\left[\sum _{q=0}^{j-\ell }\frac{s(q+p,p)}{(q+p)!}\left(\genfrac{}{}{0pt}{}{p}{j-\ell -q}\right)\right]\frac{{(lnx)}^{\ell -p}}{(\ell -p)!}\right\}\hfill \\ \hfill & \times \sum _{\ell =0}^{k-j}{\alpha }^{\ell }{(1+x)}^{\ell }\sum _{p=0}^{\ell }\left[\sum _{q=0}^{k-j-\ell }\frac{s(q+p,p)}{(q+p)!}\left(\genfrac{}{}{0pt}{}{p}{k-j-\ell -q}\right)\right]\frac{{[ln(1+x)]}^{\ell -p}}{(\ell -p)!}.\hfill \end{array}$$

The proof of Theorem 4 is, thus, complete. □

Remark 7. 

Since

$${(1+x)}^{\alpha x}={(1+x)}^{\alpha (1+x)}{(1+x)}^{-\alpha }$$

and

$$x^{\alpha (1+x)}=x^{\alpha x}{x}^{\alpha },$$

by virtue of Leibnitz’s rule for differentiation and with the help of (22) and (23), we can easily compute the nth derivatives of the power-exponential functions ${(1+x)}^{\alpha x}$ and $x^{\alpha (1+x)}$ using

$$\begin{array}{c}{\left[{(1+x)}^{\alpha x}\right]}^{\left(n\right)}=n!{(1+x)}^{\alpha x-n}\sum _{k=0}^n\frac{{⟨-\alpha ⟩}_{n-k}}{(n-k)!}\sum _{\ell =0}^k{\alpha }^{\ell }{(1+x)}^{\ell }\hfill \\ \hfill \times \sum _{j=0}^{\ell }\left[\sum _{q=0}^{k-\ell }\frac{s(q+j,j)}{(q+j)!}\left(\genfrac{}{}{0pt}{}{j}{k-\ell -q}\right)\right]\frac{{[ln(1+x)]}^{\ell -j}}{(\ell -j)!}\end{array}$$

(24)

and

$$\begin{array}{c}{\left[x^{\alpha (1+x)}\right]}^{\left(n\right)}=n!x^{\alpha (1+x)-n}\sum _{k=0}^n\frac{{⟨\alpha ⟩}_{n-k}}{(n-k)!}\sum _{\ell =0}^k{\alpha }^{\ell }{x}^{\ell }\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \sum _{j=0}^{\ell }\left[\sum _{q=0}^{k-\ell }\frac{s(q+j,j)}{(q+j)!}\left(\genfrac{}{}{0pt}{}{j}{k-\ell -q}\right)\right]\frac{{(lnx)}^{\ell -j}}{(\ell -j)!}\end{array}$$

(25)

respectively.

Remark 8. 

In theory, comparing coefficients of ${\alpha }^k$ in (21) with corresponding ones in (13) for $0\le k\le n$, we can derive a closed-form formula of partial Bell polynomials

$$B_{n,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))$$

for $n\ge k\ge 0$. In practice, it seems to be complicated to carry out this idea.

Remark 9. 

Making use of the formula

$$\frac{1}{k!}{\left(\sum _{m=1}^{\infty }{a}_m\frac{v^m}{m!}\right)}^k=\sum _{n=k}^{\infty }{B}_{n,k}(a_1,a_2,\cdots ,a_{n-k+1})\frac{v^n}{n!},k\ge 0$$

listed in [8] (p. 133) yields

$$B_{n+k,k}(a_1,a_2,\cdots ,a_{n+1})=\left(\genfrac{}{}{0pt}{}{n+k}{k}\right)\underset{v\to 0}{lim}\frac{{\mathrm{d}}^n}{\mathrm{d}{v}^n}{\left[\sum _{m=0}^{\infty }{a}_{m+1}\frac{v^m}{(m+1)!}\right]}^k.$$

Taking

$$(a_1,a_2,a_3,a_4,\cdots ,a_n,\cdots )=({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),{\mathcal{H}}_2\left(x\right),{\mathcal{H}}_3\left(x\right),\cdots ,{\mathcal{H}}_{n-1}\left(x\right),\cdots )$$

results in

$$\begin{array}{c}{B}_{n+k,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_n\left(x\right))=\left(\genfrac{}{}{0pt}{}{n+k}{k}\right)\underset{v\to 0}{lim}\frac{{\mathrm{d}}^n}{\mathrm{d}{v}^n}{\left[\sum _{m=0}^{\infty }{\mathcal{H}}_m\left(x\right)\frac{v^m}{(m+1)!}\right]}^k\\ \begin{array}{cc}& =\left(\genfrac{}{}{0pt}{}{n+k}{k}\right)\underset{v\to 0}{lim}\frac{{\mathrm{d}}^n}{\mathrm{d}{v}^n}{\left[\sum _{m=0}^{\infty }\left({\int }_0^{\infty }\frac{{\mathrm{e}}^u-1-u}{{\mathrm{e}}^u}{u}^{m-1}{\mathrm{e}}^{-xu}\mathrm{d}u\right)\frac{v^m}{(m+1)!}\right]}^k\hfill \\ & =\left(\genfrac{}{}{0pt}{}{n+k}{k}\right)\underset{v\to 0}{lim}\frac{{\mathrm{d}}^n}{\mathrm{d}{v}^n}{\left\{{\int }_0^{\infty }\frac{{\mathrm{e}}^u-1-u}{{\mathrm{e}}^u}\left[\sum _{m=0}^{\infty }{u}^{m-1}\frac{v^m}{(m+1)!}\right]{\mathrm{e}}^{-xu}\mathrm{d}u\right\}}^k\hfill \\ & =\left(\genfrac{}{}{0pt}{}{n+k}{k}\right)\underset{v\to 0}{lim}\frac{{\mathrm{d}}^n}{\mathrm{d}{v}^n}{\left[{\int }_0^{\infty }\frac{{\mathrm{e}}^u-1-u}{u}\frac{{\mathrm{e}}^{uv}-1}{uv}{\mathrm{e}}^{-(x+1)u}\mathrm{d}u\right]}^k\hfill \\ & =\left(\genfrac{}{}{0pt}{}{n+k}{k}\right)\underset{v\to 0}{lim}\frac{{\mathrm{d}}^n}{\mathrm{d}{v}^n}{\left[{\int }_0^{\infty }\frac{{\mathrm{e}}^u-1-u}{u}\left({\int }_1^e{\theta }^{uv-1}\mathrm{d}\theta \right){\mathrm{e}}^{-(x+1)u}\mathrm{d}u\right]}^k.\hfill \end{array}\end{array}$$

This is an alternative possibility to derive a closed-form formula of partial Bell polynomials $B_{n,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))$ for $n\ge k\ge 0$ and $x>0$.

5. A Closed-Form Formula of ${\mathit{B}}_{\mathit{n},\mathit{k}}({\mathcal{H}}_{\mathbf{0}}\left(\mathit{x}\right),{\mathcal{H}}_{\mathbf{1}}\left(\mathit{x}\right),\cdots ,{\mathcal{H}}_{\mathit{n}-\mathit{k}}\left(\mathit{x}\right))$

In this section, we present a closed-form and explicit formula of the partial Bell polynomials $B_{n,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))$ for $n\ge k\ge 0$.

Theorem 5. 

For $n\ge k\ge 0$ and $x>0$, we have

$$\begin{array}{c}{B}_{n,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))\hfill \\ \hfill ={(-1)}^{n-k}n!\sum _{q=0}^k\frac{1}{q!}{\left[ln\left(1+\frac{1}{x}\right)-\frac{1}{1+x}\right]}^q\sum _{r+t=k-q}{(-1)}^t\sum _{\ell +m=n-q}\frac{Q(r,t;\ell ,m)}{x^{\ell -r}{(1+x)}^{m-t}},\end{array}$$

(26)

where

$$\begin{array}{c}Q(r,t;\ell ,m)=\left[\sum _{\sigma =0}^r\frac{{(-1)}^{\sigma }}{(r-\sigma )!}\sum _{\tau =0}^{\ell -r}\frac{s(\tau +\sigma ,\sigma )}{(\tau +\sigma )!}\left(\genfrac{}{}{0pt}{}{\sigma }{\ell -r-\tau }\right)\right]\sum _{i+j=t}\frac{1}{j!}\sum _{\lambda +\mu =m}\frac{1}{(\mu -j)!}\hfill \\ \hfill \times \left[\sum _{\sigma =0}^i\frac{{(-1)}^{\sigma }}{(i-\sigma )!}\sum _{\tau =0}^{\lambda -i}\frac{s(\tau +\sigma ,\sigma )}{(\tau +\sigma )!}\left(\genfrac{}{}{0pt}{}{\sigma }{\lambda -i-\tau }\right)\right]\left[\sum _{p=0}^j{(-1)}^p\frac{\left(\genfrac{}{}{0pt}{}{j}{p}\right)}{\left(\genfrac{}{}{0pt}{}{\mu -p}{\mu -j}\right)}s(\mu -p,j-p)\right].\end{array}$$

(27)

Proof. 

By virtue of the identities (5), (6), and (4) in sequence, we acquire

$$\begin{array}{cc}\hfill & B_{n,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),{\mathcal{H}}_2\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))\hfill \\ \hfill & =\sum _{q=0}^k\left(\genfrac{}{}{0pt}{}{n}{q}\right){\mathcal{H}}_0^q\left(x\right)B_{n-q,k-q}(0,{\mathcal{H}}_1\left(x\right),{\mathcal{H}}_2\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))\hfill \\ \hfill & =\sum _{q=0}^k\left(\genfrac{}{}{0pt}{}{n}{q}\right){\mathcal{H}}_0^q\left(x\right)B_{n-q,k-q}(0,\frac{0!}{x}-\frac{0!}{1+x}-\frac{1!}{{(1+x)}^2},\frac{1!}{x^2}-\frac{1!}{{(1+x)}^2}\hfill \\ \hfill & -\frac{2!}{{(1+x)}^3},\cdots ,\frac{(n-k-1)!}{x^{n-k}}-\frac{(n-k-1)!}{{(1+x)}^{n-k}}-\frac{(n-k)!}{{(1+x)}^{n-k+1}})\hfill \\ \hfill & =\sum _{q=0}^k\left(\genfrac{}{}{0pt}{}{n}{q}\right){\mathcal{H}}_0^q\left(x\right)\sum _{r+t=k-q}\sum _{\ell +m=n-q}\left(\genfrac{}{}{0pt}{}{n-q}{\ell }\right)B_{\ell ,r}\left(0,\frac{0!}{x},\frac{1!}{x^2},\cdots ,\frac{(\ell -r-1)!}{x^{\ell -r}}\right)\hfill \\ \hfill & \times B_{m,t}\left(0,-\frac{0!}{1+x}-\frac{1!}{{(1+x)}^2},\cdots ,-\frac{(m-t-1)!}{{(1+x)}^{m-t}}-\frac{(m-t)!}{{(1+x)}^{m-t+1}}\right)\hfill \\ \hfill & =\sum _{q=0}^k\left(\genfrac{}{}{0pt}{}{n}{q}\right){\mathcal{H}}_0^q\left(x\right)\sum _{r+t=k-q}\sum _{\ell +m=n-q}\left(\genfrac{}{}{0pt}{}{n-q}{\ell }\right)B_{\ell ,r}\left(0,\frac{0!}{x},\frac{1!}{x^2},\cdots ,\frac{(\ell -r-1)!}{x^{\ell -r}}\right)\hfill \\ \hfill & \times \sum _{i+j=t}\sum _{\lambda +\mu =m}\left(\genfrac{}{}{0pt}{}{m}{\lambda }\right)B_{\lambda ,i}\left(0,-\frac{0!}{1+x},-\frac{1!}{{(1+x)}^2},\cdots ,-\frac{(\lambda -i-1)!}{{(1+x)}^{\lambda -i}}\right)\hfill \\ \hfill & \times B_{\mu ,j}\left(0,-\frac{1!}{{(1+x)}^2},-\frac{2!}{{(1+x)}^3},\cdots ,-\frac{(\mu -j)!}{{(1+x)}^{\mu -j+1}}\right)\hfill \\ \hfill & =\sum _{q=0}^k\left(\genfrac{}{}{0pt}{}{n}{q}\right){\mathcal{H}}_0^q\left(x\right)\sum _{r+t=k-q}\sum _{\ell +m=n-q}{(-1)}^t\left(\genfrac{}{}{0pt}{}{n-q}{\ell }\right)\frac{B_{\ell ,r}(0,0!,1!,\cdots ,(\ell -r-1)!)}{x^{\ell -r}{(1+x)}^{m-t}}\hfill \\ \hfill & \times \sum _{i+j=t}\sum _{\lambda +\mu =m}\left(\genfrac{}{}{0pt}{}{m}{\lambda }\right)B_{\lambda ,i}(0,0!,1!,\cdots ,(\lambda -i-1)!)B_{\mu ,j}(0,1!,2!,\cdots ,(\mu -j)!).\hfill \end{array}$$

Further making use of the Formulas (7) and (10), we arrive at

$$\begin{array}{cc}\hfill & B_{n,k}({\mathcal{H}}_0\left(x\right),{\mathcal{H}}_1\left(x\right),{\mathcal{H}}_2\left(x\right),\cdots ,{\mathcal{H}}_{n-k}\left(x\right))\hfill \\ \hfill & =\sum _{q=0}^k\left(\genfrac{}{}{0pt}{}{n}{q}\right){\mathcal{H}}_0^q\left(x\right)\sum _{r+t=k-q}{(-1)}^t\sum _{\ell +m=n-q}[\left(\genfrac{}{}{0pt}{}{n-q}{\ell }\right)B_{\ell ,r}(0,0!,1!,\cdots ,(\ell -r-1)!)\hfill \\ \hfill & \times \sum _{i+j=t}\sum _{\lambda +\mu =m}\left(\genfrac{}{}{0pt}{}{m}{\lambda }\right)B_{\lambda ,i}(0,0!,1!,\cdots ,(\lambda -i-1)!)\hfill \\ \hfill & \times B_{\mu ,j}(0,1!,2!,\cdots ,(\mu -j)!)]\frac{1}{x^{\ell -r}{(1+x)}^{m-t}}\hfill \\ \hfill & ={(-1)}^{n-k}\sum _{q=0}^k\left(\genfrac{}{}{0pt}{}{n}{q}\right){\left[ln\left(1+\frac{1}{x}\right)-\frac{1}{1+x}\right]}^q\sum _{r+t=k-q}{(-1)}^t\hfill \\ \hfill & \times \sum _{\ell +m=n-q}\{\left(\genfrac{}{}{0pt}{}{n-q}{\ell }\right)\left[\ell !\sum _{\sigma =0}^r\frac{{(-1)}^{\sigma }}{(r-\sigma )!}\sum _{\tau =0}^{\ell -r}\frac{s(\tau +\sigma ,\sigma )}{(\tau +\sigma )!}\left(\genfrac{}{}{0pt}{}{\sigma }{\ell -r-\tau }\right)\right]\hfill \\ \hfill & \times \sum _{i+j=t}\sum _{\lambda +\mu =m}\left(\genfrac{}{}{0pt}{}{m}{\lambda }\right)\left[\lambda !\sum _{\sigma =0}^i\frac{{(-1)}^{\sigma }}{(i-\sigma )!}\sum _{\tau =0}^{\lambda -i}\frac{s(\tau +\sigma ,\sigma )}{(\tau +\sigma )!}\left(\genfrac{}{}{0pt}{}{\sigma }{\lambda -i-\tau }\right)\right]\hfill \\ \hfill & \times \left[\left(\genfrac{}{}{0pt}{}{\mu }{j}\right)\sum _{p=0}^j{(-1)}^p\frac{\left(\genfrac{}{}{0pt}{}{j}{p}\right)}{\left(\genfrac{}{}{0pt}{}{\mu -p}{\mu -j}\right)}s(\mu -p,j-p)\right]\}\frac{1}{x^{\ell -r}{(1+x)}^{m-t}}\hfill \\ \hfill & ={(-1)}^{n-k}\sum _{q=0}^k\frac{n!}{q!}{\left[ln\left(1+\frac{1}{x}\right)-\frac{1}{1+x}\right]}^q\sum _{r+t=k-q}{(-1)}^t\hfill \\ \hfill & \times \sum _{\ell +m=n-q}\{\left[\sum _{\sigma =0}^r\frac{{(-1)}^{\sigma }}{(r-\sigma )!}\sum _{\tau =0}^{\ell -r}\frac{s(\tau +\sigma ,\sigma )}{(\tau +\sigma )!}\left(\genfrac{}{}{0pt}{}{\sigma }{\ell -r-\tau }\right)\right]\hfill \\ \hfill & \times \sum _{i+j=t}\sum _{\lambda +\mu =m}\left[\sum _{\sigma =0}^i\frac{{(-1)}^{\sigma }}{(i-\sigma )!}\sum _{\tau =0}^{\lambda -i}\frac{s(\tau +\sigma ,\sigma )}{(\tau +\sigma )!}\left(\genfrac{}{}{0pt}{}{\sigma }{\lambda -i-\tau }\right)\right]\hfill \\ \hfill & \times \left[\frac{1}{j!(\mu -j)!}\sum _{p=0}^j{(-1)}^p\frac{\left(\genfrac{}{}{0pt}{}{j}{p}\right)}{\left(\genfrac{}{}{0pt}{}{\mu -p}{\mu -j}\right)}s(\mu -p,j-p)\right]\}\frac{1}{x^{\ell -r}{(1+x)}^{m-t}}.\hfill \end{array}$$

The closed-form Formula (26) is derived. The proof of Theorem 5 is complete. □

6. A Closed-Form Formula of the nth Derivative of ${(\mathit{1}+\mathit{x})}^{\mathit{\alpha }/\mathit{x}}$

Combining Formula (26) in Theorem 5 with Formula (13) in Theorem 1, we can easily deduce an alternative closed-form and explicit formula of the power-exponential function $h_{\alpha }\left(x\right)={\left(1+\frac{1}{x}\right)}^{\alpha x}$.

Corollary 1. 

For $\alpha \in \mathbb{R}$ and $x>0$, the nth derivative of the power-exponential function $h_{\alpha }\left(x\right)={\left(1+\frac{1}{x}\right)}^{\alpha x}$ can be computed using

$$\begin{array}{c}{h}_{\alpha }^{\left(n\right)}\left(x\right)=n!h_{\alpha }\left(x\right)\sum _{k=0}^n{\alpha }^k\sum _{q=0}^k\frac{1}{q!}{\left[ln\left(1+\frac{1}{x}\right)-\frac{1}{1+x}\right]}^q\hfill \\ \hfill \times \sum _{r+t=k-q}{(-1)}^t\sum _{\ell +m=n-q}\frac{Q(r,t;\ell ,m)}{x^{\ell -r}{(1+x)}^{m-t}},\end{array}$$

(28)

where $n\ge 0$ is an integer and $Q(r,t;\ell ,m)$ is defined using (27).

Finally, we derive a closed-form formula of the nth derivative of ${(1+x)}^{\alpha /x}$ for $n\ge 0$, $x>0$, and $\alpha \in \mathbb{R}$.

Theorem 6. 

For $\alpha \in \mathbb{R}$ and $x>0$, we have the nth derivative formula

$$\begin{array}{c}{\left[{(1+x)}^{\alpha /x}\right]}^{\left(n\right)}={(-1)}^{n}n!\frac{{(1+x)}^{\alpha /x}}{x^n}\sum _{\kappa =0}^n\left(\genfrac{}{}{0pt}{}{n-1}{\kappa -1}\right)\sum _{k=0}^{\kappa }\frac{{\alpha }^k}{x^k}\hfill \\ \hfill \times \sum _{q=0}^k\frac{1}{q!}{\left[ln(1+x)-\frac{x}{1+x}\right]}^q\sum _{r+t=k-q}{(-1)}^t\sum _{\ell +m=\kappa -q}\frac{Q(r,t;\ell ,m)}{{(1+x)}^{m-t}},\end{array}$$

(29)

where $n\ge 0$ is an integer and $Q(r,t;\ell ,m)$ is defined using (27).

Proof. 

It is clear that

$${(1+x)}^{\alpha /x}=h_{\alpha }\left(\frac{1}{x}\right).$$

Therefore, by virtue of the Faà di Bruno Formula (3), the identity (4), and (11) in sequence, we reveal that

$$\begin{array}{cc}\hfill {\left[{(1+x)}^{\alpha /x}\right]}^{\left(n\right)}& =\sum _{\kappa =0}^n{h}_{\alpha }^{\left(\kappa \right)}\left(\frac{1}{x}\right)B_{n,\kappa }\left(-\frac{1!}{x^2},\frac{2!}{x^3},\cdots ,{(-1)}^{n-\kappa +1}\frac{(n-\kappa +1)!}{x^{n-\kappa +2}}\right)\hfill \\ \hfill & =\sum _{\kappa =0}^n{h}_{\alpha }^{\left(\kappa \right)}\left(\frac{1}{x}\right)\frac{{(-1)}^n}{x^{n+\kappa }}{B}_{n,\kappa }(1!,2!,\cdots ,(n-\kappa +1)!)\hfill \\ \hfill & =\sum _{\kappa =0}^n\left(\genfrac{}{}{0pt}{}{n-1}{\kappa -1}\right)\frac{n!}{\kappa !}\frac{{(-1)}^n}{x^{n+\kappa }}{h}_{\alpha }^{\left(\kappa \right)}\left(\frac{1}{x}\right).\hfill \end{array}$$

From the closed-form Formula (28), we deduce

$$\begin{array}{c}{h}_{\alpha }^{\left(\kappa \right)}\left(\frac{1}{x}\right)=\kappa !h_{\alpha }\left(\frac{1}{x}\right)\sum _{k=0}^{\kappa }{\alpha }^k{x}^{\kappa -k}\sum _{q=0}^k\frac{1}{q!}{\left[ln(1+x)-\frac{x}{1+x}\right]}^q\hfill \\ \hfill \times \sum _{r+t=k-q}{(-1)}^t\sum _{\ell +m=\kappa -q}\frac{Q(r,t;\ell ,m)}{{(1+x)}^{m-t}}.\end{array}$$

Consequently, we conclude

$$\begin{array}{c}{\left[{(1+x)}^{\alpha /x}\right]}^{\left(n\right)}={(-1)}^n\frac{n!}{x^n}{h}_{\alpha }\left(\frac{1}{x}\right)\sum _{\kappa =0}^n\left(\genfrac{}{}{0pt}{}{n-1}{\kappa -1}\right)\sum _{k=0}^{\kappa }\frac{{\alpha }^k}{x^k}\hfill \\ \hfill \times \sum _{q=0}^k\frac{1}{q!}{\left[ln(1+x)-\frac{x}{1+x}\right]}^q\sum _{r+t=k-q}{(-1)}^t\sum _{\ell +m=\kappa -q}\frac{Q(r,t;\ell ,m)}{{(1+x)}^{m-t}}.\end{array}$$

Formula (29) is, thus, proved. The proof of Theorem 6 is complete. □

7. Conclusions

In this paper, via Formula (13) for the nth derivative of the power-exponential function ${\left(1+\frac{1}{x}\right)}^{\alpha x}$, we discovered the relation (16) for the nth derivative of the power-exponential function ${\left(1+\frac{1}{x}\right)}^{\alpha x}$, found a sufficient and necessary condition $0<\alpha \le {\alpha }^{*}\in (2,3)$ in Theorem 3 for the power-exponential function ${\left(1+\frac{1}{x}\right)}^{\alpha x}$ to be a Bernstein function, and derived a closed-form formula (21) for the nth derivative of the power-exponential function ${\left(1+\frac{1}{x}\right)}^{\alpha x}$.

The derivative Formulas (24) and (25) are also useful and interesting.

Formula (26) in Theorem 5, Formula (28) in Corollary 1, and the closed-form Formula (29) in Theorem 6 are also our main results of this paper.