Analysis of the Total Leakage Characteristics of Finger Seal Considering Fractal Wear and Fractal Porous Media Seepage Effects
Abstract
1. Introduction
2. Basic Situation of Finger Seal
3. Analysis Method of Total Leakage Characteristics of Finger Seal
3.1. Mathematical Model for the Main Leakage Rate of Finger Seal
3.2. Mathematical Model for the Side Leakage Rate of Finger Seal
3.3. Mathematical Model for Total Leakage Rate of Finger Seal
4. Numerical Calculation Method for Dynamic Performance of Finger Seal
4.1. Finite Element Calculation Model for Dynamic Performance of Finger Seal
4.2. Boundary Condition
4.3. Setting of Load Step and Extraction of Calculation Results
5. Results and Discussion
5.1. Verification of the Accuracy of Theoretical Models
5.2. Analysis of Factors Influencing the Main Leakage Rate of Finger Seals
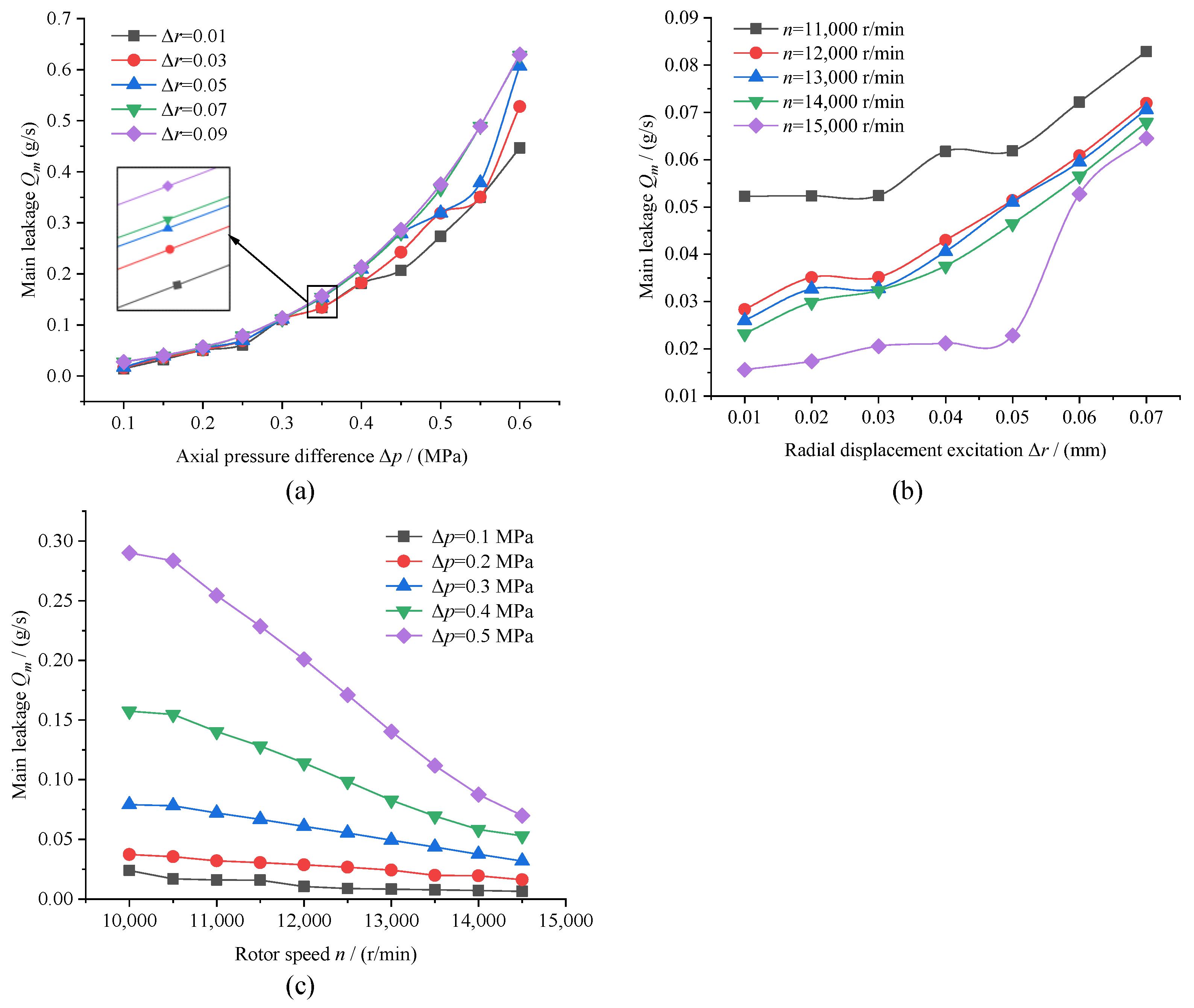
5.2.1. Working Conditions
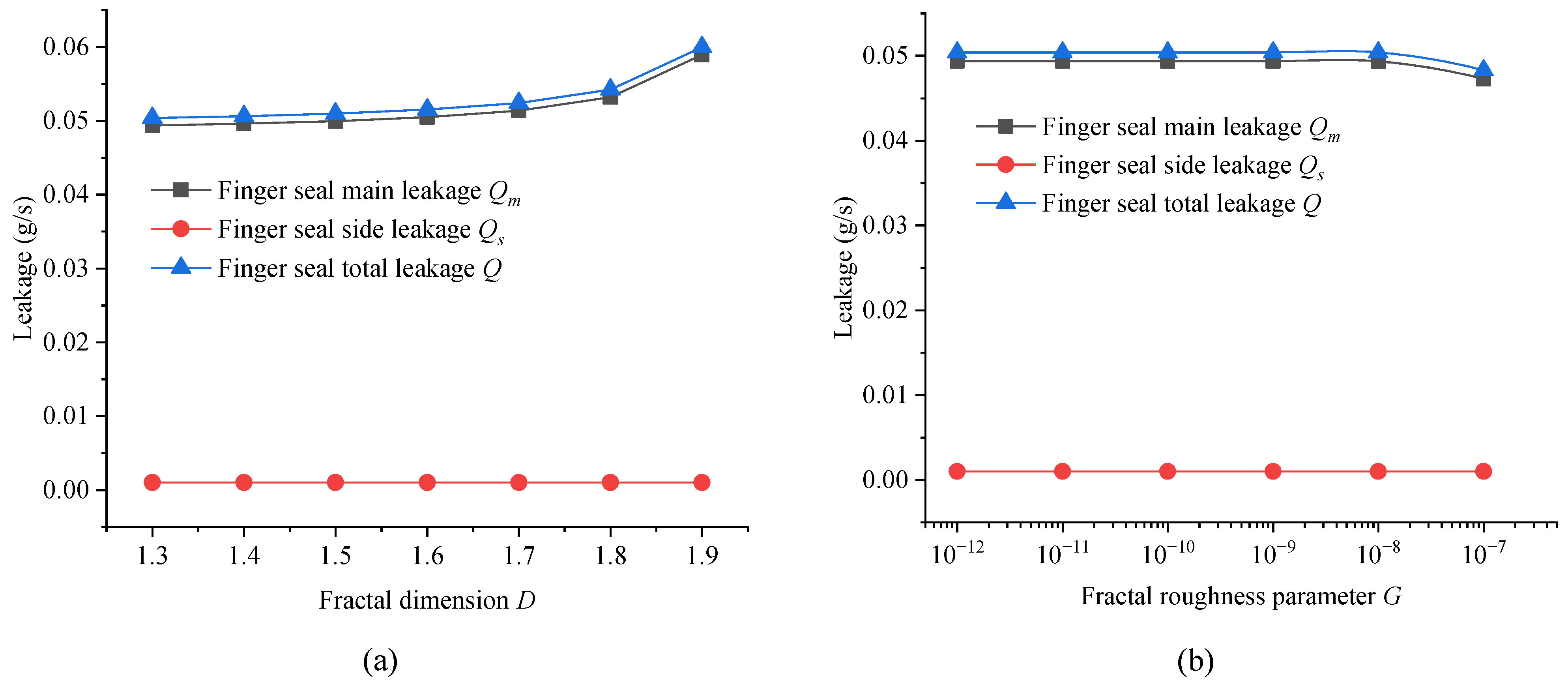
5.2.2. Fractal Dimension
5.2.3. Fractal Roughness Parameter
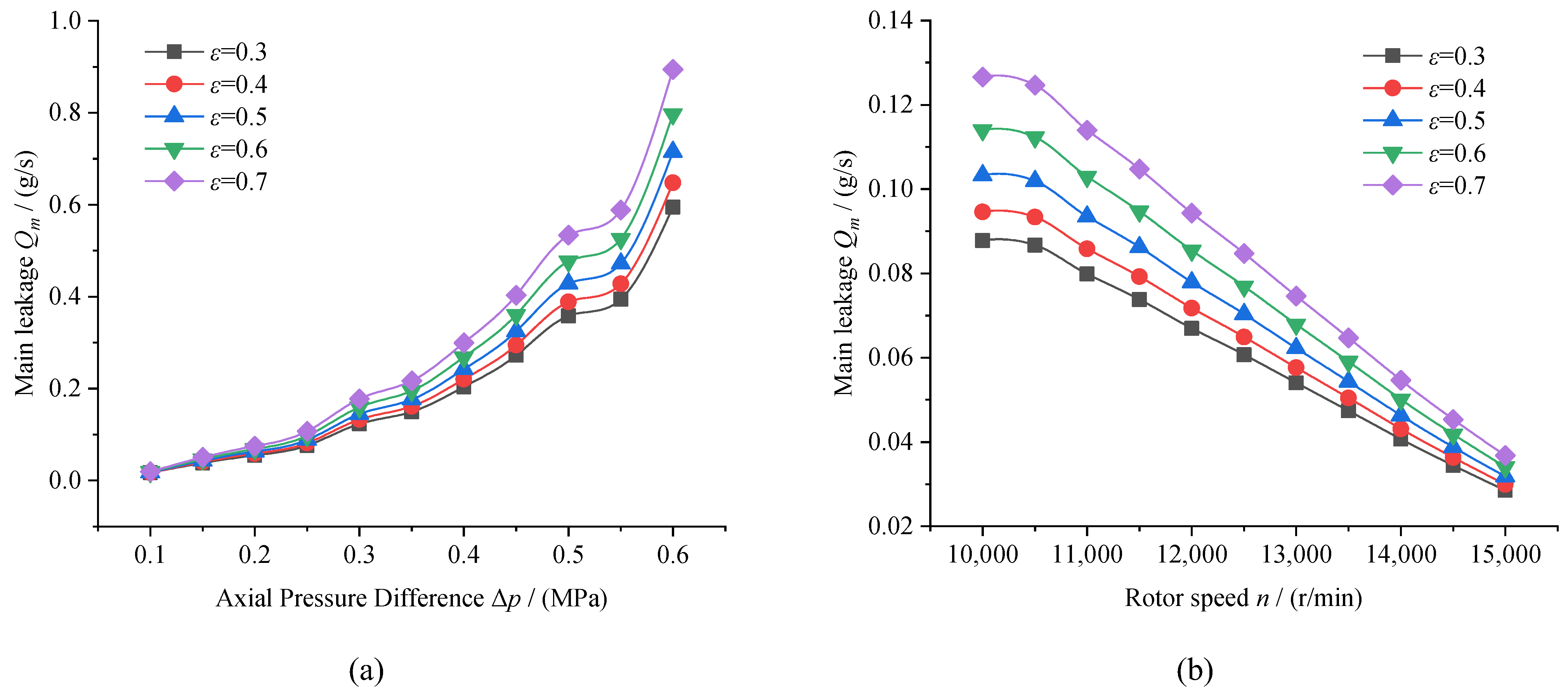
5.2.4. Eccentricity
5.3. Analysis of Factors Influencing the Side Leakage Rate of Finger Seals
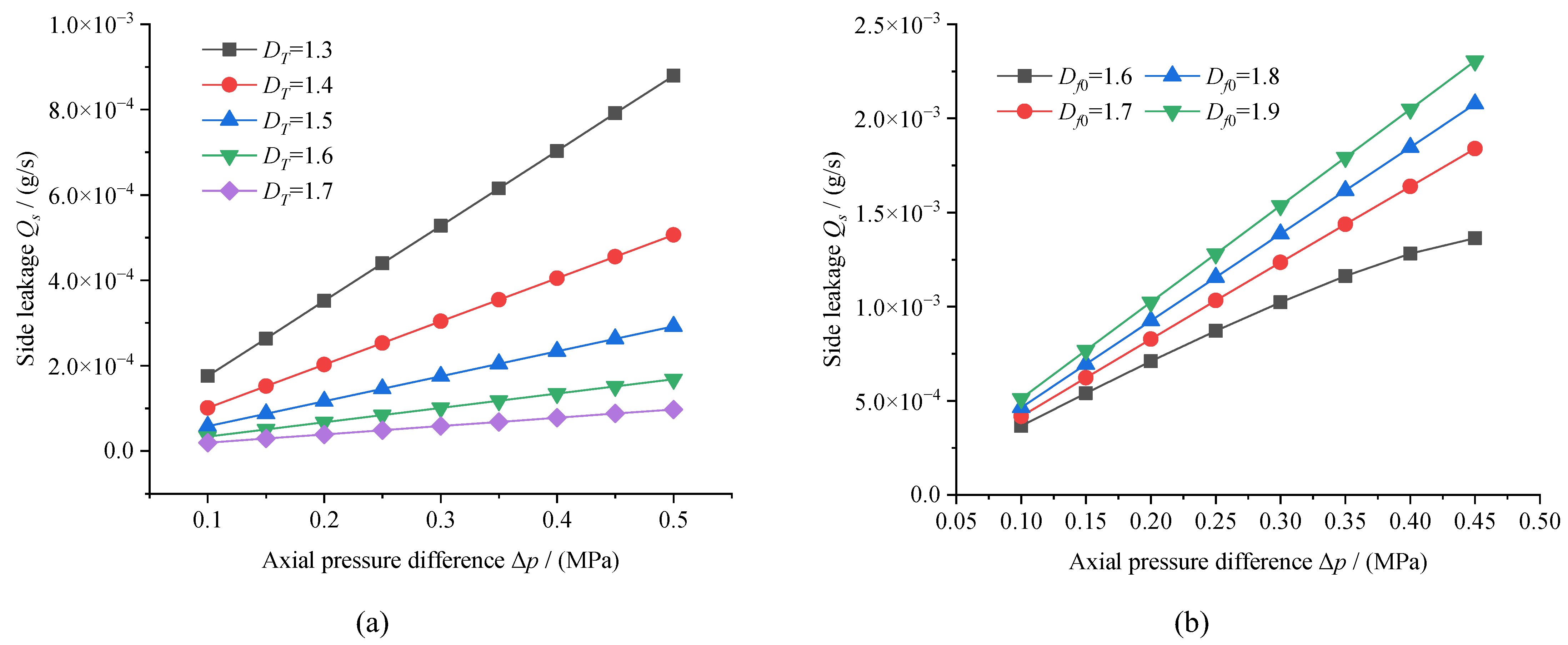
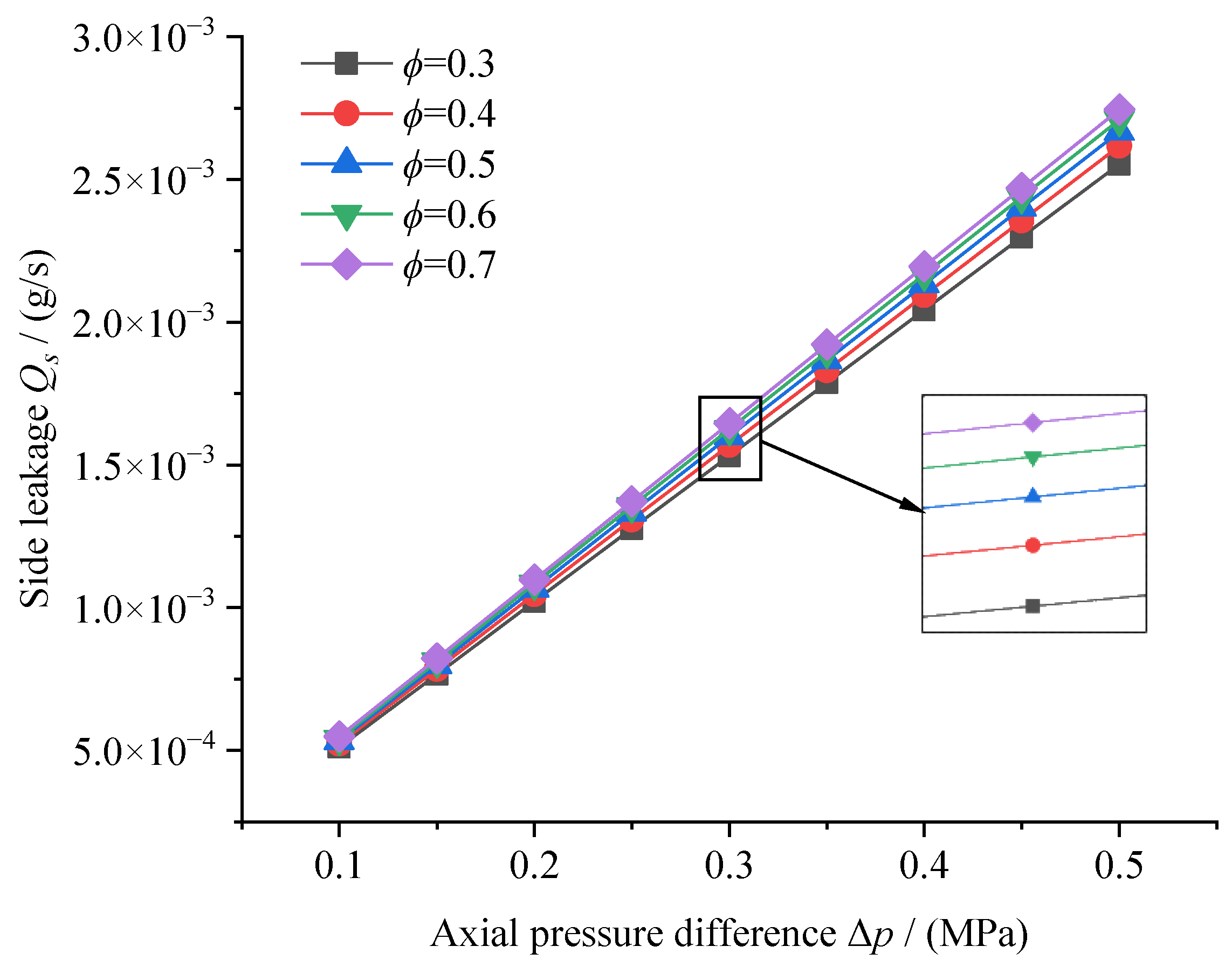
5.3.1. Axial Pressure Difference and Fractal Characteristic Parameters
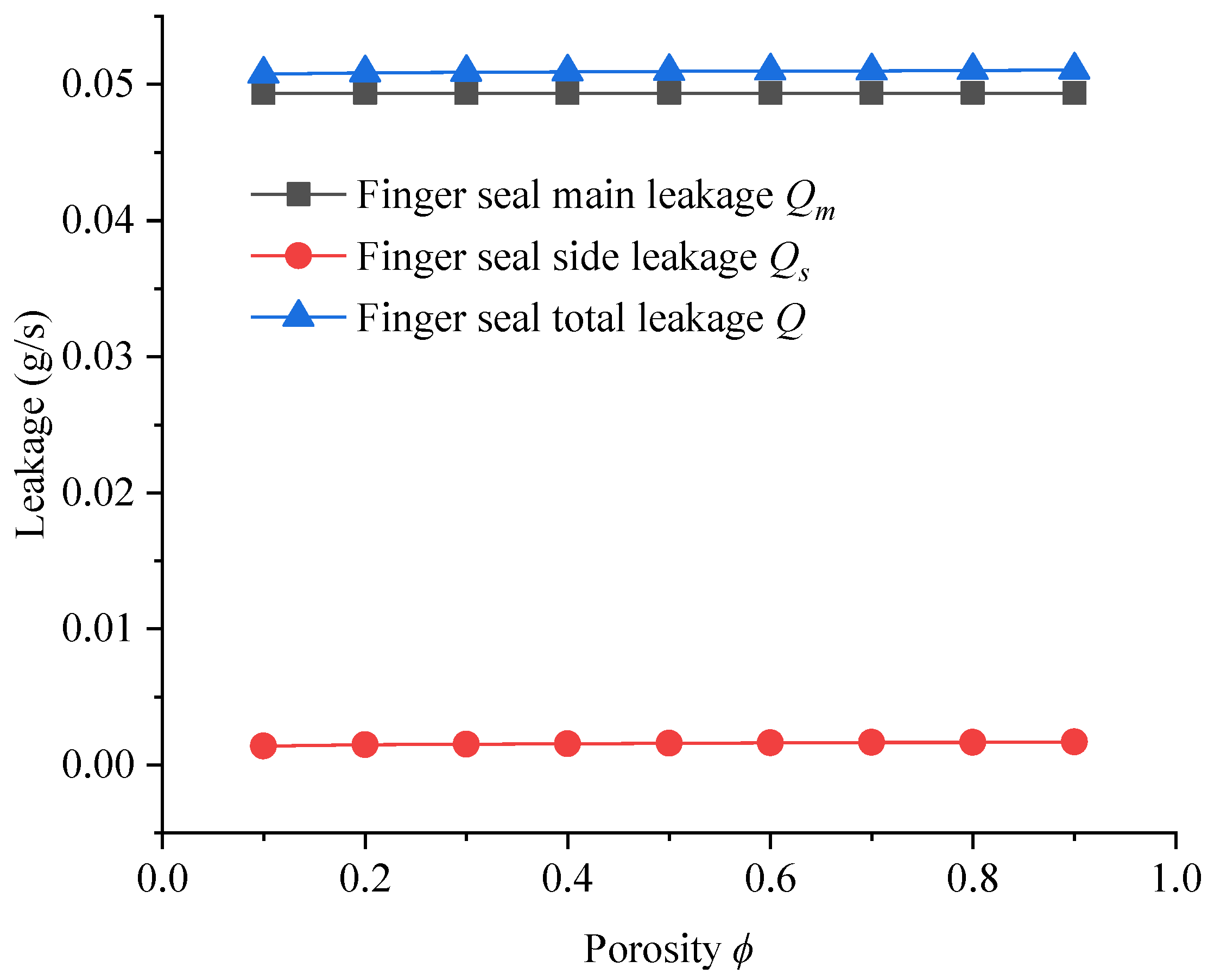
5.3.2. Porosity
5.4. Analysis of Influencing Factors on Leakage Performance of Finger Seal
5.4.1. Working Conditions
5.4.2. Fractal Feature Parameters
5.4.3. Porosity
6. Conclusions
- The maximum error rate between the numerical calculation and the experimental value of the mathematical model of the FS total leakage rate is 2.2%, which is less than 5%, and the mathematical model of the FS total leakage rate is feasible. However, the model is only applicable to the study of the leakage rate during the fully elastic deformation phase of the asperity, and the use of this model assumes that the contact surface has fractal characteristics. The FS main leakage rate mathematical model is used in the same way as the FS total leakage rate mathematical model.
- A mathematical model for the FS side leakage rate considering the seepage effect of fractal porous media takes into account the physical characteristics of isotropic porous media before and after loading, and the model can better reflect the FS side leakage characteristics, but the model does not take into account the physical characteristics of each anisotropic porous media and the non-Darcy seepage characteristics of porous media.
- In the analysis of the FS total leakage performance under various parameters, the FS main leakage rate is above 95% and the FS side leakage rate is below 5%. Thus, the FS’s main leakage rate is much larger than the FS’s side leakage rate, so the density of the material used for the FS can be improved to reduce the porosity, or non-metallic materials (such as C/C composite materials, etc.) can be used to reduce the FS wear rate and thus improve the sealing performance.
- In this study, the fractal characteristic parameters are used to characterise the contact surface morphology, which in turn reflects the leakage characteristics of the FS. It is recommended that in subsequent studies, the arithmetic mean roughness Ra or the effective root mean square surface roughness σ be used to characterise the contact surface topography and then Ra or σ be used to characterise the leakage performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.D.; Wang, Z.G. Development and Prospect of Brush Seal in Aero-engine. Lubr. Eng. 2005, 5, 203–205. [Google Scholar]
- Chupp, R.; Farshad, G.; Moore, G. Applying Abradable Seals to Industrial Gas Turbines. In Proceedings of the 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Indianapolis, IN, USA, 7–10 July 2002. [Google Scholar]
- Chupp, R.E.; Hendricks, R.C.; Lattime, S.B.; Steinetz, B.M. Sealing in turbomachinery. J. Propuls. Power 2006, 22, 313–349. [Google Scholar] [CrossRef]
- Chen, G.D.; Su, H.; Zhang, Y.C. Analysis and Design of Finger Seal; Northwestern Polytechnical University Press: Xi’an, China, 2012; pp. 40–55. [Google Scholar]
- Zhang, Y.C.; Zhang, Y.T.; Wang, T.; Cui, Y.H.; Liu, K. Experimental Study on Performances of Carbon Seal and Finger Seal under High-speed and High-pressure Condition. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Bristol, UK, 18–20 May 2018. [Google Scholar]
- Proctor, M.P.; Kumar, A.; Delgado, I.R. High-Speed, High-Temperature Finger Seal Test Results. J. Propuls. Power 2004, 20, 312–318. [Google Scholar] [CrossRef]
- Zhou, K.; Li, N.; Guo, W.; Pan, J.; Tan, J. Experimental Investigation on Static and Dynamic Characteristics of Finger Seals. Lubr. Eng. 2018, 43, 132–136. [Google Scholar]
- Proctor, M.P.; Delgado, I.R. Preliminary Test Results of Non-Contacting Finger Seal on Herringbone-Grooved Rotor. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Hartford, CT, USA, 21–23 July 2008. [Google Scholar]
- Wang, L.N.; Chen, G.D.; Su, H.; Lu, F. Transient Performance Analysis of Finger Seal Considering Compressed Fluid in the Leakage Gap Effect. J. Aerosp. Power 2015, 30, 2004–2010. [Google Scholar]
- Du, C.H.; Ji, H.H.; Hu, Y.P.; Luo, J.; Ma, D.; Tang, L.P.; Liao, K. Experiment on Axis Locus of Rotor and Leakage Characteristics of Finger Seal. J. Aerosp. Power 2016, 31, 2575–2584. [Google Scholar]
- Bai, H.L. Experimental and Numerical Study on Leakage Characteristics of Finger Seal. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2007; pp. 32–47. (In Chinese). [Google Scholar]
- Hu, T.X.; Zhou, K.; Li, N.; Pan, J. Numerical Calculation and Experimental Study on Leakage Characteristic of Finger Seal. J. Propuls. Technol. 2020, 41, 1089–1096. [Google Scholar]
- Wang, Q.; Hu, Y.P.; Ji, H.H. An Anisotropic Porous Media Model for Leakage Analysis of Finger Seal. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 280–292. [Google Scholar] [CrossRef]
- Chen, G.D.; Xu, H.; Yu, L.; Xiao, Y.X.; Zhou, L.J. On Selecting Proper Shape of Finger Seal. J. Northwestern Polytech. Univ. 2002, 20, 218–221. [Google Scholar]
- Su, H. Structural Design Performance Analysis and Tests of Finger Seal. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2007; pp. 35–43. (In Chinese). [Google Scholar]
- Zhang, Y.C.; Yin, M.H.; Zeng, Q.R.; Wang, T.; Wang, R. Theoretical and Experimental Investigation of Variable Stiffness Finger Seal. Tribol. Trans. 2020, 63, 634–646. [Google Scholar] [CrossRef]
- Yin, M.H.; Zhang, Y.C.; Zhou, R.M.; Zhai, Z.Y.; Wang, J.L.; Cui, Y.H.; Li, D.S. Friction Mechanism and Application of PTFE Coating in Finger Seal. Tribol. Trans. 2021, 65, 260–269. [Google Scholar] [CrossRef]
- Zhao, H.L.; Su, H.; Chen, G.D. Analysis of Total Leakage of Finger Seal with Side Leakage Flow. Tribol. Int. 2020, 150, 106371. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Liu, K.; Zhou, L.J.; Hu, H.T. Analysis of Leakage Characteristics of Finger Seal Based on System Responses. J. Aerosp. Power 2013, 28, 205–210. [Google Scholar]
- Persson, B.N.J. Leakage of Metallic Seals: Role of Plastic Deformations. Tribol. Lett. 2016, 63, 42. [Google Scholar] [CrossRef]
- Du, C.H.; Ji, H.H.; Hu, Y.P.; Luo, J.; Ma, D.; Tang, L.P.; Liao, K. Experiment of Wearing Characteristics and its Effect on Leakage of Finger Seal. J. Aerosp. Power 2017, 32, 53–59. [Google Scholar]
- Wang, L.N.; Sun, H.C.; Sun, W.; Zhou, X.Q.; Cui, Y.H.; Sun, L.C.; Meng, D.H. Fluid-solid Coupling Performance Analysis of Finger Seal under Considering Progressive Wear Effect. Lubr. Eng. 2021, 46, 47–53. [Google Scholar]
- Wang, Q.; Ji, H.H.; Hu, Y.P.; Du, C.H. Transient Leakage Characteristics Analysis of Finger Seal Considering Wear Effects. J. Propuls. Technol. 2020, 41, 2815–2826. [Google Scholar]
- Sun, J.J.; Gu, B.Q.; Wie, L. Leakage Model of Contacting Mechanical Seal Based on Fractal Geometry Theory. J. Chem. Ind. Eng. 2006, 57, 1626–1631. [Google Scholar]
- Ge, S.R.; Zhu, H. Fractal in Tribology; China Machine Press: Beijing, China, 2005; pp. 126–154. [Google Scholar]
- Persson, B.N.J.; Yang, C. Theory of the leak-rate of seals. J. Phys. Condens. Matter 2008, 20, 315011. [Google Scholar] [CrossRef]
- Maleki, I.; Wolski, M.; Woloszynski, T.; Podsiadlo, P.; Stachowiak, G. A Comparison of Multiscale Surface Curvature Characterization Methods for Tribological Surfaces. Tribol. Online 2019, 14, 8–17. [Google Scholar] [CrossRef]
- Lv, B.; Han, K.; Wang, Y.Z.; Li, X.L. Analysis and Experimental Verification of the Sealing Performance of PEM Fuel Cell Based on Fractal Theory. Fractal Fract. 2023, 7, 401. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Ding, X.X.; Wang, S.P. Prediction of Leakage Rate and Film Thickness of Mechanical Seal Based on Fractal Contact Theory. Lubr. Eng. 2022, 47, 156–163. [Google Scholar]
- Li, X.P.; Yang, Z.M.; Wang, L.L.; Yang, Y.X. Leakage Model of Contacting Mechanical Seal Based on Fractal Theory. J. Northeast. Univ. (Nat. Sci.) 2019, 40, 526–530. [Google Scholar]
- Sun, J.J. Research on Mechanical Seal Leakage Prediction Theory and Its Application. Ph.D. Thesis, Nanjing Tech University, Nanjing, China, 2006. [Google Scholar]
- Feng, X.; Gu, B.Q. Research on Leakage Model of Metallic Gasket Seal. Lubr. Eng. 2006, 8, 78–80. [Google Scholar]
- Ni, X.Y.; Sun, J.J.; Ma, C.B.; Zhang, Y.Y. Wear Model of a Mechanical Seal Based on Piecewise Fractal Theory. Fractal Fract. 2023, 7, 251. [Google Scholar] [CrossRef]
- Bai, H.L.; Wang, W.; Zhang, Z.S.; Hu, G.Y. Analysis of Leakage Flow through Finger Seal Based on Porous Medium. J. Aerosp. Power 2016, 31, 1303–1308. [Google Scholar]
- Bai, H.L.; Ji, H.H.; Ji, G.J.; Cao, G.Z. Experimental Investigation on Leakage Characteristics of Finger Seal. J. Aerosp. Power 2009, 24, 532–536. [Google Scholar]
- Zhao, H.L.; Chen, G.D.; Su, H. Analysis of Total Leakage Performance of Finger Seal Considering the Rough Seepage Effect. J. Mech. Eng. 2020, 56, 152–161. [Google Scholar]
- Lv, X.K.; Yang, W.J.; Xu, G.L.; Huang, X.M. The Influence of Characteristic of Rough Surface on Gas Sealing Performance in Seal Structure. J. Mech. Eng. 2015, 51, 110–115. [Google Scholar] [CrossRef]
- Bao, C.Y.; Meng, X.K.; Li, J.Y.; Peng, X.D. The Leakage Performance Analysis of Mechanical Seals under Hydrostatic Pressures Based on Porous Media Model. Lubr. Eng. 2015, 40, 57–63. [Google Scholar]
- Huang, X.M.; Yao, B.; Xu, G.L.; Lu, X.K. Research on Leakage of Metallic Gasket Based on Fractal Porous Seepage. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2016, 44, 1–5. [Google Scholar]
- Ning, C.X. Hydraulic and Pneumatic Technology; Chemical Industry Press: Beijing, China, 2017; pp. 24–27. [Google Scholar]
- Zhang, Y.C.; Liu, K.; Hu, H.T.; Song, F. Quasi-Dynamic Performances Analysis of Finger Seal Based on Finite Element Simulation. J. Propuls. Technol. 2016, 37, 2352–2358. [Google Scholar]
- Zhang, X.L. Study on Wear Performance of Finger Seal Contact Pair. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2020; pp. 46–52. (In Chinese). [Google Scholar]
- Archard, J.F. Elastic Deformation and the Laws of Friction. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 243, 190–205. [Google Scholar]
- Lei, J.J.; Liu, M.H.; Hu, X.P.; Wang, J.; Wang, X.L. Analysis of Wear Characteristics of Elliptic Arc Finger Seal Based on Fractal Theory. J. Mech. Eng. 2023, 59, 144–157. [Google Scholar]
- Dong, L. A Research for Fractal Geometry Models of Elastic-Plastic Contact and Wear Prediction. Master’s Thesis, Sichuan University, Chengdu, China, 2000; pp. 20–21. (In Chinese). [Google Scholar]
- Wei, L.; Gu, B.Q.; Liu, Q.H.; Zhang, P.G.; Fang, G.M. Correction of contact fractal model for friction faces of mechanical seals. CIESC J. 2013, 64, 1723–1729. [Google Scholar]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]
- Sayles, R.S.; Thomas, T.R. Surface topography as a nonst ationary random process. Nature 1978, 271, 431–434. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Role of Fractal Geometry in Roughness Characterization and Contact Mechanics of Surfaces. Trans. Asme J. Tribol. 1990, 112, 205–216. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Fractal Model of Elastic-Plastic Contact Between Rough Surfaces. J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Xu, G.L.; Zhu, Y.P.; Fang, L.; Du, Y.; Huang, X.M. Three-dimensional Fractal Reconstruction Technique and Leakage Characteristics of Micro-pore Sealing Interfaces. Chin. J. Comput. Phys. 2019, 36, 440–448. [Google Scholar]
- Ji, Z.B.; Sun, J.J.; Lu, J.H.; Ma, C.B.; Yu, Q.P. Predicting Method for Static Leakage of Contacting Mechanical Seals Interface Based on Percolation Theory. Tribology 2017, 37, 734–742. [Google Scholar]
- Zhou, X.; Pang, H.W.; Liu, H.Y. Leak Rate Prediction of Orbicular Seal Jonint. J. Astronaut. 2007, 28, 762–766. [Google Scholar]
- Yu, B.M.; Li, J.H. Some Fractal Characters of Porous Media. Fractals-Complex Geom. Patterns Scaling Nat. Soc. 2001, 9, 365–372. [Google Scholar] [CrossRef]
- Yu, B.M.; Xu, P.; Zou, M.Q.; Cai, J.C.; Zheng, Q. Transport Physics in Fractal Porous Media; Science Press: Beijing, China, 2014; pp. 7–8. [Google Scholar]
- Li, C.; Shen, Y.Q.; Qiu, S.X.; Yu, B.M.; Xu, P. Mapping Correlation Between Heat Conduction and Fluid Flow Through Unsaturated Porous Media. J. Eng. Thermophys. 2022, 43, 2742–2750. [Google Scholar]
- Qiu, S.X.; Xu, P.; Yang, M. The Effective Gas Permeability of Porous Media with Multi-scale Pore Structure. J. Eng. Thermophys. 2019, 40, 1375–1379. [Google Scholar]
- Xu, P.; Li, C.H.; Liu, H.C.; Qiu, S.X.; Yu, B.M. Fractal Features of the Effective Gas Transport Coefficient for Multiscale Porous Media. Earth Sci. 2017, 42, 1373–1378. [Google Scholar]
- Yu, B.M.; Cheng, P. A Fractal Permeability Model for Bi-dispersed Porous Media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Yu, B.M.; Li, J.H. A Geometry Model for Tortuosity of Flow Path in Porous Media. Chin. Phys. Lett. 2004, 21, 1569–1571. [Google Scholar]
- Yu, B.M. Fractal Character for Tortuous Streamtubes in Porous Media. Chin. Phys. Lett. 2005, 22, 158–160. [Google Scholar]
- Zhang, Y.C.; Chen, G.D.; Shen, X.L. Analysis of Dynamic Performance and Leakage for Finger Seal. Acta Aeronaut. Astronaut. Sin. 2009, 30, 2193–2199. [Google Scholar]
- Wang, H.Y.; Chen, G.D.; Zhang, Y.C. Sensitivity Analysis of Finger Seal Performances and Construction Parameters. Lubr. Eng. 2008, 33, 11–13. [Google Scholar]
- Zhang, M.C. Performance Analysis and Optimization of the Extended Rotary Finger Seal. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2020; pp. 11–36. (In Chinese). [Google Scholar]
- Wang, L.N. Research on Dynamic Performance of C/C Composite Finger Seal under Considering Work Status. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2016; pp. 99–108. (In Chinese). [Google Scholar]
- Lu, F. Study on Wear and Dynamic Performance of C/C Composite Finger Seal. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2017; pp. 111–126. (In Chinese). [Google Scholar]
- Zhi, B.W. Study on the Effect of Surface Texture on the Tribological Characteristics of Contact Finger Seal. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2022; pp. 57–63. (In Chinese). [Google Scholar]
- Zong, Z.K.; Su, H. Geometric Feature and Structure Optimization of Arc Finger Seal. Acta Aeronaut. Astronaut. Sin. 2010, 31, 393–399. [Google Scholar]
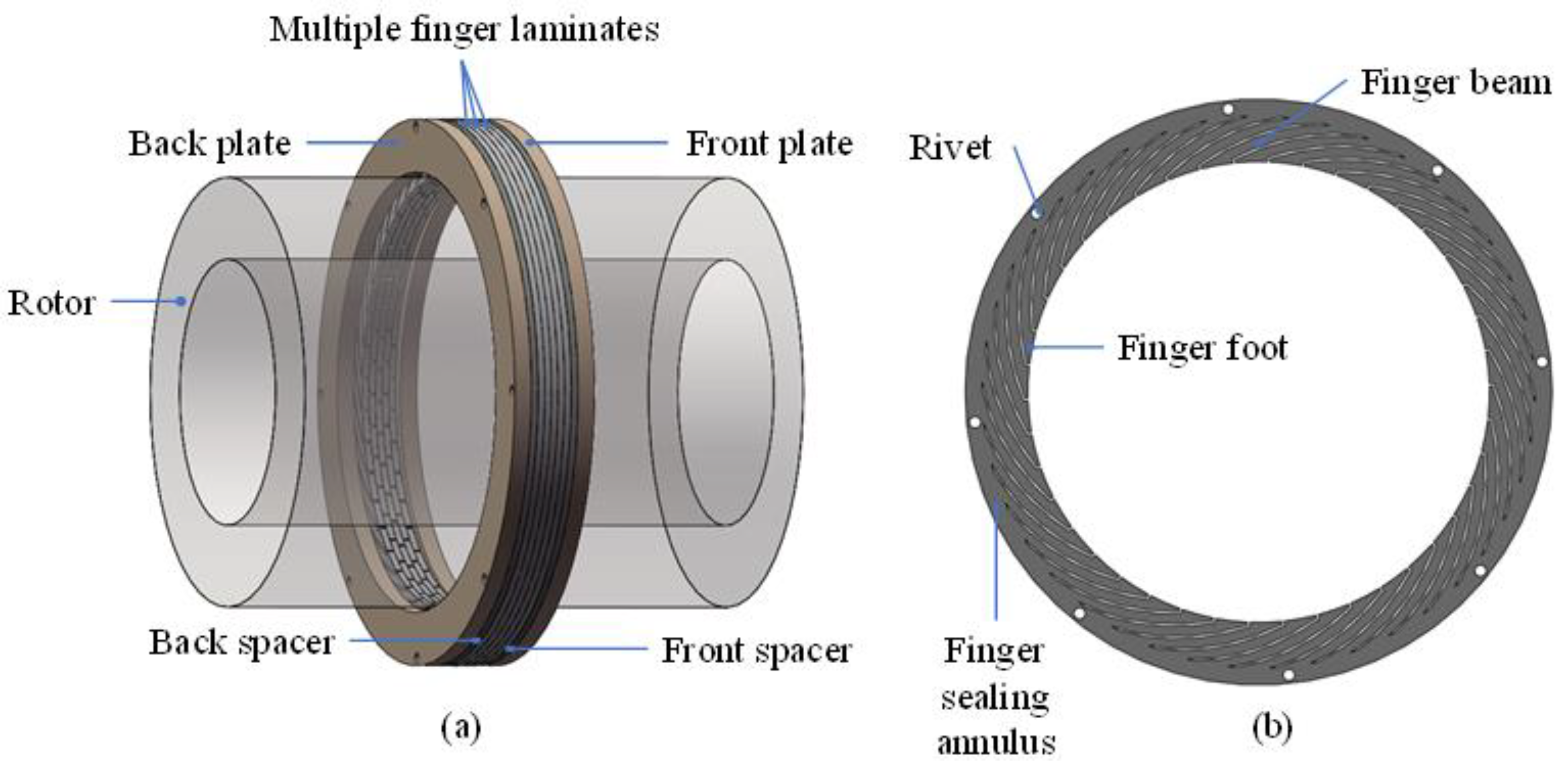

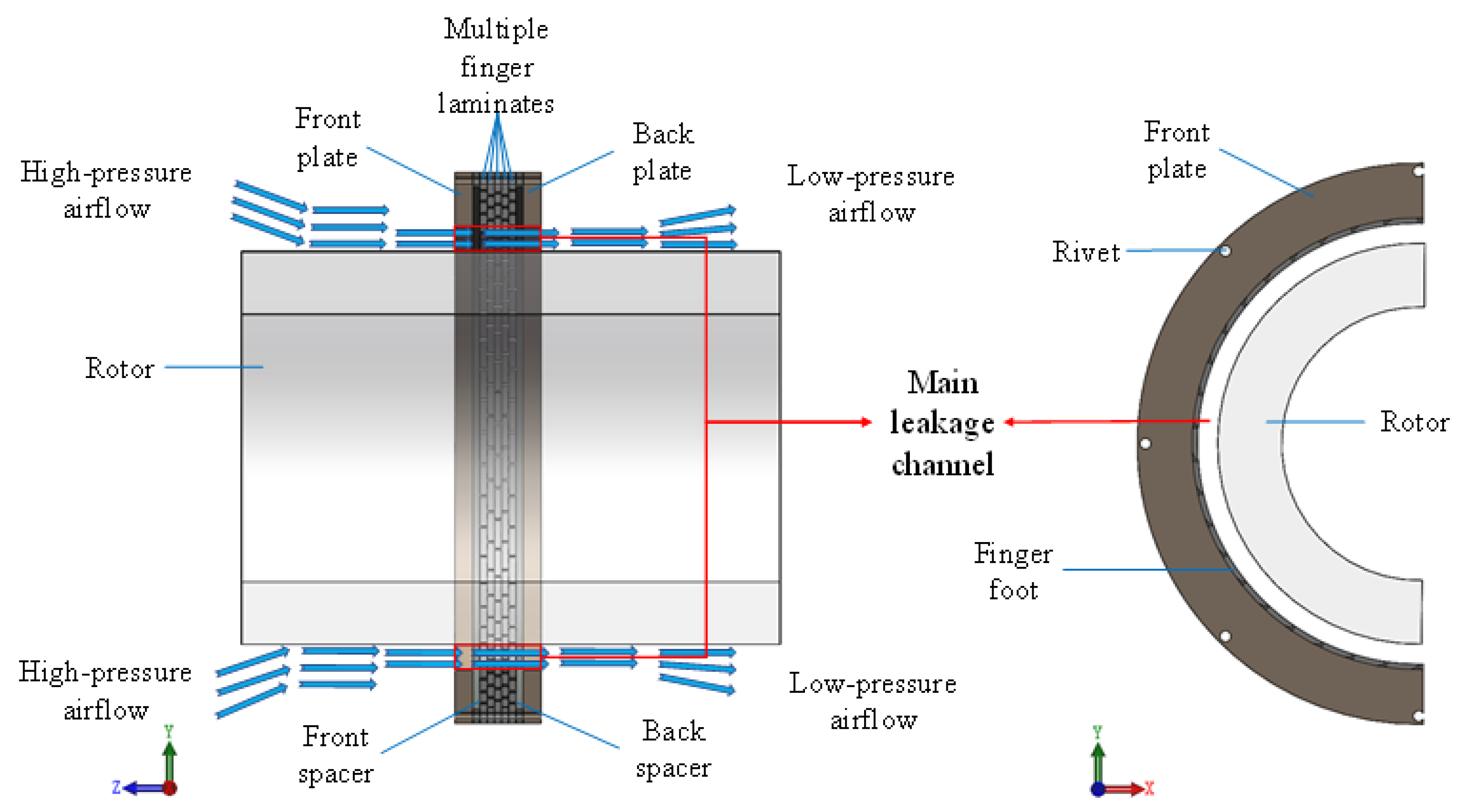
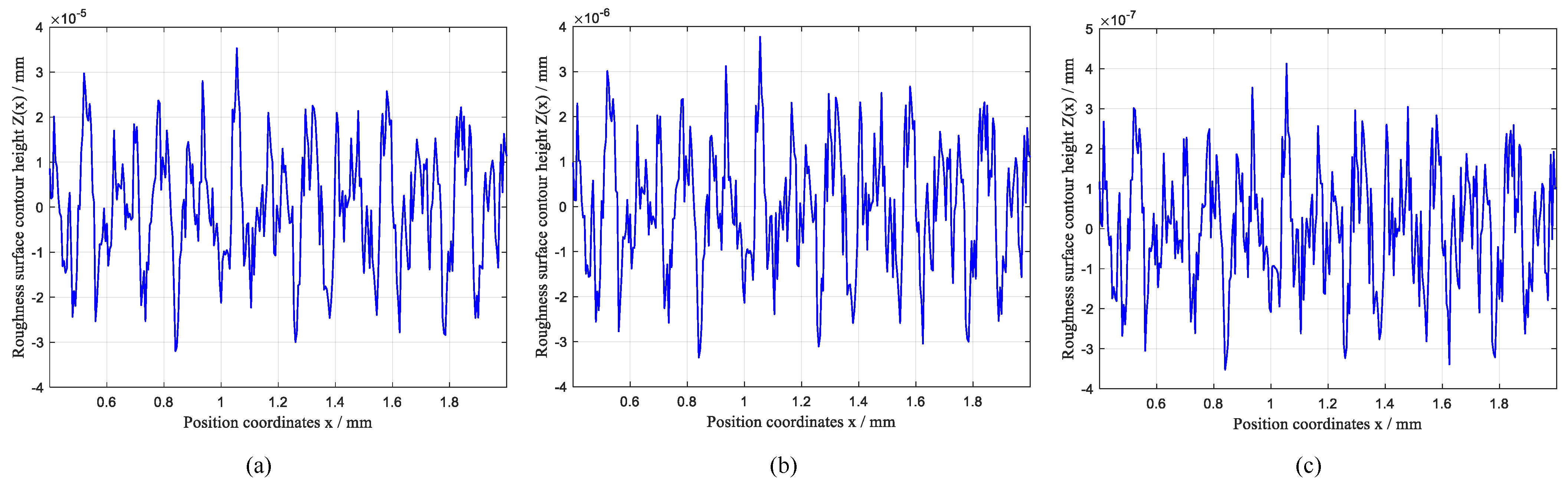

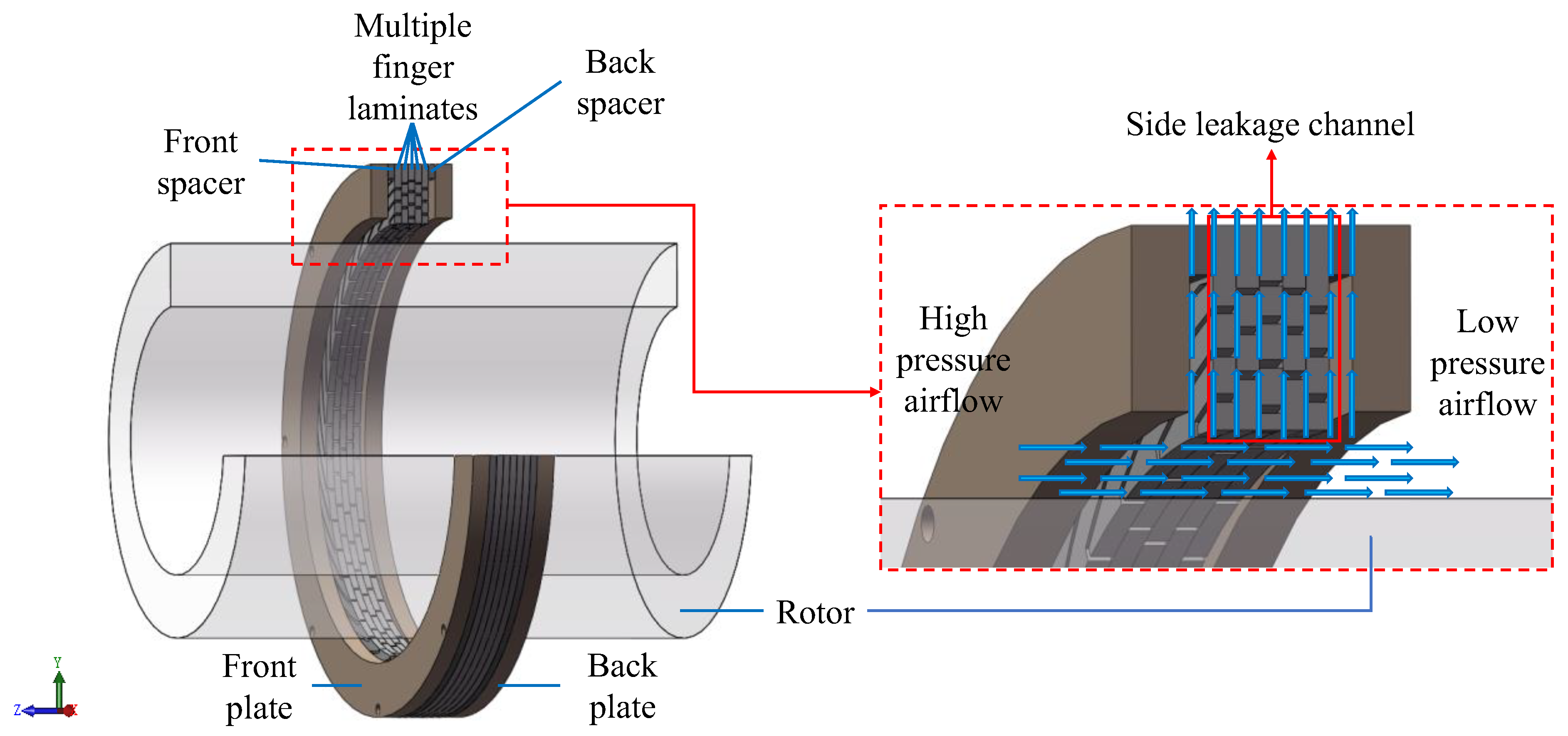
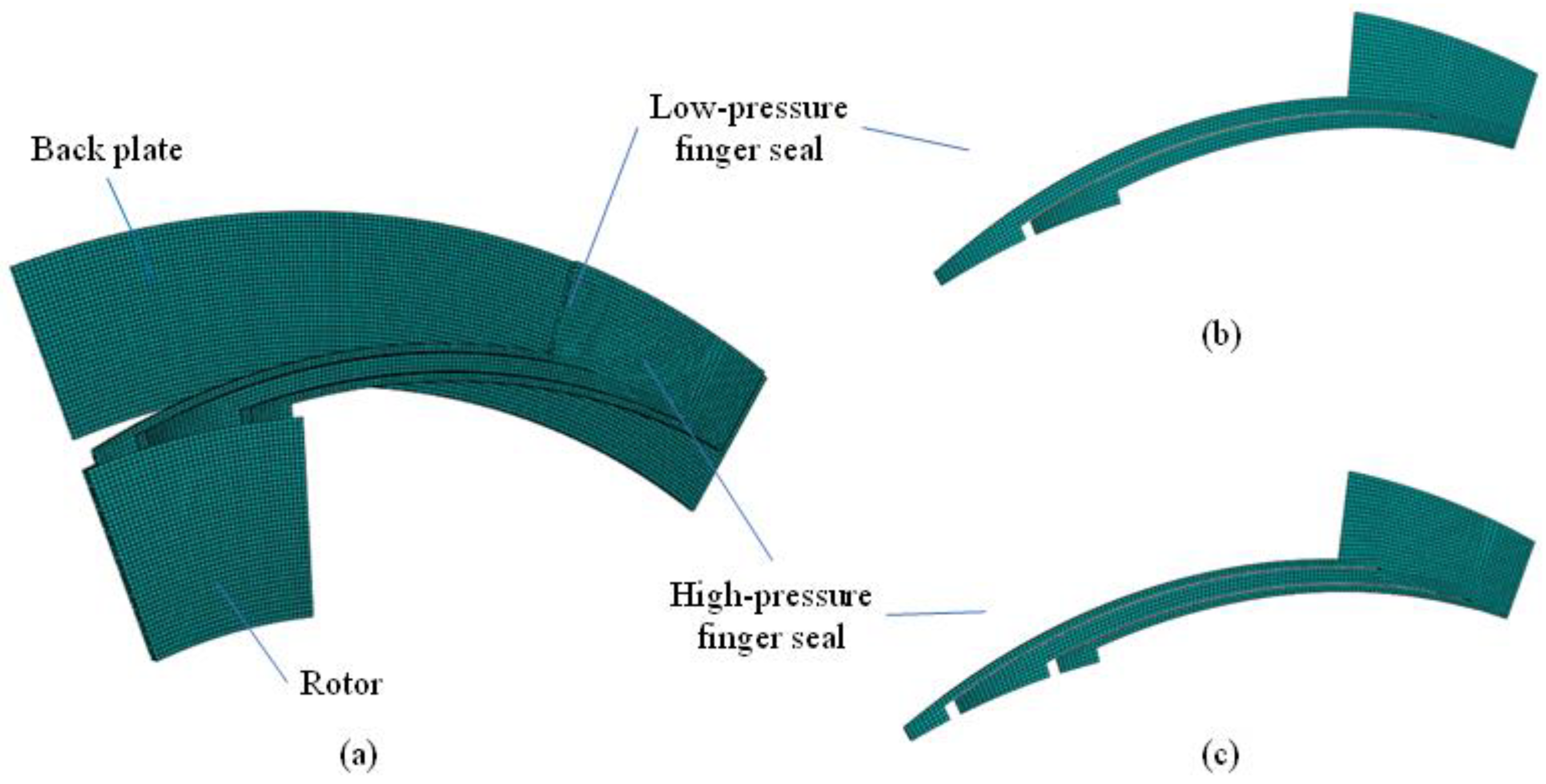




| Parameters | Units | Values |
|---|---|---|
| Radius of the outer circle/Dw | mm | 77 |
| Radius of the root circle/Df | mm | 68.75 |
| Radius of the inner circle/Dr | mm | 60.5 |
| Radius of the base circle/Dcc | mm | 11 |
| Arc radius/Rc | mm | 63 |
| Rotor radius/r | mm | 59.5 |
| Gap width/Ia | mm | 2 |
| Clearance angle/α | ° | 0.2 |
| Downstream protection height/gd | mm | 1.2 |
| Height of the heel/xg | mm | 1.2 |
| Number of finger beams/Nfb | 42 |
| Axial Pressure Differences (MPa) | Main Leakage Rate Ratio (%) | Side Leakage Rate Ratio (%) |
|---|---|---|
| 0.1 | 97.90 | 2.10 |
| 0.15 | 98.63 | 1.37 |
| 0.2 | 98.71 | 1.29 |
| 0.25 | 98.77 | 1.23 |
| 0.3 | 99.09 | 0.91 |
| 0.35 | 99.25 | 0.75 |
| 0.4 | 99.39 | 0.61 |
| 0.45 | 99.51 | 0.49 |
| 0.5 | 99.59 | 0.41 |
| Radial Displacement Excitation (mm) | Main Leakage Rate Ratio (%) | Side Leakage Rate Ratio (%) |
|---|---|---|
| 0.01 | 96.21 | 3.79 |
| 0.02 | 96.96 | 3.04 |
| 0.03 | 96.97 | 3.03 |
| 0.04 | 97.54 | 2.46 |
| 0.05 | 98.03 | 1.97 |
| 0.06 | 98.31 | 1.69 |
| 0.07 | 98.57 | 1.43 |
| 0.08 | 98.78 | 1.22 |
| 0.09 | 98.78 | 1.22 |
| Rotor Speed (r/min) | Main Leakage Rate Ratio (%) | Side Leakage Rate Ratio (%) |
|---|---|---|
| 10,000 | 98.72 | 1.28 |
| 10,500 | 98.71 | 1.29 |
| 11,000 | 98.60 | 1.40 |
| 11,500 | 98.49 | 1.51 |
| 12,000 | 98.35 | 1.65 |
| 12,500 | 98.18 | 1.82 |
| 13,000 | 97.97 | 2.03 |
| 13,500 | 97.70 | 2.30 |
| 14,000 | 97.35 | 2.65 |
| 14,500 | 96.89 | 3.11 |
| 15,000 | 96.30 | 3.70 |
| Fractal Dimension | Main Leakage Rate Ratio (%) | Side Leakage Rate Ratio (%) |
|---|---|---|
| 1.3 | 97.97 | 2.03 |
| 1.4 | 97.98 | 2.02 |
| 1.5 | 97.99 | 2.01 |
| 1.6 | 98.01 | 1.99 |
| 1.7 | 98.05 | 1.95 |
| 1.8 | 98.11 | 1.89 |
| 1.9 | 98.29 | 1.71 |
| Fractal Roughness Parameter | Main Leakage Rate Ratio (%) | Side Leakage Rate Ratio (%) |
|---|---|---|
| 1 × 10−7 | 97.88 | 2.12 |
| 1 × 10−8 | 97.97 | 2.03 |
| 1 × 10−9 | 97.97 | 2.03 |
| 1 × 10−10 | 97.97 | 2.03 |
| 1 × 10−11 | 97.97 | 2.03 |
| 1 × 10−12 | 97.97 | 2.03 |
| Porosity | Main Leakage Rate Ratio (%) | Side Leakage Rate Ratio (%) |
|---|---|---|
| 0.1 | 97.25 | 2.75 |
| 0.2 | 97.09 | 2.91 |
| 0.3 | 96.99 | 3.01 |
| 0.4 | 96.92 | 3.08 |
| 0.5 | 96.86 | 3.14 |
| 0.6 | 96.81 | 3.19 |
| 0.7 | 96.77 | 3.23 |
| 0.8 | 96.74 | 3.26 |
| 0.9 | 96.70 | 3.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, J.; Liu, M.; Chang, W.; Wan, Y. Analysis of the Total Leakage Characteristics of Finger Seal Considering Fractal Wear and Fractal Porous Media Seepage Effects. Fractal Fract. 2023, 7, 494. https://doi.org/10.3390/fractalfract7070494
Lei J, Liu M, Chang W, Wan Y. Analysis of the Total Leakage Characteristics of Finger Seal Considering Fractal Wear and Fractal Porous Media Seepage Effects. Fractal and Fractional. 2023; 7(7):494. https://doi.org/10.3390/fractalfract7070494
Chicago/Turabian StyleLei, Junjie, Meihong Liu, Wei Chang, and Yongneng Wan. 2023. "Analysis of the Total Leakage Characteristics of Finger Seal Considering Fractal Wear and Fractal Porous Media Seepage Effects" Fractal and Fractional 7, no. 7: 494. https://doi.org/10.3390/fractalfract7070494
APA StyleLei, J., Liu, M., Chang, W., & Wan, Y. (2023). Analysis of the Total Leakage Characteristics of Finger Seal Considering Fractal Wear and Fractal Porous Media Seepage Effects. Fractal and Fractional, 7(7), 494. https://doi.org/10.3390/fractalfract7070494









