Determination of Integrity Index Kv in CHN-BQ Method by BP Neural Network Based on Fractal Dimension D
Abstract
:1. Introduction
2. Fractal Dimensions D of Structural Planes
2.1. Fractal Theory and Fractal Dimension D
2.2. Fractal Characteristics of Structural Plane Distribution
2.3. Determination of Fractal Dimension D Based on Structural Plane Network Simulation
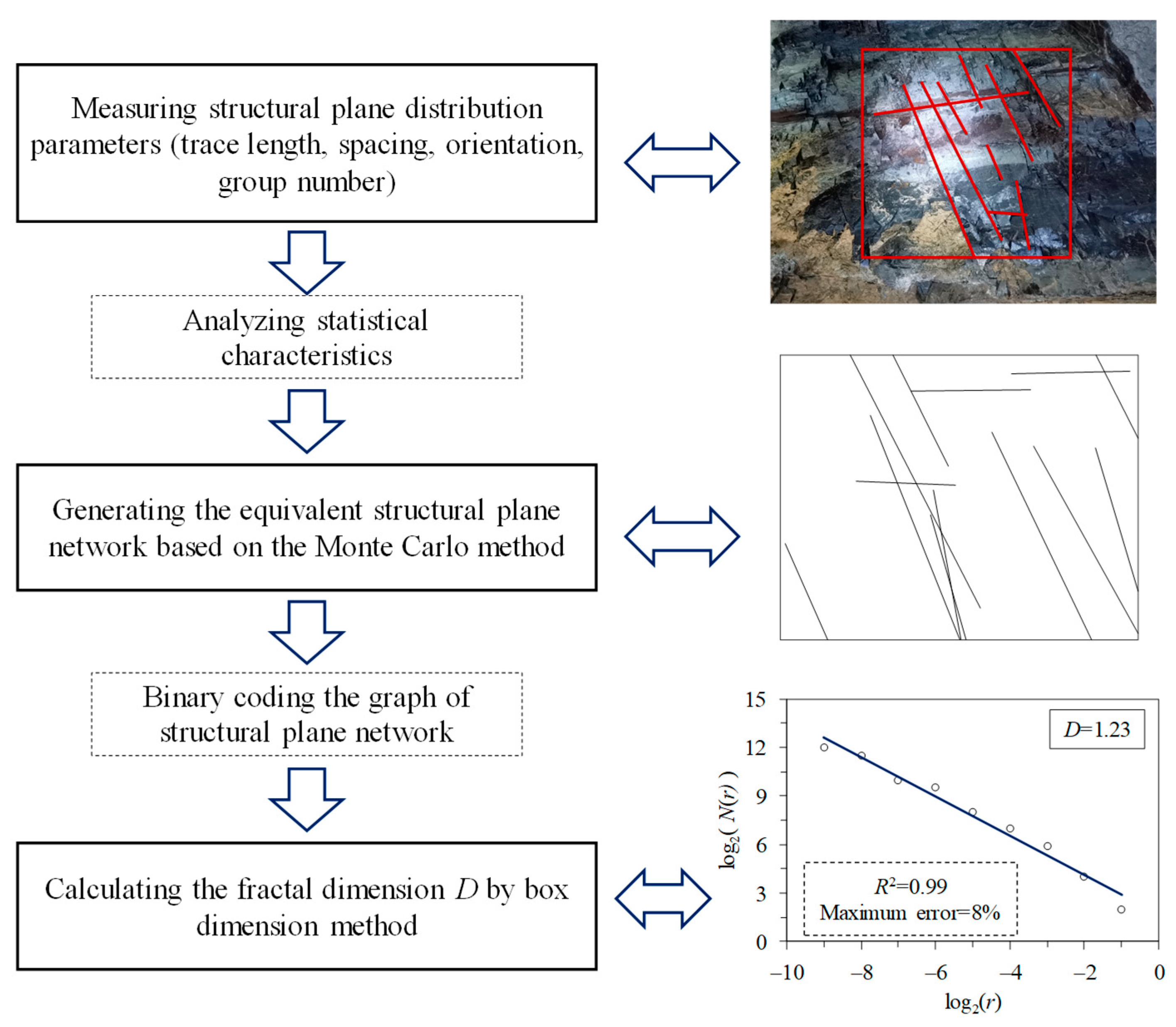
- Measurements of the structural plane distribution parameters
- 2.
- Generation of the equivalent structural plane network
- 3.
- Calculation of the fractal dimension D
3. Correlation of Fractal Dimension D with Integrity Index Kv
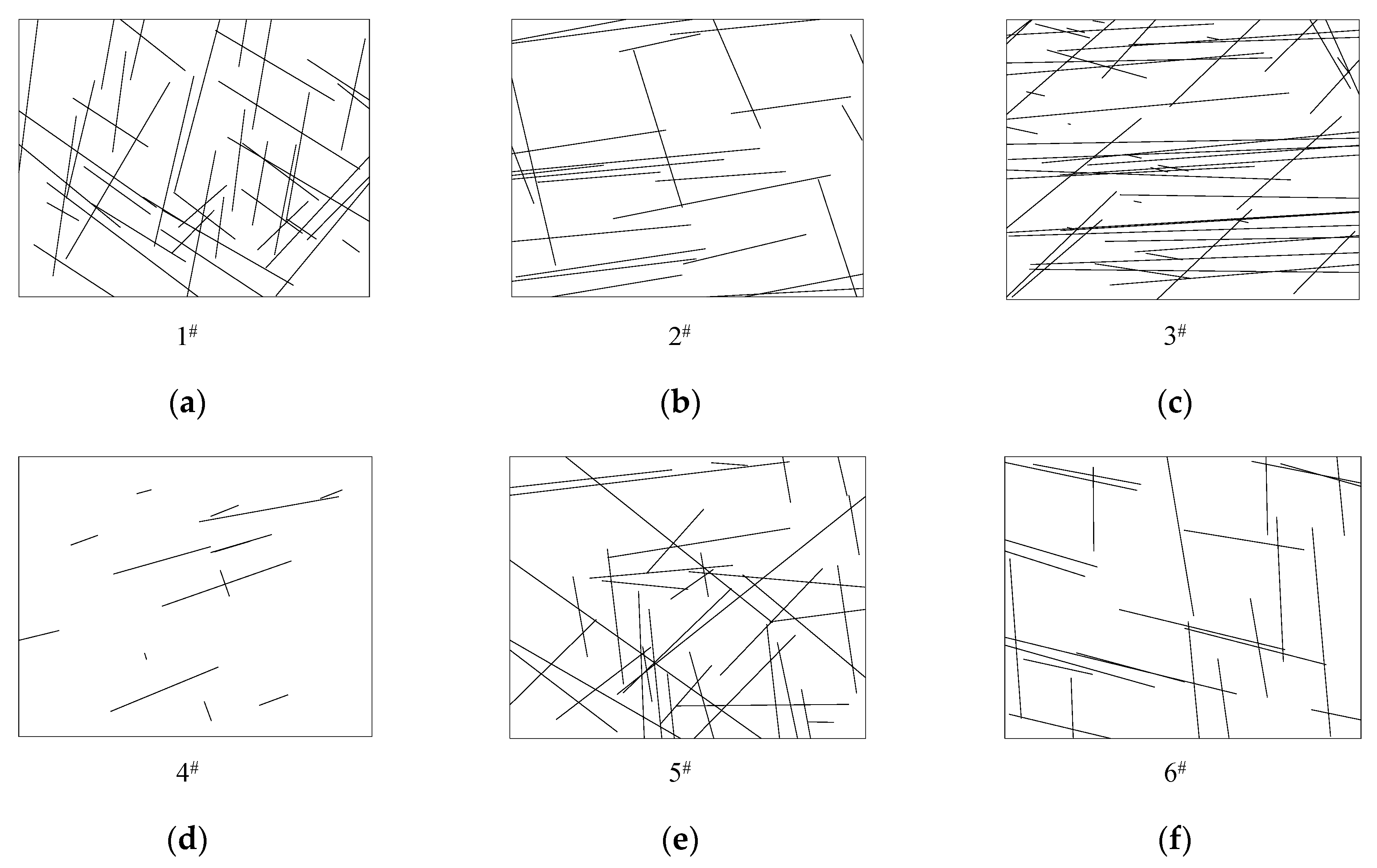
3.1. Acquisition and Treatment of Structural Plane Distribution Parameters
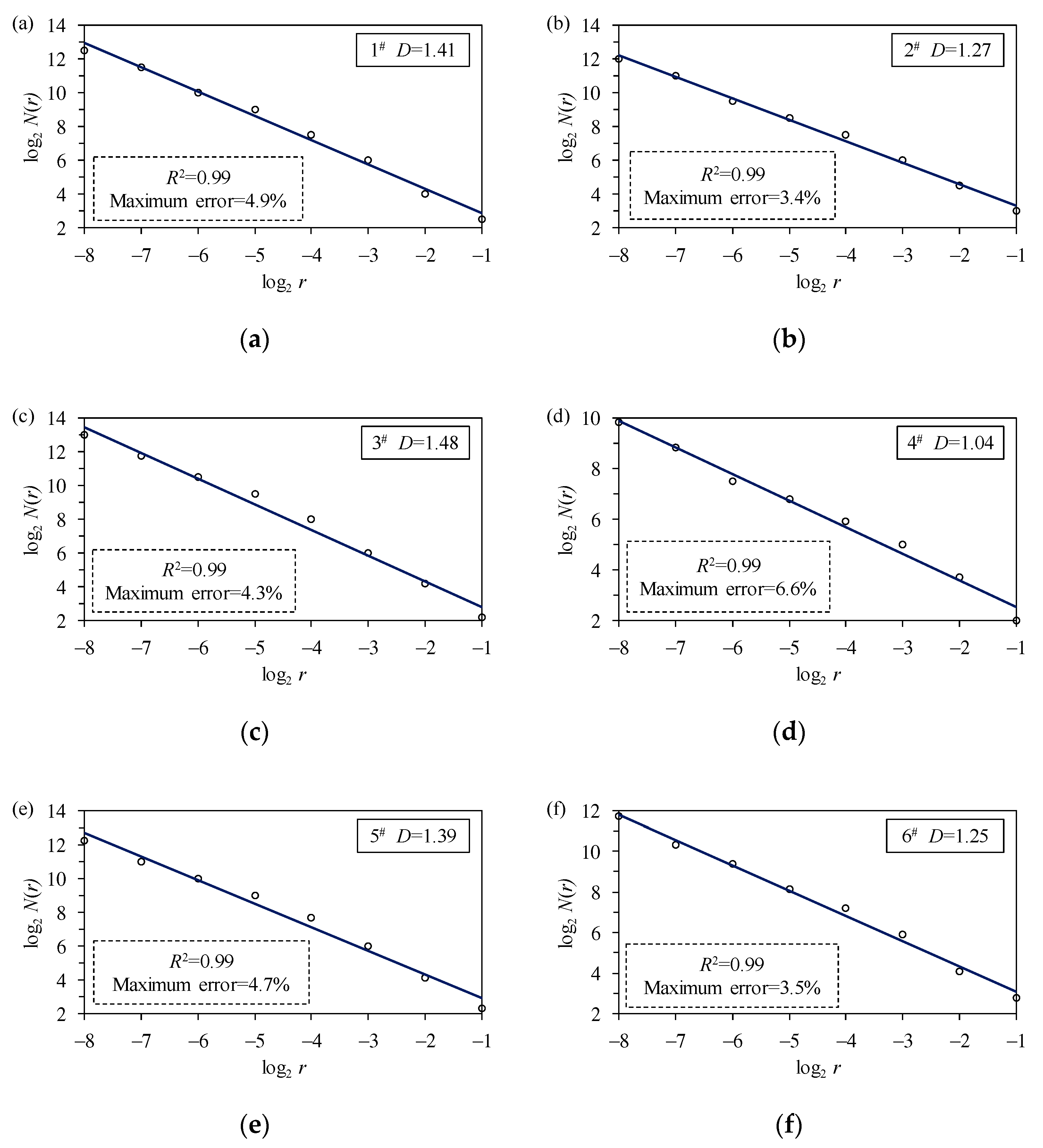
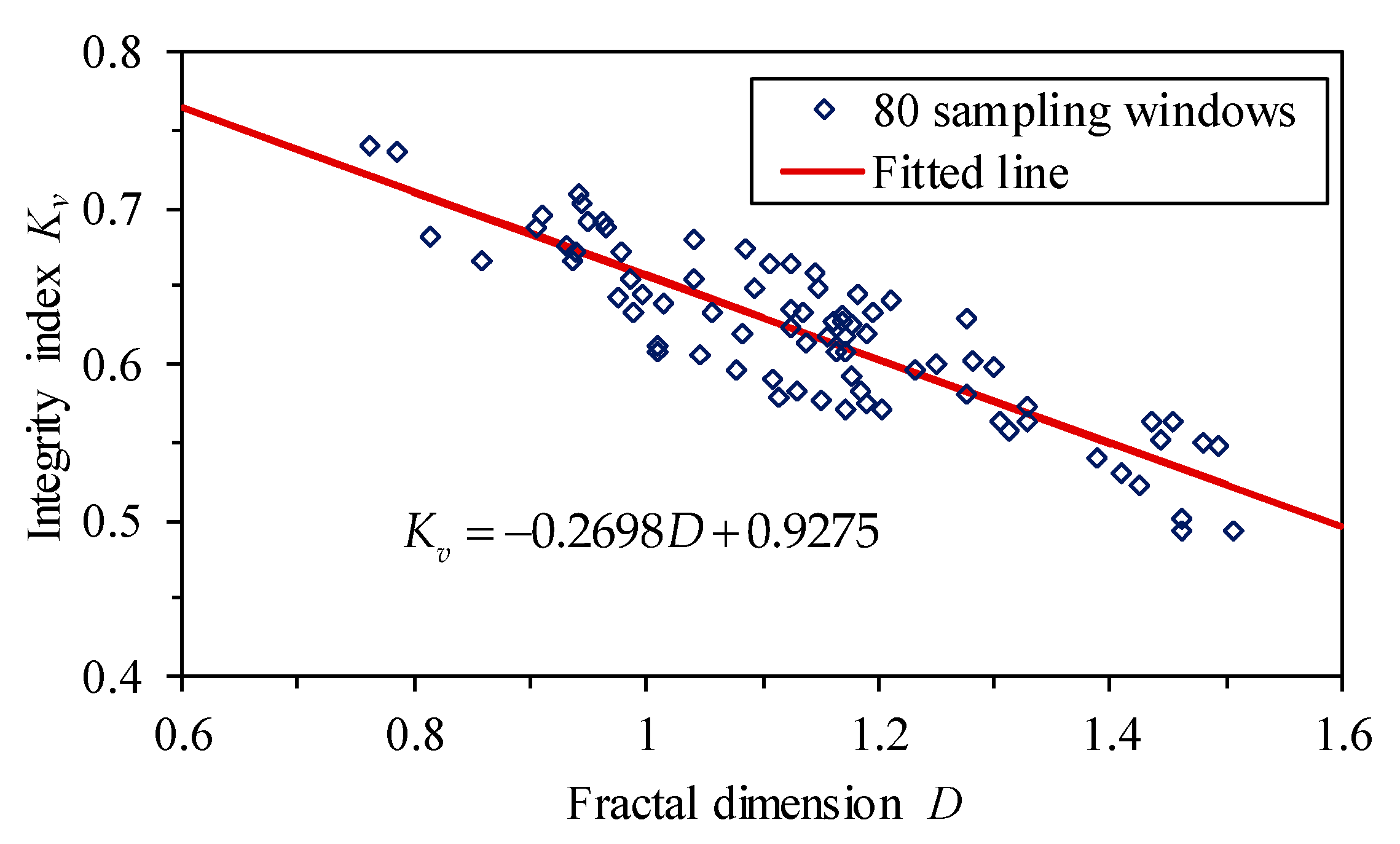
3.2. Quantitative Correlation between D and Kv
4. Prediction of Kv by BP Neural Network
5. Application of BP Neural Network for Predicting Kv in Jiulaopo Tunnel
6. Discussions
7. Conclusions
- The fractal dimension D correlates well with the integrity index Kv, with a maximum relative error of 8.21%. Meanwhile, the larger fractal dimension D corresponds to the smaller Kv and the more fractured rock mass. The fractal dimension D of the structure plane contains rich information on the rock mass, and it can effectively reflect the integrity, uniformity, and other characteristics of the rock mass.
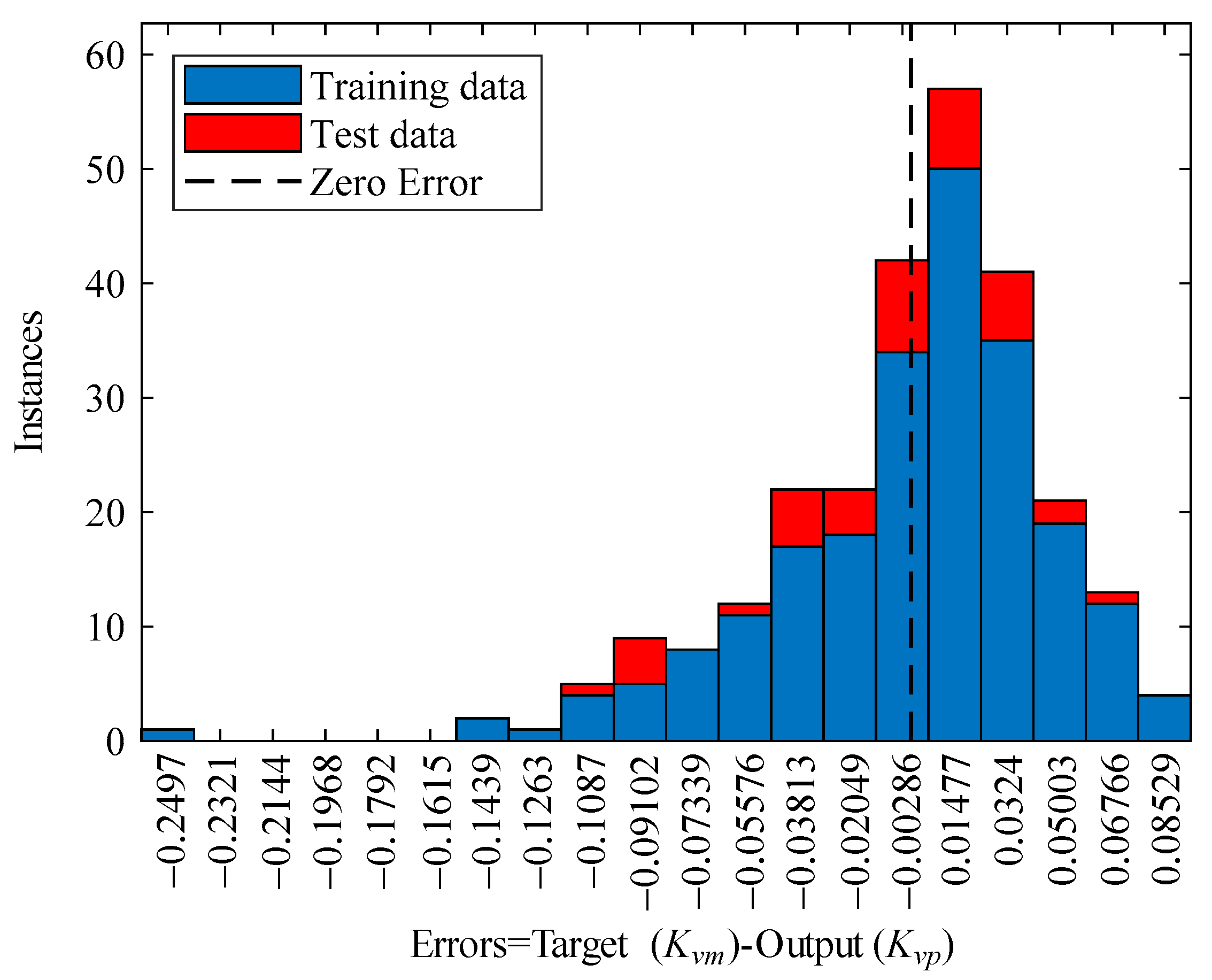
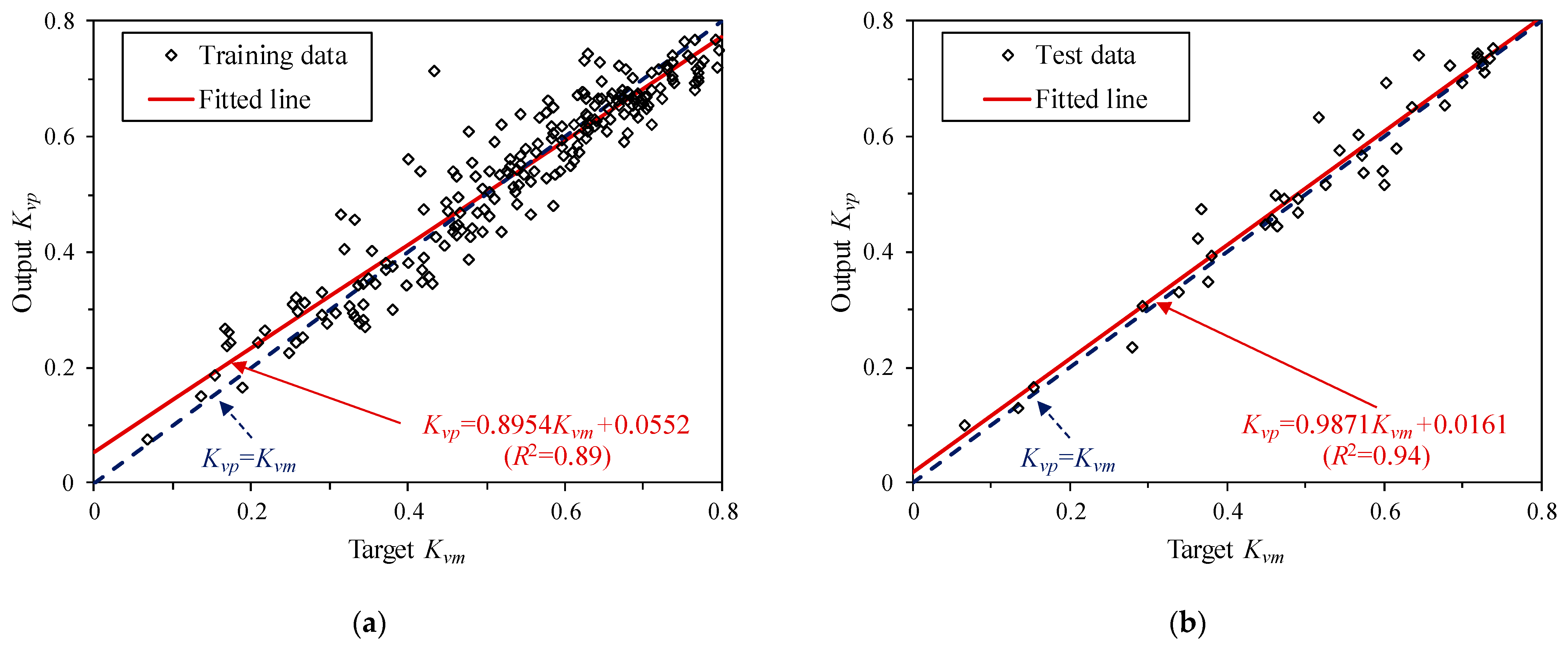
- The BP neural network for predicting Kv is well trained. The correlation coefficient R2 between the predicted Kvp by the BP neural network and the measured Kvm is 0.93, and the average relative error is 7.51%. Compared with the Kvd determined directly by fractal dimension D, there is a large error in Kvd, especially when Kv is less than 0.5. The BP neural network for predicting Kv, which considers both geometric characteristics of structural planes and structural plane conditions, is more accurate than determining Kv by fractal dimension D.
- The BP neural network for predicting Kv is applied to the Jiulaopo Tunnel. The maximum relative error between the measured Kvm and the predicted Kvp is 5.13%, and the average relative error is 2.71% for the 10 sampling windows. It shows that the BP neural network for predicting Kv performs well in rock engineering and can predict Kv accurately.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Singh, B.; Goel, R.K. Engineering Rock Mass Classification: Tunnelling, Foundations and Landslides; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Zhang, L.Y. Evaluation of rock mass deformability using empirical methods—A review. Undergr. Space 2017, 2, 1–15. [Google Scholar] [CrossRef]
- Deere, D.U. Technical description of rock cores for engineer purposes. Rock Mech. Eng. Geol. 1964, 1, 17–22. [Google Scholar]
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. Rock Eng. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Brown, E.; Hoek, E. Strength of rock and rock masses. ISRM News J. 1994, 2, 4–16. [Google Scholar]
- Hoek, E.; Kaiser, P.; Bawden, W. Support of Underground Wxcavations in Hard Rock; A. A. Balkema: Rotterdam, The Netherlands, 1995. [Google Scholar]
- Bieniawski, Z.T. Engineering classification of jointed rock masses. Civ. Eng. S. Afr. 1973, 15, 333–343. [Google Scholar]
- Bieniawski, Z.T. Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering; John Wiley and Sons: New York, NY, USA, 1989. [Google Scholar]
- Wu, A.Q.; Zhao, W.; Zhang, Y.H.; Fu, X. A detailed study of the CHN-BQ rock mass classification method and its correlations with RMR and Q system and Hoek-Brown criterion. Int. J. Rock Mech. Min. Sci. 2023, 162, 105290. [Google Scholar] [CrossRef]
- Shen, Y.-J.; Yan, R.-X.; Yang, G.-S.; Xu, G.-L.; Wang, S.-Y. Comparisons of Evaluation Factors and Application Effects of the New [BQ]GSI System with International Rock Mass Classification Systems. Geotech. Geol. Eng. 2017, 35, 2523–2548. [Google Scholar] [CrossRef]
- Cui, Z.; Sheng, Q.; Zhang, G.-M.; Liu, H. A modified rock mass classification considering seismic effects in the basic quality (BQ) system. Bull. Eng. Geol. Environ. 2021, 80, 2249–2260. [Google Scholar] [CrossRef]
- Wu, A.Q.; Liu, F.Z. Advancement and application of the standard of engineering classification of rock masses. Chin. J. Rock Mech. Eng. 2012, 31, 1513–1523. [Google Scholar]
- Shen, Y.J.; Yang, G.S.; Yan, R.X. Revised BQ system in China and its correlation to international rock mass classification systems. In Proceedings of the World Mining Congress, Canadian Institute of Mining, Metallurgy and Petroleum, Montreal, QC, Canada, 11–15 August 2013. [Google Scholar]
- Yan, R.X.; Shen, Y.J. Correlation of revised BQ system in China and the international rock mass classification systems. J. Civ. Eng. Res. 2015, 5, 33–38. [Google Scholar]
- Zhou, F.J.; Chen, J.P.; Xu, L.M. Study of rock masses quality evaluation based on 3D fractal dimension of rock discontinuity distribution. Rock Soil Mech. 2012, 33, 2315–2322. [Google Scholar]
- Ghosh, A.; Daemen, J.J. Fractal characteristics of rock discontinuities. Eng. Geol. 1993, 34, 1–9. [Google Scholar] [CrossRef]
- Sun, S.Q.; Li, S.C.; Li, L.P.; Shi, S.S.; Liu, H.L.; Hu, J.; Zhou, S. Structural planes surveying and fractal dimension characteristics of tunnel face based on digital photogrammetry. Arab. J. Geosci. 2018, 11, 622. [Google Scholar] [CrossRef]
- Bagde, M.; Raina, A.; Chakraborty, A.; Jethwa, J. Rock mass characterization by fractal dimension. Eng. Geol. 2002, 63, 141–155. [Google Scholar] [CrossRef]
- Ehlen, J. Fractal analysis of joint patterns in granite. Int. J. Rock Mech. Min. Sci. 2000, 37, 909–922. [Google Scholar] [CrossRef]
- La Pointe, P. A method to characterize fracture density and connectivity through fractal geometry. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1988, 25, 421–429. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, Z.; Dong, Y.; Liang, W.; Feng, Z. Three-dimensional fractal distribution of the number of rock-mass fracture surfaces and its simulation technology. Comput. Geotech. 2015, 65, 136–146. [Google Scholar] [CrossRef]
- Xie, H.; Wang, J.-A.; Xie, W.-H. Fractal effects of surface roughness on the mechanical behavior of rock joints. Chaos Solitons Fractals 1997, 8, 221–252. [Google Scholar] [CrossRef]
- Lee, Y.-H.; Carr, J.R.; Barr, D.J.; Haas, C.J. The fractal dimension as a measure of the roughness of rock discontinuity profiles. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1990, 27, 453–464. [Google Scholar] [CrossRef]
- Nayak, S.R.; Mishra, J.; Palai, G. Analysing roughness of surface through fractal dimension: A review. Image Vis. Comput. 2019, 89, 21–34. [Google Scholar] [CrossRef]
- Brown, S.R. A note on the description of surface roughness using fractal dimension. Geophys. Res. Lett. 1987, 14, 1095–1098. [Google Scholar] [CrossRef]
- Li, Y.R.; Huang, R.Q. Relationship between joint roughness coefficient and fractal dimension of rock fracture surfaces. Int. J. Rock Mech. Min. Sci. 2015, 75, 15–22. [Google Scholar] [CrossRef] [Green Version]
- Hirata, T.; Satoh, T.; Ito, K. Fractal structure of spatial distribution of microfracturing in rock. Geophys. J. Int. 1987, 90, 369–374. [Google Scholar] [CrossRef]
- Xie, H.P.; Liu, J.F.; Ju, Y.; Li, J.G.; Xie, L.Z. Fractal property of spatial distribution of acoustic emissions during the failure process of bedded rock salt. Int. J. Rock Mech. Min. Sci. 2011, 48, 1344–1351. [Google Scholar] [CrossRef]
- Li, W.; Zhao, H.; Wu, H.; Wang, L.; Sun, W.; Ling, X. A novel approach of two-dimensional representation of rock fracture network characterization and connectivity analysis. J. Pet. Sci. Eng. 2019, 184, 106507. [Google Scholar] [CrossRef]
- Hong, K.; Han, E.; Kang, K. Determination of geological strength index of jointed rock mass based on image processing. J. Rock Mech. Geotech. Eng. 2017, 9, 702–708. [Google Scholar] [CrossRef]
- Carr, J.R.; Wardner, J.B. Rock mass classification using fractal dimension. In Proceedings of the 28th US Symposium on Rock Mechanics (USRMS), Tucson, AZ, USA, 29 June–1 July 1987. [Google Scholar]
- Hamdi, E.; du Mouza, J. A methodology for rock mass characterisation and classification to improve blast results. Int. J. Rock Mech. Min. Sci. 2005, 42, 177–194. [Google Scholar] [CrossRef]
- Lian, J.F.; Shen, N.Q.; Zhang, J.K. Application research on fractal theory in rockmass quality evaluation. Chin. J. Rock Mech. Eng. 2001, 20, 1695–1698. [Google Scholar]
- Liu, Y.Z.; Sheng, J.L.; Ge, X.R.; Wang, S.L. Evaluation of rock mass quality based on fractal dimension of rock mass discontinuity distribution. Rock Soil Mech. 2007, 28, 971–975. [Google Scholar]
- Liebovitch, L.S.; Toth, T. A fast algorithm to determine fractal dimensions by box counting. Phys. Lett. A 1989, 141, 386–390. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Ji, H.G.; Li, W.G.; Hou, K.K.; Hao, X.J. Research on Rapid Evaluation of Rock Mass Quality Based on Ultrasonic Borehole Imaging Technology and Fractal Method. Adv. Mater. Sci. Eng. 2021, 2021, 8063665. [Google Scholar] [CrossRef]
- Ai, T.; Zhang, R.; Zhou, H.W.; Pei, J.L. Box-counting methods to directly estimate the fractal dimension of a rock surface. Appl. Surf. Sci. 2014, 314, 610–621. [Google Scholar] [CrossRef]
- Yu, B.M.; Li, J.H. Some fractal characters of porous media. Fractals 2001, 9, 365–372. [Google Scholar] [CrossRef]
- Stigsson, M.; Ivars, D.M. A Novel Conceptual Approach to Objectively Determine JRC Using Fractal Dimension and Asperity Distribution of Mapped Fracture Traces. Rock Mech. Rock Eng. 2018, 52, 1041–1054. [Google Scholar] [CrossRef] [Green Version]
- Sanei, M.; Faramarzi, L.; Goli, S.; Fahimifar, A.; Rahmati, A.; Mehinrad, A. Development of a new equation for joint roughness coefficient (JRC) with fractal dimension: A case study of Bakhtiary Dam site in Iran. Arab. J. Geosci. 2015, 8, 465–475. [Google Scholar] [CrossRef]
- Liu, B.; Wang, R.; Zhao, G.; Guo, X.; Wang, Y.; Li, J.; Wang, S. Prediction of rock mass parameters in the TBM tunnel based on BP neural network integrated simulated annealing algorithm. Tunn. Undergr. Space Technol. 2019, 95, 103103. [Google Scholar] [CrossRef]
- Zhou, J.; Bejarbaneh, B.Y.; Armaghani, D.J.; Tahir, M.M. Forecasting of TBM advance rate in hard rock condition based on artificial neural network and genetic programming techniques. Bull. Eng. Geol. Environ. 2019, 79, 2069–2084. [Google Scholar] [CrossRef]
- Lemy, F.; Hadjigeorgiou, J. Discontinuity trace map construction using photographs of rock exposures. Int. J. Rock Mech. Min. Sci. 2003, 40, 903–917. [Google Scholar] [CrossRef]
- Sonmez, H.; Gokceoglu, C.; Nefeslioglu, H.A.; Kayabasi, A. Estimation of rock modulus: For intact rocks with an artificial neural network and for rock masses with a new empirical equation. Int. J. Rock Mech. Min. Sci. 2006, 43, 224–235. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Wu, Q.M.; Zhang, Q.; Gong, Z.C. Estimation of Rock Mass Rating System with an Artificial Neural Network. In Proceedings of the Advances in Neural Networks—ISNN 2009: 6th International Symposium on Neural Networks, Wuhan, China, 26–29 May 2009. [Google Scholar] [CrossRef]
- Khatik, V.M.; Nandi, A.K. A generic method for rock mass classification. J. Rock Mech. Geotech. Eng. 2018, 10, 102–116. [Google Scholar] [CrossRef]
- He, M.M.; Zhang, Z.Q.; Li, N. Deep Convolutional Neural Network-Based Method for Strength Parameter Prediction of Jointed Rock Mass Using Drilling Logging Data. Int. J. Géoméch. 2021, 21, 04021111. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension; W. H. Freeman and Company: San Francisco, CA, USA, 1977. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Xie, H. Fractals in Rock Mechanics; Balkema: Rotterdam, The Netherlands, 2020. [Google Scholar]
- Falconer, K. Fractal Geometry—Mathematical Foundations and Applications; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Kulatilake, P.H.; Fiedler, R.; Panda, B.B. Box fractal dimension as a measure of statistical homogeneity of jointed rock masses. Eng. Geol. 1997, 48, 217–229. [Google Scholar] [CrossRef]
- Gao, M.-Z.; Zhang, J.-G.; Li, S.-W.; Wang, M.; Wang, Y.-W.; Cui, P.-F. Calculating changes in fractal dimension of surface cracks to quantify how the dynamic loading rate affects rock failure in deep mining. J. Cent. South Univ. 2020, 27, 3013–3024. [Google Scholar] [CrossRef]
- Wang, P. The Network Simulation of Jointed Rock Mass Discontinuities. Master’s Thesis, Tongji University, Shanghai, China, 2008. [Google Scholar]
- Song, L.J. Description of Joint Geometry Character and Study on the Model of Joint Geometric Parameters Based on Fractal Theory. Ph.D. Thesis, Chengdu University of Technology, Chengdu, China, 2013. [Google Scholar]
- Priest, S.D.; Hudson, J. Discontinuity spacings in rock. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1976, 13, 135–148. [Google Scholar] [CrossRef]
- Dong, S.; Yi, X.; Feng, W. Quantitative Evaluation and Classification Method of the Cataclastic Texture Rock Mass Based on the Structural Plane Network Simulation. Rock Mech. Rock Eng. 2018, 52, 1767–1780. [Google Scholar] [CrossRef]
- Chen, S.-H.; Feng, X.-M.; Isam, S. Numerical estimation of REV and permeability tensor for fractured rock masses by composite element method. Int. J. Numer. Anal. Methods Géoméch. 2008, 32, 1459–1477. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P. A new computer code for discrete fracture network modelling. Comput. Geosci. 2013, 36, 292–301. [Google Scholar] [CrossRef]
- Liu, R.C.; Jiang, Y.J.; Li, B.; Wang, X.S. A fractal model for characterizing fluid flow in fractured rock masses based on randomly distributed rock fracture networks. Comput. Geotech. 2015, 65, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Wu, N.; Liang, Z.Z.; Zhang, Z.H.; Li, S.H.; Lang, Y.X. Development and verification of three-dimensional equivalent discrete fracture network modelling based on the finite element method. Eng. Geol. 2022, 306, 106759. [Google Scholar] [CrossRef]
- ISRM. Suggested methods for the quantitative description of discontinuities in rock masses. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1978, 15, 319–368. [Google Scholar]
- Véhel, J.L.; Legrand, P. Signal and Image processing with FracLab. Signal and image processing with FracLab. FRACTAL04, Thinking in Patterns: Complexity and Fractals in Nature. In Proceedings of the 8th International Multidisciplinary Conference, Baia Mare, Romania, 4–6 September 2004. [Google Scholar]
- Celada, B.; Tardáguila, I.; Varona, P.; Rodríguez, A.; Bieniawski, Z. Innovating tunnel design by an improved experience-based RMR system. In Proceedings of the World Tunnel Congress, Foz do Iguaçu, Brazil, 9–15 May 2014. [Google Scholar]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Proceedings of the 1989 IEEE International Joint Conference on Neural Networks, Washington, DC, USA, 18–22 June 1989. [Google Scholar]
- Zhang, Q.; Huang, X.B.; Zhu, H.H.; Li, J.C. Quantitative assessments of the correlations between rock mass rating (RMR) and geological strength index (GSI). Tunn. Undergr. Space Technol. 2019, 83, 73–81. [Google Scholar] [CrossRef]
- Mackay, D.J.C. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Foresee, F.D.; Hagan, M.T. Gauss-Newton approximation to Bayesian learning. In Proceedings of the International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 12 June 1997. [Google Scholar] [CrossRef]
- Guo, L.; Li, X.Z.; Zhou, Y.Y.; Zhang, Y.S. Generation and verification of three-dimensional network of fractured rock masses stochastic discontinuities based on digitalization. Environ. Earth Sci. 2015, 73, 7075–7088. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Wang, X.J.; Zhu, H.H.; Cai, W.Q.; Li, X.J. Estimation of three-dimensional diameter distributions of multiple fracture sets clustered by a multi-level clustering method. Acta Geotech. 2023, 12, 15–31. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, X.J.; Zhu, H.H.; Zhang, K.S.; Li, X.J. Mixture distribution model for three-dimensional geometric attributes of multiple discontinuity sets based on trace data of rock mass. Eng. Geol. 2022, 311, 106915. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, X.J.; He, L.; Tian, L.G. Estimation of Fracture Orientation Distributions from a Sampling Window Based on Geometric Probabilistic Method. Rock Mech. Rock Eng. 2021, 54, 3051–3075. [Google Scholar] [CrossRef]
- Basirat, R.; Goshtasbi, K.; Ahmadi, M. Determination of the Fractal Dimension of the Fracture Network System Using Image Processing Technique. Fractal Fract. 2019, 3, 17. [Google Scholar] [CrossRef] [Green Version]




| No. | Number of Dominant Set (Amount) | Dominant Set | Direction (Normal Distribution) | Trace Length (Lognormal Distribution) | Spacing (Negative Exponential Distribution) (m) | ||
|---|---|---|---|---|---|---|---|
| Mean (°) | Standard Deviation (°) | Mean (m) | Standard Deviation (m) | ||||
| 1# | 3 | 1 | 138.93 | 3.18 | 1.70 | 0.95 | 0.228 |
| 2 | 52.71 | 3.22 | 1.81 | 1.10 | 0.670 | ||
| 3 | 81.34 | 1.67 | 1.99 | 0.67 | 0.292 | ||
| 2# | 2 | 1 | 9.30 | 2.85 | 2.69 | 1.46 | 0.258 |
| 2 | 107.71 | 4.73 | 2.20 | 1.19 | 0.755 | ||
| 3# | 4 | 1 | 114.07 | 4.61 | 0.63 | 1.00 | 1.435 |
| 2 | 49.18 | 2.52 | 2.62 | 1.12 | 0.384 | ||
| 3 | 165.36 | 2.61 | 0.58 | 0.82 | 0.316 | ||
| 4 | 3.70 | 3.11 | 5.54 | 0.60 | 0.223 | ||
| 4# | 2 | 1 | 105.74 | 4.27 | 0.81 | 1.12 | 1.460 |
| 2 | 21.51 | 4.05 | 1.11 | 1.13 | 0.419 | ||
| 5# | 4 | 1 | 135.06 | 3.47 | 4.71 | 1.14 | 0.920 |
| 2 | 9.40 | 2.79 | 3.22 | 1.07 | 0.997 | ||
| 3 | 48.80 | 3.72 | 2.15 | 1.16 | 0.551 | ||
| 4 | 96.11 | 2.78 | 2.18 | 1.40 | 0.324 | ||
| 6# | 2 | 1 | 161.87 | 3.60 | 2.17 | 1.00 | 0.338 |
| 2 | 93.62 | 3.28 | 2.71 | 0.83 | 0.471 | ||
| Rock Mass Integrity | Intact | Less Intact | Less Fractured | Fractured | Very Fractured |
|---|---|---|---|---|---|
| Integrity index Kv | >0.75 | 0.75~0.55 | 0.55~0.35 | 0.35~0.15 | ≤0.15 |
| Fractal dimension D | <0.66 | 0.65~1.40 | 1.40~2.14 | 2.14~2.88 | ≥2.88 |
| No. | Integrity Index Kv | Relative Error (%) | |||
|---|---|---|---|---|---|
| Kvm | Kvp | Kvd | Kvm − Kvp | Kvm − Kvd | |
| 1 | 0.07 | 0.10 | 0.41 | 51.05 | 519.22 |
| 2 | 0.14 | 0.13 | 0.43 | 4.81 | 220.35 |
| 3 | 0.15 | 0.17 | 0.44 | 7.42 | 187.59 |
| 4 | 0.28 | 0.24 | 0.43 | 15.52 | 55.44 |
| 5 | 0.29 | 0.31 | 0.48 | 4.67 | 63.85 |
| 6 | 0.34 | 0.33 | 0.48 | 2.70 | 42.56 |
| 7 | 0.36 | 0.42 | 0.52 | 16.31 | 43.86 |
| 8 | 0.37 | 0.48 | 0.45 | 29.12 | 23.33 |
| 9 | 0.38 | 0.35 | 0.46 | 7.86 | 21.32 |
| 10 | 0.38 | 0.39 | 0.50 | 2.99 | 30.99 |
| 11 | 0.45 | 0.45 | 0.50 | 0.51 | 11.91 |
| 12 | 0.46 | 0.46 | 0.53 | 0.00 | 16.12 |
| 13 | 0.46 | 0.50 | 0.50 | 7.91 | 7.53 |
| 14 | 0.46 | 0.45 | 0.49 | 3.93 | 6.10 |
| 15 | 0.47 | 0.49 | 0.52 | 4.34 | 10.06 |
| 16 | 0.49 | 0.49 | 0.50 | 0.46 | 2.49 |
| 17 | 0.49 | 0.47 | 0.53 | 4.64 | 7.06 |
| 18 | 0.52 | 0.63 | 0.52 | 22.53 | 0.87 |
| 19 | 0.53 | 0.52 | 0.56 | 1.74 | 6.18 |
| 20 | 0.54 | 0.58 | 0.59 | 5.87 | 8.36 |
| 21 | 0.57 | 0.60 | 0.61 | 6.01 | 7.81 |
| 22 | 0.57 | 0.57 | 0.56 | 1.19 | 1.57 |
| 23 | 0.58 | 0.54 | 0.54 | 6.74 | 6.83 |
| 24 | 0.60 | 0.54 | 0.55 | 9.91 | 8.63 |
| 25 | 0.60 | 0.52 | 0.59 | 14.05 | 2.04 |
| 26 | 0.60 | 0.69 | 0.68 | 15.13 | 13.13 |
| 27 | 0.62 | 0.58 | 0.65 | 5.92 | 6.23 |
| 28 | 0.64 | 0.65 | 0.65 | 2.15 | 1.93 |
| 29 | 0.64 | 0.74 | 0.57 | 14.87 | 11.97 |
| 30 | 0.68 | 0.65 | 0.67 | 3.70 | 1.39 |
| 31 | 0.68 | 0.72 | 0.70 | 5.33 | 2.91 |
| 32 | 0.70 | 0.69 | 0.59 | 0.98 | 15.11 |
| 33 | 0.72 | 0.74 | 0.68 | 2.54 | 5.21 |
| 34 | 0.73 | 0.71 | 0.65 | 2.19 | 10.52 |
| 35 | 0.72 | 0.74 | 0.61 | 3.36 | 15.94 |
| 36 | 0.72 | 0.74 | 0.62 | 1.93 | 14.39 |
| 37 | 0.73 | 0.72 | 0.65 | 0.57 | 10.18 |
| 38 | 0.74 | 0.74 | 0.67 | 0.10 | 9.29 |
| 39 | 0.74 | 0.75 | 0.74 | 1.89 | 0.08 |
| Average | 7.51 | 36.68 | |||
| No. | Rating in R3 | Structural Plane Distribution Parameters | Integrity Index Kv | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Continuity | Roughness | Infilling | Weathering | R3 | Number of Dominant Set (Amount) | Direction | Trace Length | Spacing (m) | D | Kvp | Kvm | Relative Error (%) | |||
| Mean (°) | Standard Deviation (°) | Mean (m) | Standard Deviation (m) | ||||||||||||
| a | 4 | 3 | 5 | 3 | 15 | 1 | 64.29 | 1.43 | 2.90 | 1.39 | 0.09 | 1.74 | 0.37 | 0.39 | 5.13 |
| b | 4 | 2 | 2 | 6 | 14 | 2 | 48.06 | 2.60 | 1.08 | 0.72 | 1.85 | 1.01 | 0.68 | 0.65 | 4.62 |
| 82.13 | 1.65 | 0.70 | 0.49 | 1.12 | |||||||||||
| c | 4 | 3 | 2 | 1 | 10 | 2 | 26.00 | 4.58 | 1.71 | 0.61 | 1.58 | 1.10 | 0.63 | 0.63 | 0 |
| 101.09 | 1.51 | 1.51 | 1.12 | 0.58 | |||||||||||
| d | 2 | 1 | 4 | 1 | 8 | 1 | 83.45 | 1.40 | 2.07 | 0.95 | 0.41 | 1.21 | 0.58 | 0.59 | 1.69 |
| e | 5 | 3 | 5 | 5 | 18 | 1 | 67.55 | 3.48 | 0.89 | 0.62 | 1.12 | 0.93 | 0.71 | 0.68 | 4.41 |
| f | 4 | 2 | 0 | 0 | 6 | 1 | 73.27 | 2.40 | 2.25 | 0.66 | 0.79 | 1.07 | 0.59 | 0.58 | 1.72 |
| g | 5 | 5 | 4 | 3 | 17 | 2 | 16.01 | 2.84 | 4.80 | 1.12 | 1.49 | 1.06 | 0.69 | 0.67 | 2.99 |
| 59.35 | 4.60 | 1.11 | 1.41 | 0.4 | |||||||||||
| h | 2 | 3 | 2 | 1 | 8 | 1 | 66.06 | 3.06 | 3.70 | 1.12 | 0.203 | 1.36 | 0.54 | 0.56 | 3.57 |
| i | 4 | 1 | 5 | 1 | 11 | 3 | 55.82 | 1.87 | 4.33 | 0.99 | 0.591 | 1.27 | 0.60 | 0.60 | 0 |
| 7.03 | 4.43 | 4.49 | 1.10 | 1.009 | |||||||||||
| 82.43 | 3.16 | 3.66 | 0.87 | 0.671 | |||||||||||
| j | 5 | 3 | 2 | 0 | 10 | 1 | 16.22 | 4.68 | 0.89 | 0.85 | 1.120 | 0.86 | 0.65 | 0.67 | 2.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Shen, Y.; Pei, Y.; Wang, X.; Wang, M.; Lai, J. Determination of Integrity Index Kv in CHN-BQ Method by BP Neural Network Based on Fractal Dimension D. Fractal Fract. 2023, 7, 546. https://doi.org/10.3390/fractalfract7070546
Zhang Q, Shen Y, Pei Y, Wang X, Wang M, Lai J. Determination of Integrity Index Kv in CHN-BQ Method by BP Neural Network Based on Fractal Dimension D. Fractal and Fractional. 2023; 7(7):546. https://doi.org/10.3390/fractalfract7070546
Chicago/Turabian StyleZhang, Qi, Yixin Shen, Yuechao Pei, Xiaojun Wang, Maohui Wang, and Jingqi Lai. 2023. "Determination of Integrity Index Kv in CHN-BQ Method by BP Neural Network Based on Fractal Dimension D" Fractal and Fractional 7, no. 7: 546. https://doi.org/10.3390/fractalfract7070546






