A Finite-Dimensional Control Scheme for Fractional-Order Systems under Denial-of-Service Attacks
Abstract
1. Introduction
- 1.
- The development of a safety control protocol for discrete-time fractional-order systems subject to external disturbance and DoS attacks is investigated in this article, with the unique properties of fractional-order calculus being taken into account.
- 2.
- The controller proposed is finite-dimensional, which makes it possible to calculate the control input with only a limited number of prior system states, making it suitable for practical use.
- 3.
- A sufficient condition is provided to guarantee the global stability of the closed-loop system, resulting in the system output eventually settling at an ultimate bound around the origin.
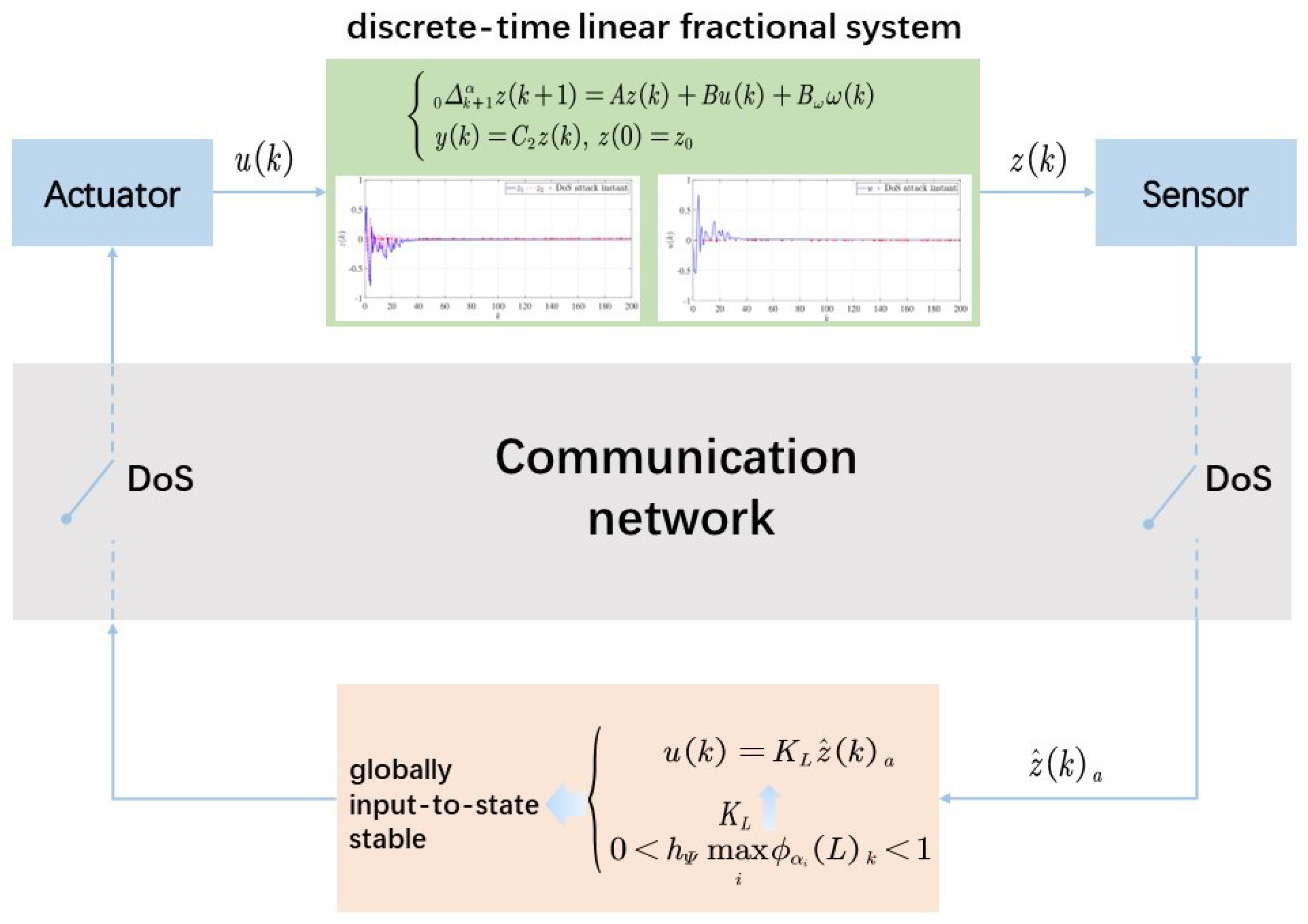
2. Problem Formulation
3. Controller Design
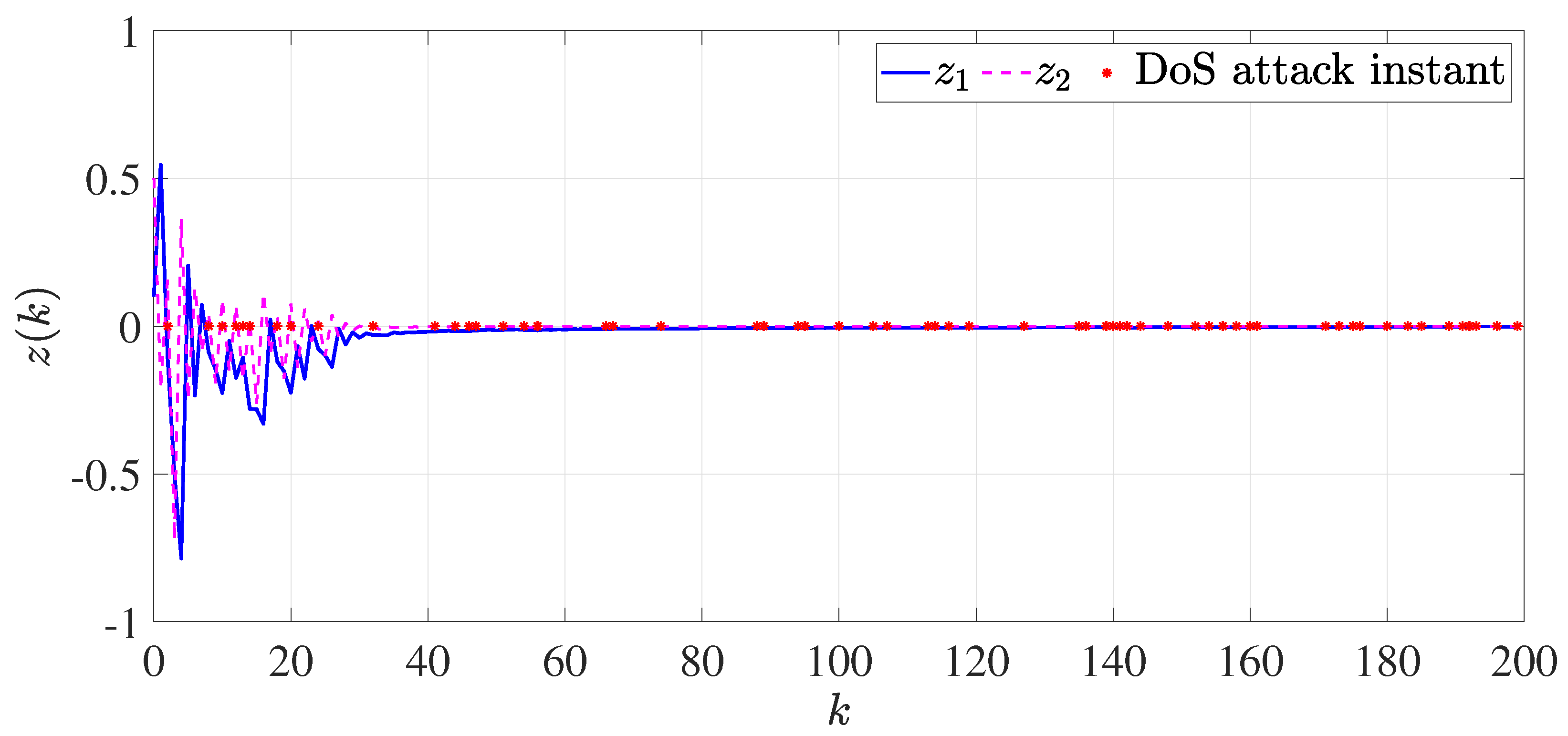
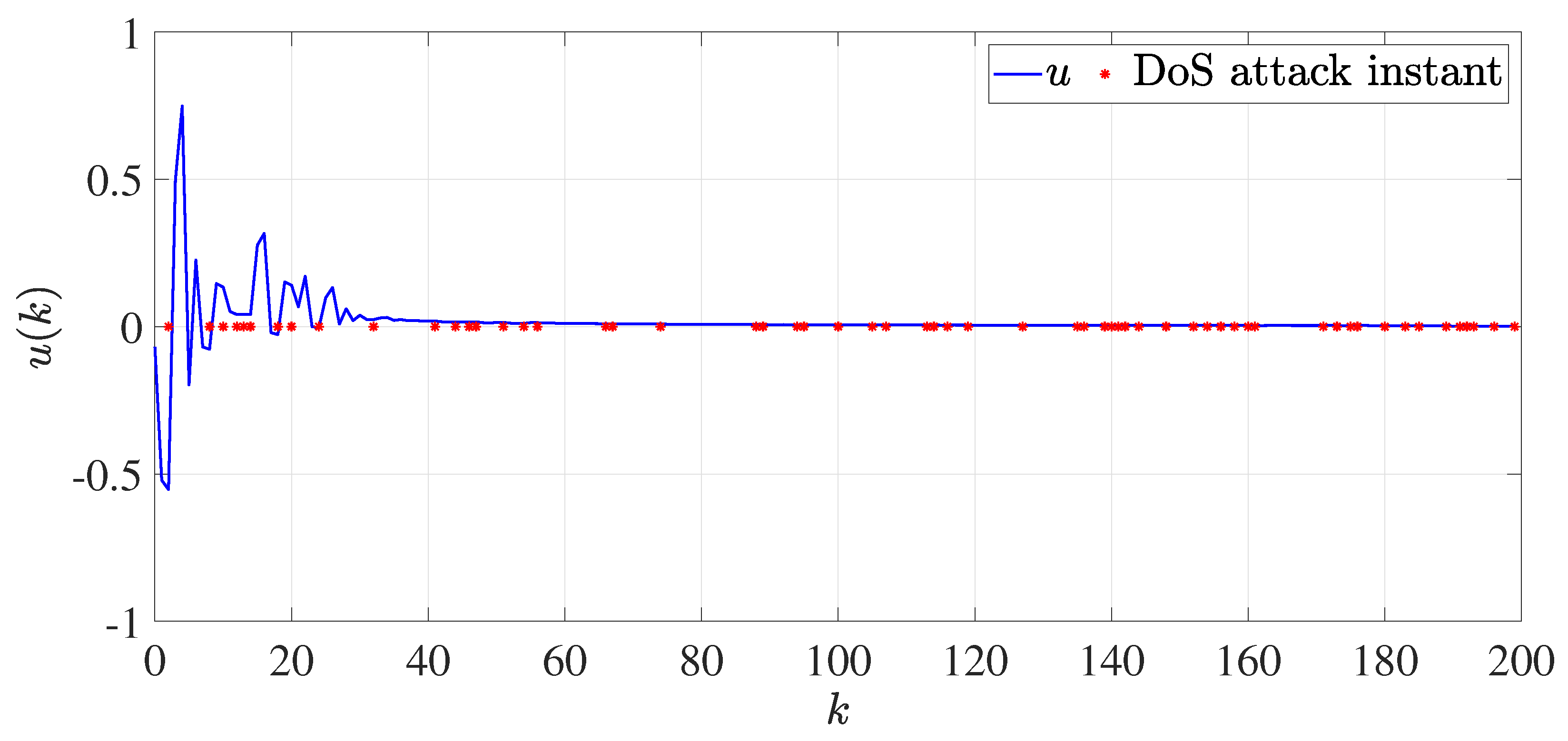
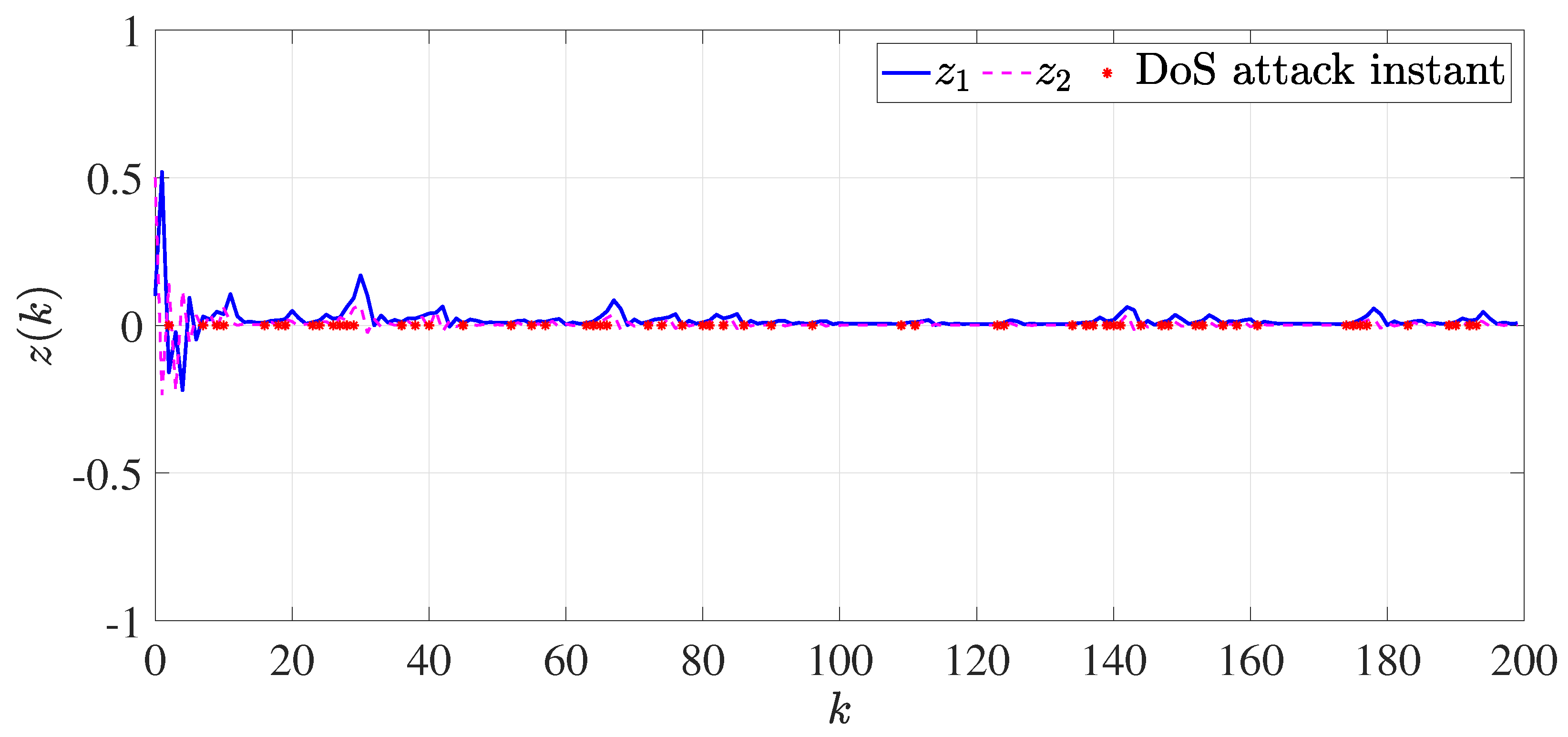
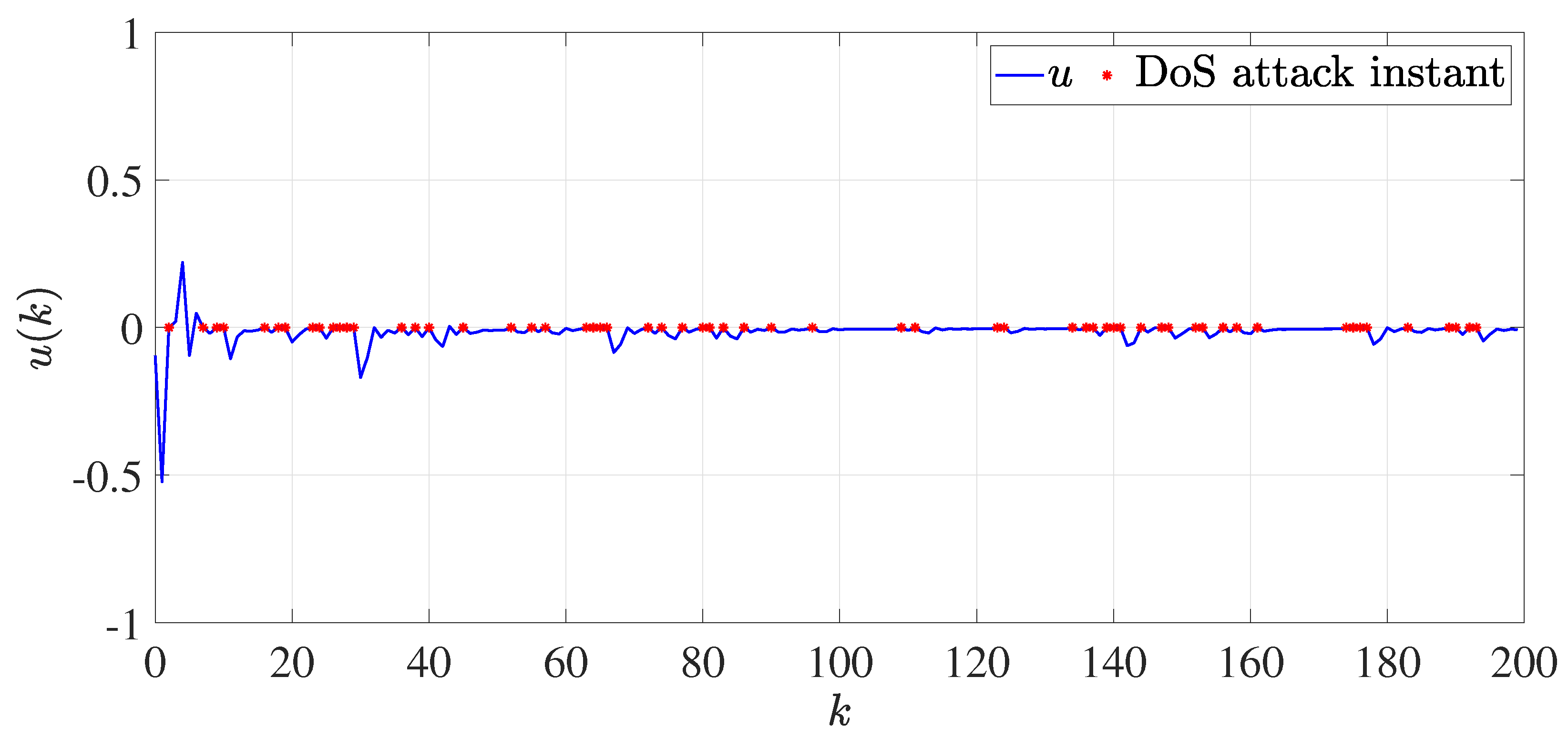
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Koeller, R. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Friedrich, C. Relaxation and retardation functions of the Maxwell model with fractional derivatives. Rheol. Acta 1991, 30, 151–158. [Google Scholar] [CrossRef]
- Cao, H.; Deng, Z.; Li, X.; Yang, J.; Qin, Y. Dynamic modeling of electrical characteristics of solid oxide fuel cells using fractional derivatives. Int. J. Hydrogen Energy 2010, 35, 1749–1758. [Google Scholar] [CrossRef]
- Hammouch, Z.; Mekkaoui, T. Circuit design and simulation for the fractional-order chaotic behavior in a new dynamical system. Complex Intell. Syst. 2018, 4, 251–260. [Google Scholar] [CrossRef]
- Butzer, P.L.; Westphal, U.; Hilfer, R.; West, B.J.; Grigolini, P.; Zaslavsky, G.M.; Douglas, J.F.; Schiessel, H.; Friedrich, C.; Blumen, A.; et al. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000; Volume 35. [Google Scholar]
- Liu, L.; Xue, D.; Zhang, S. General type industrial temperature system control based on fuzzy fractional-order PID controller. Complex Intell. Syst. 2021, 9, 2585–2597. [Google Scholar] [CrossRef]
- Guo, D.; Yang, G.; Feng, X.; Han, X.; Lu, L.; Ouyang, M. Physics-based fractional-order model with simplified solid phase diffusion of lithium-ion battery. J. Energy Storage 2020, 30, 101404. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Chen, Z. Experimental study of fractional-order models for lithium-ion battery and ultra-capacitor: Modeling, system identification, and validation. Appl. Energy 2020, 278, 115736. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Hakkar, N.; Dhayal, R.; Debbouche, A.; Torres, D.F. Approximate controllability of delayed fractional stochastic differential systems with mixed noise and impulsive effects. Fractal Fract. 2023, 7, 104. [Google Scholar] [CrossRef]
- Johnson, M.; Vijayakumar, V. An analysis on the optimal control for fractional stochastic delay integrodifferential systems of order 1 < γ < 2. Fractal Fract. 2023, 7, 284. [Google Scholar] [CrossRef]
- Kavitha, K.; Vijayakumar, V. An analysis regarding to approximate controllability for Hilfer fractional neutral evolution hemivariational inequality. Qual. Theory Dyn. Syst. 2022, 21, 80. [Google Scholar] [CrossRef]
- Guechi, S.; Dhayal, R.; Debbouche, A.; Malik, M. Analysis and optimal control of φ-Hilfer fractional semilinear equations involving nonlocal impulsive conditions. Symmetry 2021, 13, 2084. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ-controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Chen, Y.; Petráš, I.; Xue, D. Fractional order control—A tutorial. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 1397–1411. [Google Scholar] [CrossRef]
- Li, X.; Wen, C.; Liu, X.K. Sampled-data control based consensus of fractional-order multi-agent systems. IEEE Control Syst. Lett. 2021, 5, 133–138. [Google Scholar] [CrossRef]
- Li, X.; Wen, C.; Liu, X.K. Finite-dimensional sampled-data control of fractional-order systems. IEEE Control Syst. Lett. 2022, 6, 181–186. [Google Scholar] [CrossRef]
- Li, X.; Wen, C.; Li, X.; Deng, C. Stabilization for a general class of fractional-order systems: A sampled-data control method. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 4643–4653. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Mittag–Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Liu, H.; Pan, Y.; Li, S.; Chen, Y. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2209–2217. [Google Scholar] [CrossRef]
- Li, X.; Wen, C.; Zou, Y. Adaptive backstepping control for fractional-order nonlinear systems with external disturbance and uncertain parameters using smooth control. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7860–7869. [Google Scholar] [CrossRef]
- Li, X.; He, J.; Wen, C.; Liu, X.K. Backstepping-based adaptive control of a class of uncertain incommensurate fractional-order nonlinear systems With external disturbance. IEEE Trans. Ind. Electron. 2022, 69, 4087–4095. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Xing, L. Backstepping-based adaptive control for uncertain fractional-order nonlinear systems. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 1–4 August 2021; pp. 12–17. [Google Scholar] [CrossRef]
- Li, X.; Wen, C.; Li, X.; He, J. Adaptive fractional-order backstepping control for a general class of nonlinear uncertain integer-order systems. IEEE Trans. Ind. Electron. 2023, 70, 7246–7256. [Google Scholar] [CrossRef]
- Kaczorek, T. Practical stability of positive fractional discrete-time linear systems. Bull. Pol. Acad. Sci. Tech. Sci. 2008, 56, 313–317. [Google Scholar]
- BusłOwicz, M.; Kaczorek, T. Simple conditions for practical stability of positive fractional discrete-time linear systems. Int. J. Appl. Math. Comput. Sci. 2009, 19, 263–269. [Google Scholar] [CrossRef]
- Guermah, S.; Djennoune, S.; Bettayeb, M. A new approach for stability analysis of linear discrete-time fractional-order systems. In New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Dordrecht, The Netherlands, 2010; pp. 151–162. [Google Scholar] [CrossRef]
- Guermah, S.; Djennoune, S.; Bettayeb, M. Discrete-time fractional-order systems: Modeling and stability issues. In Advances in Discrete Time Systems; InTech: London, UK, 2012; pp. 183–212. [Google Scholar] [CrossRef]
- Sopasakis, P.; Ntouskas, S.; Sarimveis, H. Robust model predictive control for discrete-time fractional-order systems. In Proceedings of the 2015 23rd Mediterranean Conference on Control and Automation (MED), Torremolinos, Spain, 16–19 June 2015; pp. 384–389. [Google Scholar] [CrossRef]
- Sopasakis, P.; Sarimveis, H. Stabilising model predictive control for discrete-time fractional-order systems. Automatica 2017, 75, 24–31. [Google Scholar] [CrossRef]
- Alessandretti, A.; Pequito, S.; Pappas, G.J.; Aguiar, A.P. Finite-dimensional control of linear discrete-time fractional-order systems. Automatica 2020, 115, 108512. [Google Scholar] [CrossRef]
- Deng, C.; Wen, C.; Zou, Y.; Wang, W.; Li, X. A hierarchical security control framework of nonlinear CPSs against DoS attacks with application to power sharing of AC microgrids. IEEE Trans. Cybern. 2022, 52, 5255–5266. [Google Scholar] [CrossRef]
- Cárdenas, A.A.; Amin, S.; Sastry, S. Research challenges for the security of control systems. In Proceedings of the 3rd Conference on Hot Topics in Security, San Jose, CA, USA, 29 July 2008; pp. 1–6. [Google Scholar]
- De Persis, C.; Tesi, P. Input-to-state stabilizing control under denial-of-service. IEEE Trans. Autom. Control 2015, 60, 2930–2944. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, G.H. Adaptive fault-tolerant control for nonlinear multi-agent systems with DoS attacks. Inf. Sci. 2020, 526, 39–53. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, L.; Feng, G. Consensus of heterogeneous linear multiagent systems subject to aperiodic sampled-data and DoS attack. IEEE Trans. Cybern. 2019, 49, 1501–1511. [Google Scholar] [CrossRef]
- Feng, Z.; Hu, G. Secure cooperative event-triggered control of linear multiagent systems under DoS attacks. IEEE Trans. Control Syst. Technol. 2020, 28, 741–752. [Google Scholar] [CrossRef]
- Chang, B.; Mu, X.; Yang, Z.; Fang, J. Event-based secure consensus of muti-agent systems under asynchronous DoS attacks. Appl. Math. Comput. 2021, 401, 126120. [Google Scholar] [CrossRef]
- Narayanan, G.; Ali, M.S.; Alsulami, H.; Stamov, G.; Stamova, I.; Ahmad, B. Impulsive security control for fractional-order delayed multi-agent systems with uncertain parameters and switching topology under DoS attack. Inf. Sci. 2022, 618, 169–190. [Google Scholar] [CrossRef]
- Bai, J.; Wu, H.; Cao, J. Secure synchronization and identification for fractional complex networks with multiple weight couplings under DoS attacks. Comput. Appl. Math. 2022, 41, 187. [Google Scholar] [CrossRef]
- Narayanan, G.; Ali, M.S.; Ahamad, S. Cyber secure consensus of discrete-time fractional-order multi-agent systems with distributed delayed control against attacks. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021; pp. 2191–2196. [Google Scholar] [CrossRef]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing; World Scientific: Hackensack, NJ, USA, 2016; Volume 4. [Google Scholar]
- Chatterjee, S.; Romero, O.; Pequito, S. A separation principle for discrete-time fractional-order dynamical systems and its implications to closed-loop neurotechnology. IEEE Control Syst. Lett. 2019, 3, 691–696. [Google Scholar] [CrossRef]
- Jiang, Z.P.; Wang, Y. Input-to-state stability for discrete-time nonlinear systems. Automatica 2001, 37, 857–869. [Google Scholar] [CrossRef]
- Mendes, E.M.; Salgado, G.H.; Aguirre, L.A. Numerical solution of Caputo fractional differential equations with infinity memory effect at initial condition. Commun. Nonlinear Sci. Numer. Simul. 2019, 69, 237–247. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Li, X.; Deng, C.; Wu, X. A Finite-Dimensional Control Scheme for Fractional-Order Systems under Denial-of-Service Attacks. Fractal Fract. 2023, 7, 562. https://doi.org/10.3390/fractalfract7070562
Zou Y, Li X, Deng C, Wu X. A Finite-Dimensional Control Scheme for Fractional-Order Systems under Denial-of-Service Attacks. Fractal and Fractional. 2023; 7(7):562. https://doi.org/10.3390/fractalfract7070562
Chicago/Turabian StyleZou, Ying, Xinyao Li, Chao Deng, and Xiaowen Wu. 2023. "A Finite-Dimensional Control Scheme for Fractional-Order Systems under Denial-of-Service Attacks" Fractal and Fractional 7, no. 7: 562. https://doi.org/10.3390/fractalfract7070562
APA StyleZou, Y., Li, X., Deng, C., & Wu, X. (2023). A Finite-Dimensional Control Scheme for Fractional-Order Systems under Denial-of-Service Attacks. Fractal and Fractional, 7(7), 562. https://doi.org/10.3390/fractalfract7070562









