Adaptive Residual Useful Life Prediction for the Insulated-Gate Bipolar Transistors with Pulse-Width Modulation Based on Multiple Modes and Transfer Learning
Abstract
1. Introduction
1.1. Research Background
1.2. Literature Review for Previous RUL Prediction Models of the IGBT Modules
1.3. Research Highlights
1.4. Contributions of the Paper
1.5. Structure of the Paper
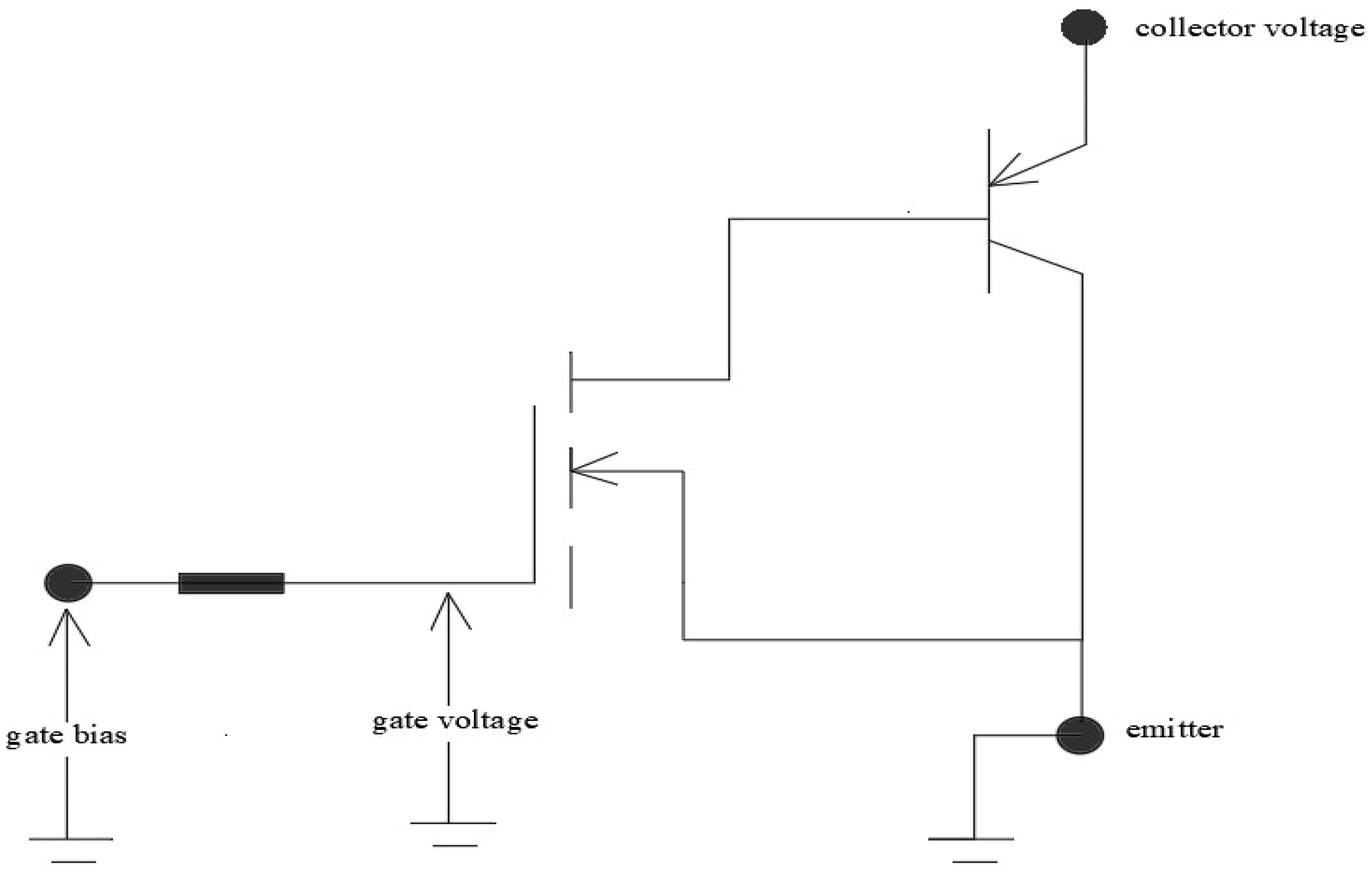
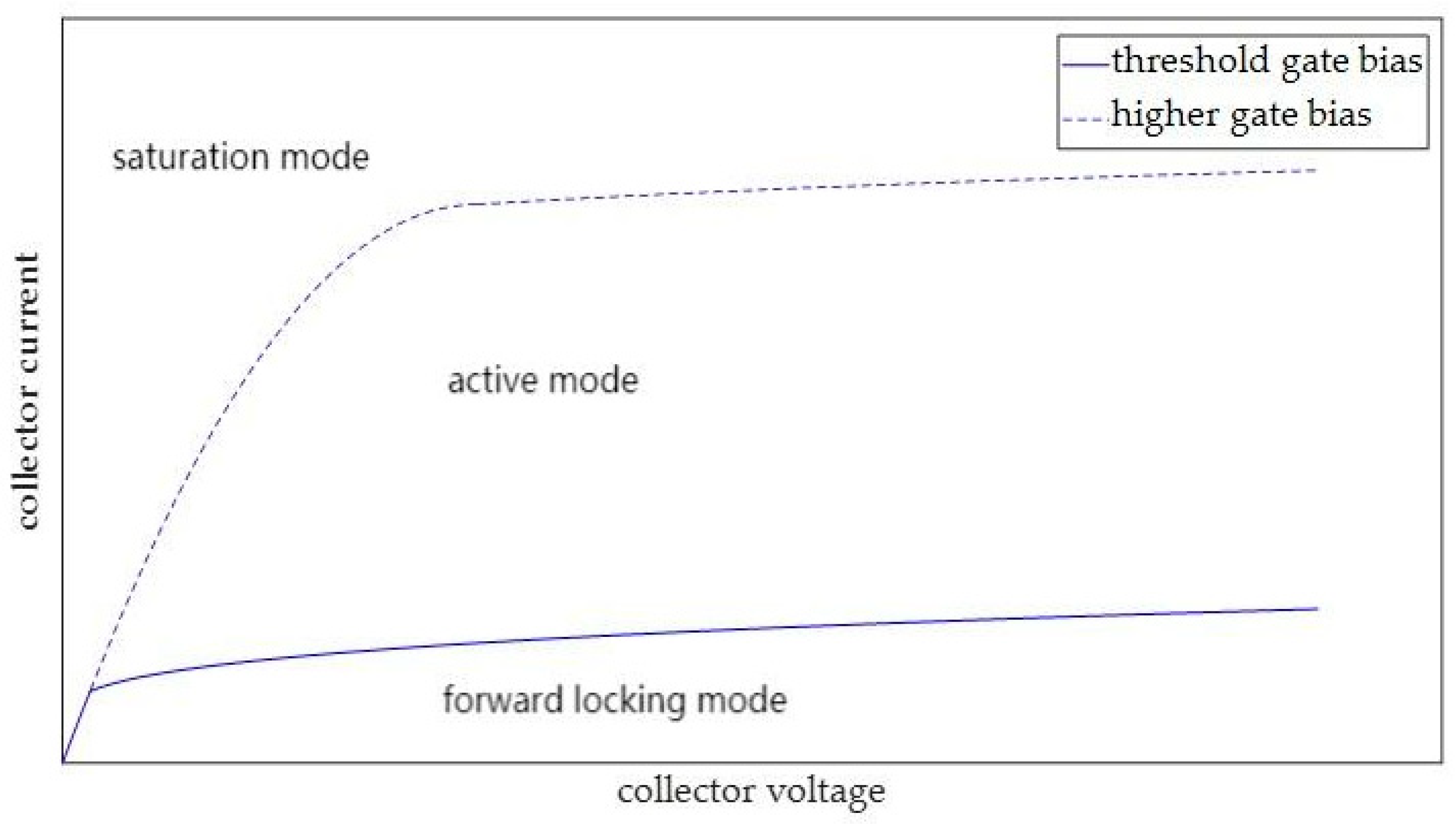
2. Markovian Mode Transition Stochastic Process for the PWM-Controlled IGBT Module
2.1. Occurrence Probabilities Estimation for the PWM-Controlled IGBT Module
2.2. Transfer Learning for the Construction of Markovian Mode Transition Stochastic Process
3. Stochasticity Modeling of the Multi-Modal IGBT Degradation with the fWm
3.1. Statistical Properties of the fWm
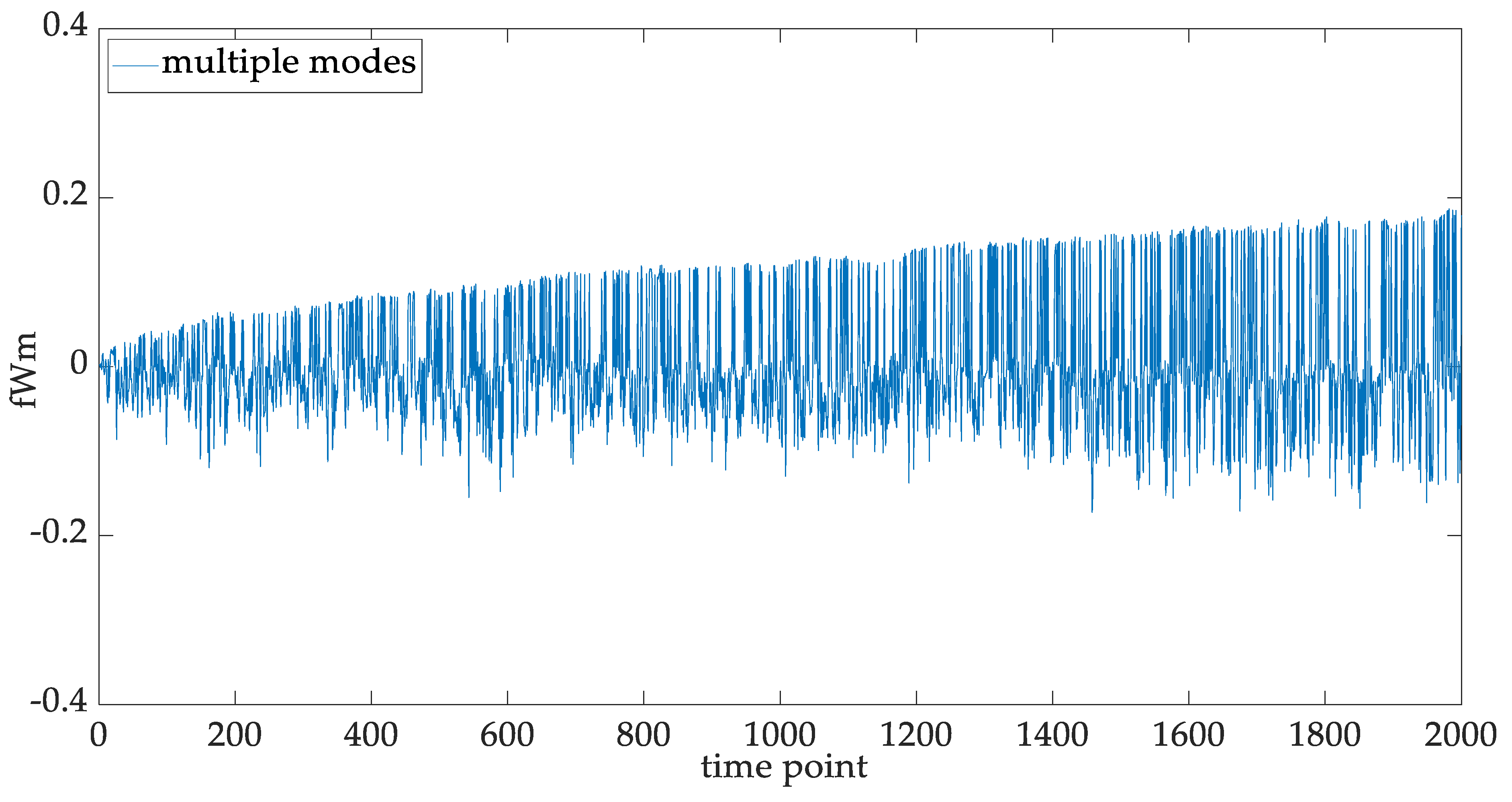
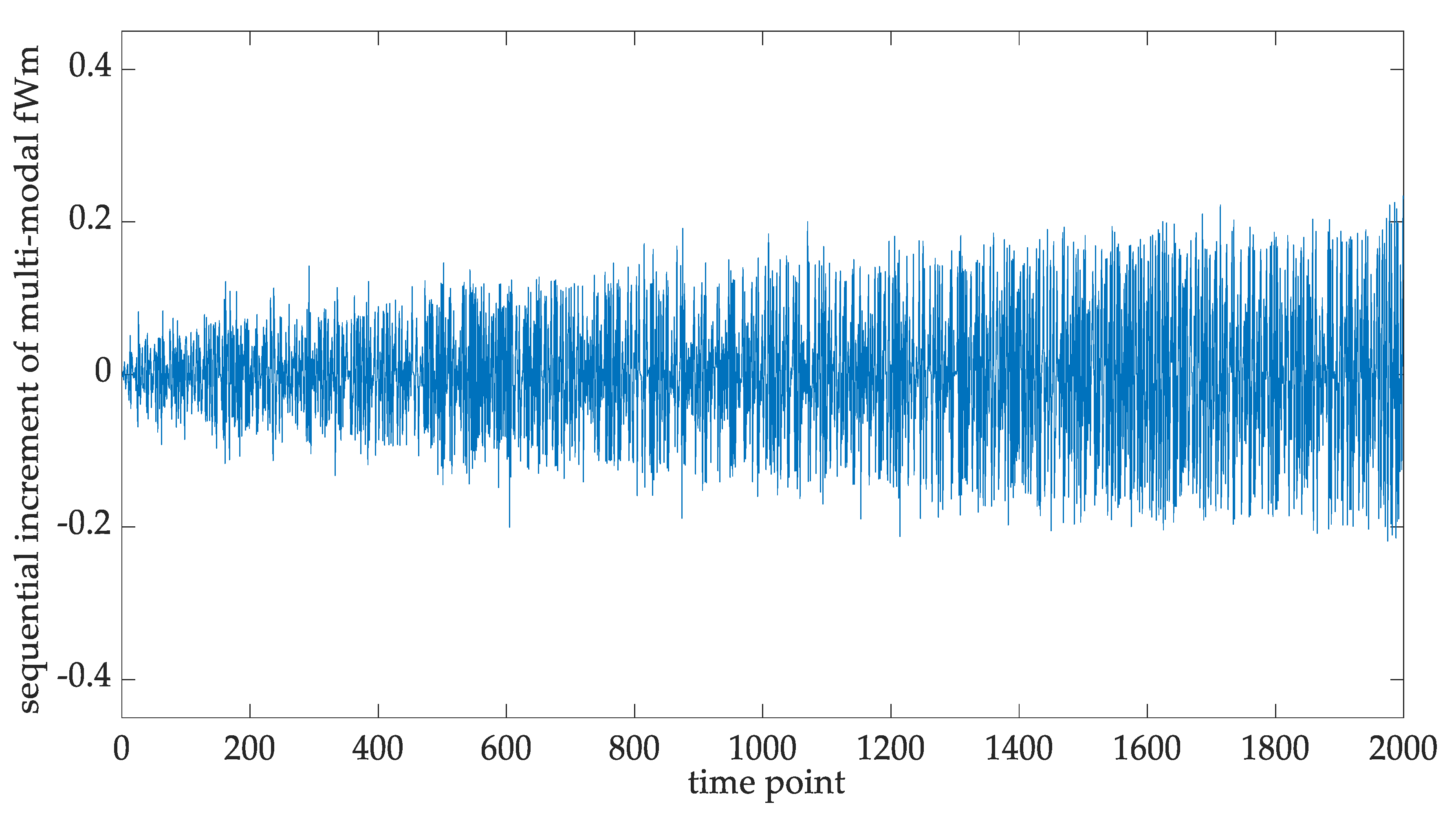
3.2. Stochaticity Modeling for the PWM-Controlled IGBT Modules with Multi-Modal fWm
4. Adaptive RUL Prediction Model for the IGBT Module with PWM Control
4.1. Adaptive Degradation Model with Multiple Modes
4.2. Adaptive RUL Prediction Model for the PWM-Controlled IGBT Module
5. Case Study
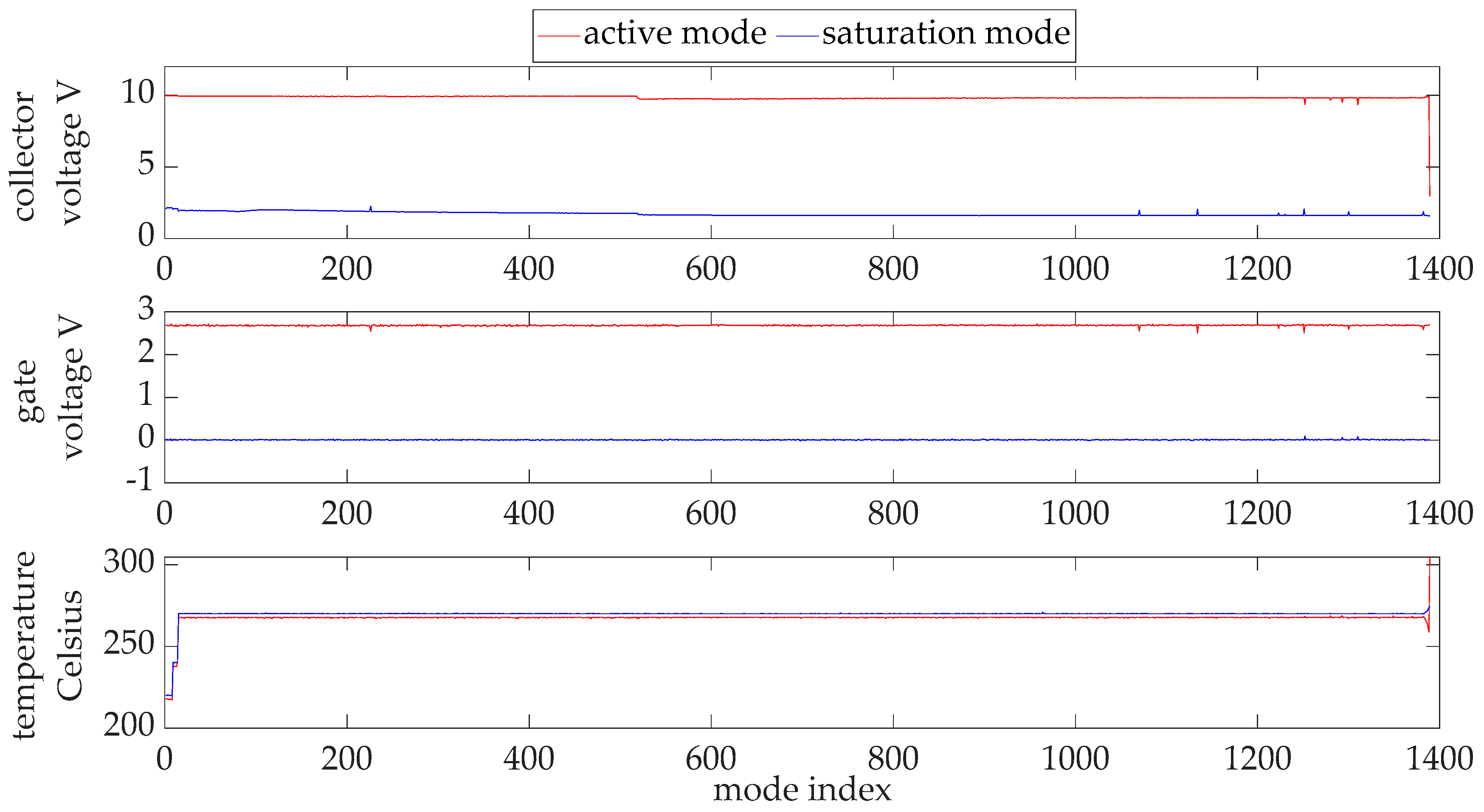
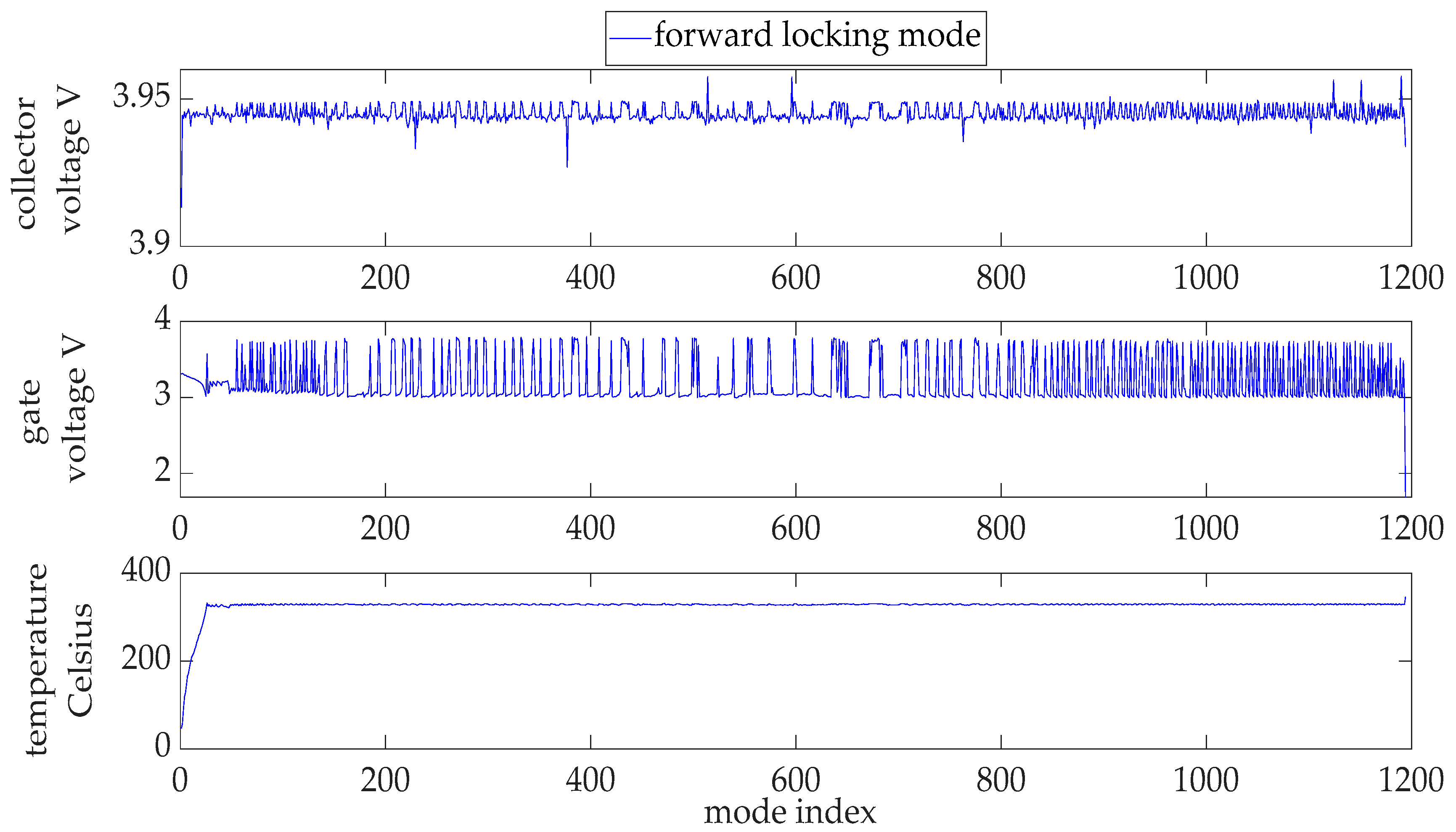
5.1. The Thermal-Accelerated IGBT Aging Data
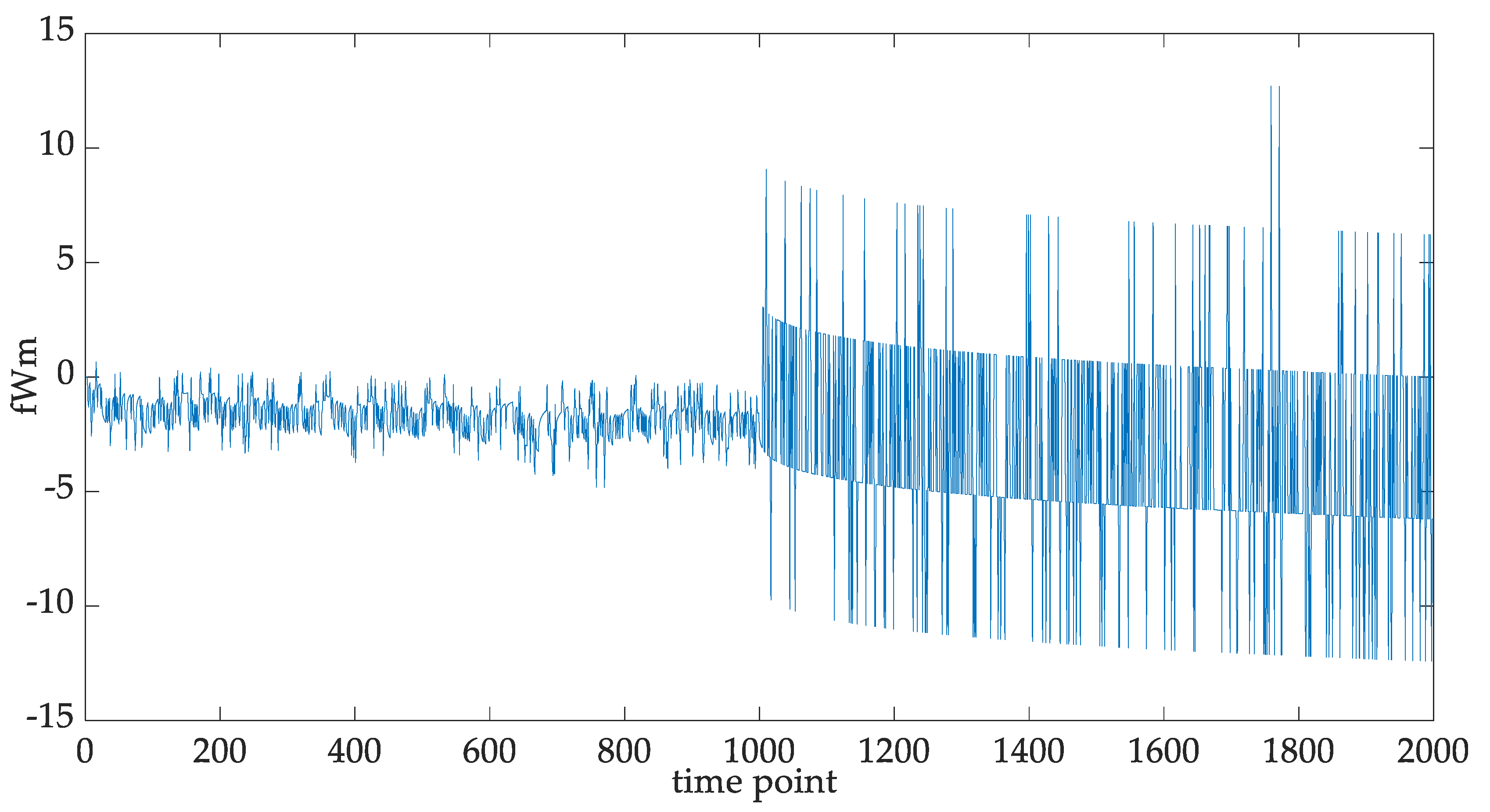
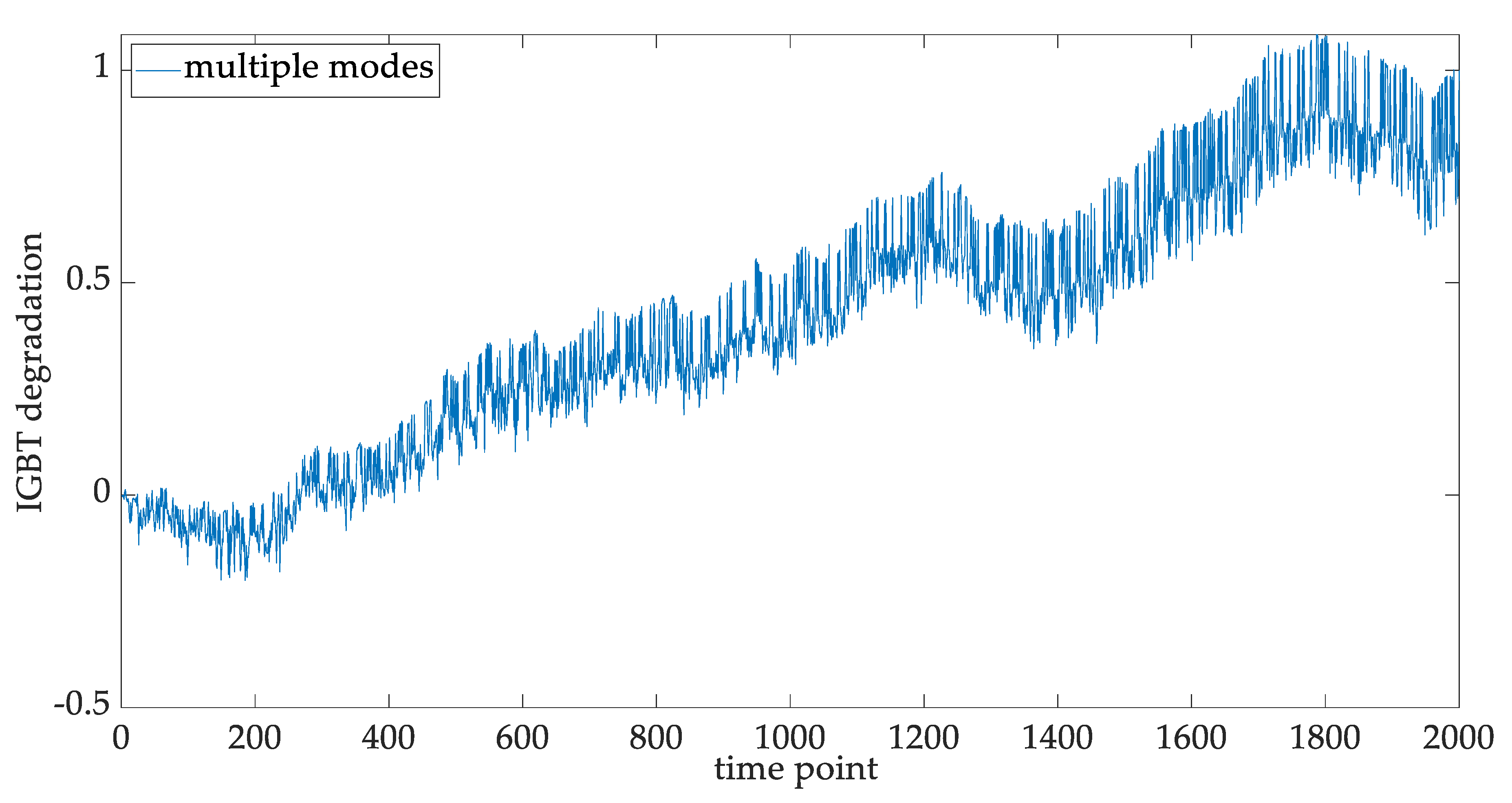
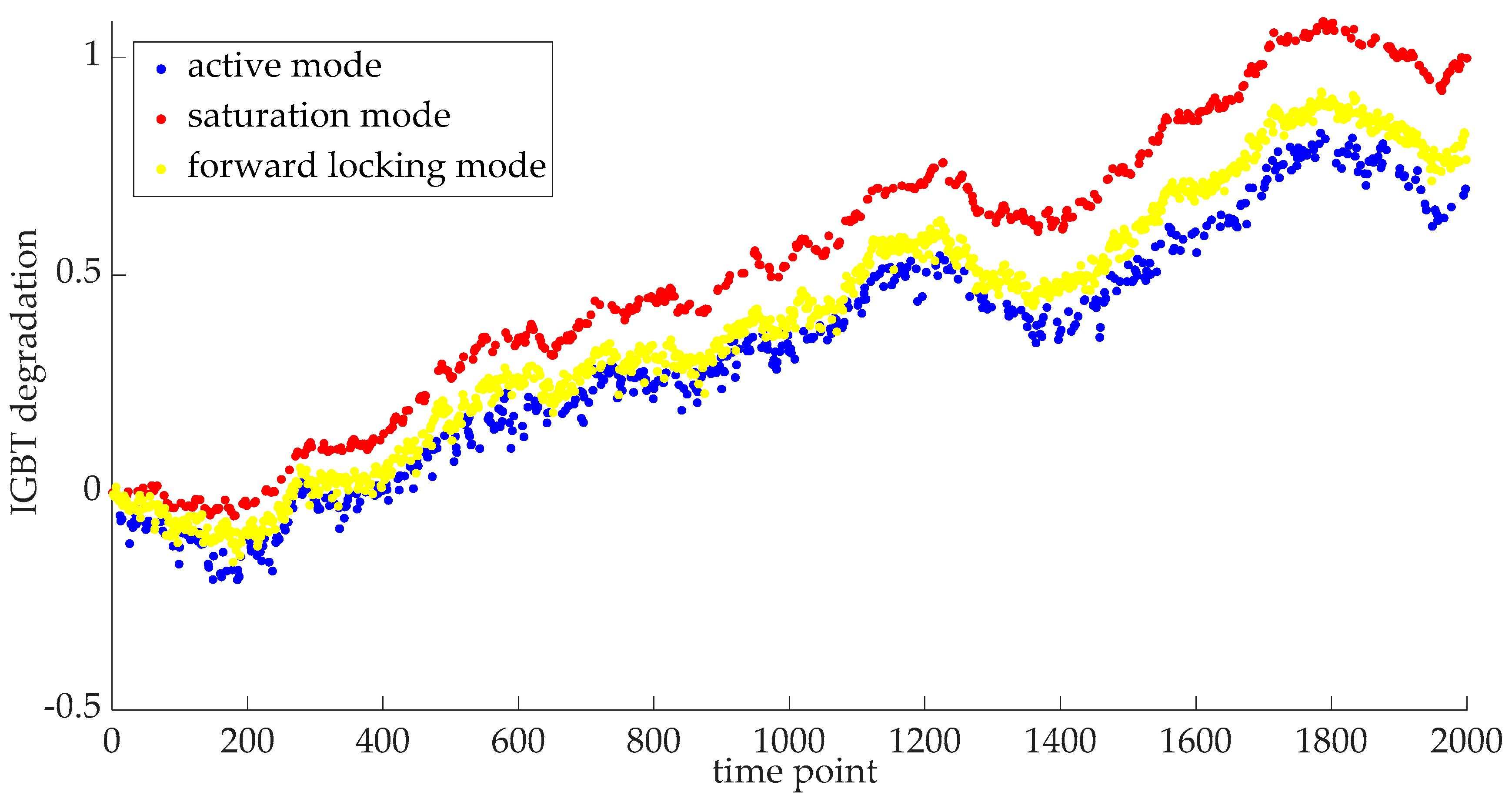
5.2. Mode Separation for the IGBT Degradation Data
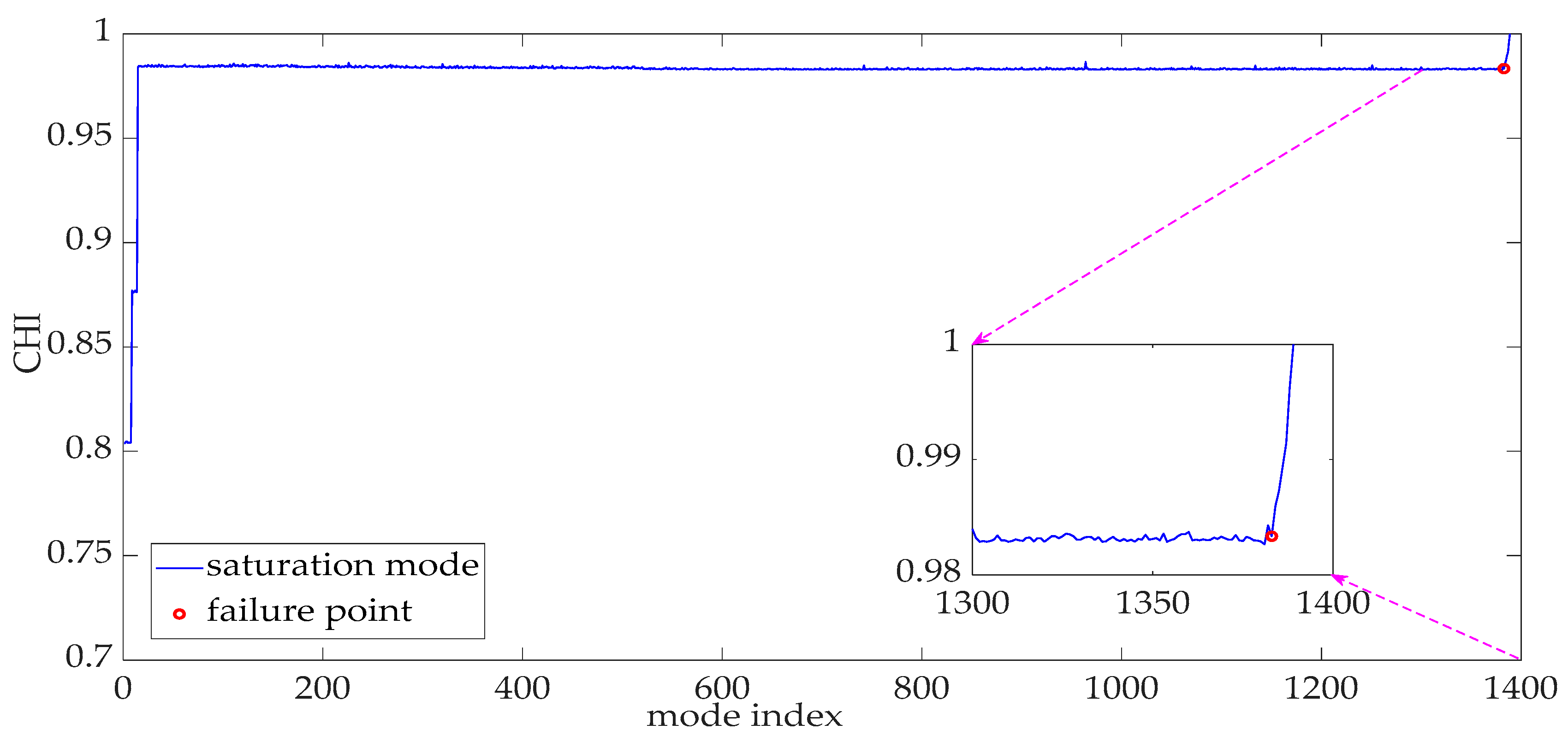
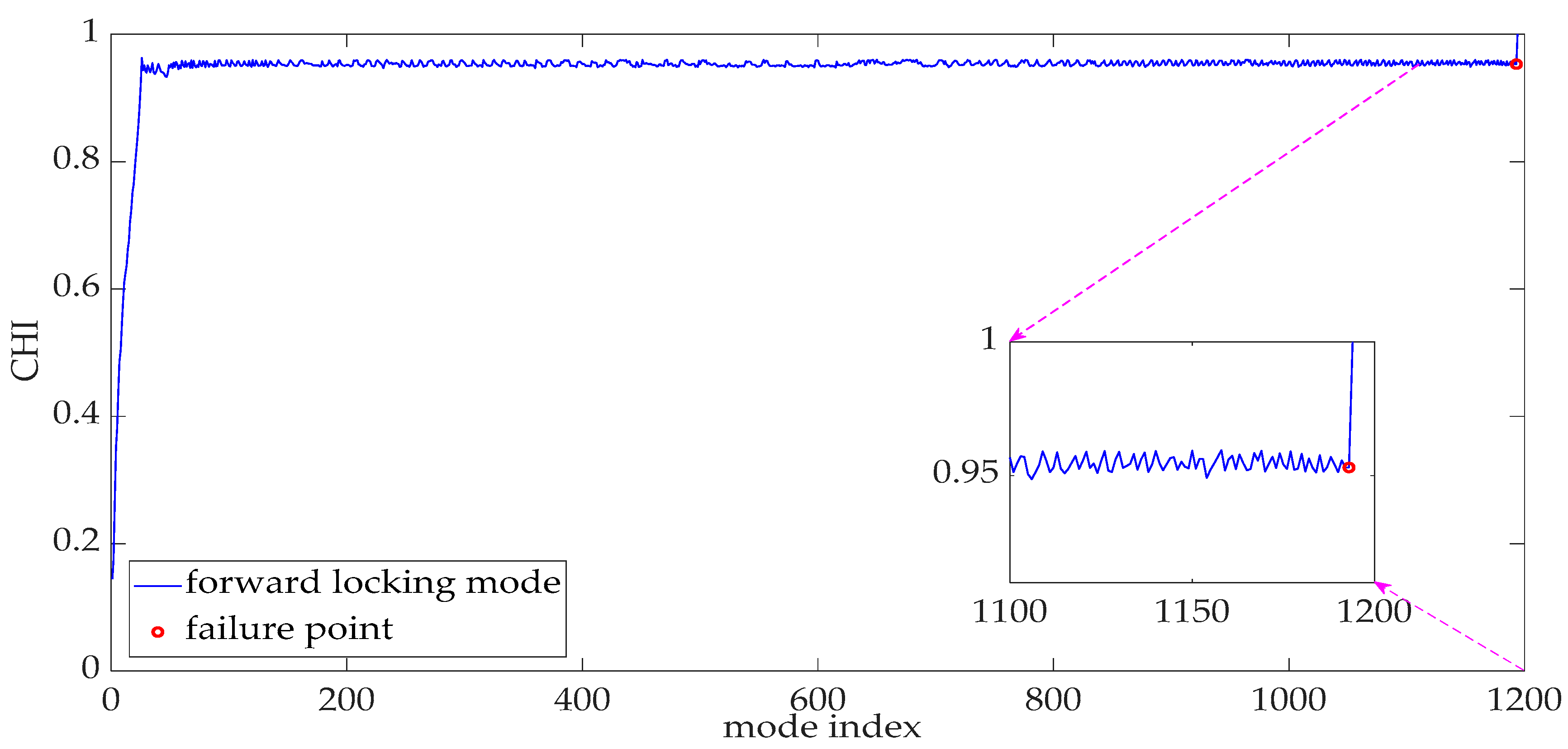
5.3. Multi-Sensor Fusion for the CHI Construction
5.4. Statistical Fitting of the Multi-Modal IGBT Degradation
5.5. Statistical Properties of the Multi-Modal IGBT Degradation
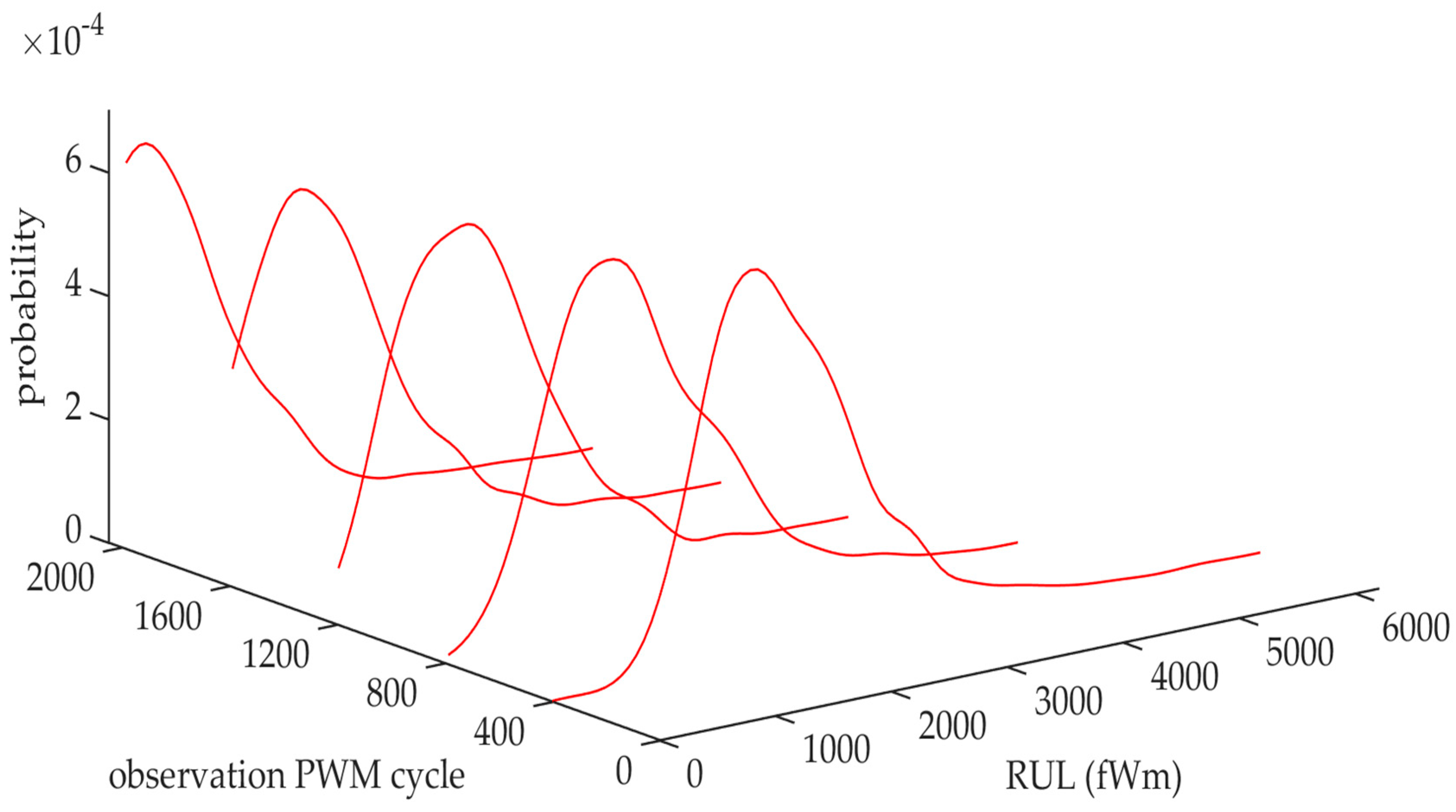
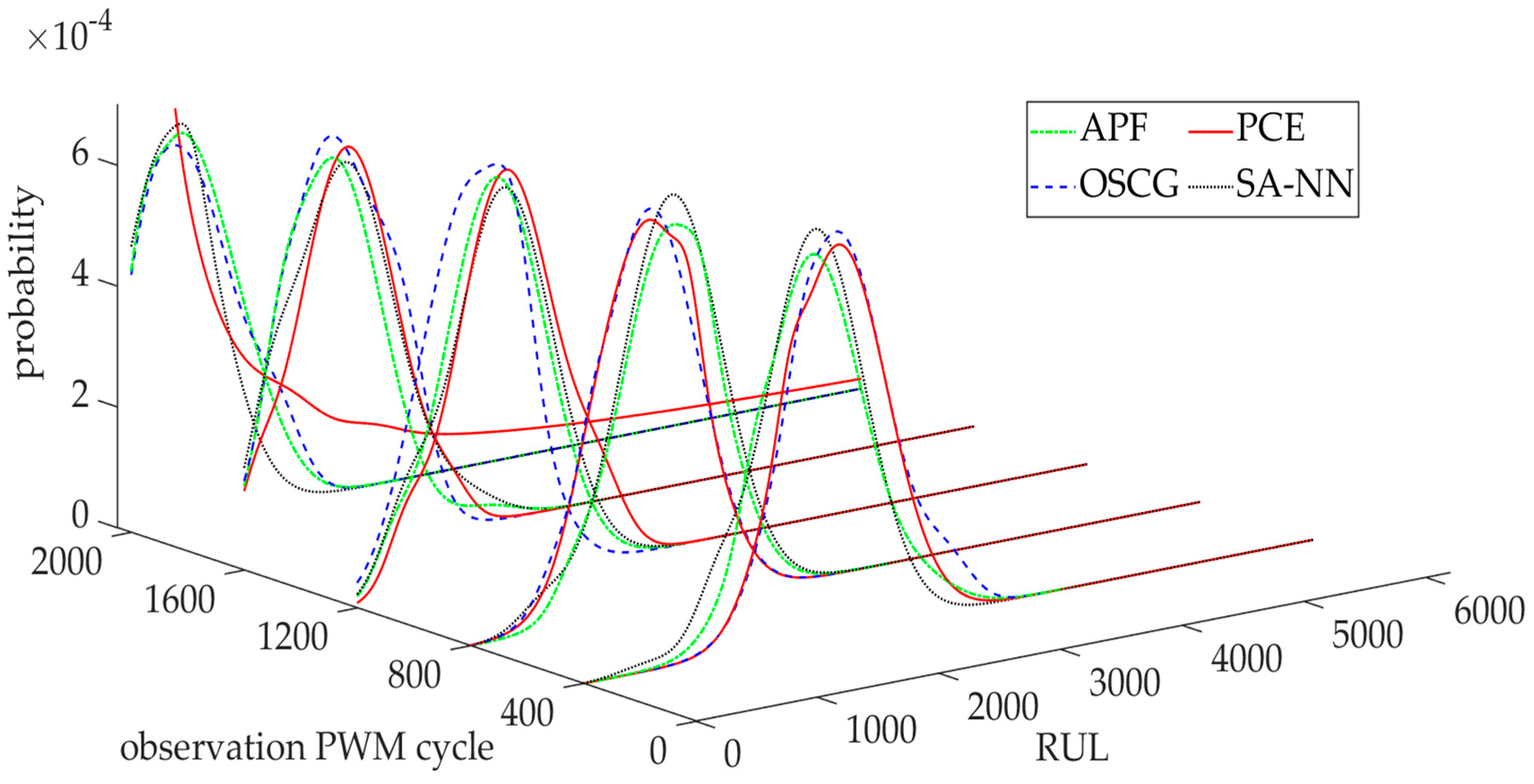
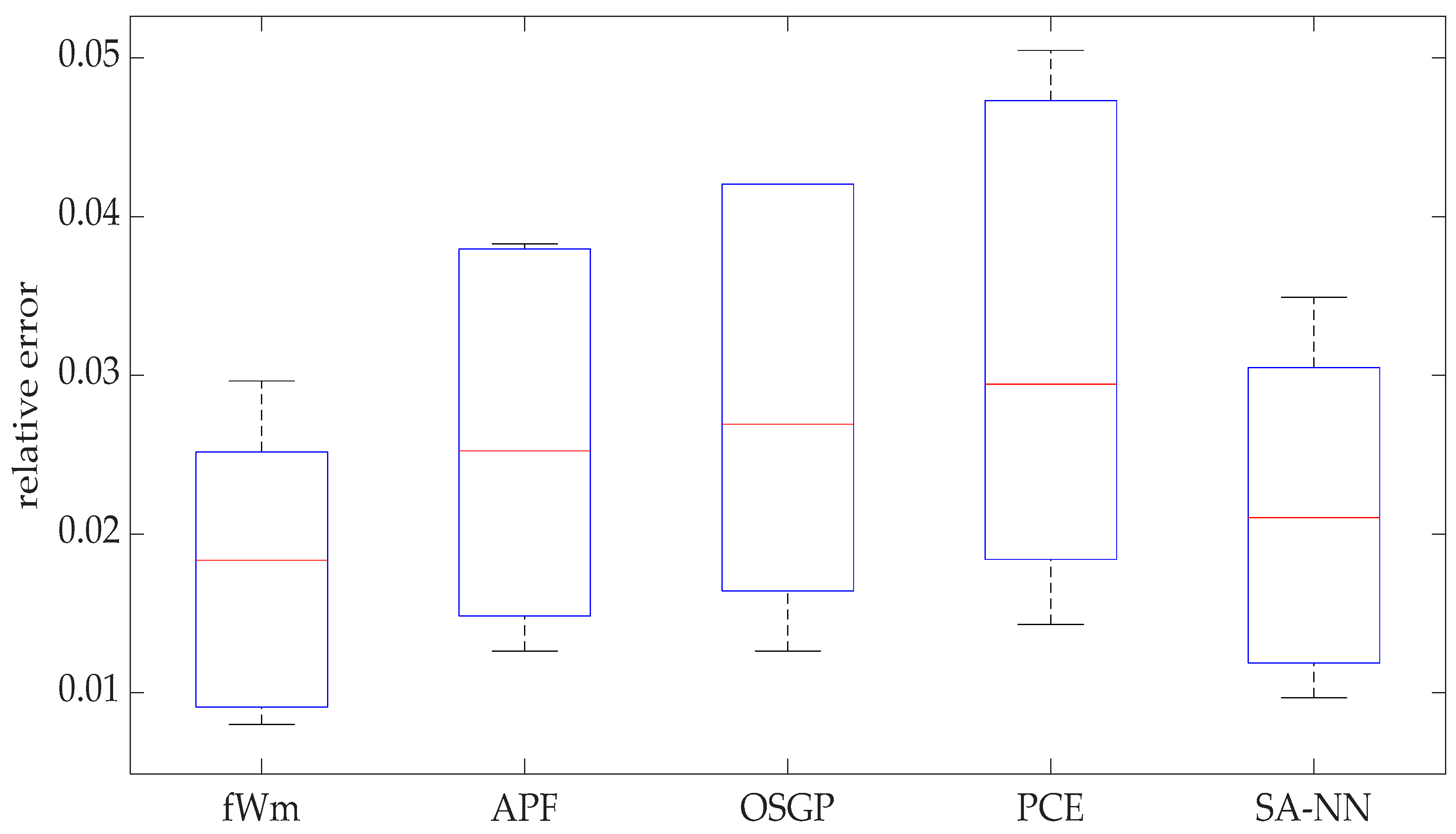
5.6. Performance Evaluation of the Proposed RUL Prediction Model
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IGBT | insulated-gate bipolar transistor |
| PWM | pulse-width modulation |
| RUL | residual useful life |
| APF | auxiliary particle filter |
| SA-NN | self-attention-based neural network |
| OSGP | optimal scale Gaussian process model |
| PCE | Poisson computationally efficient model |
| fWm | fractional Weibull motion |
| CHI | complex health indicator |
| FT | failure threshold |
| EOL | end of life |
| probability density function | |
| RMSE | root mean-squared error |
| MAE | mean absolute error |
| std | standard deviation |
References
- Han, L.B.; Liang, L.; Kang, Y.; Qiu, Y.F. A Review of SiC IGBT: Models, Fabrications, Characteristics, and Applications. IEEE Trans. Power Electron. 2020, 36, 2080–2093. [Google Scholar] [CrossRef]
- Oh, H.; Han, B.; McCluskey, P.; Han, C.; Youn, B.D. Physics-of Failure, Condition Monitoring and Prognostics of Insulated Gate Bipolar Transistor Modules: A Review. IEEE Trans. Power Electron. 2014, 30, 2413–2426. [Google Scholar] [CrossRef]
- Mauro, C. Selected failure mechanisms of modern power modules. Microelectron. Reliab. 2002, 42, 653–667. [Google Scholar] [CrossRef]
- Fischer, K.; Pelka, K.; Puls, S.; Poech, M.H.; Mertens, A.; Bartschat, A.; Tegtmeier, B.; Broer, C.; Wenske, J. Exploring the Causes of Power-Converter Failure in Wind Turbines based on Comprehensive Field-Data and Damage Analysis. Energies 2019, 12, 593. [Google Scholar] [CrossRef]
- Lei, Y.G.; Li, N.P.; Guo, L.; Li, N.B.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Wu, M.Z.; Li, Y.W.; Konstantinou, G. A Comprehensive Review of Capacitor Voltage Balancing Strategies for Multilevel Converters Under Selective Harmonic Elimination PWM. IEEE Trans. Power Electron. 2020, 36, 2748–2767. [Google Scholar] [CrossRef]
- Moinul, S.H.; Seungdeng, C.; Jeihoon, B. Auxiliary Particle Filtering-Based Estimation of Remaining Useful Life of IGBT. IEEE Trans. Power Electron. 2018, 65, 2693–2703. [Google Scholar] [CrossRef]
- Xiao, D.Y.; Qin, C.J.; Ge, J.W.; Xie, P.C.; Huang, Y.X.; Liu, C.L. Self-attention-based adaptive remaining useful life prediction for IGBT with Monte Carlo drop-out. Knowl.-Based Syst. 2022, 239, 107902. [Google Scholar] [CrossRef]
- Li, L.L.; Zhang, X.B.; Tseng, M.L.; Zhou, Y.T. Optimal scale Gaussian process regression model in Insulated Gate Bipolar Transistor remaining life prediction. Appl. Soft Comput. 2019, 78, 261–273. [Google Scholar] [CrossRef]
- Alghassi, A.; Perinpanayagam, S.; Samie, M.; Screenuch, T. Computationally Efficient, Real-Time, and Embeddable Prognostic Techniques for Power Electronics. IEEE Trans. Power Electron. 2015, 30, 2623–2634. [Google Scholar] [CrossRef]
- Xi, X.; Zhou, D.; Chen, M.; Balakrishnan, N. Remaining useful life prediction for fractional degradation processes under varying modes. Can. J. Chem. Eng. 2020, 98, 1351–1364. [Google Scholar] [CrossRef]
- Zhang, H.W.; Zhou, D.H.; Chen, M.Y.; Shang, J. FBM-Based Remaining Useful Life Prediction for Degradation Processes With Long-Range Dependence and Multiple Modes. IEEE Trans. Reliab. 2018, 68, 1021–1033. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Peng, Z.; Guan, Y.; Wu, L.F. A Nonlinear Prediction Method of Lithium-ion Battery Remaining Useful Life Considering Recovery Phenomenon. Int. J. Electrochem. Sci. 2020, 15, 8674–8693. [Google Scholar] [CrossRef]
- Duan, S.W.; Song, W.Q.; Zio, E.; Cattani, C.; Li, M. Product technical life prediction based on multi-modes and fractional Levy stable Motion. Mech. Syst. Signal Process. 2021, 161, 107974. [Google Scholar] [CrossRef]
- Rahimo, M.T.; Shammas, N.Y.A. Freewheeling diode reverse-recovery failure modes in IGBT applications. IEEE Trans. Ind. Appl. 2021, 37, 661–670. [Google Scholar] [CrossRef]
- Hao, J.; Rongshun, J.; Randy, G.; Keisuke, N.; Guangliang, L. Transferring policy of deep reinforcement learning from simulation to reality for robotics. Nat. Mach. Intell. 2022, 4, 1077–1087. [Google Scholar] [CrossRef]
- Ding, Y.F.; Jia, M.P.; Miao, Q.H.; Huang, P. Remaining useful life estimation using deep metric transfer learning for kernel regression. Reliab. Eng. Syst. Saf. 2021, 212, 107583. [Google Scholar] [CrossRef]
- Pan, T.Y.; Chen, J.L.; Ye, Z.S.; Li, A.M. A multi-head attention network with adaptive meta-transfer learning for RUL prediction of rocket engines. Reliab. Eng. Syst. Saf. 2022, 225, 108610. [Google Scholar] [CrossRef]
- Pan, D.W.; Li, H.F.; Wang, S.J. Transfer Learning-Based Hybrid Remaining Useful Life Prediction for Lithium-Ion Batteries Under Different Stresses. IEEE Trans. Instrum. Meas. 2022, 71, 3501810. [Google Scholar] [CrossRef]
- Makogin, V.; Oesting, M.; Rapp, A.; Spodarev, E. Long range dependence for stable random processes. J. Time Ser. Anal. 2020, 42, 161–185. [Google Scholar] [CrossRef]
- Wang, W.B.; Carr, M.; Xu, W.J.; Kobbacy, K. A model for residual life prediction based on Brownian motion with an adaptive drift. Microelectron. Reliab. 2011, 51, 285–293. [Google Scholar] [CrossRef]
- Li, Q.; Ma, Z.H.; Li, H.K.; Liu, X.J.; Guan, X.C.; Tian, P.H. Remaining useful life prediction of mechanical system based on performance evaluation and geometric fractional Lévy stable motion with adaptive nonlinear drift. Mech. Syst. Signal Process. 2023, 184, 109679. [Google Scholar] [CrossRef]
- Wang, H.; Ma, X.B.; Zhao, Y. An improved Wiener process model with adaptive drift and diffusion for online remaining useful life prediction. Mech. Syst. Signal Process. 2019, 127, 370–387. [Google Scholar] [CrossRef]
- Li, T.M.; Si, X.S.; Pei, H.; Sun, L. Data-model interactive prognosis for multi-sensor monitored stochastic degrading devices. Mech. Syst. Signal Process. 2022, 167, 108526. [Google Scholar] [CrossRef]
- Rao, Z.; Huang, M.; Zha, X.M. IGBT Remaining Useful Life Prediction Based on Particle Filter With Fusing Precursor. IEEE Access 2020, 8, 154281–154289. [Google Scholar] [CrossRef]
- Bayraktav, E.; Poor, V.H.; Rao, R. Prediction and tracking of long-range dependent sequences. Syst. Control Lett. 2005, 54, 1083–1090. [Google Scholar] [CrossRef]
- Li, K.X. Stochastic delay fractional evolution equations driven by fractional Brownian motion. Math. Methods Appl. Sci. 2015, 38, 158291. [Google Scholar] [CrossRef]
- Sonnenfeld, G.; Goebel, K.; Celaya, J. An Agile Accelerated Aging, Characterization and Scenario Simulation System for Gate Controlled Power Transistors. In Proceedings of the 43rd Annual IEEE AUTOTESTCON Conference, Salt Lake City, UT, USA, 31 October 2008. [Google Scholar] [CrossRef]
- Chen, Z.H.; Zheng, S.R. Lifetime Distribution Based Degradation Analysis. IEEE Trans. Reliab. 2005, 54, 3–10. [Google Scholar] [CrossRef]
- Paparoditis, E.; Politis, D.N. The asymptotic size and power of the augmented Dickey-Fuller test for a unit root. Econom. Rev. 2018, 37, 955–973. [Google Scholar] [CrossRef]
- Serroukh, A.; Walden, A.T.; Percival, D.B. Statistical Properties and Uses of the Wavelet Variance Estimator for the Scale Analysis of Time Series. J. Am. Stat. Assoc. 2000, 95, 184–196. [Google Scholar] [CrossRef]
- Chaari, R.; Briat, O.; Vinassa, J.M. Capacitance recovery analysis and modelling of supercapacitors during cycling ageing tests. Energy Convers. Manag. 2014, 82, 37–45. [Google Scholar] [CrossRef]
- Rao, K.S.; Mohapatra, Y.N. Disentangling degradation and auto-recovery of luminescence in Alq(3) based organic light emitting diodes. J. Lumin. 2014, 145, 793–796. [Google Scholar] [CrossRef]
- Kleeberger, V.B.; Barke, M.; Werner, C.; Schmitt, L.D.; Schlichtmann, U. A compact model for NBTI degradation and recovery under use profile variations and its application to aging analysis of digital integrated circuits. Microelectron. Reliab. 2014, 54, 1083–1089. [Google Scholar] [CrossRef]










| Weibull | Exponential | Gaussian | Lognormal | |
|---|---|---|---|---|
| RMSE | 17.0788 | 128.1649 | 70.4507 | 71.0164 |
| 0.9812 | 0 | 0.6796 | 0.6745 |
| Weibull | Exponential | Gaussian | Lognormal | |
|---|---|---|---|---|
| RMSE | 19.7875 | 23.2325 | 22.4567 | 22.5057 |
| 0.2684 | 0 | 0.0577 | 0.0536 |
| Weibull | Exponential | Gaussian | Lognormal | |
|---|---|---|---|---|
| RMSE | 10.3302 | 13.5106 | 12.8000 | 13.0980 |
| 0.4075 | 0 | 0.0903 | 0.0475 |
| Active Mode | Saturation Mode | Forward Locking Mode | |
|---|---|---|---|
| skewness | −9.6191 | −10.5156 | −9.4602 |
| kurtosis | 109.1250 | 115.7426 | 101.8027 |
| Hurst exponent | 0.8644 | 0.9981 | 0.6399 |
| Maximum | Mean | Std | MAE | RMSE | |
|---|---|---|---|---|---|
| fWm | 0.0296 | 0.0178 | 0.0092 | 42.3548 | 46.6874 |
| APF | 0.0383 | 0.0259 | 0.0120 | 61.6 | 66.7083 |
| OSGP | 0.0421 | 0.0283 | 0.0136 | 67.2 | 73.1574 |
| PCE | 0.0505 | 0.0320 | 0.0159 | 76.2 | 83.3847 |
| SA-NN | 0.0349 | 0.0214 | 0.0107 | 51 | 55.8194 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, W.; Gao, Y.; Song, W.; Zio, E.; Li, G.; Liu, J.; Kudreyko, A. Adaptive Residual Useful Life Prediction for the Insulated-Gate Bipolar Transistors with Pulse-Width Modulation Based on Multiple Modes and Transfer Learning. Fractal Fract. 2023, 7, 614. https://doi.org/10.3390/fractalfract7080614
Deng W, Gao Y, Song W, Zio E, Li G, Liu J, Kudreyko A. Adaptive Residual Useful Life Prediction for the Insulated-Gate Bipolar Transistors with Pulse-Width Modulation Based on Multiple Modes and Transfer Learning. Fractal and Fractional. 2023; 7(8):614. https://doi.org/10.3390/fractalfract7080614
Chicago/Turabian StyleDeng, Wujin, Yan Gao, Wanqing Song, Enrico Zio, Gaojian Li, Jin Liu, and Aleksey Kudreyko. 2023. "Adaptive Residual Useful Life Prediction for the Insulated-Gate Bipolar Transistors with Pulse-Width Modulation Based on Multiple Modes and Transfer Learning" Fractal and Fractional 7, no. 8: 614. https://doi.org/10.3390/fractalfract7080614
APA StyleDeng, W., Gao, Y., Song, W., Zio, E., Li, G., Liu, J., & Kudreyko, A. (2023). Adaptive Residual Useful Life Prediction for the Insulated-Gate Bipolar Transistors with Pulse-Width Modulation Based on Multiple Modes and Transfer Learning. Fractal and Fractional, 7(8), 614. https://doi.org/10.3390/fractalfract7080614











