Abstract
In this paper, global dynamics of fractional-order discrete maps is analyzed by an extended generalized cell mapping (EGCM) method. Considering the lack of valid global analysis methods, the EGCM method is used to explore the global dynamics for fractional-order discrete maps. Firstly, considering the slowly convergence speed of solution of fractional-order discrete maps, the one-step mapping time of the EGCM method should be sufficient long to guarantee the precision of the results. Secondly, global dynamics of three typical fractional-order discrete maps is analyzed by the EGCM method. The stable and the unstable invariant sets can be obtained by the method. The results confirm their previous results, and furthermore obtain the global dynamics in the interesting region which includes attractors, saddles, basin boundaries and domains of attraction. These indicate that the EGCM method is also valid and efficient for fractional-order discrete maps.
1. Introduction
Fractional calculus was proposed in the 17th century and is thought to be the generalization of classical calculus. The early studies of fractional calculus are very slow and mainly focus on the theories of pure mathematics. Fractional calculus has received more and more attentions in recent decades. Compared with classical calculus, fractional calculus for modeling many practical problems is a powerful and effective tool to deal with the memory and heredity in processes. For a dynamical system with fractional calculus operator, the derivative order can be taken as a system parameter which can enrich and complicate the dynamics of a system [1]. Therefore, fractional-order systems can enhance the security of information and usually are used in the secure communication. Moreover, rich dynamical behaviors also exist in numerous fractional-order nonlinear systems.
fractional-order systems including continuous systems and discrete maps are mainly studied deeply by many researchers. The research history of fractional-order continuous systems is almost as long as the integer-order nonlinear systems. However, the fractional-order discrete maps have drawn attention only in the last decade. Recently, a number of maps with discrete fractional calculus were proposed and analyzed, such as Logistic map, Lorenz map, Lozi map, sine map, and so on [2,3,4,5,6,7,8,9]. In Refs. [10,11,12], researchers attempted to establish an elementary discrete fractional calculus theory framework. The discrete fractional calculus compared with the continuous ones can avoid the computational errors caused by the numerical discretization [13]. Therefore, the investigation of discrete maps with fractional calculus is very vital for the development of fractional dynamics.
In the field of nonlinear dynamics, global dynamics analysis is very important for a dynamical system. For the purpose of having a comprehensive understanding of the behavior of a nonlinear dynamical system, it is necessary to detect a lot of trajectories beginning with different initial conditions in the state space and obtain the corresponding flow modes in the space. Generally speaking, the trajectories finally come to stay in some stable states, namely, the attractors. If global analysis of a dynamical system needs to be obtained, all of these results have to be determined. As we known that numerical computation plays a crucial part in solving complex engineering problems, and is the main approach for global analysis of a nonlinear system. The cell mapping method has its advantages in this respect. In the early 1980′s, a global analysis method based on the cell mapping methodology was proposed by C. S. Hsu for nonlinear integer-order systems [14]. Then, Hsu introduced the Markov chain theory to the method in [15,16], namely, the generalized cell mapping (GCM) method. Stable and unstable states for a dynamics system can be obtained by GCM method. Subsequently, the method was further developed by many researchers. In [17,18], a point mapping under cell reference method was developed which can avoid the error generated by the roughness of the cells. A generalized cell mapping digraphs method based on the GCM and digraph theory was presented in [19]. Considering the complexity of global dynamics analysis for higher-dimensional dynamical systems, a parallel subdomain synthesis of cell mapping method was developed in [20]. Nowadays, the GCM method is a valid global dynamics analysis tool for classical continuous and discrete dynamical systems.
In [21], authors studied the dynamics of sine and standard maps in fractional form. In which, they chose 121 different initial conditions and plotted the corresponding stable states in one Figure. The authors attempted to explore the dynamics of fractional-order discrete maps from a global perspective. So far, the report of global dynamics of fractional-order discrete maps is very few. The primary cause is that the operator of fractional calculus has the non-local property. It is very fit for modeling practical issues in nature and science but a challenge for numerical calculation which will cause the huge computation time. Therefore, effective numerical methods are needed to be developed for this kind of systems. In [22,23,24], we proposed a global dynamics method for fractional-order continuous systems based on the GCM method and the improved predictor-corrector algorithm, namely, an EGCM method. Global bifurcations and crises are determined accurately for systems with continuous fractional calculus by using the EGCM method. Compared with the direct numerical integration method, the EGCM method is an efficient tool to determine the global properties for a fractional-order continuous system. Naturally, one question may be presented: whether the EGCM method for the fractional-order continuous systems is also valid for the discrete ones.
Inspired by the above discussion, we attempt to apply the EGCM method to investigate the dynamics of fractional-order discrete maps with Caputo difference operators from a global perspective. There is one important point to notice about the EGCM method using for the fractional-order discrete maps. The one-step mapping time in the EGCM method need to be sufficient long to guarantee the precision of the results due to the slowly convergence speed of solution of fractional-order discrete maps. Global dynamics of three typical fractional-order discrete maps is analyzed by the EGCM method. These analyses illustrate the reported results, and furthermore obtain the global properties of these typical fractional-order discrete maps. The results indicate that the EGCM method is valid and efficient for this kind of systems.
The article is arranged as follows. The related preliminary knowledge for fractional-order discrete maps is introduced in Section 2. Global dynamics of three typical fractional-order discrete maps are studied by the EGCM method in Section 3. The stable and the unstable invariant sets are determined via the method. These results confirm the reported results, and furthermore gain the global dynamics of the maps including the attractors, saddles, basin boundaries, and domains of attraction for these fractional-order discrete maps. The conclusion and discussion are given in Section 4.
2. Primary Fundamental of Discrete Fractional Calculus
In this section, the operator of discrete fractional calculus and related theories used in this paper will be introduced.
Firstly, represents order discrete fractional calculus with Caputo type operator for a function , and [25]. It can be represented by the following equation
here represents a fractional order, . denotes the starting point, , and . The fractional sum of in (1) is defined as
where , [26,27], and denotes the falling function defined based on the Gamma function as
The numerical solutions of a fractional-order map are determined by the method reported in [28,29,30]. A fractional difference equation with Caputo difference operatoris described as
The equivalent discrete integral equation is
where .
It is worth mentioning that the main benefit of employing the Caputo difference operator in this paper is that the initial value of a fractional difference equation does not need to be specified. The initial conditions take on the same form as those for the integer-order ones. If you want to get more details for this kind of difference operator, please refer to Ref. [31]. Formula (5) degenerates to an integer difference equation when the order . Furthemore, the obvious difference between integer-order and fractional-order maps is the non-local property of the fractional calculus. This means that the current state depends on all of the historical iterations begining with the initial condition.
3. Global Dynamics of fractional-order Discrete Maps
3.1. The EGCM Method
For a fractional-order continuous system, the EGCM is a powerful global dynamics analysis method. The main idea of the method is to cover the continuous state space of a fractional-order system by the discrete state cells. The original system is converted to the corresponding discrete cell mapping ones by generating the GCM system. The point mapping at a certain amount of sample points in a cell are used to define a one-step transition probability matrix. Then a finite time homogeneous Markov chain can be obtained. Then the cell mapping system can be used to investigate the global dynamics of a fractional-order system [22,23,24]. The coexist attractors, regular or chaotic saddles, basin boundaries, and domains of attraction for a fractional-order continuous system can be determined by using the EGCM method.
In the following, we will apply the EGCM method to study the global properties for the fractional-order discrete maps. Generally speaking, a fractional-order map is described by the following difference equations:
here is the vector of fractional orders, and . represents a k—dimensional state vector, the time variable , is an m—dimensional parameter vector, and a vector-valued function of , , and .
A bounded area is considered as the interesting region in the EGCM method. A group of uniform grid lines are used to cover the region . Then we can get a number of rectangular paralleled pipes, namely, the cells. A positive integer ranging from 1 to is used to identify every cell [22,23]. For a cell in the cell state space, a certain amount of sample points is taken based on the uniform sample method. The image point for every sample point is obtained via the Formula (5) with the one-step mapping time.
For a fractional-order discrete map, the one-step mapping time in the EGCM method means the iterated time. In order to get a suitable one-step mapping time, facts from two aspects need to be mentioned. Firstly, considering the slowly convergence speed of solution of this kind of systems, the one-step mapping time should be sufficient long to ensure the accuracy of the results. Secondly, several necessary numerical simulation tests are carried out to get a suitable one-step mapping time which can ensure no coarse or wrong points in the basin boundary. It should be mentioned that the one-step mapping time of GCM method is also chosen by the numerical tests [14,15,16]. Based on these, a suitable one-step mapping time is chosen for a fractional-order discrete map.
The next procedures include generating of one-step transition probability matrix, obtaining the adjacency matrix of the one-step mapping digraph, computing the transitive closure matrix of the one-step mapping digraph, and so on. If you want to know more details about the EGCM method, please refer to the Refs. [22,23,24].
3.2. Global Dynamics of Three fractional-order Discrete Maps
Global dynamics of three fractional-order discrete maps will be studied by the EGCM method in this subsection. The correctness and efficiency of the method are illustrated by these results. It should be mentioned that the numerical orbits in the rest of the paper which apparently show some regular behavior are so called periodic-like orbits. It has been discussed by Danca and Kuznetsov in [32].
3.2.1. Global Dynamics of a fractional-order Duffing Map
The Duffing system is a famous and typical nonlinear dynamical system, which has very simple structure and rich dynamics. In [29], a Duffing system with Caputo fractional difference was analyzed in detail. The fractional-order Duffing map can be given by the following fractional difference equations:
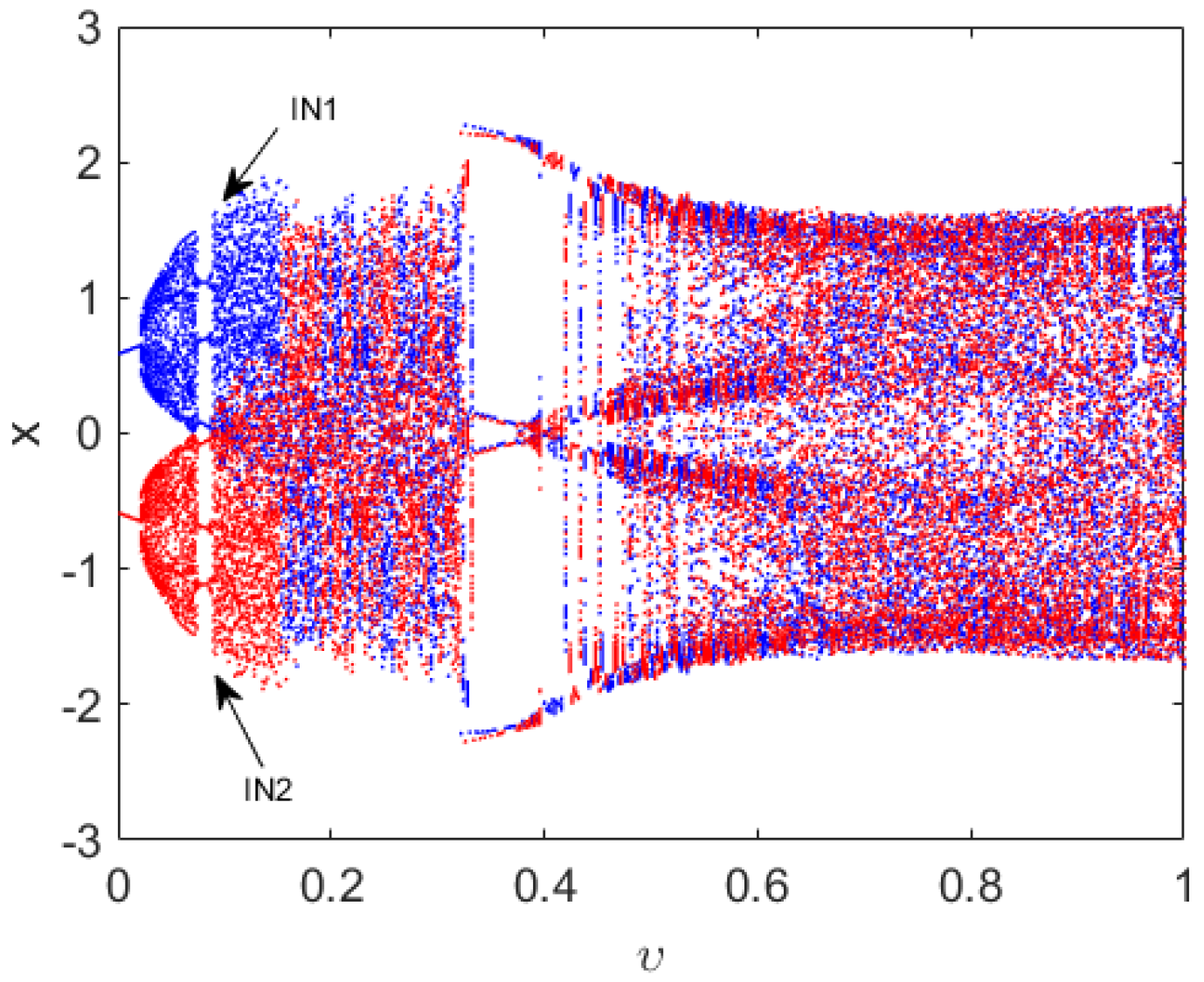
here and are system parameters. In this paper, the start point is set as 0. When parameters are fixed as , a bifurcation diagram versus the order starting from two initial conditions and is obtained (see Figure 1 in which blue and red mean the stable solutions starting from the and , respectively). It is clear that the map has fixed point attractors and chaotic attractors when the derivative order increases from 0 to 1.
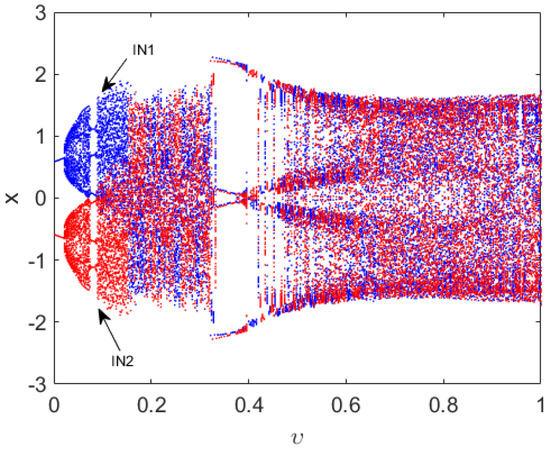
Figure 1.
The bifurcation diagram versus parameter for map (7) with initial conditions and . Blue and red mean the stable solutions starting from the and , respectively.
In order to study the global dynamics of fractional-order discrete map (7), we turn to the EGCM method. Here, the interesting region is chosen as , cells with sampling points in each cell are used to cover the interesting region . The following numerical simulation tests are carried out to obtain a suitable one-step mapping time for map (7). When the order is taken as , the map has two fixed point attractors. In this case, the basin boundaries are plotted in Figure 2 for the one-step mapping times (Figure 2a) and (Figure 2b), respectively. It is clear that there are some wrong points on the basin boundary which appear in the upper right and lower left corners of the interesting region when . Therefore, the one-step mapping time is reasonable for the global dynamics analysis of map (7).
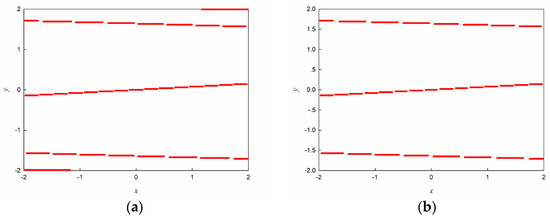
Figure 2.
The basin boundaries of map (7) with different one-step mapping times: (a) ; (b) .
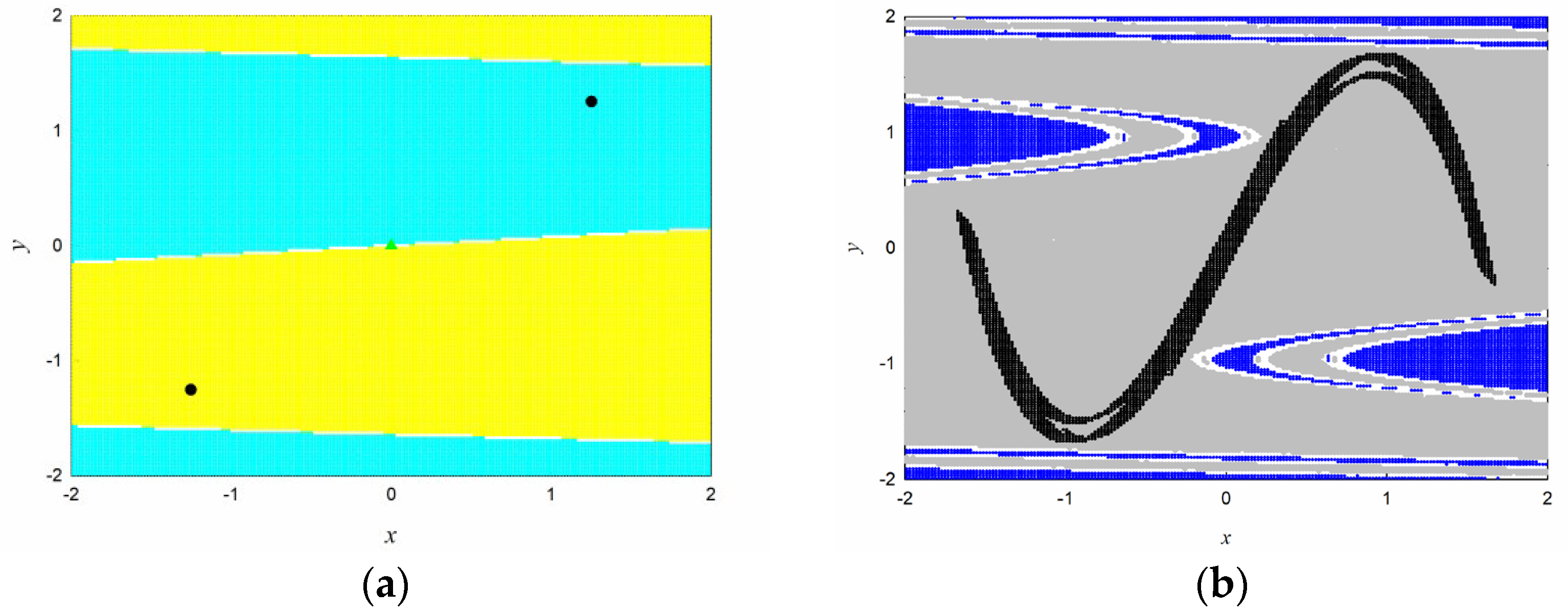
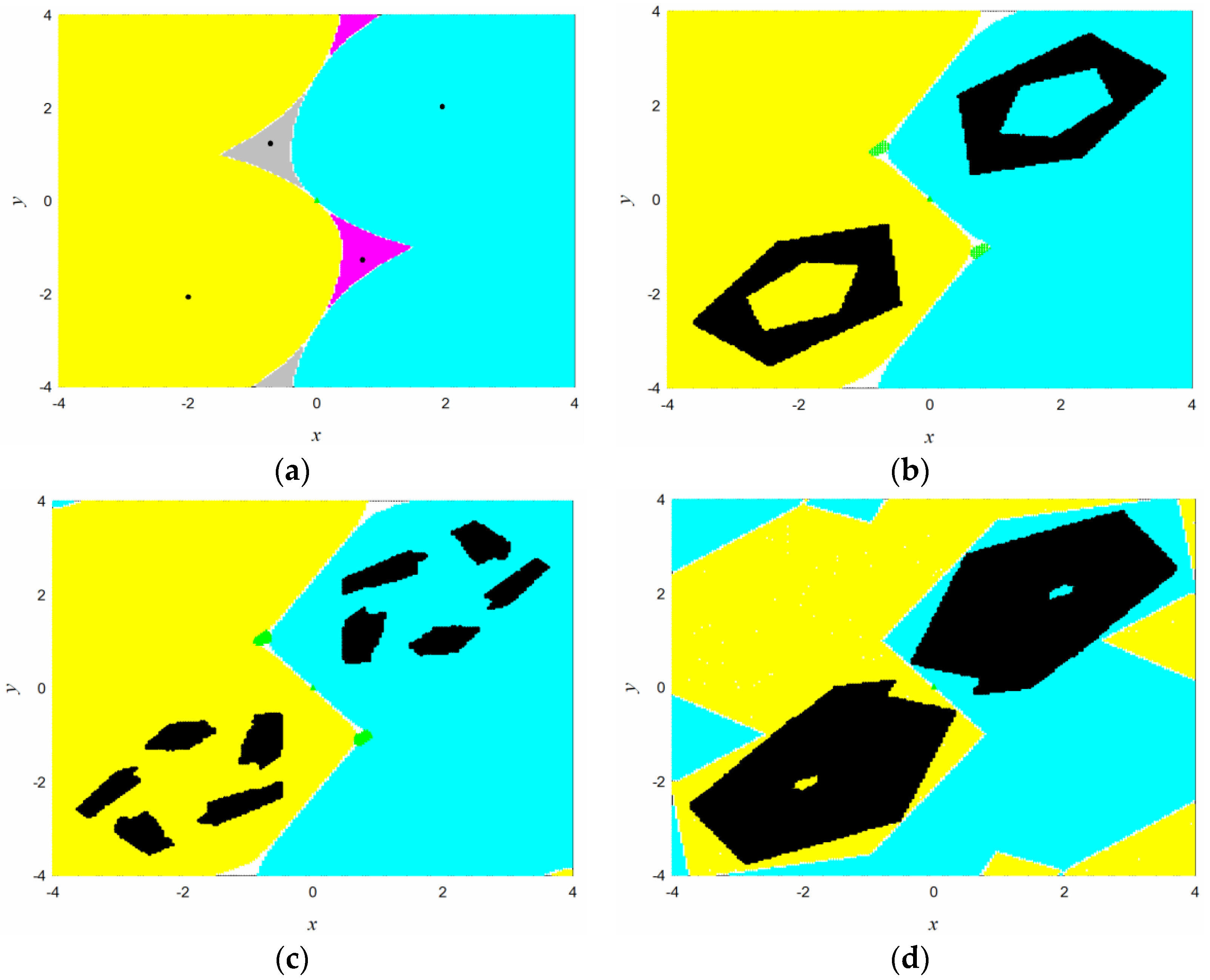
The global dynamics of fractional-order discrete map (7) with different values of the order is depicted in Figure 3. Two fixed points and a regular saddle on the basin boundary coexist in the interesting region with . When the order is taken as , there is only a chaotic attractor in the state space. In Figure 3, black denotes the attractors, yellow, cyan, and gray the corresponding domains of attraction. White denotes the boundary, green ‘▲’ the saddle, and blue the domain of attraction of the sink cell. The results confirm those of reported in Ref. [29], and furthermore the domains of attraction, basin boundaries, and regular saddle are also determined by the EGCM method. According to the analysis, we can get a explicit understanding of the global dynamics evolution for map (7).
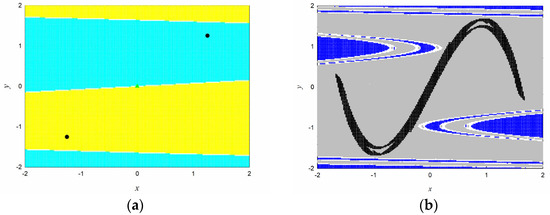
Figure 3.
The global dynamics of map (7) with different values of the fractional orders: (a) ; (b) . Black denotes the attractors, yellow and cyan the corresponding domains of attraction. Green means the saddle. White denotes the boundary and blue the domain of attraction of the sink cell.
3.2.2. Global Dynamics of a fractional-order Noninvertible Map of Cubic Type
A fractional-order noninvertible map of cubic type was presented in [33], which leads to equations in the following form:
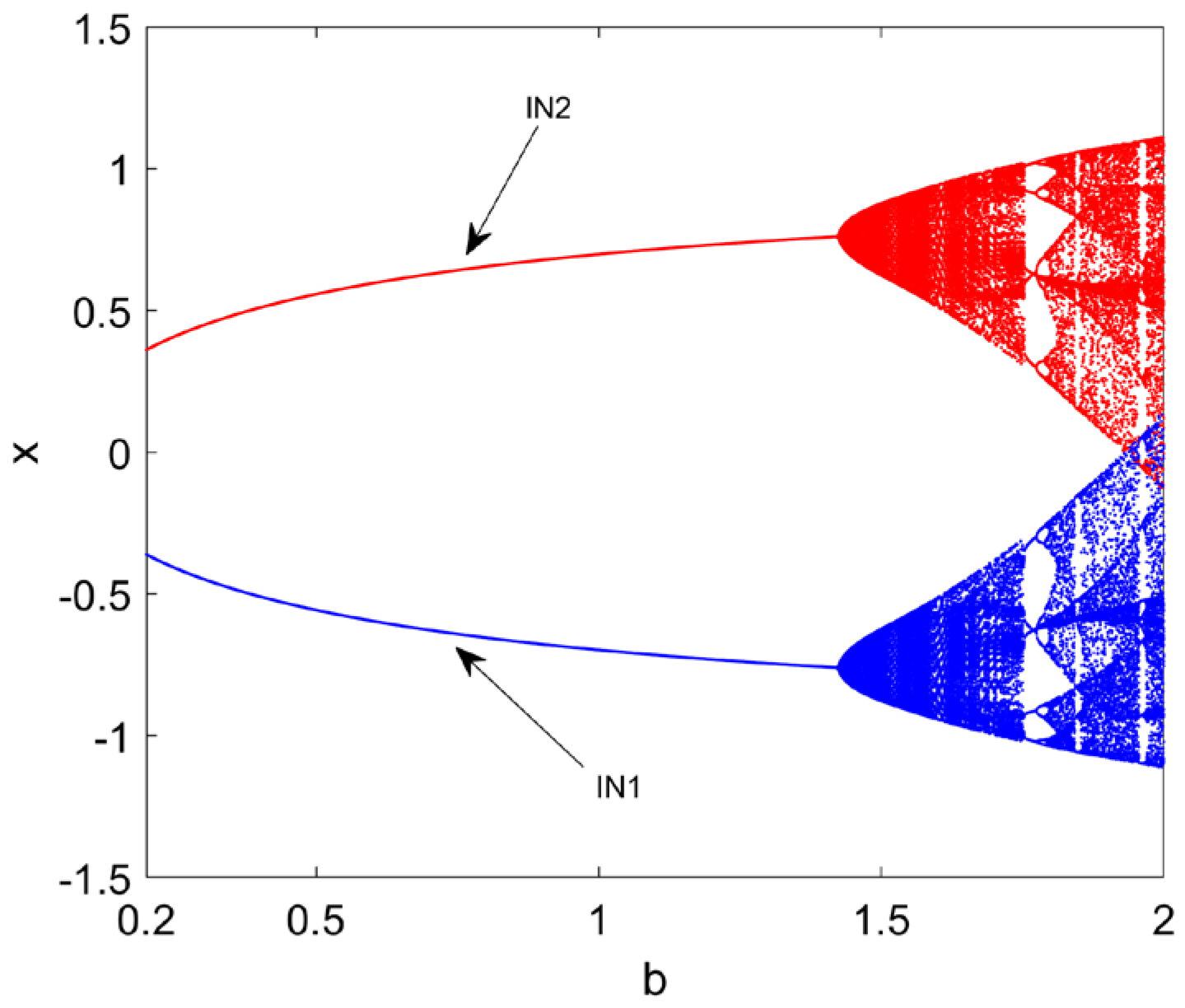
where are state variables, system parameters, and the derivative order. When and , the bifurcation diagram versus for the map with two initial conditions and is shown in Figure 4. We can see that there are two symmetry evolution orbits when , which means that two attractors coexist in the state space. However, the domains of attraction for different attractors, the corresponding boundaries, and unstable saddles cannot be determined from the analysis of local dynamics. Therefore, we will use the EGCM method to get the global properties of the map. The interesting region is taken as .
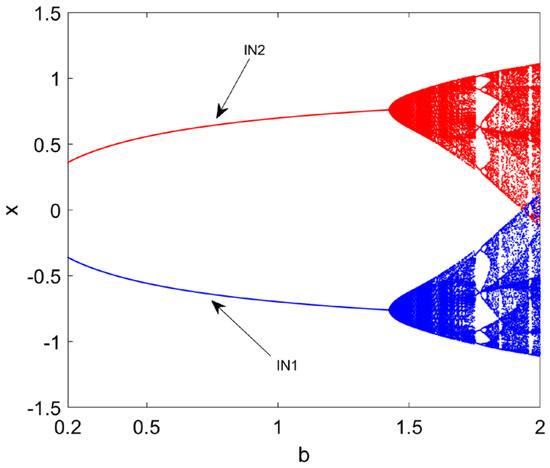
Figure 4.
The bifurcation diagram of map (8) starting from the initial conditions and when the parameter is varied.
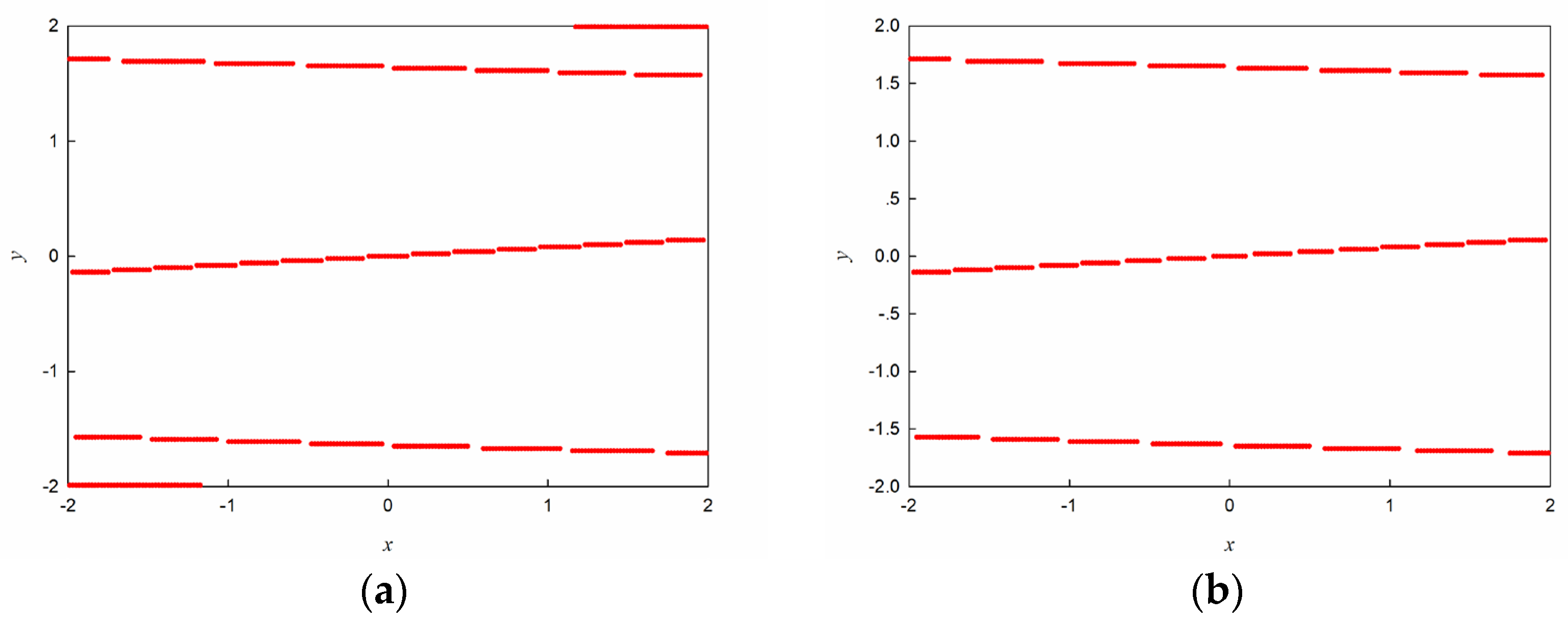
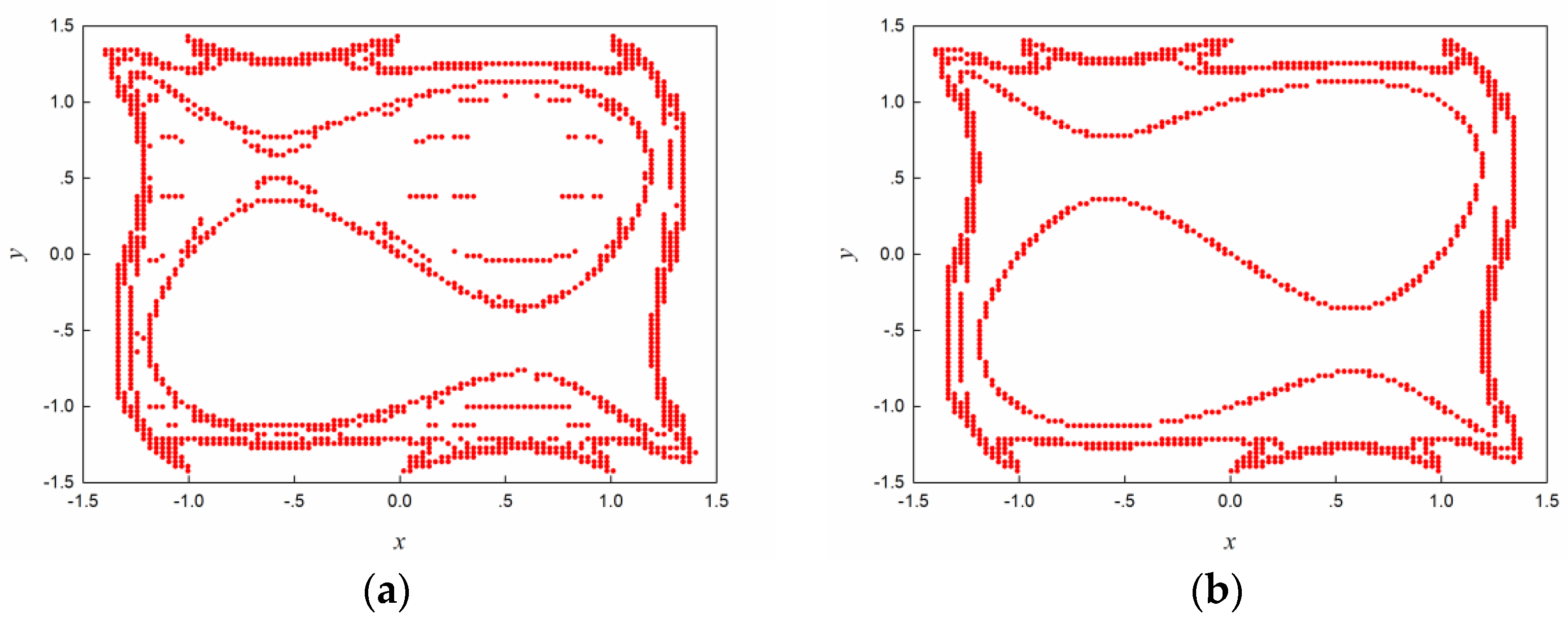
In order to determine a reasonable one-step mapping time for map (8), the following numerical simulation tests are performed. For the sake of convenience, we will use cells with sampling points in each cell to cover the interesting region. For the clarity and simplicity, we only plot the basin boundaries of the map when with different one-step mapping times, see Figure 5. From which, we can see that there are some inaccurate and coarse points on the basin boundary when the one-step mapping time is chosen as (Figure 5a). The basin boundary becomes smooth as increases to 4000 (Figure 5b). Based on these, the one-step mapping time will be chosen as 4000 for map (8).
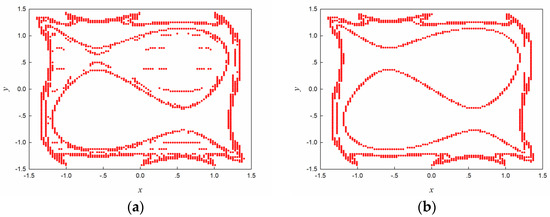
Figure 5.
The basin boundaries of map (8) with different one-step mapping times: (a) ; (b) .
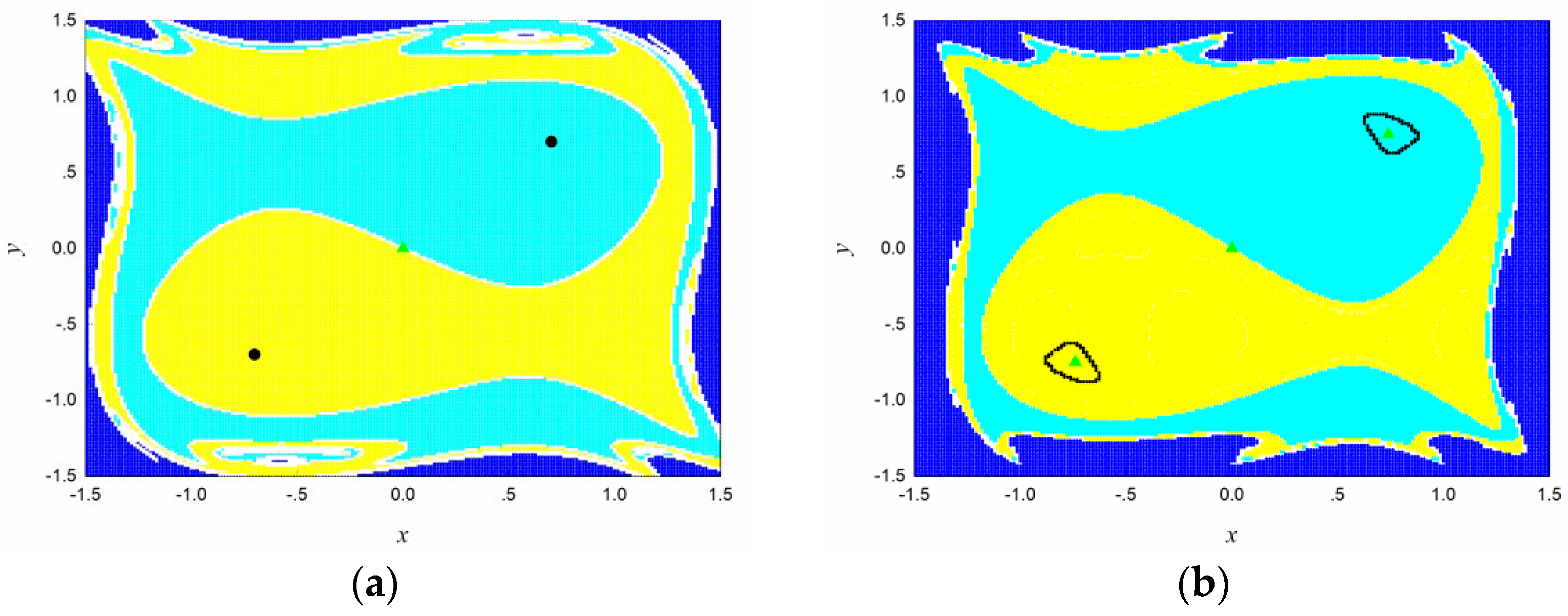
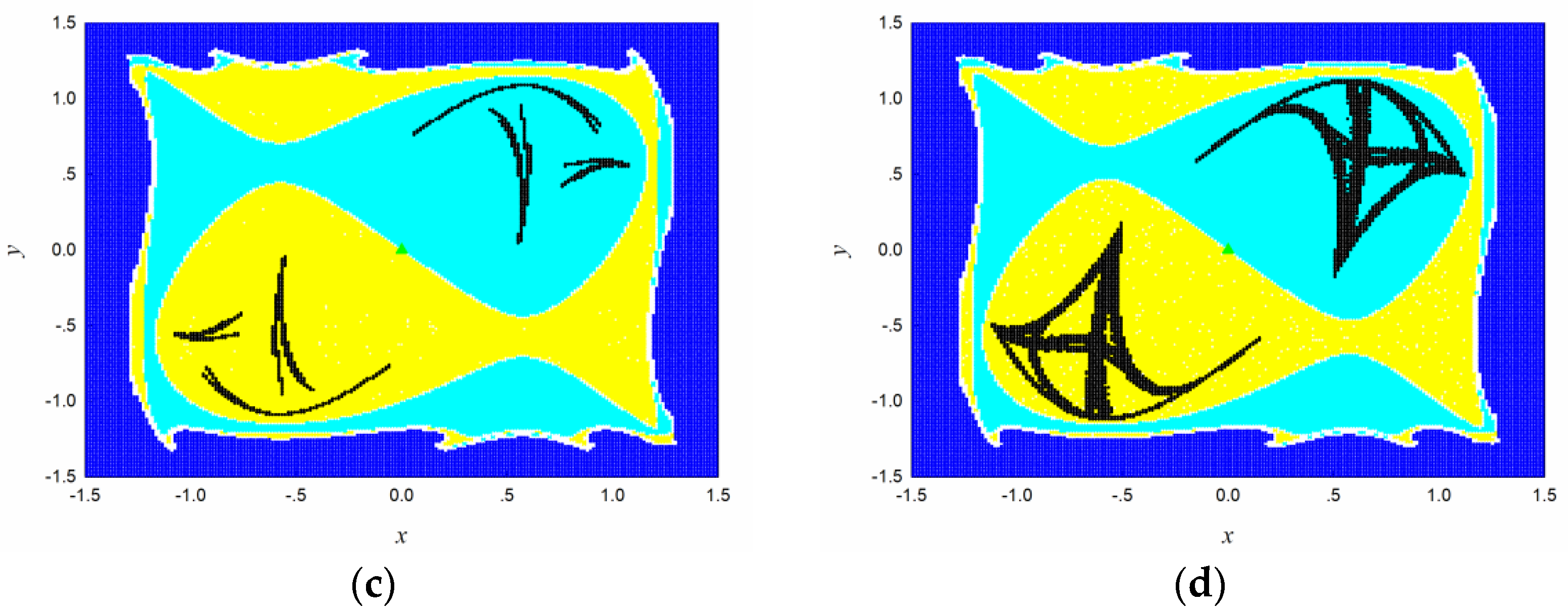
The interesting region is covered by cells. Every cell is divided by sampling points uniformly. The attractors, basin boundaries, the basins of attraction, and the saddles are plotted for different values of parameter in Figure 6. From which we can see that the map has two fixed points attractors and one saddle in the basin boundary for (Figure 6a). When the parameter increases to 1.5, two limit cycles attractors, two saddles in the basins of attraction, and one saddle in the boundary coexist in the region (Figure 6b). When , there are two chaotic attractors composed by three parts and a saddle in the basin boundary (Figure 6c). As parameter increases to 2, the three parts for the two chaotic attractors convert to a whole one in their corresponding basins of attraction (Figure 6d).
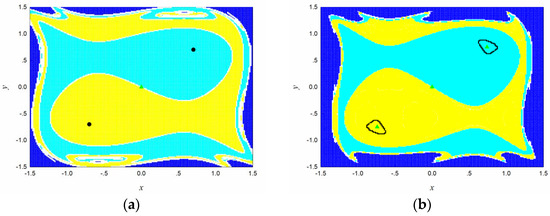
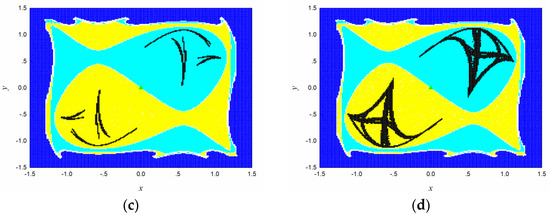
Figure 6.
The global dynamics of map (8) with different values of parameter : (a) ; (b) ; (c) ; (d) . Black denotes the attractors, Yellow and cyan the corresponding basins of attraction. White denotes the boundary, green ‘▲’ the saddle, and blue the domain of attraction of the sink cell.
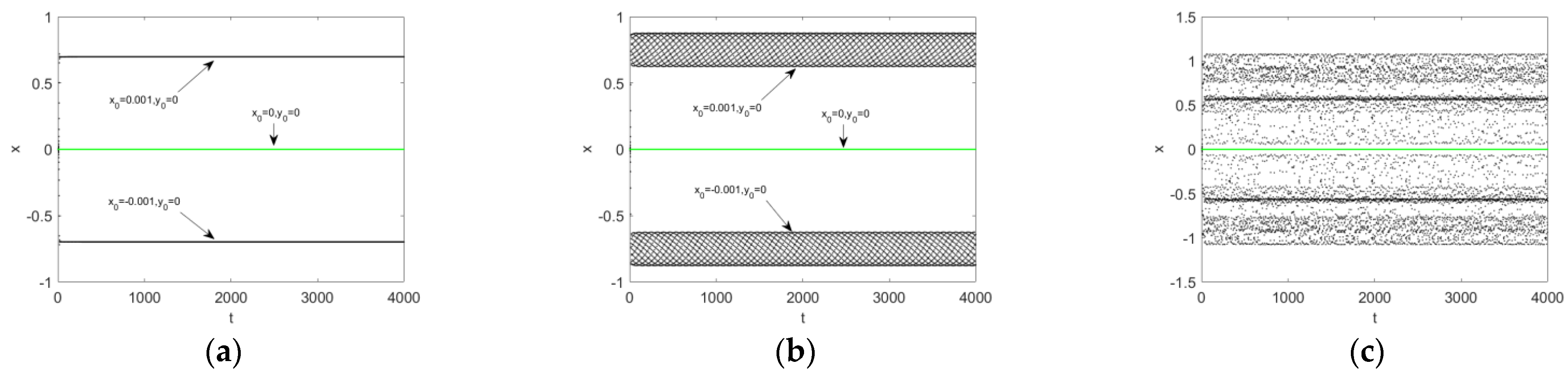
From Figure 6, we can see that the regular saddle in the basin boundary is the equilibrium .The fact can be verified by the following numerical simulations, see Figure 7. Three initial conditions and are used in here. Form the figure, we can see that the trajectory (green points) will converge to the saddle point if and only if the initial condition is taken as . The trajectories (black points) starting from and converge to the corresponding limit attractors when , and to the chaotic attractor when . These results verify the fact that the equilibrium is indeed a saddle point, namely, any small disturbance on the initial condition will lead to the convergence of trajectory to the stable invariant sets.
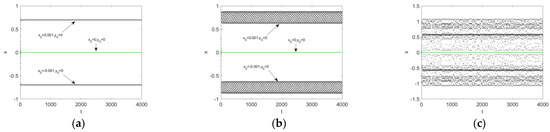
Figure 7.
The solution trajectories of the map versus the time for different values of parameter : (a) ; (b) ; (c) . Black means the stable solutions starting from and . Green means the stable solutions starting from .
3.2.3. Global Dynamics of a fractional-order Piecewise-Linear Map
A fractional-order piecewise-linear map was studied in [34], which leads to the following equations:
where are system parameters. is a characteristic function, which can be defined as
here and denote the slopes of the inner and outer sets of the original Chua circuit, respectively. In [34], authors analyzed the dynamics of the map with one initial condition . The values of system parameters are fixed as . The map has a chaotic double scroll attractor with order .
In the EGCM method, the interesting region is taken as , and covered by cells with sampling points in each cell. The one-step mapping time is chosen as . The attractors, basin boundaries, the basins of attraction, and saddles with different values of the order are shown in Figure 8. It can be seen that four fixed point attractors (black points) and one saddle (green triangle) in the basin boundary coexist when , see Figure 8a. The corresponding basins of attraction for every attractor are depicted by yellow, pink, gray, and cyan points. The basin boundary is denoted by white points.
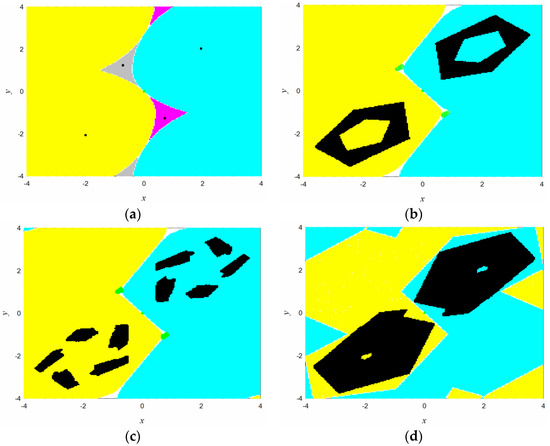
Figure 8.
The global dynamics of map (9) with different values of the order : (a) ; (b) ; (c) ; (d) . Black denotes the attractors, yellow, pink, gray, and cyan the corresponding basins of attraction. White denotes the boundary, and green ‘▲’ the saddle.
When the fractional order is taken as or , two chaotic attractors and three regular saddles can be observed in the interesting region (Figure 8b,c). There are two chaotic attractors and a saddle in the basin boundary when (Figure 8d). The attractors with different values of the order confirm the results reported in [34]. In addition, the basins of attraction, boundaries and saddles are also obtained by the EGCM method. This implies that the EGCM method is also valid for a fractional-order map with piecewise-linear function.
3.2.4. Analysis and Comparision
The research results in this subsection have shown that the EGCM method can be used to study the global dynamics for discrete maps with fractional calculus. The local dynamics of these typical fractional-order discrete maps has been studied previously using only one or several initial points by the direct numerical integration method in [29,33,34]. The global dynamics obtained via the EGCM method confirm the reported results, and further determine the global properties including attractors, saddles, basin boundaries and domains of attraction in the state space. The important benefits of the EGCM method comparing with the direct integration method in Refs. [29,33,34] are to change the continuous state space of a map with Caputo difference operator into limited discrete state cells. Based on these, it can greatly decrease the computational cost when investigate the global dynamics of the fractional-order discrete map only by one-step mappings.
4. Conclusions and Discussion
In this paper, the EGCM method is used to explore the global dynamics analysis for fractional-order discrete maps. Considering the lack of effective global analysis methods for discrete maps with fractional calculus, the EGCM method is applied to study the global dynamics for this kind of systems. Firstly, considering the slowly convergence speed of solution of fractional-order discrete maps, the one-step mapping time need to be sufficient long to guarantee the precision of the results. Secondly, global dynamics of three typical fractional-order discrete maps is analyzed by the EGCM method. The stable and the unstable invariant sets can be determined via the method. The results confirm the reported results, and furthermore determine the global dynamics in the region including the attractors, saddles, basins boundaries and domains of attraction. These results indicate that the EGCM method is valid and efficient for fractional-order discrete maps.
The investigation of global dynamics implies a large scale computation in the cell state space. Furthermore, the long memory property of fractional calculus results in the accumulated calculation of historical states, which will cause the huge or unaccepted calculation cost. Therefore, the global properties analysis for a nonlinear system with fractional calculus is difficult to obtain. Taking advantage of the EGCM method, the analysis of global dynamics for fractional-order discrete maps becomes convenient and efficient. Based on the results in this paper, we can draw a conclusion that the EGCM method supplies an effective mean to obtain the global dynamics for fractional-order continuous systems and discrete maps. It is very vital for the application of fractional-order systems in science and engineering.
Author Contributions
All authors contributed to the study conception and design. Methodology and investigation were performed by X.L. The first draft of the manuscript was written by X.L. and D.T. Supervision, review and editing were completed by L.H. All authors commented on previous versions of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (NSFC) under the grant No. 11702194 and Natural Science Foundation of Shaanxi Province under the grant No. 2023-JC-YB-075.
Data Availability Statement
The datasets generated during the current study are not publicly available due to the huge data but are available from the corresponding author on reasonable request.
Acknowledgments
The authors would like to thank the anonymous reviewers for the constructive suggestions that are helpful to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Z.; Wang, X.; Li, Y.; Huang, X. Stability and hopf bifurcation of fractional-order complex-valued single neuron model with time delay. Int. J. Bifurc. Chaos 2017, 27, 1750209. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete fractional logistic system and its chaos. Nonlinear Dyn. 2014, 75, 283–287. [Google Scholar] [CrossRef]
- Hu, T. Discrete chaos in fractional Hénon system. Appl. Math. 2014, 5, 2243–2248. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Odibat, Z.; Pham, V.T.; Grassi, G. On the dynamics, control and synchronization of fractional-order Ikeda system. Chaos Soliton Fract. 2019, 123, 108–115. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Chaos synchronization of the discrete fractional logistic system. Signal Process 2014, 102, 96–99. [Google Scholar] [CrossRef]
- Edelman, M. Fractional Systems and fractional attractors. Part I: Families of Systems. Discontinuity Nonlinearity Complex. 2012, 1, 305–324. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete chaos in fractional delayed logistic system. Nonlinear Dyn. 2015, 80, 1697–1703. [Google Scholar] [CrossRef]
- Edelman, M. Fractional systems and fractional attractors. Part II: Fractional difference families of Systems. Discontinuity Nonlinearity Complex. 2015, 4, 391–402. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Bendoukha, S.; Grassi, G.; Lozi, R.P.; Pham, V.T. On fractional-order discrete-time systems: Chaos, stabilization and synchronization. Chaos Soliton Fract. 2019, 119, 150–162. [Google Scholar] [CrossRef]
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing; World Scientific Publishing: Hackensack, NJ, USA, 2016. [Google Scholar]
- Edelman, M.; Macau, E.E.; Sanjuan, M.A. (Eds.) Chaotic, Fractional, and Complex Dynamics: New Insights and Perspectives; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Othman, A.A.; Khennaoui, A.A.; Ouannas, A.; Pham, V.T. Infinite line of equilibriums in a novel fractional system with coexisting infinitely many attractors and initial offset boosting. Int. J. Nonlinear Sci. Numer. Simul. 2023, 24, 373–391. [Google Scholar]
- Hsu, C.S. Cell-to-Cell Mapping: A Method of Global Analysis for Nonlinear Systems; Springer: New York, NY, USA, 1987. [Google Scholar]
- Hsu, C.S. Global analysis by cell mapping. Int. J. Bifurc. Chaos 1992, 2, 727–771. [Google Scholar] [CrossRef]
- Hsu, C.S. Global analysis of dynamical systems using posets and digraphs. Int. J. Bifurc. Chaos 1995, 5, 1085–1118. [Google Scholar] [CrossRef]
- Jiang, J.; Xu, J.X. A method of point mapping under cell reference for global analysis of nonlinear dynamical systems. Phys. Lett. A 1994, 188, 137–145. [Google Scholar] [CrossRef]
- Jiang, J.; Xu, J.X. An iterative method of point mapping under cell reference for the global analysis of non-linear dynamical systems. J. Sound Vib. 1996, 194, 605–622. [Google Scholar] [CrossRef]
- Hong, L.; Xu, J.X. Crises and chaotic transients studied by the generailized cell mapping diagraph method. Phys. Lett. A 1999, 262, 361–375. [Google Scholar] [CrossRef]
- Li, Z.G.; Kang, J.Q.; Jiang, J.; Hong, L. Parallel subdomain synthesis of cell mapping for capturing global invariant sets in higher-dimensional dynamical systems. Int. J. Bifurc. Chaos 2022, 32, 2250231. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D.; Zeng, S.D. Discrete chaos in fractional sine and standard systems. Phys. Lett. A 2014, 378, 484–487. [Google Scholar] [CrossRef]
- Liu, X.J.; Hong, L.; Jiang, J. Global bifurcations in fractional-order chaotic systems with an extended generalized cell mapping method. Chaos 2016, 26, 084304. [Google Scholar] [CrossRef]
- Liu, X.J.; Hong, L.; Jiang, J.; Yang, L.X. Global dynamics of fractional-order systems with an extended generalized cell mapping method. Nonlinear Dyn. 2016, 83, 1419–1428. [Google Scholar] [CrossRef]
- Liu, X.J.; Hong, L.; Tang, D.F.; Yang, L.X. Crises in a fractional-order piecewise system. Nonlinear Dyn. 2021, 103, 2855–2866. [Google Scholar] [CrossRef]
- Abdeljawad, T. Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Gray, H.I.; Zhang, N.F. On a new definition of the fractional difference. Math. Comput. 1988, 50, 513–529. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. Univalent functions, fractional calculus, and their applications. In Chichester: Eills Howard; Chichester/Society of Chemical Industry: London, UK, 1989; pp. 139–152. [Google Scholar]
- Anastassiou, G.A. Principles of delta fractional calculus on time scales and inequalities. Math. Comput. Model. 2010, 52, 556–566. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Pham, V.T. The discrete fractional duffing system: Chaos, 0–1 test, C0 complexity, entropy, and control. Chaos 2020, 30, 083131. [Google Scholar] [CrossRef] [PubMed]
- Čermák, J.; Györi, I.; Něchvátal, L. On explicit stability condition for a linear fractional difference system. Fract. Calc. Appl. Anal. 2015, 18, 651–672. [Google Scholar] [CrossRef]
- Rahmat, M.R.S.; Noorani, M.S.M. Caputo type fractional difference operator and its application on discrete time scales. Adv. Diff. Eqs. 2015, 2015, 1–15. [Google Scholar]
- Danca, M.F.; Kuznetsov, N. D3 Dihedral Logistic system of fractional order. Mathematics 2022, 10, 213. [Google Scholar] [CrossRef]
- Liu, X.J.; Hong, L.; Yang, L.X.; Tang, D.F. A fractional-order discrete noninvertible system of cubic type: Dynamics, control, and synchronization. Complexity 2020, 2020, 2935192. [Google Scholar]
- Ouannas, A.; Khennaoui, A.A.; Bendoukha, S.; Grassi, G. On the dynamics and control of a fractional form of the discrete double scroll. Int. J. Bifurc. Chaos 2019, 29, 1950078. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).