Ulam-Type Stability Results for Variable Order Ψ-Tempered Caputo Fractional Differential Equations
Abstract
:1. Introduction
2. -Tempered Fractional Calculus of Variable Order
2.1. Some Results on Caputo-Type Fractional Derivatives of Constant Order
2.2. Some Results for Variable Order of Fractional Derivatives
3. Differential Equations with Variable Order of the Fractional Derivative
Definition of Approximate Solutions of the Initial Value Problem (8)
- -
- for we have ;
- -
- for we have
4. Ulam-Type Stability of Approximate Solutions
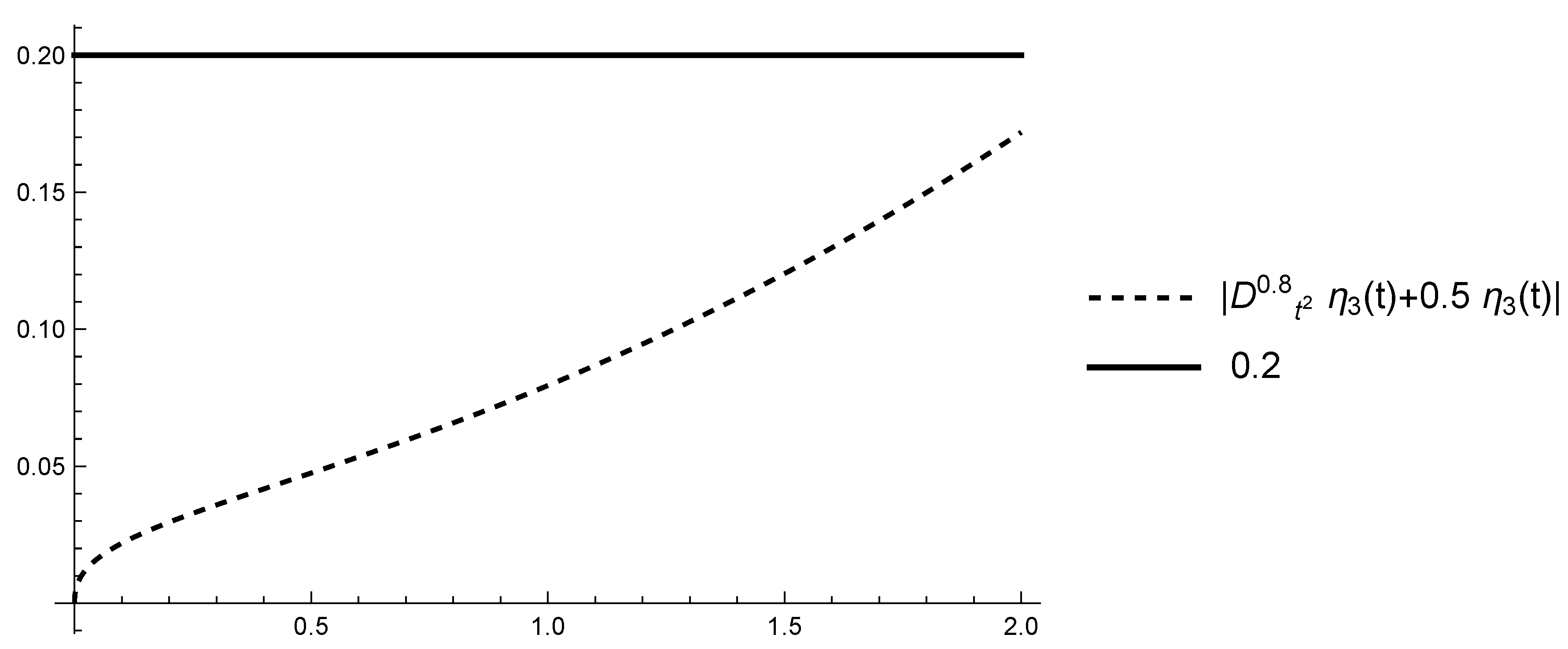
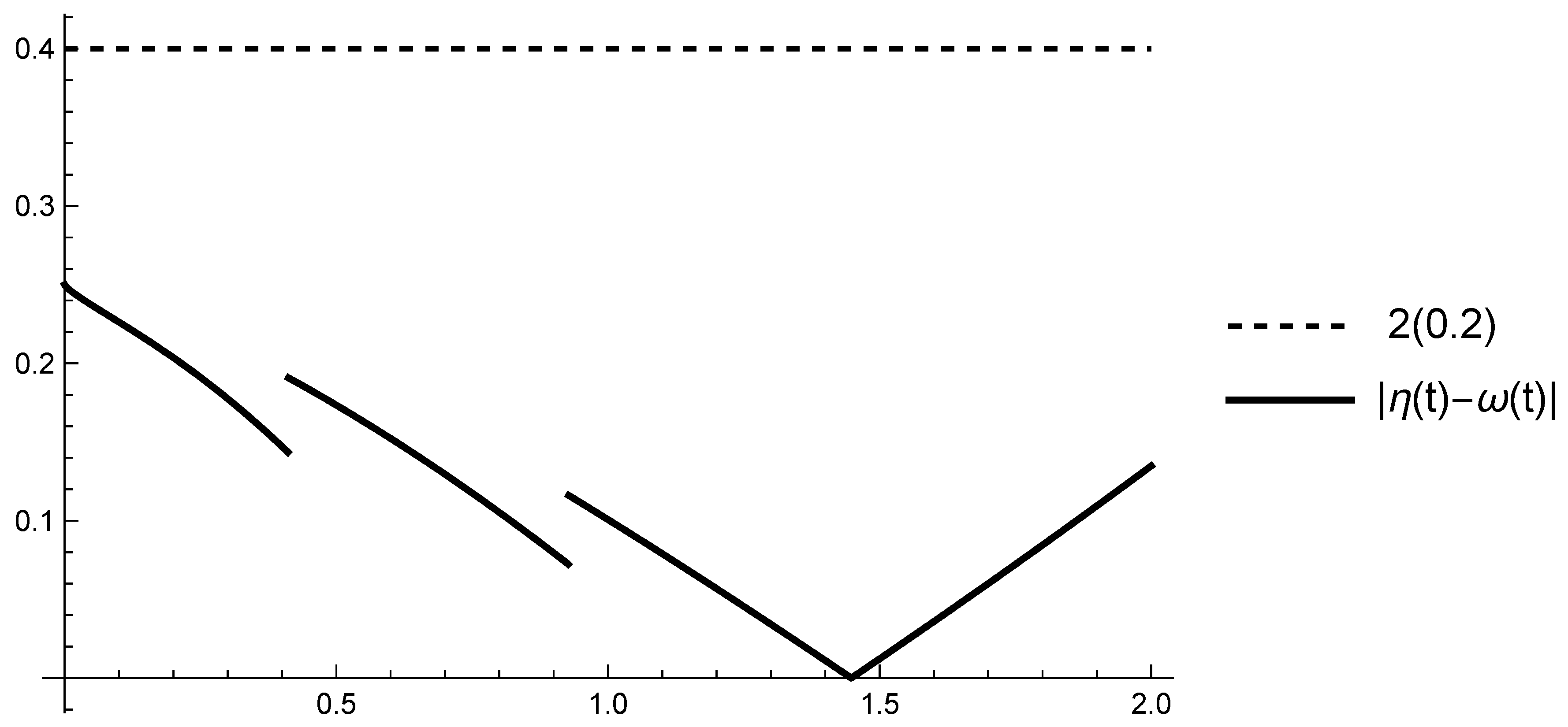
5. Piecewise Constant Order of the Fractional Derivative
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Garrappa, R.; Giusti, A.; Mainardi, F. Variable-order fractional calculus: A change of perspective. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105904. [Google Scholar] [CrossRef]
- Sun, H.G.; Chang, A.; Chang, Y.; Chen, W. A review of variable-order fractional differential equations: Mathematical foundations, physical models, numebriacl methods and applications. Frac. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications ofvariable-order fractional operators: A review. Proc. R. Soc. A 2020, 476, 20190498. [Google Scholar] [CrossRef] [PubMed]
- Samko, S.; Ross, B. Integration and differentiation to a variable fractional order. Integral Transform. Spec. Funct. 1993, 4, 277–300. [Google Scholar] [CrossRef]
- Tavares, D.; Almeida, R.; Torres, D.F.M. Caputo derivatives of fractional variable order: Numerical approximations. Commun. Nonlinear Sci. Numer. Simul. 2016, 35, 69–87. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Initialization, conceptualization, and ap plication in the generalized fractional calculus. Crit. Rev. Biomed. Eng 2007, 35, 477–553. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, L. Unique existence result of approximate solution to initial value problem for fractional differential equation of variable order involving the derivative arguments on the half-axis. Mathematics 2019, 7, 286. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier B.V.: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Drivatives; Gordon and Breach Science Publishers: Longhorne, PA, USA, 1993. [Google Scholar]
- Agarwal, R.; Hristova, S.; O’Regan, D. Boundary Value Problems for Fractional Differential Equations of Caputo Type and Ulam Type Stability: Basic Concepts and Study. Axioms 2023, 12, 226. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Hristova, S. Ulam-Type Stability for a Boundary-Value Problem for Multi-Term Delay Fractional Differential Equations of Caputo Type. Axioms 2022, 11, 742. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Hristova, S. Boundary Value Problem for Multi-Term Nonlinear Delay Generalized Proportional Caputo Fractional Differential Equations. Fractal Fract. 2022, 6, 691. [Google Scholar] [CrossRef]
- Fedotov, A.I. Substantiation of a Quadrature-Difference Method for Solving Integro-Differential Equations with Derivatives of Variable Order. Comput. Math. Math. Phys. 2022, 62, 548–563. [Google Scholar] [CrossRef]
- Telli, B.; Souid, M.; Alzabut, J.; Khan, H. Existence and uniqueness theorems for a variable-order fractional differential equation with delay. Axioms 2023, 12, 339. [Google Scholar] [CrossRef]
- Refice, A.; Souid, M.; Yakar, A. Some qualitative properties of nonlinear fractional integro-differential equations of variable order. Intern. J. Optim. Contr. Theor. Appl. 2021, 11, 68–78. [Google Scholar] [CrossRef]
- Fahad, H.M.; Fernandez, A.; ur Rehman, M.; Siddiqi, M. Tempered and Hadamard-type fractional calculus with respect to functions. Mediterr. J. Math. 2021, 18, 143. [Google Scholar] [CrossRef]
- Mali, A.D.; Kucche, K.D.; Fernandez, A.; Fahad, H.M. On tempered fractional calculus with respect to functions and the associated fractional differential equations. Math. Meth. Appl. Sci. 2022, 45, 11134–11157. [Google Scholar] [CrossRef]
- Fernandez, A.; Ustaoglu, C. On some analytic properties of tempered fractional calculus. J. Comput. Appl. Math. 2020, 366, 112400. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; Oliveira, E.C.D. A Gronwall inequality and the Cauchy-type problem by means of ψ-Hilfer operator. Differ. Equ. Appl. 2019, 11, 87–106. [Google Scholar]
- Almeida, R. A Caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar] [CrossRef]
- Sarwar, S. On the Existence and Stability of Variable Order Caputo Type Fractional Differential Equations. Fractal Fract. 2022, 6, 51. [Google Scholar] [CrossRef]
- Refice, A.; Souid, M.S.; Stamova, I. On the boundary value problems of Hadamard fractional differential equations of variable order via Kuratowski MNC technique. Mathematics 2021, 9, 1134. [Google Scholar] [CrossRef]
- Hristova, S.; Benkerrouche, A.; Souid, M.S.; Hakem, A. Boundary value problems of Hadamard fractional differential equations of variable order. Symmetry 2021, 13, 896. [Google Scholar] [CrossRef]
- Benia, K.; Souid, M.S.; Jarad, F.; Alqudah, M.A.; Abdeljawad, T. Boundary value problem of weighted fractional derivative of a function with a respect to another function of variable order. J. Ineq. Appl. 2023, 2023, 127. [Google Scholar] [CrossRef]
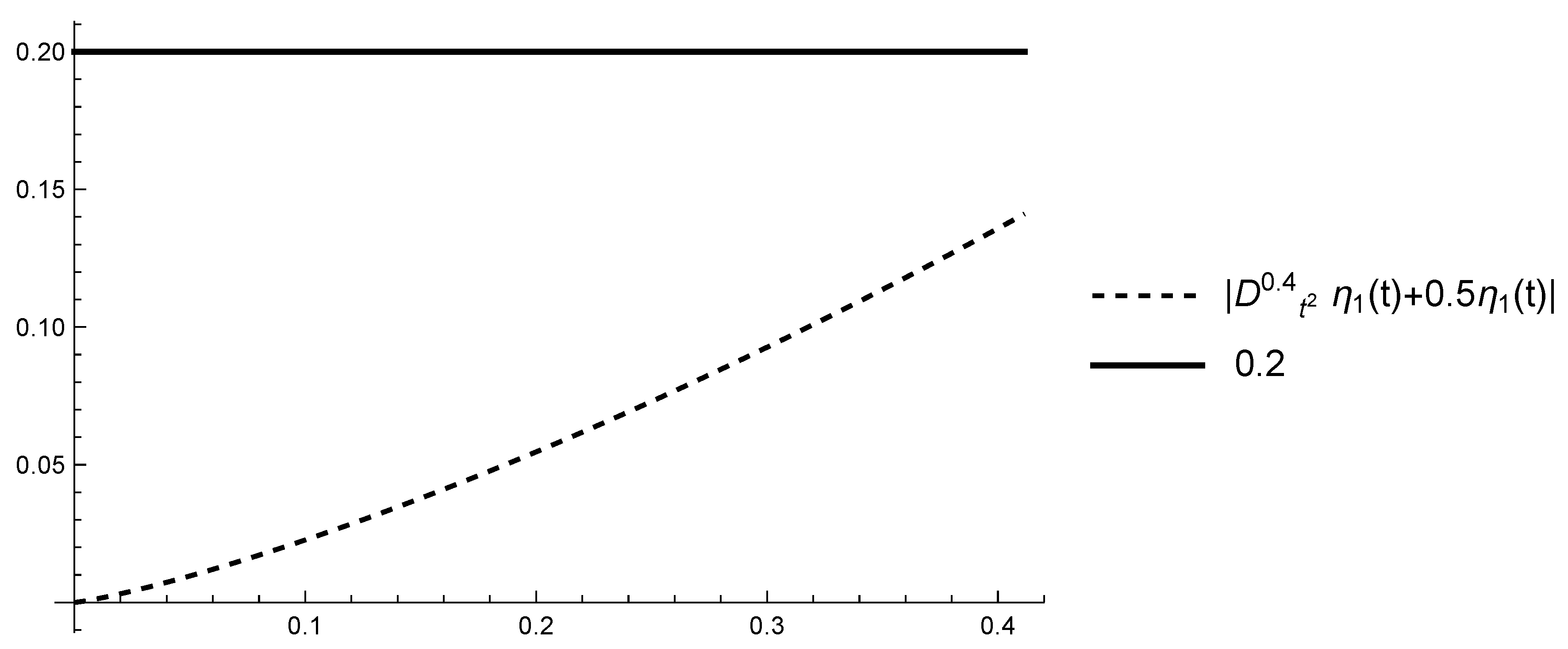

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
O’Regan, D.; Hristova, S.; Agarwal, R.P. Ulam-Type Stability Results for Variable Order Ψ-Tempered Caputo Fractional Differential Equations. Fractal Fract. 2024, 8, 11. https://doi.org/10.3390/fractalfract8010011
O’Regan D, Hristova S, Agarwal RP. Ulam-Type Stability Results for Variable Order Ψ-Tempered Caputo Fractional Differential Equations. Fractal and Fractional. 2024; 8(1):11. https://doi.org/10.3390/fractalfract8010011
Chicago/Turabian StyleO’Regan, Donal, Snezhana Hristova, and Ravi P. Agarwal. 2024. "Ulam-Type Stability Results for Variable Order Ψ-Tempered Caputo Fractional Differential Equations" Fractal and Fractional 8, no. 1: 11. https://doi.org/10.3390/fractalfract8010011






