A Novel Numerical Method for Solving Nonlinear Fractional-Order Differential Equations and Its Applications
Abstract
:1. Introduction
- The development of a fast algorithm that can be applied to numerical methods for solving ABC FDEs.
- The development of a fast PCM and its application to ABC fractional-order PDEs (FPDEs) and fractional dynamical systems.
- Error estimates for both conventional and fast PCMs.
- The conventional PCM for solving ABC FDEs is suggested.
- The fast algorithm for the computation of the memory term is proposed, and the fast PCM only requires a computational cost of .
- Truncation and global error analyses for both conventional and fast PCMs are provided, achieving a uniform accuracy of order regardless of the fractional order .
- We apply the proposed fast PCM to sub-diffusion FPDEs to demonstrate the efficiency of the proposed method.
- The proposed fast PCM is implemented to handle the fractional Rössler dynamical system, and the performance of the fast algorithm is verified.
2. Fast Predictor-Corrector Scheme
2.1. Description of Predictor-Corrector Scheme
2.2. Sum-of-Exponentials Approximation of the Power Function
2.3. Description of Fast Predictor-Corrector Scheme
3. Error Analysis
3.1. Truncation and Global Error Analyses for the Conventional PCM
3.2. Global Error Analysis for the Fast PCM
4. Numerical Results
- Maximum norm error:
- Discrete norm error:
4.1. Nonlinear ABC Fractional-Order Initial Value Problems
- The numerical results obtained with the ABC-FPCM show little difference from those obtained with the ABC-PCM.
- The computational costs, obtained by measuring the CPU time (in seconds) executed by the conventional PCM and the fast PCM versus the total number of steps N on the log-log scale in Example 2, are depicted in Figure 1. The figure shows that the CPU consumption rate of the fast PCM is , whereas that of the conventional PCM is .
4.2. Application to Fractional Order PDEs
- Theoretically, the rate of convergence for the second-order central difference quotient is , and the convergence rates for the proposed methods are shown to be 2. Thus, the global order of convergence for both (25) and (26) is expected to be 2 when either or h is fixed. In the tables, one can see that the rates of convergence computed by the ABC-FPCM and ABC-PCM are approximately 2 in both cases where is fixed and h is fixed. This verifies that the global estimates of our proposed methods are valid in solving sub-diffusion FPDEs.
- The gap between the CPU time executed by the ABC-PCM and that executed by the ABC-FPCM is evident in the tables. Particularly, the difference between them drastically increases as is fixed. This verifies that the proposed fast PCM is more efficient compared to the conventional PCM.
- Furthermore, the ABC-FPCM is much more efficient in terms of memory management compared to the existing method because it requires storing all previous values (, , and ) to calculate by using the ABC-PCM efficiently. On the other hand, the APC-FPCM requires only local values.
- Figure 2 shows the effect of fractional order and types of fractional derivatives for , , , and . The first row depicts the evolution of the system for . We can see that the spiral pattern is broken when , and an irregular pattern appears when .
- The second and third rows describe the evolution of the system for the ABC and Liouville–Caputo fractional derivatives of order , respectively. In the fractional-order system, similar to the case of , the spiral pattern is broken over time.
- In addition, in the fractional systems, a spiral pattern exists at , but the spiral pattern disappears at . This phenomenon is similar to the case where , , and has a wider pattern.
- It can be seen that the solution of the problem equipped with the ABC derivative is slower and wider than the solution of the problem equipped with the Liouville–Caputo derivative.
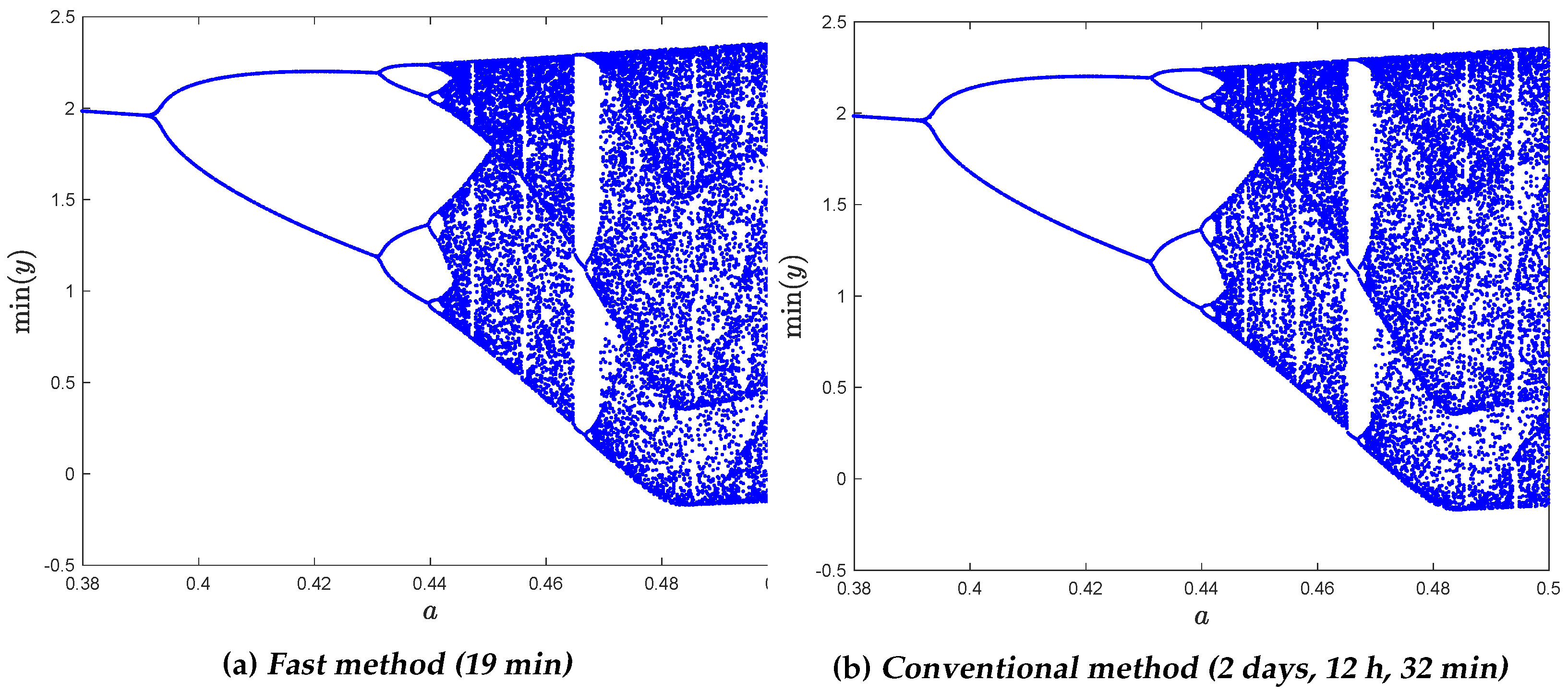
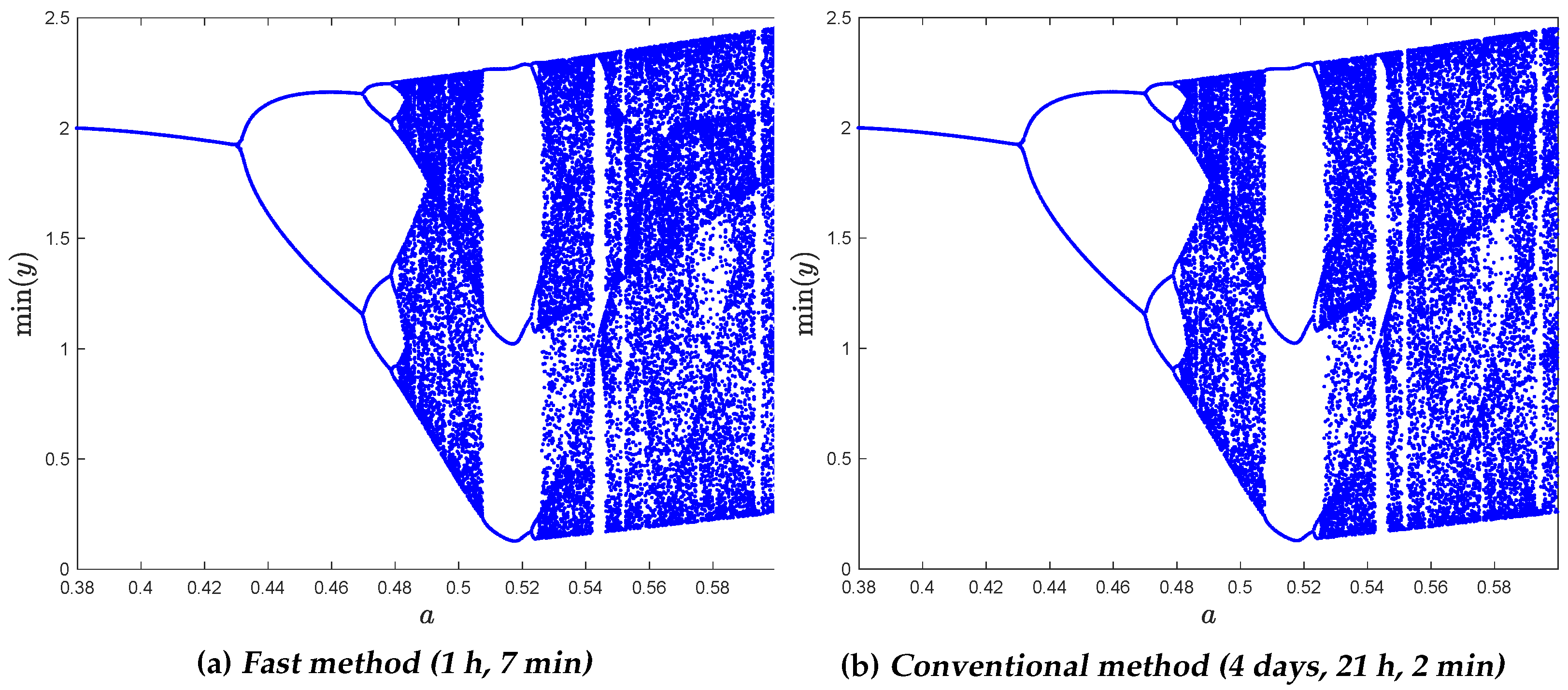
4.3. Application to Fractional Dynamical Systems
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Additional Information on the Sum-of-Exponentials Approximation
- The reachability Gramian
- The observability Gramian
- are basis independent.
- In a lot of instances, not only the eigenvalues of P and Q but also the Hankel singular values decrease very quickly.
- Note that one of properties of the balanced basis is that hard-to-reach states are hard to observe. Therefore, we obtain the reduced model by using the Hankel singular values, except for the small ones.
| Theorem 1 | ||||||||
| 84 | 2.85 | 119 | 2.74 | 147 | 2.87 | 182 | 2.91 | |
| 182 | 5.29 | 238 | 6.15 | 308 | 7.97 | 378 | 9.39 | |
| 273 | 8.01 | 378 | 1.07 | 462 | 1.10 | 567 | 1.30 | |
| 15 | 1.01 | 19 | 9.18 | 23 | 1.11 | 27 | 1.14 | |
| 26 | 1.60 | 32 | 1.50 | 39 | 9.14 | 46 | 1.21 | |
| 37 | 1.10 | 47 | 8.56 | 54 | 7.89 | 64 | 1.16 | |
| 14 | 1.62 | 19 | 1.52 | 22 | 1.72 | 26 | 1.75 | |
| 25 | 3.23 | 31 | 2.99 | 38 | 1.57 | 45 | 2.20 | |
| 36 | 2.12 | 46 | 1.64 | 53 | 1.44 | 62 | 2.10 | |
| 14 | 3.19 | 18 | 2.96 | 21 | 3.35 | 25 | 3.41 | |
| 25 | 6.46 | 30 | 5.62 | 37 | 3.56 | 43 | 4.48 | |
| 35 | 5.44 | 44 | 4.22 | 52 | 4.47 | 61 | 4.31 | |
| T | 10 | |||||||
|---|---|---|---|---|---|---|---|---|
| Theorem 1 | ||||||||
| 98 | 2.85 | 119 | 2.74 | 133 | 2.74 | 147 | 2.74 | |
| 210 | 6.09 | 238 | 6.15 | 280 | 6.15 | 308 | 6.15 | |
| 336 | 8.84 | 378 | 1.07 | 420 | 1.07 | 462 | 1.07 | |
| 16 | 2.24 | 19 | 1.48 | 21 | 2.33 | 23 | 1.76 | |
| 29 | 1.15 | 32 | 2.78 | 36 | 2.51 | 39 | 1.89 | |
| 42 | 1.39 | 47 | 1.14 | 50 | 2.16 | 54 | 2.20 | |
| 16 | 3.89 | 19 | 3.37 | 20 | 6.79 | 22 | 5.16 | |
| 29 | 2.54 | 31 | 6.58 | 35 | 8.26 | 38 | 6.23 | |
| 41 | 2.77 | 46 | 2.56 | 49 | 5.90 | 53 | 7.82 | |
| 15 | 7.04 | 18 | 4.08 | 19 | 1.23 | 21 | 9.38 | |
| 28 | 5.32 | 30 | 1.05 | 34 | 1.66 | 37 | 1.27 | |
| 40 | 6.80 | 44 | 6.08 | 48 | 1.27 | 52 | 1.70 | |
| Algorithm A1: Balanced truncation method [42] |
Data: The desired error , quadrature points , and weights . Result: Reduced quadrature points and weights . Set , , and ; Solve two Lyapunov equations and ; Compute two singular-value decompositions of and ; Set and ; Compute a singular-value decomposition of , where ; Find k such that ; Form a matrix J, where , and otherwise; Set and ; Set , , and ; Compute the eigenvalue decomposition of ; Set ; Form and ; Set ; |
References
- Goychuk, I.; Heinsalu, E.; Patriarca, M.; Schmid, G.; Hänggi, P. Current and universal scaling in anomalous transport. Phys. Rev. E 2006, 73, 020101. [Google Scholar] [CrossRef]
- Klages, R.; Radons, G.; Sokolov, I.M. Anomalous Transport: Foundations and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zaslavsky, G.M. Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 2002, 371, 461–580. [Google Scholar] [CrossRef]
- Caputo, M. Models of flux in porous media with memory. Water Resour. Res. 2000, 36, 693–705. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer Science & Business Media: Cham, Switzerland, 2010. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Machado, J.A.T. Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Cham, Switzerland, 2011. [Google Scholar]
- Giusti, A. A comment on some new definitions of fractional derivative. Nonlinear Dyn. 2018, 93, 1757–1763. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J. Fractional derivatives with no-index law property: Application to chaos and statistics. Chaos Solitons Fractals 2018, 114, 516–535. [Google Scholar] [CrossRef]
- Srivastava, H.M. Some parametric and argument variations of the operators of fractional calculus and related special functions and integral transformations. J. Nonlinear Convex Anal. 2021, 22, 1501–1520. [Google Scholar]
- Srivastava, H.M. An introductory overview of fractional-calculus operators based upon the Fox-Wright and related higher transcendental functions. J. Adv. Eng. Comput. 2021, 5, 135–166. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Gómez, J.F. Fractional Derivatives with Mittag-Leffler Kernel: Trends and Applications in Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Gómez-Aguilar, J.; Atangana, A. Fractional Derivatives with the Power-Law and the Mittag–Leffler Kernel Applied to the Nonlinear Baggs–Freedman Model. Fractal Fract. 2018, 2, 10. [Google Scholar] [CrossRef]
- Owolabi, K.M. Modelling and simulation of a dynamical system with the Atangana-Baleanu fractional derivative. Eur. Phys. J. Plus 2018, 133, 15. [Google Scholar] [CrossRef]
- Alqahtani, R.T. Atangana-Baleanu derivative with fractional order applied to the model of groundwater within an unconfined aquifer. J. Nonlinear Sci. Appl. 2016, 9, 3647–3654. [Google Scholar] [CrossRef]
- Saad, K.M.; Khader, M.; Gómez-Aguilar, J.; Baleanu, D. Numerical solutions of the fractional Fisher’s type equations with Atangana-Baleanu fractional derivative by using spectral collocation methods. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 023116. [Google Scholar] [CrossRef] [PubMed]
- Baleanu, D.; Jajarmi, A.; Hajipour, M. On the nonlinear dynamical systems within the generalized fractional derivatives with Mittag–Leffler kernel. Nonlinear Dyn. 2018, 94, 397–414. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Djida, J.; Atangana, A.; Area, I. Numerical computation of a fractional derivative with non-local and non-singular kernel. Math. Model. Nat. Phenom. 2017, 12, 4–13. [Google Scholar] [CrossRef]
- Nguyen, T.B.; Jang, B. A high-order predictor-corrector method for solving nonlinear differential equations of fractional order. Fract. Calc. Appl. Anal. 2017, 20, 447–476. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.; Jang, B. An efficient numerical approach for solving two-point fractional order nonlinear boundary value problems with Robin boundary conditions. Adv. Differ. Equ. 2021, 193. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J.; Kim, H.; Jang, B. A fast and high-order numerical method for nonlinear fractional-order differential equations with non-singular kernel. Appl. Numer. Math. 2021, 163, 57–76. [Google Scholar] [CrossRef]
- Sun, Z.z.; Wu, X. A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 2006, 56, 193–209. [Google Scholar] [CrossRef]
- Cui, M. Compact finite difference method for the fractional diffusion equation. J. Comput. Phys. 2009, 228, 7792–7804. [Google Scholar] [CrossRef]
- Brunner, H.; Hairer, E.; Nørsett, S. Runge-Kutta theory for Volterra integral equations of the second kind. Math. Comput. 1982, 39, 147–163. [Google Scholar] [CrossRef]
- Capobianco, G.; Conte, D.; Del Prete, I.; Russo, E. Fast Runge–Kutta methods for nonlinear convolution systems of Volterra integral equations. BIT Numer. Math. 2007, 47, 259–275. [Google Scholar] [CrossRef]
- Deng, J.; Zhao, L.; Wu, Y. Efficient algorithms for solving the fractional ordinary differential equations. Appl. Math. Comput. 2015, 269, 196–216. [Google Scholar] [CrossRef]
- Kumar, P.; Agrawal, O.P. An approximate method for numerical solution of fractional differential equations. Signal Process. 2006, 86, 2602–2610. [Google Scholar] [CrossRef]
- Li, C.; Chen, A.; Ye, J. Numerical approaches to fractional calculus and fractional ordinary differential equation. J. Comput. Phys. 2011, 230, 3352–3368. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A. Chaotic behaviour in system of noninteger-order ordinary differential equations. Chaos Solitons Fractals 2018, 115, 362–370. [Google Scholar] [CrossRef]
- lknur Koca. Efficient numerical approach for solving fractional partial differential equations with non-singular kernel derivatives. Chaos Solitons Fractals 2018, 116, 278–286. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, J.; Zhang, Q.; Zhang, Z. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Commun. Comput. Phys. 2017, 21, 650–678. [Google Scholar] [CrossRef]
- Cao, J.; Xu, C. A high order schema for the numerical solution of the fractional ordinary differential equations. J. Comput. Phys. 2013, 238, 154–168. [Google Scholar] [CrossRef]
- Garvie, M.R. Finite-difference schemes for reaction–diffusion equations modeling predator–prey interactions in M ATLAB. Bull. Math. Biol. 2007, 69, 931–956. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Chen, D.; Ma, M.; Zhang, X.; Wu, Y. Feigenbaum’s constants in reverse bifurcation of fractional-order Rössler system. Chaos Solitons Fractals 2017, 99, 116–123. [Google Scholar] [CrossRef]
- Laub, A.; Heath, M.; Paige, C.; Ward, R. Computation of system balancing transformations and other applications of simultaneous diagonalization algorithms. IEEE Trans. Autom. Control 1987, 32, 115–122. [Google Scholar] [CrossRef]
- Gugercin, S.; Antoulas, A.C. A survey of model reduction by balanced truncation and some new results. Int. J. Control 2004, 77, 748–766. [Google Scholar] [CrossRef]
- Enns, D.F. Model reduction with balanced realizations: An error bound and a frequency weighted generalization. In Proceedings of the 23rd IEEE Conference on Decision and Control, Las Vegas, NV, USA, 12–14 December 1984; IEEE: Manhattan, NY, USA,, 1984; pp. 127–132. [Google Scholar]
- Xu, K.; Jiang, S. A bootstrap method for sum-of-poles approximations. J. Sci. Comput. 2013, 55, 16–39. [Google Scholar] [CrossRef]


| The number of exponentials in [35] | ||||||||
| 25 | 29 | 33 | 37 | 30 | 35 | 40 | 44 | |
| 34 | 40 | 45 | 51 | 39 | 46 | 52 | 59 | |
| 43 | 51 | 58 | 66 | 49 | 57 | 65 | 74 | |
| The number of exponentials in our method | ||||||||
| 18 | 19 | 21 | 23 | 19 | 21 | 23 | 25 | |
| 30 | 34 | 37 | 43 | 31 | 34 | 39 | 43 | |
| 45 | 50 | 53 | 60 | 45 | 50 | 54 | 60 | |
| The number of exponentials in [35] | ||||||||
| 25 | 34 | 43 | 55 | 30 | 41 | 52 | 66 | |
| 34 | 45 | 58 | 69 | 39 | 51 | 65 | 81 | |
| 40 | 51 | 64 | 79 | 43 | 57 | 72 | 84 | |
| The number of exponentials in our method | ||||||||
| 18 | 21 | 25 | 30 | 19 | 21 | 27 | 30 | |
| 30 | 37 | 43 | 49 | 31 | 37 | 44 | 50 | |
| 40 | 48 | 56 | 82 | 41 | 48 | 58 | 82 | |
| ABC-FPCM | ABC-PCM | |||||||
|---|---|---|---|---|---|---|---|---|
| roc | roc | roc | roc | |||||
| h | ||||||||
| 1/10 | 3.37 | - | 1.85 | - | 3.37 | - | 1.85 | - |
| 1/20 | 9.03 | 1.90 | 4.92 | 1.91 | 9.03 | 1.90 | 4.92 | 1.91 |
| 1/40 | 1.71 | 2.40 | 1.14 | 2.11 | 1.71 | 2.40 | 1.14 | 2.11 |
| 1/80 | 3.98 | 2.10 | 2.67 | 2.09 | 3.98 | 2.10 | 2.67 | 2.09 |
| 1/160 | 9.35 | 2.09 | 6.33 | 2.08 | 9.35 | 2.09 | 6.33 | 2.08 |
| 1/320 | 2.21 | 2.08 | 1.51 | 2.07 | 2.21 | 2.08 | 1.51 | 2.07 |
| 1/640 | 5.28 | 2.07 | 3.61 | 2.06 | 5.28 | 2.07 | 3.61 | 2.06 |
| h | ||||||||
| 1/10 | 7.35 | - | 4.93 | - | 7.35 | - | 4.93 | - |
| 1/20 | 1.55 | 2.24 | 1.11 | 2.15 | 1.55 | 2.24 | 1.11 | 2.15 |
| 1/40 | 3.53 | 2.14 | 2.56 | 2.11 | 3.53 | 2.14 | 2.56 | 2.11 |
| 1/80 | 8.24 | 2.10 | 6.02 | 2.09 | 8.24 | 2.10 | 6.02 | 2.09 |
| 1/160 | 1.95 | 2.08 | 1.43 | 2.07 | 1.95 | 2.08 | 1.43 | 2.07 |
| 1/320 | 4.70 | 2.06 | 3.46 | 2.05 | 4.70 | 2.06 | 3.46 | 2.05 |
| 1/640 | 1.14 | 2.04 | 8.41 | 2.04 | 1.14 | 2.04 | 8.41 | 2.04 |
| h | ||||||||
| 1/10 | 1.82 | - | 1.38 | - | 1.82 | - | 1.38 | - |
| 1/20 | 3.95 | 2.21 | 2.99 | 2.21 | 3.95 | 2.21 | 2.99 | 2.21 |
| 1/40 | 9.17 | 2.11 | 6.84 | 2.13 | 9.17 | 2.11 | 6.84 | 2.13 |
| 1/80 | 2.21 | 2.05 | 1.62 | 2.08 | 2.21 | 2.05 | 1.62 | 2.08 |
| 1/160 | 5.41 | 2.03 | 3.93 | 2.04 | 5.42 | 2.03 | 3.94 | 2.04 |
| 1/320 | 1.35 | 2.01 | 9.68 | 2.02 | 1.34 | 2.01 | 9.67 | 2.03 |
| 1/640 | 3.39 | 1.99 | 2.41 | 2.01 | 3.33 | 2.01 | 2.39 | 2.01 |
| ABC-FPCM | ABC-PCM | |||||||
|---|---|---|---|---|---|---|---|---|
| roc | roc | roc | roc | |||||
| h | ||||||||
| 1/10 | 5.14 | - | 2.47 | - | 5.14 | - | 2.47 | |
| 1/20 | 2.00 | 1.36 | 8.53 | 1.54 | 2.00 | 1.36 | 8.53 | 1.54 |
| 1/40 | 5.59 | 1.84 | 2.29 | 1.90 | 5.59 | 1.84 | 2.29 | 1.90 |
| 1/80 | 1.34 | 2.06 | 5.56 | 2.04 | 1.34 | 2.06 | 5.56 | 2.04 |
| 1/160 | 3.20 | 2.07 | 1.36 | 2.03 | 3.20 | 2.07 | 1.36 | 2.03 |
| 1/320 | 7.81 | 2.03 | 3.36 | 2.02 | 7.81 | 2.03 | 3.36 | 2.02 |
| 1/640 | 1.93 | 2.02 | 8.31 | 2.02 | 1.93 | 2.02 | 8.31 | 2.02 |
| h | ||||||||
| 1/10 | 1.09 | - | 5.72 | - | 1.09 | - | 5.72 | - |
| 1/20 | 2.88 | 1.93 | 1.45 | 1.98 | 2.88 | 1.93 | 1.45 | 1.98 |
| 1/40 | 6.89 | 2.06 | 3.51 | 2.04 | 6.89 | 2.06 | 3.51 | 2.04 |
| 1/80 | 1.66 | 2.05 | 8.49 | 2.05 | 1.66 | 2.05 | 8.49 | 2.05 |
| 1/160 | 4.03 | 2.04 | 2.06 | 2.04 | 4.03 | 2.04 | 2.06 | 2.04 |
| 1/320 | 9.84 | 2.04 | 5.03 | 2.04 | 9.84 | 2.04 | 5.03 | 2.04 |
| 1/640 | 2.41 | 2.03 | 1.23 | 2.03 | 2.41 | 2.03 | 1.23 | 2.03 |
| h | ||||||||
| 1/10 | 4.37 | - | 2.03 | - | 4.37 | - | 2.03 | - |
| 1/20 | 8.14 | 2.42 | 3.70 | 2.46 | 8.14 | 2.42 | 3.70 | 2.46 |
| 1/40 | 1.51 | 2.43 | 6.97 | 2.41 | 1.51 | 2.43 | 6.97 | 2.41 |
| 1/80 | 2.94 | 2.36 | 1.39 | 2.32 | 2.94 | 2.37 | 1.39 | 2.32 |
| 1/160 | 6.05 | 2.28 | 2.97 | 2.23 | 6.04 | 2.28 | 2.96 | 2.23 |
| 1/320 | 1.29 | 2.23 | 6.54 | 2.18 | 1.31 | 2.20 | 6.63 | 2.16 |
| 1/640 | 2.74 | 2.23 | 1.46 | 2.17 | 2.99 | 2.13 | 1.54 | 2.10 |
| ABC-FPCM | ABC-PCM | ABC-FPCM | ABC-PCM | ||||||||||
| h | roc | CT(s) | roc | CT(s) | roc | CT(s) | roc | CT(s) | |||||
| 1/10 | 1.81 | - | 1.017 | 1.81 | - | 1.101 | 1.52 | - | 1.005 | 1.52 | - | 1.149 | |
| 1/20 | 4.96 | 1.87 | 1.975 | 4.96 | 1.87 | 2.639 | 3.82 | 1.99 | 2.115 | 3.82 | 1.99 | 2.508 | |
| 1/40 | 1.33 | 1.89 | 3.866 | 1.33 | 1.89 | 4.971 | 9.57 | 2.00 | 3.935 | 9.57 | 2.00 | 4.648 | |
| 1/80 | 3.56 | 1.91 | 7.997 | 3.56 | 1.91 | 10.120 | 2.40 | 2.00 | 8.206 | 2.40 | 2.00 | 10.139 | |
| 1/160 | 9.59 | 1.89 | 15.985 | 9.59 | 1.89 | 25.011 | 6.02 | 1.99 | 15.744 | 6.02 | 1.99 | 20.843 | |
| roc | CT(s) | roc | CT(s) | roc | CT(s) | roc | CT(s) | ||||||
| 1/10 | 9.67 | - | 3.761 | 9.67 | - | 62.772 | 1.00 | - | 3.875 | 1.00 | - | 61.249 | |
| 1/20 | 2.42 | 2.00 | 7.065 | 2.42 | 2.00 | 70.675 | 2.51 | 2.00 | 7.113 | 2.51 | 2.00 | 69.826 | |
| 1/40 | 6.05 | 2.00 | 13.893 | 6.05 | 2.00 | 90.210 | 6.27 | 2.00 | 13.590 | 6.27 | 2.00 | 86.519 | |
| 1/80 | 1.51 | 2.00 | 26.930 | 1.51 | 2.00 | 121.949 | 1.57 | 2.00 | 26.398 | 1.57 | 2.00 | 119.277 | |
| 1/160 | 3.78 | 2.00 | 29.859 | 3.78 | 2.00 | 153.570 | 3.92 | 2.00 | 21.083 | 3.92 | 2.00 | 155.221 | |
| ABC-FPCM | ABC-PCM | ABC-FPCM | ABC-PCM | ||||||||||
| h | roc | CT(s) | roc | CT(s) | roc | CT(s) | roc | CT(s) | |||||
| 1/10 | 1.19 | - | 0.101 | 1.19 | - | 0.079 | 7.64 | - | 0.101 | 7.64 | - | 0.069 | |
| 1/20 | 3.44 | 1.79 | 0.165 | 3.44 | 1.79 | 0.123 | 1.96 | 1.97 | 0.162 | 1.96 | 1.97 | 0.131 | |
| 1/40 | 9.07 | 1.92 | 0.368 | 9.07 | 1.92 | 0.324 | 4.79 | 2.03 | 0.290 | 4.79 | 2.03 | 0.312 | |
| 1/80 | 2.31 | 1.98 | 0.628 | 2.31 | 1.98 | 0.690 | 1.17 | 2.03 | 0.608 | 1.17 | 2.03 | 0.720 | |
| 1/160 | 5.79 | 1.99 | 1.207 | 5.79 | 1.99 | 1.807 | 2.89 | 2.02 | 1.183 | 2.89 | 2.02 | 1.797 | |
| roc | CT(s) | roc | CT(s) | roc | CT(s) | roc | CT(s) | ||||||
| 1/10 | 1.12 | - | 0.834 | 1.12 | - | 48.032 | 1.08 | - | 0.720 | 1.08 | - | 53.056 | |
| 1/20 | 2.70 | 2.06 | 0.642 | 2.70 | 2.06 | 53.879 | 2.60 | 2.05 | 0.779 | 2.60 | 2.05 | 52.112 | |
| 1/40 | 6.71 | 2.01 | 0.959 | 6.71 | 2.01 | 60.800 | 6.47 | 2.01 | 0.971 | 6.47 | 2.01 | 60.103 | |
| 1/80 | 1.68 | 2.00 | 1.391 | 1.68 | 2.00 | 69.584 | 1.62 | 2.00 | 1.479 | 1.62 | 2.00 | 64.850 | |
| 1/160 | 4.20 | 2.00 | 2.493 | 4.20 | 2.00 | 81.508 | 4.04 | 2.00 | 2.515 | 4.04 | 2.00 | 75.244 | |
| T | 125 | 250 | 500 | 1000 |
|---|---|---|---|---|
| Scheme 2 [37] | 17.03 | 35.22 | 74.13 | 155.21 |
| ABC-PCM | 52.41 | 149.55 | 495.41 | 1668.56 |
| ABC-FPCM | 55.23 | 109.69 | 223.01 | 547.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Kim, H.; Jang, B. A Novel Numerical Method for Solving Nonlinear Fractional-Order Differential Equations and Its Applications. Fractal Fract. 2024, 8, 65. https://doi.org/10.3390/fractalfract8010065
Lee S, Kim H, Jang B. A Novel Numerical Method for Solving Nonlinear Fractional-Order Differential Equations and Its Applications. Fractal and Fractional. 2024; 8(1):65. https://doi.org/10.3390/fractalfract8010065
Chicago/Turabian StyleLee, Seyeon, Hyunju Kim, and Bongsoo Jang. 2024. "A Novel Numerical Method for Solving Nonlinear Fractional-Order Differential Equations and Its Applications" Fractal and Fractional 8, no. 1: 65. https://doi.org/10.3390/fractalfract8010065
APA StyleLee, S., Kim, H., & Jang, B. (2024). A Novel Numerical Method for Solving Nonlinear Fractional-Order Differential Equations and Its Applications. Fractal and Fractional, 8(1), 65. https://doi.org/10.3390/fractalfract8010065






