Variable-Step Multiscale Katz Fractal Dimension: A New Nonlinear Dynamic Metric for Ship-Radiated Noise Analysis
Abstract
:1. Introduction
2. Methodology
2.1. KFD
2.2. VSMKFD
3. The Simulated Signal Analysis
3.1. The Chirp Signal Experiment
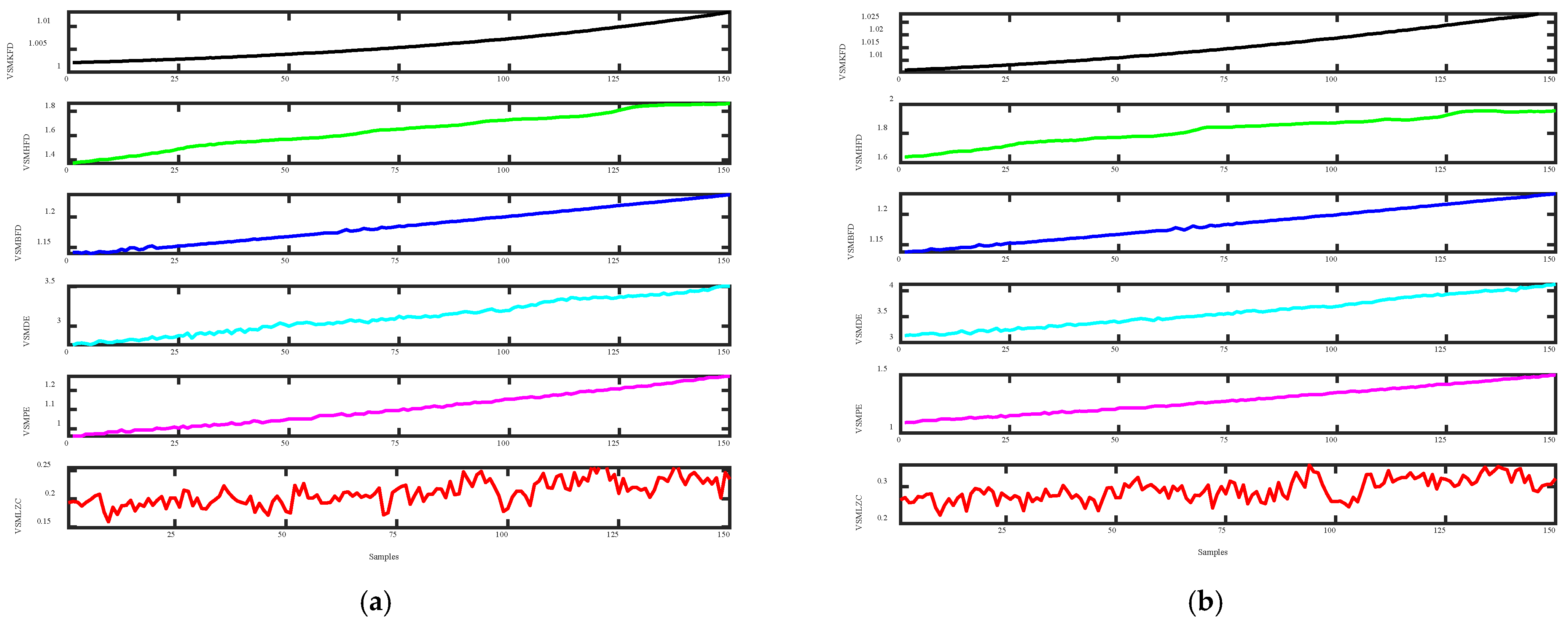
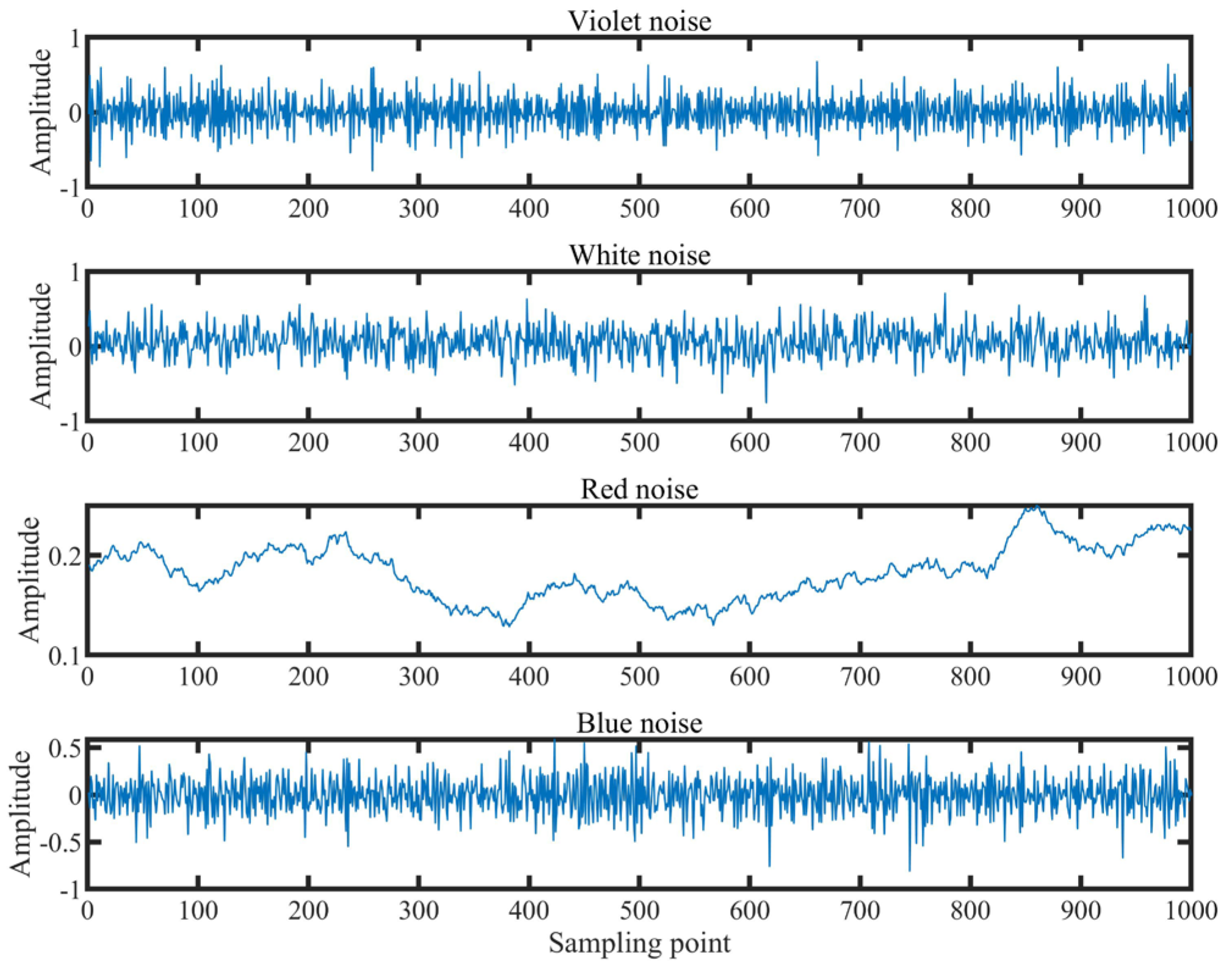
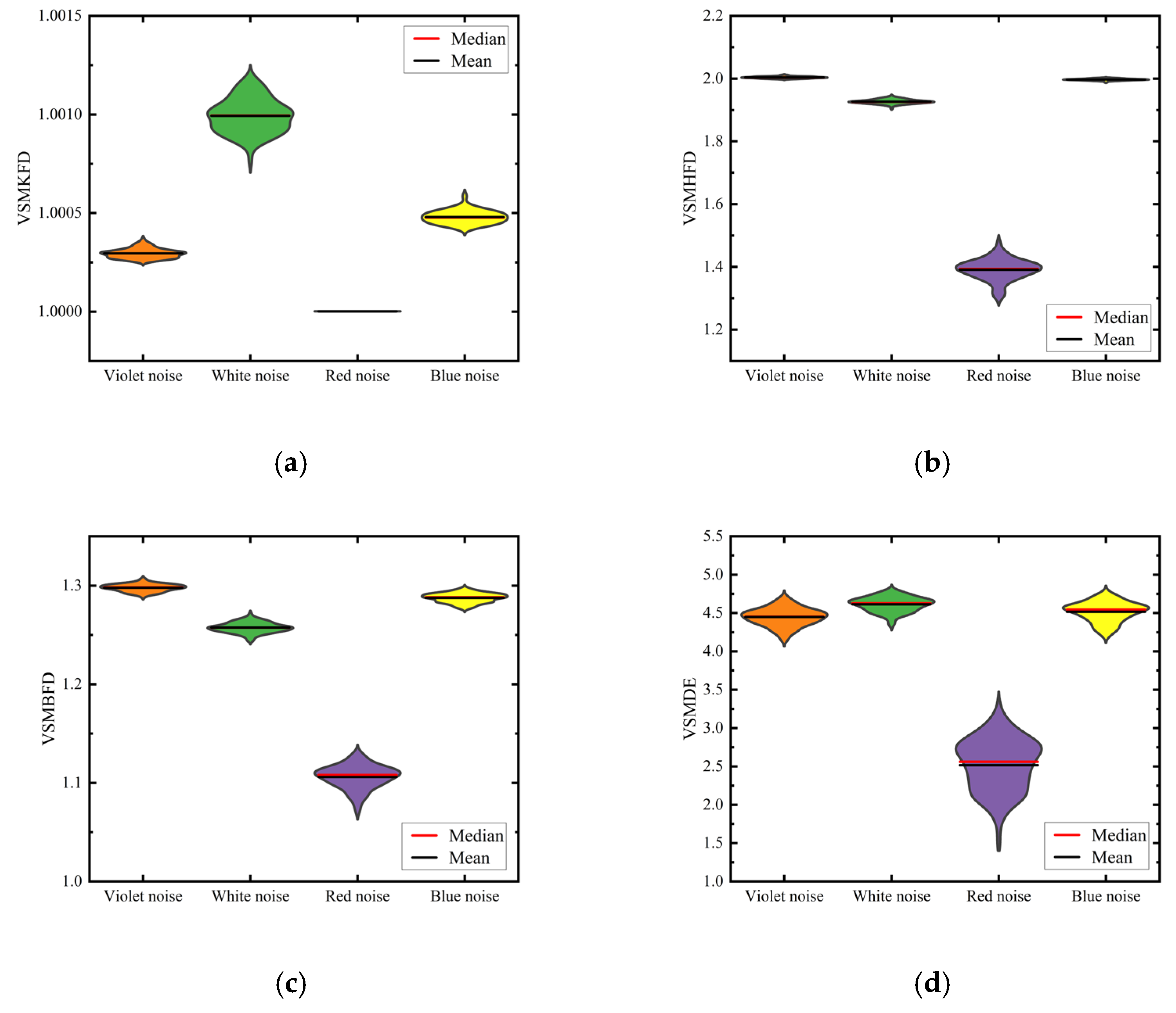
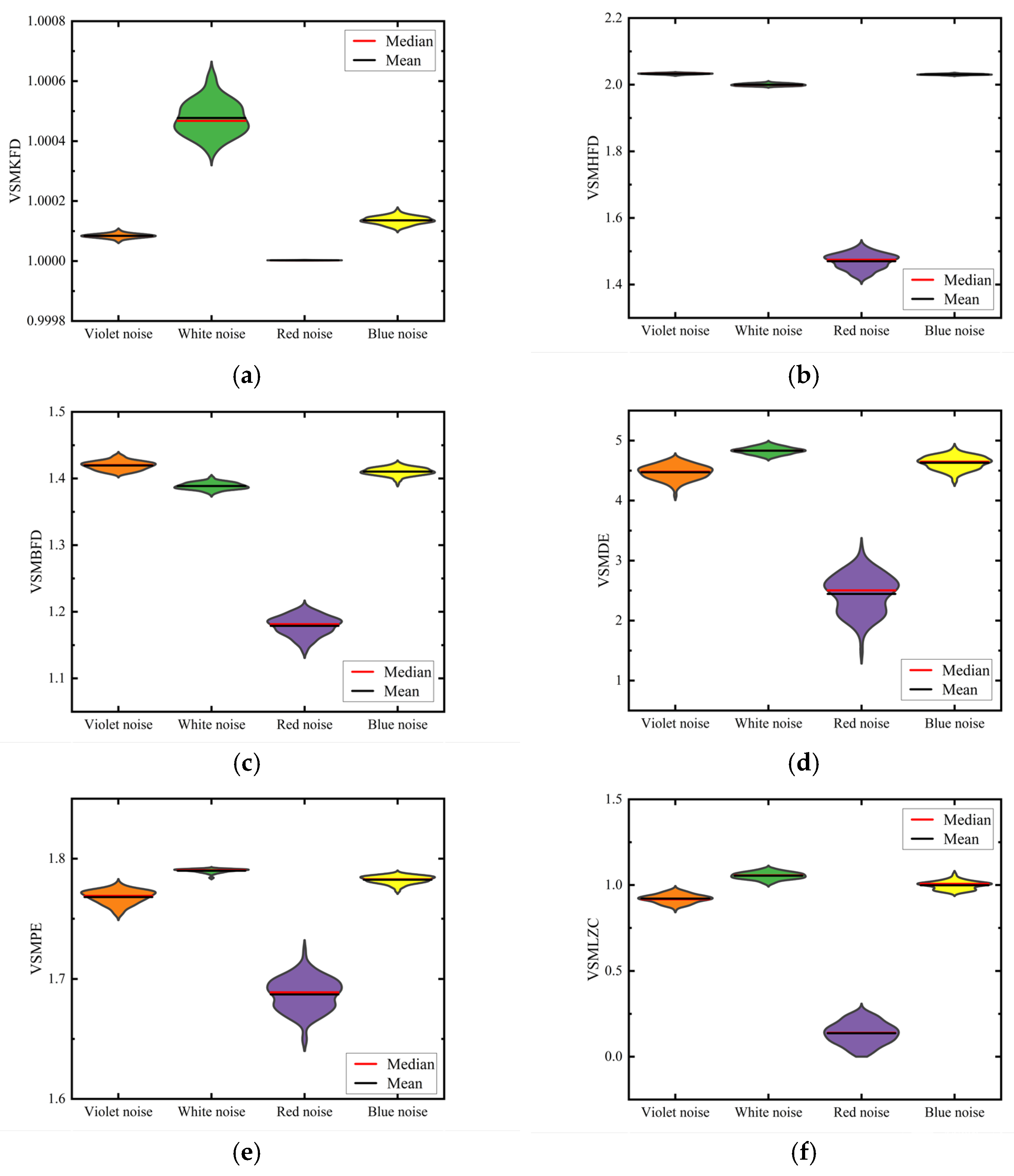
3.2. The Noise Signal Classification Experiment
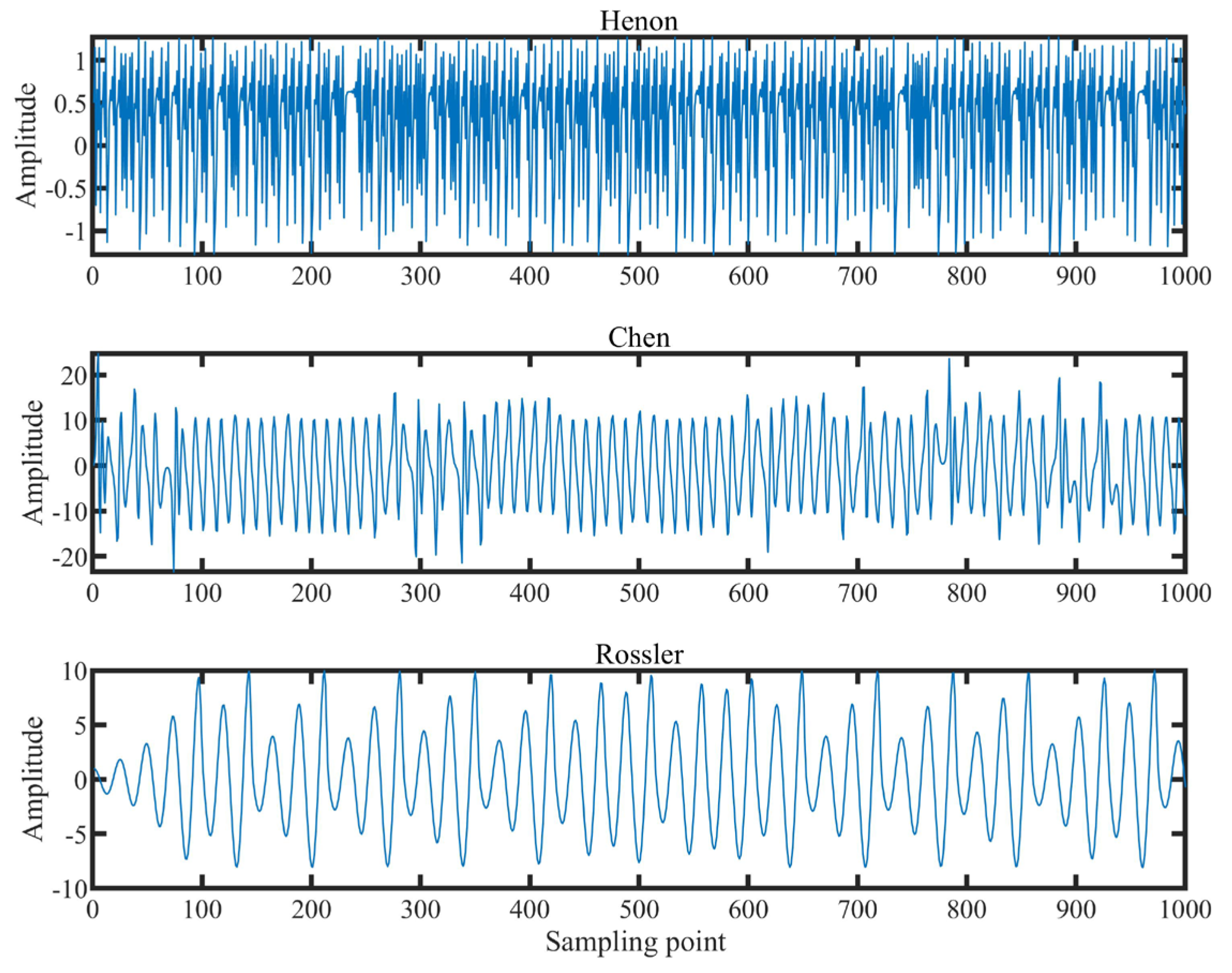
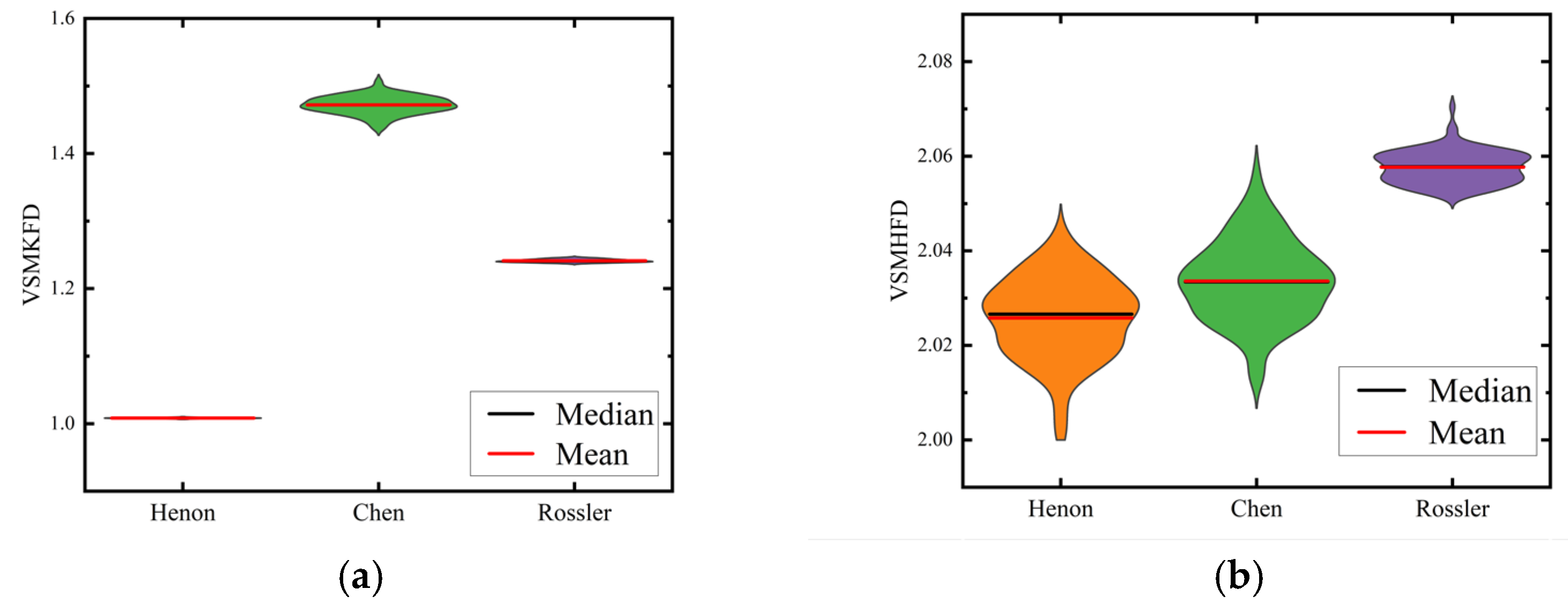
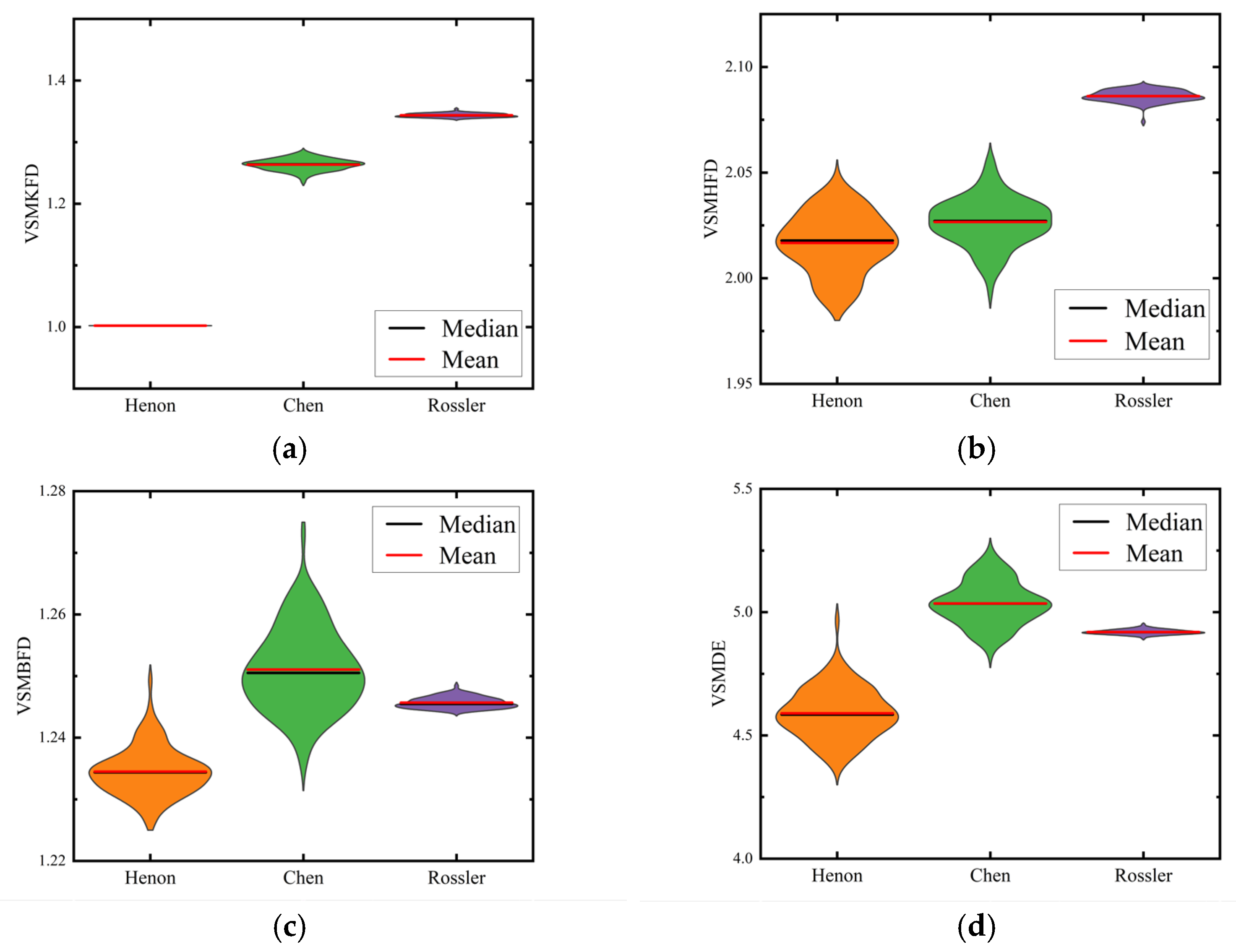
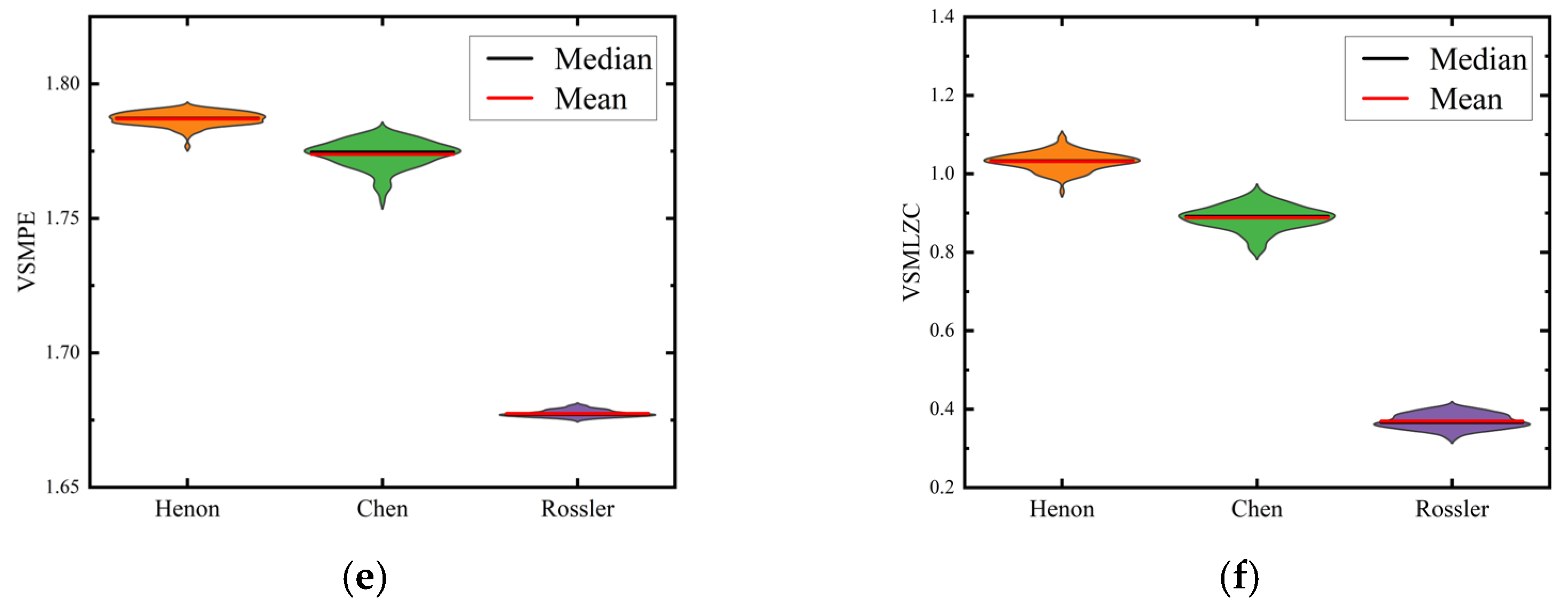
3.3. The Chaotic Signal Classification Experiment
4. The Feature Extraction Experiment on Ship-Radiated Noise
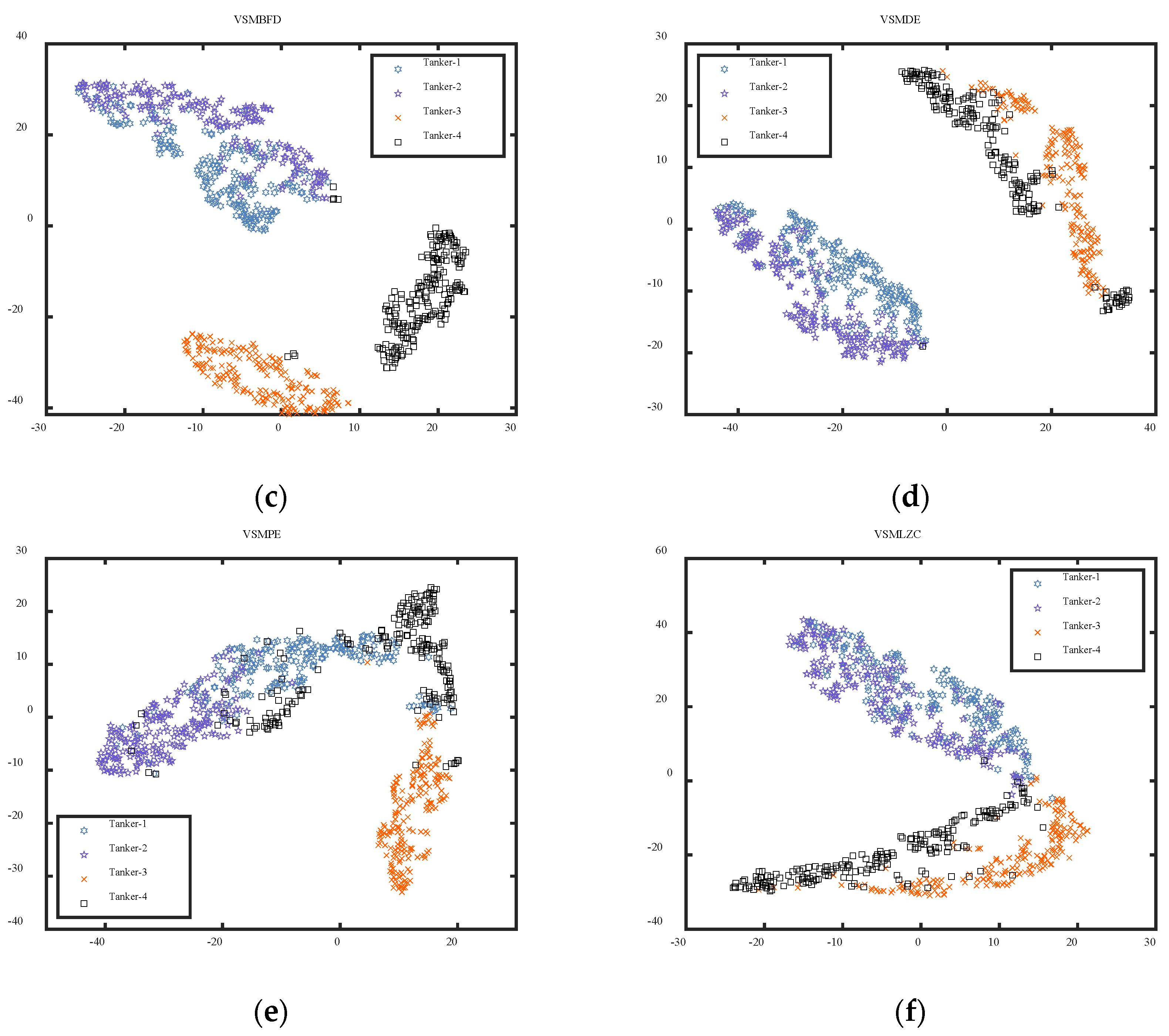
4.1. Case 1: Different Categories of Ship-Radiated Noise
4.2. Case 2: Same Categories of Ship-Radiated Noise
5. Conclusions
- (1)
- The VSMKFD was proposed by combining a variable-step multiscale process with KFD, which can improve the feature extraction performance of KFD and fully exploit signal information buried in multiscale.
- (2)
- It is validated that the VSMKFD is able to effectively reflect the frequency change of the chirp signal and has a stronger distinguishing capability for noise signals and chaotic signals than other nonlinear dynamic metrics.
- (3)
- The VSMKFD outperforms the VSMHFD, VSMBFD, VSMDE, VSMPE, and VSMLZC in classifying different and the same categories of SRN and achieves the highest recognition rate and more stable performance, which effectively improves the feature extraction performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| SRN | ship-radiated noise |
| LZC | Lempel–Ziv complexity |
| SE | sample entropy |
| FE | fuzzy entropy |
| PE | permutation entropy |
| DE | dispersion entropy |
| PLZC | permutation Lempel–Ziv complexity |
| DLZC | dispersion Lempel–Ziv complexity |
| NCDF | normal cumulative distribution function |
| DELZC | dispersion entropy-based Lempel–Ziv complexity |
| FDLZC | fluctuation-based dispersion Lempel–Ziv complexity |
| KFD | Katz fractal dimension |
| BFD | box fractal dimension |
| HFD | Higuchi fractal dimension |
| VSMKFD | variable-step multiscale Katz fractal dimension |
| VSMHFD | variable-step multiscale Higuchi fractal dimension |
| VSMBFD | variable-step multiscale box fractal dimension |
| VSMDE | variable-step multiscale dispersion entropy |
| VSMPE | variable-step multiscale permutation entropy |
| VSMLZC | variable-step multiscale Lempel–Ziv complexity |
References
- Li, G.; Hou, Y.; Yang, H. A novel method for frequency feature extraction of ship radiated noise based on variational mode decomposition, double coupled Duffing chaotic oscillator and multivariate multiscale dispersion entropy. Alex. Eng. J. 2022, 61, 6329–6347. [Google Scholar] [CrossRef]
- Gassmann, M.; Wiggins, S.M.; Hildebrand, J.A. Deep-water measurements of container ship radiated noise signatures and directionality. J. Acoust. Soc. Am. 2017, 142, 1563–1574. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zeng, X. Robust underwater noise targets classification using auditory inspired time-frequency analysis. Appl. Acoust. 2014, 7, 68–76. [Google Scholar] [CrossRef]
- Yuan, F.; Ke, X.; Cheng, E. Joint Representation and Recognition for Ship-Radiated Noise Based on Multimodal Deep Learning. J. Mar. Sci. Eng. 2019, 7, 380. [Google Scholar] [CrossRef]
- Ke, X.; Yuan, F.; Cheng, E. Integrated optimization of underwater acoustic ship-radiated noise recognition based on two-dimensional feature fusion. Appl. Acoust. 2020, 159, 107057. [Google Scholar] [CrossRef]
- Li, Y.; Geng, B.; Tang, B. Simplified coded dispersion entropy: A nonlinear metric for signal analysis. Nonlinear Dyn. 2023, 111, 9327–9344. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Zhou, Y. A Novel Denoising Method for Ship-Radiated Noise. J. Mar. Sci. Eng. 2023, 11, 1730. [Google Scholar]
- Li, Y.; Tang, B.; Jiao, S.; Su, Q. Snake Optimization-Based Variable-Step Multiscale Single Threshold Slope Entropy for Complexity Analysis of Signals. IEEE Trans. Instrum. Meas. 2023, 72, 6505313. [Google Scholar] [CrossRef]
- Siddagangaiah, S.; Li, Y.; Guo, X.; Chen, X.; Zhang, Q.; Yang, K.; Yang, Y. A complexity-based approach for the detection of weak signals in ocean ambient noise. Entropy 2016, 18, 101. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Y.; Sun, X.; Chen, M.; Bu, Q.; Gong, B. Integrating test device and method for creep failure and ultrasonic response of methane hydrate-bearing sediments. Rev. Sci. Instrum. 2023, 94, 025105. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Xue, Q.; Xu, B.; He, C.; Liu, F.; Ju, B.; Lu, S.; Liu, Y. Feature Extraction Using Hierarchical Dispersion Entropy for Rolling Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Richman, J.S.; Randall, M.J. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Simons, S.; Abásolo, D. Distance-Based Lempel-Ziv Complexity for the Analysis of Electroencephalograms in Patients with Alzheimer’s Disease. Entropy 2017, 19, 129. [Google Scholar] [CrossRef]
- Bai, Y.; Liang, Z.; Li, X. A Permutation Lempel-Ziv complexity measure for EEG analysis. Biomed. Signal Process. Control 2015, 19, 102–114. [Google Scholar] [CrossRef]
- Mao, X.; Shang, P.; Xu, M.; Peng, C. Measuring time series based on multiscale dispersion Lempel-Ziv complexity and dispersion entropy plane. Chaos Solitons Fractals 2020, 137, 109868. [Google Scholar] [CrossRef]
- Li, Y.; Geng, B.; Jiao, S. Dispersion entropy-based Lempel-Ziv complexity: A new metric for signal analysis. Chaos Solitons Fractals 2022, 161, 112400. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, S.; Geng, B. Refined composite multiscale fluctuation-based dispersion Lempel-Ziv complexity for signal analysis. ISA Trans. 2023, 133, 273–284. [Google Scholar] [CrossRef] [PubMed]
- Mendelbrot, B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed]
- Katz, M.J. Fractals and the analysis of waveforms. Comput. Biol. Med. 1988, 18, 145–156. [Google Scholar] [CrossRef] [PubMed]
- Gagnepain, J.J.; Roques-Carmes, C.F. Fractal approach to two-dimensional and three-dimensional surface roughness. Wear 1986, 109, 119–126. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D Nonlinear Phenom. 1988, 37, 277–283. [Google Scholar] [CrossRef]
- Hu, J.; Tung, W.; Gao, J. Detection of low observable targets within sea clutter by structure function based multifractal analysis. IEEE Trans. Antenn. Propag. 2006, 54, 136–143. [Google Scholar] [CrossRef]
- Burlaga, L.; Klein, L. Fractal structure of the inter planetary magnetic field. J. Geophys. Res. Space Phys. 1986, 91, 347–350. [Google Scholar] [CrossRef]
- Shi, C.-T. Signal Pattern Recognition Based on Fractal Features and Machine Learning. Appl. Sci. 2018, 8, 1327. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. Multiscale Entropy Approaches and Their Applications. Entropy 2020, 22, 644. [Google Scholar] [CrossRef]
- Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Lee, K.-Y.; Peng, C.-K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Li, Y.; Liang, L.; Zhang, S. Hierarchical Refined Composite Multi-Scale Fractal Dimension and Its Application in Feature Extraction of Ship-Radiated Noise. Remote Sens. 2023, 15, 3406. [Google Scholar] [CrossRef]
- Su, Z.; Shi, J.; Luo, Y.; Shen, C.; Zhu, Z. Fault severity assessment for rotating machinery via improved Lempel-Ziv complexity based on variable-step multiscale analysis and equiprobable space partitioning. Meas. Sci. Technol. 2022, 33, 055018. [Google Scholar] [CrossRef]
- Hénon, M. A two-dimensional mapping with a strange attractor. Commun. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Chen, C.-T. Signals and Systems; Oxford University Press: New York, NY, USA, 2004; p. 453. [Google Scholar]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- National Park Service. Available online: https://www.nps.gov/index.htm (accessed on 28 July 2023).
- Muhammad, I.; Zheng, J.; Shahid, A.; Muhammad, I.; Zafar, M.; Umar, H. DeepShip: An underwater acoustic benchmark dataset and a separable convolution based autoencoder for classification. Expert. Syst. Appl. 2021, 183, 115270. [Google Scholar]





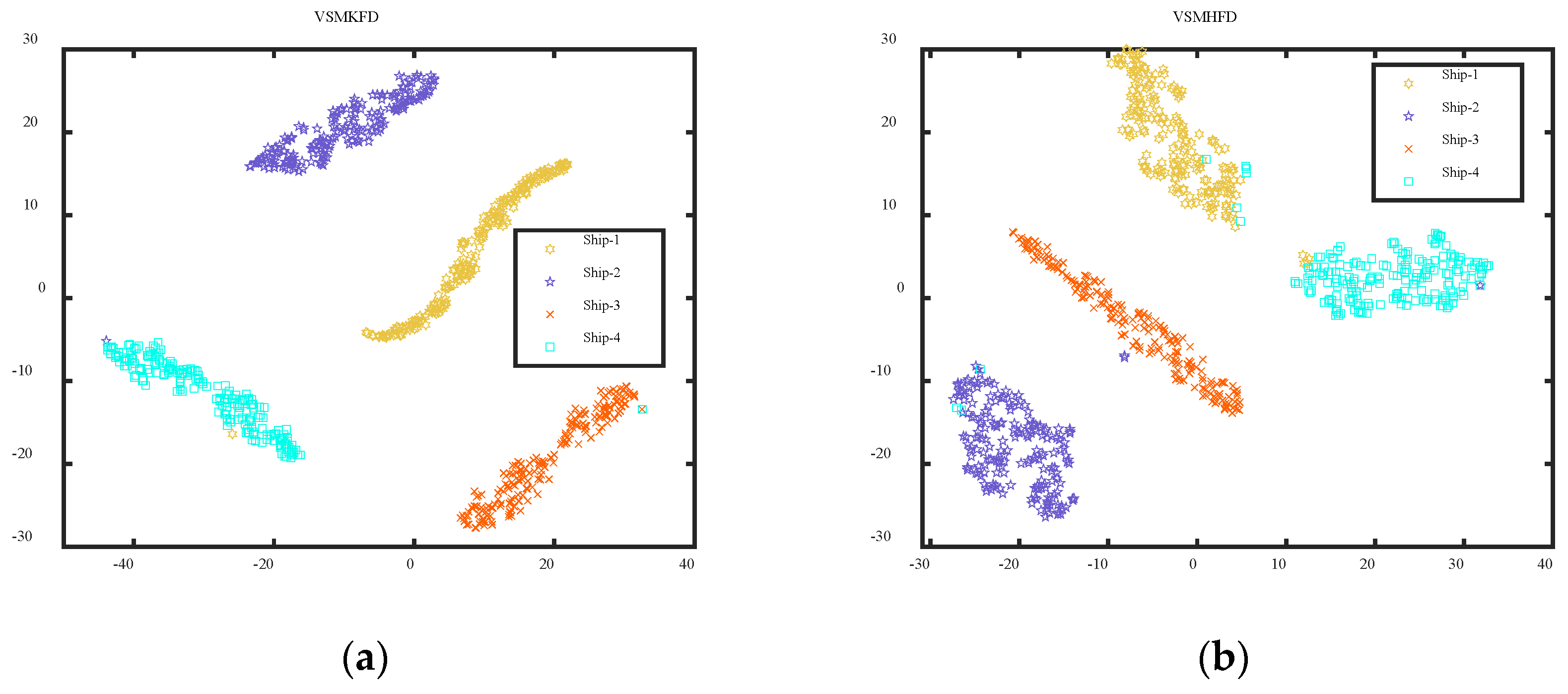
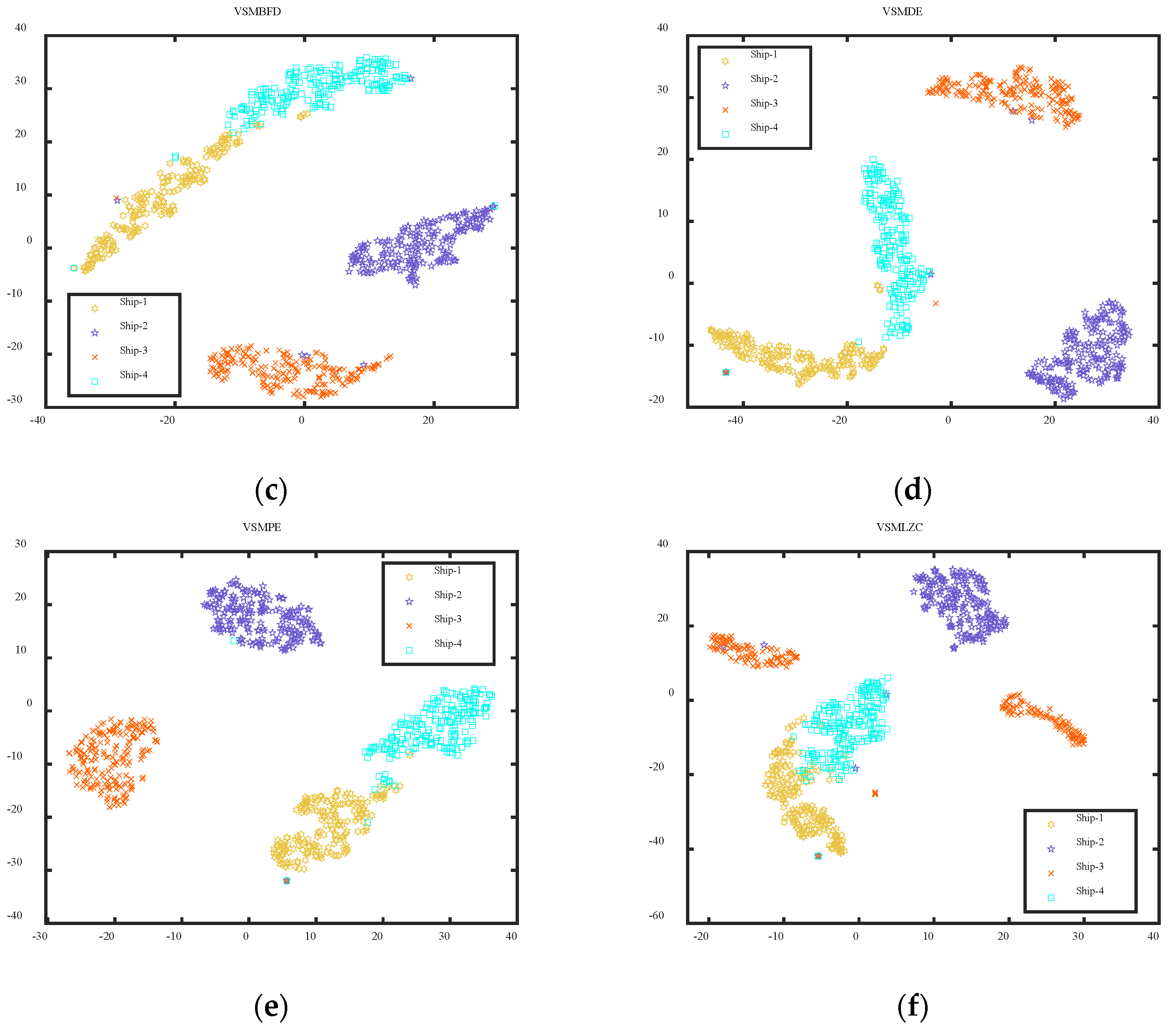
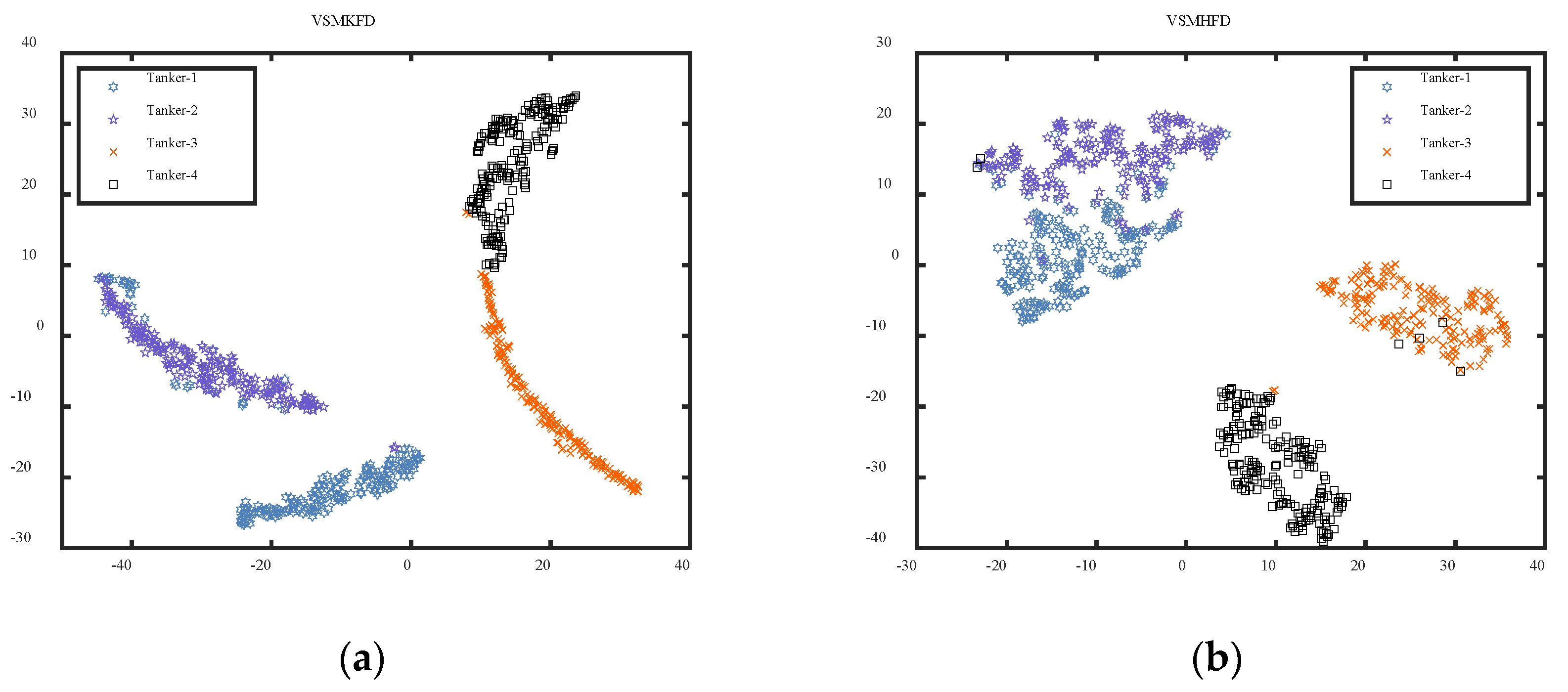
| Metrics | Number of Extracted Features | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| VSMKFD | 98.75 | 99.50 | 99.50 | 99.50 | 99.50 | 99.50 | 99.50 | 99.50 | 99.50 | 99.25 |
| VSMHFD | 94.25 | 98.25 | 99.00 | 99.00 | 99.25 | 99.25 | 99.25 | 99.25 | 99.00 | 99.00 |
| VSMBFD | 97.25 | 97.75 | 97.50 | 97.50 | 97.50 | 96.50 | 95.50 | 95.25 | 95.00 | 95.00 |
| VSMDE | 97.00 | 98.25 | 98.75 | 98.75 | 98.50 | 98.25 | 98.25 | 98.25 | 98.00 | 97.75 |
| VSMPE | 92.75 | 96.75 | 98.25 | 98.25 | 98.25 | 98.25 | 98.25 | 98.00 | 98.25 | 97.75 |
| VSMLZC | 90.50 | 95.50 | 95.75 | 95.75 | 95.75 | 96.00 | 95.50 | 95.25 | 95.25 | 95.25 |
| Metrics | Number of Extracted Features | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| VSMKFD | 96.75 | 98.50 | 99.25 | 99.25 | 99.25 | 99.25 | 99.00 | 98.75 | 98.75 | 98.50 |
| VSMHFD | 68.50 | 93.75 | 95.00 | 95.00 | 95.25 | 95.00 | 95.00 | 94.75 | 94.25 | 93.50 |
| VSMBFD | 70.25 | 91.00 | 92.25 | 92.25 | 92.25 | 91.75 | 91.25 | 90.75 | 90.50 | 90.50 |
| VSMDE | 65.00 | 88.00 | 89.25 | 88.75 | 89.25 | 88.75 | 88.25 | 87.25 | 87.25 | 86.00 |
| VSMPE | 66.00 | 81.25 | 86.00 | 87.25 | 87.00 | 87.25 | 86.00 | 85.25 | 84.50 | 83.00 |
| VSMLZC | 59.50 | 78.00 | 80.00 | 79.75 | 80.00 | 80.00 | 78.25 | 78.00 | 78.00 | 75.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhou, Y.; Jiao, S. Variable-Step Multiscale Katz Fractal Dimension: A New Nonlinear Dynamic Metric for Ship-Radiated Noise Analysis. Fractal Fract. 2024, 8, 9. https://doi.org/10.3390/fractalfract8010009
Li Y, Zhou Y, Jiao S. Variable-Step Multiscale Katz Fractal Dimension: A New Nonlinear Dynamic Metric for Ship-Radiated Noise Analysis. Fractal and Fractional. 2024; 8(1):9. https://doi.org/10.3390/fractalfract8010009
Chicago/Turabian StyleLi, Yuxing, Yuhan Zhou, and Shangbin Jiao. 2024. "Variable-Step Multiscale Katz Fractal Dimension: A New Nonlinear Dynamic Metric for Ship-Radiated Noise Analysis" Fractal and Fractional 8, no. 1: 9. https://doi.org/10.3390/fractalfract8010009
APA StyleLi, Y., Zhou, Y., & Jiao, S. (2024). Variable-Step Multiscale Katz Fractal Dimension: A New Nonlinear Dynamic Metric for Ship-Radiated Noise Analysis. Fractal and Fractional, 8(1), 9. https://doi.org/10.3390/fractalfract8010009







