The Averaging Principle for Caputo Type Fractional Stochastic Differential Equations with Lévy Noise
Abstract
:1. Introduction
2. Preliminaries
3. Averaging Principle
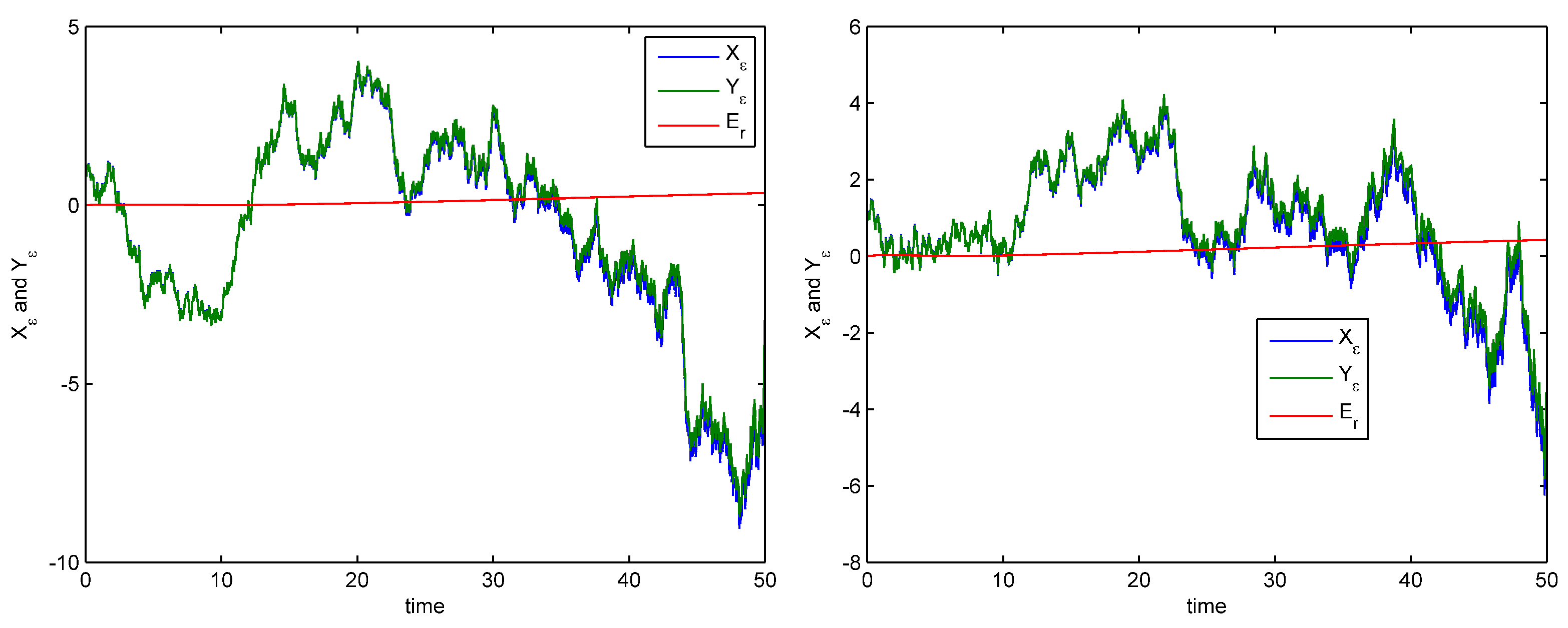
4. An Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, W.; Xu, W.; Zhang, S. The averaging principle for stochastic differential equations with Caputo fractional derivative. Appl. Math. Lett. 2019, 93, 79–84. [Google Scholar] [CrossRef]
- Guo, Z.; Hu, J.; Yuan, C. Averaging principle for a type of Caputo fractional stochastic differential equations. Chaos 2021, 31, 053123. [Google Scholar] [CrossRef] [PubMed]
- Gao, P. Averaging principle for multiscale stochastic reaction-diffusion-advection equations. Math. Methods Appl. Sci. 2019, 42, 1122–1150. [Google Scholar] [CrossRef]
- Luo, D.; Zhu, Q.; Zhang, Z. An averaging principle for stochastic fractional differential equations with time-delays. Appl. Math. Lett. 2020, 105, 106290. [Google Scholar] [CrossRef]
- Ahmed, H.M.; Zhu, Q. The averaging principle of Hilfer fractional stochastic delay differential equations with Poisson jumps. Appl. Math. Lett. 2021, 112, 106755. [Google Scholar] [CrossRef]
- Xu, W.; Xu, W. An effective averaging theory for fractional neutral stochastic equations of order 0<α<1 with Poisson jumps. Appl. Math. Lett. 2020, 106, 106344. [Google Scholar]
- Xu, W.; Xu, W.; Lu, K. An averaging principle for stochastic differential equations of fractional order 0<α<1. Fract. Calc. Appl. Anal. 2020, 23, 908–919. [Google Scholar]
- Li, M.; Wang, J. The existence and averaging principle for Caputo fractional stochastic delay differential systems. Fract. Calc. Appl. Anal. 2023, 26, 893–912. [Google Scholar] [CrossRef]
- Wang, Q.; Han, Z.; Zhang, X.; Yang, Y. Dynamics of the delay-coupled bubble system combined with the stochastic term. Chaos Solitons Fractals 2021, 148, 111053. [Google Scholar] [CrossRef]
- Xiao, G.; Fečkan, M.; Wang, J. On the averaging principle for stochastic differential equations involving Caputo fractional derivative. Chaos 2022, 32, 101105. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q. Stability of stochastic differential equations with Lévy noise. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 5211–5216. [Google Scholar]
- Xu, Y.; Duan, J.; Xu, W. An averaging principle for stochastic dynamical systems with Lévy noise. Physica D 2011, 240, 1395–1401. [Google Scholar] [CrossRef]
- Shen, G.; Xu, W.; Wu, J. An averaging principle for stochastic differential delay equations driven by time-changed Lévy noise. Acta Math. Sci. 2022, 42, 540–550. [Google Scholar] [CrossRef]
- Shen, G.; Xiao, R.; Yin, X. Averaging principle and stability of hybrid stochastic fractional differential equations driven by Lévy noise. Int. J. Syst. Sci. 2020, 51, 2115–2133. [Google Scholar] [CrossRef]
- Xu, W.; Duan, J.; Xu, W. An averaging principle for fractional stochastic differential equations with Lévy noise. Chaos 2020, 30, 083126. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Fu, H.; Wang, W. An averaging principle for caputo fractional stochastic differential equations with compensated Poisson random measure. J. Partial. Differ. Equ. 2022, 35, 1–10. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Ye, H.; Gao, J.; Ding, Y. A generalized Gronwall inequality and its application to a fractional differential equation. J. Math. Anal. Appl. 2007, 328, 1075–1081. [Google Scholar] [CrossRef]
- Umamaheswari, P.; Balachandran, K.; Annapoorani, N. Existence and stability results for Caputo fractional stochastic differential equations with Lévy noise. Filomat 2020, 34, 1739–1751. [Google Scholar] [CrossRef]
- Freidlin, M.I.; Wentzell, A.D. Random Perturbations of Dynamical Systems, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Application, 2nd ed.; Horwood Publishing Limited: Chichester, UK, 2007. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, L.; Xiao, G. The Averaging Principle for Caputo Type Fractional Stochastic Differential Equations with Lévy Noise. Fractal Fract. 2024, 8, 595. https://doi.org/10.3390/fractalfract8100595
Ren L, Xiao G. The Averaging Principle for Caputo Type Fractional Stochastic Differential Equations with Lévy Noise. Fractal and Fractional. 2024; 8(10):595. https://doi.org/10.3390/fractalfract8100595
Chicago/Turabian StyleRen, Lulu, and Guanli Xiao. 2024. "The Averaging Principle for Caputo Type Fractional Stochastic Differential Equations with Lévy Noise" Fractal and Fractional 8, no. 10: 595. https://doi.org/10.3390/fractalfract8100595
APA StyleRen, L., & Xiao, G. (2024). The Averaging Principle for Caputo Type Fractional Stochastic Differential Equations with Lévy Noise. Fractal and Fractional, 8(10), 595. https://doi.org/10.3390/fractalfract8100595




