Formation of Optical Fractals by Chaotic Solitons in Coupled Nonlinear Helmholtz Equations
Abstract
1. Introduction
2. The Methodology of RMESEM
3. Establishing Optical Soliton Solutions for CNHEs
- Case 1:
- Case 2:
- Case 3:
- Case 4:
- Cluster 1.1: For and ,
- Cluster 1.2: For and ,
- Cluster 1.3: For and ,
- Cluster 1.4: For , when ,
- Cluster 1.5: For , , and ,
- Cluster 2.1: For and ,
- Cluster 2.2: For and ,
- Cluster 2.3: For , , and ,
- Cluster 2.4: For , , and ,
- Cluster 2.5: For , , and ,
- Cluster 3.1: For and ,
- Cluster 3.2: For and ,
- Cluster 3.3: For and ,
- Cluster 3.4: For , when ,
- Cluster 3.5: For , , and ,
- Cluster 3.6: For , , and ,
- Cluster 3.7: For , , and ,
- Cluster 4.1: For ,
- Cluster 4.2: For and ,
- Cluster 4.3: For and ,
- Cluster 4.4: For , when ,
- Cluster 4.5: For , , and ,
- Cluster 4.6: For , , and ,
- Cluster 4.7: For , , and ,
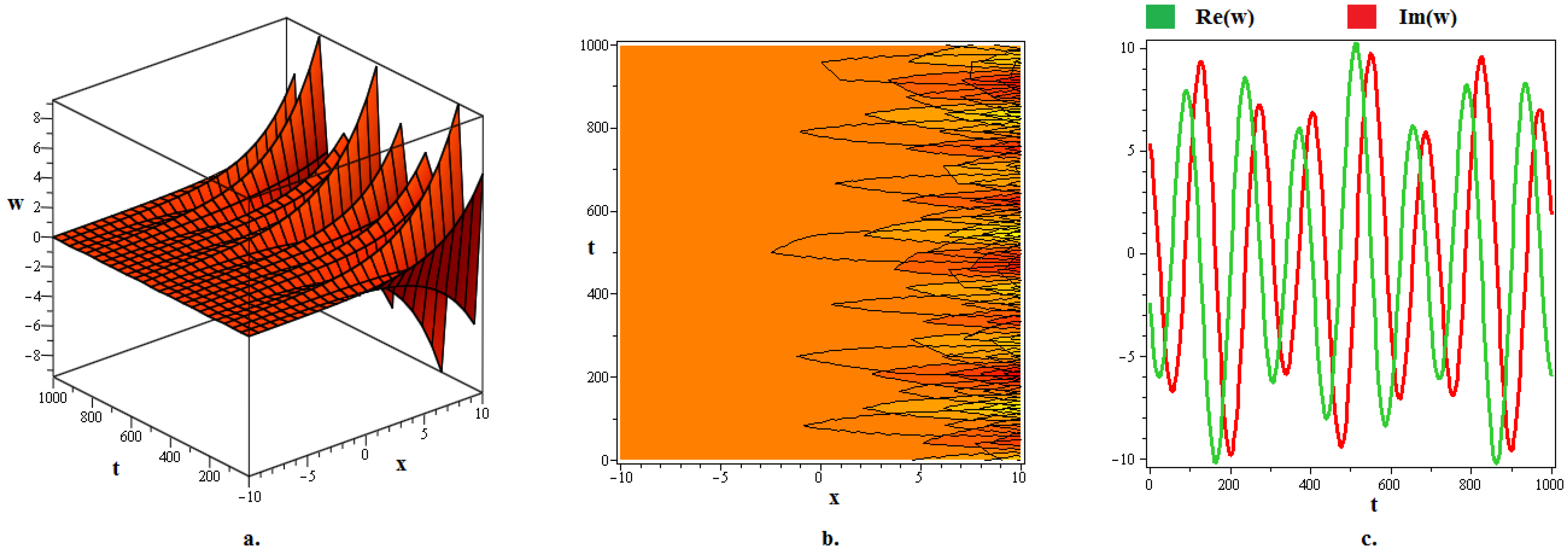
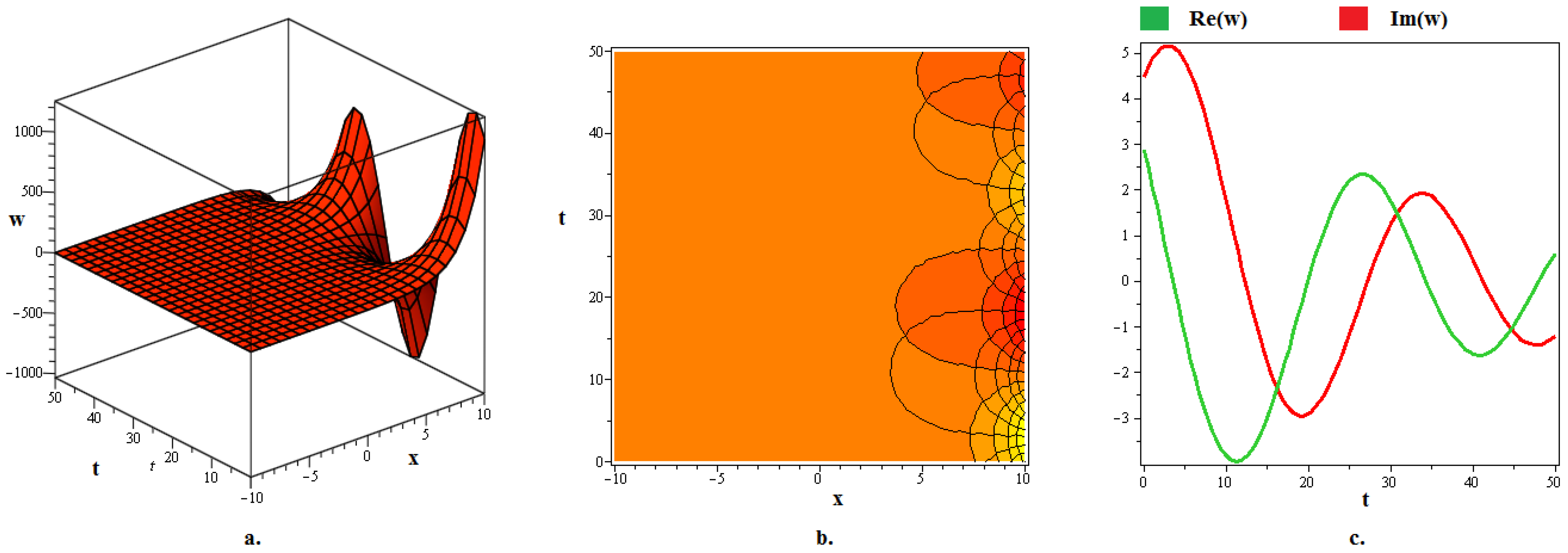
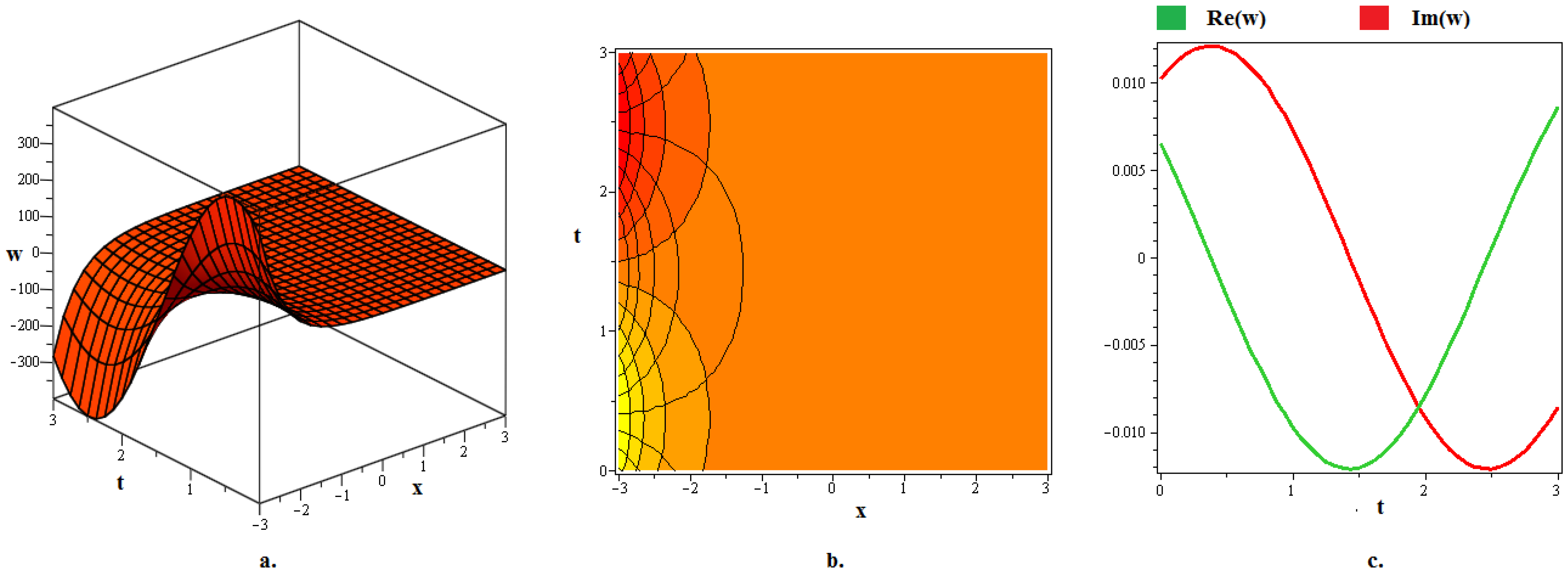
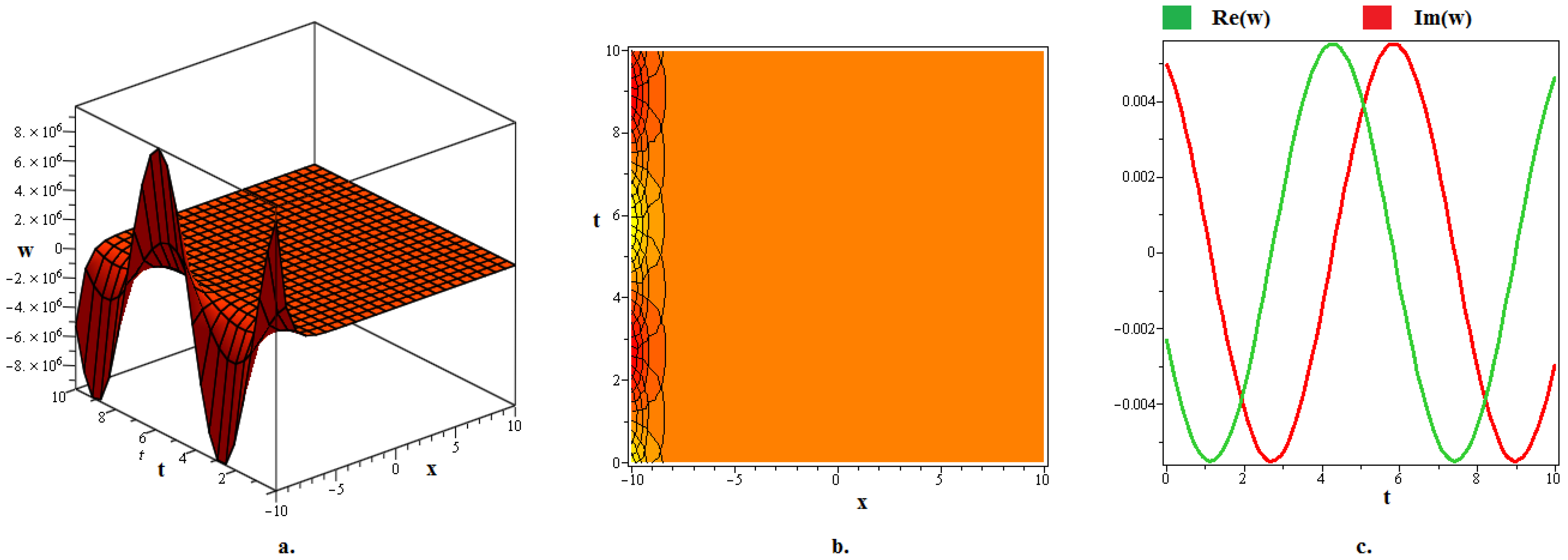
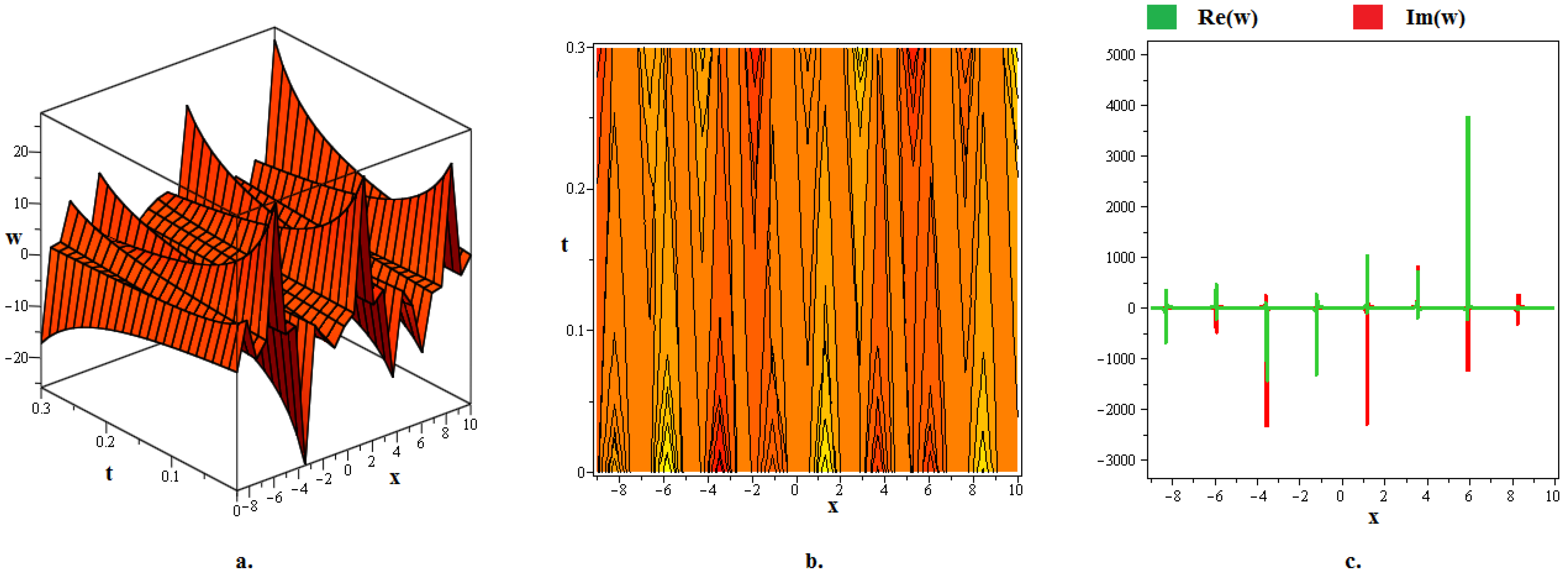
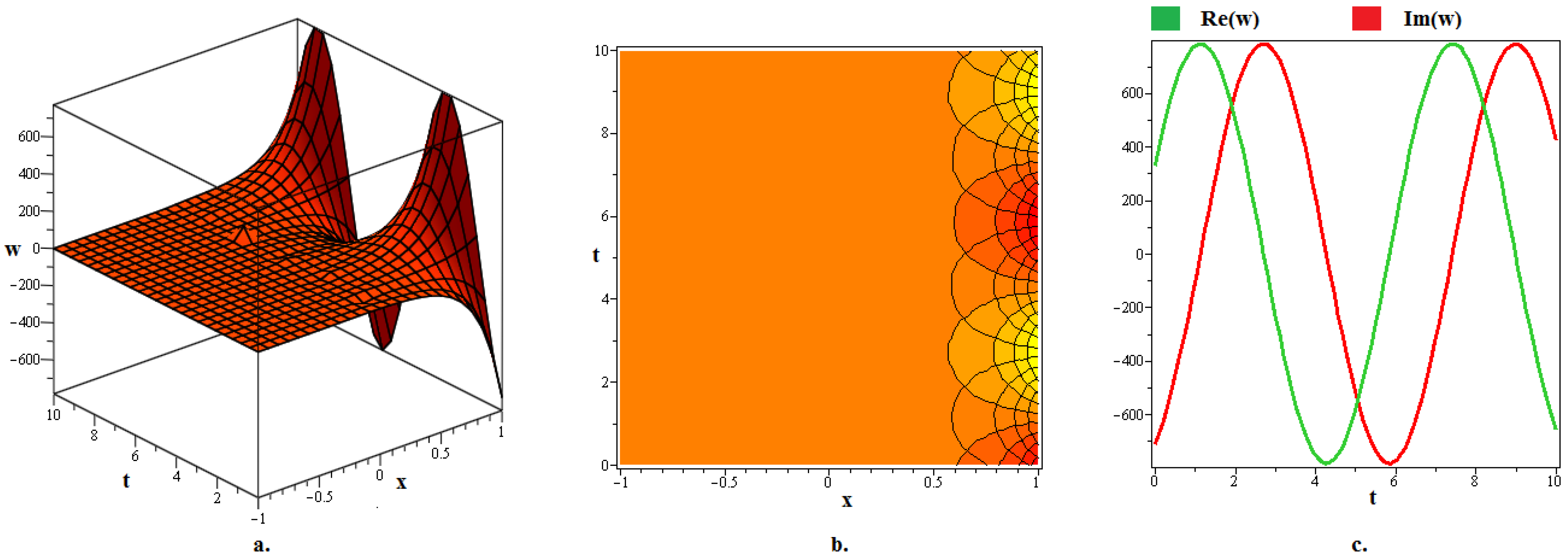
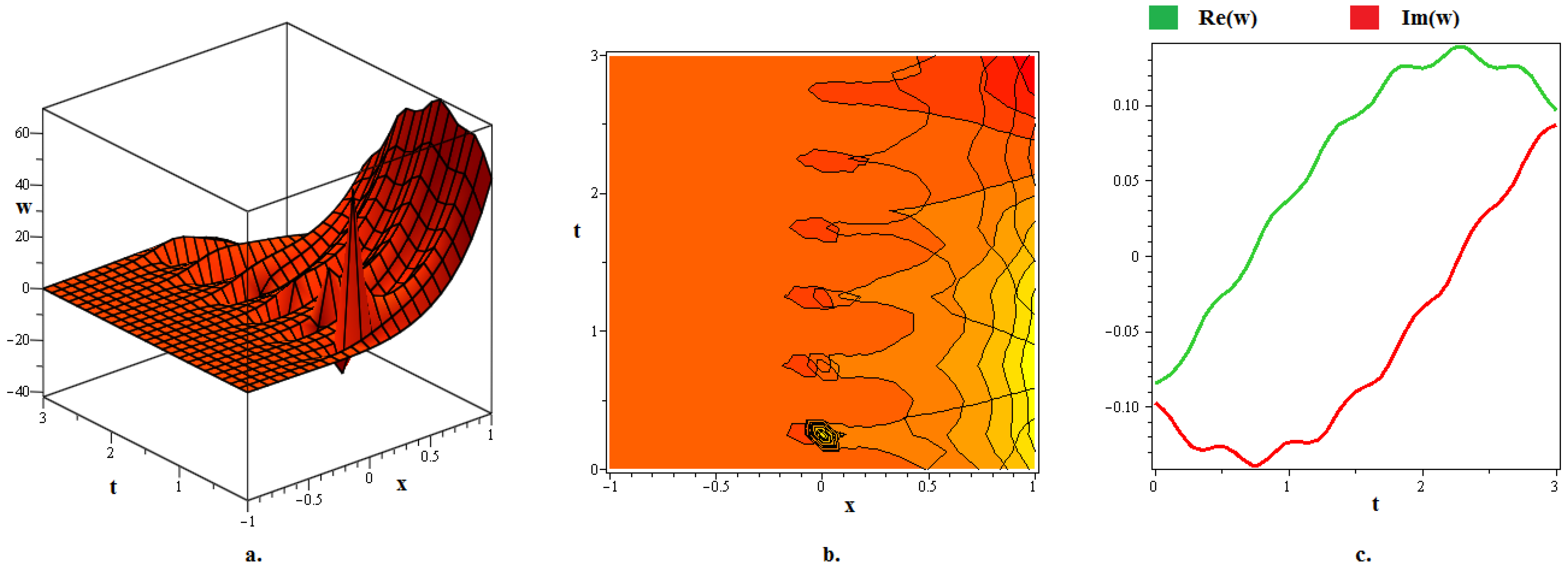
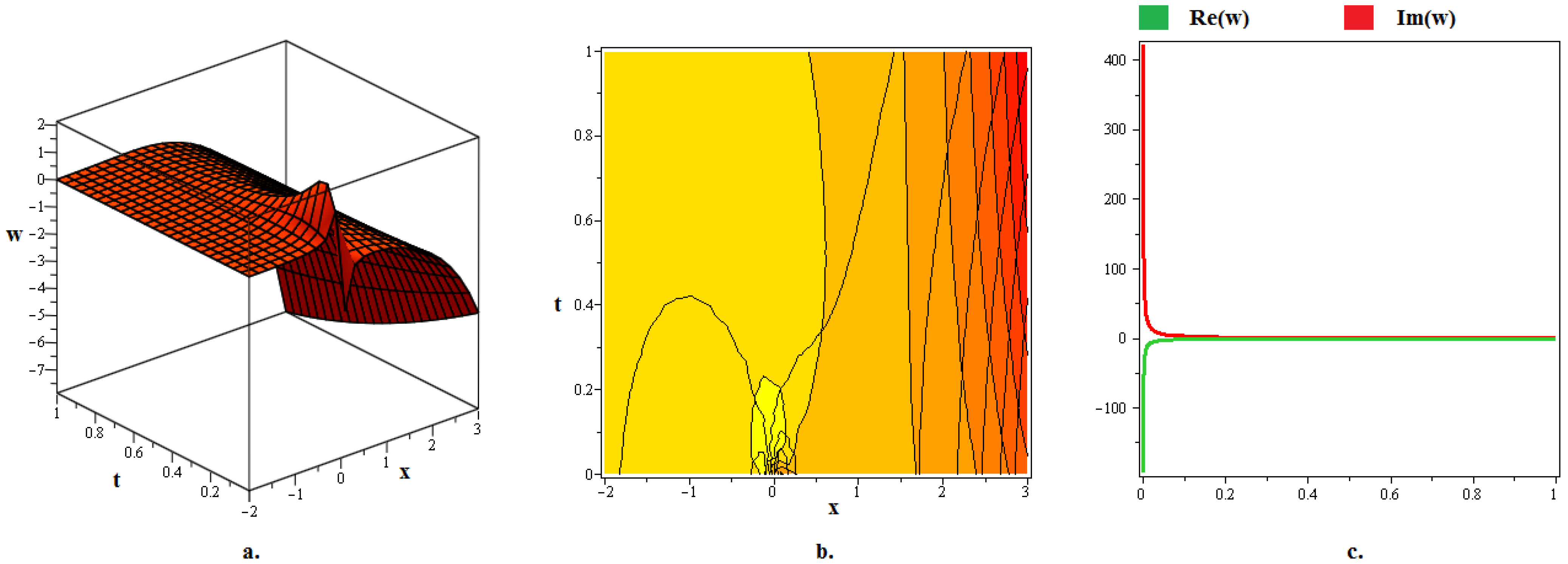
4. Discussion and Graphs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- For the Solutions of Case 1, Case 3, and Case 4:
References
- Abdelrahman, M.A.; Mohammed, W.W.; Alesemi, M.; Albosaily, S. The effect of multiplicative noise on the exact solutions of nonlinear Schrödinger equation. AIMS Math. 2021, 6, 2970–2980. [Google Scholar] [CrossRef]
- Alomair, R.A.; Hassan, S.Z.; Abdelrahman, M.A. A new structure of solutions to the coupled nonlinear Maccari’s systems in plasma physics. AIMS Math. 2020, 7, 8588–8606. [Google Scholar] [CrossRef]
- Navier, C.L. Navier Stokes Equation; Chez Carilian-Goeury: Paris, France, 1838. [Google Scholar]
- Hafez, M.G.; Alam, M.N.; Akbar, M.A. Traveling wave solutions for some important coupled nonlinear physical models via the coupled Higgs equation and the Maccari system. J. King Saud-Univ.-Sci. 2015, 27, 105–112. [Google Scholar] [CrossRef]
- El-Naggar, A.M.; Ismail, G.M. Analytical solution of strongly nonlinear Duffing oscillators. Alex. Eng. J. 2016, 55, 1581–1585. [Google Scholar] [CrossRef]
- Xiao, Y.; Barak, S.; Hleili, M.; Shah, K. Exploring the dynamical behaviour of optical solitons in integrable kairat-II and kairat-X equations. Phys. Scr. 2024, 99, 095261. [Google Scholar] [CrossRef]
- Ali, R.; Barak, S.; Altalbe, A. Analytical study of soliton dynamics in the realm of fractional extended shallow water wave equations. Phys. Scr. 2024, 99, 065235. [Google Scholar] [CrossRef]
- Akbar, M.A.; Akinyemi, L.; Yao, S.W.; Jhangeer, A.; Rezazadeh, H.; Khater, M.M.; Ahmad, H.; Mustafa Inc. Soliton solutions to the Boussinesq equation through sine-Gordon method and Kudryashov method. Results Phys. 2021, 25, 104228. [Google Scholar] [CrossRef]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Differ. Equ. 2015, 2015, 117. [Google Scholar] [CrossRef]
- Khan, H.; Barak, S.; Kumam, P.; Arif, M. Analytical solutions of fractional Klein-Gordon and gas dynamics equations, via the (G′/G)-expansion method. Symmetry 2019, 11, 566. [Google Scholar] [CrossRef]
- Khan, H.; Baleanu, D.; Kumam, P.; Al-Zaidy, J.F. Families of travelling waves solutions for fractional-order extended shallow water wave equations, using an innovative analytical method. IEEE Access 2019, 7, 107523–107532. [Google Scholar] [CrossRef]
- Hammad, M.M.A.; Shah, R.; Alotaibi, B.M.; Alotiby, M.; Tiofack, C.G.L.; Alrowaily, A.W.; El-Tantawy, S.A. On the modified versions of -expansion technique for analyzing the fractional coupled Higgs system. AIP Adv. 2013, 13, 105131. [Google Scholar] [CrossRef]
- Ali, R.; Tag-eldin, E. A comparative analysis of generalized and extended -Expansion methods for travelling wave solutions of fractional Maccari’s system with complex structure. Alex. Eng. J. 2023, 79, 508–530. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Cinar, M.; Secer, A.; Ozisik, M.; Bayram, M. Derivation of optical solitons of dimensionless Fokas-Lenells equation with perturbation term using Sardar sub-equation method. Opt. Quantum Electron. 2022, 54, 402. [Google Scholar] [CrossRef]
- Barman, H.K.; Islam, M.E.; Akbar, M.A. A study on the compatibility of the generalized Kudryashov method to determine wave solutions. Propuls. Power Res. 2021, 10, 95–105. [Google Scholar] [CrossRef]
- Shi-qiang, D. Poincare-Lighthill-Kuo method and symbolic computation. Appl. Math. Mech. 2001, 22, 261–269. [Google Scholar] [CrossRef]
- Hietarinta, J. Introduction to the Hirota bilinear method. In Integrability of Nonlinear Systems, Proceedings of the CIMPA School Pondicherry University, India, 8–26 January 1996; Springer: Berlin/Heidelberg, Germany, 2007; pp. 95–103. [Google Scholar]
- Bilal, M.; Iqbal, J.; Ali, R.; Awwad, F.A.; AIsmail, E.A. Exploring Families of Solitary Wave Solutions for the Fractional Coupled Higgs System Using Modified Extended Direct Algebraic Method. Fractal Fract. 2023, 7, 653. [Google Scholar] [CrossRef]
- Aldandani, M.; Altherwi, A.A.; Abushaega, M.M. Propagation patterns of dromion and other solitons in nonlinear Phi-Four (ϕ4) equation. AIMS Math. 2024, 9, 19786–19811. [Google Scholar] [CrossRef]
- Mirzazadeh, M. Modified simple equation method and its applications to nonlinear partial differential equations. Inf. Sci. Lett. 2014, 3, 1. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Al-Nowehy, A.G. The Modified Simple Equation Method, the Exp-Function Method, and the Method of Soliton Ansatz for Solving the Long-Short Wave Resonance Equations. Z. Naturforschung A 2016, 71, 103–112. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Seven common errors in finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3507–3529. [Google Scholar] [CrossRef]
- Navickas, Z.; Ragulskis, M. Comments on “A new algorithm for automatic computation of solitary wave solutions to nonlinear partial differential equations based on the Exp-function method”. Appl. Math. Comput. 2014, 243, 419–425. [Google Scholar] [CrossRef]
- Antonova, A.O.; Kudryashov, N.A. Generalization of the simplest equation method for nonlinear non-autonomous differential equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 4037–4041. [Google Scholar] [CrossRef]
- Navickas, Z.; Marcinkevicius, R.; Telksniene, I.; Telksnys, T.; Ragulskis, M. Structural stability of the hepatitis C model with the proliferation of infected and uninfected hepatocytes. Math. Comput. Model. Dyn. Syst. 2024, 30, 51–72. [Google Scholar] [CrossRef]
- Martin-Vergara, F.; Rus, F.; Villatoro, F.R. Fractal structure of the soliton scattering for the graphene superlattice equation. Chaos Solitons Fractals 2021, 151, 111281. [Google Scholar] [CrossRef]
- Wang, K. A new fractal model for the soliton motion in a microgravity space. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 442–451. [Google Scholar] [CrossRef]
- Zheng, C.L. Coherent soliton structures with chaotic and fractal behaviors in a generalized (2+ 1)-dimensional Korteweg de-Vries system. Chin. J. Phys. 2003, 41, 442–455. [Google Scholar]
- Bunde, A.; Havlin, S. (Eds.) Fractals in Science; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Stanley, H.E. Fractal landscapes in physics and biology. Phys. Stat. Mech. Its Appl. 1992, 186, 1–32. [Google Scholar] [CrossRef]
- Bizzarri, M.; Giuliani, A.; Cucina, A.; D’Anselmi, F.; Soto, A.M.; Sonnenschein, C. Fractal analysis in a systems biology approach to cancer. In Seminars in Cancer Biology; Academic Press: Cambridge, MA, USA, 2011; Volume 21, pp. 175–182. [Google Scholar]
- Abraham, N.B.; Firth, W.J. Overview of transverse effects in nonlinear-optical systems. JOSA B 1990, 7, 951–962. [Google Scholar] [CrossRef]
- Alsaud, H.; Youssoufa, M.; Inc, M.; Inan, I.E.; Bicer, H. Some optical solitons and modulation instability analysis of (3+ 1)-dimensional nonlinear Schrödinger and coupled nonlinear Helmholtz equations. Opt. Quantum Electron. 2024, 56, 1138. [Google Scholar] [CrossRef]
- Tamilselvan, K.; Kanna, T.; Khare, A. Nonparaxial elliptic waves and solitary waves in coupled nonlinear Helmholtz equations. Commun. Nonlinear Sci. Numer. Simul. 2016, 39, 134–148. [Google Scholar] [CrossRef]
- Singh, S.; Kaur, L.; Sakthivel, R.; Murugesan, K. Computing solitary wave solutions of coupled nonlinear Hirota and Helmholtz equations. Phys. Stat. Mech. Its Appl. 2020, 560, 125114. [Google Scholar] [CrossRef]
- Saha, N.; Roy, B.; Khare, A. Coupled Helmholtz equations: Chirped solitary waves. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 113104. [Google Scholar] [CrossRef] [PubMed]
- Yamaguti, M.; Yoshihara, H.; Niahida, T. Periodic solutions of Duffing equation. CiNii J. 1988, 673, 80–95. [Google Scholar]


| S. No. | Cluster | Constraint(s) | ||
|---|---|---|---|---|
| 1 | Trigonometric Solutions | |||
| , | , | |||
| , | , | |||
| , | , | |||
| . | . | |||
| 2 | Hyperbolic Solutions | |||
| , | , | |||
| , | , | |||
| , | ||||
| . | ||||
| 3 | Rational Solutions | |||
| , | , | |||
| , & | , | , | ||
| , & | . | . | ||
| 4 | Exponential Solutions | |||
| , & , | , | , | ||
| , & , | . | . | ||
| 5 | Rational-Hyperbolic Solutions | |||
| , & , | , | , | ||
| . | . |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Sawalha, M.M.; Noor, S.; Alqudah, M.; Aldhabani, M.S.; Shah, R. Formation of Optical Fractals by Chaotic Solitons in Coupled Nonlinear Helmholtz Equations. Fractal Fract. 2024, 8, 594. https://doi.org/10.3390/fractalfract8100594
Al-Sawalha MM, Noor S, Alqudah M, Aldhabani MS, Shah R. Formation of Optical Fractals by Chaotic Solitons in Coupled Nonlinear Helmholtz Equations. Fractal and Fractional. 2024; 8(10):594. https://doi.org/10.3390/fractalfract8100594
Chicago/Turabian StyleAl-Sawalha, M. Mossa, Saima Noor, Mohammad Alqudah, Musaad S. Aldhabani, and Rasool Shah. 2024. "Formation of Optical Fractals by Chaotic Solitons in Coupled Nonlinear Helmholtz Equations" Fractal and Fractional 8, no. 10: 594. https://doi.org/10.3390/fractalfract8100594
APA StyleAl-Sawalha, M. M., Noor, S., Alqudah, M., Aldhabani, M. S., & Shah, R. (2024). Formation of Optical Fractals by Chaotic Solitons in Coupled Nonlinear Helmholtz Equations. Fractal and Fractional, 8(10), 594. https://doi.org/10.3390/fractalfract8100594









