Nerve Signal Transferring Mechanism and Mathematical Modeling of Artificial Biological System Design
Abstract
1. Introduction
2. Physiological Basis of Muscle Contraction
3. Theoretical Approaches and Problem Statement
4. Mechanical Analysis
5. Mathematical Modeling
5.1. Numerical Approaches
5.2. Algebraix Equations with Matrix
6. Nerve Signal Transferring Mechanism
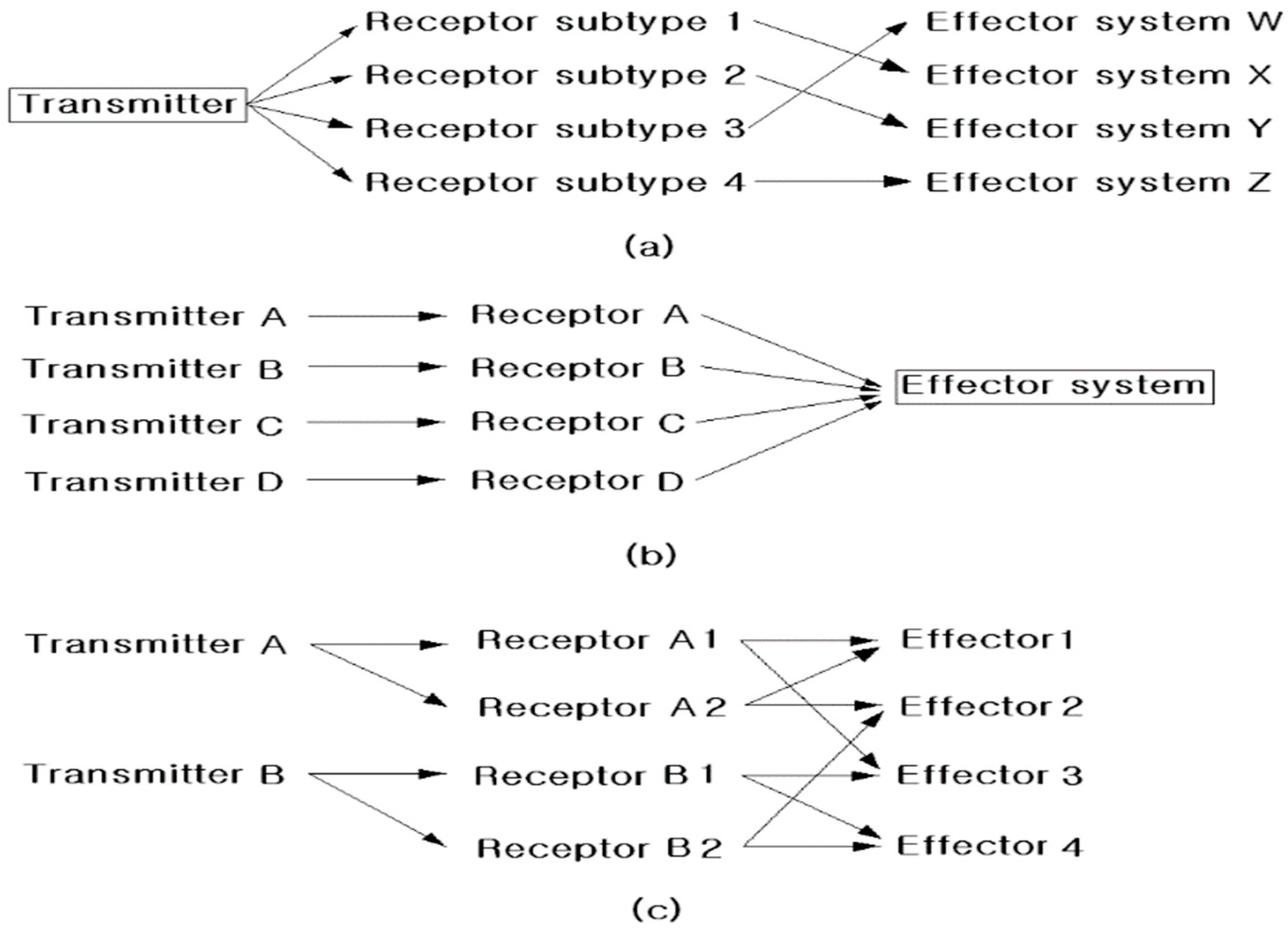
6.1. Nerve Signal on Biological System
6.2. Transferring Mechanism
- •
- Vm is the resting membrane potential,
- •
- R is the gas constant,
- •
- T is the absolute temperature in Kelvin,
- •
- F is the Faraday’s constant,
- •
- P is the permeability coefficient for each ion species,
- •
- [X+] in/out [X+] in/out represents the intracellular/extracellular concentration of each ion species.
- •
- H = value of the Planck constant (6.626068 × 10−34 Js) [23],
- •
- Λ = wavelength (Potassium for K; 6.142 × 10−10 m
- •
- Sodium for Na; 11.885 × 10−10 m,
- •
- Chloride for Cl; 4.7182 × 10−10 m) [24]
- •
- m = non-zero rest atomic mass
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bear, M.F.; Connors, B.W.; Paradiso, M.A. Neuroscience Exploring the Brain, 2nd ed.; Lippincott Williams & Wilkins: Baltimore, Maryland, 2001. [Google Scholar]
- Bloch, S.C. Excel for Engineers and Scientists, 2nd ed.; John Wiley and Sons, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Wei, H.; Shi, R.; Sun, L.; Yu, H.; Gong, J.; Liu, C.; Xu, Z.; Ni, Y.; Xu, J.; Xu, W. Mimicking efferent nerves using a graphdiyne-based artificial synapse with multiple ion diffusion dynamics. Nat. Commun. 2021, 12, 1068. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Liu, Y.; Qu, X.; Shi, B.; Zheng, Q.; Lin, X.; Chao, S.; Wang, C.; Zhou, J.; Sun, Y.; et al. Ultra-stretchable and fast self-healing ionic hydrogel in cryogenic environments for artificial nerve fiber. Adv. Mater. 2022, 34, 2105416. [Google Scholar] [CrossRef] [PubMed]
- Singleton, B.; Alkahby, H. Observation of Signal Transmission on the Nerve Axon with time delay. Int. J. Evol. Equ. 2011, 6, 319. [Google Scholar]
- Gandevia, S.C.; McCloskey, D.I.; Burke, D. Kinaesthetic signals and muscle contraction. Trends Neurosci. 1992, 15, 62–65. [Google Scholar] [CrossRef] [PubMed]
- Soendenbroe, C.; Andersen, J.L.; Mackey, A.L. Muscle-nerve communication and the molecular assessment of human skeletal muscle denervation with aging. Am. J. Physiol.-Cell Physiol. 2021, 321, C317–C329. [Google Scholar] [CrossRef] [PubMed]
- Gash, M.C.; Kandle, P.F.; Murray, I.V.; Varacallo, M. Physiology, muscle contraction. In StatPearls [Internet]; StatPearls Publishing: Treasure Island, FL, USA, 2023. [Google Scholar]
- O’Bryan, R.; Kincaid, J. Nerve conduction studies: Basic concepts and patterns of abnormalities. Neurol. Clin. 2021, 39, 897–917. [Google Scholar] [CrossRef] [PubMed]
- Lanigan, L.G.; Russell, D.S.; Woolard, K.D.; Pardo, I.D.; Godfrey, V.; Jortner, B.S.; Butt, M.T.; Bolon, B. Comparative pathology of the peripheral nervous system. Vet. Pathol. 2021, 58, 10–33. [Google Scholar] [CrossRef] [PubMed]
- Cuccurullo, S.J. (Ed.) Physical Medicine and Rehabilitation Board Review; Demos Medical Pub: New York, NY, USA, 2004. [Google Scholar]
- Souza, M.L.; Freitas, C.F.; Domingos MA, O.; Nunes-Tavares, N.; Hasson-Voloch, A.; Nasciutti, L.E.; Silva, L.C.F. Identification and distribution of chondroitin sulfate in the three electric organs of the electric eel, Electrophorus electricus (L.). Comp. Biochem. Physiol. Part B Biochem. Mol. Biol. 2007, 146, 227–233. [Google Scholar] [CrossRef] [PubMed]
- Garcia, A.L. Numerical Methods for Physics; Prentice Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
- Edwards, C.H.; Penney, D.E. Elementary Differential Equations with Boundary Value Problems, 4th ed.; Upper Saddle River & Prentice-Hall, Inc.: Hoboken, NJ, USA, 2000; pp. 101–365. [Google Scholar]
- Natanson, G. X-Jacobi Differential Polynomial System Formed by Solutions of Heun Equation at Fixed Values of Accessory Parameter. 2018. Available online: https://www.researchgate.net/profile/Gregory-Natanson/publication/327235393_X1-Jacobi_Differential_Polynomial_System_Formed_by_Solutions_of_Heun_Equation_at_Fixed_Values_of_Accessory_Parameter/links/6663410ca54c5f0b9456679a/X1-Jacobi-Differential-Polynomial-System-Formed-by-Solutions-of-Heun-Equation-at-Fixed-Values-of-Accessory-Parameter.pdf (accessed on 3 November 2024).
- Hatfield, B.D.; Jaquess, K.J.; Lo, L.C.; Oh, H. The cognitive and affective neuroscience of superior athletic performance. In Handbook of Sport Psychology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020; pp. 487–512. [Google Scholar]
- Park, J. Mathematical Modeling of Nerves Signal on the Design of Artificial Arms. Ph.D. Dissertation, University of Advancing Technology, Tempe, AZ, USA, 2009. [Google Scholar]
- Mermelstein, C.; Costa, M.; Neto, V. The cytoskeleton of the electric tissue of Electrophorus electricus, L. Ann. Acad. Bras. Cienc. 2000, 72, 341351. [Google Scholar] [CrossRef] [PubMed]
- Rosenberg, R.L.; Tomiko, S.A.; Agnew, W.S. Single-channel properties of the reconstituted voltage-regulated Na channel isolated from the electroplax of Electrophorus electricus. Proc. Natl. Acad. Sci. USA 1984, 81, 55945598. [Google Scholar] [CrossRef] [PubMed]
- Keynes, R.; Ferreira, H. Membrane potentials in the electroplates of the electric eel. J. Physiol. 1953, 119, 315351. [Google Scholar] [CrossRef] [PubMed]
- Gotter, A.; Kaetzel, M.; Dedman, J. Electrophorus electricus as a model system for the study of membrane excitability. Comp. Biochem. Physiol. 1998, 119, 225–241. [Google Scholar] [CrossRef] [PubMed]
- Jeong, T. Time-series Data Classification and Analysis associated with Machine Learning Algorithms for Cognitive Perception and Phenomenon. IEEE Access 2020, 8, 222417–222428. [Google Scholar] [CrossRef]
- Sherif, K.; Nachbagauer, K.; Steiner, W. On the rotational equations of motion in rigid body dynamics when using Euler parameters. Nonlinear Dyn. 2015, 81, 343–352. [Google Scholar] [CrossRef] [PubMed]
- Henry Moseley Finds a Property to Justify the Term Atomic Number. Available online: http://www.rsc.org/education/teachers/learnnet/periodictable/ (accessed on 3 November 2024).
- Logg, A. Automating the finite element method. Arch. Comput. Methods Eng. 2007, 14, 93–138. [Google Scholar] [CrossRef]
- Malak, D.; Akan, O.B. Communication theoretical understanding of intra-body nervous nanonetworks. IEEE Commun. Mag. 2014, 52, 129–135. [Google Scholar] [CrossRef]
- Web Associates. Anthropometric Source Book. National Aeronautics and Space Administration I (NASA no. 1024). 1978. Available online: https://ntrs.nasa.gov/citations/19790003563 (accessed on 3 November 2024).
- Weir, R.F. Design of Artificial Arms and Hands for Prosthetic Applications: Standard Handbook of Biomedical Engineering and Design; McGraw-Hill Standard Handbooks: New York, NY, USA, 2003. [Google Scholar]
- Ewart, H.S.; Klip, A.M.I.F.U. Hormonal regulation of the Na (+)-K (+)-ATPase: Mechanisms underlying rapid and sustained changes in pump activity. Am. J. Physiol.-Cell Physiol. 1995, 269, C295–C311. [Google Scholar] [CrossRef] [PubMed]
- McDowell, M.A.; Fryar, C.D.; Ogden, C.L.; Flegal, K.M. Anthropometric reference data for children and Adults: United States, 2003–2006. Natl. Health Stat. Rep. 2008, 10, 5. [Google Scholar]
- Saeed, M. Three-Dimensional Elements Finite Element Analysis, Theory and Application with ANSYS; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Gordon, A.M.; Huxley, A.F.; Julian, F.J. The variation in isometric tension with sarcomere length in vertebrate muscle fibers. J. Physiol. 2000, 184, 170–192. [Google Scholar] [CrossRef] [PubMed]
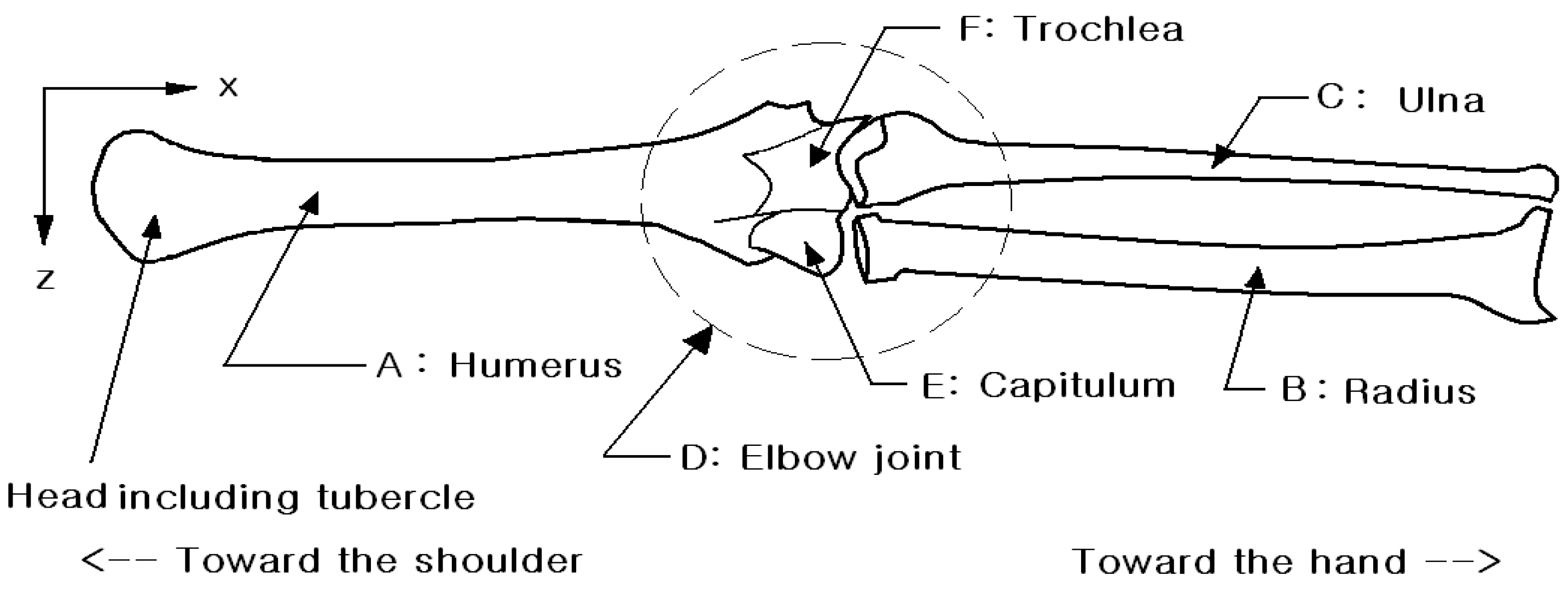
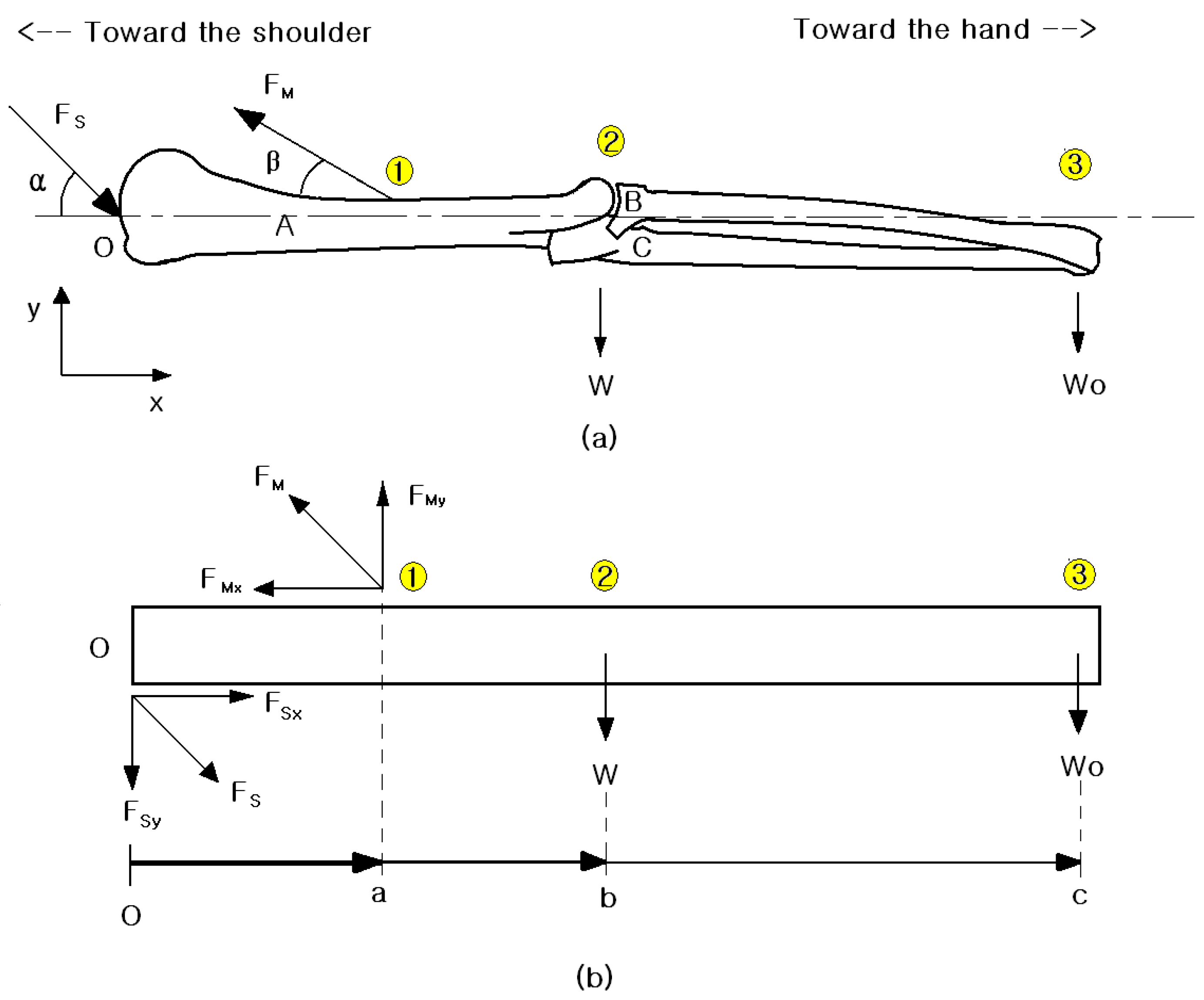


| Bone | Element | Node (i) | Node (j) | Coordination | Angle (°) |
|---|---|---|---|---|---|
| Humerus (θ) | A | 1 | 2 | x, y | 0, 45, 90 |
| Radius (δ) | B | 3 | 5 | x, y | 0, 45, 90, 135 |
| Ulna (λ) | C | 4 | 6 | x, y | 0, 45, 90, 135 |
| Radius and Ulna (ω) | B and C | 5 | 6 | y, z | 0, 90, 180 |
| Potassium (K) | Sodium (Na) | Chloride (Cl) | |
|---|---|---|---|
| Ionic concentrations (M), [1] | 1.00 × 10 | 1.50 × 10−1 | 1.30 × 10−1 |
| Reference energy (eV), [1] | −0.8 | 0.62 | −0.65 |
| Calculated energy (eV) | −0.56 | 1.69 | −0.804 |
| Amplitude | Negative | Positive | Negative |
| Muscle State | Ions | Flow Direction | Inside the Membrane Energy | Amplitude |
|---|---|---|---|---|
| Extend | K+ | Efflux | Increase | Positive |
| Cl− | Influx | Decrease | Negative | |
| Na+ | Negative | |||
| Flex | K+ | Influx | Decrease | Negative |
| Cl− | Efflux | Increase | Positive | |
| Na+ | Positive |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Yoo, S.; Jeong, T. Nerve Signal Transferring Mechanism and Mathematical Modeling of Artificial Biological System Design. Fractal Fract. 2024, 8, 648. https://doi.org/10.3390/fractalfract8110648
Park J, Yoo S, Jeong T. Nerve Signal Transferring Mechanism and Mathematical Modeling of Artificial Biological System Design. Fractal and Fractional. 2024; 8(11):648. https://doi.org/10.3390/fractalfract8110648
Chicago/Turabian StylePark, Jeongseop, Sehwan Yoo, and Taikyeong Jeong. 2024. "Nerve Signal Transferring Mechanism and Mathematical Modeling of Artificial Biological System Design" Fractal and Fractional 8, no. 11: 648. https://doi.org/10.3390/fractalfract8110648
APA StylePark, J., Yoo, S., & Jeong, T. (2024). Nerve Signal Transferring Mechanism and Mathematical Modeling of Artificial Biological System Design. Fractal and Fractional, 8(11), 648. https://doi.org/10.3390/fractalfract8110648





