Soliton Solutions and Chaotic Dynamics of the Ion-Acoustic Plasma Governed by a (3+1)-Dimensional Generalized Korteweg–de Vries–Zakharov–Kuznetsov Equation
Abstract
1. Introduction
2. Dynamics of the Aforementioned Model
3. Periodic Orbits
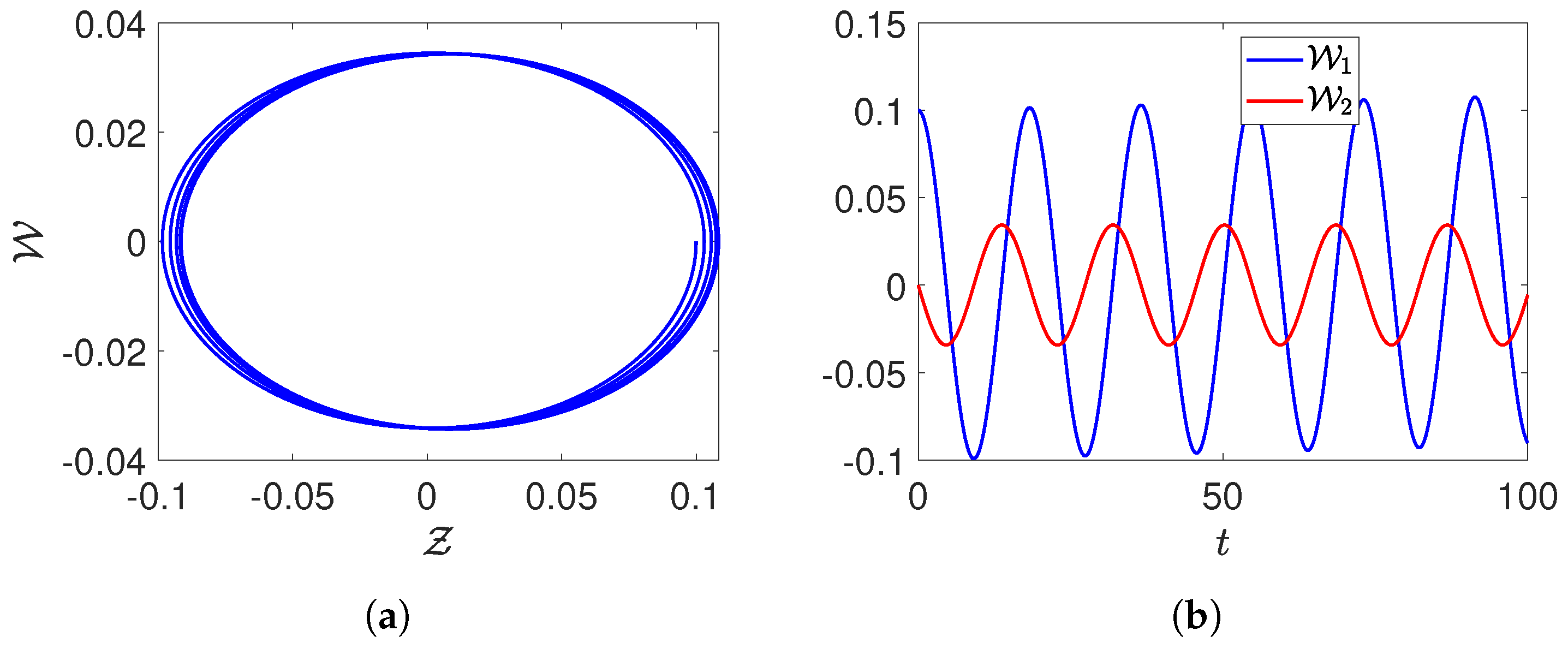
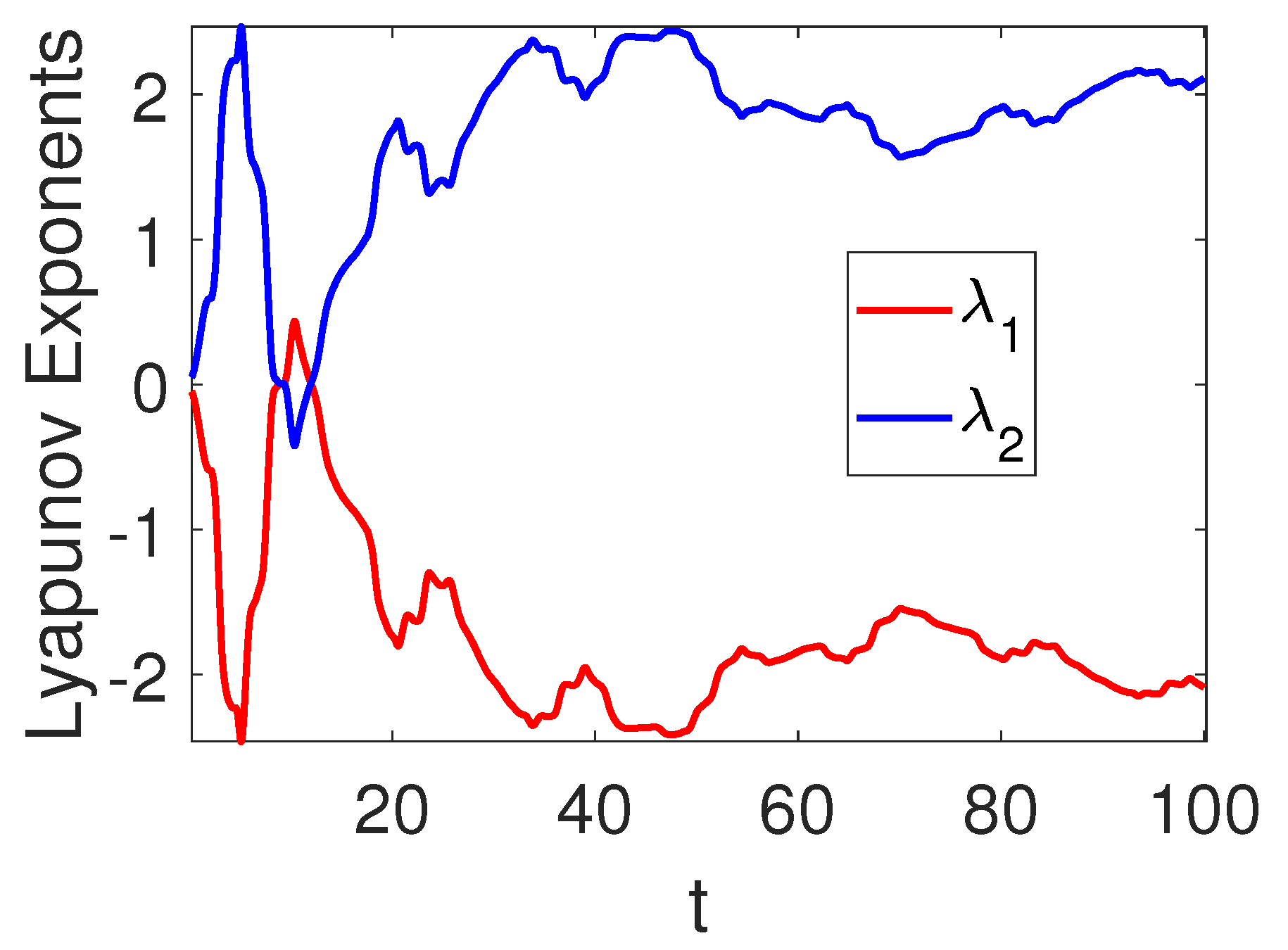
3.1. Transition from Order to Chaos
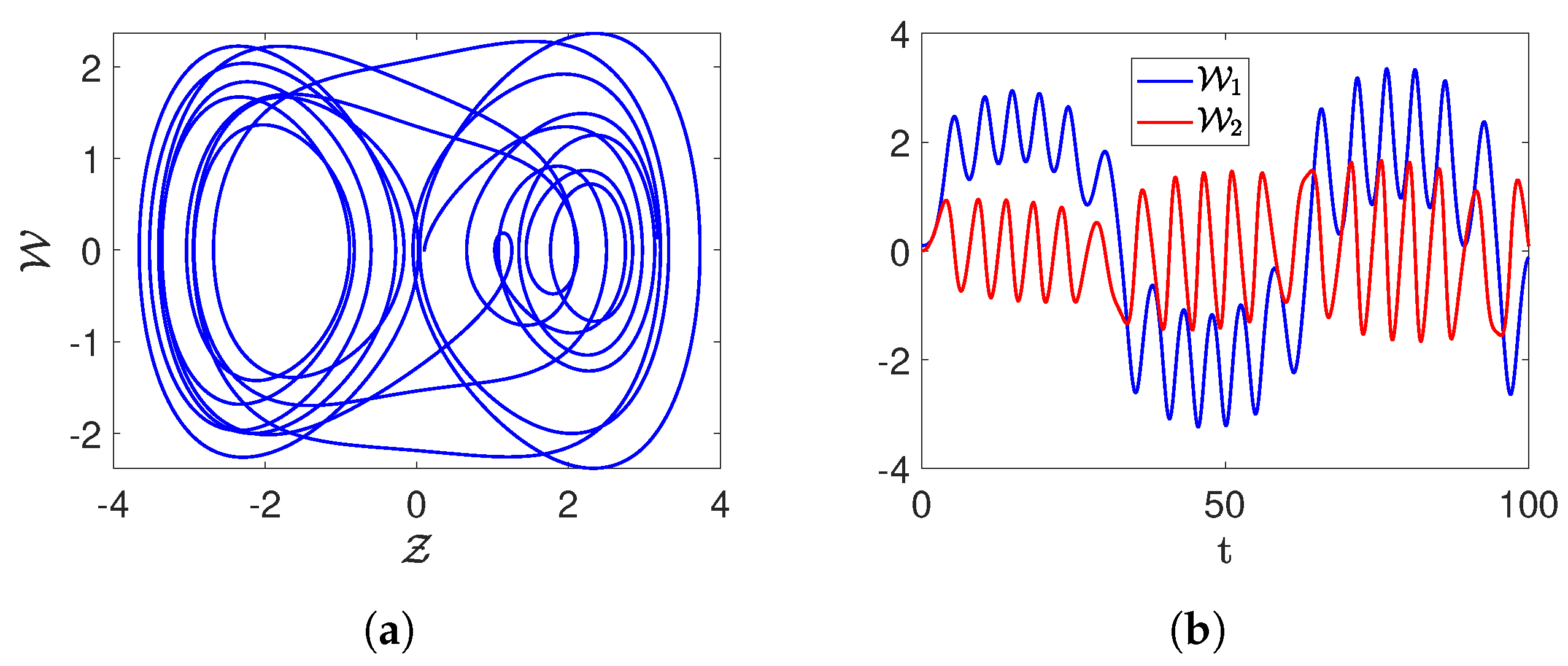
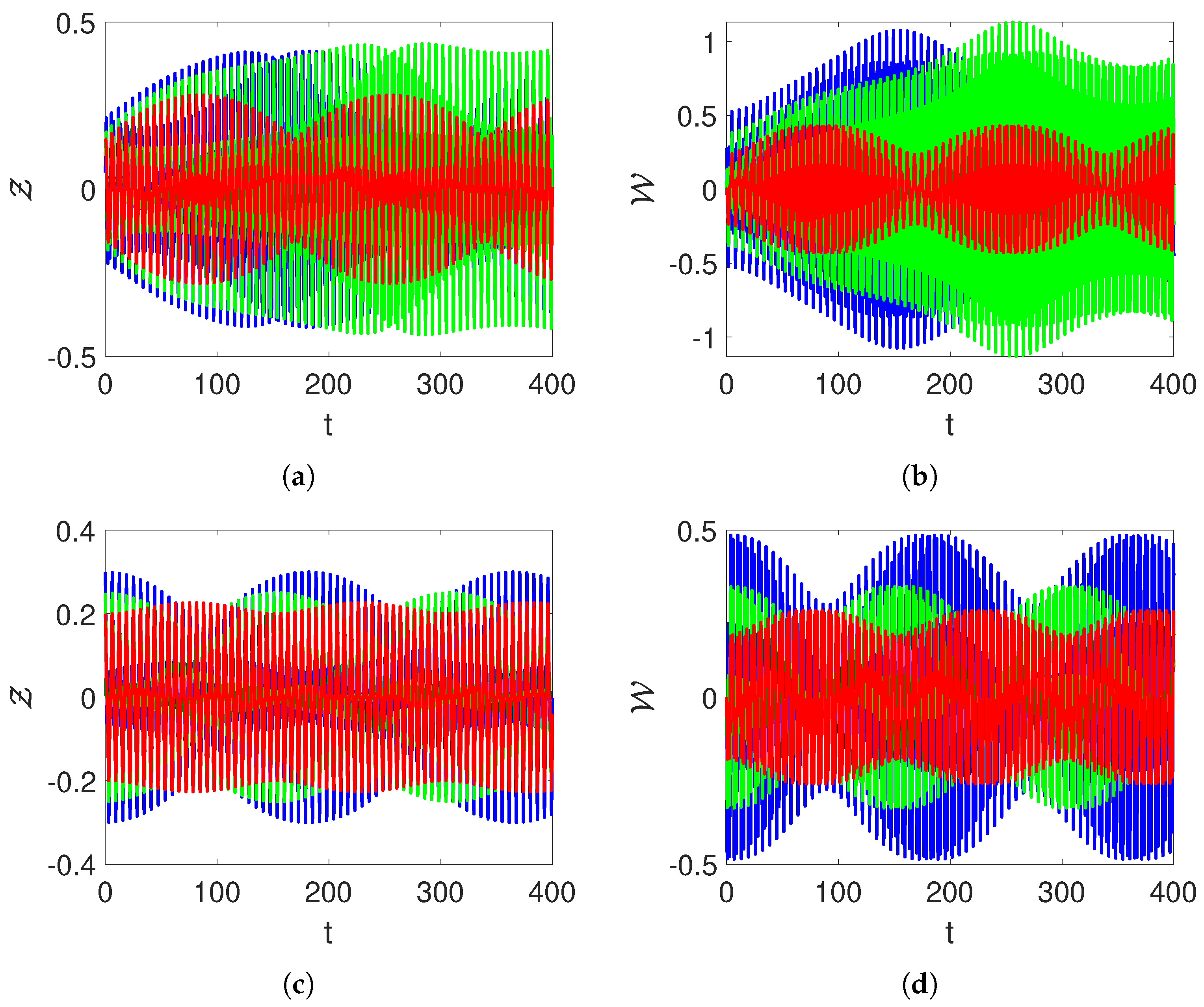
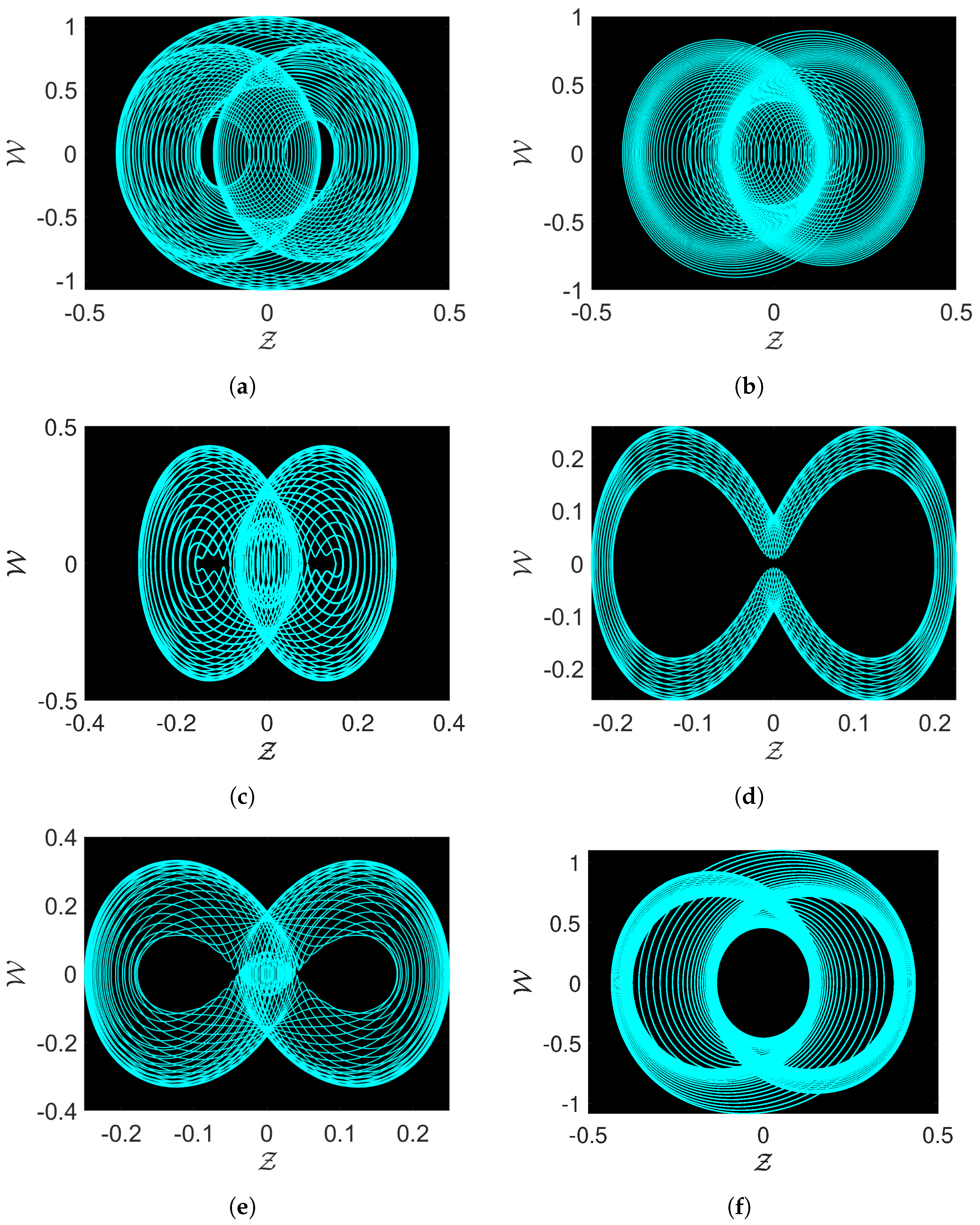
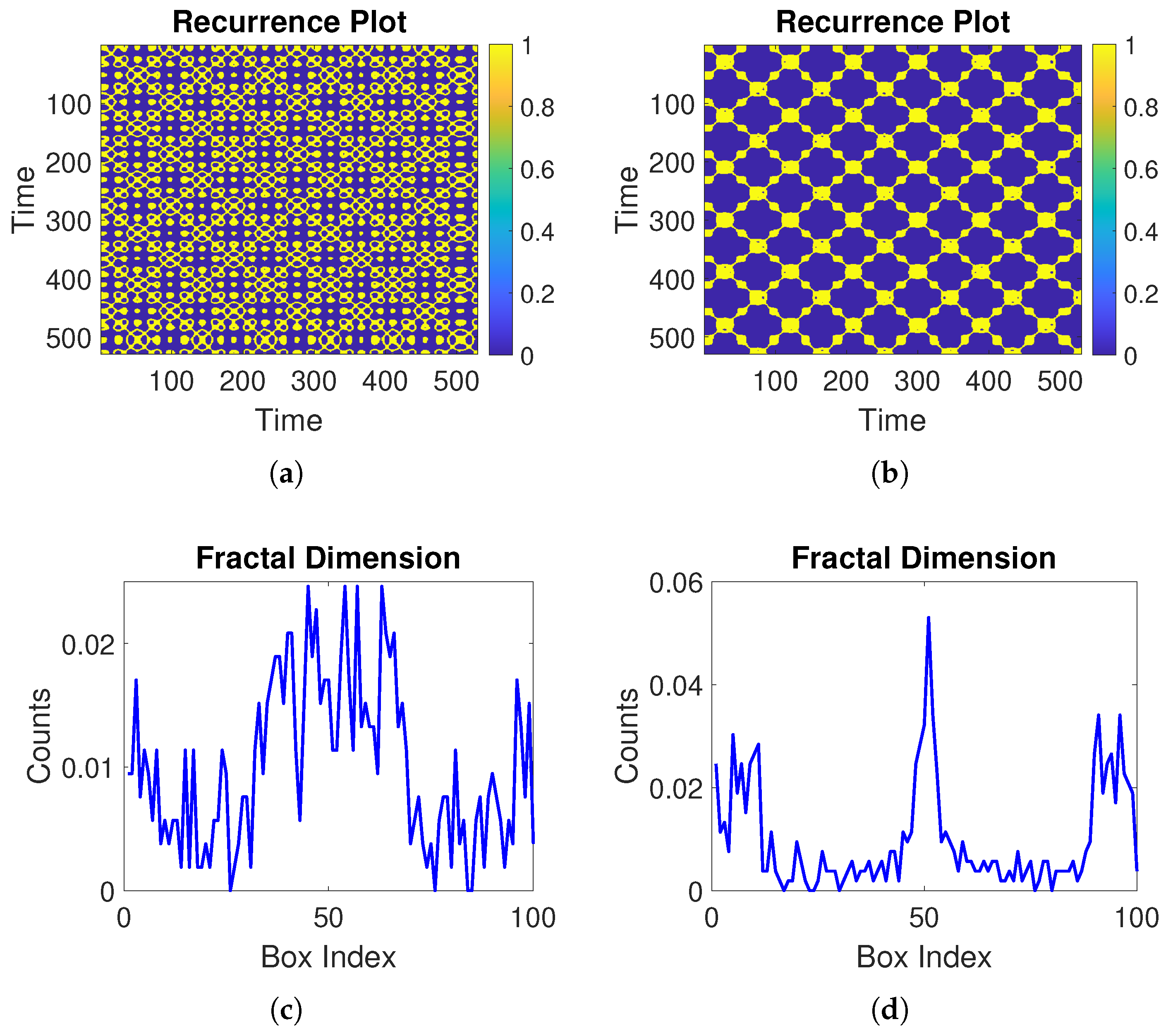
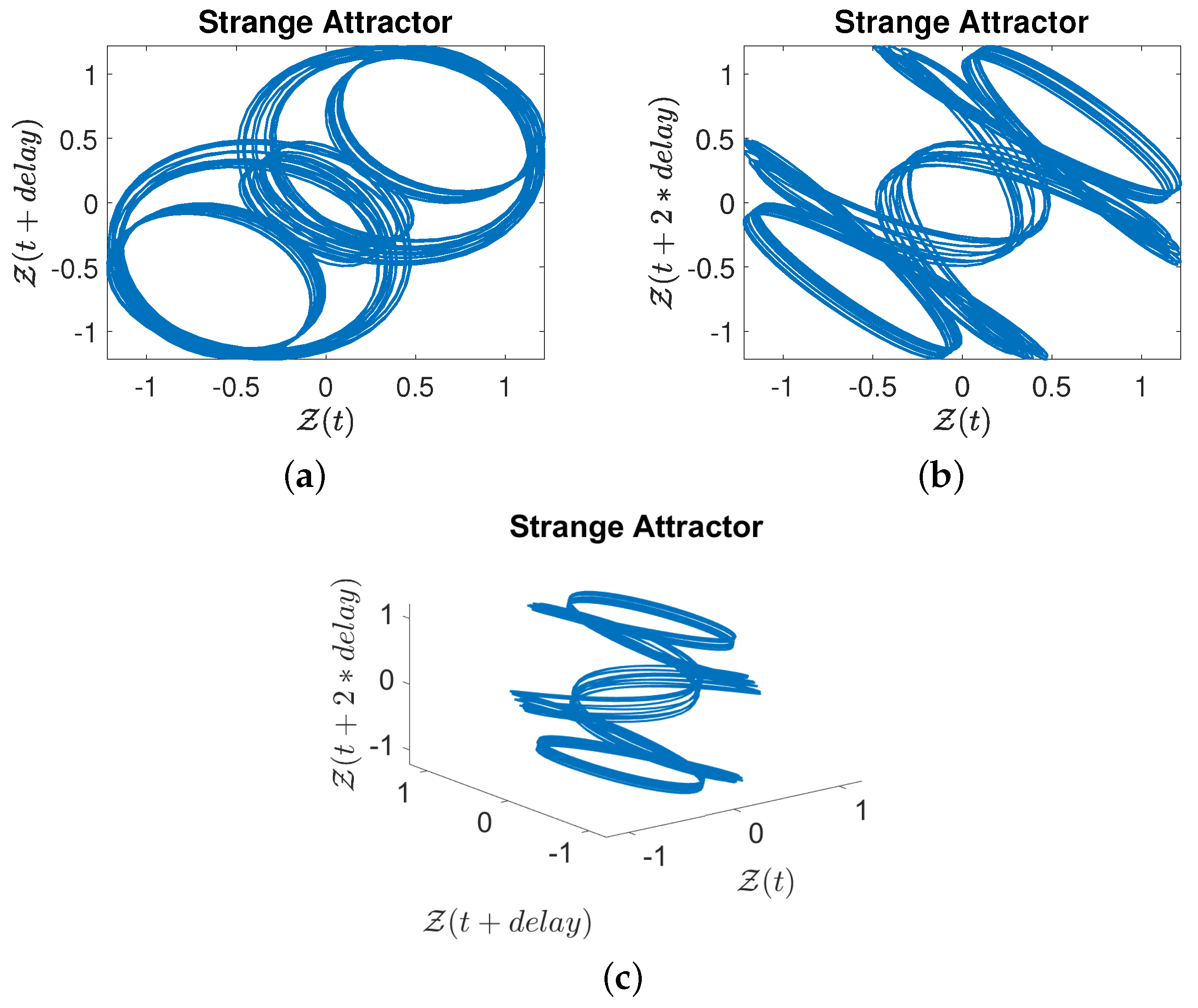
3.2. Chaos and Other Novel Dynamics of the Proposed System
3.3. Sensitivity
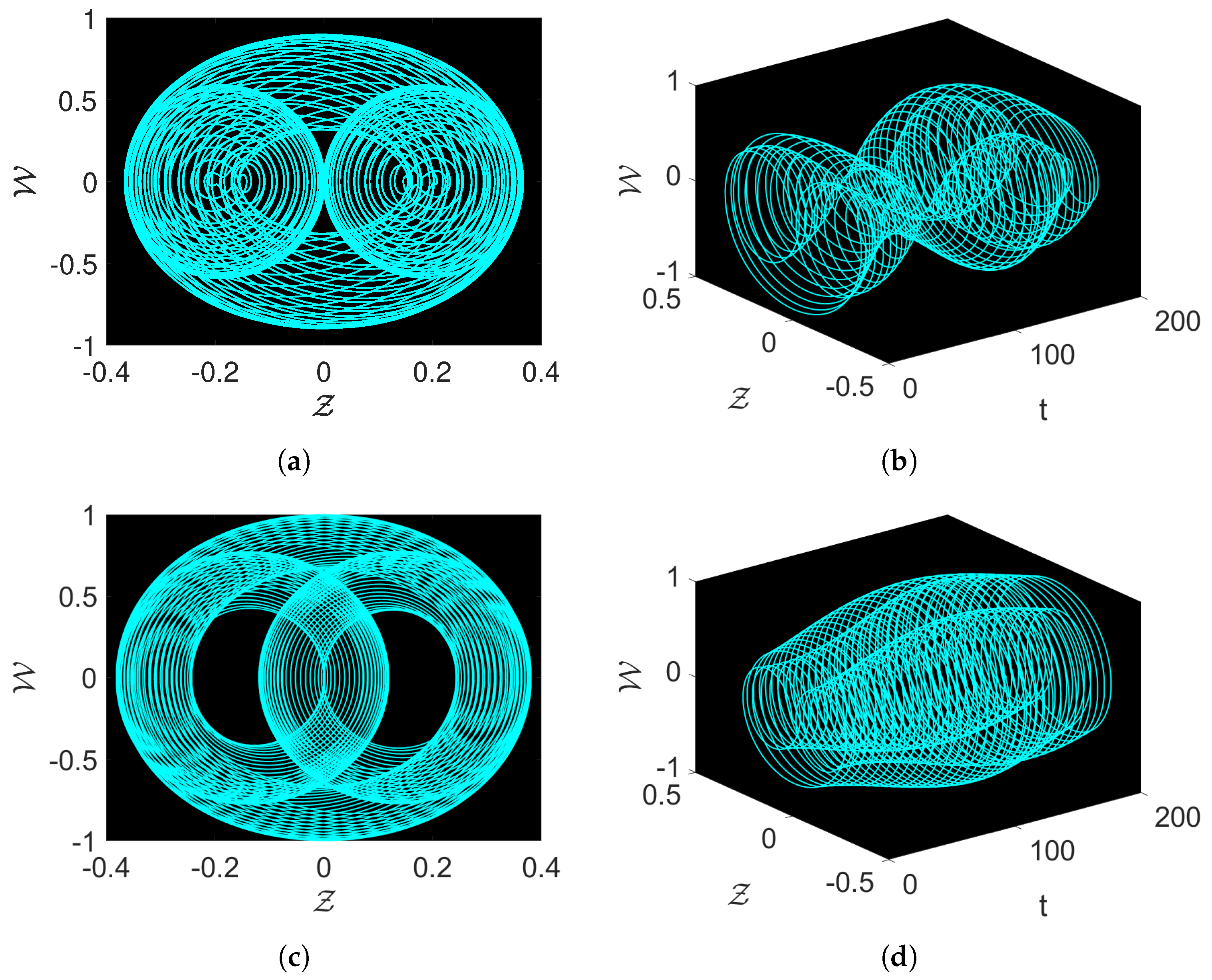
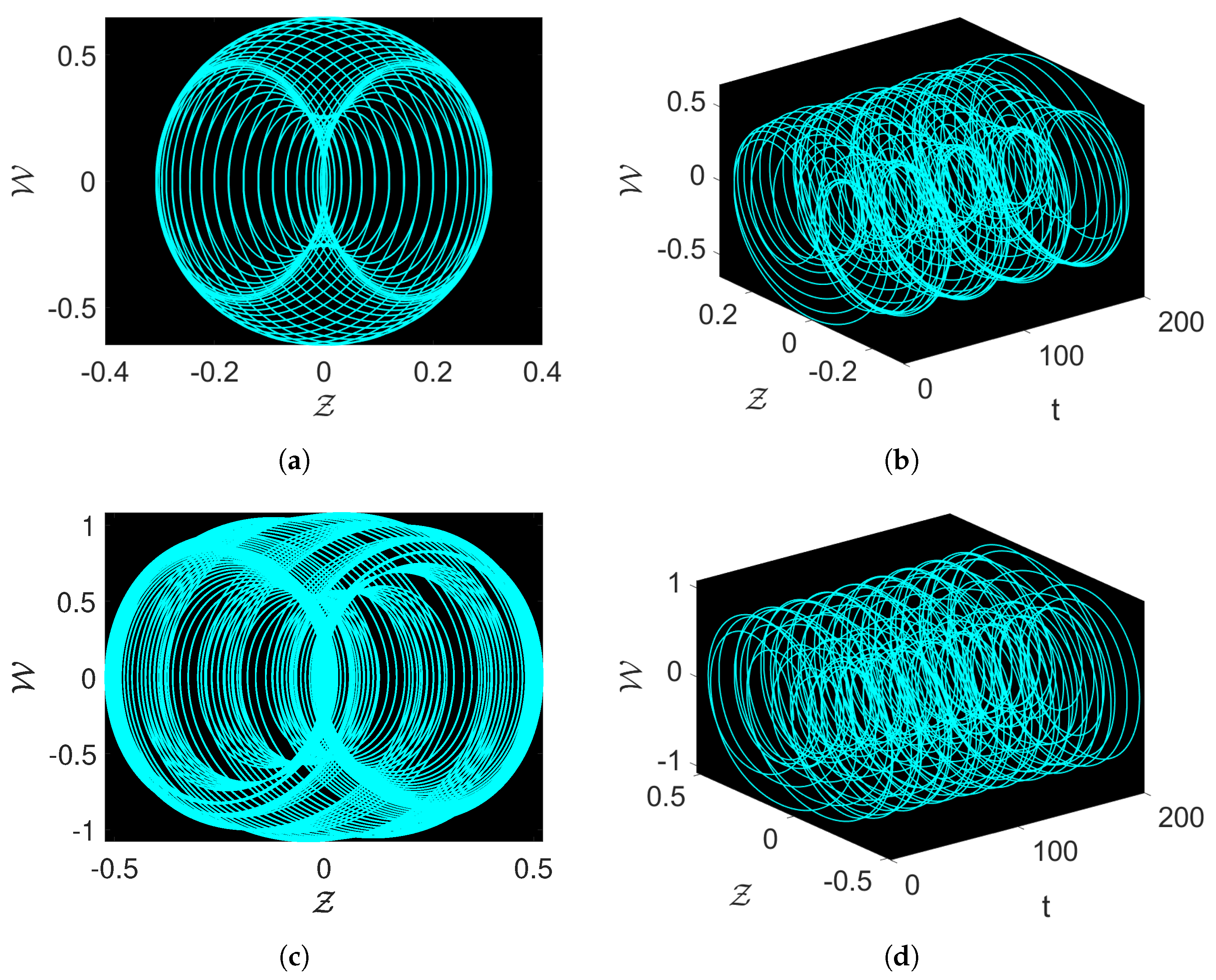
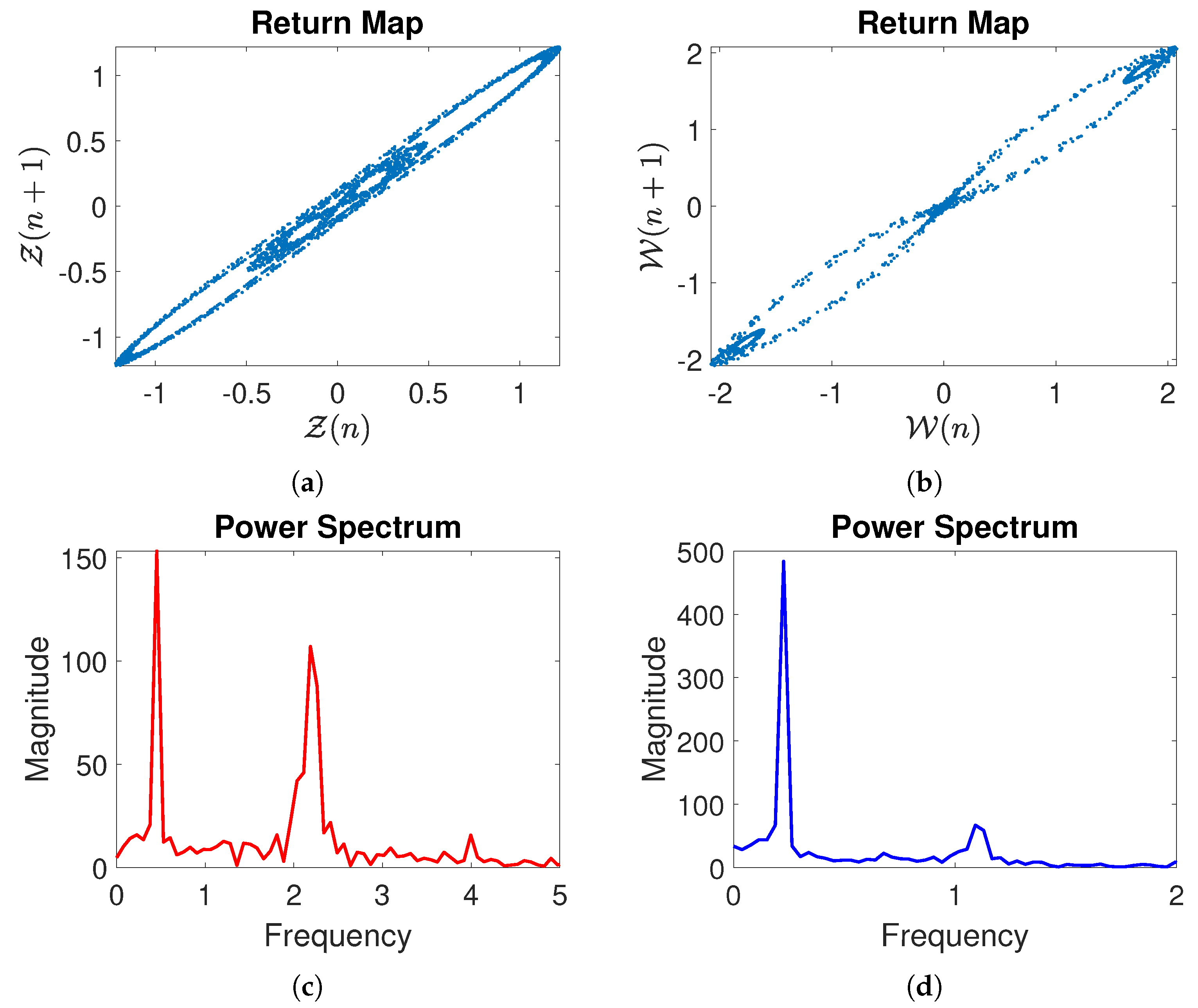
3.4. Novel Dynamical Analysis of the Proposed System
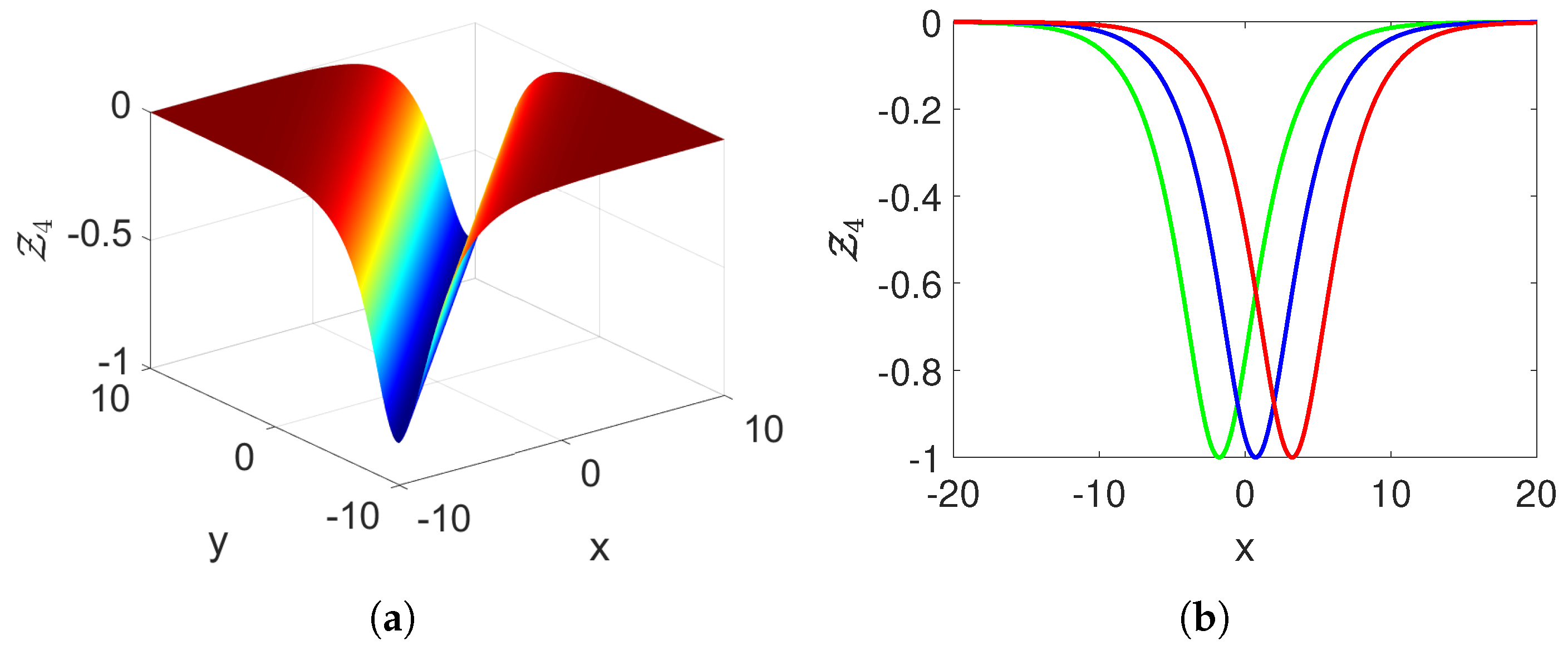
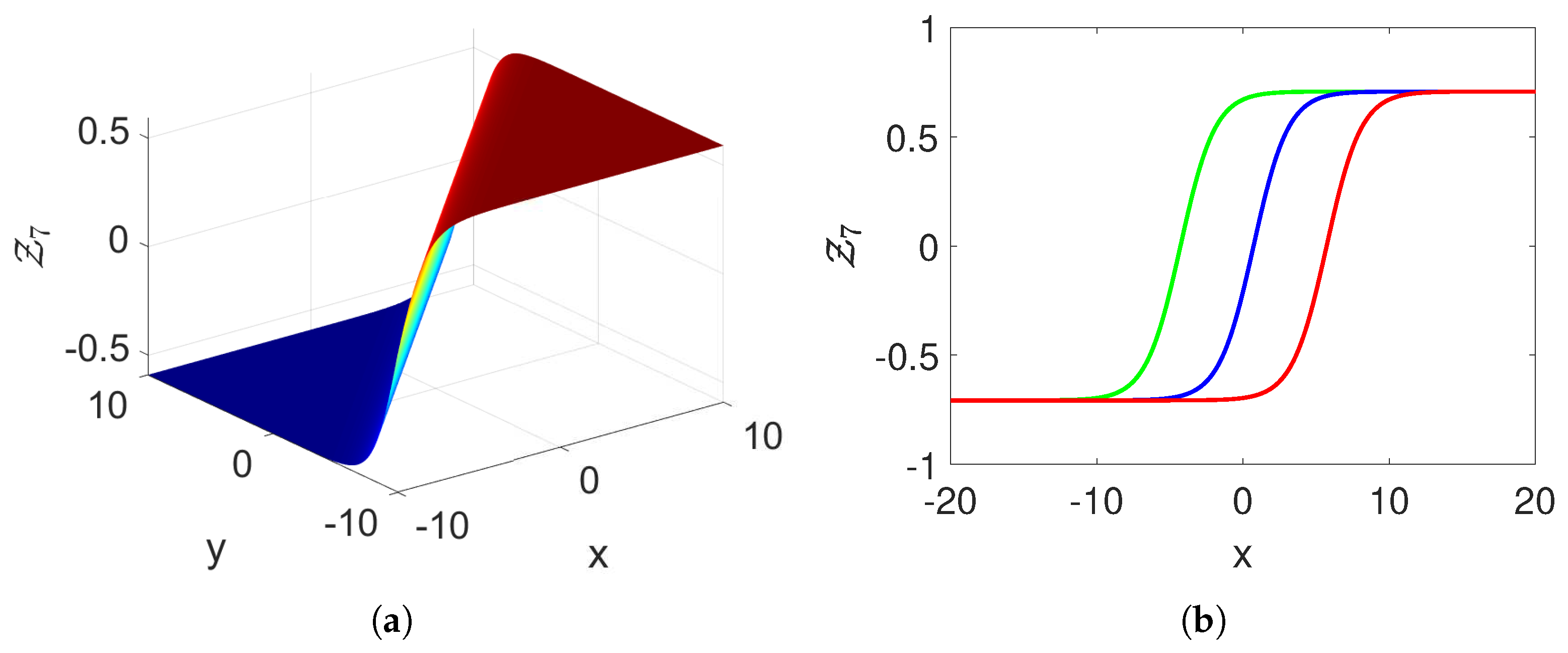
4. Soliton Solutions for the Suggested Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmad, H.; Khan, T.A.; Stanimirovic, P.S.; Shatanawi, W.; Botmart, T. New approach on conventional solutions to nonlinear partial differential equations describing physical phenomena. Results Phys. 2022, 41, 105936. [Google Scholar] [CrossRef]
- Alam, M.N.; Bonyah, E.; Fayz-Al-Asad, M.; Osman, M.S.; Abualnaja, K.M. Stable and functional solutions of the Klein-Fock-Gordon equation with nonlinear physical phenomena. Phys. Scr. 2021, 96, 055207. [Google Scholar] [CrossRef]
- Fadhal, E.; Akbulut, A.; Kaplan, M.; Awadalla, M.; Abuasbeh, K. Extraction of exact solutions of higher order Sasa-Satsuma equation in the sense of beta derivative. Symmetry 2022, 14, 2390. [Google Scholar] [CrossRef]
- Mhadhbi, N.; Gana, S.; Alsaeedi, M.F. Exact solutions for nonlinear partial differential equations via a fusion of classical methods and innovative approaches. Sci. Rep. 2024, 14, 6443. [Google Scholar] [CrossRef]
- Prakash, P.; Priyendhu, K.S.; Sahadevan, R. Generalized separation of variable methods with their comparison: Exact solutions of time-fractional nonlinear PDEs in higher dimensions. Fract. Calc. Appl. Anal. 2024, 1–51. [Google Scholar] [CrossRef]
- Ma, W.-X. The inverse scattering transform and soliton solutions of a combined modified Korteweg–de Vries equation. J. Math. Anal. Appl. 2019, 471, 796–811. [Google Scholar] [CrossRef]
- Li, J.; Xu, C.; Lu, J. The exact solutions to the generalized (2 + 1)-dimensional nonlinear wave equation. Results Phys. 2024, 58, 107506. [Google Scholar] [CrossRef]
- Hussain, A.; Ali, H.; Usman, M.; Zaman, F.D.; Park, C. Some New Families of Exact Solitary Wave Solutions for Pseudo-Parabolic Type Nonlinear Models. J. Math. 2024, 2024, 5762147. [Google Scholar] [CrossRef]
- Kaplan, M.; Akbulut, A. A mathematical analysis of a model involving an integrable equation for wave packet envelope. J. Math. 2022, 2022, 3486780. [Google Scholar] [CrossRef]
- Zhang, H.; Jing, M.; Dong, S.; Dong, D.; Liu, Y.; Meng, Y. Stability and evolutionary trend of Hopf bifurcations in double-input SEPIC DC–DC converters. Int. J. Bifurc. Chaos 2019, 29, 1950192. [Google Scholar] [CrossRef]
- Khan, A.; Saifullah, S.; Ahmad, S.; Khan, M.A.; Rahman, M.U. Dynamical properties and new optical soliton solutions of a generalized nonlinear Schrödinger equation. Eur. Phys. J. Plus 2023, 138, 1059. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Ahmad, S.; Saifullah, S.; Shokri, A. Periodic solitons of Davey Stewartson Kadomtsev Petviashvili equation in (4+1)-dimension. Results Phys. 2023, 50, 106547. [Google Scholar] [CrossRef]
- Saifullah, S.; Alqarni, M.M.; Ahmad, S.; Baleanu, D.; Khan, M.A.; Mahmoud, E.E. Some more bounded and singular pulses of a generalized scale-invariant analogue of the Korteweg–de Vries equation. Results Phys. 2023, 52, 106836. [Google Scholar] [CrossRef]
- Saifullah, S.; Ahmad, S.; Khan, M.A.; ur Rahman, M. Multiple solitons with fission and multi waves interaction solutions of a (3+1)-dimensional combined pKPBKP integrable equation. Phys. Scr. 2024, 99, 065242. [Google Scholar] [CrossRef]
- Baber, M.Z.; Ahmed, N.; Xu, C.; Iqbal, M.S.; Sulaiman, T.A. A computational scheme and its comparison with optical soliton solutions for the stochastic Chen–Lee–Liu equation with sensitivity analysis. Mod. Phys. Lett. B 2024, 2450376. [Google Scholar] [CrossRef]
- Tariq, K.U.; Wazwaz, A.M.; Kazmi, S.R. On the dynamics of the (2+ 1)-dimensional chiral nonlinear Schrödinger model in physics. Optik 2023, 285, 170943. [Google Scholar] [CrossRef]
- Ding, C.-C.; Zhou, Q.; Triki, H.; Sun, Y.; Biswas, A. Dynamics of dark and anti-dark solitons for the x-nonlocal Davey–Stewartson II equation. Nonlinear Dyn. 2023, 111, 2621–2629. [Google Scholar] [CrossRef]
- Chen, X.; Guo, Y.; Zhang, T. Some new kink type solutions for the new (3+ 1)-dimensional Boiti–Leon–Manna–Pempinelli equation. Nonlinear Dyn. 2023, 111, 683–695. [Google Scholar] [CrossRef]
- Muflih Alqahtani, A.; Akram, S.; Alosaimi, M. Study of bifurcations, chaotic structures with sensitivity analysis and novel soliton solutions of non-linear dynamical model. J. Taibah Univ. Sci. 2024, 18, 2399870. [Google Scholar] [CrossRef]
- Chahlaoui, Y.; Ali, A.; Javed, S. Study the behavior of soliton solution, modulation instability and sensitive analysis to fractional nonlinear Schrödinger model with Kerr Law nonlinearity. Ain Shams Eng. J. 2024, 15, 102567. [Google Scholar] [CrossRef]
- Borhan, J.R.M.; Mamun Miah, M.; Duraihem, F.Z.; Iqbal, M.A.; Ma, W.X. New Optical Soliton Structures, Bifurcation Properties, Chaotic Phenomena, and Sensitivity Analysis of Two Nonlinear Partial Differential Equations. Int. J. Theor. Phys. 2024, 63, 183. [Google Scholar] [CrossRef]
- Li, P.; Shi, S.; Xu, C.; Rahman, M.U. Bifurcations, chaotic behavior, sensitivity analysis and new optical solitons solutions of Sasa-Satsuma equation. Nonlinear Dyn. 2024, 112, 7405–7415. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, Y.; Lin, J.; Pang, Y.; Liu, Z.; Shen, J.; Liao, M.; Li, P.; Qin, Y. Bifurcation investigation and control scheme of fractional neural networks owning multiple delays. Comput. Appl. Math. 2024, 43, 1–33. [Google Scholar] [CrossRef]
- Shukla, V.K.; Joshi, M.C.; Mishra, P.K.; Xu, C. Adaptive fixedtime difference synchronization for different classes of chaotic dynamical systems. Phys. Scr. 2024, 99, 095264. [Google Scholar] [CrossRef]
- Baber, M.Z.; Yasin, M.W.; Xu, C.; Ahmed, N.; Iqbal, M.S. Numerical and Analytical Study for the Stochastic Spatial Dependent Prey–Predator Dynamical System. J. Comput. Nonlinear Dyn. 2024, 19, 101003. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamza, A.E.; Rabih, M.N.A.; Alsulami, A.; Mustafa, A.; Aldwoah, K.; Saber, H. Soliton Solutions and Chaotic Dynamics of the Ion-Acoustic Plasma Governed by a (3+1)-Dimensional Generalized Korteweg–de Vries–Zakharov–Kuznetsov Equation. Fractal Fract. 2024, 8, 673. https://doi.org/10.3390/fractalfract8110673
Hamza AE, Rabih MNA, Alsulami A, Mustafa A, Aldwoah K, Saber H. Soliton Solutions and Chaotic Dynamics of the Ion-Acoustic Plasma Governed by a (3+1)-Dimensional Generalized Korteweg–de Vries–Zakharov–Kuznetsov Equation. Fractal and Fractional. 2024; 8(11):673. https://doi.org/10.3390/fractalfract8110673
Chicago/Turabian StyleHamza, Amjad E., Mohammed Nour A. Rabih, Amer Alsulami, Alaa Mustafa, Khaled Aldwoah, and Hicham Saber. 2024. "Soliton Solutions and Chaotic Dynamics of the Ion-Acoustic Plasma Governed by a (3+1)-Dimensional Generalized Korteweg–de Vries–Zakharov–Kuznetsov Equation" Fractal and Fractional 8, no. 11: 673. https://doi.org/10.3390/fractalfract8110673
APA StyleHamza, A. E., Rabih, M. N. A., Alsulami, A., Mustafa, A., Aldwoah, K., & Saber, H. (2024). Soliton Solutions and Chaotic Dynamics of the Ion-Acoustic Plasma Governed by a (3+1)-Dimensional Generalized Korteweg–de Vries–Zakharov–Kuznetsov Equation. Fractal and Fractional, 8(11), 673. https://doi.org/10.3390/fractalfract8110673






