Integrable Riesz Fractional-Order Generalized NLS Equation with Variable Coefficients: Inverse Scattering Transform and Analytical Solutions
Abstract
:1. Introduction
2. ADR and the Derivation of vcRfgNLS Equation
3. IST and Analytical Solutions for the vcRfgNLS Equation
4. Explicit Form of the vcRfgNLS Equation
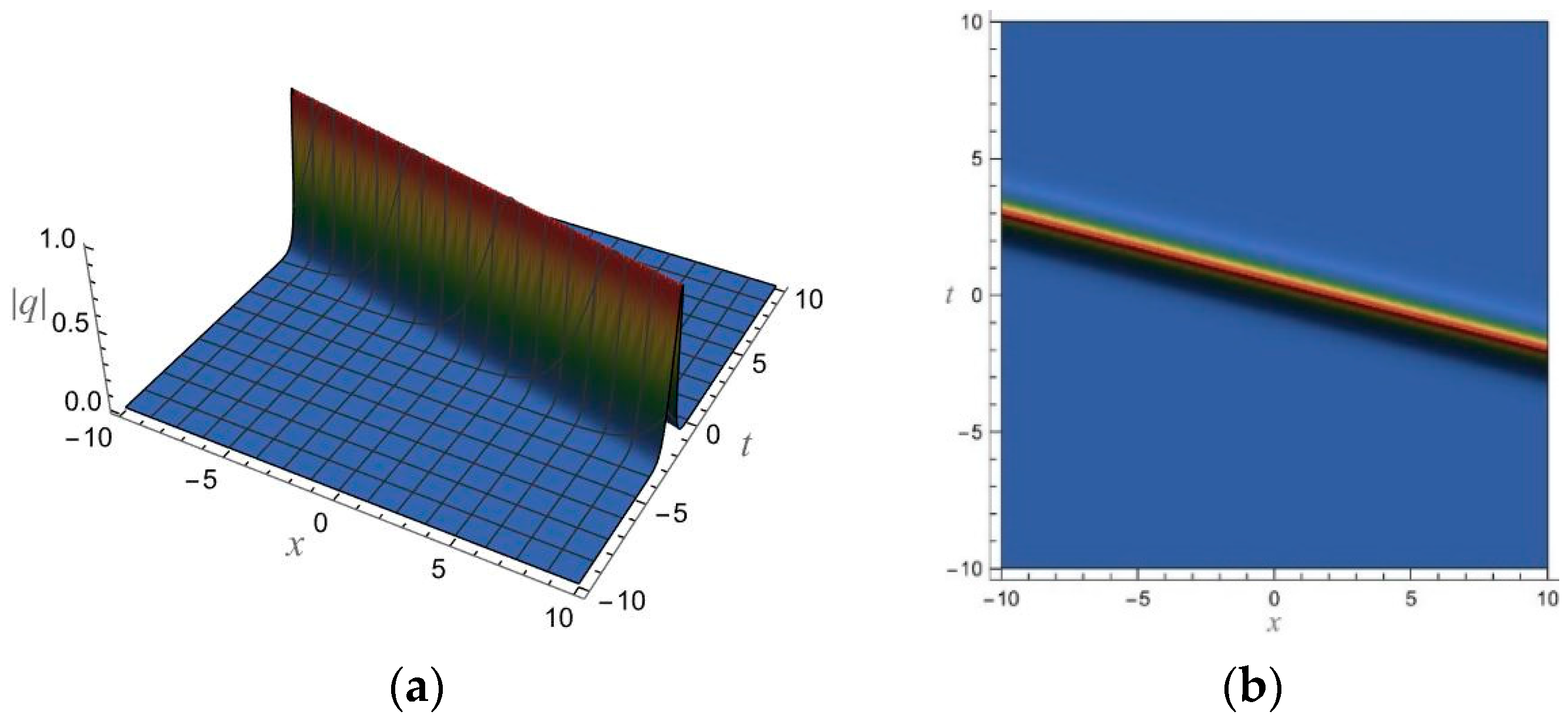
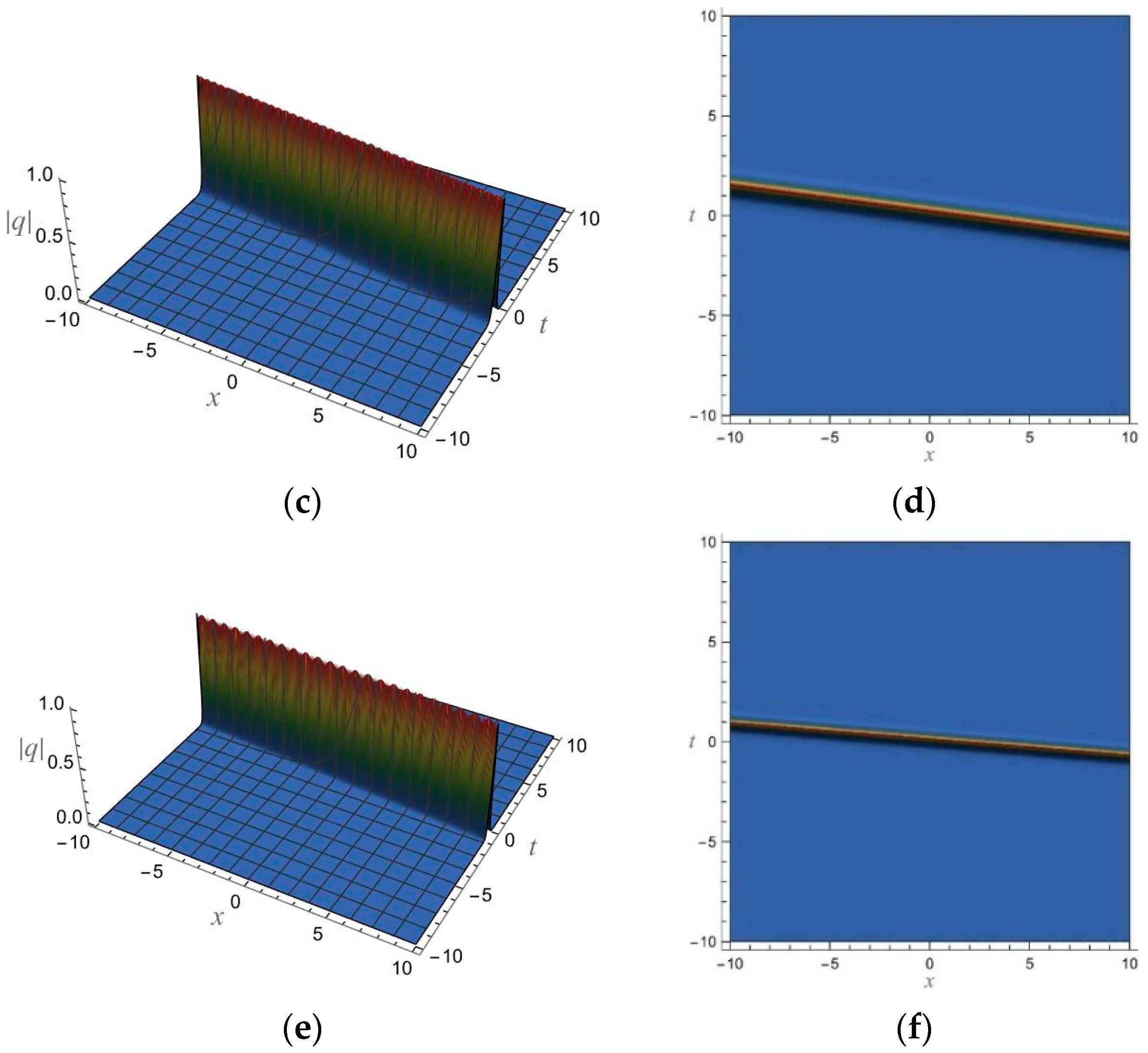
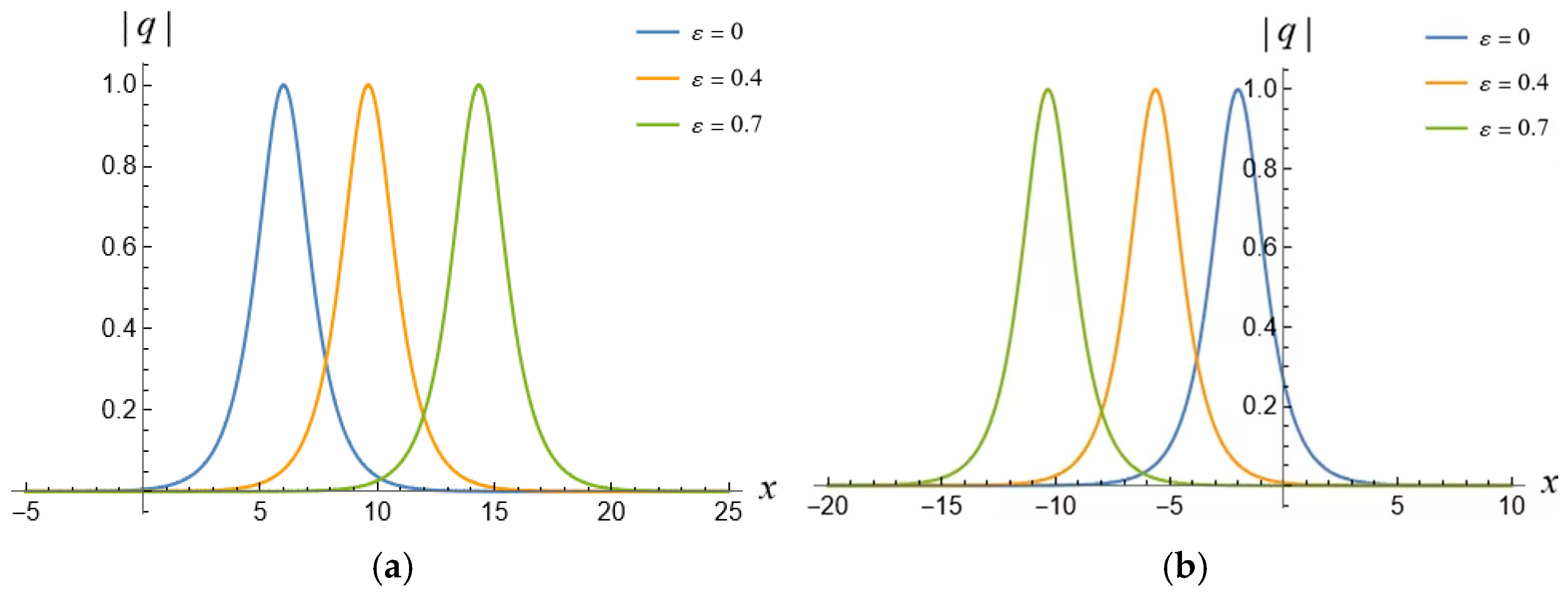
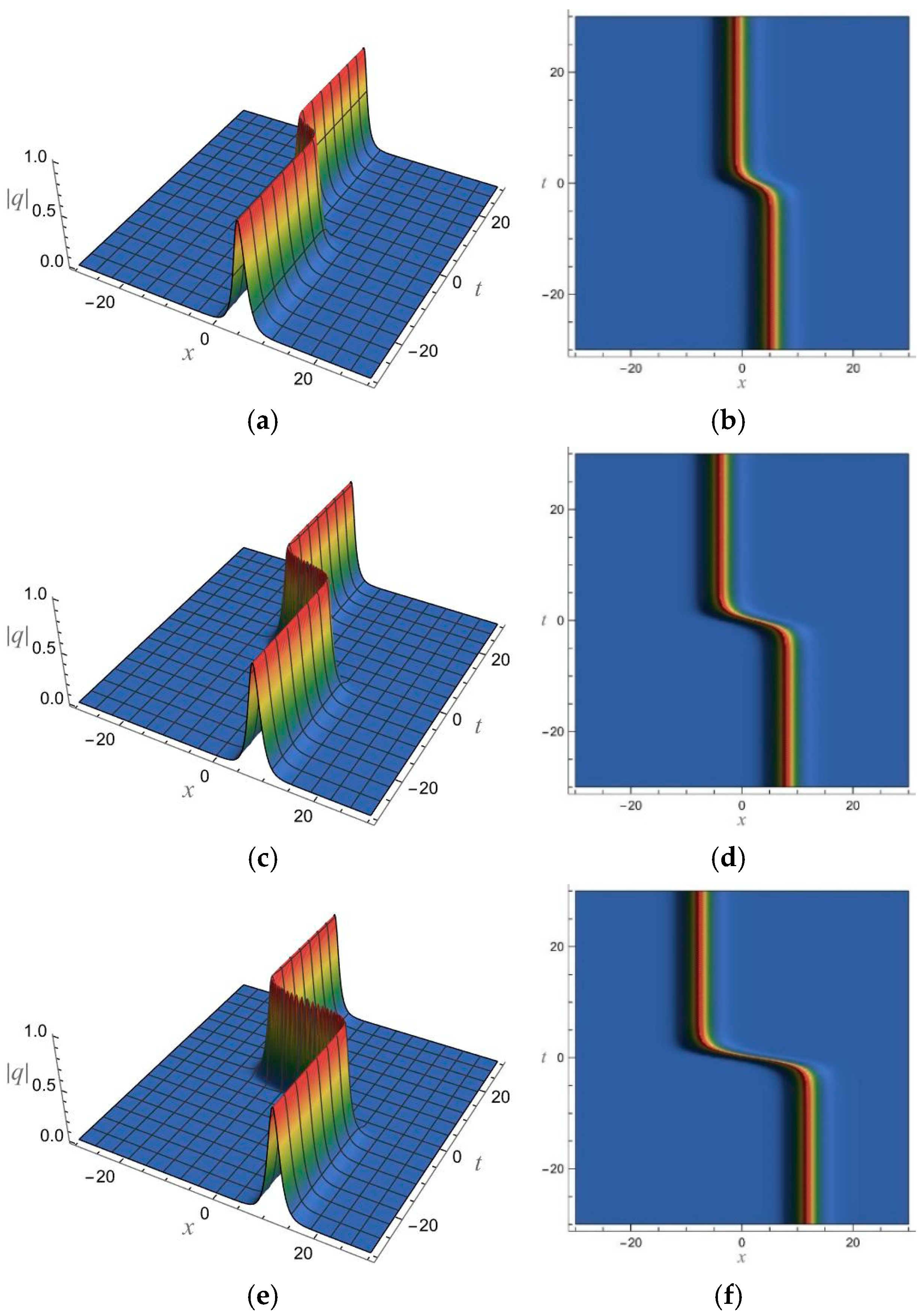
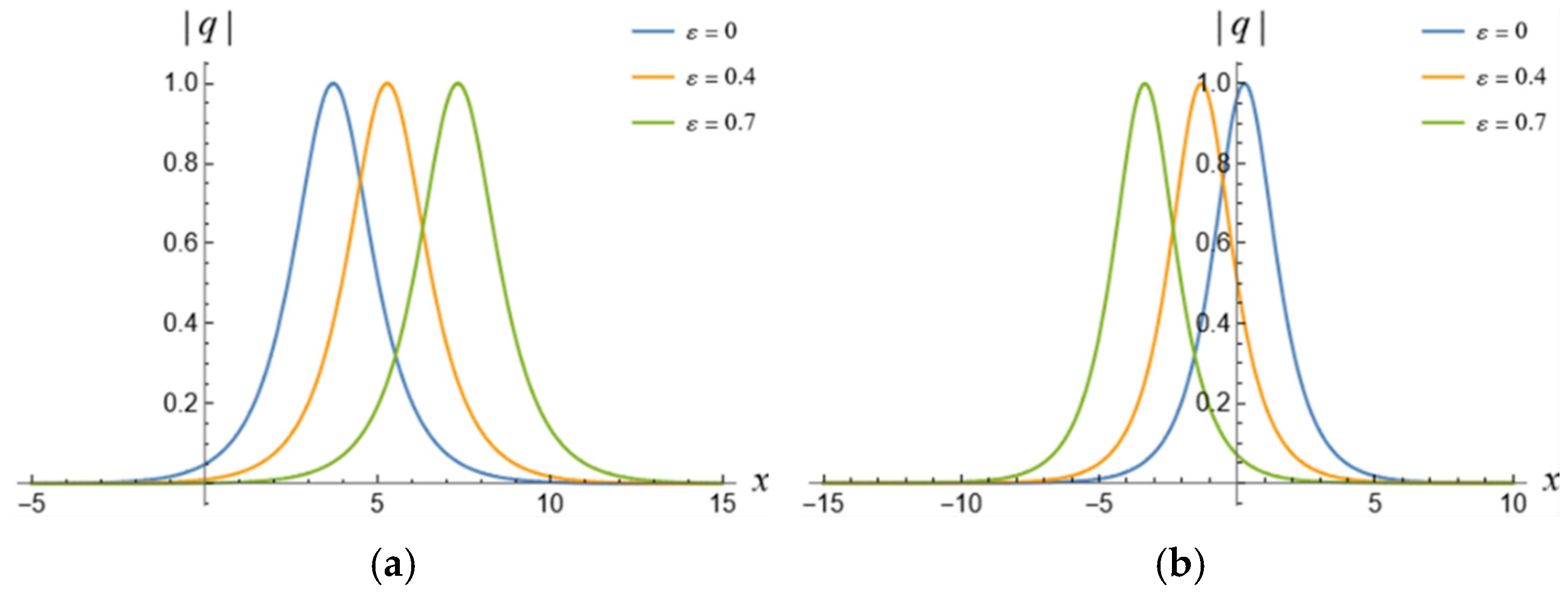
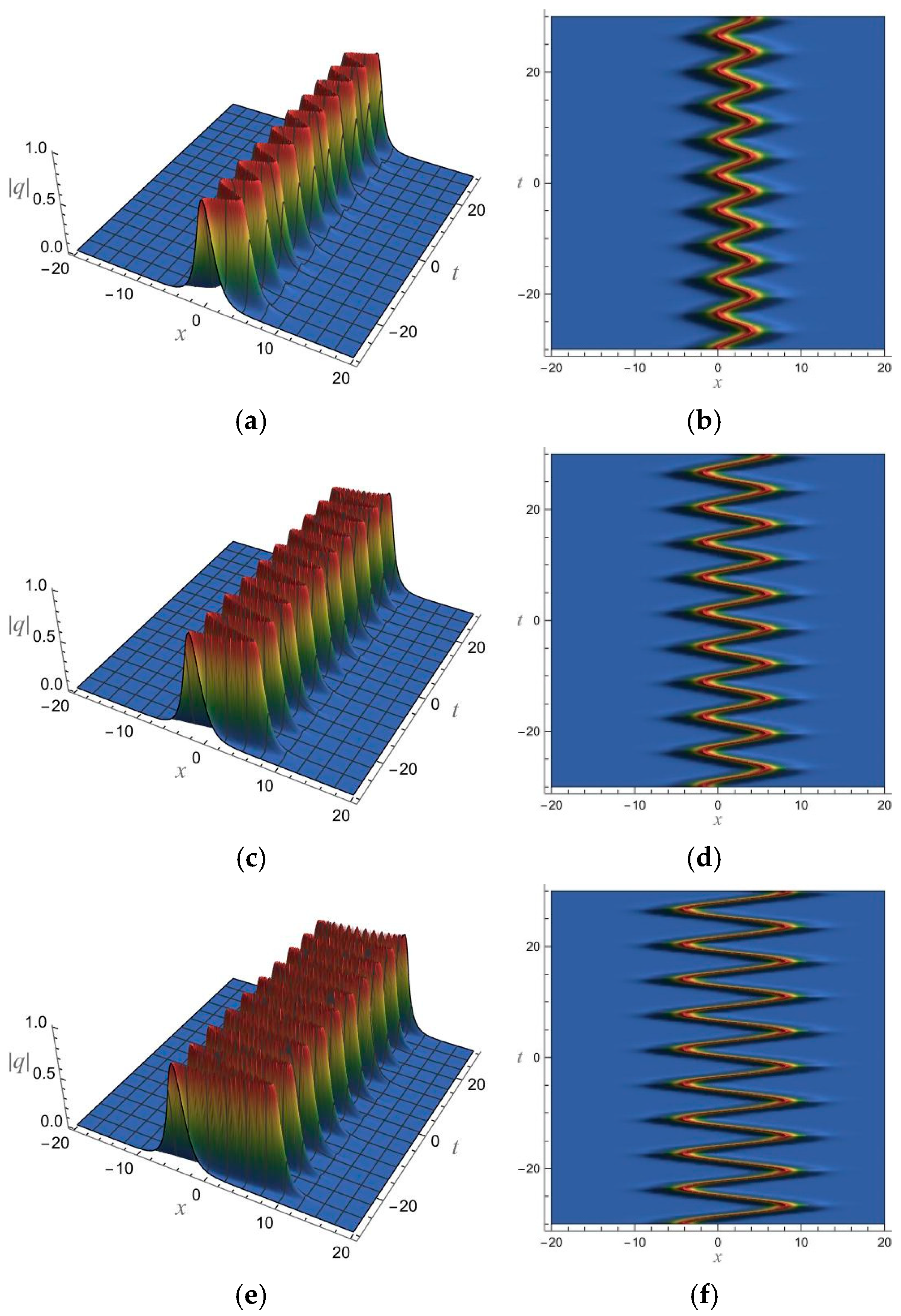
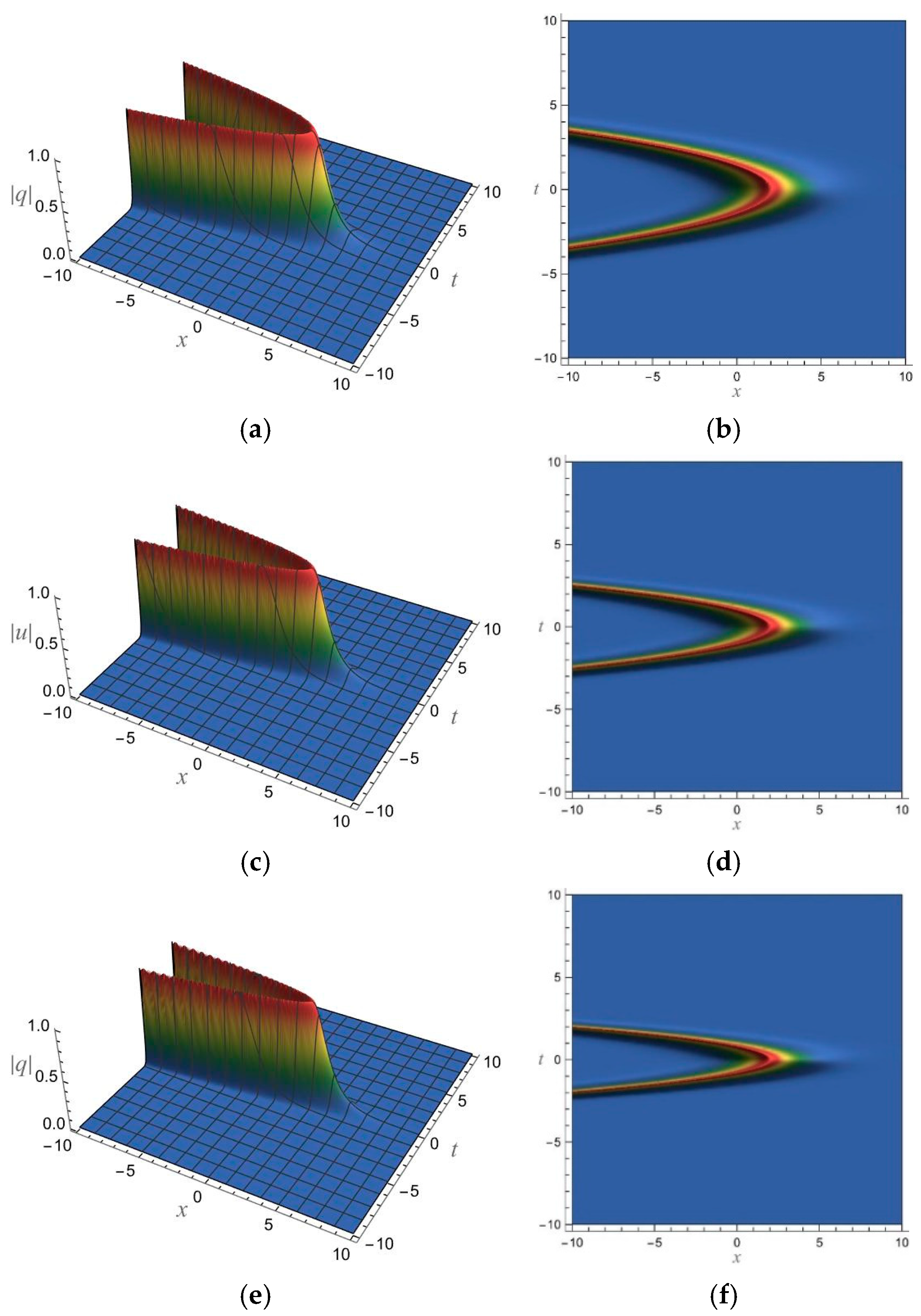
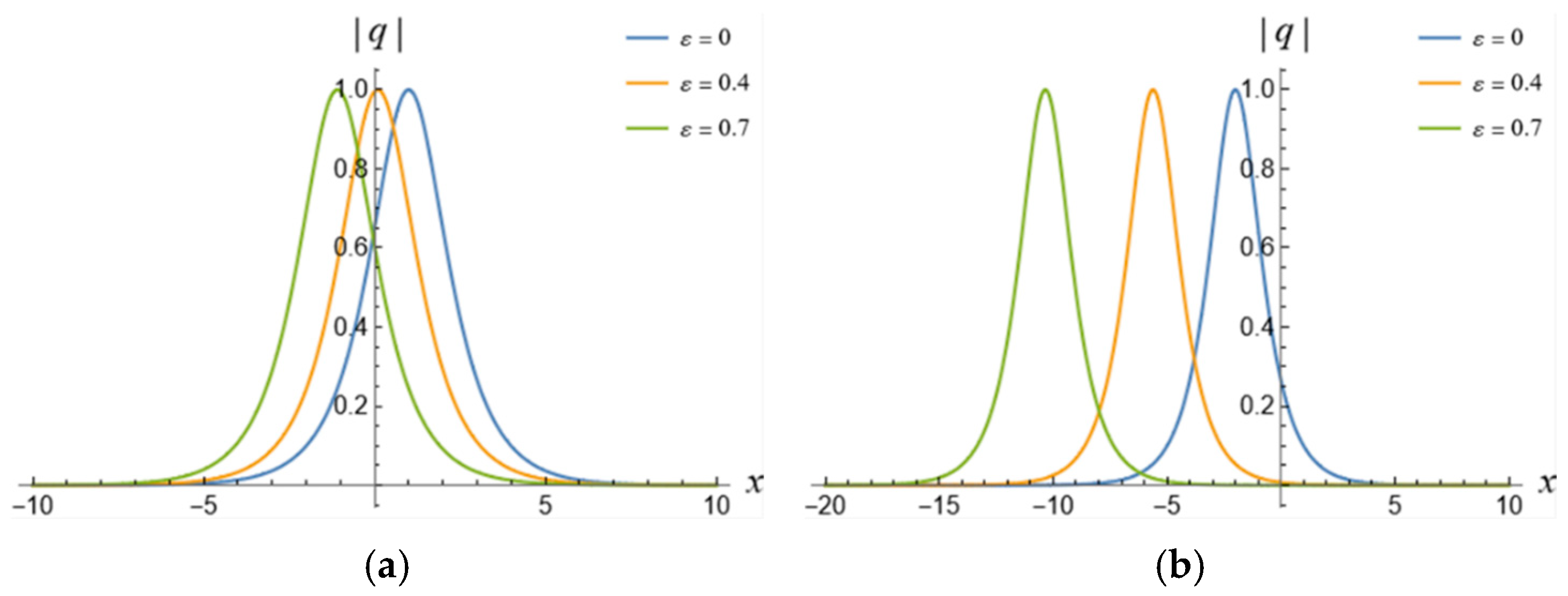
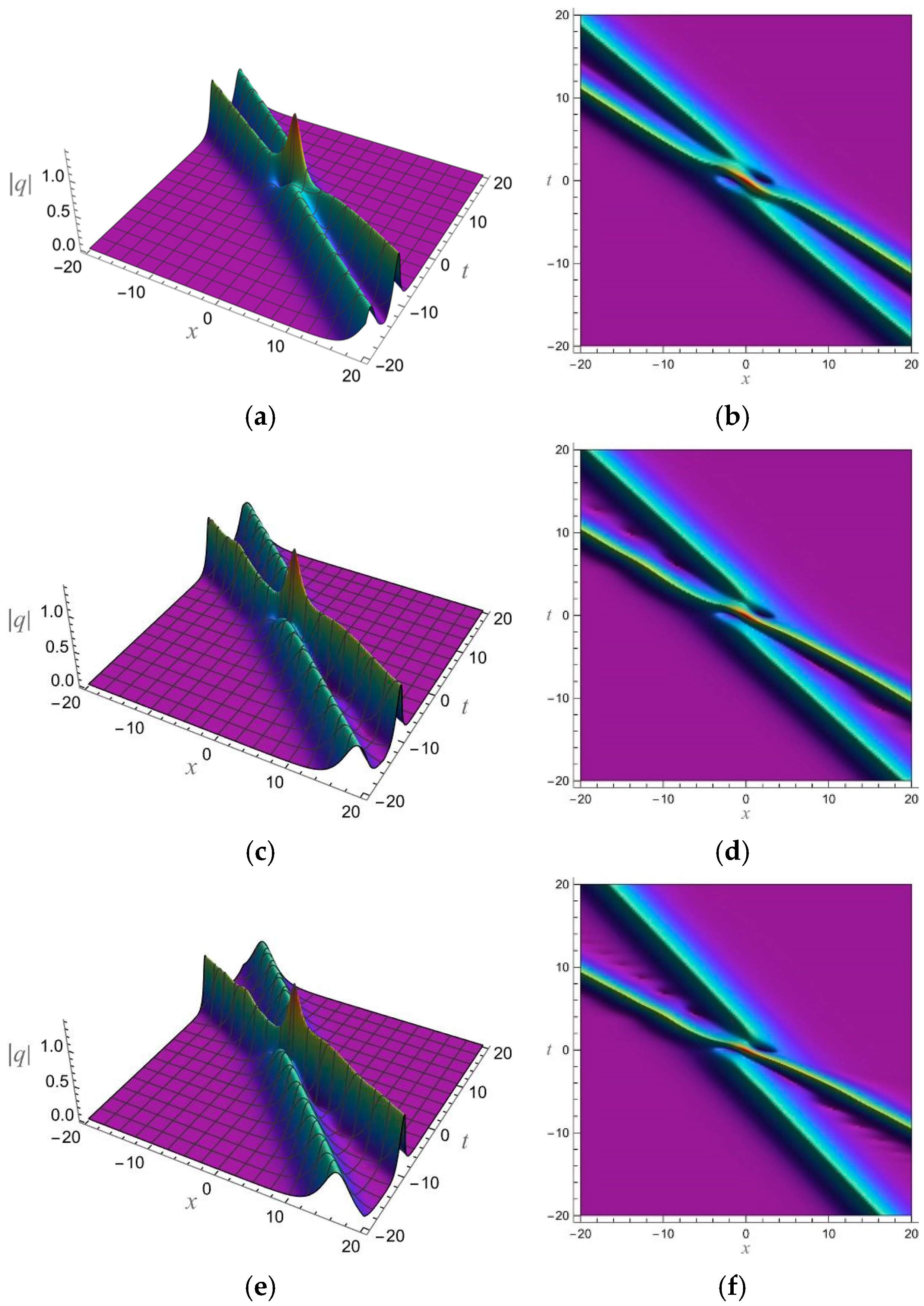
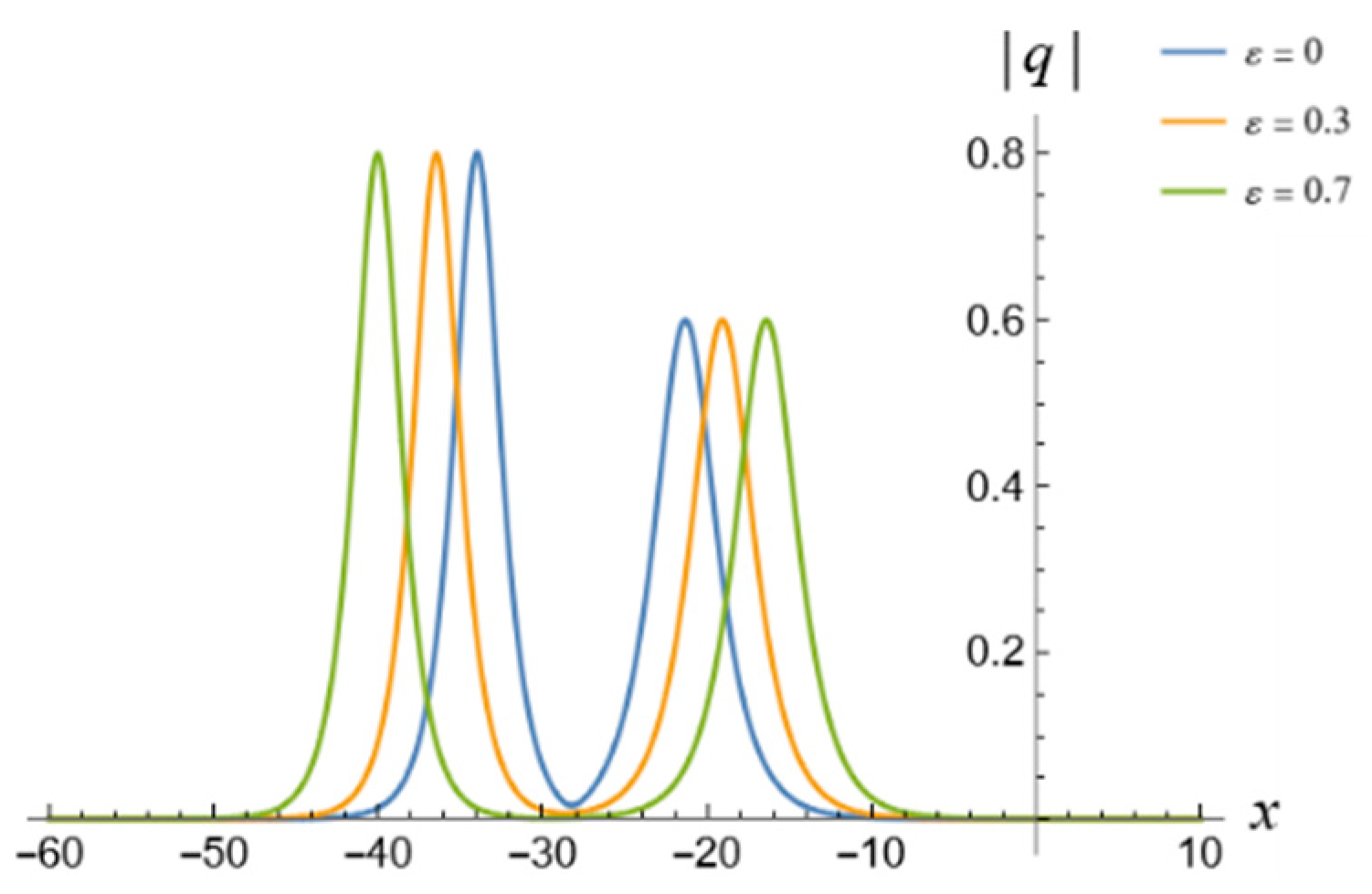
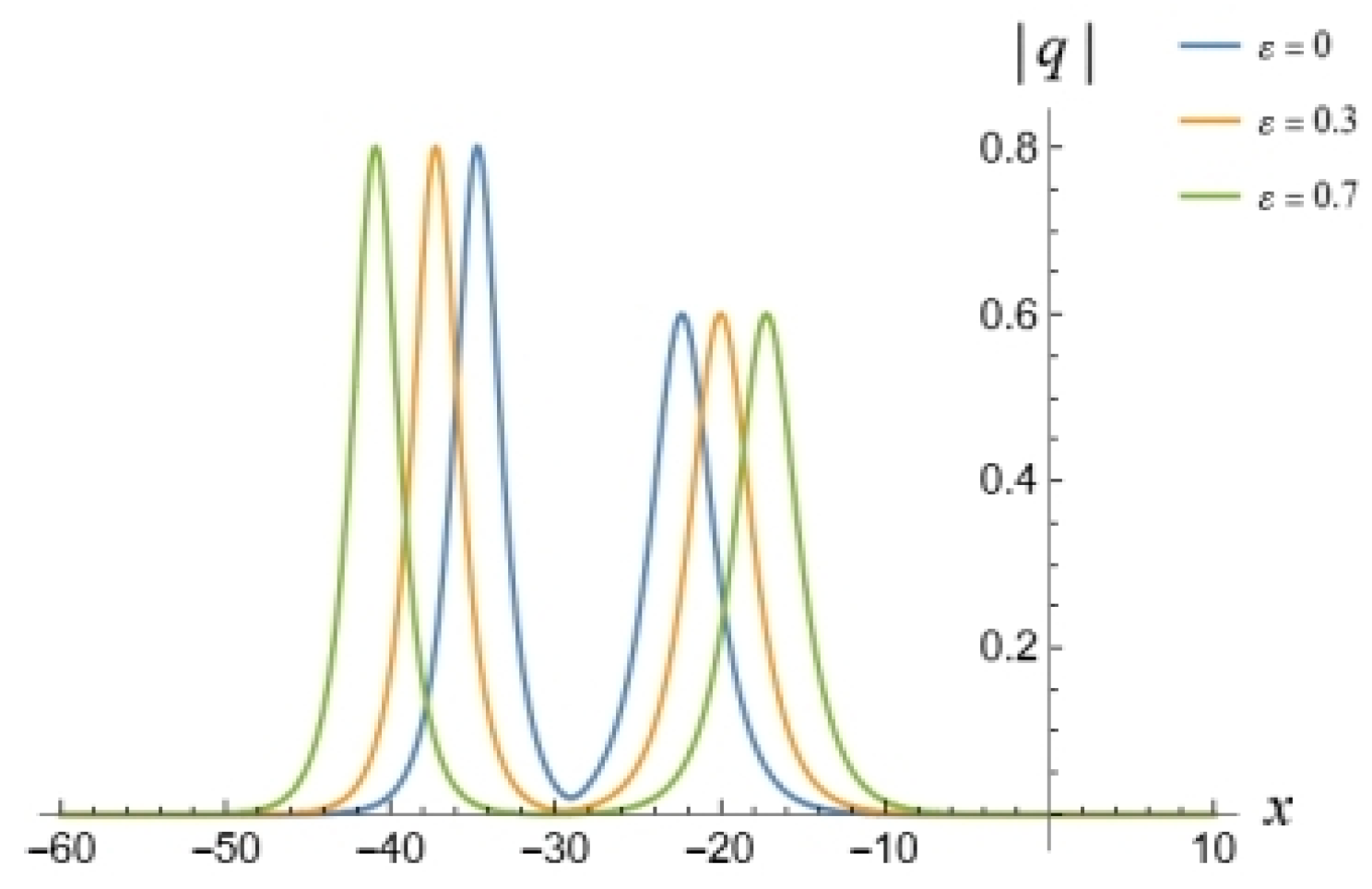
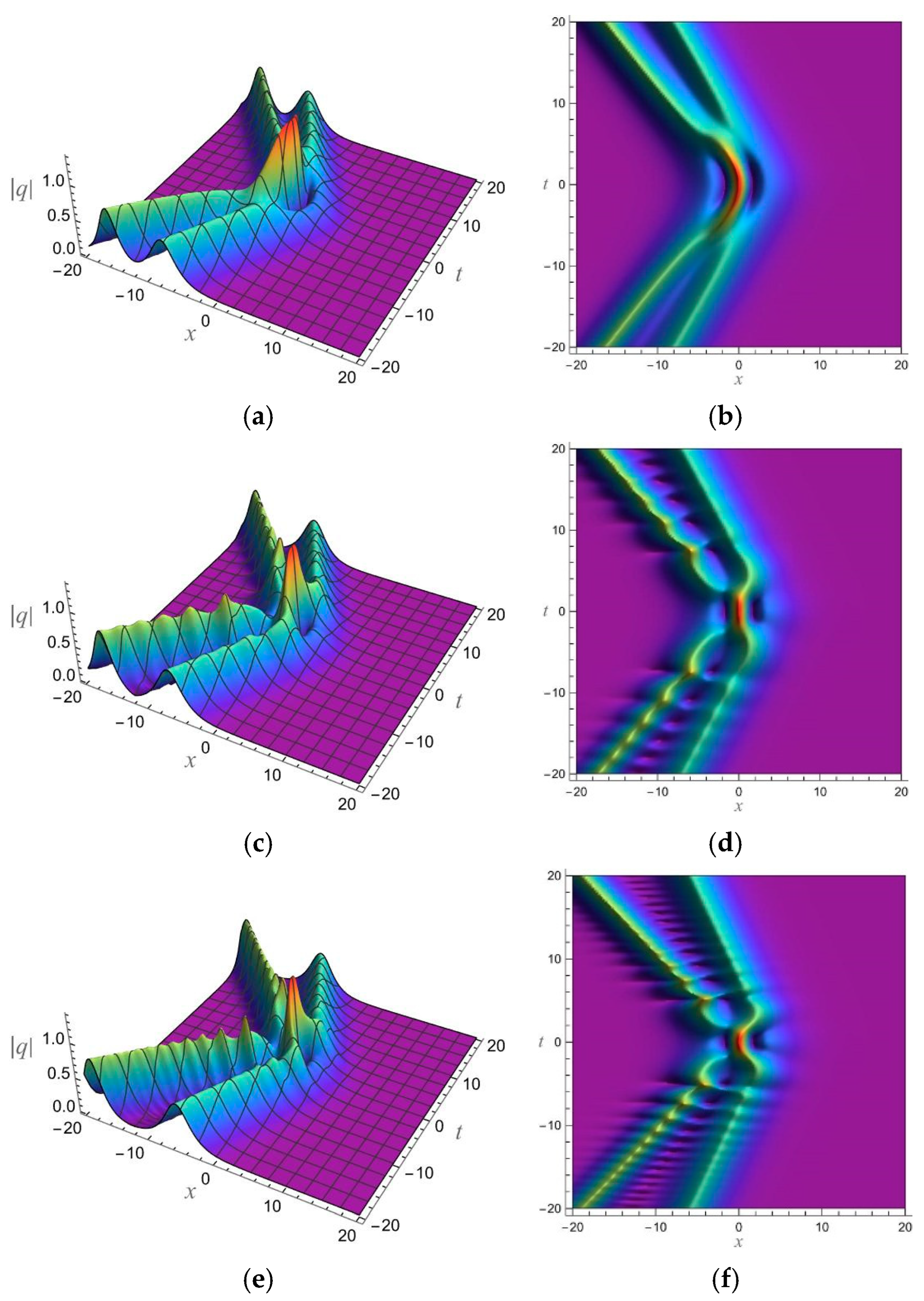
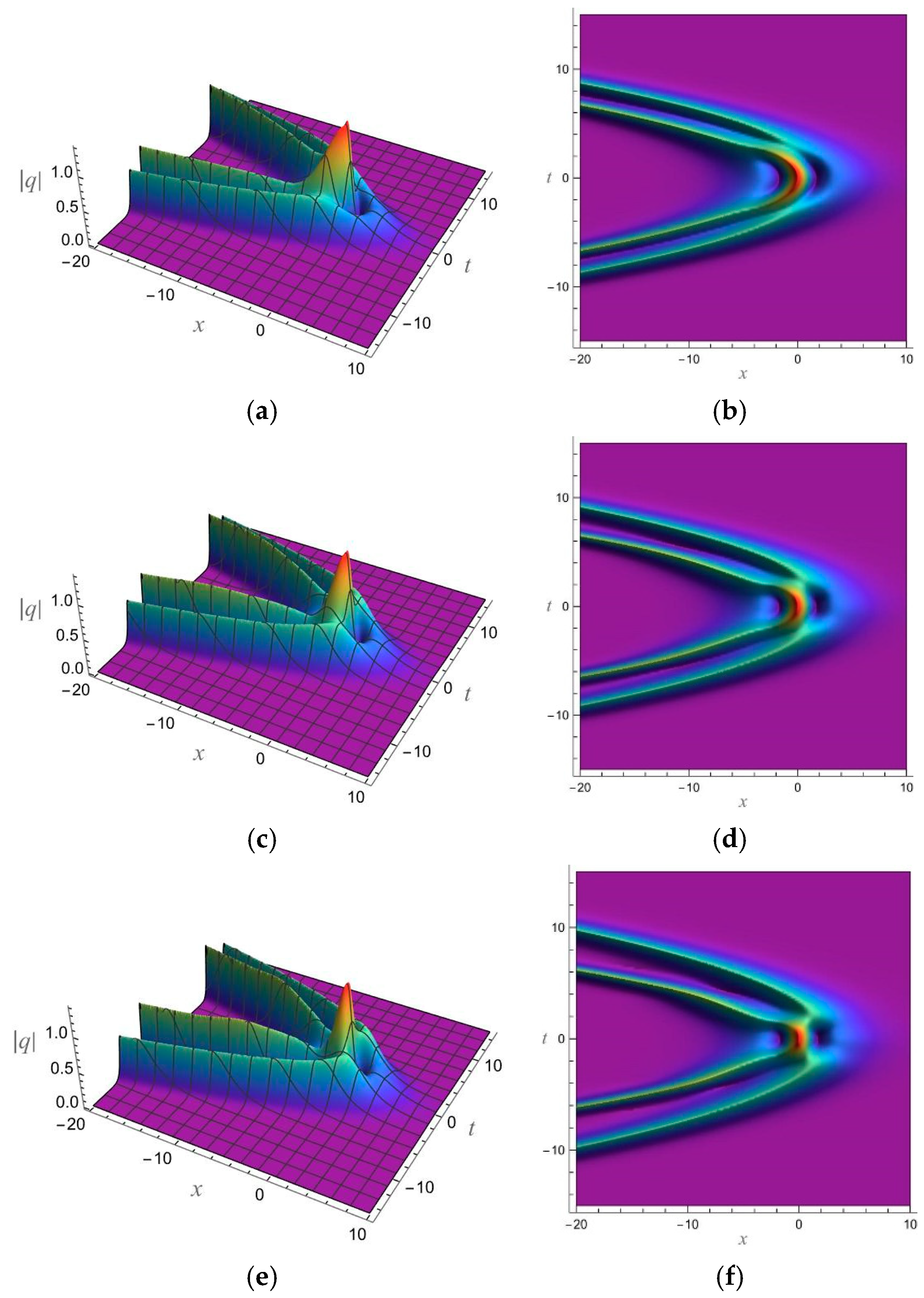
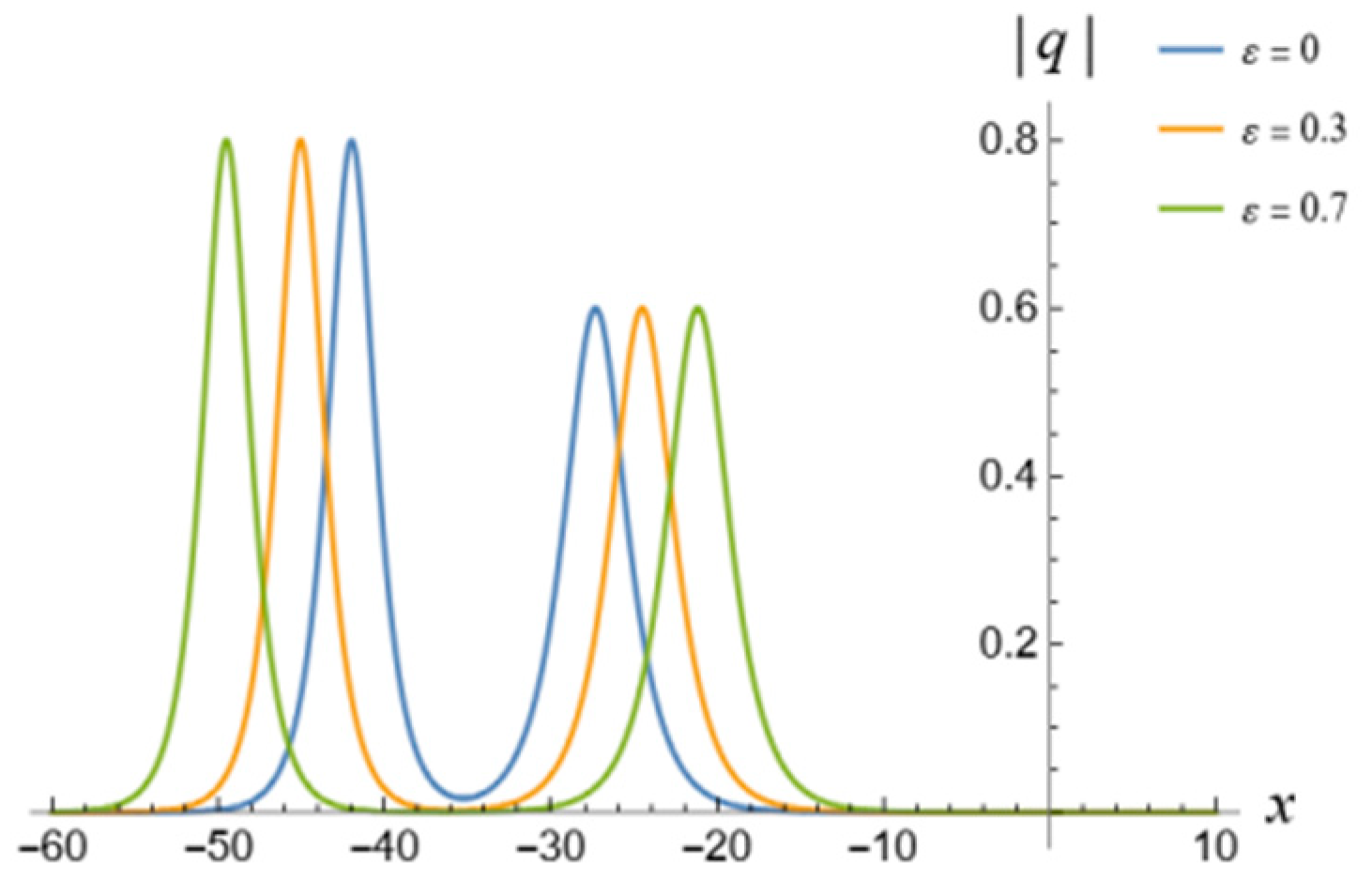
5. 1-Soliton Solution and 2-Soliton Solution of the vcRfgNLS Equation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ablowitz, M.J. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Carrillo, J.A.; Manresa, M.D.P.; Figalli, A.; Mingione, G. Nonlocal and Nonlinear Diffusions and Interactions: New Methods and Directions; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Bronski, J.C.; Carr, L.D.; Deconinck, B.; Kutz, J.N. Bose-einstein condensates in standing waves: The cubic nonlinear Schrödinger equation with a periodic potential. Phys. Rev. Lett. 2001, 86, 1402–1405. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimensional self-focusing and one dimensional self-modulation of waves in nonlinear media. J. Exp. Theor. Phys. 1972, 34, 62–69. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- West, B.J. Colloquium: Fractional calculus view of complexity: A tutorial. Rev. Mod. Phys. 2014, 86, 1169–1186. [Google Scholar] [CrossRef]
- Zhong, W.P.; Belić, M.R.; Malomed, B.A.; Zhang, Y.Q.; Huang, T.W. Spatiotemporal accessible solitons in fractional dimensions. Phys. Rev. E 2016, 94, 012216. [Google Scholar]
- Metzler, R.; Joseph, K. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar]
- Lischke, A.; Pang, G.F.; Gulan, M.; Song, F.Y.; Glusa, C.; Zheng, X.N.; Mao, Z.P.; Cai, W.; Meerschaertd, M.M.; Ainswortha, M.; et al. What is the fractional Laplacian? A comparative review with new results. J. Comput. Phys. 2020, 404, 109009. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Sikorskii, A. Stochastic Models for Fractional Calculus; Walter de Gruyter GmbH & Co KG: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar]
- Khawaja, U.A.; Al-Refai, M.; Carr, L.D. High-accuracy power series solutions with arbitrarily large radius of convergence for the fractional nonlinear Schrödinger-type equations. J. Phys. A Math. Theor. 2018, 51, 235201. [Google Scholar] [CrossRef]
- Li, P.F.; Malomed, B.A.; Mihalache, D. Vortex solitons in fractional nonlinear Schrödinger equation with the cubic-quintic nonlinearity. Chaos Solitons Fractals 2020, 137, 109783. [Google Scholar] [CrossRef]
- Qiu, Y.; Malomed, B.A.; Mihalache, D.; Zhu, X.; Peng, X.; He, Y. Stabilization of single-and multi-peak solitons in the fractional nonlinear Schrödinger equation with a trapping potential. Chaos Solitons Fractals 2020, 140, 110222. [Google Scholar] [CrossRef]
- Li, P.F.; Malomed, B.A.; Mihalache, D. Symmetry-breaking bifurcations and ghost states in the fractional nonlinear Schrödinger equation with a PT-symmetric potential. Opt. Lett. 2021, 46, 3267–3270. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Been, J.B.; Carr, L.D. Fractional integrable nonlinear soliton equation. Phys. Rev. Lett. 2022, 128, 184101. [Google Scholar] [CrossRef] [PubMed]
- Ablowitz, M.J.; Been, J.B.; Carr, L.D. Integrable fractional modified Korteweg–de Vries, sine-Gordon, and sinh-Gordon equations. J. Phys. A Math. Theor. 2022, 55, 384010. [Google Scholar] [CrossRef]
- Riesz, M. L’intégrale de Riemann-Liouville et le problème de Cauchy. Acta Math. 1949, 81, 1–222. [Google Scholar] [CrossRef]
- Cai, M.; Li, C.P. On Riesz derivative. Fract. Calc. Appl. Anal. 2019, 22, 287–301. [Google Scholar] [CrossRef]
- Weng, W.F.; Zhang, M.H.; Zhang, G.Q.; Yan, Z.Y. Dynamics of fractional N-soliton solutions with anomalous dispersions of integrable fractional higher-order nonlinear Schrödinger equations. Chaos 2022, 32, 123110. [Google Scholar] [CrossRef]
- Mou, D.S.; Dai, C.Q.; Wang, Y.Y. Integrable fractional n-component coupled nonlinear Schrödinger model and fractional n-soliton dynamics. Chaos Solitons Fractals 2023, 171, 113451. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Been, J.B.; Carr, L.D. Fractional integrable and related discrete nonlinear Schrodinger equations. Phys. Lett. A 2022, 452, 12845. [Google Scholar] [CrossRef]
- Kruglov, V.I.; Peacock, A.C.; Harvey, J.D. Exact self-similar solutions of the generalized nonlinear Schrödinger equation with distributed coefficients. Phys. Rev. Lett. 2003, 90, 113902. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, S. Analytical method for generalized nonlinear Schrödinger equation with time-varying coefficients: Lax representation, Riemann–Hilbert problem solutions. Mathematics 2022, 10, 1043. [Google Scholar] [CrossRef]
- Serkin, V.N.; Hasegawa, A. Novel soliton solutions of the nonlinear Schrödinger equation model. Phys. Rev. Lett. 2000, 85, 4502–4505. [Google Scholar] [CrossRef]
- Li, Y.S. Solitons and Integrable Systems; Shanghai Science and Technology Education Press: Shanghai, China, 1999. [Google Scholar]
- Chen, D.Y. Introduction of Soliton; Science Press: Beijing, China, 2006. [Google Scholar]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. The inverse scattering transform—Fourier analysis for nonlinear problems. Stud. Appl. Math. 1974, 53, 249–315. [Google Scholar] [CrossRef]
- Kaup, D. Closure of the squared Zakharov–Shabat eigenstates. J. Math. Anal. Appl. 1975, 54, 849–864. [Google Scholar] [CrossRef]
- Zeng, L.W.; Shi, J.C.; Lu, X.W.; Cai, Y.; Zhu, Q.F.; Chen, H.Y.; Long, H.; Li, J.Z. Stable and oscillating solitons of PT-symmetric couplers with gain and loss in fractional dimension. Nonlinear Dyn. 2021, 103, 1831–1840. [Google Scholar] [CrossRef]
- Wu, G.Z.; Dai, C.Q. Nonautonomous soliton solutions of variable-coefficient fractional nonlinear Schrödinger equation. Appl. Math. Lett. 2020, 106, 106365. [Google Scholar] [CrossRef]
- Heydari, M.H.; Atangana, A. A cardinal approach for nonlinear variable-order time fractional Schrodinger equation defined by Atangana-Baleanu-Caputo derivative. Chaos Soliton. Fract. 2019, 128, 339–348. [Google Scholar] [CrossRef]
- Hong, B.J. Exact solutions for the conformable fractional coupled nonlinear Schrödinger equations with variable coefficients. J. Low Freq. Noise Vib. Act. Control. 2023, 42, 628–641. [Google Scholar] [CrossRef]
- Tian, F.Z.; Wang, Y.L.; Li, Z.Y. Numerical simulation of soliton propagation behavior for the fractional-in-space NLSE with variable coefficients on unbounded domain. Fractal Fract. 2024, 8, 163. [Google Scholar] [CrossRef]
- Liu, M.W.; Wang, H.T.; Yang, H.J.; Liu, W.J. Study on propagation properties of fractional soliton in the inhomogeneous fiber with higher-order effects. Nonlinear Dyn. 2024, 112, 1327–1337. [Google Scholar] [CrossRef]
- Tang, W.F.; Wang, Y.L.; Li, Z.Y. Numerical simulation of fractal wave propagation of a multi-dimensional nonlinear fractional-in-space Schrödinger equation. Phys. Scr. 2023, 98, 045205. [Google Scholar] [CrossRef]
- García-Ferrero, M.A.; Rüland, A. Strong unique continuation for the higher order fractional Laplacian. Math. Eng. 2019, 1, 715–774. [Google Scholar]
- Wang, H.M.; Chen, H.J.; Li, T. Numerical simulation for the wave of the variable coefficient nonlinear Schrödinger equation based on the lattice Boltzmann method. Mathematics 2024, 12, 3807. [Google Scholar] [CrossRef]
- Yu, F.J.; Li, L.; Zhang, J.F.; Yan, J.W. Fractional-order effect on soliton wave conversion and stability for the two-Levy-index fractional nonlinear Schrödinger equation with PT-symmetric potential. Phys. D 2024, 460, 134089. [Google Scholar] [CrossRef]



| Time | Velocity and Amplitude with | Velocity and Amplitude with | Velocity and Amplitude with |
|---|---|---|---|
| −100 | −1.48803 × 10−43; 1 | −2.83269 × 10−43; 1 | −4.59083 × 10−43; 1 |
| −10 | −1.816 × 10−4; 1 | −3.45703 × 10−4; 1 | −5.60266 × 10−4; 1 |
| −1 | −1.29611; 1 | −2.46734; 1 | −3.99871; 1 |
| 0 | −2; 1 | −3.80731; 1 | −6.17034; 1 |
| 5 | −2.69506 × 10−2; 1 | −5.13045 × 10−2; 1 | −8.31471 × 10−2; 1 |
| 200 | −5.53559 × 10−87; 1 | −1.05378 × 10−86; 1 | −1.70782 × 10−86; 1 |
| 1000 | −2.0030383559 × 10−424; 1 | −3.8614765923 × 10−424; 1 | −6.2640077051 × 10−424; 1 |
| Height and Time | Width with | Width with | Width with |
|---|---|---|---|
| 0.1; −5 | 5.98642 | 5.98644 | 5.98643 |
| 0.1; 0 | 5.986443 | 5.986443 | 5.986443 |
| 0.1; 10 | 5.98644 | 5.986443 | 5.98644 |
| 0.2; −5 | 4.58486 | 4.58483 | 4.58484 |
| 0.2; 0 | 4.584862 | 4.584862 | 4.584862 |
| 0.2; 10 | 4.58486 | 4.58486 | 4.58487 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, S.; Xu, B. Integrable Riesz Fractional-Order Generalized NLS Equation with Variable Coefficients: Inverse Scattering Transform and Analytical Solutions. Fractal Fract. 2025, 9, 228. https://doi.org/10.3390/fractalfract9040228
Li H, Zhang S, Xu B. Integrable Riesz Fractional-Order Generalized NLS Equation with Variable Coefficients: Inverse Scattering Transform and Analytical Solutions. Fractal and Fractional. 2025; 9(4):228. https://doi.org/10.3390/fractalfract9040228
Chicago/Turabian StyleLi, Hongwei, Sheng Zhang, and Bo Xu. 2025. "Integrable Riesz Fractional-Order Generalized NLS Equation with Variable Coefficients: Inverse Scattering Transform and Analytical Solutions" Fractal and Fractional 9, no. 4: 228. https://doi.org/10.3390/fractalfract9040228
APA StyleLi, H., Zhang, S., & Xu, B. (2025). Integrable Riesz Fractional-Order Generalized NLS Equation with Variable Coefficients: Inverse Scattering Transform and Analytical Solutions. Fractal and Fractional, 9(4), 228. https://doi.org/10.3390/fractalfract9040228






